ELSA: Expanded Latent Space Autoencoder for Image Feature

Extraction and Classiﬁcation

Emerson Vilar de Oliveira

, Dunfrey Pires Arag

and Luiz Marcos Garcia Gonc¸alves

Universidade Federal do Rio Grande do Norte, Av. Salgado Filho, 3000, Campus Universit

ario, 59.078-970, Natal, Brazil

Keywords:

Autoencoder, Stacked Autoencoder, Latent Space, Image Classiﬁcation, Feature Extraction.

Abstract:

In the ﬁeld of computer vision, image classiﬁcation has been aiding in the understanding and labeling of im-

ages. Machine learning and artiﬁcial intelligence algorithms, especially artiﬁcial neural networks, are widely

used tools for this task. In this work, we present the Expanded Latent space Autoencoder (ELSA). The ELSA

network consists of more than one autoencoder in its internal structure, concatenating their latent spaces and

constructing an expanded latent space. The expanded latent space aims to extract more information from input

data. Thus, this expanded latent space can be used by other networks for general tasks such as prediction and

classiﬁcation. To evaluate these capabilities, we created an image classiﬁcation network for the FashionM-

NIST and MNIST datasets, achieving 99.97 and 99.98 accuracy for the test dataset. The classiﬁer trained with

the expanded latent space dataset outperforms some models in public benchmarks.

1 INTRODUCTION

Image classiﬁcation, one of the fundamental pillars

of computer vision, remains a relevant topic in the

contemporary technological landscape. As society

becomes digitally driven, the availability of visual

data grows exponentially, making the ability to extract

meaningful information from images undeniable. In-

terconnected with this necessity in advance in the ﬁeld

of extract information is the ability to classify images

efﬁciently and increasingly accurately. For both chal-

lenging tasks may involve the use of sophisticated al-

gorithms and advanced machine-learning techniques

in an attempt to fulﬁll its objectives. Among these

techniques, artiﬁcial neural networks, including Con-

volutional Neural Networks (CNNs), gain signiﬁcant

prominence due to their adaptive capability and a

range of different models for various applications.

The relevance of image classiﬁcation can extend

beyond visual categorization. Applications range

from medical diagnostics (Miranda et al., 2016;

Deepa et al., 2011) to industrial automation (Liu et al.,

2023; Turay and Vladimirova, 2022), where the abil-

ity to distinguish patterns and identify objects in im-

ages has transformed entire industries (Germain and

Aguilera, 2012). In healthcare, image classiﬁcation

systems have played a relevant role in recognizing

https://orcid.org/0000-0001-8400-7119

https://orcid.org/0000-0002-2401-6985

https://orcid.org/0000-0002-7735-5630

medical conditions, potentially providing faster and

more accurate diagnoses (Sharma and Jindal, 2011;

Mehdy et al., 2017). Furthermore, industrial automa-

tion, driven by computer vision algorithms, has ex-

perienced signiﬁcant gains in efﬁciency and reliabil-

ity (Garibotto et al., 2013).

Regardless of the adopted model, application, or

use, submitted data requires prior analysis and en-

gineering in design and acquisition. A dataset that

is not sufﬁciently representative can accentuate the

model’s sensitivity to noisy or incomplete input data,

leading to unsatisfactory results (Huang et al., 2015;

Najafabadi et al., 2015; Jain et al., 2020). In situ-

ations where data is poorly organized or designed,

convergence in prediction becomes more challenging.

However, persistent challenges in image classiﬁca-

tion stimulate the continuous search for innovations.

The internal complexity of image diversity, the pres-

ence of noise in data, and the need for adaptability to

new contexts demand increasingly sophisticated ap-

proaches.

Considering these challenges, we propose the Ex-

panded Latent space Auto-encoder (ELSA) neural

network. ELSA is based on comprising more than

one auto-encoder in its structure, leveraging the vari-

ability of these structures to extract information from

input data and form an expanded latent space. The

expanded latent space is made by concatenating each

latent space of the internal auto-encoders. This as-

sembled ELSA approach turns up the application into

scenarios where there is not a considerable amount

Vilar de Oliveira, E., Aragão, D. and Gonçalves, L.

ELSA: Expanded Latent Space Autoencoder for Image Feature Extraction and Classiﬁcation.

DOI: 10.5220/0012455300003660

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 19th Inter national Joint Conference on Computer Vision, Imaging and Computer Graphics Theor y and Applications (VISIGRAPP 2024) - Volume 3: VISAPP, pages

703-710

ISBN: 978-989-758-679-8; ISSN: 2184-4321

703

of data possible, aiming at extracting more informa-

tion from input data. Additionally, on the incremental

variable approach, it is unnecessary to retrain an au-

toencoder for previously known variables, being nec-

essary only for newly added features. We applied the

model to image classiﬁcation task using the Fashion-

MNIST and MNIST datasets to evaluate the network.

2 RELATED WORKS

In the literature on image classiﬁcation, a substantial

body of work applies machine learning techniques to

this task, from developing advanced architectures of

CNNs to new data pre-processing data strategies. The

analysis of these studies reveals a continuous empha-

sis on the search for more robust and accurate mod-

els, considering the complexity and diversity of image

datasets.

As an autoencoder work related to the classiﬁca-

tion task, (Zhao et al., 2015) proposed a stack of au-

toencoders in a supervised, semi-supervised, and un-

supervised learning approach, using a convolutional

network for encoding and a deconvolutional network

for input reconstruction. The autoencoder combined

with pooling layers produces what the authors call

”what” and ”where” variable sets. The ”what” is

fed to the next layer, and then its output is passed

to its complementary variable (where), which passes

its output to the next decoding layer. The work pre-

sented consistent results on the MNIST, CIFAR-10,

and CIFAR-100 datasets (Zhao et al., 2015). Other

works utilize autoencoder versatility in various appli-

cations (Zhou et al., 2019; Liang et al., 2017; Yang

et al., 2022).

Similarly, convolutional networks are widely ap-

plied in image classiﬁcation and computer vision

(Hussain et al., 2019; Gavrikov and Keuper, 2022;

Zhang et al., 2018; Lei et al., 2019). (Li et al., 2014)

designed a custom CNN with shallow convolution

layers to classify lung images with interstitial lung

disease. The authors claim that the proposed architec-

ture learns automatically and efﬁciently the intrinsic

features of lung images, and the same architecture is

generalized for classifying other medical images (Li

et al., 2014).

Beyond those directly proposing neural network

architectures for classiﬁcation, some works use differ-

ent machine learning techniques to improve the train-

ing of other networks (Huang et al., 2021; Louizos

et al., 2021; Dieuleveut et al., 2021). (Shi et al.,

2022) employed Bayesian learning to model person-

alized federated learning, proposing a framework to

solve a problem modeled using Bregman divergence

regularization. The authors empirically tested the pro-

posed methodology alongside non-neural network al-

gorithms on datasets like FMIST, MNIST, Sent140,

and CIFAR-10, stating that the proposal signiﬁcantly

outperforms other personalized federated learning al-

gorithms (Shi et al., 2022).

Similarly, some studies propose combinations of

optimized gradient adjustment algorithms and other

approaches to promote deep learning of networks

(Kwon et al., 2021; Pham and Le, 2021; Ram

et al., 2021; Belhasin et al., 2022). (Tseng et al.,

2022) investigated some commonly used optimiz-

ers and proposed Perturbed Unit Gradient Descent

(PUGD). Through analysis and experiments, the au-

thors showed that the proposed method makes locally

bounded weight updates, thus controlled but poten-

tially leading models to a ﬂat minimum, where the

error remains approximately constant. The authors

tested the methodology on datasets such as Tiny Im-

ageNet, CIFAR-10, and CIFAR-100 (Tseng et al.,

2022).

This overview of works establishes the backdrop

for our research, showing a snapshot of the networks

and methodologies variety present in the lecture for

the image classiﬁcation problem.

3 EXPANDED-LATENT SPACE

AUTOENCODER (ELSA)

ELSA is based on Pereira et al.(Pereira et al., 2020),

and as extension it uses n = 1, 2, . . . , N internal au-

toencoders, where the same input is presented to each

of them individually. After showing an input to the

internal autoencoders, an average of the produced nu-

merical decoders outputs is taken to preserve the same

input dimensionality. In parallel, the algorithm con-

catenate the encoded latent spaces of the internal au-

toencoders. The ﬁnal output of the ELSA is a decoded

vector that attempts to copy the input and an ampli-

ﬁed latent space vector. The decoded vector has the

same dimension as the input, and the latent space vec-

tor has dimension N × latent space size, where N is

the numbers of internal autoencoders. Figure 1 shows

a representative diagram in ﬂowchart form of how we

present the inputs to the expanded latent space autoen-

coder.

To verify that each internal autoencoder brings

new information to the expanded latent space, we

trained a network using only the label 0 of the MNIST

dataset (explained further in the experiments). We

only used two internal autoencoders to train this net-

work. Table 1 shows the hyperparameters details used

for this network training.

VISAPP 2024 - 19th International Conference on Computer Vision Theory and Applications

704

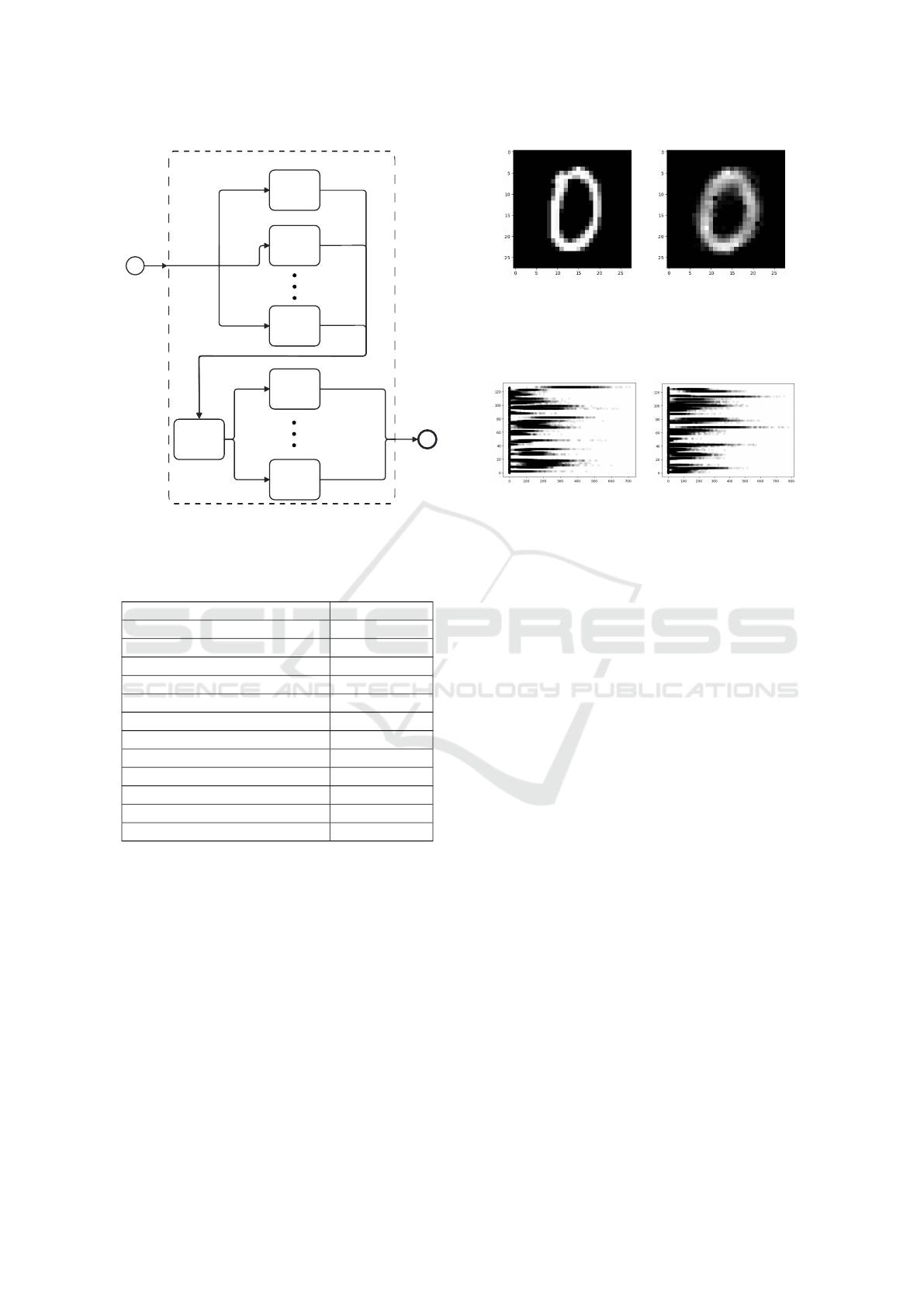
Expanded Latent-Space Autoencoder

autoencoder 1

autoencder 2

autoencoder N

autoencoders

outputs

concatenated

encoded

decoded mean

input

encoded 1,

decoded 1

encoded 2,

decoded 2

encoded N,

decoded N

encoded 1,

encoded 2,

encoded N

decoded 1,

decoded 2,

decoded N

N * latent space

dimension

decoded mean,

input

output

Figure 1: Representative ﬁgure of the sequence ﬂowchart of

entries into ELSA.

Table 1: Table of network hyperparameters used to demon-

strate how we create the expanded latent space.

Hyperparameter Value

Data train length 600

Data validation length 100

Data test length 1009

ELSA input size 784 (28 * 28)

ELSA hidden layer size 256

ELSA latent space size 128

Activation function ReLU

Internal Autoencoders number 2

Epochs 70

Learning rate 0.004

Loss function RMSE

Seed generator 5

After 70 epochs of training, the network presented

a training RMSE of 47.36 for input image reconstruc-

tion. This value should not be considered high, as the

values of each pixel in the image range from 0 to 255

in grayscale.We arrived at these hyperparameter val-

ues through trial and error, but they can be assigned

using a grid search, aiming to reduce the image recon-

struction error. All hyperparameters can be changed

and optimized, but it is relevant to point out that if the

number of hidden layers and their neurons substan-

tially increases, it is interesting to reduce the learning

rate to avoid high gradient variance. Furthermore, by

increasing the number of internal autoencoders, train-

ing time can exponentially grow and not result in a

considerable improvement. Figures 2a and 2b show

(a) Original input. (b) Output model copy.

Figure 2: Visual sample of an input and an output used in

training the network to verify that each internal autoencoder

brings new information to the expanded latent space.

(a) Latent Space 1. (b) Latent Space 2.

Figure 3: Visual sample of the latent space of each of the

internal autoencoders. We used a scatter plot with an alpha

of 0.07 to overlap the latent spaces.

an input and an output (image reconstruction) from

the trained network, respectively.

Starting from Figure 2, we can observe the model

could copy its input to its output satisfactorily. With

this, we have to verify whether the internal autoen-

coders of this ELSA network generate individual la-

tent spaces with different values. We will make sure

of that, suggesting that each of the internal autoen-

coders adds new information to the expanded latent

space. Figures 3a and 3b show a plot of the overlap

of the latent spaces generated for a test dataset with

1009 zero-digit images.

Figure 3 shows that the latent spaces generated by

internal autoencoder 1 for the test dataset have con-

centration values at different points than the internal

autoencoder 2. Thus, the expanded latent space is the

two latent spaces concatenation. Therefore, we can

reasonably assume that each autoencoder adds differ-

ent information to the expanded latent space. For this

network, the ﬁnal latent space has N = 2 internal au-

toencoders multiplied by the size of each of their la-

tent spaces, thus 2× 128, totaling a dimension of 256.

ELSA may be able to extract more information

from a limited training set, i.e., with fewer inputs

and requiring fewer training epochs, resulting in a

shorter training time and lower network complexity.

In addition to the image reconstruction error for the

training dataset already presented, the trained net-

work achieved a 48.89 RMSE reconstruction error for

the validation dataset and 48.62 for the test dataset.

ELSA: Expanded Latent Space Autoencoder for Image Feature Extraction and Classiﬁcation

705

This behavior suggests that ELSA, even trained with

a smaller portion of samples, is capable of generaliz-

ing what it learned to a set of new and more extensive

unseen inputs.

3.1 Multivariable ELSA

Once we train an ELSA network for a speciﬁc feature,

the network can generate expanded latent space rep-

resentations for each presented data. Similarly to the

previous example shown in Section 3 for the label 0 of

the MNIST dataset, all other labels (from 1 to 9) can

have their own ELSA that can encode them individu-

ally. Then, all input data in the entire training dataset

can pass through to their respective ELSA networks

and generate an encoded dataset with the expanded

latent spaces. With this ﬁnal encoded dataset, it is

possible to train a reduced number of neurons predic-

tor or classiﬁer networks. Consequently, the ELSA

network can generate a dataset that makes training

less costly and faster when speed is needed. Addition-

ally, absorbing each feature (the labels of the MINIST

dataset, for example) in a unique ELSA can be used

when one does not want to retrain an entire model

with the complete dataset when adding a new feature

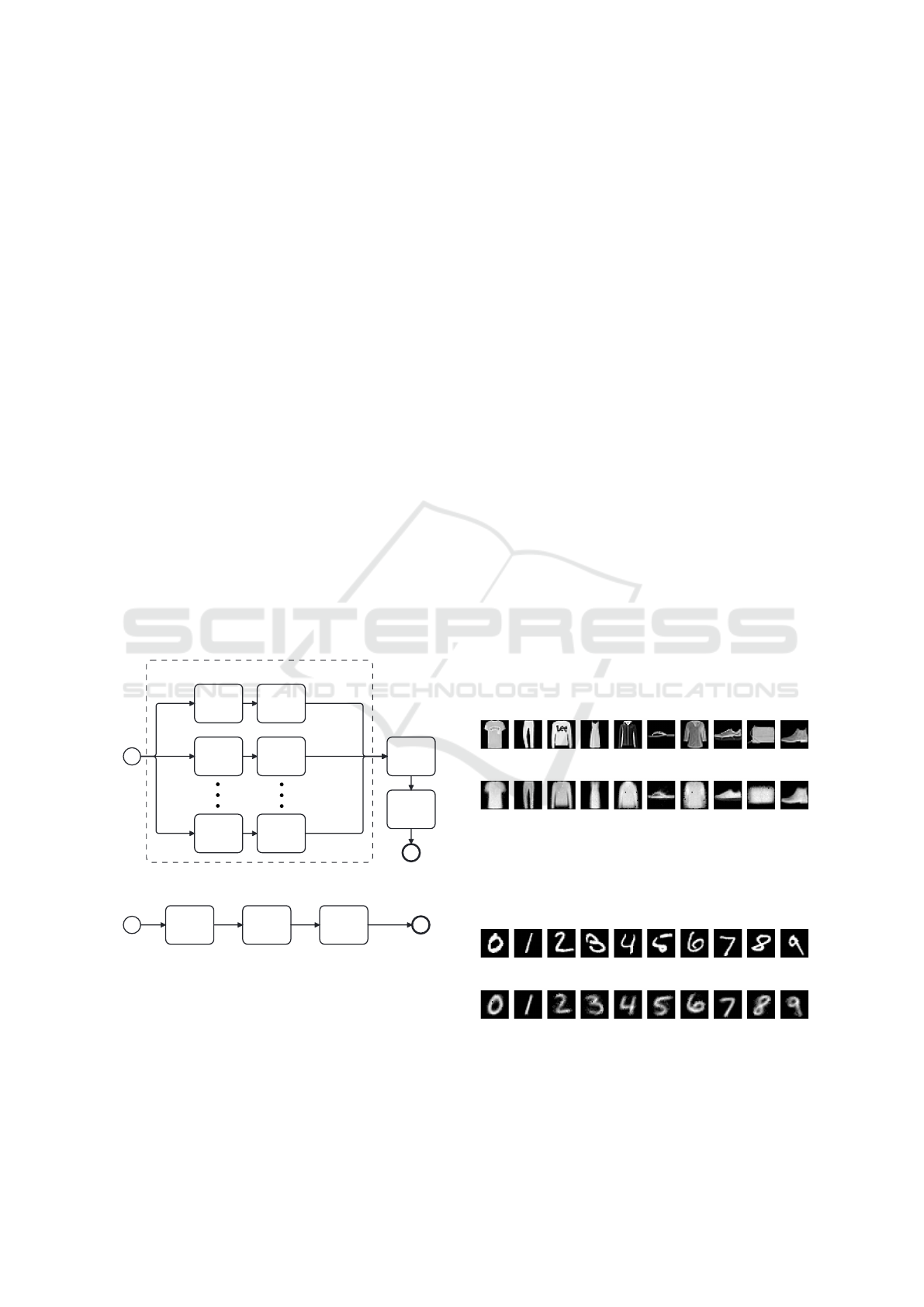
(label) to the predictor model. Figure 4 shows the

operational structure of a multi-variable model with

ELSA networks.

ELSA N

ELSA 2

ELSA 1

ELSA 1 train

ELSA 2 train

Expanded

Latent Space

and label

association

Expanded

Latent Space

dataset

Classifier Model

Train

Entire

Expanded

Latent Space

Dataset

Generation

label N data

label 0 data

label 1 data

Multi-Variabel

ELSA model

expanded latent

space 2

expanded latent

space 1

expanded latent

space N

label class

Figure 4: Flowchart representation of how a multi-variable

ELSA network works.

From Figure 4, we can see that we can train N

ELSA models to represent each input label. With this,

we can think of the ELSA network as multi-variable

since it is sufﬁcient to use an ELSA network for each

label separately and then create a dataset with the ex-

panded latent spaces (presenting all samples to their

respective ELSA networks). Then, we can associate

each expanded latent space with their labels and use

them to train a predictor model.

4 EXPERIMENTS AND RESULTS

To evaluate the ELSA network’s ability to absorb fea-

tures and generate a representation in an expanded la-

tent space, we applied it to the image classiﬁcation

of well-known MNIST (Deng, 2012) and FashionM-

NIST (Xiao et al., 2017) datasets. Both datasets con-

tain grayscale images with 28 × 28 pixels dimension.

The MNIST dataset consists of images of Arabic nu-

merals from 0 to 9, where each label represents its

respective numeral. The FashionMNIST dataset has

clothing image items, where labels 0 to 9 represent

T-shirt/top, Trouser, Pullover, Dress, Coat, Sandal,

Shirt, Sneaker, Bag, Ankle boot, respectively. Similar

to the example used in Section 3, we trained an ELSA

network for each of the 10 classes in the datasets, us-

ing the same architecture presented in Table 1. We

do not normalize the data, only resized it to match

with the ﬁrst network layer, changing from (28 × 28

to (1 × 784). Figure 5 shows one data input from

each label from FashionMNIST dataset and they re-

construction from it respective ELSA network.

From Figure 5a it is possible see the original input

samples from FashinMNIST data from each of the ten

labels. Figure 5b shows that each ELSA network was

able to do a satisfactory reconstruction for it respec-

tive label input. Figure 6 shows one data input from

(a) First FashionMNIST test dataset input sample.

(b) Reconstructed ELSA to each ﬁrst FashionMNIST test

dataset input sample.

Figure 5: Original dataset test input samples from Fashion-

MNIST dataset and the reconstruction (internal ELSA de-

coders mean) image from each trained ELSA network.

(a) First MNIST test dataset input sample.

(b) Reconstructed ELSA to each ﬁrst MNIST test dataset

input sample.

Figure 6: Original dataset test input samples from MNIST

dataset and the reconstruction (internal ELSA decoders

mean) image from each trained ELSA network.

VISAPP 2024 - 19th International Conference on Computer Vision Theory and Applications

706

Figure 7: Boxplot of the distributions obtained in the ex-

periment for classifying the FashionMNIST and MNIST

datasets.

each label from MNIST dataset and they reconstruc-

tion from it respective ELSA network.

From Figure 6a it is possible see the original in-

put samples from MNIST data from each of the ten

hand write digits. Figure 6b shows that each ELSA

network was able to do a satisfactory reconstruction

for it respective label input.

After training the ten ELSA networks, the train-

ing dataset with 60, 000 entries was divided in half

for training and validation, resulting in 30, 000 en-

tries for each. The test dataset retained its original

size of 10, 000 entries. We individually presented all

training, validation, and test entries to their respec-

tive trained networks for each label. We obtained the

expanded latent space representation for each dataset

input as mentioned in Section 3.1. Subsequently, we

created a dataset with the expanded latent spaces and

their respective labels.

To evaluate the obtained expanded latent spaces,

we trained 50 classiﬁer networks responsible for indi-

cating the label to which each entry belongs. All net-

works have the same architecture of a fully connected

layer with 256 MLP (fully connected) inputs that re-

duce to 10 outputs. We subjected this output to a Log-

Softmax function for classiﬁcation. For all networks,

we used Negative Log-Likelihood as the loss func-

tion, the Adam optimization algorithm (Kingma and

Ba, 2017), 0.009 as the learning rate, and 5 epochs

presenting the entire training and validation dataset.

The model parameters (weights) were adjusted every

1, 000 entries, meaning batch training. We extracted

the ﬁnal classiﬁcation accuracy for the test dataset

from each network as the evaluation metric. All these

50 networks are identical except for the weight initial-

ization seed, which we chose to vary from 1 to 100

with a sampling interval of 2, i.e., S = 1, 2, . . . , 98, 99.

Finally, to avoid overﬁtting networks, we considered

only accuracies below 99.99 as valid.

We do not perform tests with other types of net-

work neurons precisely because ELSA’s proposal is

also to be a computationally simple model, not us-

ing various techniques such as batch normalization,

attention, or complex deep learning networks, such as

CNN, LSTM, Transformers, and even so manages to

achieve good results in feature extraction and image

classiﬁcation, explaining that the latent space expan-

sion technique alone can be efﬁcient.

Following the experiment detailed above, Figure

7 shows the boxplot of the two distributions obtained

from the accuracies (already ﬁltered) in networks

trained with their respective datasets.

Figure 7 shows the boxplot representing the Fash-

ionMNIST dataset experiment has a lower RMSE

mean, median, and a more distant interquartile range

than the MNIST dataset boxplot. The difference can

Figure 8: Confusion matrix for training the classiﬁer net-

work for FashionMNIST with the 13 integer seed.

Figure 9: Confusion matrix for training the classiﬁer net-

work for MNIST with the 35 integer seed.

ELSA: Expanded Latent Space Autoencoder for Image Feature Extraction and Classiﬁcation

707

Table 2: Table of benchmark works for the FashionMNIST dataset.

Model Accuracy Paper

ELSA (our model) 99.97* Expanded Latent-Sapce Autoencoder

pFedBreD ns mg 99.06 Personalized Federated Learning with Hidden Information on

Personalized Prior (Shi et al., 2022)

Fine-Tuning DARTS 96.91 Fine-Tuning DARTS for Image Classiﬁcation (Tanveer et al.,

2021)

Shake-Shake 96.41 Sharpness-Aware Minimization for Efﬁciently Improving Gener-

alization (Foret et al., 2020)

Inception v3 94.44 CNN Filter DB: An Empirical Investigation of Trained Convolu-

tional Filters (Gavrikov and Keuper, 2022)

StiDi-BP in R-CSNN 92.8 Spike time displacement based error backpropagation in convo-

lutional spiking neural networks (Mirsadeghi et al., 2023)

Table 3: Table of benchmark works for the MNIST dataset.

Model Accuracy Paper

ELSA (our model) 99.98* Expanded Latent-Sapce Autoencoder

Branching/Merging CNN +

Homogeneous Vector Cap-

sules

99.87 No Routing Needed Between Capsules (Byerly et al., 2021)

EnsNet (Ensemble learning

in CNN augmented with

fully connected subnet-

works)

99.84 Ensemble learning in CNN augmented with fully connected sub-

networks (Hirata and Takahashi, 2023)

Efﬁcient-CapsNet 99.84 Efﬁcient-CapsNet: Capsule Network with Self-Attention Rout-

ing (Mazzia et al., 2021)

SOPCNN (Only a single

Model)

99.83 Stochastic Optimization of Plain Convolutional Neural Networks

with Simple methods (Assiri, 2020)

RMDL (30 RDLs) 99.82 RMDL: Random Multimodel Deep Learning for Classiﬁca-

tion (Kowsari et al., 2018)

happen due to the label complexity to be encoded by

ELSA networks, as FashionMNIST consists of im-

ages of clothing items that may, in normalized scale,

resemble each other. However, MNIST images of

handwritten Arabic numerals have non-similar con-

tours and shapes. In terms of values, the average accu-

racies represented by the triangle inside the box were

99.65 and 99.75 for FashionMNIST and MNIST, re-

spectively. Similarly, the median accuracies repre-

sented by the horizontal line inside the box were

99.81 and 99.87 for FashionMNIST and MNIST, re-

spectively. As the chosen network, we selected the

one whose weight initialization seed provided the

highest accuracy value.

For the FashionMNIST dataset, the seed that pro-

vided the best accuracy value was 13. Figure 8 shows

the confusion matrix obtained from the network’s

classiﬁcation for the 10, 000 entries in the test dataset.

From Figure 8, we can observe that the predictive

network made errors in classifying three out of the

1, 000 entries in the test dataset, resulting in a ﬁnal

accuracy of 99.97%.

For the MNIST dataset, the seed that provided the

best accuracy value was 35. Figure 9 shows the confu-

sion matrix obtained from the network’s classiﬁcation

for the 10, 000 entries in the test dataset.

Figure 9 shows the predictive network made errors

in classifying two out of the 10, 000 entries in the test

dataset, resulting in a ﬁnal accuracy of 99.98%.

To assess the model’s quality generated from our

methodology compared to other classiﬁcation mod-

els, we used two benchmarks related to the datasets

on the Papers With Code

website. Table 2 shows

the models and works found in the benchmark for the

FashionMNIST dataset

, including our model in or-

der of higher accuracy.

From Table 2, we can see that our model achieved

an accuracy result higher than those presented in this

benchmark by 0.91%. Table 3 shows the models

and works found in the benchmark for the MNIST

https://paperswithcode.com/

https://paperswithcode.com/sota/image-classiﬁcation-

on-fashion-mnist?metric=Accuracy

VISAPP 2024 - 19th International Conference on Computer Vision Theory and Applications

708

dataset

, including our model in order of higher accu-

racy.

Table 3 shows that our model achieved an accu-

racy result higher than those presented in this bench-

mark by 0.11%.

5 CONCLUSION

In this work, we proposed a new network based

on autoencoder models for creating an expanded la-

tent space applied to image classiﬁcation. From the

conducted experiment, we observed that the trained

ELSA networks demonstrated reasonable proﬁciency

to feature extraction from the input data. Also, this

feature extraction provided a considerable improve-

ment in classifying grayscale images from the Fash-

ionMNIST and MNIST datasets. The prominent ac-

curacy values in the image classiﬁcation task to the

dataset can be attributed to the expanded latent spaces

generated by individual ELSA networks for each la-

bel. By reconstructing the input into its output, the

ELSA network could extract information contained

in the images, and by generating the expanded latent

space, it provided the predictive network with a possi-

bly better representation of the entries. Furthermore,

the ELSA network generalized its reconstruction and

representation well to a larger dataset despite being

trained with a reduced dataset. This behavior is sim-

ilar to natural language processing models that gen-

erate word and the sentence embedding. In future

work, we will further investigate the limits of how

much the ELSA network can reduce the training en-

try quantity while maintaining a good representation

in its expanded latent space. Additionally, we will

subject it to tests with other image datasets and dif-

ferent case studies involving time series and natural

language processing.

ACKNOWLEDGEMENTS

This work has been developed with partial support

of Coordination of Higher Education Personnel Im-

provement (CAPES-Brazil), grants number 001 and

88881.506890/2020-01, and by National Research

Council (CNPq-Brazil) grant number 311640/2018-4.

https://paperswithcode.com/sota/image-classiﬁcation-

on-mnist

REFERENCES

Assiri, Y. (2020). Stochastic optimization of plain convo-

lutional neural networks with simple methods. arXiv

preprint arXiv:2001.08856.

Belhasin, O., Bar-Shalom, G., and El-Yaniv, R. (2022).

Transboost: Improving the best imagenet performance

using deep transduction. Advances in Neural Informa-

tion Processing Systems, 35:28363–28373.

Byerly, A., Kalganova, T., and Dear, I. (2021). No routing

needed between capsules. Neurocomputing, 463:545–

553.

Deepa, S., Devi, B. A., et al. (2011). A survey on artiﬁ-

cial intelligence approaches for medical image classi-

ﬁcation. Indian Journal of Science and Technology,

4(11):1583–1595.

Deng, L. (2012). The mnist database of handwritten digit

images for machine learning research. IEEE Signal

Processing Magazine, 29(6):141–142.

Dieuleveut, A., Fort, G., Moulines, E., and Robin, G.

(2021). Federated-em with heterogeneity mitigation

and variance reduction. Advances in Neural Informa-

tion Processing Systems, 34:29553–29566.

Foret, P., Kleiner, A., Mobahi, H., and Neyshabur, B.

(2020). Sharpness-aware minimization for efﬁ-

ciently improving generalization. arXiv preprint

arXiv:2010.01412.

Garibotto, G., Murrieri, P., Capra, A., De Muro, S., Petillo,

U., Flammini, F., Esposito, M., Pragliola, C., Di Leo,

G., Lengu, R., et al. (2013). White paper on industrial

applications of computer vision and pattern recogni-

tion. In Image Analysis and Processing–ICIAP 2013:

17th International Conference, Naples, Italy, Septem-

ber 9-13, 2013, Proceedings, Part II 17, pages 721–

730. Springer.

Gavrikov, P. and Keuper, J. (2022). Cnn ﬁlter db: An em-

pirical investigation of trained convolutional ﬁlters. In

Proceedings of the IEEE/CVF Conference on Com-

puter Vision and Pattern Recognition, pages 19066–

19076.

Germain, J. C. and Aguilera, J. M. (2012). Identifying

industrial food foam structures by 2d surface image

analysis and pattern recognition. Journal of Food En-

gineering, 111(2):440–448.

Hirata, D. and Takahashi, N. (2023). Ensemble learning

in cnn augmented with fully connected subnetworks.

IEICE TRANSACTIONS on Information and Systems,

106(7):1258–1261.

Huang, J., Li, Y.-F., and Xie, M. (2015). An empirical anal-

ysis of data preprocessing for machine learning-based

software cost estimation. Information and software

Technology, 67:108–127.

Huang, Y., Chu, L., Zhou, Z., Wang, L., Liu, J., Pei, J.,

and Zhang, Y. (2021). Personalized cross-silo fed-

erated learning on non-iid data. In Proceedings of

the AAAI conference on artiﬁcial intelligence, volume

35.9, pages 7865–7873.

Hussain, M., Bird, J. J., and Faria, D. R. (2019). A

study on cnn transfer learning for image classiﬁca-

tion. In Advances in Computational Intelligence Sys-

ELSA: Expanded Latent Space Autoencoder for Image Feature Extraction and Classiﬁcation

709

tems: Contributions Presented at the 18th UK Work-

shop on Computational Intelligence, September 5-7,

2018, Nottingham, UK, pages 191–202. Springer.

Jain, A., Patel, H., Nagalapatti, L., Gupta, N., Mehta, S.,

Guttula, S., Mujumdar, S., Afzal, S., Sharma Mittal,

R., and Munigala, V. (2020). Overview and impor-

tance of data quality for machine learning tasks. In

Proceedings of the 26th ACM SIGKDD international

conference on knowledge discovery & data mining,

pages 3561–3562.

Kingma, D. P. and Ba, J. (2017). Adam: A method for

stochastic optimization.

Kowsari, K., Heidarysafa, M., Brown, D. E., Meimandi,

K. J., and Barnes, L. E. (2018). Rmdl: Random mul-

timodel deep learning for classiﬁcation. In Proceed-

ings of the 2nd international conference on informa-

tion system and data mining, pages 19–28.

Kwon, J., Kim, J., Park, H., and Choi, I. K. (2021). Asam:

Adaptive sharpness-aware minimization for scale-

invariant learning of deep neural networks. In Interna-

tional Conference on Machine Learning, pages 5905–

5914. PMLR.

Lei, X., Pan, H., and Huang, X. (2019). A dilated cnn model

for image classiﬁcation. IEEE Access, 7:124087–

124095.

Li, Q., Cai, W., Wang, X., Zhou, Y., Feng, D. D., and Chen,

M. (2014). Medical image classiﬁcation with convo-

lutional neural network. In 2014 13th international

conference on control automation robotics & vision

(ICARCV), pages 844–848. IEEE.

Liang, P., Shi, W., and Zhang, X. (2017). Remote sens-

ing image classiﬁcation based on stacked denoising

autoencoder. Remote Sensing, 10(1):16.

Liu, Y., Wang, X., Zhang, Z., and Deng, F. (2023). A review

of deep leaning in image classiﬁcation for mineral ex-

ploration. Minerals Engineering, 204:108433.

Louizos, C., Reisser, M., Soriaga, J., and Welling, M.

(2021). An expectation-maximization perspective on

federated learning. arXiv preprint arXiv:2111.10192.

Mazzia, V., Salvetti, F., and Chiaberge, M. (2021).

Efﬁcient-capsnet: Capsule network with self-attention

routing. Scientiﬁc reports, 11(1):14634.

Mehdy, M., Ng, P., Shair, E., Saleh, N., Gomes, C., et al.

(2017). Artiﬁcial neural networks in image processing

for early detection of breast cancer. Computational

and mathematical methods in medicine, 2017.

Miranda, E., Aryuni, M., and Irwansyah, E. (2016). A sur-

vey of medical image classiﬁcation techniques. In

2016 international conference on information man-

agement and technology (ICIMTech), pages 56–61.

IEEE.

Mirsadeghi, M., Shalchian, M., Kheradpisheh, S. R., and

Masquelier, T. (2023). Spike time displacement-based

error backpropagation in convolutional spiking neural

networks. Neural Computing and Applications, pages

1–16.

Najafabadi, M. M., Villanustre, F., Khoshgoftaar, T. M.,

Seliya, N., Wald, R., and Muharemagic, E. (2015).

Deep learning applications and challenges in big data

analytics. Journal of big data, 2(1):1–21.

Pereira, I. G., Guerin, J. M., Silva J

unior, A. G., Gar-

cia, G. S., Piscitelli, P., Miani, A., Distante, C., and

Gonc¸alves, L. M. G. (2020). Forecasting covid-19

dynamics in brazil: a data driven approach. Interna-

tional Journal of Environmental Research and Public

Health, 17(14):5115.

Pham, H. and Le, Q. (2021). Autodropout: Learning

dropout patterns to regularize deep networks. In Pro-

ceedings of the AAAI Conference on Artiﬁcial Intelli-

gence, volume 35.11, pages 9351–9359.

Ram

e, A., Sun, R., and Cord, M. (2021). Mixmo: Mixing

multiple inputs for multiple outputs via deep subnet-

works. In Proceedings of the IEEE/CVF International

Conference on Computer Vision, pages 823–833.

Sharma, D. and Jindal, G. (2011). Identifying lung cancer

using image processing techniques. In International

Conference on Computational Techniques and Arti-

ﬁcial Intelligence (ICCTAI), volume 17, pages 872–

880. Citeseer.

Shi, M., Zhou, Y., Ye, Q., and Lv, J. (2022). Personalized

federated learning with hidden information on person-

alized prior. arXiv preprint arXiv:2211.10684.

Tanveer, M. S., Khan, M. U. K., and Kyung, C.-M. (2021).

Fine-tuning darts for image classiﬁcation. In 2020

25th International Conference on Pattern Recognition

(ICPR), pages 4789–4796. IEEE.

Tseng, C.-H., Liu, H.-C., Lee, S.-J., and Zeng, X. (2022).

Perturbed gradients updating within unit space for

deep learning. In 2022 International Joint Conference

on Neural Networks (IJCNN), pages 01–08. IEEE.

Turay, T. and Vladimirova, T. (2022). Toward performing

image classiﬁcation and object detection with convo-

lutional neural networks in autonomous driving sys-

tems: A survey. IEEE Access, 10:14076–14119.

Xiao, H., Rasul, K., and Vollgraf, R. (2017).

Fashion-mnist: a novel image dataset for bench-

marking machine learning algorithms. cite

arxiv:1708.07747Comment: Dataset is freely avail-

able at https://github.com/zalandoresearch/fashion-

mnist Benchmark is available at http://fashion-

mnist.s3-website.eu-central-1.amazonaws.com/.

Yang, Z., Wu, X., Huang, P., Zhang, F., Wan, M., and Lai, Z.

(2022). Orthogonal autoencoder regression for image

classiﬁcation. Information Sciences, 618:400–416.

Zhang, M., Li, W., and Du, Q. (2018). Diverse region-based

cnn for hyperspectral image classiﬁcation. IEEE

Transactions on Image Processing, 27(6):2623–2634.

Zhao, J., Mathieu, M., Goroshin, R., and Lecun, Y. (2015).

Stacked what-where auto-encoders. arXiv preprint

arXiv:1506.02351.

Zhou, S., Xue, Z., and Du, P. (2019). Semisupervised

stacked autoencoder with cotraining for hyperspec-

tral image classiﬁcation. IEEE Transactions on Geo-

science and Remote Sensing, 57(6):3813–3826.

VISAPP 2024 - 19th International Conference on Computer Vision Theory and Applications

710