A Learning Powered Bi-Level Approach for Dynamic Electricity Pricing
Patrizia Beraldi
a
, Luigi Gallo and Alessandra Rende
Department of Mechanical, Energy and Management Engineering, University of Calabria, Italy
Keywords:
Bi-Level Optimization, Electricity Tariffs, Solar Production, Forecasting, Machine Learning Techniques.
Abstract:
This paper presents a comprehensive approach to electricity tariff determination by integrating advanced Arti-
ficial Intelligence (AI) techniques with Bi-Level (BL) optimization. More specifically, AI techniques are used
to obtain accurate forecasts of photovoltaic panel generation, which are then used as input parameters for a
deterministic BL problem that models the interaction between a power supplier and a residential prosumer.
To handle the high complexity of the BL formulations, the model is first reformulated into a single-level struc-
ture, and then linearized using an approach based on the application of the dual reformulation. An intensive
experimental phase is carried out on a real case study to test the effectiveness of the proposed methodology
and to quantify the impact of the forecast techniques on the supplier strategy.
1 INTRODUCTION
Climate change and environmental degradation pose
a severe threat to Europe and the rest of the world.
In response to these challenges, the European Cli-
mate Law, effective since 29 July 2021, has estab-
lished the intermediate target of reducing net green-
house gas emissions by at least 55% by the year 2030,
compared to levels recorded in 1990. Furthermore,
this legislation has set the ambitious goal of attain-
ing a climate neutral European Union by 2050. In
the energy transition, end-users are acknowledged as
key stakeholders. Nowadays, a growing number of
consumers are evolving into prosumers, i.e. con-
sumers that also produce energy, primarily from re-
newable energy sources (RES), as, for example, Pho-
tovoltaic (PV) panels. Additionally, prosumers often
possess a battery energy storage (BES) device to com-
pensate for the non-programmability of green energy
production, which is by nature intermittent and un-
predictable. Indeed, prosumers can accumulate self-
produced energy and use it later when needed, and
purchase electricity during off-peak hours when the
prices are lower, thus reducing the electricity bill. In
addition, the recent integration of advanced commu-
nications, metering, and control automation provides
prosumers with the technical support to optimize the
load management, exploiting the flexibility of con-
trollable loads. Many modern appliances are, indeed,
deemed for control and they can be properly sched-
a
https://orcid.org/0000-0002-1672-4033
uled during hours when electricity prices are lower
or when self-produced energy is available, leading to
significant cost savings. Proactive prosumers are of-
ten referred to as prosumagers, as they are called to
optimize the management of their home energy sys-
tems in response to the market signals. Prosumers can
act individually or collectively, as a single entity, as,
for example, a local energy community coordinated
by aggregator acting as intermediary with the mar-
ket. In this paper, we study the interaction between an
aggregator and a homogeneous group of residential
prosumagers, comparable in terms of location, con-
sumption patterns, flexibility and behaviour. A sim-
ilar interaction can also be envisaged with a retailer,
although the ultimate goal of aggregators and retail-
ers may be different, as the former are designed to be
non-profit organisations. Nonetheless, both entities
aim to maximize their net profit, which, in the case of
the aggregator, could potentially be reinvested in the
community, for example, incentivising future invest-
ments in RES. In this paper, we focus on the electric-
ity pricing problem analyzed from the perspective of
an aggregator. In the text, the terms aggregator and re-
tailer are used interchangeably. Specifically, we focus
on a dynamic pricing scheme with rates that vary over
time. Time-of-use (ToU), critical-peak pricing (CPP)
and real-time pricing (RTP) are commonly used time-
based pricing structures. We consider a RTP scheme,
where the aggregator dynamically determines the sell-
ing prices offered to the clients for each period of a
planning horizon. Such a pricing scheme is expected
390
Beraldi, P., Gallo, L. and Rende, A.
A Learning Powered Bi-Level Approach for Dynamic Electricity Pricing.
DOI: 10.5220/0012465700003639
Paper published under CC license (CC BY-NC-ND 4.0)
In Proceedings of the 13th International Conference on Operations Research and Enterprise Systems (ICORES 2024), pages 390-397
ISBN: 978-989-758-681-1; ISSN: 2184-4372
Proceedings Copyright © 2024 by SCITEPRESS – Science and Technology Publications, Lda.

to become a common practice in smart grids as it
represents a mean to incentive price-based demand-
response programs. Prosumers can, indeed, be moti-
vated to change their habitual consumption patterns
in response to economic signals, thereby favouring
the transition from the conventional “supply follows
load” paradigm to the “load follows supply” one in
the long run. Due to the increasing relevance, the
electricity pricing problem has been the subject of in-
tensive research in recent years. The problem involves
two different players tied by a hierarchical relation.
The retailer/aggregator plays the role of leader, decid-
ing first, whereas the prosumer the role of follower.
To account for such a relation, we formulate the prob-
lem by the Bi-Level (BL) paradigm (Colson et al.,
2007). Specifically, the leader solves the Upper Level
(UL) problem aimed at defining the electricity rates
and the procurement plan that bears the maximum
profit. In taking the best decision, he conjectures the
possible reaction of the follower to the offered rates
as this affects the objective function. Indeed, the fol-
lower, on the basis of the offered rates, decides the
management of his home energy system including the
load scheduling. The aim of this Lower Level (LL)
problem is the minimization of the daily electricity
bill. Since variation of the controllable loads with the
respect to the ideal consumption procures a discom-
fort, a penalization term is also considered in the fol-
lower’s objective function. Different recent contribu-
tions propose BL formulations for the electricity pric-
ing problem. For example, in (Grimm et al., 2021) the
authors compare different pricing schemes and show
that the RTP structure guarantees the highest addi-
tional revenue for the retailer, but also the largest price
volatility for the prosumer. (Soares et al., 2020) pro-
pose a BL formulation where in the UL problem the
retailer establishes the ToU tariff that maximizes the
profit, whereas at the LL, the consumer, as follower,
reacts to this price by determining the operation of the
controllable loads in order to minimize the electricity
bill and a discomfort cost. (Ferrara et al., 2021) pro-
pose a BL formulation where the leader owns a local
energy production system to optimally manage, with
the aim of reducing the amount of energy to purchase
from the wholesale market to cover the follower re-
quest who is also equipped with a renewable energy
system and can control the flexible loads. More re-
cently, (Beraldi and Khodaparasti, 2023a) propose a
BL formulation for defining RTP tariffs offered to a
follower representative of a residential prosumager
who reacts to price signal by scheduling the flexi-
ble appliances. Unlike other contributions, the leader
owns a local energy system that must be properly
managed with the aim of maximizing the daily profit.
The contributions mentioned above share the assump-
tion of perfect information of the parameters involved
in the decision process, thus neglecting the impact
that uncertainty in market prices and weather-related
variables may have in defining the optimal tariff. Only
a few recent contributions, acknowledging the im-
portance of explicitly dealing with uncertainty, pro-
pose stochastic BL formulations. Here, we men-
tion the recent contribution by (Beraldi and Khoda-
parasti, 2023b) who propose a stochastic formulation
for the definition of time-variant tariffs. Specifically,
the leader solves a two-stage problem to define the
optimal procurement plan, considering both the day-
ahead and the real-time market, and maximizing a
safety measure that controls the expected profit that
can be gained in a given percentage of worst case re-
alizations. The follower reacts to the offered tariffs
by optimally managing his home energy system with
the aim of reducing the expected electricity bill. In
(Sarfarazi et al., 2023) the authors provide a stochas-
tic BL formulation where the aggregator sets real-
time selling and buying prices, whereas users mod-
ify their consumption and their grid feed-in through
the use of battery storage systems, to minimize their
costs. Scenario based framework is introduced to take
into account the uncertainty about market prices, local
market generation levels and user electricity demand.
In (Feng and Ruiz, 2023) a stochastic BL approach
to determine electricity tariffs for energy community
members is proposed. Proactive prosumers are as-
sumed to be equipped with PV panels, storage de-
vices and hydrogen systems. Although stochastic BL
formulations have been shown to perform better than
their deterministic counterparts (Beraldi and Khoda-
parasti, 2023b), their solution poses severe computa-
tional challenges. Deterministic BL problems have
been proved to be NP-hard, thus the explicit consid-
eration of uncertainty introduces an additional layer
of complexity, preventing the solution of large-scale
instances that take into account a significant number
of possible future scenarios. Nevertheless, the pricing
problem should be solved on a daily basis to generate
electricity rates for the following day, thus imposing a
limit on the computational time. To address this chal-
lenge, we incorporate uncertainty into the decision
process by employing forecasts of the random param-
eters (Samal et al., 2021). In particular, we assume to
know the wholesale electricity prices as they are an-
nounced in advance one day-ahead, whereas weather-
related variables, i.e. the solar production, are con-
sidered as random and are forecast. The proposed
approach relies on the idea of integrating prediction
and optimization. In particular, we apply the classical
”predict, then optimize” paradigm, where prediction
A Learning Powered Bi-Level Approach for Dynamic Electricity Pricing
391

is performed first and then the forecast values are used
in the BL optimization model. A strong advantage of
the considered approach compared to more advanced
frameworks that jointly perform predictions and opti-
mization relies on the observation that the optimiza-
tion problem is not ”altered”. This represents an im-
portant element in our case given the difficulty related
to the solution of the BL problems. The contributions
of this paper are summarized below:
• We apply machine learning (ML) techniques to
derive day-ahead accurate PV power production
forecasts serving as input parameters for the BL
model.
• We formulate and solve the learning powered BL
formulation once derived the corresponding sin-
gle level reformulation.
• We test the proposed approach on a realistic case
study and we derive useful insights.
The rest of the paper is organized as follows. Section
2 outlines the proposed methodology: first, we de-
tail the techniques used for PV prediction, and, then,
we present the BL formulation, followed by the used
solution approach. Numerical results of experiments
carried out on a realistic case study are presented and
discussed in Section 3. Conclusions and future re-
search directions are discussed in Section 4.
2 THE PROPOSED APPROACH
We consider an aggregator facing the problem of
defining electricity rates for a homogeneous group
of smart prosumers represented by a reference pro-
sumager. As the aim is to offer RTP rates, the prob-
lem has to be solved every day, using each time up-
dated information. Figure 1 shows the scheme of the
proposed approach. It consists of two main modules.
In particular, Module 1 refers to the forecast of the
uncertain parameters entering as input of Module 2,
where rates are determined by the solution of a BL
problem. Boxes under the two modules refer to the
solution techniques. Specifically, Machine Learning
is used for forecasting, whereas the solution of the BL
problem is carried out by using a commercial solver
once that a single-level reformulation is obtained.
2.1 Forecasting the Solar Production
In the last decades, several methods have been pro-
posed for PV power prediction (Ahmed et al., 2020).
The methods are based on two main approaches: the
physical approach and the data-driven one. While the
former requires prior knowledge of the PV material
Figure 1: Structure of the proposed approach.
properties and the metadata, along with the need of
weather condition data, the latter requires operational
data to train/calibrate the coefficients of the models
which are then used to generate the predictions. In
this paper, we focus on day-ahead solar power fore-
casting. Specifically, the PV production of the next
day is generated one day in advance. We adopt the
data-driven approach and, specifically, we apply fore-
casting techniques belonging to the class of Machine
Learning, as they provide (see, e.g. (Das et al., 2018))
better results, although they are more computationally
demanding. In particular, we consider four ML tech-
niques: Multivariate Linear Regression (MLR), Sup-
port Vector Regression (SVR), Random Forest (RF)
and Artificial Neural Networks (ANNs).
• MLR: It is a simple and widely applied model in
solar forecasting. Specifically, the MLR forecasts
the PV production by considering a linear rela-
tionship between the target variable and a set of
independent variables (predictors). In our case,
the slope and the intercept are determined in the
training phase minimizing the sum of squared
residuals between the predicted values and the ac-
tual values, according to the Ordinary Least of
Squares (OLS) algorithm.
• SVR: It is a kernel based forecast technique that
evolved from the Support Vector Machine, which
is typically used for classification problems. Sim-
ilar to SVM, the SVR constructs a set of hyper-
planes in a multidimensional space in order to de-
rive the relationship between predictors and the
target variable. In this study, we consider the Ra-
dial Basis kernel function (Scott et al., 2023).
• ANN: The architecture of the ANNs allows to
build complex nonlinear relationships between
predictors and the target variables, without assum-
ing any form of relationship between these vari-
able. ANN consists of an input layer that re-
ceives the input data, and an output layer that
provides the predictions. Moreover, there is a
ICORES 2024 - 13th International Conference on Operations Research and Enterprise Systems
392

predefined number of hidden layers that trans-
form the weighted sum of inputs, using an activa-
tion function. In this study, we consider a back-
propagation algorithm to learn the weights that
minimize the difference between the actual val-
ues of target variable and the resulting values of
output layer of the net.
• RF: Random forest is an ensemble method that
combines the results of multiple decision trees to
determine the result. The training set is recur-
sively partitioned to classify the target data on the
basis of one or more predictor variables, gener-
ating a number of trees. A tree generated may
be identical or different to another tree generated
during the execution of the algorithm. Only one
tree is selected and used to make the prediction,
and the selection is made using the majority vot-
ing criterion: the most frequent tree is selected.
The tree generation algorithm is implemented us-
ing the Gini index and the minimum number of
elements in a leaf node as stopping criteria.
2.2 The BL Formulation
Forecasts generated by applying the algorithms intro-
duced in the previous subsection represent the values
in input to Module 2, where electricity rates are deter-
mined by applying the BL formulation. We assume
to consider hourly-rate and we denote by r
t
the rate
offered by the aggregator at time period t of a given
planning horizon (1 day). Bound constraints are im-
posed on the offered rates:
R
min
t
≤ r
t
≤ R
max
t
∀t (1)
Here R
min
t
is a lower bound defined increasing the av-
erage market prices by a percentage accounting for
taxes and leverages, whereas R
max
t
accounts for mar-
ket competition and eventual caps agreed with the fol-
lower in advance. Moreover, we impose a threshold Γ
on the average price that can be reached during a day:
1
T
T
∑
t=1
r
t
≤ Γ (2)
The aim of the leader is to maximize the daily profit
defined as difference between revenues deriving from
the electricity selling and procurement costs, i.e. pur-
chasing electricity from the market.
maxF =
T
∑
t = 1
(r
t
E
t
− P
M
t
E
t
) (3)
Here P
M
t
denotes the market prices, whereas E
t
de-
notes the energy amount required by the follower.
Such a variable is not under the leader control, but
for given values of the electricity rates represents the
solution of the LL problem. Specifically, the follower
reacts to the offered rates by managing the home en-
ergy system composed by a BES of a given nominal
capacity C and a system of PV panels with a power
production G
t
forecast by Module 1. The aim is to
minimize the daily electricity bill by exploiting the
stored electricity and the load flexibility. In partic-
ular, we assume that the follower’s loads are parti-
tioned into inflexible and flexible loads on the basis
of their level of control. Inflexible demand or base
load is associated with a consumption that cannot be
controlled (e.g. refrigerators, centralized heating and
cooling systems, lighting for essential areas), whereas
flexible demand refers to an energy consumption that
can be shifted. For a given time period t, ideal flexible
load value is denoted by x
id
t
, whereas we denote by w
t
the base load. Variation from the ideal consumption
produces a discomfort that should be also taken into
account in the follower’s objective function. For each
period t of the time horizon, the prosumager has to
take three types of decision on:
• the amount to buy from the retailer E
t
;
• the operation of the flexible loads, controlled by
the variables x
t
, x
+
t
, x
−
t
;
• the management of the BES, represented by the
state of charge, soc
t
, and the power charged z
c
t
,
and discharged from the battery z
d
t
.
The following constraints are included into the LL
problem:
x
t
= x
id
t
+ x
+
t
− x
−
t
∀t (h
1t
) (4)
T
∑
t = 1
x
t
=
T
∑
t = 1
x
id
t
(h
2
) (5)
w
t
+ x
t
≤ Q ∀t (h
3t
) (6)
E
t
= x
t
+ w
t
− G
t
− z
d
t
+ z
d
t
− z
c
t
∀t (h
4t
) (7)
soc
t
= (1 − α) soc
t−1
+ η
c
z
c
t
−
z
d
t
η
d
∀t (h
5t
)
(8)
µ
1
C ≤ soc
t
≤ µ
2
C ∀t (h
6t
, h
7t
) (9)
z
c
t
≤ τ
c
C ∀t (h
8t
) (10)
z
d
t
≤ τ
d
C ∀t (h
9t
) (11)
E
t
, x
t
, x
+
t
, x
−
t
, z
d
t
, z
c
t
≥ 0 ∀t (12)
Constraints (4) refer to the flexible loads and model
the hourly deviation between the ideal consumption,
whereas constraints (5) ensure that, considering the
entire time horizon, the total consumption is satis-
fied. An upper bound Q on the consumption of the
follower, is set by constraint (6), for each period t
of the time horizon. The amount of electricity to
A Learning Powered Bi-Level Approach for Dynamic Electricity Pricing
393

purchase from the leader is defined by constraints
(7). Besides PV production, demand can be covered
by the power discharged from the BES, whereas the
amount in excess is stored and used later. Constraints
(8) refer to the management of the BES consider-
ing a self-discharge rate α, a charging efficiency η
c
and a discharging efficiency η
d
. The initial condi-
tion for the state of charge of the battery is defined as
soc
0
= µ
1
C. Constraints (9) guarantee that the state-
of-charge of the battery, soc
t
, remains within mini-
mum and maximum levels, determined as a function
of the nominal capacity C through the coefficients µ
1
and µ
2
, while constraints (10)–(11) set upper bounds
on the total power charged and discharged, defined
as a percentage (charging rate τ
c
and discharging rate
τ
d
) of the nominal capacity. Given the communicated
rates r
t
, the aim of the follower is to minimize the ob-
jective function:
min f =
T
∑
t = 1
[ r
t
E
t
+ ρ
1
x
−
t
+ ρ
2
x
+
t
] (13)
Here, two goals are considered related to the cost and
discomfort, respectively. This latter corresponds to
the figurative cost of changing the consumption pat-
tern from the ideal one. More in detail, the figurative
cost is defined by penalizing positive (x
+
t
) and nega-
tive (x
−
t
) deviations of the actual load from the pre-
ferred value x
id
t
through the coefficients ρ
1
and ρ
2
.
2.2.1 The Solution Approach
To solve the proposed BL formulation we apply a tra-
ditional approach relying on the derivation of a single
level reformulation. We note that for fixed values of
the electricity rates r
t
, the LL problem is a linear prob-
lem. We can therefore derive the corresponding dual
problem reported below:
maxz =
T
∑
t = 1
h
1t
x
id
t
+ h
2
T
∑
t = 1
x
id
t
+
T
∑
t = 1
h
3t
(w
t
− Q)
+
T
∑
t = 1
h
4t
(G
t
− w
t
) + h
51
soc
0
(1 − α) +
+ µ
1
C
T
∑
t = 1
h
6t
+ − µ
2
C
T
∑
t = 1
h
7t
+
− τ
c
C
T
∑
t = 1
h
8t
− τ
d
C
T
∑
t = 1
h
9t
(14)
s.t.
− h
4t
≤ r
t
∀t (15)
h
1t
+ h
2
− h
3t
+ h
4t
≤ 0 ∀t (16)
h
1t
≤ ρ
1
∀t (17)
− h
1t
≤ ρ
2
∀t (18)
h
4t
− η
c
h
5t
− h
8t
≤ 0 ∀t (19)
− h
4t
+
1
η
d
h
5t
− h
9t
≤ 0 ∀t (20)
h
5t
− (1 − α) h
5 t+1
+
+ h
6t
− h
7t
= 0 ∀t ∈ {1, T − 1} (21)
h
5T
+ h
6T
− h
7T
= 0 (22)
h
1t
, h
2
, h
4t
, h
5t
f ree (23)
h
3t
, h
6t
, h
7t
, h
8t
, h
9t
≥ 0 (24)
We observe that the LL problem is always feasible
and bounded. Thus, based on the strong duality theo-
rem, both the primal and the dual problems have op-
timal solutions and the corresponding objective func-
tion values are equal. The single-level reformulation
is obtained by adding to the UL constraints, the pri-
mal LL constraints (4)-(12), the corresponding dual
constraints (15)-(24) and equating the primal (13) and
dual objective functions (14). We observe that the
single-level reformulation contains a bilinear term de-
riving from the product of the r
t
and E
t
variables, that
we may linearize by adopting a dual approach. More
specifically, the auxiliary variable ω
t
= r
t
E
t
is intro-
duced, together with the following set of constraints:
r
t
= (λ
1
+ λ
2
)L
1
+ (λ
3
+ λ
4
)U
1
(25)
E
t
= (λ
1
+ λ
3
)L
2
+ (λ
2
+ λ
4
)U
2
(26)
4
∑
i=1
λ
i
= 1 (27)
ω
t
= λ
1
L
1
L
2
+ λ
2
L
1
U
2
+ λ
3
U
1
L
2
+ λ
4
U
1
U
2
(28)
λ
i
≥ 0 i = 1, ..., 4 (29)
where L
1
and U
1
are defined from 1, while L
2
is as-
sumed to be 0, and U
2
to be equal to the prosumer’s
maximum total consumption Q.
3 NUMERICAL RESULTS
This section is devoted to the presentation and dis-
cussion of the computational experiments carried out
to assess the effectiveness of the proposed approach
on a realistic case study. The techniques used to fore-
cast the PV power production have been implemented
by using the software R version 4.3.0 (R Core Team,
2023), whereas the model and the solution algorithm
have been coded in GAMS 38 and solved using ILOG
CPLEX (Bussieck and Meeraus, 2007). All the exper-
iments have been performed on a 64-bit HP Pavilion
Laptop 15-eg2xxx with 12th Gen Intel(R) Core(TM)
i7-1255U 1.70 GHz and a RAM of 16 GB.
ICORES 2024 - 13th International Conference on Operations Research and Enterprise Systems
394

3.1 Case Study and Data Setting
The case study concerns a retailer operating in the
Italian electricity market that wants to offer RTP tar-
iffs to affiliated end users, represented by a refer-
ence prosumager. The tariffs are communicated the
day before the commitment and are, therefore, dy-
namically determined. Following the organization
of the Italian market, we consider hourly time steps.
The results reported in the following refer to an au-
tumn day, specifically 30th October 2019, for which
the real values are available. In particular, day-
ahead electricity prices are available on the website
of the Italian ”Gestore dei mercari elettrici”(GME)
1
for download. Starting from these values, proper
bounds on the rates have been determined. R
min
t
has been set to R
min
t
= min
t∈T
P
M
t
(1 + β), whereas
R
max
t
= max
t∈T
K P
M
t
(1 + β). Finally, Γ = U (1 +
β)
1
T
∑
T
t = 1
P
M
t
, where β, K and U are parameters un-
der the decision maker control. In our experiments,
we have considered the values 1.3, 1.2 and 1.2, re-
spectively.
Tariffs are offered to a reference prosumager,
who reacts to the price signals by managing his
domestic energy system with the aim of minimizing
the electricity bill. In the experiments, we have
considered a reference prosumager with an energy
system composed of a BES with nominal capacity
of 3.8 kW and a system of PV panels. Technical
parameters concerning the management of the BES
are reported in the Appendix, together with other
parameters defining prosumer features. The amount
of electricity the follower purchases from the leader
depends on his self-production that is forecast. In
the experiments, we have considered a reference PV
module whose main characteristics are reported in the
note
2
. Prediction has been carried out considering
four main predictor variables, i.e. hour of the day,
relative humidity (%), temperature (°C), radiance
on tilt surface. As each predictor varies in different
scale, a normalization step has been preliminary
carried out. The data span a period of 3 years,
from 01/01/2017 to 31/12/2019, for a total of 23832
records. The data set has been divided into two
subsets, with observations from 2017 and 2018 used
for the training and validation phases, and data from
2019 used for testing. Approximately 57% of the
data set is used as the training set, a further 6%
as the validation set and the remaining 37% as the
test set. The ML techniques have been evaluated
1
https://www.mercatoelettrico.org/it
2
Schuco module, series MPE 240 PG 60 FA with size
1.995 x 998 mm, nominal power equal to 240 W, under stan-
dard test condition
Table 1: Performance metrics of the ML techniques.
ML technique RMSPE MAPE R
2
MLR 23.5 11.4 97.2
SVR 10.8 5.5 97.9
ANN 46.2 31.9 93.4
RF 9.7 5.7 97.5
by using three traditional metrics: the root mean
square percentage error (RMSPE), the mean absolute
percentage error (MAPE), and R squared (R
2
). More
specifically, the metrics are defined as:
RMSPE =
v
u
u
t
1
M
M
∑
j = 1

y
j
− ˆy
j
y
j

2
MAPE =
1
M
M
∑
j=1





y
j
− ˆy
j
y
j





R
2
= 1 −
∑
M
j=1
(y
j
− ˆy
j
)
2
∑
M
j=1
(y
j
− ¯y)
2
Here M denotes the number of data points of the test
set, whereas y
j
, ˆy
j
represent the j-th actual and pre-
dicted value. Finally, ¯y denotes the expected value
of the target variable. Better performance are associ-
ated with lower values of the RMSPE and MAPE and
higher values of R
2
. The results are reported in Table
1. As evident, the MLR and ANN techniques perform
poorly, while the other methods provide accurate fore-
casts. Specifically, the SVR technique outperforms
the other methods, reporting the lowest MAPE value
and the highest value of R
2
. Moreover, it also ranks
second in the RMSPE metric. The RF method also
performs well on the RMSPE metric and provides
comparable values for the other two metrics.
Accuracy can be also appreciated by looking at the
plot in Figure 2 where we report the real production
in comparison to forecast one obtained by applying
the different techniques. Looking at the Figure, we
may note that the ANN tends to overestimate the PV
production in the central hours of the day.
Forecast values are used by the leader who, in
defining the electricity tariffs, anticipates the pro-
sumager reaction. Clearly errors in the prediction
negatively impact on his profit requiring the re-
course to balancing market to compensate any short-
age and/or surplus deriving from a difference between
the initial requirement and the real ones.
3.2 Results of the BL Formulation
Different experiments have been carried out as func-
tion of the technique used to forecast the PV produc-
A Learning Powered Bi-Level Approach for Dynamic Electricity Pricing
395

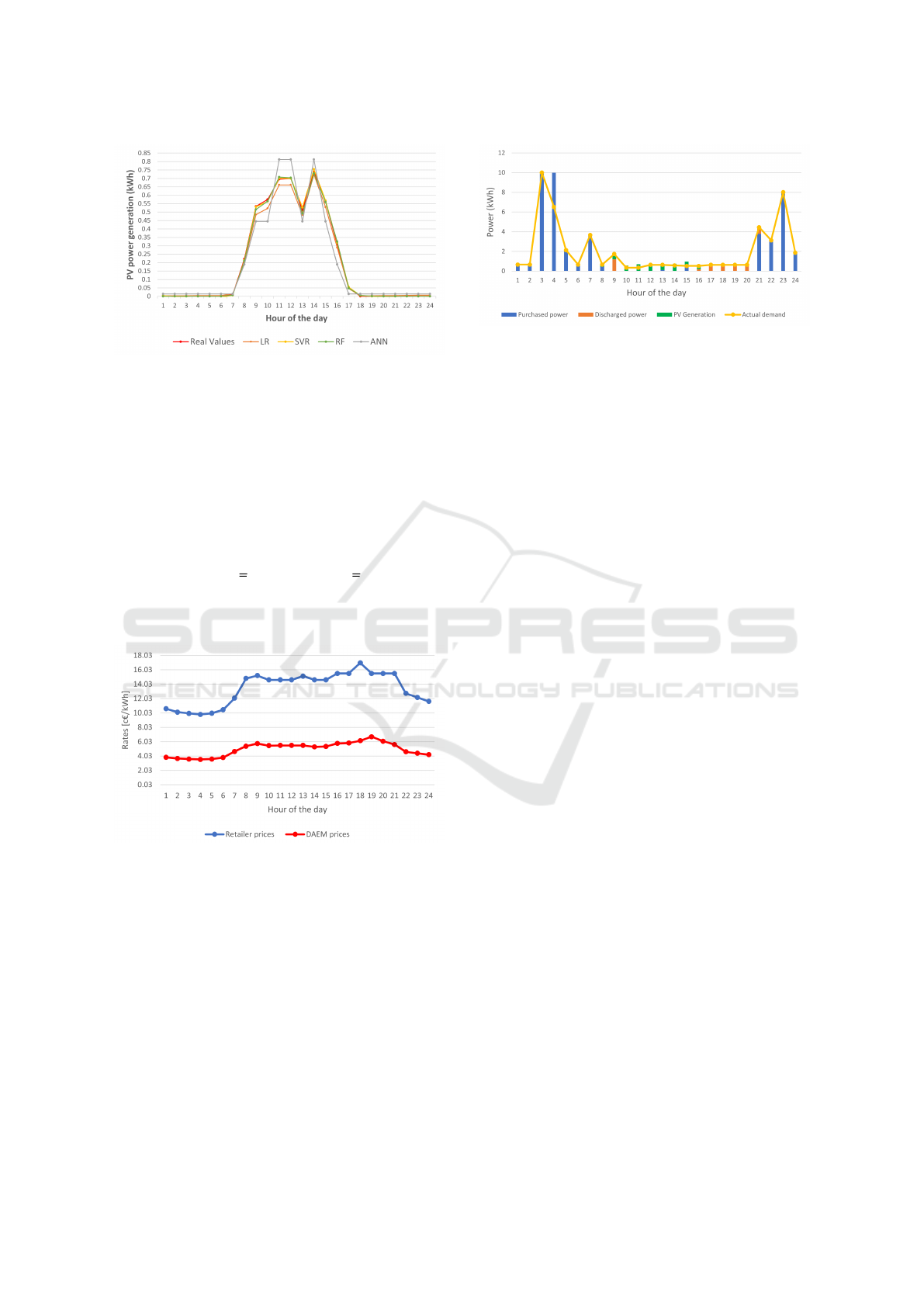
Figure 2: Actual vs. predicted PV Production.
tion. The results have been compared with those ob-
tained when considering the real data to gain insight
on the impact of the prediction accuracy on the rec-
ommendation provided to the end-user. In what fol-
lows, we report the results obtained adopting the SVR
technique that, at least considering the data used here,
represents the most performing approach. Similar re-
sults have been obtained considering the other tech-
niques, which provide anyhow good predictions. Fig-
ure 3 shows the electricity tariffs offered by the leader,
ranging from 9.82 c C/kWh to 16.99 c C/kWh. In the
same Figure we also report the wholesale electricity
prices. As evident, the rates and prices show a similar
trend.
Figure 3: Offered rates and DAEM prices.
Given the offered tariffs, Figure 4 shows the reac-
tion of the follower. Specifically, we report the con-
sumption pattern after performing eventual shifting of
the flexible loads and we show how the demand is sat-
isfied. In detail, in high price periods 8, 9, 20 and 21,
the ideal loads are partially shifted towards period 4,
which is characterised by the minimum price, and pe-
riods 3 and 5, which present the second and the third
lowest values. The solution indicates to shift the 59.4
% of the total flexible demand. Moreover, in these
high price hours, the demand is also met by discharg-
ing the battery, which is charged through the electric-
ity supply in period 4 and 15 and with the PV gen-
Figure 4: Prosumager’s demand satisfaction.
eration when this overcomes the demand of the same
period.
Additional experiments have been performed with
the aim of measuring the impact of the forecast tech-
niques on the leader’s strategy. More specifically, we
have compared the cost of the leader’s supply plan
when considering the real PV production and when
considering the different prediction techniques. The
results show that the increase is very low for all the
techniques , which the exception of the ANN one. In
that case, at least for the case study considered in our
tests, an increase of around 4 % has been registered.
Clearly, the higher the share of the renewable produc-
tion, the higher the negative effect produced by not
accurate prediction.
4 CONCLUSIONS AND FUTURE
RESEARCH DIRECTIONS
The paper presents a BL approach for the pricing
problem faced by an aggregator who wants to deter-
mine real time electricity rates to offer to aggregated
end-users represented by a reference prosumager. The
problem is solved every day using, each time, more
updated information and the offered rates are com-
municated the day-ahead. Uncertainty in weather-
related variables is dealt by applying ML techniques
that provide accurate forecast which are then used as
input data for the BL problem. This predict and opti-
mize approach allows to explicitly account for uncer-
tainty keeping the original structure of the BL prob-
lem. The problem is solved by a commercial solver
once derived the corresponding single-level reformu-
lation. Several experiments have been carried out to
assess the efficiency of the proposed approach on a
realistic test case, where the leader is presented by a
retailer operating in the Italian electricity market and
the follower is a prosumager owing a domestic energy
system. Specifically, the performance of the four ML
techniques has been measured and compared by ap-
plying traditional measures. The results show that all
ICORES 2024 - 13th International Conference on Operations Research and Enterprise Systems
396

the methods provide accurate forecast, especially the
SVR and the RF approaches. The experiments show
how the quality of the forecasts impacts on the rec-
ommendations provided by the model when imple-
mented on a real setting. Inaccurate predictions im-
pose the recourse to the balancing market to compen-
sate any shortage/surplus of the required power, de-
termining a reduction of the leader’s profit. Different
issues are currently under investigation and represent
future developments. First of all, the BL problem can
be extended to a multi-follower setting so to consider
a more general configuration where different types of
followers are jointly considered and the leader can of-
fer specialized tariffs. The problem would be more
complex if we consider the possibility that the fol-
lowers may sell energy to the aggregation. An addi-
tional interesting extension would be to define com-
prehensive tariffs that cover both electricity and gas
by exploiting the close relationship between the two
markets.
ACKNOWLEDGEMENTS
We acknowledge the financial support from: PNRR
MUR project PE0000013-FAIR .
REFERENCES
Ahmed, R., Sreeram, V., Mishra, Y., and Arif, M. (2020).
A review and evaluation of the state-of-the-art in pv
solar power forecasting: Techniques and optimiza-
tion. Renewable and Sustainable Energy Reviews,
124:109792.
Beraldi, P. and Khodaparasti, S. (2023a). A bi-level
model for the design of dynamic electricity tar-
iffs with demand-side flexibility. Soft Computing,
27:12925–12942.
Beraldi, P. and Khodaparasti, S. (2023b). Designing elec-
tricity tariffs in the retail market: A stochastic bi-level
approach. International Journal of Production Eco-
nomics, 257(108759).
Bussieck, M. R. and Meeraus, A. (2007). Algebraic Mod-
eling for IP and MIP (GAMS). In Annals of Oper-
ations Research, volume 149(1), special edition His-
tory of Integer Programming: Distinguished Personal
Notes and Reminiscences, Guest Editors: Kurt Spiel-
berg and Monique Guignard-Spielberg, pages 49–56.
Kluwer Academic Publishers-Plenum Publishers.
Colson, B., Marcotte, P., and Savard, G. (2007). An
overview of bilevel optimization. Annals of opera-
tions research, 153(1):235–256.
Das, U. K., Tey, K. S., Seyedmahmoudian, M., Mekhilef,
S., Idris, M. Y. I., Van Deventer, W., Horan, B., and
Stojcevski, A. (2018). Forecasting of photovoltaic
power generation and model optimization: A review.
Renewable and Sustainable Energy Reviews, 81:912–
928.
Feng, W. and Ruiz, C. (2023). Risk management of en-
ergy communities with hydrogen production and stor-
age technologies. Applied Energy, 348:121494.
Ferrara, M., Violi, A., Beraldi, P., Carrozzino, G., and
Ciano, T. (2021). An integrated decision approach for
energy procurement and tariff definition for prosumers
aggregations. Energy economics, 97(105034).
Grimm, V., Orlinskaya, G., Schewe, L., Schmidt, M., and
Z
¨
ottl, G. (2021). Optimal design of retailer-prosumer
electricity tariffs using bilevel optimization. Omega,
102(102327).
R Core Team (2023). R: A Language and Environment for
Statistical Computing. R Foundation for Statistical
Computing, Vienna, Austria.
Samal, D., Bisoi, R., and Sahu, B. (2021). Identification
of nonlinear dynamic system using machine learning
techniques. International Journal, 12(1):23–43.
Sarfarazi, S., Mohammadi, S., Khastieva, D., Hesamzadeh,
M. R., Bertsch, V., and Bunn, D. (2023). An optimal
real-time pricing strategy for aggregating distributed
generation and battery storage systems in energy com-
munities: A stochastic bilevel optimization approach.
International Journal of Electrical Power & Energy
Systems, 147:108770.
Scott, C., Ahsan, M., and Albarbar, A. (2023). Machine
learning for forecasting a photovoltaic (pv) generation
system. Energy, 278:127807.
Soares, I., Alves, M. J., and Antunes, C. H. (2020). De-
signing time-of-use tariffs in electricity retail markets
using a bi-level model – estimating bounds when the
lower level problem cannot be exactly solved. Omega,
93:102027.
APPENDIX
In the numerical experiments, we have used the fol-
lowing parameters in the constraints related to the
storage management. In particular, the values of the
efficiency rates i.e. η
c
, η
d
have been set to 0.98,
whereas the operation ranges are set to µ
1
= 5% and
µ
2
= 95%. Finally, the charging and discharging co-
efficients (τ
c
, τ
d
) have been set equal to 95% of the
BES capacity C. The values of base load w
t
and ideal
flexible load x
id
t
, for each period of the time horizon,
have been derived from data reported in (Soares et al.,
2020). The maximum total prosumer’s consumption
(Q) is set to 10 kWh, whereas the parameters ρ
1
and
ρ
2
are assumed to be equal to 0.01 and 0.005, respec-
tively.
A Learning Powered Bi-Level Approach for Dynamic Electricity Pricing
397