A Soft Constraint-Based Framework for Ethical Reasoning

Hiroshi Hosobe

1 a

and Ken Satoh

Faculty of Computer and Information Sciences, Hosei University, Tokyo, Japan

National Institute of Informatics, Tokyo, Japan

Keywords:

Ethical Norm, Constraint Programming, Soft Constraint.

Abstract:

Artiﬁcial intelligence is becoming more widely used for making decisions in many application areas, where

it often needs to consider legal rules and ethical norms. However, ethical norms are more difﬁcult to treat

than legal rules that have logical nature. Taheri et al. proposed a framework that formalized several important

aspects of ethical decision making. However, their framework is still not powerful enough for more general

problem solving. In this paper, we propose a soft constraint-based framework for ethical reasoning. Espe-

cially by devising the notion of norm constraints, we integrate Taheri et al.’s framework into Borning et al.’s

constraint hierarchy framework for treating soft constraints. We also present a case study on the application

of our framework to ethical reasoning.

1 INTRODUCTION

Artiﬁcial intelligence is becoming more widely used

for making decisions in many application areas,

where it often needs to consider legal rules and ethical

norms. To treat legal rules, legal reasoning has long

been studied. An effective and promising approach is

logic programming. For example, a Prolog-based sys-

tem was developed for the purpose of reasoning about

the Japanese civil code (Satoh et al., 2010).

Ethical reasoning also has been studied. How-

ever, ethical norms are more difﬁcult to treat than le-

gal rules that have logical nature. One problem is that

ethical norms are not explicitly speciﬁed unlike legal

rules that are speciﬁed in laws. Another more essen-

tial problem is that how to represent and evaluate eth-

ical norms is unclear. Another is that there are many

kinds of ethical norms that should be simultaneously

considered but that might be conﬂicting.

To tackle these problems, Taheri et al. proposed a

framework for ethical decision making (Taheri et al.,

2023). Their framework formalized several important

aspects of ethical decision making including how to

organize ethical norms, how to evaluate choices ac-

cording to individual norms, how to aggregate such

evaluations for different classes of norms, and how

to determine the best choices according to the entire

norms.

https://orcid.org/0000-0002-7975-052X

However, Taheri et al.’s framework is still not

powerful enough for more general problem solving.

Basically, what the framework does is to compare

choices according to given norms. Therefore, it needs

to be combined with another method to handle rules

and knowledge other than ethical norms. In fact, in

addition to the ethical decision making framework,

they needed to use a planner and a legal checker to

develop a multi-agent real-time compliance mecha-

nism (Hayashi et al., 2023). The ethical decision mak-

ing framework worked as an ethical checker to select

the ethically best plans from the legal plans generated

by the planner and the legal checker.

In this paper, we propose a soft constraint-based

framework for ethical reasoning. Our goal is to con-

struct a unifying framework that enables expressive

ethical decision making as well as powerful constraint

programming. Especially by devising the notion of

norm constraints, we integrate Taheri et al.’s frame-

work into Borning et al.’s constraint hierarchy frame-

work (Borning et al., 1992) for treating soft con-

straints. The resulting framework has twofold charac-

ters. On one hand, it can be regarded as an extension

of Taheri et al.’s ethical decision making framework to

constraint-based reasoning. On the other hand, it can

be regarded as a special case of Borning et al.’s con-

straint hierarchy framework with concrete application

to ethical reasoning.

The rest of this paper is organized as follows. Sec-

tion 2 describes previous research that is related to our

1354

Hosobe, H. and Satoh, K.

A Soft Constraint-Based Framework for Ethical Reasoning.

DOI: 10.5220/0012474100003636

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 16th International Conference on Agents and Artiﬁcial Intelligence (ICAART 2024) - Volume 3, pages 1354-1361

ISBN: 978-989-758-680-4; ISSN: 2184-433X

work. Section 3 brieﬂy explains Taheri et al.’s frame-

work and Borning et al.’s framework. Section 4 pro-

poses our soft constraint-based framework for ethical

reasoning. Section 5 presents a case study on the ap-

plication of our framework to ethical reasoning. Sec-

tion 6 discusses our framework. Finally, Section 7

gives conclusions and future work.

2 RELATED WORK

Satoh et al. proposed the use of constraints for le-

gal and ethical reasoning (Satoh et al., 2021). More

speciﬁcally, they proposed to use hard constraints

for legal rules and to use soft constraints for ethical

norms. They showed their concept by developing a

system based on abductive planning with event cal-

culus (Eshghi, 1988). However, their treatment of

soft constraints was still limited as compared to other

soft constraint frameworks such as constraint hierar-

chies (Borning et al., 1992).

Fungwacharakorn et al. proposed the use of

constraint hierarchies to treat ethical norms (Fung-

wacharakorn et al., 2022a; Fungwacharakorn et al.,

2022b). They represented ethical norms as soft con-

straints and studied the property of fundamental revi-

sions and the debugging of represented norms. How-

ever, they used logical constraints that were evaluated

as true or false, and did not consider more general soft

constraints that could be evaluated in a more detailed

manner as shown in this paper.

3 PRELIMINARIES

In this section, we explain two frameworks as prelim-

inaries to our framework.

3.1 Ethical Decision Making

First, we brieﬂy explain Taheri et al.’s ethical deci-

sion making framework, which was originally pro-

posed in (Taheri et al., 2023) and also was brieﬂy

explained in (Hayashi et al., 2023). The framework

treats various ethical norms such as data minimality,

data sensitivity, gender fairness, racial fairness, and

even system performance. In addition, it provides a

mechanism for organizing such norms into multiple

norm classes (that can be hierarchically structured).

For example, data minimality and data sensitivity can

be classiﬁed in a norm class called privacy. There

may be other norm classes such as fairness and per-

formance.

Norms are represented as a tuple of norm classes

N = hN

,...,N

i, where l is some positive inte-

ger, and each N

indicates a norm class consisting of

norms. Each norm is used to rank alternatives (or

choices to be compared in decision making) in a given

set A. A norm class aggregates the results of the rank-

ings of the norms in the class by using a voting mech-

anism. The framework especially chooses Copeland’s

rule (Saari and Merlin, 1996) for this purpose. Intu-

itively, Copeland’s rule computes the Copeland score

s(a,N

) of an alternative a ∈ A according to a norm

class N

. A higher Copeland score of a indicates that

a is better.

The framework selects the best alternatives by us-

ing a relation called superiority for comparing al-

ternatives according to norm classes with an order,

which is deﬁned as follows.

Deﬁnition 1 (superiority). Given alternatives a,a

∈

A, a tuple N = hN

,...,N

i of norm classes, and

a partial order <

on {1,...,l}, the superiority of a

over a

according to N with <

is deﬁned as

superior(a,a

,N,<

) ≡

∃k ∈ {1,...,l}(∀i ∈ {1,...,l}

(i <

k → s(a,N

) = s(a

))∧

s(a,N

) > s(a

)).

3.2 Constraint Hierarchies

Next, we brieﬂy explain Borning et al.’s constraint hi-

erarchy framework (Borning et al., 1992). Let X be a

set of variables. How to assign values to variables is

expressed as a valuation that is a function from vari-

ables to their values. Let Θ be the set of all the valu-

ations. Then a valuation θ ∈ Θ obtains the value of a

variable x ∈ X as θ(x). Let C be a set of constraints.

How much a constraint is satisﬁed by a valuation is

given by an error function e. Speciﬁcally, e(c,θ) re-

turns a non-negative real number: returning 0 means

that c is exactly satisﬁed by θ; returning a larger num-

ber means that c is less satisﬁed.

A constraint hierarchy is typically represented as

H = hH

,...,H

i, where l is some positive inte-

ger, and each H

, called a level, is a set of constraints.

Level H

consists of required (or hard) constraints

that must be exactly satisﬁed while each H

with i ≥ 1

consists of preferential (or soft) constraints that can

be relaxed if necessary. A typical constraint hierar-

We simpliﬁed the formulation of the superiority rela-

tion by using a partial order and a standard deﬁnition of lex-

icographic ordering. The original framework (Taheri et al.,

2023) gives a more complex formulation of this relation by

using a total preorder.

A Soft Constraint-Based Framework for Ethical Reasoning

1355

chy is totally ordered, which means that a preferen-

tial level H

with smaller i consists of more important

constraints.

In this paper, we treat partially ordered hierar-

chies. A partially ordered hierarchy is represented

as hH, <

i, where H = hH

,...,H

i, and <

is a

partial order on {0,1,. ..,l} with 0 as the only small-

est element. The intuitive meaning of the required

level H

is the same as in the case of totally ordered

hierarchies. By contrast, the importance of the pref-

erential levels is speciﬁed by partial order <

; that is,

if i <

j, H

has more important constraints than H

To deﬁne solutions to a partially ordered hierar-

chy, the notion of consistent totally ordered hierar-

chies is used. Given a partially ordered hierarchy

hH,<

i, hH,<

i is a consistent totally ordered hi-

erarchy if <

is a total order on {0, 1, . . . , l} with 0

as the smallest element and there is a bijective map-

ping m of type {0,1,...,l} → {0,1,...,l} such that

i <

j → m(i) <

m( j).

Intuitively, a consistent to-

tally ordered hierarchy is a modiﬁcation of a partially

ordered hierarchy that rearranges preferential levels

in a total order in such a way that any pair of ordered

levels in the original partially ordered hierarchy will

keep the same order in the resulting totally ordered

hierarchy.

The importance of constraints in a constraint hi-

erarchy is evaluated by a comparator better. In-

tuitively, better(θ,θ

,hH,<

i) judges whether a

valuation θ is better than another θ

with respect to al-

ternative valuations S

according to a totally ordered

hierarchy hH,<

i that is consistent with a partially

ordered hierarchy hH,<

i. It should be noted that the

better comparator internally uses the error function e

to evaluate individual constraints.

The solution set of a partially ordered hierarchy

is deﬁned as the union of the solution sets of all the

totally ordered constraint hierarchies consistent with

the original partially ordered hierarchy.

Deﬁnition 2 (solution). Given a partially ordered hi-

erarchy hH, <

i, the set S

(hH,<

i) of all the solu-

tions to hH,<

i is deﬁned as

(hH,<

i) =

[

hH,<

i∈H

(hH,<

where H is the set of all the totally ordered hierar-

We simpliﬁed the deﬁnition of consistent totally or-

dered hierarchies by removing a possible operation of merg-

ing levels. This operation may impose a problem, which is

discussed in (Borning et al., 1992). Chiu and Lee also dis-

cuss the problem and present a more complex deﬁnition of

solutions (Chiu and Lee, 1998).

chies consistent with hH,<

i and

(hH,<

i) ={θ ∈ S

|∀θ

∈ S

(¬better(θ

,θ,S

,hH,<

i))}

where

= {θ ∈ Θ |∀c ∈ H

(e(c,θ) = 0)}.

In this deﬁnition, S

indicates the set of all the

valuations that satisfy the required constraints. Also,

(hH,<

i) indicates the set of all the solutions to

a totally ordered hierarchy hH, <

i, which is deter-

mined by collecting the “best” valuations from S

4 PROPOSED FRAMEWORK

In this section, we propose a soft constraint-based

framework for ethical reasoning. To begin with, we

introduce a new kind of constraints called norm con-

straints. Intuitively, a norm constraint evaluates a

given valuation according to the associated norm and

assigns a rank to the valuation. Let C

norm

be a set

of norm constraints. Then the meaning of norm con-

straints is deﬁned with a ranking function r. Intu-

itively, r(c, θ) obtains the rank of a valuation θ ac-

cording to a norm constraint c. Ranks are expressed

with positive integers, and a smaller positive integer

indicates a better rank, typically with 1 as the best.

This is formally deﬁned as follows.

Deﬁnition 3 (ranking function). Let Z

be the set of

all the positive integers. A ranking function r is a

function of type C

norm

× Θ → Z

We use the notion of partially ordered hierarchies,

which we explained in Subsection 3.2. Therefore,

we deﬁne a constraint hierarchy as a pair hH, <

where H = hH

,...,H

i and <

is a partial or-

der on {0, 1, . . . , l} with 0 as the only smallest ele-

ment. We assume that the required level H

consists

of only ordinary constraints and that the other lev-

els H

,...,H

, called the norm levels, consist of only

norm constraints

To evaluate how much a valuation satisﬁes a norm

level, we use a combining function g that computes

the Copeland score of the valuation according to the

norm level. Intuitively, g(θ,S

) computes the

Copeland score of a valuation θ with respective to al-

ternative valuations S

according to a norm level H

This is deﬁned as follows.

Deﬁnition 4 (combining function). Given a valuation

θ, a set S

of valuations with θ (i.e., θ ∈ S

), and a set

of norm constraints, the combining function g is

deﬁned as

g(θ,S

) =

∑

∈S

\{θ}

p(θ,θ

)

ICAART 2024 - 16th International Conference on Agents and Artiﬁcial Intelligence

1356

where

p(θ,θ

) =







1 if w(θ,θ

) > w(θ

,θ,H

)

1/2 if w(θ,θ

) = w(θ

,θ,H

)

0 otherwise

where

w(θ,θ

) =



{c ∈ H

|r(c, θ) < r(c,θ

)}



This deﬁnition is based on an adaptation of

Copeland scores to our framework. Function

w(θ,θ

) uses the ranking function r to compute

the number of the wins of θ against θ

according to

the norm constraints in H

. Function p(θ, θ

) com-

putes the elemental score of θ against θ

according to

. Finally, function g(θ,S

) accumulates the el-

emental scores to compute the Copeland score of θ

according to H

Next, we deﬁne a comparator better for our

framework. Although we treat a partially ordered hi-

erarchy, we deﬁne it for a totally ordered hierarchy by

following the original framework.

Deﬁnition 5 (comparator). Given a constraint hierar-

chy hH, <

i, valuations θ and θ

, a set S

of valua-

tions with θ and θ

(i.e., θ,θ

∈ S

), and a total order

consistent with <

, the comparator better is de-

ﬁned as

better(θ,θ

,hH,<

i) ≡

∃k ∈ {1,...,l}(∀i ∈ {1,...,l}

(i <

k → g(θ,S

) = g(θ

)) ∧

g(θ,S

) > g(θ

)).

This comparator is deﬁned as the lexicographic or-

dering using the total order and the Copeland scores

of norm levels. The nature of the lexicographic order-

ing more highly evaluates a valuation if it obtains a

higher Copeland score at an upper level.

We deﬁne solutions to a constraint hierarchy in the

same way as solutions to a partially ordered hierarchy

in the original framework. Speciﬁcally, the set of all

the solutions to a given constraint hierarchy hH,<

is S

(hH,<

i), which is formulated by Deﬁnition 2.

Finally, we present a theorem that relates our

framework with Taheri et al.’s ethical decision mak-

ing framework. It allows us to regard our framework

as an extension of Taheri et al.’s framework.

Theorem 1. Let A be an arbitrary set of alterna-

tives, N = hN

,...,N

i be an arbitrary tuple of

norm classes, and <

be an arbitrary partial order

on {1, . . . , l}. Let X = {x} be the set of a variable

x, and Θ be the set of all the valuations from X to

A. Regard the norms in N as norm constraints and

the ranking of alternatives in A by norms in N as a

ranking function r. Let H = h

0,N

,...,N

i be a

constraint hierarchy. Then the following holds:

(hH,<

i) = {θ ∈ Θ | θ(x) = a ∧

∀a

∈ A(¬superior(a

,a,N,<

))}.

Intuitively, this theorem says that the constraint

hierarchy constructed from an ethical decision mak-

ing problem based on Taheri et al.’s framework ob-

tains the same set of solutions as the original prob-

lem. Note that the resulting constraint hierarchy has

only one variable and no required constraints.

5 CASE STUDY

In this section, we conduct a case study on the appli-

cation of the proposed framework to ethical reason-

ing.

5.1 Modeling a Problem

This case study uses a problem adapted from Hayashi

et al.’s use case of their multi-agent real-time compli-

ance mechanism (Hayashi et al., 2023). It supposes a

job recommendation service operated by an employ-

ment platform company and performs legal and ethi-

cal reasoning. They implement this service as a dis-

tributed system consisting of multiple nodes in dif-

ferent regions, some of which are inside the Euro-

pean Union (EU) and the others of which are out-

side. They want to process their customers’ data by

using a remote processing node. Although both their

user node and the remote processing node are inside

the EU, some of the intermediate nodes between these

nodes are outside the EU. Since the data include the

customers’ privacy information, they need to treat the

data by following legal rules such as the EU’s Gen-

eral Data Protection Regulation (GDPR). In addition,

they want to treat the data by respecting ethical norms

such as privacy and fairness.

This use case is represented as a simpliﬁed

problem illustrated in Figure 1. The company

has two datasets, data1 and data2, at the user

node. While they can use data1 for two purposes,

recommendation and analysis, they are legally al-

lowed to use data2 only for analysis. The remote

processing nodes can execute two kinds of processes,

process1 and process2, which have different charac-

teristics. The user node and the processing node are

connected along two routes, one with node1 and the

other with node2 as an intermediate node. While

node1 is inside the EU, node2 is outside the EU.

When they process a dataset, it is transferred from

the user node to the processing node via either node1

A Soft Constraint-Based Framework for Ethical Reasoning

1357

User node

Node 1

Node 2

Processing

node

Dataset 1

Dataset 2

Process 1

Process 2

Non-EU

Figure 1: Problem of legal and ethical reasoning for a job

recommendation service adapted from Hayashi et al.’s use

case of their compliance mechanism (Hayashi et al., 2023).

or node2, then it is processed by either process1 or

process2 at the processing node, and the result is re-

turned to the user node via either node1 or node2.

Now we model this problem as a constraint hierar-

chy by using our framework. First, we introduce ﬁve

variables with ﬁnite domains, d ∈ {data1,data2}, u ∈

{recommendation,analysis}, n,m ∈ {node1,node2},

and p ∈ {process1, process2}. Variable d indicates

which of datasets data1 and data2 is used. Variable u

indicates for which of purposes recommendation and

analysis the dataset should be used. Variables n and

m indicate which of intermediate nodes node1 and

node2 should be used when the dataset is transferred

to the processing node and when it is returned to the

user node respectively. Variable p indicates which of

processes process1 and process2 should be used when

the dataset is processed at the processing node.

Next, to express the legal rule, we introduce the

following required constraint:

d = data2 → u = analysis. (1)

This constraint means that data2 is legally allowed to

be used only for analysis.

In the following, we associate norm con-

straints with symbolic norms to distinguish how

important they are. Speciﬁcally, we have six sym-

bolic norms, data minimality, data sensitivity,

transfer safety, node safety, algo unbiasedness,

and transfer eﬃciency. More generally, norms

data minimality, data sensitivity, transfer safety,

and node safety are related to the ethical norm of

privacy, algo unbiasedness (for algorithmic unbiased-

ness) is related to fairness, and transfer eﬃciency is

related to performance. (In the next subsection, we

consider such a classiﬁcation of the norms.)

We represent each norm constraint as a sequence

of more primitive constraints separated with either re-

lation of  or ◦. Relation  indicates that satisfying its

left-hand side is better than satisfying its right-hand

side, and relation ◦ indicates that satisfying its left-

hand side is as good as satisfying its right-hand side

in the sense of the associated norm.

To represent ethical norms in this problem, we in-

troduce the following norm constraints:

data minimality (d = data1)  (d = data2) (2)

data sensitivity (d = data1)  (d = data2) (3)

transfer safety (n = node1 ∧ m = node1) 

(n = node1 ∧ m = node2) ◦

(n = node2 ∧ m = node1) 

(n = node2 ∧ m = node2) (4)

node safety (n = node1 ∧ m = node1) 

(n = node1 ∧ m = node2) ◦

(n = node2 ∧ m = node1) 

(n = node2 ∧ m = node2) (5)

algo unbiasedness (p = process1) 

(p = process2) (6)

transfer eﬃciency (n = node2 ∧ m = node2) 

(n = node1 ∧ m = node2) ◦

(n = node2 ∧ m = node1) 

(n = node1 ∧ m = node1). (7)

Intuitively, constraints (2) and (3) mean that, in the

senses of data minimality and data sensitivity re-

spectively, using data1 is better than using data2.

Constraints (4) and (5) mean that, in the senses

of transfer safety and node safety respectively, us-

ing node1 twice is the best, using node2 only once

is the second best, and using node2 twice is the

worst. Constraint (6) means that, in the sense of

algo unbiasedness, using process1 is better than us-

ing process2. Constraint (7) means that, in the sense

of transfer eﬃciency, using node2 twice is the best,

using node1 only once is the second best, and using

node1 twice is the worst.

This problem especially considers the case where

a dataset is used for the purpose of recommendation,

which is expressed by further introducing the follow-

ing required constraint:

u = recommendation. (8)

Now the entire problem has nearly been modeled as

a constraint hierarchy consisting of two required con-

straints (1) and (8) and six norm constraints (2) to (7)

although norm levels are yet to be introduced.

5.2 Solving the Problem

We solve the problem modeled in the previous sub-

section.

First, we satisfy the required constraints

In this paper, we manually solve the problem by fol-

lowing the formulation of our framework, without introduc-

ing a concrete algorithm.

ICAART 2024 - 16th International Conference on Agents and Artiﬁcial Intelligence

1358

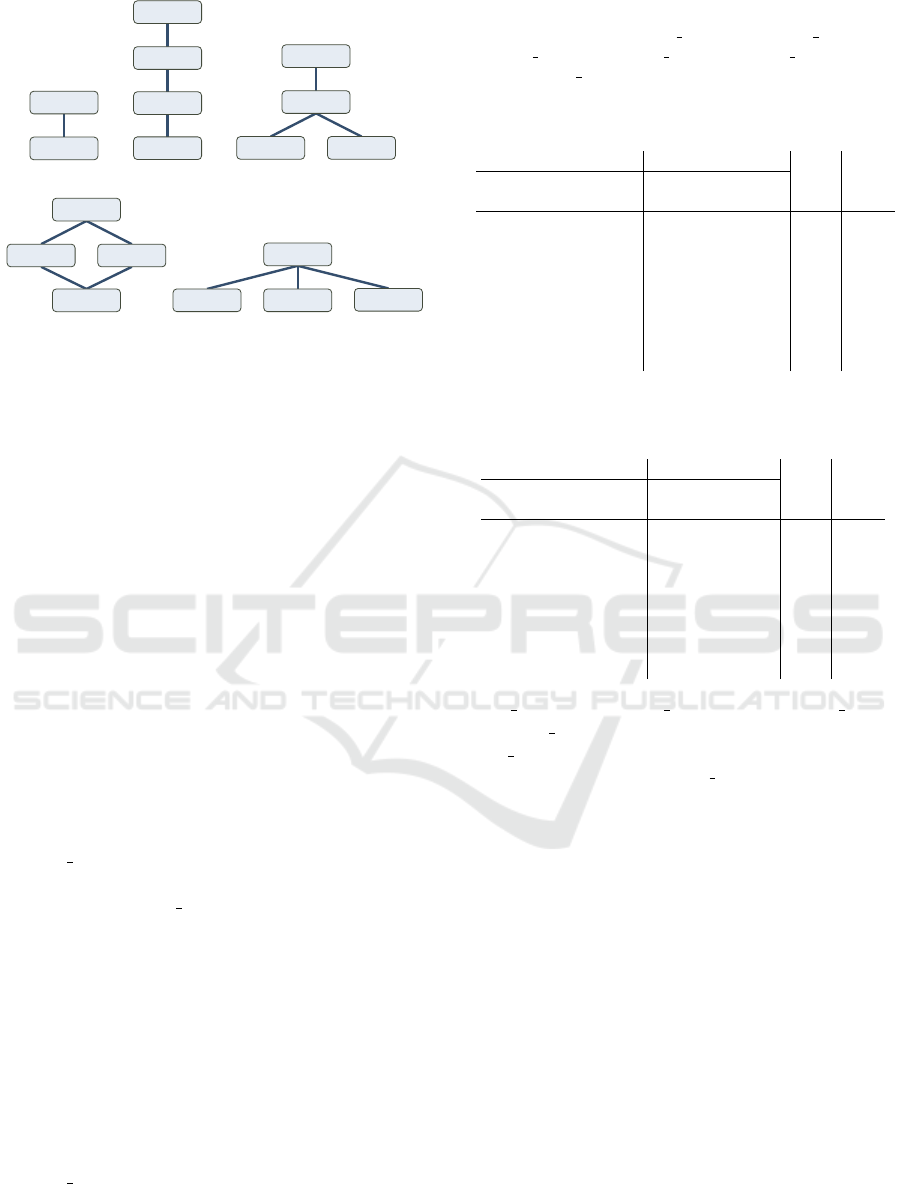
required

all norms

required

privacy

fairness

performance

required

privacy

fairness performance

(a) (b) (c)

required

privacy fairness

performance

required

privacy fairness

performance

(d) (e)

Figure 2: Structures of constraint hierarchies.

(1) and (8). Constraint (8) uniquely determines u

as recommendation, which further determines d as

data1 because of constraint (1) and the domain of d.

There are still eight potential solutions that can assign

different combinations of values to variables n, m, and

p. Their values need to be determined by further con-

sidering the norm constraints.

To show the effects of our framework, we con-

sider different structures of constraint hierarchies.

First, we suppose the simplest case where all the

six norms belong to one norm level as shown in

Figure 2(a). In this case, all the norms are aggre-

gated to compare the potential solutions that satisfy

the required constraints, which determines the solu-

tions to the constraint hierarchy. Table 1 shows this

process. Initially, each potential solution is associ-

ated with the six ranks that are indicated as norm-

wise ranks in this table. For example, potential

solution hd, u, n, m, pi = hdata1, recommendation,

node1, node1, process1i has the ﬁrst rank for norm

transfer safety since assigning node1 to both n and m

is speciﬁed as the best by the norm constraint (4) as-

sociated with transfer safety. Next, for each potential

solution, its Copeland score is computed from their

norm-wise ranks. Finally, hd, u, n, m, pi = hdata1,

recommendation, node1, node1, process1i is deter-

mined as only the solution to the constraint hierar-

chy since it was given the highest Copeland score

of 7.0. Intuitively, this solution means that data1

should be used for recommendation, should be trans-

ferred to the processing node via node1, should be

processed by process1, and should be returned to the

user node via node1. Note that this solution is given

the ﬁrst norm-wise ranks by the ﬁve norms other than

transfer eﬃciency.

Next, we consider a case where there are three

norm levels, privacy, fairness, and performance.

In this case, level privacy consists of four norms

Table 1: Case where all the six norms belong to one

norm level. Norms data minimality, data sensitivity,

transfer safety, node safety, algo unbiasedness,

and transfer eﬃciency and variable values data1,

recommendation, node1, node2, process1, and process2

are abbreviated as dm, ds, ts, ns, au, te, d1, rec, n1, n2,

p1, and p2 respectively.

Potential solution Norm-wise ranks Cope- Level-

land wise

hd, u, n, m, pi dm ds ts ns au te score rank

hd1, rec, n1, n1, p1i 1 1 1 1 1 3 7.0 1

hd1, rec, n1, n2, p1i 1 1 2 2 1 2 5.0 2

hd1, rec, n2, n1, p1i 1 1 2 2 1 2 5.0 2

hd1, rec, n2, n2, p1i 1 1 3 3 1 1 2.5 4

hd1, rec, n1, n1, p2i 1 1 1 1 2 3 4.5 3

hd1, rec, n1, n2, p2i 1 1 2 2 2 2 2.0 5

hd1, rec, n2, n1, p2i 1 1 2 2 2 2 2.0 5

hd1, rec, n2, n2, p2i 1 1 3 3 2 1 0.0 6

Table 2: Case where four out of the six norms belong to

norm level privacy. The norms and the variable values are

abbreviated in the same way as in Table 1.

Potential solution Norm-wise ranks Cope- Level-

land wise

hd, u, n, m, pi dm ds ts ns score rank

hd1, rec, n1, n1, p1i 1 1 1 1 6.5 1

hd1, rec, n1, n2, p1i 1 1 2 2 3.5 2

hd1, rec, n2, n1, p1i 1 1 2 2 3.5 2

hd1, rec, n2, n2, p1i 1 1 3 3 0.5 3

hd1, rec, n1, n1, p2i 1 1 1 1 6.5 1

hd1, rec, n1, n2, p2i 1 1 2 2 3.5 2

hd1, rec, n2, n1, p2i 1 1 2 2 3.5 2

hd1, rec, n2, n2, p2i 1 1 3 3 0.5 3

data minimality, data sensitivity, transfer safety,

and node safety, level fairness consists of one norm

algo unbiasedness, and level performance consists of

the other one norm transfer eﬃciency. Since lev-

els privacy and fairness consist of only one norm,

their level-wise rankings of the potential solutions are

the same as the underlying norm-wise rankings due

to the nature of Copeland’s rule. For level privacy,

we need to compute its level-wise ranking, which is

shown in Table 2. In the same way as the previ-

ous case, the four norm-wise ranks are aggregated to

calculate their Copeland scores, which separates the

potential solutions into three ranks. Especially, note

that two potential solutions hd, u, n, m, pi = hdata1,

recommendation, node1, node1, process1i, hdata1,

recommendation, node1, node1, process2i are given

the ﬁrst level-wise rank in this case.

To handle the three norm levels, we further con-

sider their partial orders. It should be noted that,

in the typical use of a constraint hierarchy, such

a partial order is determined at its modeling stage.

However, in the following, we show all the possi-

ble partial orders to illustrate our framework. Since

there are three norm levels, we can consider the

A Soft Constraint-Based Framework for Ethical Reasoning

1359

following three subcases: (A) they are totally or-

dered, e.g., privacy <

fairness <

performance as

shown in Figure 2(b); (B) two of them are in-

comparable, e.g., privacy <

fairness ∧ privacy <

performance with incomparable norms fairness and

performance as shown in Figure 2(c), which is de-

noted as privacy <

{fairness,performance} below,

and also, e.g., privacy <

performance ∧ fairness <

performance with incomparable norms privacy and

fairness as shown in Figure 2(d), which is de-

noted as {privacy,fairness} <

performance below;

as shown in Figure 2(e), which is denoted as

{privacy,fairness,performance} below.

We ﬁrst consider subcase (A). In this subcase,

we can determine solutions in the same way as nor-

mal, totally ordered constraint hierarchies, which

is achieved by using lexicographic ordering. Ta-

ble 3 shows this process. In this table, each po-

tential solution is associated with three level-wise

ranks. For example, potential solution hd,u,n,m, pi =

hdata1, recommendation, node1, node1, process1i

has the ﬁrst rank for privacy, the ﬁrst rank for

fairness, and the third rank for performance. The

ﬁnal ranks of the potential solutions are determined

as the “lexicographic ranks” according to the used

order of the norm levels. For example, for or-

der privacy <

fairness <

performance, potential

solution hd, u, n, m, pi = hdata1, recommendation,

node1, node1, process1i is given the ﬁrst lexico-

graphic rank since its level-wise ranks 1, 1, and 3 (in

the order of the norm levels) is lexicographically bet-

ter than those of the other potential solutions. Such

potential solutions given the ﬁrst ranks are ﬁnally de-

termined as the solutions to the constraint hierarchy

according to the associated order of the norm lev-

els. Note that different lexicographic ranks can be

obtained for different orders of norm levels.

Finally, we consider subcases (B) and (C). In

these subcases, we determine solutions by using the

notion of partially ordered hierarchies. Table 4

shows this process. In this table, each partially

ordered hierarchy is associated with consistent to-

tally ordered hierarchies. For example, partially or-

dered hierarchy privacy <

{fairness,performance}

have two consistent totally ordered hierarchies,

privacy <

fairness <

performance and privacy <

performance <

fairness. Solutions to a partially

ordered hierarchies are obtained by collecting the

solutions to all the consistent totally ordered hi-

erarchies. For example, partially ordered hierar-

chy privacy <

{fairness,performance} has only one

solution hd, u, n, m, pi = hdata1, recommendation,

node1, node1, process1i since it is only the solution

to both of its consistent totally ordered hierarchies.

Note that different solutions can be obtained for dif-

ferent partially ordered hierarchies. Also, note that

subcase (C) (shown in Figure 2(e)) obtained the dif-

ferent solution set (with two solutions) from that of

the simplest case (shown in Figure 2(a)) of having all

the six norms in one level (with only one solution).

6 DISCUSSION

In our framework, we treated only norm constraints at

preferential levels of constraint hierarchies. However,

we can modify our framework to allow other kinds of

constraints at preferential levels. This can be realized

by separating different kinds of constraints into dif-

ferent levels, as already suggested for the purpose of

user interface applications (Hosobe et al., 1994). For

example, we can use ordinary constraints at stronger

levels and norm constraints at weaker levels.

We did not present a concrete algorithm for solv-

ing constraint hierarchies based on our framework.

For this purpose, we think that an SMT- or SAT-

based approach will be promising. In this approach,

a constraint hierarchy is ﬁrst encoded as an SMT

or SAT problem and then is solved by an external

SMT or SAT solver. Especially, the hill climbing

method (Hosobe and Satoh, 2022) is plausible be-

cause it is simple and applicable to various constraint

hierarchies. Also, it might be possible to use binary

search-based methods (Hosobe and Satoh, 2023) to

construct a more efﬁcient algorithm although it will

be more difﬁcult and challenging.

7 CONCLUSIONS AND FUTURE

WORK

In this paper, we proposed a soft constraint-based

framework for ethical reasoning. By devising the no-

tion of norm constraints, we integrated Taheri et al.’s

ethical decision making framework into Borning et

al.’s constraint hierarchy framework. We also pre-

sented a case study on the application of our frame-

work to ethical reasoning.

Our future work includes the development of a

constraint solver based on our framework. Another

direction is to integrate our framework into hierarchi-

cal constraint logic programming (Wilson and Born-

ing, 1993) to enable more expressive modeling of eth-

ical reasoning problems. It is also necessary to evalu-

ate the usefulness of our framework by applying it to