Scalable Verification of Social Explainable AI by Variable Abstraction
Wojciech Jamroga
1,2 a
, Yan Kim
2 b
and Damian Kurpiewski
1 c
1
Institute of Computer Science, Polish Academy of Science, Warsaw, Poland
2
Interdisciplinary Centre for Security, Reliability, and Trust, SnT, University of Luxembourg, Luxembourg
Keywords:
Multi-Agent Systems, Formal Verification, Social Explainable AI, Strategic Ability, Model Checking.
Abstract:
Social Explainable AI (SAI) is a new direction in artificial intelligence that emphasises decentralisation, trans-
parency, social context, and focus on the human users. SAI research is still at an early stage, and concentrates
mainly on delivering the intended functionalities. At the same time, formal analysis and verification of the
proposed solutions is rare. In this paper, we present an approach to formal verification of SAI protocols by
means of temporal model checking. We use agent graphs to model benign as well as malicious behaviors of
the participants, branching-time logic formulas to express interesting properties of the protocol, and the state
of the art temporal model checker UPPAAL to verify those formulas. As usual in such cases, state-space explo-
sion and the resulting complexity of verification is a major problem. We show how to mitigate the complexity
through state abstraction, and demonstrate the advantages in practice by using a novel tool for user-friendly
abstractions EASYABSTRACT4UPPAAL.
1 INTRODUCTION
Artificial intelligence solutions have become ubiqui-
tous in daily life, including social media, car navi-
gation, recommendation algorithms, etc. Moreover,
AI provides back-end solutions to many business pro-
cesses, resulting in a huge societal and economic im-
pact. Social Explainable AI (SAI) is a new, power-
ful idea in artificial intelligence research (Social Ex-
plainable AI, CHIST-ERA, 24; Contucci et al., 2022).
SAI emphasises decentralisation, human-centricity,
and explainability, which is in line with the trend to
move away from classical, centralised machine learn-
ing. This is essential – not only for technical reasons
like scalability, but also to meet the more and more
stringent ethical requirements with respect to trans-
parency and trustworthiness of data storage and com-
putation (Drainakis et al., 2020; Ottun et al., 2022).
Even more importantly, SAI tries to put the human
user in the spotlight, and move the focus away from
the technological infrastructure (Conti and Passarella,
2018; Toprak et al., 2021; Fuchs et al., 2022).
Social Explainable AI is a new concept, and a sub-
ject of ongoing research. It remains to be seen if it
will deliver effective, transparent, and mindful AI so-
a
https://orcid.org/0000-0001-6340-8845
b
https://orcid.org/0000-0001-7523-8783
c
https://orcid.org/0000-0002-9427-2909
lutions. SAI should be extensively studied, includ-
ing formal verification of relevant requirements. Im-
portantly, this should encompass the possible side ef-
fects of interaction that involves AI components and
human users in complex environments. In particu-
lar, one should carefully analyse the possibilities of
adversarial misuse and abuse of the interaction, e.g.,
by means of impersonation or man-in-the-middle at-
tacks (Dolev and Yao, 1983; Gollmann, 2011). In
those scenarios, one or more nodes of the interaction
network are taken over by a malicious party that tries
to disrupt communication, corrupt data, and/or spread
false information. The design of SAI must be resis-
tant to such abuse; otherwise it contains a vulnera-
bility which will be sooner or later exploited. While
the topic of adversarial attacks on machine learning
algorithms is an established topic of research (Good-
fellow et al., 2018; Kianpour and Wen, 2019; Kumar
et al., 2020), the research on SAI has mainly focused
on its expected functionalities and ideal environments
of execution.
1
This is probably because SAI environ-
ments are very complex: both conceptually, computa-
tionally, and socially. Thus, a realistic study of their
possible unintended behaviors is very challenging.
(Kurpiewski et al., 2023) proposed that SAI can
benefit from the use of formal methods to analyze
1
With the notable exception of (Kurpiewski et al.,
2023).
Jamroga, W., Kim, Y. and Kurpiewski, D.
Scalable Verification of Social Explainable AI by Variable Abstraction.
DOI: 10.5220/0012474800003636
Paper published under CC license (CC BY-NC-ND 4.0)
In Proceedings of the 16th International Conference on Agents and Artificial Intelligence (ICAART 2024) - Volume 1, pages 149-158
ISBN: 978-989-758-680-4; ISSN: 2184-433X
Proceedings Copyright © 2024 by SCITEPRESS – Science and Technology Publications, Lda.
149

the behaviours that can possibly emerge. In par-
ticular, a SAI protocol can be seen as an exam-
ple of a multi-agent system (Weiss, 1999; Shoham
and Leyton-Brown, 2009) that includes human as
well as artificial agents interacting in a mixed so-
cial/computational environment. Consequently, one
can use model checking (Clarke et al., 2018), which
is arguably the most successful framework of formal
verification, to specify, visualise, and analyse SAI
designs with respect to the relevant properties. The
study in (Kurpiewski et al., 2023) concentrated on the
verification of properties related to strategic ability of
agents and their groups to achieve their goals (Bulling
et al., 2015), using appropriate model checking tools,
such as STV (Kurpiewski et al., 2021).
The results were promising, but also showed that
the high computational complexity of verification for
strategic properties only allows for the analysis of
very simple models. In this paper, we propose to fo-
cus on temporal instead of strategic model checking.
This way, we lose some of the expressivity with re-
spect to which requirements can be analyzed, but we
gain on the feasibility of the verification process. We
use multi-agent graphs (Jamroga and Kim, 2023a) to
specify the agents and their interaction, and formu-
las of branching-time temporal logic CTL (Emerson,
1990) to formalize the interesting properties. Fur-
ther, we apply the state of the art model checker UP-
PAAL (Behrmann et al., 2004) to automatically ver-
ify those properties. Despite lower verification com-
plexity, the formal models of SAI still suffer from the
so called state space explosion (Clarke et al., 2018).
To mitigate it, we use the recent experimental model
reduction tool EASYABSTRACT4UPPAAL (Jamroga
and Kim, 2023b) that clusters similar states of the
formal model in a provably correct and user-friendly
way.
2 SOCIAL EXPLAINABLE AI
(SAI)
SAI Social Explainable AI (Social Explainable AI,
CHIST-ERA, 24; Contucci et al., 2022; Fuchs et al.,
2022), SAI in short, is a powerful idea whose goal
is to address important drawbacks of the currently
dominant AI approaches. First and foremost, the
current machine learning-based systems are predom-
inantly centralised. The huge size of data collections
used in the learning process, as well as the complex-
ity of the resulting AI models (typically, deep neural
networks), make the resulting AI systems effectively
black boxes, i.e., systems that do their job remarkably
well, but resist deeper interpretation by users and even
by machine learning experts. This naturally raises
issues of safety and trustworthiness. Moreover, that
often requires to store a large collection of sensitive
data in a single, central location, which in turn raises
the questions of feasibility, privacy, data protection,
as well as compliance with legal regulations regard-
ing data ownership.
In contrast, SAI envisions novel machine
learning-based AI systems with the following foci:
Individuation. The main architecture is based on
“Personal AI Valets” (PAIVs) associated with hu-
man users, and each acting as the user’s proxy in
a complex ecosystem of interacting agents;
Personalisation. Each PAIV processes the data
through an explainable AI model tailored to the
specific characteristics of its user;
Purposeful interaction. The machine learning and
decision making in PAIVs is obtained through in-
teraction, starting from the local AI models and
making them interact with each other;
Human-centricity. AI algorithms and PAIV interac-
tions are driven by quantifiable models of the indi-
vidual and social behaviour of their human users;
Explainability by Design. Machine Learning tech-
niques produce explainable AI models through
quantifiable human behavioural models and net-
work science analysis.
The current attempts at building SAI (Palmieri
et al., 2023a; Palmieri et al., 2023b) use gossip
learning as the ML regime for PAIVs (Social AI
gossiping. Micro-project in Humane-AI-Net, 2022;
Heged
¨
us et al., 2019; Heged
¨
us et al., 2021). An
experimental simulation tool to assess the effective-
ness of the process and functionality of the result-
ing AI components is available in (Lorenzo et al.,
2022). In this paper, we focus on modeling the multi-
agent interaction in the learning process, and for-
mal verification of the interaction by model checking.
We model the network of PAIVs as an asynchronous
multi-agent graph (Jamroga and Kim, 2023a), MAS
graph in short, and formalise its properties as formu-
las of branching-time temporal logic CTL (Emerson,
1990). Then, we use the state-of-art model checker
UPPAAL (Behrmann et al., 2004) to verify interesting
properties of SAI, and the recent experimental model
reduction tool EASYABSTRACT4UPPAAL (Jamroga
and Kim, 2023b) to mitigate the complexity of the
verification process.
The formal framework is introduced in Section 3.
In Section 4, we present our MAS graphs for SAI,
including models of possible adversarial behaviors,
inspired by (Kurpiewski et al., 2023). In Section 5,
ICAART 2024 - 16th International Conference on Agents and Artificial Intelligence
150

we formalise several properties and conduct model
checking experiments.
3 FORMAL FRAMEWORK
We will now present a brief overview of the formal
machinery used in the rest of the paper. For more de-
tails and in-depth discussions, we refer the interested
reader to (Emerson, 1990; Jamroga and Kim, 2023a;
Jamroga and Kim, 2023b).
3.1 Agent Graphs and MAS Models
MAS graphs and Templates. To specify the possible
behaviours of the system, we use MAS graphs (Jam-
roga and Kim, 2023a), based on standard models of
concurrency (Priese, 1983), and compatible with UP-
PAAL model specifications (Behrmann et al., 2004).
A MAS graph is a multiset of agent graphs that
can share a set of global variables. Each agent graph
includes finitely many locations and private vari-
ables (with distinguished initial location and initial
evaluation that maps variables to initial values from
their domain) which, together, define its local state
space. Moreover, edges between locations determine
the local transition relation. Each edge can be la-
belled with a randomized selection command (a pair
of variable and range, from which it can bound to a
value), boolean precondition (a condition over vari-
ables, which must hold if the edge is to be taken), syn-
chronisation command (the name of a synchroniza-
tion channel followed by ‘!’ for sending or ‘?’ for
receiving), and/or a postcondition updating the values
of some variables. A synchronizing edge can only be
taken with a complementary one in another agent. An
example agent graph is shown in Fig. 1. The locations
are graphically depicted as nodes, an initial location is
marked with double circle.
A MAS template treats each agent graph as a tem-
plate, and specifies the number of its instances that
occur in the verified system (each differing only by
the value of the special parameter variable id).
MAS Models. Every MAS graph G can be trans-
formed to its combined MAS graph representing the
behaviour of the system as a whole. Technically,
the combined MAS graph is a single agent graph
comb(G) given by the asynchronous product of the
agent graphs in G.
2
Each location in comb(G) is a
tuple of agents’ locations in G. Moreover, the set of
2
By construction, all synchronisation-type edge labels
are disposed of in combined MAS graph.
Figure 1: A template of AI agent in meta-configuration:
reversed-cascade-network, sharing via average, no attacker.
variables in comb(G) is the union of all variables oc-
curring in G. A global model of G is obtained from
comb(G) by unfolding it to the labelled transition sys-
tem where states are defined by combined locations
and valuations of all the variables. Such models are
usually huge due to the well-known state-space ex-
plosion. Very often, this is the main bottleneck of the
verification procedure.
More formally, model M is a tuple (St,I, →
,AP, L), where St is the finite set of global states,
I ⊆ St non-empty set of initial states, →⊆ St × St
serial transition relation, AP set of atomic proposi-
tions and L : St → 2
AP
labelling function. A path
is an infinite sequence of states λ = s
0
,s
1
,. . ., such
that s
i
∈ St and s
i
→ s
i+1
for every i; by λ[i] = s
i
and λ[i, ∞] = s
i
,s
i+1
.. . we denote i-th state and suf-
fix starting from i-th state in λ respectively. A set of
all paths in M that start from state s is denoted by
Paths(s).
3.2 Branching-Time Logic ACTL
To express requirements, we use the universal frag-
ment of the branching-time logic CTL (Emerson,
1990), denoted ACTL, with A (“for every path”) as
the only path quantifier. The syntax for ACTL is
Scalable Verification of Social Explainable AI by Variable Abstraction
151

given by the following grammar:
ϕ ::= true | false | p | ¬p | ϕ∧ ϕ | ϕ ∨ ϕ | Aψ
ψ ::= Xϕ | ϕUϕ | ϕRϕ
where ϕ and ψ are state and path formulae respec-
tively, p is an atomic proposition, and X, U, R stand
respectively for “next,” “until,” and “release.”
Let M = (St, I,→,AP, L) be a model and p ∈ AP
be an atomic proposition. The semantics of ACTL is
given with respect to states s and paths λ in a model
M:
M, s |= p s iff p is on the list of labels L(s);
M, s |= ¬p iff p is not on the list of labels L(s);
M, s |= Aψ iff, for each λ ∈ Paths(s), we have M,λ |=
ϕ;
M, λ |= ϕ iff, M, λ[0] |= ϕ;
M, λ |= AXϕ iff, M, λ[1] |= ϕ;
M, λ |= ϕ
1
Uϕ
2
iff, there is i ≥ 0 with M, λ[i, ∞] |= ϕ
2
,
and for all 0 ≤ j < i it holds M, λ[ j, ∞] |= ϕ
1
;
M, λ |= ϕ
1
Rϕ
2
iff, for all i ≥ 0, we have M, λ[i, ∞] |=
ϕ
2
or exists j ≥ 0 such that M, λ[ j, ∞] |= ϕ
1
and
M, λ[k,∞] |= ϕ
2
for all k ≤ j.
The clauses for Boolean connectives are standard.
Additional temporal operators “sometime” and “al-
ways” can be defined as Fϕ ≡ >Uϕ and Gϕ ≡ ϕR ⊥
respectively. Model M satisfies formula ϕ (written
M |= ϕ) iff M, s
0
|= ϕ for all s
0
∈ I.
It must be noted that UPPAAL uses a nonstandard
interpretation of formulas using the AF combination
of quantifiers, as it admits non-maximal runs in the in-
terpretation of “for every path.” Fortunately, we have
come up with a fix that restores the standard seman-
tics. We present it in Section 5.
3.3 User-Friendly State Abstraction
To mitigate the impact of state-space explosion, we
use state abstraction, i.e., a method that reduces the
state space by clustering similar concrete states in the
MAS model into a single abstract state. In order for
the scheme to be practical, it must be easy to use.
Moreover, it has to avoid the generation of the full
concrete model, i.e., circumvent the complexity bot-
tleneck. This has been recently implemented in an
open-access tool EASYABSTRACT4UPPAAL (Jam-
roga and Kim, 2023b) that employs the abstrac-
tion scheme of (Jamroga and Kim, 2023a), and pro-
duces specifications of two abstract models: a may-
abstraction (that overapproximates the concrete states
and transitions) and a must-abstraction (that underap-
proximates them). Consequently, if a universal CTL
formula is true in the may-abstraction, then it must
be true in the concrete model, and if it is false in the
must-abstraction, then it must be false in the concrete
model (Jamroga and Kim, 2023a).
Variable Removal. The abstraction scheme behind
EASYABSTRACT4UPPAAL is based on the assump-
tion that the verifier gets a domain expert’s advice
about what information to remove from the MAS
graph. The most natural way is to select some model
variables for removal, or merge those variables into
a new variable containing less information than the
original ones.
In the simplest variant, the abstraction concerns a
complete removal of some variables from the MAS
model. For example, one might remove completion,
mstatus from the agent graph in Fig. 1, i.e., the
agent’s memory of how much data was collected and
whether the learning went well. The abstraction pro-
cedure takes the combined MAS graph comb(G), for
each location ` (starting from `
0
) computes an approx-
imation of the reachable values for the set of selected
variables V , and then processes the edges of comb(G)
by substituting the occurrences of v ∈ V with the val-
ues u ∈ appr(v,`) in the approximation set of the in-
cident source location `.
3
If appr(v,`) overapproxi-
mates (resp. underapproximates) the actual reachable
values of v at `, then the resulting model is a may
(resp. must)-abstraction of G.
Variable Merge and Scoping. More generally, a sub-
set of variables can be merged into a fresh variable by
means of a user-defined mapping function.
Additionally, the user can specify the scope of the
abstraction, i.e., a subset of locations in the MAS
graph where the abstraction will be applied.
Abstraction on MAS Templates. In some cases,
approximation of variable domains on the combined
MAS graph is computationally infeasible due to the
size of the combined MAS graph. Then, one can try to
compute the approximation directly on the MAS tem-
plate by the right approximation of the synchroniza-
tion edges. However, this might result with largely
suboptimal abstract models, i.e., ones more likely to
produce inconclusive verification results.
4 FORMAL MODELS OF SAI
In this section we describe our new formal models of
SAI. The models are aimed at representing both the
3
Internally, some linear order ≺ is defined over the vari-
able set Var. Intuitively, this allows to treat any variable
subset V ⊆ Var and its evaluation as vectors. Thus, a pair of
variables v, v
0
∈ V , s.t. v ≺ v
0
, can be substituted with values
u and u
0
iff {u,u
0
} ∈ appr({v,v
0
},`).
ICAART 2024 - 16th International Conference on Agents and Artificial Intelligence
152

intended and adversarial behavior of PAIVs. The for-
mer is modeled through so called “honest” AI agents.
For the latter, we use two kinds of malicious AI
agents: an “impersonator” and a “man-in-the-middle”
attacker. Our new models have been strongly in-
spired by (Kurpiewski et al., 2023), where SAI were
specified using Asynchronous Multi-Agent Systems
(AMAS) and verified using the STV model checker.
In this work, we use MAS Graphs for the modelling
part, and the UPPAAL model checker for verification.
MAS Graphs allow for more flexibility than AMAS
in the specification of the formal model. Moreover,
UPPAAL better avoids the state-space explosion than
STV. In consequence, we have been able to create and
verify richer and more sophisticated models of SAI
than (Kurpiewski et al., 2023), e.g., by considering
different topologies of sharing the machine learning
models between agents. Moreover, temporal verifi-
cation of MAS Graphs admits practical model reduc-
tions of (Jamroga and Kim, 2023a; Jamroga and Kim,
2023b), which we employ in this paper to mitigate the
complexity of the verification process.
A preliminary take on MAS Graph-based models
and abstraction for SAI was reported in (Jamroga and
Kim, 2023b), but that was only done to demonstrate
the functionality of the abstraction tool.
We begin with a high-level overview of the system
and AI agent behaviour. Then, we provide several
variants for the lower-level specification, which will
further establish the scope for experiments in Sec-
tion 5.
4.1 AI Agents
The system is composed of a number AI agents, each
having a unique identifier. An example agent graph
template for an AI agent is shown in Fig. 1.
The local model of an AI agent involves three sub-
sequent phases: data gathering, learning and sharing.
During the data gathering phase agent collects the
data required for the learning. The amount of data is
represented by a local variable data, which is incre-
mented by taking the corresponding transition multi-
ple times. When the gathering phase is finished, the
data gets processed and categorized as either incom-
plete, complete or excessive. Next, in the learning
phase, the agent proceeds with training its machine
learning component (ML-component in short), based
on the previously acquired data. Depending on data
completeness and the number of learning iterations,
the quality of the ML-component is adjusted. No-
tably, the learning process does not affect the qual-
ity when no data has been acquired, and overtraining
generally decreases the quality of the component.
It is also possible for an agent to completely skip
data gathering and/or learning phases.
Afterwards, in the sharing phase, the agent shares
its ML-component with other AI agents. Here we
assume the case of asymmetric exchange, where
the sender sends its ML-component and the receiver
merges it with its own component. Which pairs of
agents can communicate (and in which order) is spec-
ified by the network topology (see the examples in
Section 4.2). Finally, the agent can return to the learn-
ing phase, or refrain from doing so.
4.2 Scenarios
We consider several scenarios with different meta-
parameters: the network topology (ring, tree,
reversed-cascade), attacker type (none, man-in-the-
middle, impersonator), and the operator for comput-
ing the outcome of sharing (minimum, average, max-
imum).
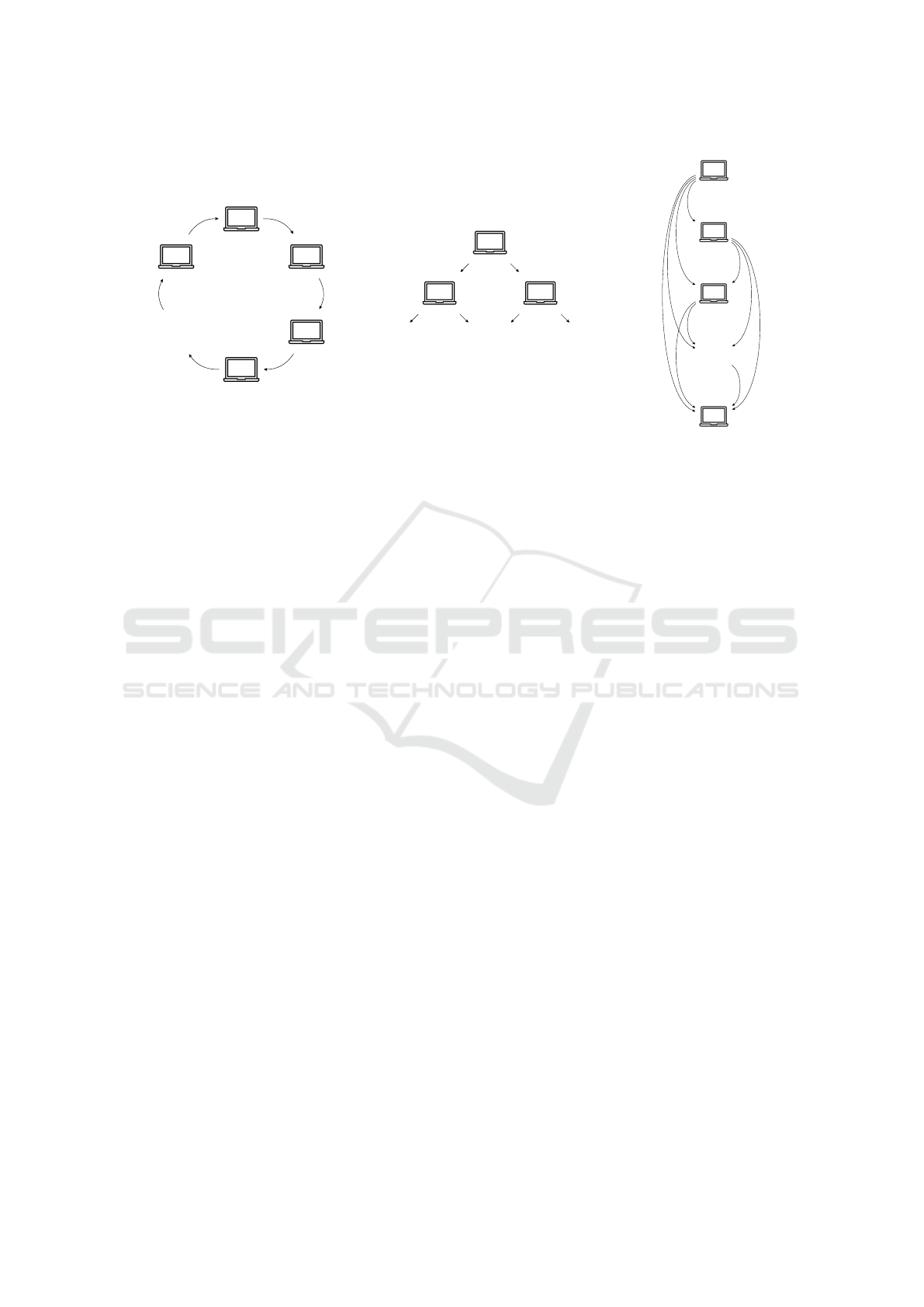
Topology. The network topology outlines the struc-
ture of communication between AI agents during the
sharing phase. Selected variants are described below
(see Fig. 2 for intuition):
• In the ring-network, each agent communicates
with the pair of adjacent agents. Without loss of
generality, we assume that agents with odd iden-
tifiers first transmit their model quality and then
proceed to receive incoming models (and con-
versely for ones with odd identifiers).
• In the tree-network, messages are sent top down,
starting from a distinguished node, called the root.
Each node has a single parent and can have up to
n-children, where n denotes the arity. Here, we
assume the case of complete binary trees, where
all levels, except possibly the last, are filled.
• In the reversed-cascade-network, each node with
identifier i receives messages from those with
id < i and then can start sending to those with
id > i.
Sharing Method. When an agent receives a machine
learning component, it merges the component with
that of its own. We specify the merging outcome by
means of its effect on the resulting ML-component
quality, taking either the maximum, the average, or
the minimum of the original and the received model
quality.
Attacker. In addition to a scenario with no attacker,
where all agents are honest and follow the protocol
as expected, we analyse those with an attacker. Here,
we utilize two well-known types of adversary: man-
in-the-middle and impersonator. Of course, this does
not constitute a complete threat analysis, but already
Scalable Verification of Social Explainable AI by Variable Abstraction
153

1
2
3
4
...
n
1
2 3
... ... ...
1
2
3
...
n
Figure 2: Informal illustration for possible message flow in (from left to right): ring, tree and reversed-cascade networks.
shows the way towards the verification of resistance
against other, more sophisticated attacks.
• Man-in-the-middle attacker can intercept the com-
munication and re-direct it, but without any
changes on the message content. As such
an attacker may also abstain from interception,
all executions that were present in the meta-
configuration without an attacker will also be
present here.
• Impersonator attacker acts in place of a selected
AI agent. It only participates in the sharing
phase(s) and exchanges messages as prescribed
by its role. However, in contrast to an hon-
est AI agent, an impersonator can forge an ML-
component of any chosen quality prior to each
transfer.
Altogether this gives 27 variants of MAS templates
(see Fig. 5 for a graphical illustration), each being pa-
rameterized by the number of AI agents. A collection
of instances from the same MAS template makes up a
family of models. We use terms meta-configuration
and t-configuration when referring to actual values
of meta-parameters and template-parameters respec-
tively.
5 EXPERIMENTS
We have performed a series of experiments with
aforementioned 27 families of SAI models. The ex-
periments were conducted using UPPAAL v4.1.24 and
EASYABSTRACT4UPPAAL on a machine with In-
tel i7-8665U 2.11 GHz CPU, 16 GB RAM, running
Ubuntu 22.04. The source code of the models (both
concrete and abstract), as well as detailed results, can
be found at https://tinyurl.com/sai-abstraction.
5.1 Requirement Specification
Deadlock-Freeness. Deadlock occurs when neither
system component can proceed. In other words, it is
a global state with no outgoing transitions. Deadlock-
freeness is achieved when the system is guaran-
teed to never reach a deadlock state. While some
model checkers provide a special atomic proposition
deadlock dedicated for deadlock states, the property
can be also simulated within “vanilla” ACTL
∗
. For
example, we can select some agent’s location(s) and
verify that it gets visited infinitely many times via the
following formula:
ϕ
1
≡ AG(false ⇒ AF
_
i∈AI
wait
i
)
Note that location “wait” of the AI template in Fig. 1
has a self-loop, and thus it is guaranteed that there
will be at least one outgoing transition. The above is a
stronger requirement than AG¬deadlock; thus, when
the former holds the latter must hold as well.
Eventually-Win. Suppose that we want to verify if
the SAI network is guaranteed to eventually reach
a “winning” state where the average ML-component
quality of the involved AI agents is greater than 0.
This can be formalized by
ϕ
2
≡ AF(avg(mqual
i
)
i∈AI
> 0)
In other words, we check if the system guarantees
progress to a state better than the initial one. Clearly,
other interpretations of a “win” can be interesting too.
Similar queries can also facilitate the analysis of sys-
tem modifications and design improvements. In order
ICAART 2024 - 16th International Conference on Agents and Artificial Intelligence
154

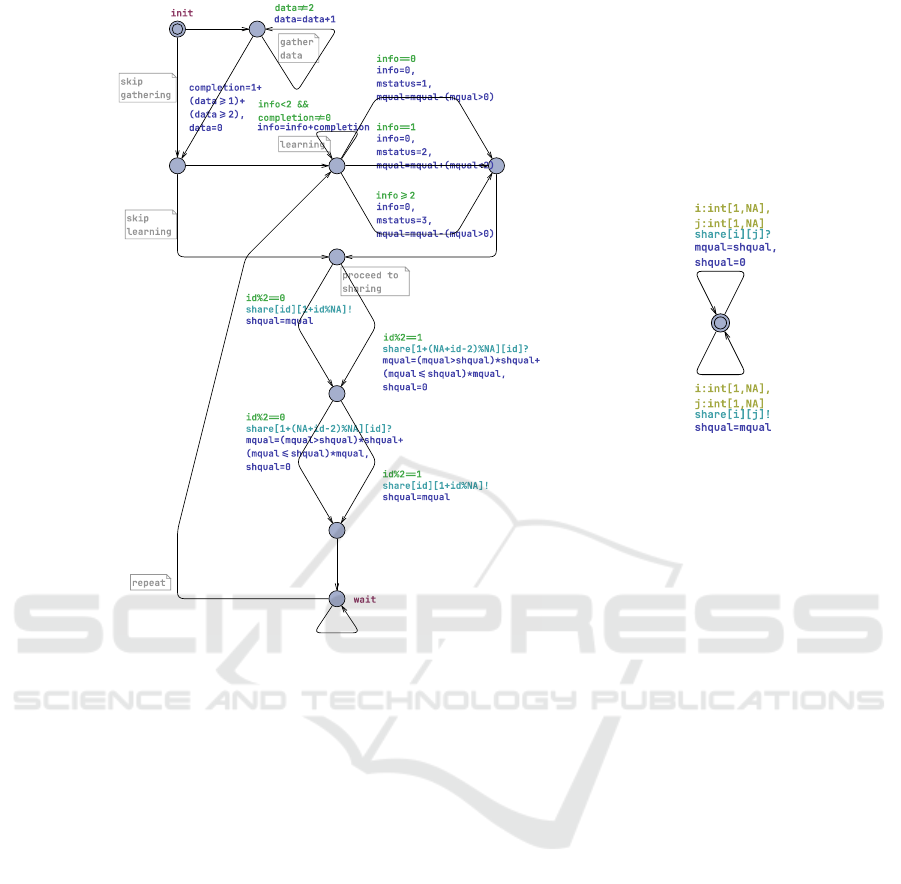
Figure 3: A template of AI agent (left) and Attacker (right) in meta-configuration: ring-network, sharing via min, man-in-the-
middle attacker. Notably, the specification of man-in-the-middle attacker remains the same for all meta-configurations.
to force standard interpretation of AF formulas we in-
troduce a benign modification to the models (just be-
fore verification) and appended each location with an
invariant over clock variable. Note, that doing had
no side effect on the state-space, and merely filtered
non-maximal paths.
Flawless-Wins. In a multi-agents system the goals
of different agents (or their coalitions) are often con-
flicting. Therefore, a guaranteed achievement of all
the goals (within every execution, no matter the cho-
sen action) seldom happens. One of the common ap-
proaches is to reason about strategic abilities: whether
there exists a strategy for the coalition that secures
a win. Despite the limitation of UPPAAL that ad-
mits only verification of temporal properties, some re-
sults can still be obtained. For example, (Jamroga and
Kim, 2023a) showed that, if the winning condition is
free of modal operators, one can manually fix the can-
didate strategy, and then using UPPAAL check if it en-
forces a win. Here, instead of trying to guess the full
strategy, we verify whether the achievement of certain
sub-goals will ultimately guarantee winning. That is,
we refine a previously introduced property and nar-
row down the scope of executions, where the winning
state is expected to eventually occur. The formula
AG(
^
i∈AI
flawless-learner
i
⇒ ϕ
2
)
says that if all AI agents performed the learning
phase perfectly then ϕ
2
is eventually guaranteed.
For technical reasons, we also need to ignore runs,
where agents self-loop in “wait” location, and ex-
press “flawless-learning” by persistent evaluation of
mstatus
i
=2. These enhancements result in formula
ϕ
3
≡ AG((
^
i∈AI
0
mstatus
i
=2) ⇒
AF((
^
i∈AI
0
mstatus
i
=2) ⇒
(avg(mqual
i
)
i∈AI’
> 0)))
where AI
0
= AI\{impersonated} in the meta-
configurations with impersonator, and AI
0
= AI oth-
erwise.
Scalable Verification of Social Explainable AI by Variable Abstraction
155

Figure 4: A template of AI agent (left) and Attacker (right) in meta-configuration: tree-network, sharing via max, impersonator
attacker. Note that specification of impersonator corresponds to sharing phase of AI agent in relevant meta-configuration.
Attacker
Topology
Sharing
Attacker
Topology
Sharing
Attacker
Topology
Sharing
Figure 5: Verification results for model checking (from left to right): ϕ
1
, ϕ
2
and ϕ
3
. Nodes in the “cube”
stand for possible meta-configurations of SAI models, (x, y, z) where coordinates map to specific element of
(none, man-in-the-middle, impersonator) × (ring, tree, r-cascade) × (min, avg, max). Each node is denoted by: black-filled
circle if given formula was satisfied on all attempted t-configurations, half-filled circle if it is satisfied for some, and empty
circle if satisfied on none of them.
5.2 Dealing with State-Space Explosion
We have utilised the open-source experimental ab-
straction tool EASYABSTRACT4UPPAAL
4
, which au-
tomatically generates reduced formal models after ap-
plying the specified variable-based abstractions. A
4
https://tinyurl.com/EasyAbstract4Uppaal
notable advantage of the tool is that it creates models
that are portable. The output models are specified in
the very same modular format as the input ones, and
can be therefore opened, inspected and further used
in UPPAAL; there is no side effect backwards depen-
dence on a third-party tool afterwards.
We have employed the following abstractions:
ICAART 2024 - 16th International Conference on Agents and Artificial Intelligence
156

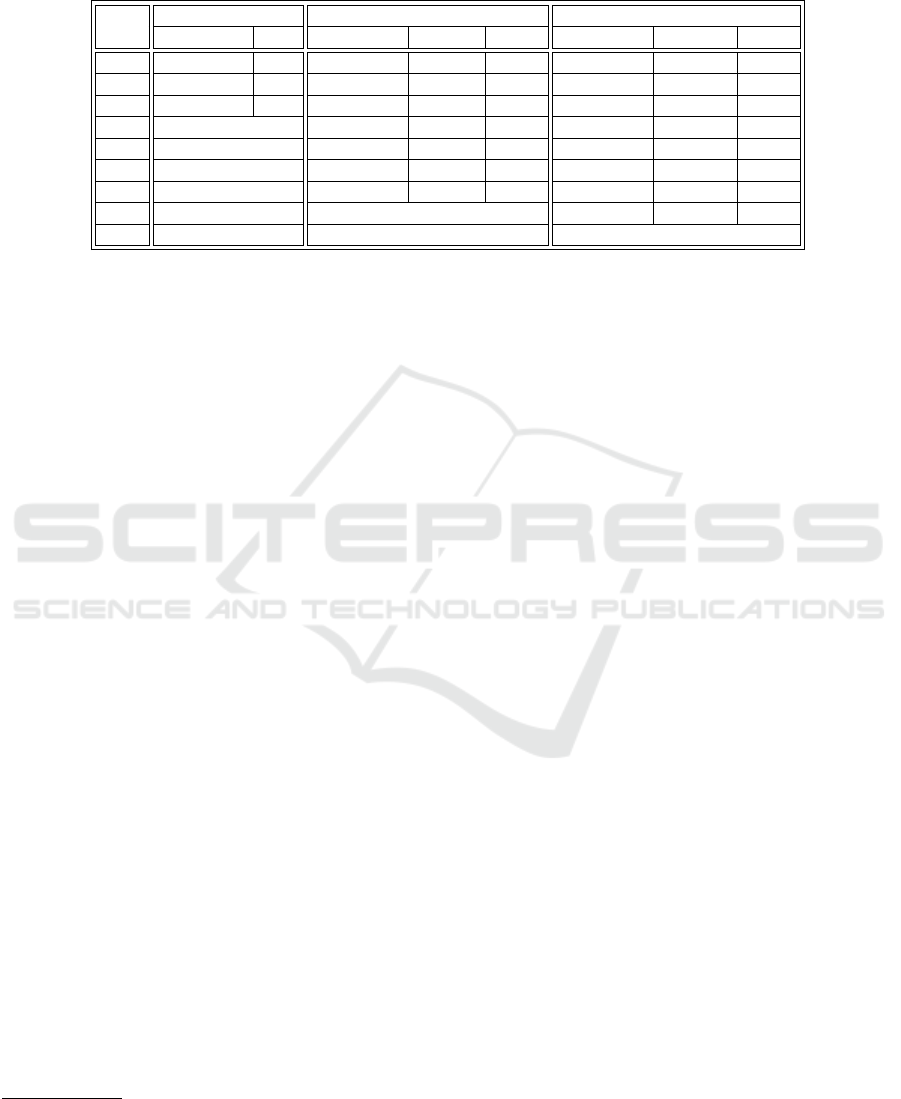
Table 1: Results of model checking ϕ
3
on meta-configuration with ring-network, sharing via average, no attacker. The column
“#Ag” denotes the t-configuration (number of AI agents), “#St” number of states in global model, “t” avg. verification time
in seconds, and “Reduct” shows the level of reduction in the state space. For all reported cases, the time for computing an
abstraction itself was negligible (less than 1 sec) and thus we omit it from the details.
#Ag
Concrete Abstract A1 Abstract A2
#St t #St Reduct t #St Reduct t
2 5832 0.1 81 72 0 53 110.03 0
3 363 013 2.3 625 580.8 0 327 1110.1 0
4 25 216 704 213 4851 5198.2 0 1995 12 639.9 0
5 memout 37 790 – 0.2 12 014 – 0.1
6 memout 299 226 – 1.9 73 154 – 0.7
7 memout 2 374 295 – 23.7 443 593 – 5.9
8 memout 19 059 651 – 251.4 2 724 787 – 46.1
9 memout memout 16 672 836 – 329.1
10 memout memout memout
A1. Removes variables completion and mstatus
from AI agent templates;
A2. Removes variables data, completion, mstatus
and info from AI agent templates;
We use the former for the verification of ϕ
1
and the
latter for ϕ
3
. In both cases, overapproximating may-
abstractions were conclusive.
5
5.3 Results and Discussion
An aggregated view of the experimental results is
shown in Fig. 5. We have been able to perform the
verification of ϕ
1
(resp. ϕ
3
) on concrete models with
up to 4 AI agents, and up to 8 (resp. 9) AI agents after
applying abstraction A1 (resp. A2). Notably, cases
when ϕ
1
and ϕ
2
were not satisfied arise only for the
t-configuration with one AI agent and only for meta-
configurations that involved the Impersonator attacker
or (in case of ϕ
1
) the tree topology of the SAI net-
work.
The verification of ϕ
2
resulted with “property not
satisfied” in all the studied cases, and the model
checker was able to quickly find and report a witness-
ing counter-example. Therefore, abstraction was not
needed for this instance of verification.
Reasoning whether the same result would hold for
a whole family of models (i.e., on every possible t-
configuration) is generally much more challenging if
feasible at all. To the best of our knowledge there
exists no universally applicable approach to achieve
that. Nonetheless, a common conjecture
6
suggests
that often it suffices to look for a fairly small (vio-
lating) counter-examples. And whilst an absence of
such counter-examples does not provide complete as-
5
Note, that attempting to verify ϕ
1
on models from A2
produces inconclusive results.
6
For example, as in (Arapinis et al., 2016).
surance, it does strengthen the confidence in the sys-
tem being compliant with the requirements.
6 CONCLUSIONS
In this paper, we have applied the formalism of MAS
graphs, together with branching-time specification of
requirements, to formally model and verify Social Ex-
plainable AI (SAI). We constructed and studied 27
variants of scalable model families, further parame-
terized by the type and number of involved AI agents.
This way, we showed how certain important prop-
erties could be specified using temporal logic and
then verified in UPPAAL. Furthermore, we used a
recently proposed user-friendly tool for practical ab-
straction EASYABSTRACT4UPPAAL to demonstrate
how to mitigate the state-space explosion. The re-
ported results are very promising: in most cases we
were able to double the number of agents that can be
handled by the model checker before running out of
memory.
In the future, we plan to conduct a more compre-
hensive analysis of the threats (e.g., consider other
types of attack models) as well as capture more nu-
anced formulas. For example, one can use temporal-
epistemic logic to express and verify starvation-
freeness, which is a much stronger requirement than
the basic notion of deadlock-freeness.
ACKNOWLEDGEMENTS
The work has been supported by NCBR Poland
and FNR Luxembourg under the PolLux/FNR-CORE
project SpaceVote (POLLUX-XI/14/SpaceVote/2023
and C22/IS/17232062/SpaceVote), by NCN Poland
under the CHIST-ERA grant CHIST-ERA-19-XAI-
Scalable Verification of Social Explainable AI by Variable Abstraction
157

010 (2020/02/Y/ST6/00064), and by the CNRS IEA
project MoSART. For the purpose of open access,
and in fulfilment of the obligations arising from the
grant agreement, the authors have applied a Creative
Commons Attribution 4.0 International (CC BY 4.0)
license to any Author Accepted Manuscript version
arising from this submission.
REFERENCES
Arapinis, M., Cortier, V., and Kremer, S. (2016). When are
three voters enough for privacy properties? In Pro-
ceedings of ESORICS, volume 9879 of Lecture Notes
in Computer Science, pages 241–260. Springer.
Behrmann, G., David, A., and Larsen, K. (2004). A tuto-
rial on UPPAAL. In Formal Methods for the Design of
Real-Time Systems: SFM-RT, number 3185 in LNCS,
pages 200–236. Springer.
Bulling, N., Goranko, V., and Jamroga, W. (2015). Logics
for reasoning about strategic abilities in multi-player
games. In Models of Strategic Reasoning. Logics,
Games, and Communities, volume 8972 of Lecture
Notes in Computer Science, pages 93–136. Springer.
Clarke, E., Henzinger, T., Veith, H., and Bloem, R., editors
(2018). Handbook of Model Checking. Springer.
Conti, M. and Passarella, A. (2018). The internet of peo-
ple: A human and data-centric paradigm for the next
generation internet. Comput. Commun., 131:51–65.
Contucci, P., Kertesz, J., and Osabutey, G. (2022). Human-
ai ecosystem with abrupt changes as a function of the
composition. PLOS ONE, 17(5):1–12.
Dolev, D. and Yao, A. C. (1983). On the security of public
key protocols. IEEE Trans. Inf. Theory, 29(2):198–
207.
Drainakis, G., Katsaros, K. V., Pantazopoulos, P., Sourlas,
V., and Amditis, A. (2020). Federated vs. centralized
machine learning under privacy-elastic users: A com-
parative analysis. In Proceedings of NCA, pages 1–8.
IEEE.
Emerson, E. (1990). Temporal and modal logic. In van
Leeuwen, J., editor, Handbook of Theoretical Com-
puter Science, volume B, pages 995–1072. Elsevier.
Fuchs, A., Passarella, A., and Conti, M. (2022). Model-
ing human behavior part I - learning and belief ap-
proaches. CoRR, abs/2205.06485.
Gollmann, D. (2011). Computer Security (3. ed.). Wiley.
Goodfellow, I. J., McDaniel, P. D., and Papernot, N. (2018).
Making machine learning robust against adversarial
inputs. Commun. ACM, 61(7):56–66.
Heged
¨
us, I., Danner, G., and Jelasity, M. (2019). Gos-
sip learning as a decentralized alternative to federated
learning. In Proceedings of IFIP DAIS, volume 11534
of Lecture Notes in Computer Science, pages 74–90.
Springer.
Heged
¨
us, I., Danner, G., and Jelasity, M. (2021). Decen-
tralized learning works: An empirical comparison of
gossip learning and federated learning. J. Parallel Dis-
tributed Comput., 148:109–124.
Jamroga, W. and Kim, Y. (2023a). Practical abstraction for
model checking of multi-agent systems. In Proceed-
ings of KR, pages 384–394.
Jamroga, W. and Kim, Y. (2023b). Practical model re-
ductions for verification of multi-agent systems. In
Proceedings of the Thirty-Second International Joint
Conference on Artificial Intelligence, IJCAI, pages
7135–7139. ijcai.org.
Kianpour, M. and Wen, S. (2019). Timing attacks on ma-
chine learning: State of the art. In IntelliSys Volume 1,
volume 1037 of Advances in Intelligent Systems and
Computing, pages 111–125. Springer.
Kumar, R. S. S., Nystr
¨
om, M., Lambert, J., Marshall, A.,
Goertzel, M., Comissoneru, A., Swann, M., and Xia,
S. (2020). Adversarial machine learning-industry per-
spectives. In IEEE Security and Privacy Workshops,
pages 69–75. IEEE.
Kurpiewski, D., Jamroga, W., and Sidoruk, T. (2023). To-
wards modelling and verification of social explainable
AI. In Proceedings of ICAART, pages 396–403.
Kurpiewski, D., Pazderski, W., Jamroga, W., and Kim, Y.
(2021). STV+Reductions: Towards practical verifi-
cation of strategic ability using model reductions. In
Proceedings of AAMAS, pages 1770–1772. ACM.
Lorenzo, V., Boldrini, C., and Passarella, A. (2022). SAI
simulator for social AI gossiping. https://zenodo.org/
record/5780042.
Ottun, A.-R., Mane, P. C., Yin, Z., Paul, S., Liyanage,
M., Pridmore, J., Ding, A. Y., Sharma, R., Nurmi,
P., and Flores, H. (2022). Social-aware federated
learning: Challenges and opportunities in collabora-
tive data training. IEEE Internet Computing, pages
1–7.
Palmieri, L., Boldrini, C., Valerio, L., Passarella, A., and
Conti, M. (2023a). Exploring the impact of disrupted
peer-to-peer communications on fully decentralized
learning in disaster scenarios. In International Con-
ference on Information and Communication Technolo-
gies for Disaster Management, ICT-DM, pages 1–6.
IEEE.
Palmieri, L., Valerio, L., Boldrini, C., and Passarella, A.
(2023b). The effect of network topologies on fully
decentralized learning: a preliminary investigation.
CoRR, abs/2307.15947.
Priese, L. (1983). Automata and concurrency. Theoretical
Computer Science, 25:221–265.
Shoham, Y. and Leyton-Brown, K. (2009). Multiagent
Systems - Algorithmic, Game-Theoretic, and Logical
Foundations. Cambridge University Press.
Social AI gossiping. Micro-project in Humane-AI-Net
(2022). Project website. https://www.ai4europe.eu/
research/research-bundles/social-ai-gossiping.
Social Explainable AI, CHIST-ERA (2021–24). Project
website. http://www.sai-project.eu/.
Toprak, M., Boldrini, C., Passarella, A., and Conti, M.
(2021). Harnessing the power of ego network layers
for link prediction in online social networks. CoRR,
abs/2109.09190.
Weiss, G., editor (1999). Multiagent Systems. A Modern
Approach to Distributed Artificial Intelligence. MIT
Press: Cambridge, Mass.
ICAART 2024 - 16th International Conference on Agents and Artificial Intelligence
158