Multi-Agent Archive-Based Inverse Reinforcement Learning by
Improving Suboptimal Experts
Shunsuke Ueki and Keiki Takadama
Department of Informatics, The University of Electro-Communications, Tokyo, Japan
Keywords:
Multi-Agent System, Reinforcement Learning, Inverse Reinforcement Learning, Maze Problem.
Abstract:
This paper proposes the novel Multi-Agent Inverse Reinforcement Learning method that can acquire reward
functions in continuous state space by improving the “suboptimal” expert behaviors. Specifically, the pro-
posed method archives the superior “individual” behaviors of the agent without taking an account of other
agents, selects the “cooperative” behaviors that can cooperate with other agents from the individual behaviors,
and improve expert behaviors according to both the individual and cooperative behaviors to obtain the better
behaviors of the agents than those of experts. The experiments based on the maze problem in a continuous
state space have been revealed the following implications (1) the suboptimal expert trajectories that may col-
lide with the other agents can be improved to the trajectories that can avoid the collision among the agents;
and (2) the number of collisions of agents and the expected return in the proposed method is smaller/larger
than those in MA-GAIL and MA-AIRL.
1 INTRODUCTION
Reinforcement Learning (RL) (Sutton and Barto,
1998) learns behaviors to maximize the expected re-
wards through trial and error in a given environment.
To obtain the optimal behavior, an appropriate reward
function should be designed, but such design is gener-
ally difficult as a size of the state-action space and/or a
complexity of environment increases. To tackle solve
this problem, Inverse Reinforcement Learning (IRL)
(Russell, 1998) was proposed to estimate the reward
function from optimal behaviors of agents called ex-
perts behaviors. Since multiple reward functions can
be derived from an expert behavior, the maximum
entropy IRL (MaxEntIRL) (Ziebart et al., 2008) was
proposed to derive an unique the reward function by
applying the maximum entropy principle. However,
MaxEntIRL works well in a discreate state space but
not in a continuous state space because the state vis-
itation frequency probabilities of “all” states should
be calculated which is impossible to cover all states
in a continuous space. To address this problem, the
sampling-based IRL with adversarial generative net-
works (Goodfellow et al., 2014) was proposed (Finn
et al., 2016) for a single agent environment, and then
Multi-Agent Adversarial IRL (MA-AIRL) was pro-
posed (Yu et al., 2019) by extending Finn’s method
to a multiagent environment. However, MA-AIRL
cannot estimates the optimal reward functions of all
agents when their expert behaviors are not optimal. In
multiagent environment, it goes without saying that
design of expert behaviors becomes difficult as the
number of agents increases and/or the environment
becomes complex because of many combinations of
cooperative behaviors. From this fact, it is crucial to
estimate the “optimal” reward functions of all agents
from their “suboptimal” expert behaviors. For this
issue, the reward function is estimated by minimiz-
ing the difference between the performance learned
from the suboptimal expert behaviors and that learned
from Nash equilibrium solutions in multiagent envi-
ronment (Wang and Klabjan, 2018). However, it is
very computationally time-consuming to calculate the
Nash equilibrium solutions, meaning that it is not re-
alistic to employ this method.
To overcome this problem, this paper proposes the
Archive Multi-Agent Inverse Reinforcement Learn-
ing (Archive MA-AIRL) which is extended from MA-
AIRL to acquire appropriate reward functions in con-
tinuous state space by improving the suboptimal ex-
pert behaviors whose computational complexity is in-
dependent of the number of agents and the size of
the state space. For this purpose, Archive MA-AIRL
archives the superior “individual” behaviors of the
agent without taking an account of other agents, se-
lects the “cooperative” behaviors that can cooperate
1362
Ueki, S. and Takadama, K.
Multi-Agent Archive-Based Inverse Reinforcement Learning by Improving Suboptimal Experts.
DOI: 10.5220/0012475100003636
Paper published under CC license (CC BY-NC-ND 4.0)
In Proceedings of the 16th International Conference on Agents and Artificial Intelligence (ICAART 2024) - Volume 3, pages 1362-1369
ISBN: 978-989-758-680-4; ISSN: 2184-433X
Proceedings Copyright © 2024 by SCITEPRESS – Science and Technology Publications, Lda.

with other agents from the individual behaviors, and
improve the suboptimal expert behaviors according to
both the individual and cooperative behaviors. To in-
vestigate the effectiveness of the Archive MA-AIRL,
this paper applies it into the continuous maze problem
This paper is organized as follows. Sections 2 and
3 describe reinforcement learning and inverse rein-
forcement learning, respectively. Section 4 proposes
the archive mechanism and Archive MA-AIRL. The
experiment is conducted and its result is discussed in
Section 5. Finally, our conclusion is given in Section
6.
2 REINFORCEMENT LEARNING
Reinforcement learning (RL) is a method in which an
agent learns a policy to maximize the reward from
trajectories by repeatedly observing a state, select-
ing an action, and acquiring a reward in the envi-
ronment. RL is modeled as Markov Decision Pro-
cesses(MDPs). In this paper, we introduce Q-learning
(Watkins and Dayan, 1992), a common method of re-
inforcement learning, in which Q values (state action
values) Q(s,a) are updated according to Eq. (1) in
the process of repeatedly observing states, selecting
actions, and obtaining rewards. We adopt the epsilon-
greedy selection method for selecting actions. In this
selection method, the agent chooses a random ac-
tion with ε probability and selects the action with the
largest Q-value with 1 − ε probability.
Q(s,a) ← Q(s, a)
+α

r + γ max
a
′
∈A(s
′
)
Q(s
′
,a
′
) − Q(s,a)

(1)
where s is the state, a is the action, s
′
is the next state,
a
′
is the next action, α (0 ≤ α ≤ 1) is the learning rate,
γ (0 ≤ γ ≤ 1) is the discount rate, r is the reward, and
A(s
′
) is the set from several reward functions..
3 INVERSE REINFORCEMENT
LEARNING
Inverse reinforcement learning (IRL) is a method for
estimating the reward function from optimal actions
by experts. IRL can be divided into three main
categories, Maximum Margin IRL (MaxMarginIRL)
(Ng and Russell, 2000), Bayesian IRL (BIRL) (Ra-
machandran and Amir, 2007), and Maximum Entropy
IRL (MaxEntIRL) (Ziebart et al., 2008). In the fol-
lowing section, we will introduce MaxEntIRL, its ex-
tension Adversarial IRL (AIRL), and furthermore, the
extension of B into a Multi-Agent System, referred to
as Multi-Agent Adversarial IRL (MA-AIRL).
3.1 Maximum Entropy IRL
(MaxEntIRL)
Maximum Entropy IRL (MaxEntIRL) is a common
method of IRL. MaxEntIRL can solve the ambiguity
of the reward function (one expert trajectory can be
acquired from several reward functions) by the maxi-
mum entropy principle. MaxEntIRL estimates the re-
ward function such that the agent trajectory and the
expert trajectory are the same. The algorithm of Max-
EntIRL is shown in Algorithm 1. The reward function
R(s) is defined by Eq. (2)
R(s) = θ
T
f
s
(2)
where θ is the parameter assigned to each state and
f
s
is the feature of the trajectory. The feature of the
trajectory f
ζ
is computed by the Eq. (3) using the
feature of the state φ(s) represented by the one-hot
vector.
f
ζ
=
∑
s∈ζ
φ(s) (3)
Maximize the entropy of the probability of exe-
cuting a certain trajectory under the parameter P(ζ|θ)
(max
θ
∑
ζ∈Z
P(ζ|θ)logP(ζ|θ)). Let the likelihood
function be
L(θ) =
∑
ζ∈Z
P(ζ|θ)
=
∑
ζ∈Z
exp(θ
T
f
ζ
)/
∑
ζ∈Z
exp(θ
T
f
ζ
) (4)
Z is the set of the agent’s trajectory. Then the
optimal parameter θ
∗
and the gradient of the log-
likelihood ∇L(θ) are as follows:
θ
∗
= argmax
θ
(
1
M
M
∑
i=1
θ
T
f
ζ
i
− log
∑
ζ∈Z
exp(θ
T
f
ζ
)
)
(5)
∇L(θ) =
1
M
M
∑
i=1
f
ζ
i
−
∑
s∈s
i
P(s
i
|θ) f
s
i
(6)
where M is the number of expert trajectories and
P(s
i
|θ) is the expected state visited frequencies (SVF)
calculated by Eq. (7) using the policy computed
π
θ
(a|s) by RL. The learning process of RL in IRL
is called inner-loop learning.
Multi-Agent Archive-Based Inverse Reinforcement Learning by Improving Suboptimal Experts
1363

Algorithm 1: MaxEntIRL.
1: Set the expert trajectory ζ
expert
.
2: Initialize the reward functions
R(s) and the reward parameters θ.
3: for cycle
:
= 0 to N
cycle
do
4: R(s) = (θ)
T
φ(s)
5: Compute policies π(s) (e.g. π(s) is calculated
by Q-learning).
6: Update reward parameters:
∇L(θ) = f
expert
−
∑
j=1
P(s
j
|θ) f
s
j
θ ← θ − α∇L(θ)
7: end for
P(s
i
|θ) =
T
∑
i=1
µ
t
(s
i
) (7)
µ
t
(s
i
) =
∑
s∈S
∑
a∈A
µ
t−1
(s)π
θ
(a|s)P(s|a,s) (8)
where T is maximum number of steps, P(s|a,s) is
state transition probability.
The parameter θ of the reward function is updated
by the product of the gradient ∇L(θ) and the learning
rate α (0 ≤ α ≤ 1).
θ ← θ − α∇L(θ) (9)
3.2 Adversarial IRL
Adversarial Inverse Reinforcement Learning (AIRL)
(Finn et al., 2016) is a form of learning and sampling-
based inverse reinforcement learning. AIRL recon-
structs the reward function based on Generative Ad-
versarial Imitation Learning (GAIL) that employs
Generative Adversarial Networks (GAN) (Goodfel-
low et al., 2014). GAIL involves a generator, which
is the agent’s policy π
θ
, and a discriminator D
ω
that
identifies pairs of states s and actions a sampled from
either the generator or an expert’s policy π
E
. Mini-
mization and maximization of θ and ω are performed
according to Equation (10).
min
θ
max
ω
E
π
E
[logD
ω
(s,a)] + E
π
θ
[log(1 − D
ω
(s,a))]
(10)
The discriminator D
ω
is expressed as D
ω
(s,a) =
exp( f
ω
(s,a))
exp( f
ω
(s,a))+q(a|s)
, where q(a|s) represents the proba-
bility computed by the generator. In AIRL, f
ω
(s,a)
is defined as f
ω,φ
= g
ω
(s
t
,a
t
) + γh
φ
(s
t+1
) − h
φ
(s
t
) to
reconstruct g
ω
(s
t
,a
t
) as the reward.
3.3 Multi-Agent Adversarial IRL
The algorithm for Multi-Agent Adversarial Inverse
Reinforcement Learning (MA-AIRL) (Yu et al.,
2019) is shown in Algorithm 2. MA-AIRL adapts the
Logistic Stochastic Best Response Equilibrium (LS-
BRE), which is well-suited for multi-agent environ-
ments, to AIRL.
π
t
(a
1
,...,a
n
|s
t
) = P
\
i
z
t,∞
(s
t
) = a
i
!
(11)
where the index i corresponds to each agent, and z
t,∞
represents the state of the t-th Markov chain at ∞
steps, calculated as follows:
z
t,(k+1)
(s
t
) ∼ P
t
i
(a
t
i
|a
t
−i
= z
t,(k)
−i
(s
t
),s
t
)
=
exp(λQ
π
t+1:T
i
(s
t
,a
t
i
,z
t,(k)
−i
(s
t
)))
∑
a
′
i
exp(λQ
π
t+1:T
i
(s
t
,a
′
i
,z
t,(k)
−i
(s
t
)))
. (12)
π
∅
represents a time-dependent policy, and
Q
π
t+1:T
i
denotes the state-action value function with
the policy entropy term added, defined as follows:
Q
π
t+1:T
i
(s
t
,a
t
i
,a
t
−i
) = r
i
(s
t
,a
t
i
,a
t
−i
)
+E
s
t+1
P(·|s
t
,a
t
)

H π
t+1
i
(·|s
t+1
)
+E
a
t+1
π(·|s
t+1
)
h
Q
π
t+2:T
i
(s
t+1
,a
t+1
)
i

. (13)
In the context of LSBRE, MA-AIRL involves
minimizing the Kullback-Leibler (KL) divergence be-
tween the probability of the expert performing trajec-
tories ζ, denoted as ˆp(ζ), and the probability of the
agent obtaining trajectories ζ, denoted as ˆp(ζ).
min
ˆ
π
1:T
D
KL
( ˆp(ζ)||p (ζ)) (14)
ˆp(ζ) =
"
η(s
1
)
T
∏
t=1
P(s
t+1
|s
t
,a
t
)π
t
−i
(a
t
−i
|s
t
)
#
·
T
∏
t=1
ˆ
π
t
i
(a
t
i
|a
t
−i
,s
t
) (15)
ˆp(ζ) ∝
"
η(s
1
)
T
∏
t=1
P(s
t+1
|s
t
,a
t
)π
t
−i
(a
t
−i
|s
t
)
#
·exp
T
∑
t=1
r
i
(s
t
,a
t
i
,a
t
−i
) (16)
ICAART 2024 - 16th International Conference on Agents and Artificial Intelligence
1364

This optimization problem can be transformed
through the entropy maximization in MaxEntIRL as
follows:
max
ω
E
ζ π
E
"
T
∑
t=1
logπ
t
(a
t
,s
t
;ω)
#
. (17)
The loss function becomes as follows:
max
ω
E
π
E
"
N
∑
i=1
T
∑
t=1
∂
∂ω
r
i
(s
t
,a
t
;ω
i
)
#
N
∑
i=1
∂
∂ω
logZ
w
i
. (18)
Similar to AIRL, we use the sampling-based esti-
mation q
θ
obtained through Z.
The discriminator learns by maximizing as fol-
lows with respect to ω.
max
ω
E
π
E
h
∑
N
i=1
log
exp( f
ω
i
(s,a))
exp( f
ω
i
(s,a))+q
θ
i
(a
i
|s)
i
+E
q
θ
h
∑
N
i=1
log
q
θ
i
(a
i
|s))
exp( f
ω
i
(s,a))+q
θ
i
(a
i
|s)
i
(19)
The generator learns by maximizing as follows
with respect to θ.
max
θ
E
q
θ
"
N
∑
i=1
f
ω
i
(s,a) − log q
θ
i
(a
i
|s)
#
(20)
In MA-AIRL, f
ω
i
,φ
i
= g
ω
i
(s
t
,a
t
) + γh
φ
i
(s
t+1
) −
h
φ
i
(s
t
) is defined to reconstruct g
ω
i
(s
t
,a
t
) as the re-
ward.
4 METHOD
4.1 Archive Multi-Agent Adversarial
Inverse Reinforcement Learning
To obtain the optimal reward function from quasi-
optimal expert trajectories, we propose Archive
Multi-Agent Adversarial Inverse Reinforcement
Learning (Archive MA-AIRL).
4.2 Archive Multi-Agent Adversarial
IRL
Archive MA-AIRL extends the MA-AIRL approach
with an archive mechanism. This mechanism archives
trajectories generated by the generator when they ex-
hibit superior performance and treats them as ex-
pert trajectories, aiming to acquire the optimal re-
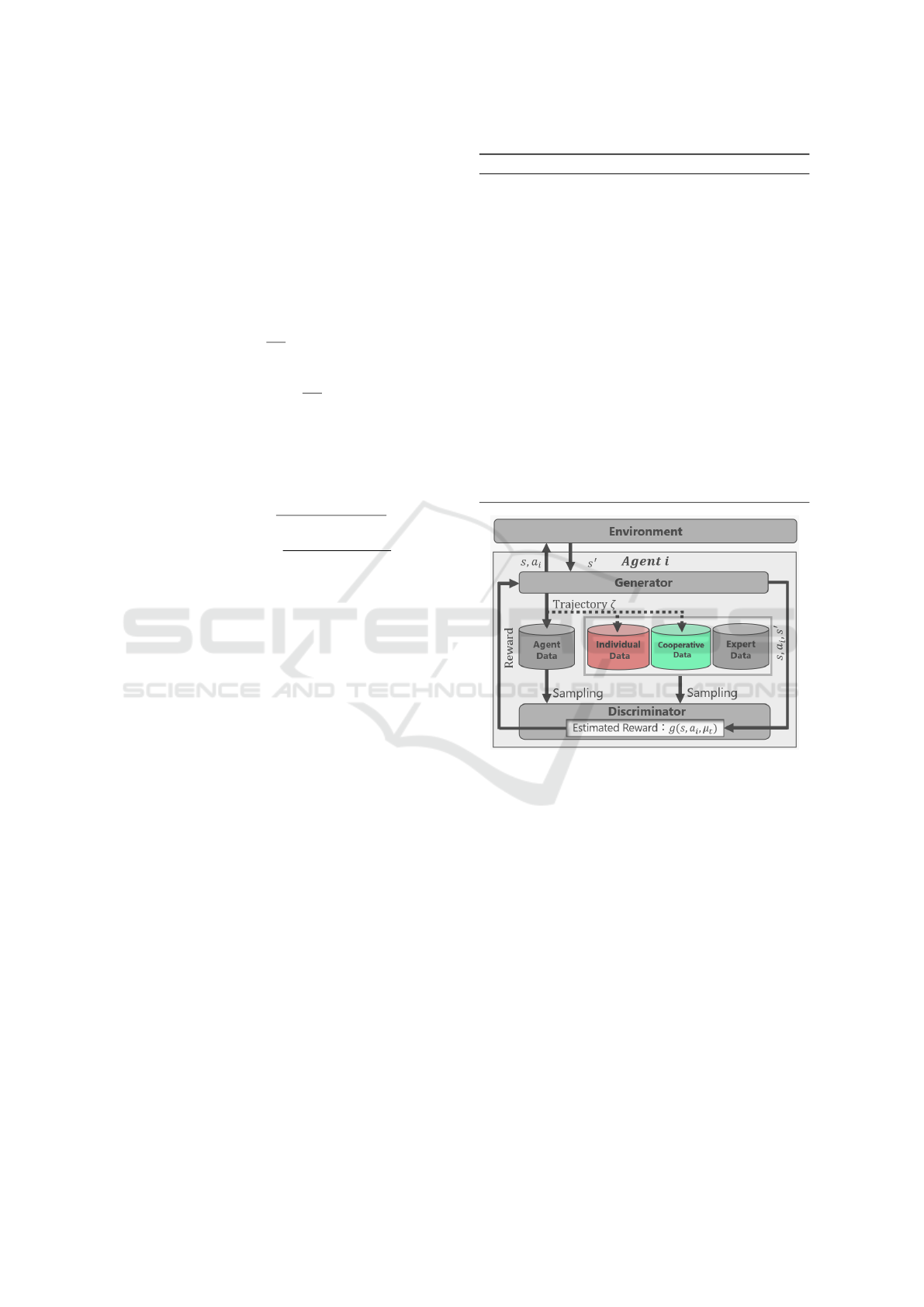
ward function. Figure 1 depicts Archive MA-AIRL.
Algorithm 2: MA-AIRL.
Set the expert trajectory D
expert
= {ζ
E
j
}.
Initialize the parameters of policies q, reward esti-
mators g and potential functions h with ω,ω, ϕ.
for iteration
:
= 0 to N
iteration
do
Sample trajectories D
π
= {ζ
j
} from π.
Sample sate-action pairs X
π
from D
π
.
Sample X
expert
from D
expert
for i
:
= 0 to N
agent
do
Update ω
i
,φ
i
to increase the objective in Eq.
19
end for
for i
:
= 0 to N
agent
do
Update reward estimates ˆr
i
(s,a
i
,s
′
) with
g
ω
i
(s,a
i
) or (logD(s, a
i
,s
′
) − log(1 −
D(s,a
i
,s
′
))).
Update ω
i
with respect to ˆr
i
(s,a
i
,s
′
)
end for
end for
Figure 1: The architecture of Archive Multi-Agent Adver-
sarial IRL.
The proposed method adds three steps to MA-AIRL:
trajectories evaluation (I), trajectories archiving (II),
and selection of expert state-action sampling for the
dataset (III).
(I) Trajectories evaluation involves assessing tra-
jectories ζ generated by the generator. Evaluation
encompasses individual evaluation functions, E
indi
,
assessing trajectories based on individual achieve-
ment of goals, and a collaborative evaluation function,
E
coop
, rating trajectories based on their collaboration
with other agents. These evaluations contribute to an
overall evaluation function, E
opt
= E
indi
+ E
coop
. For
example, in a maze problem, E
indi
might prioritize
quicker goal achievement, while E
coop
might empha-
size avoiding collisions with other agents.
(II) Trajectories archiving involves saving se-
quences with evaluated scores exceeding a certain
threshold into either individual archives D
indi
or op-
Multi-Agent Archive-Based Inverse Reinforcement Learning by Improving Suboptimal Experts
1365

timal archives D
opt
, based on evaluations from (I).
D
indi
stores trajectories with individual evaluations
E
indi
surpassing a specific threshold, while D
opt
re-
tains trajectories with overall evaluations E
entire
ex-
ceeding a set threshold. Individual and collabora-
tive archives operate on a per-agent basis to archive
trajectories. If the number of trajectories within the
archive exceeds the predefined limit set by the user,
low-rated trajectories are removed from the archive.
Consequently, the low-rated trajectories gradually get
replaced by higher-rated ones.
(III) Selection of expert state-action sampling for
the dataset involves choosing datasets used in the dis-
criminator’s training based on the following rules:
For all agents, if trajectories archived in the opti-
mal archive D
opt
exist, only D
opt
is sampled. If no
agent has trajectories archived in D
opt
but trajecto-
ries exist in the individual archive D
indi
for all agents,
either D
indi
or the initially provided expert dataset
D
expert
is sampled. If no agent has trajectories in
both D
opt
and D
indi
, only the initially provided expert
dataset D
expert
is sampled. Sampling is performed by
randomly selecting state-action pairs from the dataset.
If the number of data samples to be collected exceeds
the total number of samples in the dataset, sampling
is conducted allowing for duplication.
4.3 Algorithm
Algorithm 3 presents the algorithm for Archive MA-
AIRL. To start, provide quasi-optimal expert trajec-
tories ζ
expert
to each of the N agents. Initialize the
parameters q for the generator’s policy and g,h for
the discriminator as θ,ω,ϕ. Execute a maximum of
N
iteration
iterations as pre-set. Sample trajectories us-
ing the policy π of the generator. Execute a maximum
of N
iteration
iterations as pre-set. Sample trajectories
using the policy π of the generator. Evaluate the sam-
pled trajectories. Save trajectories with high individ-
ual evaluations into the individual archive D
indi
and
those with high overall evaluations into the optimal
archive D
opt
. Sample data from the sampled agent’s
trajectories to match the batch size for learning. For
all agents, if trajectories are archived in the optimal
archive D
opt
, only sample from D
opt
. If trajectories
archived in the optimal archive D
opt
are not available
for any agent, and trajectories archived in the indi-
vidual archive D
indi
exist for all agents, sample from
either the individual archive D
indi
or the initially pro-
vided expert dataset D
expert
. If trajectories archived
in either the optimal archive D
opt
for any agent or
the individual archive D
indi
for any agent are unavail-
able, sample solely from the initially provided expert
dataset D
expert
. Update ω
i
,φ
i
for each agent. Update
Algorithm 3: Archive MA-AIRL.
Set the expert trajectory D
expert
= {ζ
E
j
}.
Initialize the parameters of policies q, reward esti-
mators g and potential functions h with θ,ω,ϕ.
for iteration
:
= 0 to N
iteration
do
Sample trajectories D
π
= {ζ
j
} from π.
Evaluate sampled trajectories D
π
Store individual data, optimum data
to D
indi
,D
opt
Sample sate-action pairs X
π
from D
π
.
if
V
N
agent
i=0
|D
opt
i
| > 0 then
Sample X
expert
from D
opt
else if
V
N
agent
i=0
|D
indi
i
| > 0 then
Sample X
expert
from D
indi
, D
expert
else
Sample X
expert
from D
expert
end if
for i
:
= 0 to N
agent
do
Update ω
i
,φ
i
to increase the objective in Eq.
(19)
end for
for i
:
= 0 to N
agent
do
Update reward estimates ˆr
i
(s,a
i
,s
′
) with
g
ω
i
(s,a
i
) or (logD(s, a
i
,s
′
) − log(1 −
D(s,a
i
,s
′
))).
Update ω
i
with respect to ˆr
i
(s,a
i
,s
′
)
end for
end for
reward functions ˆr
i
for each agent. Also, update ω
i
with the updated reward functions ˆr
i
.
5 EXPERIMENT
Verifying whether the proposed method can acquire
the optimal trajectories of actions when given subop-
timal experts in a continuous state space maze prob-
lem.
5.1 Problem Settings
Each agent can choose to move up, down, left, right,
or take no action at each step, applying a force of 1N
in the selected direction. The environment is set with
specific start and goal locations, and a game consists
of 50 steps. After reaching the goal, agents don’t
remain in the environment. Agents cannot be out-
side the environment. The environment involves two
agents, Agent 0 and Agent 1, with Agent 0 starting
at the top left with the goal at the bottom right, while
Agent 1 starts at the top right with the goal at the bot-
tom left.
ICAART 2024 - 16th International Conference on Agents and Artificial Intelligence
1366

Figure 2: Example of expert trajectory
(a) MA-GAIL
(b) MA-AIRL
(c) Archvie
MA-AIRL
Figure 3: Results of sampled trajectory from learned policy.
The true reward function provides a +100 reward
upon reaching the goal, a negative reward based on
the distance to the goal, and a -100 reward for col-
lisions. Initially, the expert provided is trained for
10e
5
steps using ACKTR (Wu et al., 2017) in a single-
agent environment based on the true reward function
(note that collisions do not occur, so negative rewards
due to collisions are not applicable). From the learned
policy, 1000 state-action pairs are sampled.
An example of trajectories sampled from the ex-
pert’s policy is depicted in Fig. 2. Agent 0 is repre-
sented in blue, Agent 1 in green, and collisions are de-
picted in red. Since the agents collide with each other,
the expert experts are considered to be quasi-optimal.
5.2 Parameter Settings
The parameters for MA-GAIL, MA-AIRL, and
Archive MA-AIRL were set as follows: discount fac-
tor of 0.99, batch size of 500 steps (This is the number
of state-action pairs sampled from the agent data and
expert data), and 550 update iterations (total timesteps
is 2.75 × 10
6
).
5.3 Experiment Results
Fig. 3 shows the trajectories sampled from policies
learned by each method. Blue represents the trajec-
tory of Agent 0, green represents the trajectory of
Agent 1, and red indicates a collision. MA-GAIL
and MA-AIRL collide with agents, but Archive MA-
AIRL does not.
Table 1 presents the results of sampling 1000 tra-
jectories from the learned policies, showing the aver-
age expected returns calculated for each agent by us-
ing true reward and the average total number of colli-
sions in 30 seeds. Based on the expected return results
in Table 1, Archive MA-AIRL outperformed Expert,
MA-GAIL and MA-AIRL. In addition, the number of
collisions is the lowest value for Archive MA-AIRL.
These indicate that Archive MA-AIRL has acquired
a better trajectory than MA-GAIL and MA-AIRL.
The difference between Archive MA-AIRL and MA-
AIRL is archive mechanism. Therefore, the archive
mechanism can contribute to obtaining a better tra-
jectory.
Fig. 4 shows the sum of expected returns in Agent
0 and Agent 1 calculated by using true reward duar-
ing learning. Fig. 5 shows the number of collisions
between Agent 0 and Agent 1 during learning. Fig. 6
shows the average number of steps to reach the goal
for A and B during learning. These values in fig-
ures are averaging 30 seeds. From Fig. 4, it is ev-
ident that around 7000 total timesteps, it surpasses
MA-GAIL and around 10000 total timesteps, it sur-
passes MA-AIRL. Until approximately 10000 total
timesteps, there isn’t a significant difference between
MA-AIRL and Archive MA-AIRL. Fig. 5 indicates
that around 7000 total timesteps, the collision count
of MA-GAIL falls below, and around 10000 total
timesteps, it falls below the collision count of MA-
AIRL. From the result of Fig. 6, all methods are able
to learn shortest trajectories. Archive MA-AIRL and
MA-AIRL converge to the shortest step count around
10000 total timesteps, while MA-GAIL converges to
the shortest step count at 15000 total timesteps.
5.4 Discussion
From the experiment results, the proposed method
was able to outperform both the experts and the
conventional methods (MA-GAIL, MA-AIRL). The
performance improvement was confirmed as the
generated trajectories were appropriately added to
the expert’s dataset through the archive mechanism.
Archive MA-AIRL can acquire more optimal non-
collision trajectories without compromising the learn-
ing efficiency of MA-AIRL by incorporating the
Archive mechanism.
Fig. 7 shows examples of three archived trajecto-
ries. These trajectories are stored in the archive and
consist of non-collision trajectories.
Fig. 8 shows trajectories sampled from policies
for the proposed method. Until agents are learn-
ing with individual data, the behavior resembled that
of the expert, resulting in collisions. However, by
Multi-Agent Archive-Based Inverse Reinforcement Learning by Improving Suboptimal Experts
1367

Table 1: Results of the average expected returns and the average total number of collisions.
Algorithm
Expected returns
Number of Collision
Agent 0 Agent 1
Expert -220.8 -220.0 3.0
MA-GAIL -119.6 -118.8 2.0
MA-AIRL -44.0 -42.8 1.3
Archive MA-AIRL 10.6 12.5 0.7
Figure 4: Expected returns for each
algorithm
Figure 5: Number of collisions for
each algorithm
Figure 6: Number of steps to reach
goal for each algorithm.
(a) Example 1
(b) Example 2
(c) Example 3
Figure 7: Examples of archived cooperative trajs.
archiving cooperative trajectories and agents learning
with them, both Agent 0 and Agent 1 learned to nav-
igate along the edges, avoiding collisions. Addition-
ally, by improving cooperative data, Agent 0 learned
shorter non-collision trajectories.
Fig. 9 shows the changes observed during the
learning with cooperative trajectories while improv-
ing them. In Fig. 9a, agents learned the trajectory that
do not collide with agents, but Agent 0 trying to go out
of area and slowed down. In Fig. 9b, agents learned a
trajectory that do not collide with agents and Agent 0
is stay in the area. Fig. 9b’trajectory is a shorter tra-
jectoryway than Fig. 9a’s trajectory, and the archive
is appropriately improved. In Fig. 9c, agents learned
short collision trajectories. Such collision trajectories
are not in the cooperative archive, but in the process
of learning short trajectories, they learned trajectories
that collide with each other. However, In Fig. 9d,
agents learned short non-collision trajectories. As a
result, it is obvious that Agent 0 has learned the short-
est trajectory from the trajectory along the edge to the
goal without collision by improving the archive.
(a) Early stage of learning
(learning with expert data)
(b) Middle stage of learn-
ing (learning with individ-
ual data)
(c) Middle stage of learn-
ing (learning with cooper-
ative data)
(d) Late stage of learning
(learning with cooperative
data)
Figure 8: The overall process of learning (Archive MA-
AIRL).
6 CONCLUSIONS
This paper proposed Archive MA-AIRL that can ac-
quire reward functions in continuous state space by
improving the “suboptimal” expert behaviors. Specif-
ically, Archive MA-AIRL archives the superior “indi-
vidual” behaviors of the agent, selects the “coopera-
tive” behaviors from the individual behaviors, and im-
ICAART 2024 - 16th International Conference on Agents and Artificial Intelligence
1368

(a) Learns non-collision
trajectories
(b) Learns a slightly
shorter trajectories
(c) Learns short collision
trajectories
(d) Learns shorter non-
collision trajectories
Figure 9: Process of improving the archive trajectories
(Archive MA-AIRL).
proves the expert behaviors according to both the in-
dividual and cooperative behaviors to obtain the bet-
ter behaviors of the agents than those of experts. For
this purpose, the discriminator in Archive MA-AIRL
evaluates whether the behaviors generated by the gen-
erator are close to the behaviors of experts improved
from both individual and collective trajectories. To in-
vestigate the effectiveness of Archive MA-AIRL, this
paper applied it into the continuous maze problem and
the following implications have been revealed: (1)
The trajectories that can avoid the collision among
the agents can be acquired from the suboptimal expert
trajectories that may collide with the other agents (2)
Archive MA-AIRL outperforms MA-GAIL and MA-
AIRL as the conventional methods in addition to the
experts from the viewpoint of the number of collisions
of agents and expected return.
What should be noticed here is that these results
have only been obtained from the simple testbeds, i.e.,
the maze problem, therefore further careful qualifica-
tions and justifications, such as complex maze prob-
lems, are needed to generalized the obtained impli-
cations. Such important directions must be pursued
in the near future in addition to (1) an exploration of
the proper evaluation of trajectories because. the in-
correct evaluation of trajectories might deteriorate the
archived trajectories and (2) an increase of the number
of agents.
REFERENCES
Finn, C., Levine, S., and Abbeel, P. (2016). Guided cost
learning: Deep inverse optimal control via policy op-
timization. In the 33rd International Conference on
Machine Learning, volume 48, pages 49–58.
Goodfellow, I. J., Pouget-Abadie, J., Mirza, M., Xu, B.,
Warde-Farley, D., Ozair, S., Courville, A., and Ben-
gio, Y. (2014). Generative adversarial nets. In Ad-
vances in Neural Information Processing Systems,
pages 2672–2680.
Ng, A. Y. and Russell, S. (2000). Algorithms for inverse re-
inforcement learning. In the 17th International Con-
ference on Machine Learning, pages 663–670.
Ramachandran, D. and Amir, E. (2007). Bayesian in-
verse reinforcement learning. In the 20th international
joint conference on Artifical intelligence, pages 2586–
2591.
Russell, S. (1998). Learning agents for uncertain environ-
ments. In the eleventh annual conference on Compu-
tational learning theory, pages 101–F103.
Sutton, R. S. and Barto, A. G. (1998). Reinforcement learn-
ing: An introduction. A Bradford Book.
Wang, X. and Klabjan, D. (2018). Competitive multi-
agent inverse reinforcement learning with sub-optimal
demonstrations. In the 35th International Conference
on Machine Learning, volume 80, pages 5143–5151.
Watkins, C. J. C. H. and Dayan, P. (1992). Q-learning. Ma-
chine Learning, 8:279–292.
Wu, Y., Mansimov, E., Liao, S., Grosse, R., and Ba, J.
(2017). Scalable trust-region method for deep rein-
forcement learning using kronecker-factored approx-
imation. In the 31st International Conference on
Neural Information Processing Systems, pages 5285–
5294.
Yu, L., Song, J., and Ermon, S. (2019). Multi-agent ad-
versarial inverse reinforcement learning. In the 36th
International Conference on Machine Learning, vol-
ume 97, pages 7194–7201.
Ziebart, B. D., Maas, A., Bagnell, J., and Dey, A. K. (2008).
Maximum entropy inverse reinforcement learning. In
the 23rd AAAI Conference on Artificial Intelligence,
pages 1433–1438.
Multi-Agent Archive-Based Inverse Reinforcement Learning by Improving Suboptimal Experts
1369