Optimization and Learning Rate Inﬂuence on Breast Cancer Image

Classiﬁcation

Gleidson Vinicius Gomes Barbosa

1 a

, Larissa Ferreira Rodrigues Moreira

1, 2 b

Pedro Moises de Sousa

1 c

, Rodrigo Moreira

1 d

and Andr

e Ricardo Backes

3 e

Institute of Exacts and Technological Sciences, Federal University of Vic¸osa, Rio Parana

ıba-MG, Brazil

Faculty of Computing (FACOM), Federal University of Uberl

andia, Uberl

andia-MG, Brazil

Department of Computing, Federal University of S

ao Carlos, S

ao Carlos-SP, Brazil

Keywords:

Breast Cancer, CNN, Explainable, Inﬂuence of Factors, Classiﬁcation.

Abstract:

Breast cancer is a prevalent and challenging pathology, with signiﬁcant mortality rates, affecting both women

and men. Despite advancements in technology, such as Computer-Aided Diagnosis (CAD) and awareness

campaigns, timely and accurate diagnosis remains a crucial issue. This study investigates the performance

of Convolutional Neural Networks (CNNs) in predicting and supporting breast cancer diagnosis, considering

BreakHis and Biglycan datasets. Through a factorial partial method, we measured the impact of optimization

and learning rate factors on the prediction model accuracy. By measuring each factor’s level of inﬂuence on

the validation accuracy response variable, this paper brings valuable insights into the relevance analyses and

CNN behavior. Furthermore, the study sheds light on the explainability of Artiﬁcial Intelligence (AI) through

factorial partial performance evaluation design. Among the results, we determine which and how much the

hyperparameters tunning inﬂuenced the performance of the models. The ﬁndings contribute to image-based

medical diagnosis ﬁeld, fostering the integration of computational and machine learning approaches to en-

hance breast cancer diagnosis and treatment.

1 INTRODUCTION

Although the cancer mortality rate is declining (Ben-

hammou et al., 2020), it represents the greatest barrier

to increasing life expectancy (Sahu et al., 2023), es-

pecially for women, where breast cancer accounts for

30% of the incidence (Clement et al., 2022). Breast

cancer is a pathology caused by the uncontrolled

spread of abnormal cells in the breast (dysplasia),

causing tumors that can invade other organs (Ben-

hammou et al., 2020). Although rare, breast cancer

can also occur in men with about 1% of cases (Alqah-

tani et al., 2022).

Despite the advancement of technology concern-

ing the treatment and diagnosis of breast cancer and

annual incentives with campaigns to carry out exams,

this pathology remains a major problem in our soci-

https://orcid.org/0009-0000-2159-335X

https://orcid.org/0000-0001-8947-9182

https://orcid.org/0000-0003-4563-0033

https://orcid.org/0000-0002-9328-8618

https://orcid.org/0000-0002-7486-4253

ety, being the most prevalent type of cancer in women

and and second in men (Batra et al., 2020)(Sahu et al.,

2023). Conventional exams require the careful anal-

ysis by a pathologist, consequently resulting in long

waiting periods from the exam to scheduling the next

appointment to present the diagnosis, considering all

procedures performed by the Brazilian Uniﬁed Health

System (SUS). Time is crucial for the patient as there

is a continuous proliferation of abnormal cells (INCA,

2021).

Furthermore, the analysis of images by the pathol-

ogist is prone to error due to eye fatigue, human error,

and device-dependent inﬂuences, which hinders such

diagnoses. Therefore, pathologists rely on Computer-

Aided Diagnosis (CAD) to assist in the task of identi-

fying and classifying problematic tissues using com-

putational resources in this task (Benhammou et al.,

2020)(Yu et al., 2023)(Sahu et al., 2023).

To achieve this, in addition to improving CAD

methods, it is important to evolve machine learn-

ing techniques to increase the accuracy rate of such

diagnoses (Backes, 2022)(Rodrigues Moreira et al.,

2023)(Gautam, 2023). Therefore, this paper proposes

792

Barbosa, G., Moreira, L., Moises de Sousa, P., Moreira, R. and Backes, A.

Optimization and Learning Rate Inﬂuence on Breast Cancer Image Classiﬁcation.

DOI: 10.5220/0012507100003660

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 19th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2024) - Volume 3: VISAPP, pages

792-799

ISBN: 978-989-758-679-8; ISSN: 2184-4321

to evaluate the performance of computational tech-

niques for predicting and supporting the diagnosis

of breast cancer using two relevant datasets. To ac-

complish this task, we employed the partial facto-

rial method and carried out experiments to measure

the impact of two factors (optimization and learning

rate) and their levels (0.001 and 0.0001) on the val-

idation accuracy response variable. This method en-

ables us to identify which factor is more relevant to

the validation accuracy variable, shedding light on is-

sues of interpretability of Convolutional Neural Net-

work (CNN) models and their behavior, as well as in-

dicating which factors are more promising in terms of

hyperparameter optimization techniques.

The main contribution of this paper is the mea-

surement of the impact of each factor, optimization

and learning rate, individually and in combination, on

the training accuracy result of the models. In addi-

tion, the use of different datasets, such as BreakHis

and Biglycan, contributes to a greater generalization

of the results, as we are not restricted to just one

type of image or context. Also, this study aims to

shed light on explaining Artiﬁcial Intelligence (AI)

through factorial partial performance evaluation. Fi-

nally, this study contributes to the area of image-based

medical diagnosis, using computational and machine-

learning approaches.

The remaining sections of this paper are organized

as follows: Section 2 provides an overview of related

works in the literature that are similar to the proposed

approach. Section 3 presents the proposed method for

evaluating CNNs. In Section 4, we present and dis-

cuss the results achieved in this work. Finally, Sec-

tion 5 concludes the discussion and offers some ﬁnal

remarks.

2 RELATED WORK

Several efforts have been directed toward develop-

ing computational methods based on Artiﬁcial Intelli-

gence (AI) to support breast cancer diagnosis, demon-

strating the potential of deep learning with Convo-

lutional Neural Networks (CNNs) to identify breast

cancer in different stages using histopathological im-

ages (Gautam, 2023)(Springenberg et al., 2023).

(Zerouaoui and Idri, 2022) used a fusion of

seven CNNs (DenseNet 201, Inception V3, Inception

ResNet V2, MobileNet V2, ResNet 50, VGG16, and

VGG19) as feature extractors and performed classi-

ﬁcation with four different classiﬁers (Decision Tree,

Support Vector Machine, K-Nearest Neighbors, and

Multilayer Perceptron).

(Abbasniya et al., 2022) employed IRv2-CXL

method for binary classiﬁcation of the BreakHis

dataset. This method combines the Inception-ResNet-

v2 architecture with an ensemble of CatBoost, XG-

Boost, and LightGBM algorithms. However, the gen-

eralizability of the ﬁndings obtained with IRv2-CXL

hasn’t been evaluated in other datasets.

(Macedo et al., 2022) evaluated ﬁve CNNs trained

on the BreakHis dataset to learn to distinguish be-

tween benign and malignant tumor nuclei. They sub-

sequently tested these CNNs on a different dataset

to classify and interpret tumor nuclei, quantifying

the number of tumor nuclei cells in the segmented

heat map generated by Grad-CAM after classiﬁca-

tion. However, they did not investigate the impact of

parameters on classiﬁcation and interpretation behav-

iors, limiting the depth of their analysis.

(Maleki et al., 2023) proposed an approach

based on transfer learning for feature extraction from

histopathological images in the BreakHis dataset.

They used the extracted features as input for the ex-

treme gradient boosting (XGBoost) classiﬁer. The

study evaluated different combinations of classiﬁers

and pre-trained networks to enhance the classiﬁcation

performance.

(Majumdar et al., 2023) introduced a novel en-

semble method based on rank fusion using the

Gamma function. It combines the conﬁdence

scores of three transfer learning-based CNN mod-

els (GoogleNet, VGG11, and MobileNetV3). They

speciﬁcally designed the ensemble model to classify

breast histopathology images into two classes.

(Silva Neto, 2022) proposed a new dataset consist-

ing of photomicrographs of the immunohistochemi-

cal expression of Biglycan (BGN) in breast tissue, in-

cluding both cancerous and non-cancerous samples.

Additionally, the study developed a CNN model in-

spired by LeNet-5 and evaluated its performance for

classiﬁcation. However, the author did not incor-

porate transfer learning and data augmentation tech-

niques to address the limited number of images in the

dataset.

Previous studies have focused on breast cancer

classiﬁcation using CNNs, but overlooked optimiza-

tion and learning rate inﬂuence. To address this is-

sue, we propose a novel approach that evaluates CNN

performance, emphasizing interpretability, behavior,

and key factors for hyperparameter optimization us-

ing partial factorial design.

3 PROPOSED APPROACH

We propose a comparative method to verify the in-

ﬂuence of the optimizer and Learning Rate (LR) fac-

Optimization and Learning Rate Inﬂuence on Breast Cancer Image Classiﬁcation

793

tors on the accuracy of different CNNs. Figure 1 il-

lustrates the proposed method, which is divided into

three (3) phases, as described as follows.

1 First Phase: consists of training and validat-

ing six (6) different CNNs using the BreakHis (Span-

hol et al., 2016) dataset, varying the optimizer param-

eters, and LR. The BreakHis breast cancer dataset

consists of 7,909 microscopic images of breast tumor

tissue from 82 patients, divided into benign (2,480 im-

ages) and malignant (5,429 images) tumors, with 700

× 460 pixels size. At the end of this phase, we veri-

ﬁed which CNN performs better in the binary classi-

ﬁcation task.

2 Second Phase: another dataset was consid-

ered, Biglycan (da Silva Neto et al., 2023), which is

also from the context of breast cancer. The Bigly-

can breast cancer dataset consists of photomicro-

graphs depicting the immunohistochemical expres-

sion of Biglycan (BGN) in breast tissue, both with

and without cancer. The dataset comprises a total of

336 images with 128 × 128 pixels size and contains

two (2) categories: malignant (203) and benign (133).

In this phase, the goal is to verify which CNN per-

forms better in the classiﬁcation task using Biglycan

dataset.

For both phases ( 1 and 2 ), we considered the

variations of the optimizer parameters – Adam and

Stochastic Gradient Descent (SGD) – and LR accord-

ing to Table 1, leading to seventy-two (72) differ-

ent training types of CNNs. Also, the datasets were

randomly partitioned into 80% for training and 20%

for testing. Finally, we resized all images to 224 ×

224 pixels size and conducted the experiments using

Python (version 3.8) and Pytorch 2.0 framework.

Table 1: Experiment Combinations for each CNN.

AlexNet EfﬁcientNet ResNet-50 ShufﬂeNet SqueezeNet VGG-16

Learning

Rate

0.01 0.01 0.01 0.01 0.01 0.01

0.001 0.001 0.001 0.001 0.001 0.001

0.0001 0.0001 0.0001 0.0001 0.0001 0.0001

Optimizer

SGD SGD SGD SGD SGD SGD

Adam Adam Adam Adam Adam Adam

Dataset

BreakHis BreakHis BreakHis BreakHis BreakHis BreakHis

Biglycan Biglycan Biglycan Biglycan Biglycan Biglycan

3 Third Phase: consists of evaluating, using

the partial factorial technique, based on the sum of

squares, which factor impacts the most on the vali-

dation accuracy response variable. For this, we re-

duced the experimental space from 72 to eight differ-

ent types of experiments. We selected the CNN with

the best classiﬁcation performance for each dataset

and submitted it to a performance validation using the

partial factorial design.

We based our reduced experimental design on a

partial factorial with two factors and two levels la-

beled as (-1) and (1) according to Table 2. The

ﬁrst factor in our study is the Optimizer, followed by

the LR. The Optimizer factor comprises two levels:

Adam and SGD. The LR factor includes the follow-

ing levels: 0.001 and 0.0001.

Table 2: Detailing of factors and levels with their Labels.

Levels

Factors

Optimizer - A SGD (-1) Adam (1)

Learning Rate (LR) - B 0.001 (-1) 0.0001 (1)

Through the partial factorial method, we com-

bined the factors and levels by providing an experi-

mental combination according to Table 3. Thus, with

a regression model, we carried out four experiments,

using the combinations of each factor and level and

measuring their inﬂuence on the Response Variable

(y).

Table 3: Experiments Combinations.

Experiment

Learning

Rate (LR)

Optimizer

Val.

Accuracy

#1 -1 (0.001) -1 (SGD) y

#2 1 (0.0001) -1 (SGD) y

#3 -1 (0.001) 1 (Adam) y

#4 1 (0.0001) 1 (Adam) y

The goal of the third phase is to conduct a perfor-

mance evaluation by doing four experiments for each

dataset, following the combination in Table 3. Ini-

tially, we consider SGD as the level of the optimiza-

tion function factor, which is an iterative method for

optimizing an objective function with differentiable

or sub-differentiable smoothness properties. It can be

considered a stochastic approximation of gradient de-

scent optimization, as it replaces the actual gradient

with an estimate of it. Especially in high-dimensional

optimization problems, this reduces the high compu-

tational cost, thus achieving faster iterations in ex-

change for a lower convergence rate. SGD is repre-

sented by Equation 1.

t+1

= w

−η

∇E(w

, b

) (1)

Where w

is the vector of parameters estimated in the

t iteration, η

is the learning rate, and ∇E(w

, b

) is the

gradient of the objective function concerning the pa-

rameters. The goal of the performance evaluation in

phase three (3) is to measure the percentage inﬂuence

of the η

(component of Equation 1) on the validation

accuracy.

The other level of the optimization function factor

that we experimented with in our performance eval-

VISAPP 2024 - 19th International Conference on Computer Vision Theory and Applications

794

Open-Source

Datasets

}

BreakHis

Biglycan

Training and Evaluating

six (6) CNNs

Feeds Setup

For each

Dataset

Performance

Evaluation

}

Influence of

Factors

Better CNNs

7909

336

}

Factors:

• Optimizer

• Learning Rate

Output

Malignant

Benign

Figure 1: Proposed method.

uation is Adam, represented by Equation 2. Adam

maintains an individual adaptive learning rate for each

parameter of the model based on ﬁrst-order moment

estimates (gradient) and second-order moment esti-

mates (moment). Additionally, it adjusts the learning

rate adaptively for each parameter, allowing larger up-

dates for common parameters and smaller updates for

less common parameters.

= θ −α

ˆm

√

ˆv + ε

(2)

Where θ is the updated parameter, θ

is the new

parameter value, α is the interactive learning rate,

ˆm represents the ﬁrst-order momentum, ˆv represents

the second-order momentum, and ε is the smoothing

term. Therefore, with the performance evaluation de-

ble to verify the percentage inﬂuence of the α (a com-

ponent of Equation 2) on the optimization function

and, consequently, on the validation accuracy.

The Partial Factorial Method. To evaluate in-

ﬂuence’s level of each factor, we used the Sum of

Squares. The regression model for the partial facto-

rial design (2

) is represented by Equation 3.

y = q

+ q

(3)

The individual coefﬁcients of each regression

component can be obtained by breaking down Equa-

tion 3. The q

value, commonly referred to as the

intercept term, signiﬁes the baseline value of the de-

pendent variable when all the other factors within the

model are held at zero. By substituting the follow-

ing four observations into the regression model, we

can obtain the values of q

, q

, and q

according

to the equations below: q

×(y

+ y

×(−y

+ y

−y

+ y

), q

×(−y

−y

+ y

), and q

×(y

−y

+ y

Using the values of q

, q

, and q

, we can

calculate the sum of squares, which represents the to-

tal variation in the response variable (y), as well as the

variations attributed to the inﬂuence of factor A, fac-

tor B, and the interaction between A and B. The total

variance of y, known as the Total Sum of Squares, is

determined by Equation 4.

SST = 2

+ 2

(4)

The Sum of Squares due to the inﬂuence of A is

= 2

·q

. The inﬂuence of A is given by

SST

Similarly, the Sum of Squares due to the inﬂuence of

B is SS

= 2

·q

, and the inﬂuence of Factor B as

SST

. Lastly, we obtain the Sum of Squares due to the

inﬂuence of Factors A and B together as SS

= 2

, and the inﬂuence of Factors A and B combined

SST

4 RESULTS AND DISCUSSION

Initially, the six different CNNs:

AlexNet (Krizhevsky et al., 2012), Efﬁcient-

Net (Tan and Le, 2020), ResNet-50 (He et al., 2016),

ShufﬂeNet (Ma et al., 2018), SqueezeNet (Han et al.,

2016), and VGG-16 (Simonyan and Zisserman,

2014)) were trained on each set of breast cancer

images (BreakHis and Biglycan), considering train-

ing with data augmentation based on horizontal

and vertical ﬂips, and random rotation (-10

◦

and

◦

). Thus, according to Table 4, we recorded the

best accuracy scores for each CNN, considering

the combinations from Table 3. As indicated in

Optimization and Learning Rate Inﬂuence on Breast Cancer Image Classiﬁcation

795

Table 4, EfﬁcientNet CNN performed the best result

on the BreakHis dataset, achieving an accuracy of

98.86%. Additionally, we report the best alpha (α)

and the best optimizer, which in this case is Adam.

Moving to the right side of Table 4, we ﬁnd that

the ShufﬂeNet performed the best on the Biglycan

dataset, achieving an accuracy of 97.06% based on

the validation accuracy.

Figure 2 presents loss and accuracy graphs to en-

rich our understanding of the generalization capacity

of the better CNNs on the evaluated datasets. For the

BreakHis, it is worth noting that CNN EfﬁcientNet

has a gradual learning process over epochs. Nonethe-

less, for the dataset Biglycan and ShufﬂeNet, it is sug-

gestive that up until the 20

epoch, there is a pro-

gressive and suggestive learning pattern. However,

in the subsequent epochs, the optimization function

behaves inconsistently, resulting in irregular weights

adjustment of the CNN throughout the epochs.

We selected the best CNN for each dataset based

on the accuracies reported in Table 4. Therefore, we

evaluated the inﬂuence of the optimizer and learning

rate (LR) factors on the accuracies of these CNNs.

The ﬁrst set of experiments aimed to ensure that

the CNNs were able to generalize on both datasets,

BreakHis and Biglycan. The accuracy achieved on the

BreakHis dataset is comparable to the state-of-the-art.

However, Biglycan presented greater challenges for

the CNNs due to its limited number of images. The

second set of experiments involved combining differ-

ent conﬁgurations and testing these combinations in a

partial factorial design.

Table 5 presents the validation accuracies for

different combinations of optimizers and learning

rates (LR). For the BreakHis dataset, the CNN that

achieved the highest performance (98.86%) was Efﬁ-

cientNet, using the Adam optimizer and LR of 0.001.

Meanwhile, the best CNN for the Biglycan dataset

was ShufﬂeNet, with an accuracy of 97.07% and us-

ing Adam optimizer and LR of 0.001. Tables 6 and 7

report the results of the second set of experiments in

phase three (3) of our method.

Table 6 reports the percentage of inﬂuence of

each factor (q

, q

, and q

) on the response vari-

able, validation accuracy. The results obtained for the

BreakHis dataset (Table 6) allow us to infer that the

inﬂuence of Factor A, i.e., the optimizer alone, rep-

resents an impact of approximately 21.41% on the

response variable, validation accuracy. On the other

hand, Factor B (learning rate – LR) isolated repre-

sents an impact of approximately 23.60% on the re-

sponse variable, validation accuracy. Lastly, we ob-

served that the inﬂuence of Factors A and B (Opti-

mization Function and Learning Rate) simultaneously

has a predominant impact of approximately 55.00%

on the response variable, validation accuracy.

We sought to understand whether this behavior

of the optimizer and learning rate factors’ inﬂuence

, q

, and q

) carries over to other problems and

datasets. Therefore, we carried out a performance

evaluation using the Biglycan dataset and reported our

ﬁndings in Table 7. We found that the inﬂuence of

the optimizer and learning rate factors changes across

problem classes and datasets. This perception is sup-

ported by the fact that the simultaneous inﬂuence of

Factors A and B (Optimizer and LR) is negligible, ac-

counting for approximately 1.79%. Meanwhile, Fac-

tor A (Optimizer) solely exerted a predominant inﬂu-

ence of approximately 96.41% on the response vari-

able, validation accuracy, for this dataset. On the

other hand, Factor B (LR) alone had a negligible in-

ﬂuence of approximately 1.79%.

Among the numerical ﬁndings suggested by our

experiments, it is possible to recognize that formal

analyses of factor inﬂuence using the partial factorial

method can help guide optimization efforts toward

factors that truely impact validation accuracy. Hy-

perparameter optimizers are recommended for ﬁne-

tuning CNNs, and the insights from our experiments

can inspire new criteria for hyperparameter optimiza-

tion, directing the tuning toward the search spaces of

factors that have a predominant inﬂuence over others.

Finally, our best results achieved for each dataset

were compared with other state-of-the-art approaches

in the literature, as presented in Table 8. Our ﬁndings

indicate that our best score exceeds the performance

of the best state-of-the-art technique reported in pre-

vious studies.

5 CONCLUSION

This paper evaluated the extent to which two factors

(optimization function and learning rate) inﬂuence the

response variable and validation accuracy. To accom-

plish this, we proposed a three-fold method, where the

initial two (2) phases involved training and validat-

ing six different CNNs using various parameter com-

binations and the two datasets, BreakHis and Bigly-

can. Subsequently, in the third phase, we selected two

(2) CNNs that outperformed the others in the classi-

ﬁcation task and conducted a performance evaluation

based on the sum of squares.

We found that the CNNs EfﬁcientNet and Shuf-

ﬂeNet empirically outperformed the others in the clas-

siﬁcation task on the BreakHis and Biglycan datasets,

achieving accuracies of 98.86% and 97.06%, both re-

spectively. Additionally, our paper introduces an in-

VISAPP 2024 - 19th International Conference on Computer Vision Theory and Applications

796

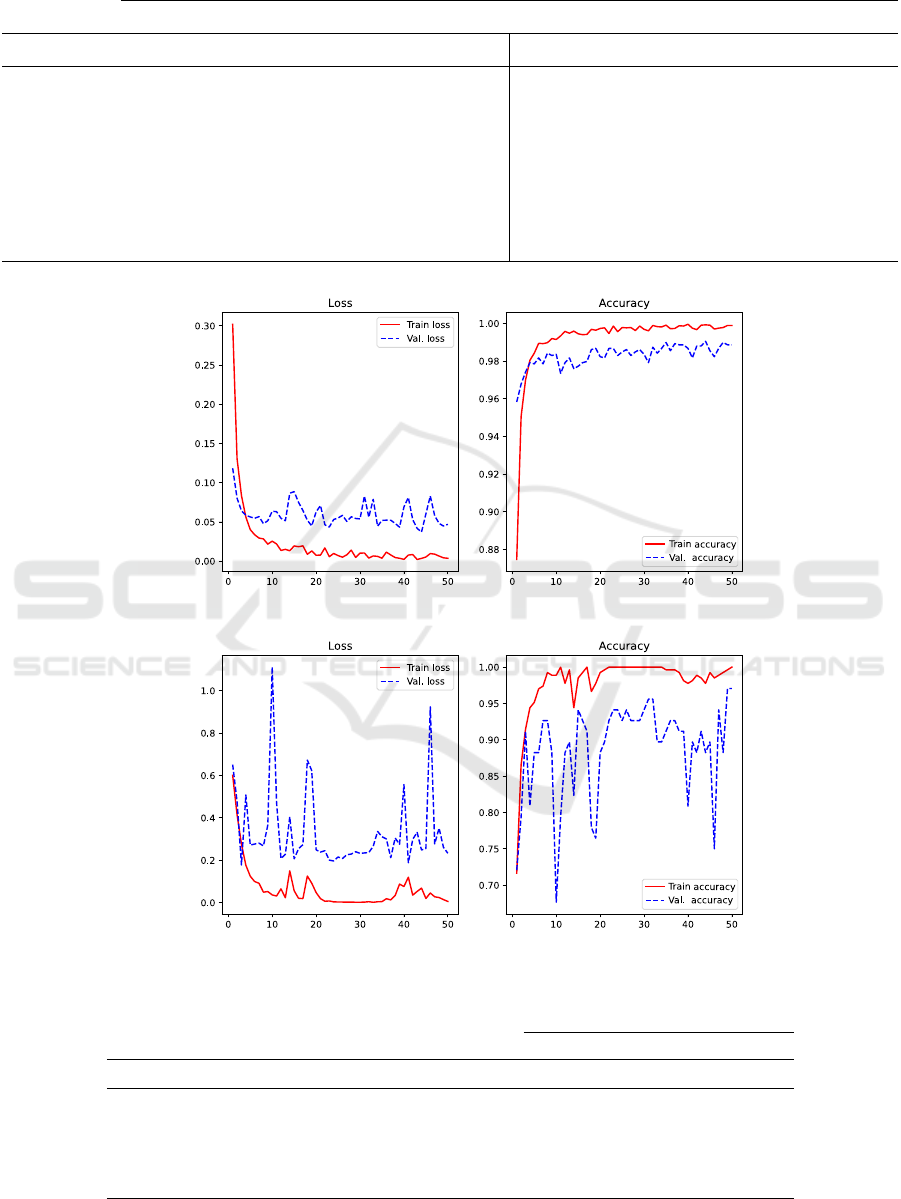
Table 4: Overall CNNs Higher Performance.

Breakhis Biglycan

CNN alfa (α) Acc. Train Acc. Val. Optimizer alfa (α) Acc. Train Acc. Val. Optimizer

AlexNet 0.0001 99.87% 97.35% SGD 0.0001 100% 91.18% Adam

EfﬁcientNet 0.0001 99.89% 98.86% Adam 0.0001 100% 94.12% Adam

ResNet-50 0.01 99.98% 98.80% SGD 0.01 100% 95.59% SGD

ShufﬂeNet 0.01 99.25% 98.29% SGD 0.001 100% 97.06% Adam

SqueezeNet 0.0001 95.84% 96.84% Adam 0.0001 100% 94.12% Adam

VGG-16 0.001 100% 98.55% SGD 0.001 100% 95.59% SGD

(a)

Epochs Epochs

(b)

Epochs Epochs

Figure 2: Generalization behavior through Loss and Accuracy Functions: (a) BreakHis; (b) Byglycan.

Table 5: Accuracies of the four (4) combinations of experiments for each dataset.

Factors Response Variable: Val. Acc.

Optimizer - A Learning Rate (LR) - B AB BreakHis Biglycan

SGD (-1) 0.001 (-1) 1 98.74% 60.29%

Adam (1) 0.001 (-1) -1 92.48% 97.06%

SGD (-1) 0.0001 (1) -1 97.41% 60.29%

Adam (1) 0.0001 (1) 1 98.86% 88.24%

Optimization and Learning Rate Inﬂuence on Breast Cancer Image Classiﬁcation

797

Table 6: Breakhis: Estimation of The Inﬂuence of Factors,

A, B, and AB Jointly.

Parameters

Estimated

Variance

Variance (%)

Val. Acc. Val. Acc.

0.9687

(Optimizer) -0.0120 21.41%

(LR) 0.0126 23.60%

(Optimizer + LR) 0.0192 55.00%

Table 7: Biglycan: Estimation of The Inﬂuence of Factors,

A, B, and AB Jointly.

Parameters

Estimated

Variance

Variance (%)

Val. Acc. Val. Acc.

0,7647

(Optimizer) 0.1618 96.41%

(LR) -0.0220 1.79%

(Optimizer + LR) -0.0225 1.79%

Table 8: Short Comparison with literature.

Dataset Method Accuracy (%)

BreakHis

(Zerouaoui and Idri, 2022) 92.56

(Abbasniya et al., 2022) 96.46

(Maleki et al., 2023) 91.9

(Majumdar et al., 2023) 98.05

Our approach 98.86

Biglycan (Silva Neto, 2022) 93

Our approach 97.06

novative approach by conducting a performance eval-

uation based on the sum of squares to estimate the

inﬂuence of the optimizer and learning rate on val-

idation accuracy. Using this method, we were able

to determine that the combined inﬂuence of the opti-

mizer and learning rate accounted for approximately

55.00% of the validation accuracy for the BreakHis

dataset. Meanwhile, the optimizer factor alone had

a predominant inﬂuence on validation accuracy, ac-

counting for approximately 96.41% in the Biglycan

dataset.

In addition to the reported quantitative results, our

method provides insights and sheds light on a rele-

vant issue in the context of optimization methods by

indicating the percentage of the relevance of a vari-

able in the optimization process and search within ﬁ-

nite spaces. This empowers new efforts in exhaustive

searches for variables that effectively impact the ob-

jective function.

In future work, we plan to evaluate the inﬂuence

of other factors such as batch size and the internal

structure of the CNN, as well as assess patterns of

inﬂuence across different datasets. In addition, we in-

tend to expand the experiments by considering mul-

ticlass classiﬁcation and expand the gathered insights

and conclusions into more general and practically us-

able heuristics.

ACKNOWLEDGMENTS

This study was ﬁnanced in part by the Coordenac¸

de Aperfeic¸oamento de Pessoal de N

ıvel Superior

– Brasil (CAPES) – Finance Code 001. Andr

e R.

Backes gratefully acknowledges the ﬁnancial support

of CNPq (Grant #307100/2021-9).

REFERENCES

Abbasniya, M. R., Sheikholeslamzadeh, S. A., Nasiri,

H., and Emami, S. (2022). Classiﬁcation of Breast

Tumors Based on Histopathology Images Using

Deep Features and Ensemble of Gradient Boosting

Methods. Computers and Electrical Engineering,

103:108382.

Alqahtani, Y., Mandawkar, U., Sharma, A., Hasan,

M. N. S., Kulkarni, M. H., and Sugumar, R.

(2022). Breast Cancer Pathological Image Clas-

siﬁcation Based on the Multiscale CNN Squeeze

Model. Computational Intelligence and Neuro-

science, 2022:7075408.

Backes, A. R. (2022). Pap-smear image classiﬁcation by

using a fusion of texture features. In 2022 35th SIB-

GRAPI Conference on Graphics, Patterns and Images

(SIBGRAPI), volume 1, pages 139–144.

Batra, K., Sekhar, S., and Radha, R. (2020). Breast can-

cer detection using cnn on mammogram images. In

Smys, S., Tavares, J. M. R. S., Balas, V. E., and

Iliyasu, A. M., editors, Computational Vision and Bio-

Inspired Computing, pages 708–716, Cham. Springer

International Publishing.

Benhammou, Y., Achchab, B., Herrera, F., and Tabik, S.

(2020). Breakhis based breast cancer automatic di-

agnosis using deep learning: Taxonomy, survey and

insights. Neurocomputing, 375:9–24.

Clement, D., Agu, E., Obayemi, J., Adeshina, S., and

Soboyejo, W. (2022). Breast cancer tumor classiﬁ-

cation using a bag of deep multi-resolution convolu-

tional features. Informatics, 9(4).

da Silva Neto, P. C., Kunst, R., Barbosa, J. L. V., Lein-

decker, A. P. T., and Savaris, R. F. (2023). Breast can-

cer dataset with biomarker biglycan. Data in Brief,

47:108978.

Gautam, A. (2023). Recent advancements of deep learn-

ing in detecting breast cancer: a survey. Multimedia

Systems, 29(3):917–943.

Han, S., Liu, X., Mao, H., Pu, J., Pedram, A., Horowitz,

M. A., and Dally, W. J. (2016). EIE: Efﬁcient Infer-

VISAPP 2024 - 19th International Conference on Computer Vision Theory and Applications

798

ence Engine on Compressed Deep Neural Network.

SIGARCH Comput. Archit. News, 44(3):243–254.

He, K., Zhang, X., Ren, S., and Sun, J. (2016). Deep Resid-

ual Learning for Image Recognition. In 2016 IEEE

Conference on Computer Vision and Pattern Recogni-

tion (CVPR), pages 770–778.

INCA, I. N. d. C. (2021). Detecc¸

ao Precoce do C

ancer,

volume 1. Minist

erio da Sa

ude.

Krizhevsky, A., Sutskever, I., and Hinton, G. E. (2012). Im-

ageNet Classiﬁcation with Deep Convolutional Neu-

ral Networks. In Pereira, F., Burges, C. J. C., Bottou,

L., and Weinberger, K. Q., editors, Advances in Neu-

ral Information Processing Systems, volume 25, pages

1097–1105. Curran Associates, Inc.

Ma, N., Zhang, X., Zheng, H.-T., and Sun, J. (2018). Shuf-

ﬂeNet V2: Practical Guidelines for Efﬁcient CNN Ar-

chitecture Design. In Proceedings of the European

Conference on Computer Vision (ECCV), pages 116–

131.

Macedo, D. C., John W. S., D. L., Santos, V. D., Tasso

L. O., M., Fernando M. P., N., Arrais, N., Vinuto,

T., and Lucena, J. (2022). Evaluating Interpretabil-

ity in Deep Learning using Breast Cancer Histopatho-

logical Images. In 2022 35th SIBGRAPI Conference

on Graphics, Patterns and Images (SIBGRAPI), vol-

ume 1, pages 276–281.

Majumdar, S., Pramanik, P., and Sarkar, R. (2023). Gamma

function based ensemble of cnn models for breast can-

cer detection in histopathology images. Expert Sys-

tems with Applications, 213:119022.

Maleki, A., Raahemi, M., and Nasiri, H. (2023). Breast can-

cer diagnosis from histopathology images using deep

neural network and XGBoost. Biomedical Signal Pro-

cessing and Control, 86:105152.

Rodrigues Moreira, L. F., Moreira, R., Travenc¸olo, B.

A. N., and Backes, A. R. (2023). An Artiﬁcial

Intelligence-as-a-Service Architecture for deep learn-

ing model embodiment on low-cost devices: A case

study of COVID-19 diagnosis. Applied Soft Comput-

ing, 134:110014.

Sahu, Y., Tripathi, A., Gupta, R. K., Gautam, P., Pateriya,

R. K., and Gupta, A. (2023). A CNN-SVM based

computer aided diagnosis of breast Cancer using his-

togram K-means segmentation technique. Multimedia

Tools and Applications, 82(9):14055–14075.

Silva Neto, P. C. d. (2022). BGNDL: Arquitetura de Deep

Learning para diferenciac¸

ao da prote

ına Biglycan em

tecido mam

ario com e sem c

ancer. Master’s thesis,

Universidade do Vale do Rio dos Sinos, Brazil.

Simonyan, K. and Zisserman, A. (2014). Very Deep Con-

volutional Networks for Large-Scale Image Recogni-

tion. CoRR, abs/1409.1556.

Spanhol, F. A., Oliveira, L. S., Petitjean, C., and Heutte,

L. (2016). A Dataset for Breast Cancer Histopatho-

logical Image Classiﬁcation. IEEE Transactions on

Biomedical Engineering, 63(7):1455–1462.

Springenberg, M., Frommholz, A., Wenzel, M., Weicken,

E., Ma, J., and Strodthoff, N. (2023). From mod-

ern cnns to vision transformers: Assessing the per-

formance, robustness, and classiﬁcation strategies of

deep learning models in histopathology. Medical Im-

age Analysis, 87:102809.

Tan, M. and Le, Q. V. (2020). EfﬁcientNet: Rethinking

Model Scaling for Convolutional Neural Networks.

Yu, D., Lin, J., Cao, T., Chen, Y., Li, M., and Zhang, X.

(2023). Secs: An effective cnn joint construction strat-

egy for breast cancer histopathological image classiﬁ-

cation. Journal of King Saud University - Computer

and Information Sciences, 35(2):810–820.

Zerouaoui, H. and Idri, A. (2022). Deep hybrid architec-

tures for binary classiﬁcation of medical breast cancer

images. Biomedical Signal Processing and Control,

71:103226.

Optimization and Learning Rate Inﬂuence on Breast Cancer Image Classiﬁcation

799