Evaluation of K-Means Time Series Clustering Based on

Z-Normalization and NP-Free

Ming-Chang Lee

1 a

, Jia-Chun Lin

2 b

and Volker Stolz

1 c

Department of Computer Science, Electrical Engineering and Mathematical Sciences, Høgskulen p

a Vestlandet (HVL),

Bergen, Norway

Department of Information Security and Communication Technology, Norwegian University of Science and Technology

(NTNU), Gjøvik, Norway

Keywords:

Time Series, Clustering, K-Means Time Series Clustering, Z-Normalization, NP-Free,

Performance Evaluation.

Abstract:

Despite the widespread use of k-means time series clustering in various domains, there exists a gap in the

literature regarding its comprehensive evaluation with different time series preprocessing approaches. This

paper seeks to ﬁll this gap by conducting a thorough performance evaluation of k-means time series clus-

tering on real-world open-source time series datasets. The evaluation focuses on two distinct techniques:

z-normalization and NP-Free. The former is one of the most commonly used approaches for normalizing time

series, and the latter is a real-time time series representation approach. The primary objective of this paper is

to assess the impact of these two techniques on k-means time series clustering in terms of its clustering quality.

The experiments employ the silhouette score, a well-established metric for evaluating the quality of clusters

in a dataset. By systematically investigating the performance of k-means time series clustering with these two

preprocessing techniques, this paper addresses the current gap in k-means time series clustering evaluation

and contributes valuable insights to the development of time series clustering.

1 INTRODUCTION

Time series clustering is a data mining technique that

involves grouping similar time series into clusters

without prior knowledge of these cluster deﬁnitions.

To elaborate, clusters are established by aggregating

time series with signiﬁcant similarity to other time

series within the same cluster while maintaining min-

imal similarity with time series in different clusters

(Aghabozorgi et al., 2015).

In recent years, there has been an increasing need

for time series clustering due to the explosion of

the Internet of Things (IoT) in diverse areas. Vast

amounts of time series data are continuously mea-

sured and collected from connected devices and sen-

sors, and they often require clustering and analy-

sis. Various clustering approaches have been intro-

duced and employed to address this demand, includ-

ing k-means (MacQueen et al., 1967) , hierarchi-

cal clustering (Kaufman and Rousseeuw, 2009), k-

https://orcid.org/0000-0003-2484-4366

https://orcid.org/0000-0003-3374-8536

https://orcid.org/0000-0002-1031-6936

Shape (Paparrizos and Gravano, 2015), Kernel K-

means (Dhillon et al., 2004), etc. Among these, k-

means is one of the most popular and widely used

techniques, known for its simplicity and efﬁciency

in partitioning time series data into distinct clusters

(Ruiz et al., 2020). However, clustering raw time se-

ries can be challenging because the scales and magni-

tudes of different time series may vary signiﬁcantly.

Hence, it becomes necessary to apply preprocessing

techniques before clustering the raw time series data.

Z-normalization is one of the most commonly

used approach for preprocessing time series (Dau

et al., 2019), and it is widely employed by many rep-

resentation approaches and clustering approaches be-

cause of its simplicity and effectiveness. However,

z-normalization may cause certain distinct time series

to become indistinguishable (Lee et al., 2023a), which

might mislead clustering approaches and negatively

impact on the performance of clustering results.

NP-Free is a real-time time series representation

approach introduced by Lee et al. (Lee et al., 2023b).

NP-Free possesses the unique capability to dynam-

ically transform any raw time series into a root-

mean-square error (RMSE) series in real time. This

Lee, M., Lin, J. and Stolz, V.

Evaluation of K-Means Time Series Clustering Based on Z-Normalization and NP-Free.

DOI: 10.5220/0012547200003654

In Proceedings of the 13th International Conference on Pattern Recognition Applications and Methods (ICPRAM 2024), pages 469-477

ISBN: 978-989-758-684-2; ISSN: 2184-4313

469

transformation ensures that the resulting RMSE se-

ries serves as an effective representation of the orig-

inal raw series. NP-Free stands out from conven-

tional representation approaches by eliminating pre-

processing steps like z-normalization. This character-

istic enables NP-Free to be an alternative to replace

z-normalization in time series clustering applications.

Considering these two distinct options for time se-

ries preprocessing, the impact of z-normalization and

NP-Free on the performance of k-means time series

clustering, especially concerning its clustering qual-

ity, remains unknown in the literature. Therefore, in

this paper, we aims to ﬁll this gap. Our goal is to an-

alyze and compare the performance of k-means time

series clustering when applied with z-normalization

and NP-Free, providing insights into how each tech-

nique inﬂuences the quality of clusters generated by

k-means time series clustering.

Two experiments, utilizing real-world open-

source time series datasets from the UEA&UCR

archive (Dau et al., 2019), were conducted. The clus-

ters generated by the two variants of k-means time

series clustering were assessed using the silhouettes

score, which is a metric used to evaluate the quality

of clusters in a dataset (Rousseeuw, 1987). The ex-

periment results shows that the cluster quality is sig-

niﬁcantly inﬂuenced by z-normalization and NP-Free.

Our evaluation analysis valuable insights to the devel-

opment of time series clustering.

The rest of the paper is organized as follows: Sec-

tion 2 covers background on k-means time series clus-

tering, z-normalization, and NP-Free. Section 3 dis-

cusses related work. Section 4 provides evaluation

details and discusses the experiments along with the

corresponding results. Finally, Section 5 concludes

this paper and outlines future work.

2 BACKGROUND

This section introduces k-means time series cluster-

ing, z-normalization, and NP-Free.

2.1 K-Means Time Series Clustering

k-means time series clustering is a unsupervised ma-

chine learning approach designed to group time series

into distinct clusters. The method, its initial formu-

lation, was ﬁrst introduced by Mac Queen in 1967

(MacQueen et al., 1967), and the approximation de-

veloped by Lloyd in 1982 (Lloyd, 1982) has proven

to be more popular in application. It is widely used

due to its ease of implementation, simplicity, and ef-

ﬁciency.

k-means minimizes the distance between each

time series and the centroid of its assigned clus-

ter, with distances computed using various metrics

such as Euclidean distance or dynamic time warping

(DTW) distance. Before initiating k-means cluster-

ing, two parameters must be determined: the num-

ber of clusters (k) and the initial centroids. While

a ﬁxed parameter conﬁguration yields a consistent

clustering result, it is important to note that differ-

ent conﬁgurations typically lead to varying outcomes.

Consequently, a common approach is to execute k-

means multiple times with different parameter con-

ﬁgurations and subsequently select the best clustering

outcome.

2.2 Z-Normalization

z-normalization (also known as z-score normaliza-

tion) is a statistical technique used in data process-

ing and analysis. It transforms data into a standard

scale with a mean of 0 and a standard deviation of

1 (Senin, 2016). The purpose of z-normalization is

to simplify the interpretation and comparison of dif-

ferent datasets, making them directly comparable. z-

normalization is typically applied to individual data

points within a dataset by subtracting the mean of the

dataset from each data point and then dividing the

result by the standard deviation. The formula of z-

normalization is shown below.

− µ

(1)

where z

is the i-th data point in a time series, µ is

the mean of all data points in the time series, σ is the

standard deviation of all the data points, and z

is the

z-normalized value (i.e., z-score) of the the i-th data

point derived from the formula.

z-normalization is considered an essential pre-

processing step for time series representation ap-

proaches because it allows these approaches to focus

on the structural similarities/dissimilarities of time

series rather than on the original data point values

(Senin, 2016). However, z-normalization has some

limitations and drawbacks, including sensitivity to

outliers, loss of the original data scale, lack of invari-

ance. Additionally, when applied to ﬂat time series, it

can amplify ﬂuctuations, such as noises, resulting in

an negative impact on data mining techniques, such

as Matrix Proﬁle (Paepe et al., 2019).

2.3 NP-Free

NP-Free (Lee et al., 2023a) is a real-time time series

representation approach. It eliminates the need for

preprocessing input time series with z-normalization

ICPRAM 2024 - 13th International Conference on Pattern Recognition Applications and Methods

470

and requires no advance parameter tuning by users.

NP-Free directly generates a representation for a raw

time series by transforming the time series into a root-

mean-square error (RMSE) series in real time.

NP-Free, using Long Short-Term Memory

(LSTM) and the Look-Back and Predict-Forward

strategy from RePAD (Lee et al., 2020), generates

representations for time series. Speciﬁcally, NP-Free

continuously predicts the next data point in the target

time series using three historical data points and

calculates the RMSE (Root Mean Square Error) value

between the observed and predicted data points.

This process converts the target time series into an

RMSE series. With its preprocessing-free approach,

NP-Free presents an alternative to z-normalization in

time series clustering applications.

3 RELATED WORK

Kapil and Chawla (Kapil and Chawla, 2016) inves-

tigated the impact of different distance functions, in-

cluding the Euclidean and Manhattan distance func-

tions, on the performance of k-means. Ahmed et al.

(Ahmed et al., 2020) conducted a review to address

the shortcomings of the k-means algorithm, speciﬁ-

cally focusing on the issues of initialization and its

inability to handle data with mixed types of features.

The authors performed an experimental analysis to in-

vestigate different versions of the k-means algorithms

for different datasets.

Kuncheva and Vetrov (Kuncheva and Vetrov,

2006) investigated the stability of clustering algo-

rithms, particularly cluster ensembles relying on k-

means clusters, in the presence of random elements

such as the target number of clusters (k) and random

initialization. Using a diverse set of 10 artiﬁcial and

10 real datasets with a modest number of clusters and

data points, the research assessed pairwise and non-

pairwise stability metrics. The study explored the re-

lationship between stability and accuracy concerning

the number of clusters (k) and proposed a new com-

bined stability index, incorporating both pairwise in-

dividual and ensemble stabilities, which shows im-

proved correlation with ensemble accuracy.

Gupta and Chandra (Gupta and Chandra, 2020)

aims to ﬁnd out the possibility of different dis-

tance/similarity metrics to be used with k-means al-

gorithm by conducting an empirical evaluation. The

study compares the accuracy, performance, and reli-

ability of 13 diverse distance or similarity measures

across six variations of data using the k-means algo-

rithm.

Vats and Sagar (Vats and Sagar, 2019) investigated

the performance of the k-means algorithm through

various implementations, including k-mean simple

(utilizing Java codes on MapReduce), k-means with

Initial Equidistant Centres (IEC), k-mean on Mahout

(leveraging a machine learning library), and k-mean

on Spark (utilizing another machine learning library).

Additionally, the study explores the behavior of k-

means algorithms concerning centroids and various

iteration levels, providing insights into their perfor-

mance across different infrastructures.

The work by Ikotun et al. (Ikotun et al., 2023)

presents a comprehensive review focused on four key

aspects: a systematic examination of the k-means

clustering algorithm and its variants, the introduction

of a novel taxonomy, in-depth analyses to validate

ﬁndings, and identiﬁcation of open issues. The review

provides a detailed examination of k-means, identi-

ﬁes research gaps, and outlines future directions to

address challenges in k-means clustering and its vari-

ants.

According to our investigation, there exists a gap

in the literature concerning the evaluation of k-means

time series clustering with different normalization

techniques. This gap highlights the need for compre-

hensive studies that compare the performance of k-

means clustering using different preprocessing tech-

niques. Such investigations could provide valuable

insights into the strengths and limitations of different

preprocessing techniques, contributing to the devel-

opment of more effective and robust clustering algo-

rithms for time series data.

4 EVALUATION

To evaluate the impact of z-normalization and NP-

Free on k-means time series clustering in terms of its

clustering quality, we conducted two experiments us-

ing two real-world open-source time series datasets

from the UEA&UCR archive (Dau et al., 2019). In

the rest of this paper, we refer to k-means time series

clustering based on z-normalization as z-kmeans, and

refer to k-means time series clustering based on NP-

Free as NPF-kmeans.

We implemented these two variants using the

k-means time series algorithm provided by tslearn

(Tavenard et al., 2020), which is a Python package

that provides machine learning tools for time series

analysis. Furthermore, the NP-Free in NPF-kmeans

was implemented in DeepLearning4J (Deeplearn-

ing4j, 2023). To ensure a fair comparison, identical

initial centroids were utilized for both z-kmeans and

NPF-kmeans. All the experiments were performed on

a laptop running MacOS Ventura 13.4 with 2.6 GHz

6-Core Intel Core i7 and 16GB DDR4 SDRAM.

In the ﬁrst experiment, we selected all time se-

Evaluation of K-Means Time Series Clustering Based on Z-Normalization and NP-Free

471

ries belonging to a class named ”class 2: Point

(FP03, MP03, FP18, and MP18)” from the

GunPointAgeSpan TRAIN.txt of the GunPointAgeS-

pan dataset

. There are 67 raw time series in this

class, each with 150 data points representing an ac-

tion performed by a person. We refer to this dataset as

GunPointPointTrain in this paper. As per the dataset

description, the time series can be categorized into

various types. However, it is important to note that

there is no label information indicating the speciﬁc

type to which each time series belongs.

In the second experiment, we selected all

time series from a class named ”class 2:

Male (MG03, MP03, MG18, MP18)” from the

GunPointMaleVersusFemale TRAIN.txt of the Gun-

PointMaleVersusFemale dataset

. In this class, there

are 64 raw time series, each comprising 150 data

points. We call this dataset GunPointMaleTrain.

Similarly, despite the dataset description suggesting

that these time series can be further divided into

different types, there is no label information in the

dateset. The reason we chose these two datasets is

that they are in a raw form, making them suitable for

conducting our evaluation.

The hyperparameter and parameter settings in

NPF-kmeans are identical to those used in NP-Free

(Lee et al., 2023a). This settings were originally sug-

gested and employed in prior studies by (Lee et al.,

2023b), (Lee et al., 2020), and (Lee et al., 2021). We

adopted these settings for our two experiments. Re-

garding the sliding window parameter w, it is recom-

mended to use a large value (Lee and Lin, 2023). In

this paper, w was set to 150, as each time series in

GunPointPointTrain and GunPointMaleTrain consists

of only 150 data points.

In order to evaluate the performance of z-kmeans

and NPF-kmeans, Silhouettes (Rousseeuw, 1987) was

used in this paper. Silhouettes is a well-known mea-

sure to evaluate the quality of clusters in unsupervised

machine learning. Silhouettes quantiﬁes how similar

each object is to its own cluster compared to other

clusters. A Silhouettes score ranges from -1 to 1. A

value near 1 indicates that each object is well matched

to its own cluster and poorly matched to neighboring

clusters, a value of 0 indicates that each object is on or

very close to the boundary between two neighboring

clusters, and a value near -1 suggests that objects may

have been assigned to the wrong cluster.

The process for calculating the Silhouettes score

The GunPointAgeSpan dataset, http://www.timeseries

classiﬁcation.com/description.php?Dataset=GunPointAg

eSpan

The GunPointMaleVersusFemale dataset, http://www.

timeseriesclassiﬁcation.com/description.php?Dataset=Gu

nPointMaleVersusFemale

to represent the overall clustering quality of a time

series clustering approach is shown as follows:

1. Select a time series i. Choose one time series from

a cluster for which we would like to calculate its

Silhouettes score.

2. Calculate a(i). Calculate the average distance of

i to all the other time series within the same clus-

ter. A smaller value indicates a better assignment

within the cluster.

3. Identify the nearest cluster to i. Compute the aver-

age distance between i and all time series in each

of the other clusters. Find the cluster that has the

minimum average distance to i. This cluster is

considered the nearest neighboring cluster to i.

4. Calculate b(i). Calculate the average distance of i

to all series in the nearest neighboring cluster.

5. Calculate s(i). Calculate the Silhouettes score of

i using (b(i) − a(i))/max{a(i), b(i)}. This result-

ing s(i) ranges from -1 to 1, where higher values

indicate better clustering.

6. Repeat steps 1 to 5 to calculate a Silhouettes score

for each time series in the dataset. Afterward,

calculate the average Silhouettes score for all the

time series. This provides an overall measure of

the clustering quality.

In this paper, we used the Silhouettes function pro-

vided by tslearn (Tavenard et al., 2020) to evaluate

z-kmeans and NPF-kmeans. Note that the random

state in tslearn is ﬁxed at a value of 1 to avoid ran-

dom execution results. Additionally, the metric for

calculating the distance between time series is set to

euclidean. It is worth mentioning that when eval-

uating NPF-kmeans, we mapped each RMSE series

back to its original raw time series and calculated the

average Silhouettes score using these raw time se-

ries. Similarly, we used the raw time series to com-

pute the average Silhouettes score of z-kmeans. This

is because using z-normalized time series to calcu-

late the average Silhouettes score for z-kmeans un-

fairly favors z-kmeans over NPF-kmeans. Recall that

z-normalization can make distinct time series seem

similar, leading to them being assigned to the same

cluster. Consequently, the overall Silhouettes score

for z-kmeans might falsely appear higher than that

of NPF-kmeans, giving the impression that z-kmeans

provides better clustering quality.

Due to the mentioned reason, we evaluated the

overall Silhouettes score of NPF-kmeans and z-

kmeans using raw time series, which resulted in

somewhat lower overall Silhouettes score. However,

this approach ensures a fair basis for comparing NPF-

kmeans and z-kmeans.

ICPRAM 2024 - 13th International Conference on Pattern Recognition Applications and Methods

472

4.1 Experiment 1

In this experiment, we evaluated the individual per-

formance of NPF-kmeans and z-kmeans on the Gun-

PointPointTrain dataset. Figure 1(a) illustrates all the

raw time series in this dataset. When NPF-kmeans

was evaluated, it ﬁrst converted each raw time series

into a RMSE series using NP-Free. Figure 1(b) shows

all the corresponding RMSE time series. On the other

hand, when z-kmeans was evaluated, it ﬁrst prepro-

cessed each raw time series by translating it into a

z-normalized series. The results can be seen in Fig-

ure 1(c). We then randomly chose 12 different values

between 13 and 33 for the parameter k in both NPF-

kmeans and z-kmeans, with the aim of evaluating the

overall Silhouettes score of the two approaches across

different settings for k. As the results listed in Table 1,

NPF-kmeans achieves a higher Silhouettes score than

z-kmeans in all the cases. Note that all the scores were

calculated based on raw time series, rather than nor-

malized ones.

Table 1: The overall Silhouettes scores of NPF-kmeans and

z-kmeans on GunPointPointTrain.

The value of k NPF-kmeans z-kmeans

13 0.4110 0.3327

14 0.4093 0.3654

15 0.5035 0.3766

17 0.4326 0.3594

19 0.3696 0.2853

20 0.3404 0.2845

21 0.3484 0.3129

22 0.3599 0.2787

26 0.3388 0.2345

28 0.3257 0.2004

29 0.3077 0.2332

33 0.2935 0.2294

We further elaborate the clustering results of NPF-

kmeans and z-kmeans when the GunPointPointTrain

dataset was partitioned into 15 clusters, as both vari-

ants achieve the highest Silhouettes score under this

setting. Figure 2 illustrates all the 15 clusters gener-

ated by NPF-kmeans where the left part of the ﬁgure

shows all the RMSE series in each cluster, whereas

the right part of the ﬁgure shows all the corresponding

raw time series in each cluster. It is clear that NPF-

kmeans effectively clustered all the raw time series,

as each time series within the same cluster is similar

to every other but less similar to any time series in

other clusters. It is important to note that this good

performance cannot be reﬂected in the overall Silhou-

ettes score of NPF-kmeans because the score was cal-

culated based on raw time series rather than RMSE

series. These scores were intended for the purpose of

comparing NPF-kmeans and z-kmeans.

Table 2 further lists the detailed clustering results

of NPF-kmeans. NPF-kmeans identiﬁed two time se-

ries as outliers (i.e., time series No. 11 and No. 21)

and therefore assigned each of them to a separated

cluster because their RMSE series are very different

from those of the rest time series, which can be ob-

served from the left part of Figure 2.

Table 2: The clustering results of NPF-kmeans on Gun-

PointPointTrain with k set to 15.

Cluster ID # of time series Time series No.

1 11 17,22,30,31,32,39,45,52,53,56,57

2 8 6,12,13,14,27,37,49,65

3 7 4,15,24,35,40,54,61

4 6 34,36,47,50,59,62

5 5 16,19,33,44,60

6 5 10,18,28,64,66

7 5 5,8,26,42,55

8 4 1,2,7,29

9 4 20,38,41,63

10 3 3,43,67

11 3 46,48,58

12 2 9,23

13 2 25,60

14 1 11

15 1 21

On the other hand, Figure 3 depicts all the 15 clus-

ters produced by z-kmeans. The left part of the ﬁgure

shows all the z-normalized time series in each cluster,

while the right part shows all the corresponding raw

time series. Detailed clustering results of z-kmeans

are presented in Table 3. It is interesting and surpris-

ing to observe that, although the z-normalized time

series in each cluster appear similar (as shown in the

left part of Figure 3), not all corresponding raw time

series within these clusters exhibit the same level of

similarity (see the the right part of Figure 3). For

instance, we can see that all z-normalized time se-

ries in cluster 2 appear signiﬁcantly similar, but the

corresponding raw time series in cluster 2 do not ex-

hibit the same phenomenon. Apparently, raw time

series No.42 and No.55 have a similar pattern with

each other, but they have a much ﬂatter pattern and

much smaller y-axis values than the rest of the raw

time series within cluster 2. Similar observations can

be made in cluster 8.

The observed phenomena were attributed to the

effects of z-normalization, which has the potential to

make distinct time series indistinguishable. This ﬁnd-

ing is consistent with studies (H

oppner, 2014) and

(Lee et al., 2023a), suggesting that z-normalization

might compromise potentially relevant properties that

differentiate time series. Consequently, this could

negatively impact subsequent data mining tasks (Dau

et al., 2019; Senin, 2016; Codecademy-Team, 2022).

Evaluation of K-Means Time Series Clustering Based on Z-Normalization and NP-Free

473

Figure 1: (a) Original raw time series in the GunPointPointTrain dataset, (b) The RMSE series of each raw time series, and

Figure 2: The clustering results of NPF-kmeans on the Gun-

PointPointTrain dataset. The left part displays RMSE series

in each cluster, while the right part shows the corresponding

raw time series.

In this experiment, z-normalization misled time

series to be wrongly clustered together into the same

cluster. This is also why we chose not to use all the z-

normalized time series for calculating the overall Sil-

houettes score of z-kmeans. The score, in this case, is

unable to accurately reﬂect the true clustering quality

of z-kmeans.

Table 3: The clustering results of z-kmeans on GunPoint-

PointTrain wiht k set to 15.

Cluster ID # of time series Time series No.

1 11 17,22,30,31,32,39,45,52,53,56,57

2 9 6,12,13,14,27,37,42,55,65

3 7 21,34,36,47,50,59,62

4 5 10,18,28,64,66

5 5 16,19,33,44,51

6 4 1,2,7,29

7 4 3,11,43,67

8 4 8,9,23,49

9 4 20,38,41,63

10 3 4,35,54

11 3 26,40,61

12 3 46,48,58

13 2 15, 24

14 2 25,60

15 1 5

In terms of time consumption for NPF-kmeans

and z-kmeans, we exclusively evaluated both variants

for their preprocessing stages, as this is the only dif-

ference between them. The average time consumption

and standard deviation for NPF-kmeans are 5.575 sec

and 1.545 sec, respectively. On the other hand, the

average time consumption and standard deviation for

z-kmeans are 0.002 sec and 0.001 sec, respectively.

Since NP-Free is based on LSTM to generate a RMSE

series for each time series, it took more time than z-

normalization.

ICPRAM 2024 - 13th International Conference on Pattern Recognition Applications and Methods

474

Figure 3: The clustering results of z-kmeans on the Gun-

PointPointTrain dataset. The left part shows z-normalized

time series in each cluster, while the right part shows the

corresponding raw time series.

4.2 Experiment 2

In this experiment, we further evaluated the cluster-

ing performance of NPF-kmeans and z-kmeans on the

GunPointMaleTrain dataset. Figure 4(a) illustrates all

the raw time series in this dataset, Figure 4(b) shows

the corresponding RMSE time series generated by

NP-Free, and Figure 4(c) depicts the corresponding

time series generated by z-normalization.

Here we randomly selected 9 different values for

parameter k, ranging from 13 to 29, for both NPF-

kmeans and z-kmeans. This was conducted for the

same purpose outlined in the ﬁrst experiment: to

evaluate the overall Silhouettes scores of the two ap-

proaches across various settings of k. As the results

shown in Table 4, NPF-kmeans provides a higher

overall Silhouettes score than z-kmeans in all the

cases. Please note that all the Silhouettes scores

shown in Table 4 might appear low, as they were

calculated using the raw time series. As mentioned

earlier, although the scores are intended to compare

NPF-kmeans and z-kmeans, they cannot be used to

accurately represent the true clustering performance

of both variants. It is evident from Table 4 that NPF-

kmeans offers better clustering quality than z-kmeans,

regardless of the value of k.

Table 4: The overall Silhouettes score of NPF-kmeans and

z-kmeans on GunPointMaleTrain.

The value of k NPF-kmeans z-kmeans

13 0.2240 0.1512

15 0.2590 0.1986

16 0.3659 0.2231

18 0.3335 0.2284

20 0.3422 0.2108

23 0.2873 0.1858

26 0.2969 0.1339

28 0.2734 0.2085

29 0.2423 0.1991

To understand why z-kmeans performed worse

than NPF-kmeans, we closely examined the cluster-

ing results of z-kmeans on the GunPointMaleTrain

dataset, taking k =16 as an example. The left part

of Figure 5 illustrates all the z-normalized time series

in clusters 2, 5, and 6, while the right part of the same

ﬁgure depicts all the corresponding raw time series in

these clusters. It is evident that all the z-normalized

time series within each of these clusters are close

to each other. This is why z-kmeans assigned these

z-normalized time series to their respective clusters.

However, if mapping these z-normalized time series

back to their original raw time series reveals that not

all the time series within each of these three clusters

were appropriately grouped together (refer to the right

part of Figure 5). In other words, z-kmeans was mis-

led by z-normalization.

Regarding time consumption for preprocessing

GunPointMaleTrain, the average time consumption

and standard deviation for NPF-kmeans are 5.515 sec

and 1.378 sec, respectively. However, for z-kmeans,

they are 0.002 sec and 0.001 sec, respectively. Simi-

lar to the result shown in the ﬁrst experiment, NPF-

kmeans required more preprocessing time than z-

kmeans due to the adoption of NP-Free.

Evaluation of K-Means Time Series Clustering Based on Z-Normalization and NP-Free

475

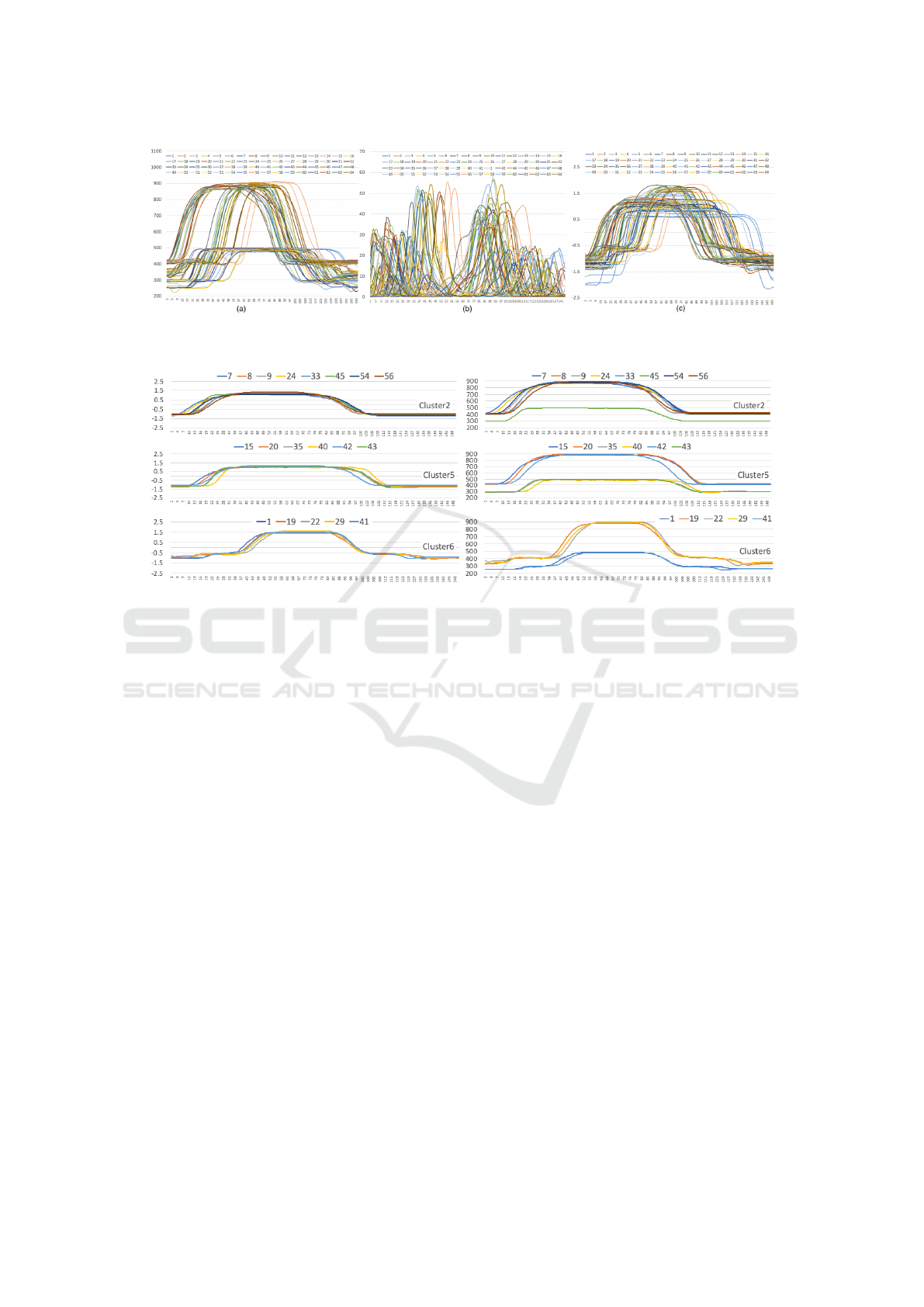
Figure 4: (a) Original raw time series in the GunPointMaleTrain dataset, (b) The RMSE series of each raw time series

generated by NP-Free, and (c) The z-normalized series of each raw time series generated by z-normalization.

Figure 5: The clustering results of z-kmeans on the GunPointMaleTrain dataset. The left part shows all the z-normalized time

series in clusters 2, 5, and 6, while the right part shows all the corresponding raw time series.

5 CONCLUSIONS AND FUTURE

WORK

In this study, we assessed the impact of utilizing

z-normalization and NP-Free as preprocessing tech-

niques on the performance of k-means time series

clustering. Two experiments were conducted us-

ing two real-world open-source time series datasets.

Our ﬁndings indicate that NPF-kmeans (k-means

based on NP-Free) exhibited superior clustering re-

sults compared to z-kmeans (k-means based on z-

normalization). The distinct advantage of NPF-

kmeans lies in its ability to provide a more faithful

representation of time series, which addresses con-

cerns associated with the potential misguidance of z-

normalization observed in z-kmeans.

However, our ﬁndings also indicate that the pre-

processing part in NPF-kmeans requires a longer time

due to the adoption of NP-Free, compared to z-

kmeans. Therefore, to enhance the efﬁciency of NPF-

kmeans when handling a large set of time series, it

is recommended to integrate NPF-kmeans with paral-

lelization in a multi-core environment or distributed

computing clusters. This integration facilitates the

acceleration of the preprocessing step, making NPF-

kmeans more scalable. Furthermore, it is recom-

mended to further enhance the performance of NP-

Free, with the goal of reducing the time required to

convert a time series into an RMSE series.

In our future work, we plan to expand our evalua-

tion by considering more time series clustering algo-

rithms, normalization techniques, datasets, and per-

formance metrics to provide a more holistic and com-

prehensive evaluation.

ACKNOWLEDGEMENTS

This work was partially conducted within the SFI-

NORCICS (https://www.ntnu.edu/norcics). This

project has received funding from the Research Coun-

cil of Norway under grant no. 310105 “Norwegian

Centre for Cybersecurity in Critical Sectors.”

REFERENCES

Aghabozorgi, S., Shirkhorshidi, A. S., and Wah, T. Y.

(2015). Time-series clustering–a decade review. In-

formation systems, 53:16–38.

ICPRAM 2024 - 13th International Conference on Pattern Recognition Applications and Methods

476

Ahmed, M., Seraj, R., and Islam, S. M. S. (2020). The

k-means algorithm: A comprehensive survey and per-

formance evaluation. Electronics, 9(8):1295.

Codecademy-Team (2022). Normalization. https://www.

codecademy.com/article/normalization. [Online;

accessed 14-September-2023].

Dau, H. A., Bagnall, A., Kamgar, K., Yeh, C.-C. M., Zhu,

Y., Gharghabi, S., Ratanamahatana, C. A., and Keogh,

E. (2019). The UCR time series archive. IEEE/CAA

Journal of Automatica Sinica, 6(6):1293–1305.

Deeplearning4j (2023). Introduction to core deeplearning4j

concepts. https://deeplearning4j.konduit.ai/. [Online;

accessed 14-September-2023].

Dhillon, I. S., Guan, Y., and Kulis, B. (2004). Kernel k-

means: spectral clustering and normalized cuts. In

Proceedings of the tenth ACM SIGKDD international

conference on Knowledge discovery and data mining,

pages 551–556.

Gupta, M. K. and Chandra, P. (2020). An empirical evalu-

ation of k-means clustering algorithm using different

distance/similarity metrics. In Proceedings of ICETIT

2019: Emerging Trends in Information Technology,

pages 884–892. Springer.

oppner, F. (2014). Less is more: similarity of time series

under linear transformations. In Proceedings of the

2014 SIAM International Conference on Data Mining,

pages 560–568. SIAM.

Ikotun, A. M., Ezugwu, A. E., Abualigah, L., Abuhaija,

B., and Heming, J. (2023). K-means clustering al-

gorithms: A comprehensive review, variants analysis,

and advances in the era of big data. Information Sci-

ences, 622:178–210.

Kapil, S. and Chawla, M. (2016). Performance evaluation

of k-means clustering algorithm with various distance

metrics. In 2016 IEEE 1st international conference

on power electronics, intelligent control and energy

systems (ICPEICES), pages 1–4. IEEE.

Kaufman, L. and Rousseeuw, P. J. (2009). Finding groups in

data: an introduction to cluster analysis. John Wiley

& Sons.

Kuncheva, L. I. and Vetrov, D. P. (2006). Evaluation of

stability of k-means cluster ensembles with respect

to random initialization. IEEE transactions on pat-

tern analysis and machine intelligence, 28(11):1798–

1808.

Lee, M.-C. and Lin, J.-C. (2023). RePAD2: Real-time,

lightweight, and adaptive anomaly detection for open-

ended time series. In Proceedings of the 8th Inter-

national Conference on Internet of Things, Big Data

and Security - IoTBDS, pages 208–217. INSTICC,

SciTePress. arXiv preprint arXiv:2303.00409.

Lee, M.-C., Lin, J.-C., and Gran, E. G. (2020). RePAD:

real-time proactive anomaly detection for time series.

In Advanced Information Networking and Applica-

tions: Proceedings of the 34th International Confer-

ence on Advanced Information Networking and Ap-

plications (AINA-2020), pages 1291–1302. Springer.

arXiv preprint arXiv:2001.08922.

Lee, M.-C., Lin, J.-C., and Gran, E. G. (2021). How far

should we look back to achieve effective real-time

time-series anomaly detection? In Advanced Infor-

mation Networking and Applications: Proceedings of

the 35th International Conference on Advanced In-

formation Networking and Applications (AINA-2021),

Volume 1, pages 136–148. Springer. arXiv preprint

arXiv:2102.06560.

Lee, M.-C., Lin, J.-C., and Stolz, V. (2023a). NP-Free:

A real-time normalization-free and parameter-tuning-

free representation approach for open-ended time se-

ries. https://arxiv.org/pdf/2304.06168.pdf. [Online;

accessed 14-September-2023].

Lee, M.-C., Lin, J.-C., and Stolz, V. (2023b). NP-

Free: A real-time normalization-free and parameter-

tuning-free representation approach for open-ended

time series. In 2023 IEEE 47th Annual Computers,

Software, and Applications Conference (COMPSAC),

pages 334–339.

Lloyd, S. (1982). Least squares quantization in pcm. IEEE

transactions on information theory, 28(2):129–137.

MacQueen, J. et al. (1967). Some methods for classiﬁcation

and analysis of multivariate observations. In Proceed-

ings of the ﬁfth Berkeley symposium on mathematical

statistics and probability, volume 1, pages 281–297.

Oakland, CA, USA.

Paepe, D. D., Avendano, D. N., and Hoecke, S. V. (2019).

Implications of z-normalization in the matrix proﬁle.

In International Conference on Pattern Recognition

Applications and Methods, pages 95–118. Springer.

Paparrizos, J. and Gravano, L. (2015). k-shape: Efﬁcient

and accurate clustering of time series. In Proceedings

of the 2015 ACM SIGMOD international conference

on management of data, pages 1855–1870.

Rousseeuw, P. J. (1987). Silhouettes: a graphical aid to

the interpretation and validation of cluster analysis.

Journal of computational and applied mathematics,

20:53–65.

Ruiz, L. G. B., Pegalajar, M., Arcucci, R., and Molina-

Solana, M. (2020). A time-series clustering methodol-

ogy for knowledge extraction in energy consumption

data. Expert Systems with Applications, 160:113731.

Senin, P. (2016). Z-normalization of time series. https:

//jmotif.github.io/sax-vsm site/morea/algorithm/znor

m.html. [Online; accessed 14-September-2023].

Tavenard, R., Faouzi, J., Vandewiele, G., Divo, F., Androz,

G., Holtz, C., Payne, M., Yurchak, R., Rußwurm, M.,

Kolar, K., and Woods, E. (2020). Tslearn, a machine

learning toolkit for time series data. Journal of Ma-

chine Learning Research, 21(118):1–6.

Vats, S. and Sagar, B. (2019). Performance evaluation of

k-means clustering on hadoop infrastructure. Journal

of Discrete Mathematical Sciences and Cryptography,

22(8):1349–1363.

Evaluation of K-Means Time Series Clustering Based on Z-Normalization and NP-Free

477