Particle and Cell Cluster Separation Based on Inertial Effects in

Rectangular Serpentine Channels

Michal Mul

ık

and Ivan Cimr

Cell-in-ﬂuid Biomedical Modelling & Computations Group, Faculty of Management Science and Informatics,

University of

Zilina, Slovakia

Keywords:

Microﬂuidics, Inertial Flow, Clusters, PyOIF, ESPResSo, Separation.

Abstract:

It is well-established that the inertial effect in microﬂuidics has a signiﬁcant impact on particle and cell cluster

separation. The outcomes are particularly dependent on the channel geometry and the particle and cell sus-

pensions introduced into the channel. In this study, we investigate various combinations related to the size of a

curved channel, ﬂuid velocity, and the size and elasticity of clusters. We quantitatively and qualitatively eval-

uate the behavior of the examined clusters with respect to separation potential. Computational results suggest

speciﬁc combinations of ﬂow parameters leading to efﬁcient particle and cell cluster separation.

1 INTRODUCTION

Under speciﬁc microﬂow conditions, ﬂuid inertia

dominates over viscous forces, allowing precise con-

trol and manipulation of suspended particles (Hood

et al., 2015). This has led to the development of tech-

niques to sort and separate particles based on size,

shape and deformability (Xu et al., 2021; Nivedita

et al., 2017; Liu et al., 2019; Warkiani et al., 2014).

Meandering channels induce complex ﬂow patterns

and particle behavior due to inertial effects of (Xiang

and Ni, 2022). Experimental studies, such as (Tri-

pathi et al., 2016) generating four Dean vortices with

two bends and (Zhang et al., 2014) focusing on high-

throughput plasma extraction using a secondary ﬂow-

assisted inertial microﬂuidic device, further investi-

gate these phenomena.

The inertial migration of particles was further ex-

plored in the work (Bug

nov

a and Cimr

ak, 2023),

which focused on solid particles and their separation

in curved channels of rectangular shape. It was ob-

served that as the particles increase in size, they tend

to concentrate and stabilize more in the center of the

channel. This leaves a signiﬁcant space for smaller

particles, which concentrate along the edges of the

channel, facilitating successful separation. The re-

sults demonstrate that not only are smaller cells capa-

ble of separating from larger ones, but in some cases,

https://orcid.org/0000-0001-5592-4524

https://orcid.org/0000-0002-0389-7891

they even leave the center of the channel completely

empty for a third type of even larger cells. This phe-

nomenon provides an intriguing possibility for triple

separation.

Over time, microﬂuidics has undergone signiﬁ-

cant breakthroughs and clariﬁcations, allowing for a

deeper exploration of phenomena and the continued

pursuit of answers to various questions. One such av-

enue includes the potential opportunity to leverage in-

ertial effects in bio-medicine or medicine in general.

In living organisms, such as the human body, iner-

tial ﬂows are encountered, for instance, at vascular

bifurcations. The fact that cells divide and travel into

different branches provides us with a suitable oppor-

tunity to investigate where they are most likely to go.

This could enable the capture of rare cells from blood

(Tanaka et al., 2012). A similar concept is mentioned

in the article (Gossett et al., 2012), where, in the dis-

cussion of cell deformation, they were able to separate

diseased red blood cells from healthy ones or search

for sepsis markers.

In the article (Bug

nov

a and Cimr

ak, 2023), de-

tailed information about inertial microﬂuidics, com-

putational models, and curved microchannels is pro-

vided. The study utilized the Lattice-Boltzmann

method, a technique also employed in our model. The

alignment of cells is correlated with the Reynolds

number, directly linked to the ﬂuid velocity. In the

model, as the ﬂuid velocity increases, the Reynolds

number becomes larger, leading to a more precise sta-

bilization of cells at a speciﬁc level within the chan-

Mulík, M. and Cimrák, I.

Particle and Cell Cluster Separation Based on Inertial Effects in Rectangular Serpentine Channels.

DOI: 10.5220/0012547300003657

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 17th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2024) - Volume 1, pages 553-560

ISBN: 978-989-758-688-0; ISSN: 2184-4305

553

nel. However, in the mentioned article, the discus-

sion remained focused on the level of small and solid

particles that did not have the opportunity to deform.

Our work investigates larger objects, which are under-

standably more prone to deformation. Therefore, we

have included this property in our examination.

Contents of this Work

In this study, we employed two geometries of sizes

160 × 80µm and 200 × 64µm. For the ﬁrst time in the

model, we introduced rounded edges to better mimic

reality, as blood vessels in the body exhibit curvature.

We opted for larger geometries compared to those in

the article (Bug

nov

a and Cimr

ak, 2023) since the

cells themselves and the subsequent cell clusters were

about two times larger. Consequently, we needed to

create a space where cell clusters would have greater

freedom in the ﬂow.

In Section 2, we brieﬂy explain inertial forces in

microﬂows. In Section 3, we will explore the funda-

mental types of channels commonly used in inertial

microﬂuidics worldwide and take a closer look at the

model we selected. Speciﬁcally, we will focus on two

channel sizes. Subsequently, we present the cell and

cell cluster model, where we utilized three sizes for

each type. Finally, we use two different values of cell

elasticity based on the well-known observation that

some cells exhibit greater deformability compared to

others when exposed to ﬂow in S channels. In the

concluding Sections 4.1 and 4.2, we comprehensively

summarize the qualitative and quantitative results ob-

tained from our work through simulations. We expect

to gain valuable insights into the spatial distribution

of the cells over time in relation to the inertial ﬂows,

namely Dean ﬂows, induced by the secondary ﬂow.

2 BASIC OVERVIEW OF

INERTIAL FOCUSING

The concentration of particles approximately 60%

away from the tube centerline in straight channels

results from a dynamic equilibrium between inertial

shear gradient lift forces, directing the particles to-

wards the wall, and wall repulsion forces generated by

elevated pressure between the particles and the chan-

nel wall (Matas et al., 2009). Modifying the channel

cross-section or introducing curvature through ser-

pentine or spiral geometries alters the distribution and

positions of lateral equilibrium, potentially expedit-

ing the lateral focusing of particles (Martel and Toner,

2014).

The forces governing this behavior encompass

three main components: the wall interaction lift

forces, the shear gradient lift forces, and the

secondary-ﬂow induced Dean drag forces. All three

mentioned mechanisms constitute a complex system

where three different principles interact, all dependent

on the particle size, channel characteristics, ﬂuid ve-

locity, and the elasticity of particles or cells. Compu-

tational modeling can analyze the impact under spe-

ciﬁc parameters and evaluate the sorting potential of

various suspensions.

3 MODEL AND

COMPUTATIONAL SETUP

3.1 Numerical Model

We employed a well-established computational

model capable of simulating ﬂuid with immersed ob-

jects. In this model, the ﬂuid is modelled by the

lattice-Boltzmann (LB) method (Arnold et al., 2013).

The cell membrane is represented by a network of tri-

angles, and their interaction is determined by elastic

coefﬁcients, allowing us to control the magnitude of

deformation forces. In our case, we additionally re-

inforced the cell interiors with edges forming tetrahe-

dral mesh to address the high ﬂuid velocity, which, in

a way, limits the deformation of cell clusters. More

detailed information on this can be found in the arti-

cles (Jan

cigov

a et al., 2020; Jancigova and Tothova,

2014; Bachrat

y et al., 2018). The mentioned model

underwent veriﬁcation and validation for its applica-

tion, as detailed in (Jan

cigov

a et al., 2020; Jan

cigov

2020; Tothova et al., 2015).

3.2 Channel Geometry

In (Bug

nov

a and Cimr

ak, 2023), the channel geom-

etry with sharp edges was used. In this work, we ex-

tended the model with rounded edges, leading to a

smoother ﬂow of the ﬂuid as shown in Figure 1. Due

to the periodicity of the channel, we will model only

two S-sections with periodical boundaries on the in-

ﬂow and outﬂow to decrease computational complex-

ity.

Due to the signiﬁcant computational demands, our

model includes only a curved section in the shape of

an ”S”, which was periodically repeated several times

until the clusters stabilized in the ﬂow. The basic idea

depicted in Figure 2 is that particles or clusters, when

initially seeded randomly in the channel near the ob-

servation line, ﬂow through one S-section towards a

BIOINFORMATICS 2024 - 15th International Conference on Bioinformatics Models, Methods and Algorithms

554

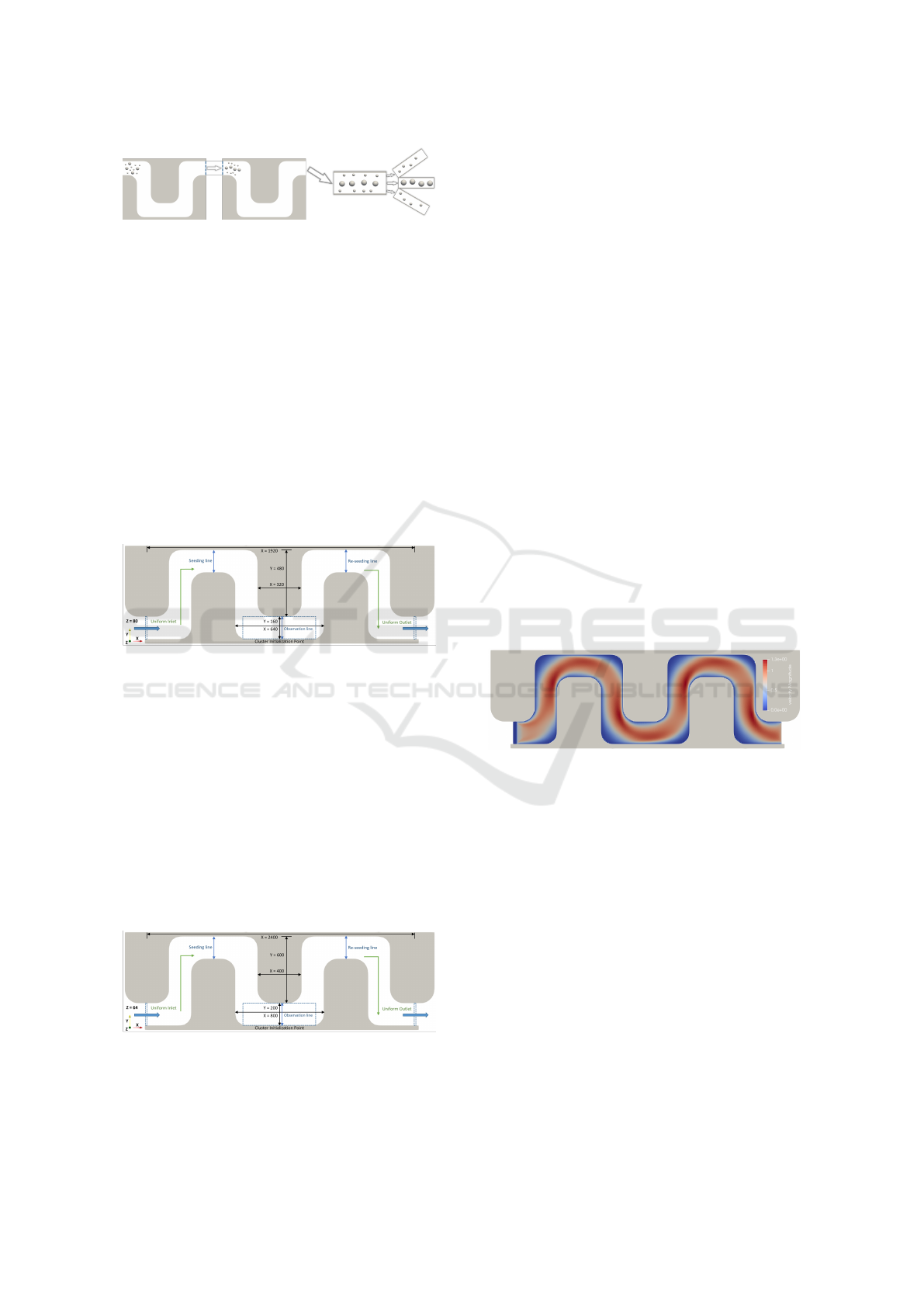
Figure 1: Separation of cells of different sizes based on the

use of a periodically repeating curved channel with round

edges in the shape of an ”S.”.

speciﬁc re-seeding line and are subsequently longi-

tudinally re-seeded back to the seeding line by al-

tering the X-coordinates while preserving the Y- and

Z-coordinates. This approach allowed us to conduct

simulations without creating an entire channel con-

sisting of 40 or 80 repeating S-sections. Moreover,

the cluster velocity in the ﬂuid is maintained after the

transfer.

In addition to the seeding and re-seeding lines,

we also consider an observation line in the middle of

the channel. If a cluster passes through this line, we

record its center coordinates in a ﬁle. The outcome

for each cluster is then its trajectory in a graph, illus-

trating where the cluster has stabilized.

Figure 2: Detailed description of cross-section 160 × 80µm.

The orientation with respect to the X, Y, and Z axes is de-

scribed by the three-dimensional axis label in the lower-left

corner of the image.

When experimenting with different sizes of the

cross section we concluded that cell clusters need suf-

ﬁcient space to rotate freely and for example, cross

section 80 × 40 used in (Bug

nov

a and Cimr

ak, 2023)

is too narrow for clusters to move out of the center

of the cross section. These preliminary tests led to

choosing two different channel sizes. The dimensions

of both geometries are detailed in Figure 2 for the

cross-section 160 × 80µm and Figure 3 for the cross-

section 200 × 64µm, where all lengths are described

in micrometers.

Figure 3: Detailed description of cross-section 200 × 64µm.

The orientation with respect to the X, Y, and Z axes is de-

scribed by the three-dimensional axis label in the lower-left

corner of the image.

3.3 Fluid Set-up

The imposition of uniform boundary conditions at the

inlet and outlet serves to determine the average veloc-

ity within the channel, a factor directly proportional

to the volumetric ﬂow rate. In the PyOIF framework,

achieving this involves implementing a specialized

velocity boundary equipped with pre-deﬁned constant

values for the velocity ﬁeld at the boundary points.

Values of the inlet conditions and the correspond-

ing Reynolds numbers are presented in Table 1.

Table 1: Fluid velocity parameters in 160 × 80µm curved

channel. Values in the other cross-section are similar.

Reynolds number [−] 19.2 37.3 48 64

Average velocity [µm/µs] 0.18 0.35 0.45 0.6

Our focus lies in examining ﬂows within scenarios

that hold physical relevance. Speciﬁcally, we investi-

gate ﬂuids with a density and viscosity akin to physi-

ological solutions or water, characterized by values of

1000kg/m

and 10

−3

Pa.s, respectively. In the sphere

of inertial microﬂuidics, where the Reynolds number

is a pertinent parameter, we adhere to ranges up to 100

(Ying and Lina, 2020). To encompass a diverse set of

conditions, we explore four distinct average velocities

within the channel, reaching up to 0.6 µm/µs, thereby

allowing the Reynolds number to vary up to 64.

Figure 4: The ﬂuid ﬂowing in the channel at the highest

Reynolds number 64. The units of the displayed scale are

in µm/µs.

A visual representation of the ﬂuid ﬂowing

throughout the simulation can be seen in Figure 4.

The more saturated red color, the higher the ﬂuid ve-

locity at that location. Flow direction is from left to

right. The areas with deep blue indicate almost zero

ﬂuid velocity.

3.4 Cell and Cluster Models

Similar to the membrane model of red blood cells

composed of triangular mesh, the cluster model is

composed of a tetrahedral mesh. Given the presence

of stiffer cancer clusters, we reinforced the cell’s in-

terior with additional edges forming complete cover

of cell’s interior by tetrahedrons to restrict excessive

deformation due to the high ﬂuid velocity in the sim-

ulation. The edges of tetrahedrons are modelled as

Particle and Cell Cluster Separation Based on Inertial Effects in Rectangular Serpentine Channels

555

springs with given relaxed length and speciﬁc stiff-

ness. To get stiffer cells or clusters, higher values of

edge stiffness was used. In Figure 5, the interiors of a

single cell and a cluster are depicted, respectively.

As a model for cancer cells, we opted for a spher-

ical shape as it closely approximates the morphology

of most real types of cancer cells within the body. The

length of tetrahedral edges was primarily determined

by the size of the object, as the number of points in

the tetrahedral network remained constant.

Figure 5: The entire cell (top left), cutaway of the cell (top

right), the entire cluster (bottom left) and a cutaway of the

cluster (bottom right). The cuts reveal the interiors ﬁlled

with walls.

Based on the actual sizes of cancer cell clusters,

we determined three basic sizes for a cluster with a

single cell and three for a cluster with two cells. On

closer inspection, in one case, the size of a single cell

is even equal to that of two cells placed side by side.

A comparison of sizes for clusters containing one or

two cells is illustrated in Figure 6.

Figure 6: The cluster containing a single cell (left), and the

cluster with two cells (right). Sizes are given in microme-

ters.

The cell adhesion in a cluster can be simulated in

two different ways. One way is to use an attractive-

repulsive Lennard-Jones or Morse-type interaction,

where two separate cells are attracted to each other

when they are far apart and repelled when they are

too close. This approach ensures that cells can slide

past each other, and at high ﬂuid velocities, it may

lead to their separation. However, the ﬂuid velocity

we use almost always separates these cells, making it

an unsuitable method.

Another way for cells to be connected in a cluster

is by such a strong bond that cells do not slide over

each other and the bond is ﬁxed. To simulate this

behavior, we used the second method of connecting

cells through a shared membrane. In this case, the en-

tire cluster behaves as one object. As seen in Figure 6

on the right, the cluster contains two connected cells.

These methods that help us simulate the cell adhesion

in a cluster are described in more detail in the article

(Jan

cigov

a et al., 2022).

4 COMPUTATIONAL RESULTS

In this section, we will delve into the results of sim-

ulations in an S-shaped curved channel. In this case,

we utilized a single basic cluster of two cells (here-

inafter referred to as the ”two-in-line” cluster). How-

ever, technically, we will also treat a single cell as

a cluster of cells composed of only one cell, which

we now refer to as ”CTC”, an acronym for ”circu-

lating tumour cell”. For each cluster type, we will

distinguish three different sizes concerning the diam-

eter. For the two-in-line cluster we used diameters of

20, 30, and 40 µm, meaning that one cell in the two-

in-line cluster had a diameter of 10, 15, and 20 µm.

For the single-cell cluster, we aimed to approach its

largest size to the smallest two-in-line cluster, so we

chose the same diameters of 10, 15, and 20 µm. The

sizes of clusters were chosen based on the article (An-

derson et al., 2017).

In addition to the cluster type and size, we incor-

porated the elasticity of the cell. Clusters were di-

vided into more and less elastic ones under the names

”solid” and ”elastic”. Solid clusters represented the

stiffest cells that had almost no possibility of defor-

mation during ﬂow in the channels, while elastic ones

had the ability to deform. It should be noted that both

types of clusters had an internal ﬁll, so we will talk

about one important and only used elastic parameter

called k

, which represents the edge stiffness. The dif-

ference between elastic cluster with k

= 0.5 and solid

cluster with k

= 1.0 can be seen in Figure 7. Top

row depicts clusters close to the channel center with

low shear rates. This implies minimal deformation of

the clusters. The second row depicts clusters at po-

sitions near the wall with high shear rates, leading to

signiﬁcant deformation of more elastic cluster while

the solid one remains fairly rigid. The simulations in

Figure 7 were conducted at Re = 64.

As mentioned before, we conducted simulations

with four ﬂuid velocities corresponding to four values

of Reynolds number, as indicated in Table 1. For com-

pleteness, it should be noted that we used two differ-

ent channel sizes with cross-sections of 160 × 80µm

and 200 × 64µm. Further details about individual

channel geometries are already described in Section

3.2.

BIOINFORMATICS 2024 - 15th International Conference on Bioinformatics Models, Methods and Algorithms

556

Figure 7: The deformation of a two-in-line cluster with k

0.5 (left column) and k

= 1.0 (right column). Deformation

at low shear rates depicted in top row and at high shear rates

in bottom row.

The initial seeding line for generating cluster posi-

tions is delineated in Figures 2 and 3. Distinct random

positions for clusters were generated for each geom-

etry. Additionally, the initial rotation of clusters was

randomized for each geometry, given the absence of

a clear explanation regarding whether the initial ro-

tation signiﬁcantly inﬂuences simulation outcomes.

As these are simple clusters composed of one or two

cells, we did not attribute signiﬁcant emphasis to this

aspect.

All numerical results were subsequently repre-

sented by graphs, facilitating comparisons. In the fol-

lowing Subsections 4.1 and 4.2, we will present the

most useful comparisons.

4.1 Quantitative Analysis of Flow

Patterns

From a quantitative perspective, we focused on ana-

lyzing data obtained from simulations, categorizing

it into ﬁve parts for better clarity: channel geome-

try, ﬂuid velocity, cluster type, cluster size, and clus-

ter elasticity, in that order. All results were primarily

compared in terms of the separation of different clus-

ters, where the main role was played by inertial ﬂow,

speciﬁcally the Dean effect.

For a general overview, each simulation included

28 clusters of cells. The simulation ran until each

cluster crossed the observation line 40 times. How-

ever, it should be noted that especially at the highest

ﬂuid velocity Re = 64 and channel size of 160 × 80µm

with CTCs, we concluded that they did not have

enough time to stabilize within 40 passes. Therefore,

we increased the number of passes to 80 for them to

stabilize more effectively within the ﬂow. For com-

parison, you can refer to Figure 8, where a signiﬁ-

cant difference between 40 and 80 passes is evident.

For all subsequent comparisons in graph form, results

from 80 passes were used.

For quantitative analysis, Figure 9 serves us the

most, where it is clearly visible that in some cases,

clusters can linger near the channel walls, creating

space in the middle of the channel for other clusters

that can be separated from the other lateral clusters.

4.1.1 Analysis of CTCs

At ﬁrst glance, CTCs in graphs (C), (D), (G), and (H)

seem to linger the most on the sides of the channel.

The only differences are the solid and elastic CTCs in

graphs (C) and (D) for the geometry of 160 × 80µm,

ﬂuid velocity Re = 64, and a diameter of 20µm, which

linger more in the middle of the channel. Based on the

obtained information, we can infer that they can be

separated from the smallest CTCs with a diameter of

10µm. It should be mentioned that in the (H) graph,

the largest CTCs at the slowest speed are scattered

across the entire width. This result is due to the small

number of passes, as the cells have not yet had time

to settle. For a better understanding, we can observe

the changes in the ongoing settling in Figure 10.

4.1.2 Analysis of Two-in-Line Clusters

In the case of two-in-line clusters, the behavior in

the ﬂow is not that straightforward. The trend for

the largest clusters remains consistent with single-cell

clusters, settling in the center of the channel. The only

instances where they concentrate at the channel edges

occur at the highest velocity, Re = 64, and a geom-

etry of 160 × 80µm, as seen in graphs (A) and (B)

in the last columns marked in red. Conversely, the

smallest two-in-line clusters marked in blue tended to

settle regularly at the channel edges. Exceptions are

speciﬁc cases, as observed in graphs (B) and (C) at

Re = 48 and graph (F) at Re = 19.2.

Medium-sized two-in-line clusters marked in yel-

low generally behaved similarly to two-in-line clus-

ters, except for isolated cases observed in graphs (A)

and (E), where the settling level coincided with the

smallest two-in-line clusters. From the analysis, it

can be inferred that there is a possibility of separat-

ing two-in-line clusters from other two-in-line clus-

ters based on their sizes, as seen in the mentioned

graph (E) at all ﬂuid velocities or at speciﬁc ﬂuid ve-

locities in graphs (A), (B), or (F).

An interesting aspect is that for two-in-line clus-

ters, elasticity plays a role for the ﬁrst time, as we

could potentially separate clusters with diameters 20

Particle and Cell Cluster Separation Based on Inertial Effects in Rectangular Serpentine Channels

557

Figure 8: Examples of a cluster formed by CTCs with a diameter of 10, 15 and 20µm, solid and elastic type, at a cross-section

of 160 × 80µm.The Y-axis represents the channel width, and the X-axis represents the number of passes. The dashed line

indicates the state after 40 passes through the channel.

Figure 9: Complete set of 96 simulations, where each graph contains exactly 12 of them. Each graph has 4 columns for 4

values of Reynolds number mentioned in Table 1 from the smallest to the largest from left to right. Each column has results

from three simulations, differing in the cluster size. Regarding the legends, blue squares represent the smallest clusters, yellow

diamonds represent medium-sized clusters, and red triangles represent the largest clusters. In general, these are analogously

transformed graphs from 8 into a concise form for better visualization, where data were taken only from the last passage of all

cells in the simulation. All graphs indicate the locations where cell clusters stabilized. The ﬁrst row of graphs A-D denotes the

last passage of cells from channels with cross-section 160 × 80µm, and the second row E-H with cross-section 200 × 64µm.

Graphs (A), (B), (E), and (F) represent the stabilization of two-in-line clusters, and graphs (C), (D), (G), and (H) of CTCs.

Regarding the elasticity of clusters, graphs (A), (C), (E), (G) are solid, and (B), (D), (F), and (H) are elastic.

Figure 10: The graphs represent the settling of elastic CTCs

over 40 passes, ranging from the slowest ﬂuid speed, where

Re = 19.2, to the fastest, where Re = 64. In this case, a

cross-section of 200 × 64µm was used, and the cells were

elastic.

and 30µm, that have different elasticity. This phe-

nomenon can be observed, for example, by comparing

graphs (E) and (F) at the lowest velocity Re = 19.2 in

case of the smallest clusters, and at all velocities in

case of medium-sized clusters, where solid clusters

concentrate on the sides of the channel, and elastic

clusters in its center.

4.1.3 Comparison Between CTC and

Two-in-Line Cluster

When comparing the same geometries but different

clusters, namely CTC and two-in-line clusters, we

come to the conclusion that separation is also possi-

ble under certain conditions. Considering the ﬁrst row

of graphs with the 160 × 80µm geometry, the smallest

two-in-line clusters with a diameter of 20µm in graphs

(A) and (B) could be separated from CTC in graphs

at a ﬂuid velocity of Re = 48. This is because CTC

would again stabilize at the sides of the channel, while

two-in-line clusters would stabilize in the center.

The same case applies to medium-sized and the

largest two-in-line clusters with diameters of 30 and

40µm. However, the largest two-in-line clusters at a

ﬂuid velocity of Re = 37.3 could be separated from

any size of CTC. The same applies to Re = 19.2 and

elastic two-in-line clusters. However, the geometry

200 × 64µm, which provides more space for cell sta-

bilization at the sides of the channel due to its wider

width, offers a more obvious separation possibility.

For the smallest elastic two-in-line cluster in graph

(F), there is an opportunity for separation at the slow-

BIOINFORMATICS 2024 - 15th International Conference on Bioinformatics Models, Methods and Algorithms

558

est ﬂuid velocity of Re = 19.2 from any size of CTC in

graphs (G) and (H). In this case, the separation possi-

bility for elastic CTC would depend on the number of

passes. The same applies when considering medium-

sized and elastic two-in-line clusters in graph (F),

where the separation is possible regardless of the ﬂuid

velocity Re chosen. However, the largest two-in-line

clusters could probably be separated most effectively

from any size of CTC, as it is independent of both

elasticity and ﬂuid velocity.

4.2 Qualitative Analysis of Flow

Patterns

From a qualitative perspective, we observed the ﬂow

of CTC and two-in-line clusters in the 160 × 80µm

channel. The movement of a single solid two-in-line

cluster can be seen at the highest velocity in Figure

11, depicting the cluster’s movement in three consec-

utive S-sections. The cluster’s motion was recorded

after approximately 20 passes, indicating a steady

ﬂow.

At ﬁrst glance, collisions with the wall can be ob-

served at each upper right turn. Two-in-line clusters,

in general, do not have a reason to rotate around their

center. Nevertheless, during gentle shear ﬂow gener-

ated by collisions and movement along the wall, the

cluster tends to rotate around its own center a few

times in succession. This rotation involves a change

in the order of cells, with the most pronounced ro-

tations occurring during the ﬁrst two upper turns, as

the cluster is aligned longitudinally along the X-axis.

In the third turn, where the cluster is aligned width-

wise, this rotation type does not occur. In this case,

the cluster appears to rotate like a wheel.

It is important to note that collisions of CTC and

clusters with walls are not entirely safe from a hu-

man health perspective. Further information on the

interactions of clusters with walls can be found in the

article (Jan

cigov

a et al., 2022).

Figure 11: Three S-shaped channel passes of the largest

solid two-in-line cluster in the geometry of 160 × 80µm at

the highest velocity of Re = 64. One cell out of two is

marked in red to better observe the movement, especially

the rotation of each cell in the cluster.

5 CONCLUSION

The basis of the work was derived from the princi-

ples of inertial ﬂows, namely Dean ﬂows. Thanks

to them, we could observe how clusters, after several

passes through the channel, slowly stabilized either

in the center or at the edges of the channel. This

phenomenon allowed us to study the separation of

cell clusters, which depended on their properties or

the properties of the surrounding environment in the

model in which we released them.

Initially, we worked on a model of a microﬂu-

idic channel in an S shape, which had rounded edges

for simpler ﬂuid ﬂow. As a next step, we created

new channel geometry sizes with dimensions of 160×

80µm and 200 × 64µm to provide more space for the

stabilization of cell clusters.

We focused mainly on studying a simple cluster

formed from a single cell, also known as CTC, and

a two-in-line cluster formed from two cells. Fluid

was released at four different velocities expressed by

the Reynolds number Re = 19.2,37.3,48, and 64, in

which we released clusters with three different cell

diameters, 10, 15, and 20µm. These clusters also had

two different elasticities, so some were solid, where

= 1.0, and others were elastic, for which k

= 0.5,

meaning they had more opportunity to deform during

the simulation than solid ones.

As for the computational complexity of each sim-

ulation, each one ran for 3 to 7 days until each clus-

ter in the simulation had a certain number of passes.

Mostly, it was 40 passes. In a speciﬁc case where it

took longer for the clusters to stabilize, we increased

the number of passes to 80.

The obtained numerical data of cluster positions

were analyzed from each simulation using appropri-

ate graphs. We summarized and combined all the

graphs, where it was very well visible which clusters

stabilized at the edges of the channel and which, on

the contrary, more in its central part with respect to

the channel height, i.e., the Y-axis. For some combi-

nations of sizes and elasticity of CTC and clusters, we

found that separation would be highly probable.

ACKNOWLEDGEMENTS

This research was supported by the Ministry of Ed-

ucation, Science, Research and Sport of the Slovak

Republic under the contract No. VEGA 1/0369/22.

Particle and Cell Cluster Separation Based on Inertial Effects in Rectangular Serpentine Channels

559

REFERENCES

Anderson, K. J., de Guillebon, A., Hughes, A. D., Wang,

W., and King, M. R. (2017). Effect of circulating

tumor cell aggregate conﬁguration on hemodynamic

transport and wall contact. Mathematical biosciences,

294:181–194.

Arnold, A., Lenz, O., Kesselheim, S., Weeber, R., Fahren-

berger, F., Roehm, D., Ko

sovan, P., and Holm, C.

(2013). ESPResSo 3.1: Molecular dynamics soft-

ware for coarse-grained models. In Meshfree Methods

for Partial Differential Equations VI, Lecture notes in

computational science and engineering, pages 1–23.

Springer Berlin Heidelberg, Berlin, Heidelberg.

Bachrat

y, H., Bachrat

a, K., Chovanec, M., Kaj

anek, F.,

Smie

skov

a, M., and Slav

ık, M. (2018). Simulation

of blood ﬂow in microﬂuidic devices for analysing of

video from real experiments. In Bioinformatics and

Biomedical Engineering, Lecture notes in computer

science, pages 279–289. Springer International Pub-

lishing, Cham.

Bug

nov

a, A. and Cimr

ak, I. (2023). Computational study

of particle separation based on inertial effects in rect-

angular serpentine channels with different aspect ra-

tios. In Proceedings of the 16th International Joint

Conference on Biomedical Engineering Systems and

Technologies (BIOSTEC 2023) - Volume 3: BIOIN-

FORMATICS, pages 284–291. INSTICC, SciTePress.

Gossett, D. R., Tse, H. T. K., Lee, S. A., Ying, Y., Lindgren,

A. G., Yang, O. O., Rao, J., Clark, A. T., and Di Carlo,

D. (2012). Hydrodynamic stretching of single cells for

large population mechanical phenotyping. Proc. Natl.

Acad. Sci. U. S. A., 109(20):7630–7635.

Hood, K., Lee, S., and Roper, M. (2015). Inertial migration

of a rigid sphere in three-dimensional poiseuille ﬂow.

J. Fluid Mech., 765:452–479.

Jan

cigov

a, I. (2020). Computational modeling of blood

ﬂow with rare cell in a microbifurcation. In Lec-

ture Notes in Computational Vision and Biomechan-

ics, Lecture notes in computational vision and biome-

chanics, pages 518–525. Springer International Pub-

lishing, Cham.

Jan

cigov

a, I., Koval

ıkov

a, K., Bohinikov

a, A., and

Cimr

ak, I. (2020). Spring-network model of red blood

cell: From membrane mechanics to validation. Int. J.

Numer. Methods Fluids, 92(10):1368–1393.

Jancigova, I. and Tothova, R. (2014). Scalability of forces in

mesh-based models of elastic objects. In 2014 ELEK-

TRO. IEEE.

Jan

cigov

a, I., Koval

ıkov

a, K., Weeber, R., and Cimr

ak, I.

(2020). Pyoif: Computational tool for modelling of

multi-cell ﬂows in complex geometries. PLoS Com-

putational Biology, 16:e1008249.

Jan

cigov

a, I., Mul

ık, M., and Cimr

ak, I. (2022). Contact

area of cell cluster in a simple bifurcation. In 2022

ELEKTRO (ELEKTRO), pages 1–5.

Liu, N., Petchakup, C., Tay, H. M., Li, K. H. H., and Hou,

H. W. (2019). Spiral inertial microﬂuidics for cell sep-

aration and biomedical applications. Applications of

Microﬂuidic Systems in Biology and Medicine, pages

99–150.

Martel, J. M. and Toner, M. (2014). Inertial focusing in

microﬂuidics. Annu. Rev. Biomed. Eng., 16(1):371–

396.

Matas, J.-P., Morris, J. F., and Guazzelli,

E. (2009). Lateral

force on a rigid sphere in large-inertia laminar pipe

ﬂow. J. Fluid Mech., 621:59–67.

Nivedita, N., Ligrani, P., and Papautsky, I. (2017). Dean

ﬂow dynamics in low-aspect ratio spiral microchan-

nels. Scientiﬁc Reports, 7(1):44072.

Tanaka, T., Ishikawa, T., Numayama-Tsuruta, K., Imai, Y.,

Ueno, H., Matsuki, N., and Yamaguchi, T. (2012).

Separation of cancer cells from a red blood cell sus-

pension using inertial force. Lab Chip, 12(21):4336–

4343.

Tothova, R., Jancigova, I., and Busik, M. (2015). Calibra-

tion of elastic coefﬁcients for spring-network model

of red blood cell. In 2015 International Conference

on Information and Digital Technologies. IEEE.

Tripathi, S., Kumar, A., Bala Varun Kumar, Y., and

Agrawal, A. (2016). Three-dimensional hydrody-

namic ﬂow focusing of dye, particles and cells in a

microﬂuidic device by employing two bends of oppo-

site curvature. Microﬂuidics and Nanoﬂuidics, 20:1–

14.

Warkiani, M. E., Guan, G., Luan, K. B., Lee, W. C., Bhagat,

A. A. S., Chaudhuri, P. K., Tan, D. S.-W., Lim, W. T.,

Lee, S. C., Chen, P. C., et al. (2014). Slanted spiral

microﬂuidics for the ultra-fast, label-free isolation of

circulating tumor cells. Lab on a Chip, 14(1):128–

137.

Xiang, N. and Ni, Z. (2022). Inertial microﬂuidics: current

status, challenges, and future opportunities. Lab on a

Chip, 22(24):4792–4804.

Xu, X., Huang, X., Sun, J., Wang, R., Yao, J., Han, W., Wei,

M., Chen, J., Guo, J., Sun, L., et al. (2021). Recent

progress of inertial microﬂuidic-based cell separation.

Analyst, 146(23):7070–7086.

Ying, Y. and Lina, Y. (2020). Inertial focusing and separa-

tion of particles in similar curved channels. Scientiﬁc

reports, natureresearch, 391:123570.

Zhang, J., Yan, S., Li, W., Alici, G., and Nguyen, N.-T.

(2014). High throughput extraction of plasma using

a secondary ﬂow-aided inertial microﬂuidic device.

RSC Adv., 4:33149–33159.

BIOINFORMATICS 2024 - 15th International Conference on Bioinformatics Models, Methods and Algorithms

560