Conformance Checking on Timed Automaton Process Models

Sohei Ito

1 a

and Kento Hamae

School of Information and Data Sciences, Nagasaki University, 1-14 Bunkyo-machi, Nagasaki City, Japan

FCC Techno, 4-25-30 Ohashi, Minami-ku, Fukuoka City, Japan

Keywords:

Conformance Checking, Timed Automaton, Business Process Model, Process Mining.

Abstract:

Conformance checking is a kind of process analysis methods that evaluate the difference between modeled

behavior and recorded behavior of a process. Usual conformance checking evaluates such difference (called

ﬁtness) based on only the order of executed tasks. Therefore, one cannot correctly evaluate ﬁtness for process

executions that violate the task completion time required by the model. In this paper, we consider process

models with time constraints given as timed automata, and propose a method for evaluating ﬁtness of timed

traces with timed automaton process models. We implement two algorithms to compute the ﬁtness we pro-

posed, namely a naive exhaustive search and A* algorithm, and show experimental results with simple process

models.

1 INTRODUCTION

A process is a collection of tasks (or activities) or-

ganized to achieve a certain goal. Processes appear

everywhere, and business processes in particular are a

prime example. Since organizations are usually com-

posed of many business processes, improving their

efﬁciency is one of the social issues that have been

addressed over the years.

A method called process mining (van der Aalst,

2016) has been attracting attention for the systematic

design, evaluation, and improvement of business pro-

cesses. Process mining is a collective term for meth-

ods that use process models and process execution

records (called event logs) to perform various analy-

ses. Event logs come from many sources: a database

system such as patient data in a hospital, a transaction

log of a trading system, an ERP system, etc.

Conformance checking is one of the methods of

process mining. It quantitatively evaluate how well a

process model conforms to the actual behavior (i.e.

event log). Process models are usually obtained

through various abstractions, and thus it is not un-

common for errors to be introduced during the mod-

eling process. Moreover, processes themselves vary

due to changes in the environment and technological

updates. For these reasons, conformance checking is

useful to analyze the difference between the model

and the process executions.

https://orcid.org/0000-0002-7029-664X

Several methods have been proposed for confor-

mance checking (Weidlich et al., 2011a; Zha et al.,

2010; Weidlich et al., 2011b; Polyvyanyy et al., 2014;

Rozinat, 2010; vanden Broucke et al., 2014b; vanden

Broucke et al., 2014a; Adriansyah, 2014; Adriansyah

et al., 2011a; Adriansyah et al., 2011b; van der Aalst

et al., 2012). However, these methods only use ac-

tivity names for conformance checking, and thus only

interested in whether the order of activities conform to

the model. In general, however, event logs contain a

lot of information, such as timestamps for each activ-

ity and unique attributes for each activity type (e.g.,

“price” for the activity “send quote”). If a process

model determines its behavior depending on such at-

tributes, it is desirable to check conformance consid-

ering not only the order of activities but also attribute

values of activities. For example, in a negotiation pro-

cess in a trading company (e.g. (Ito et al., 2018)),

a salesperson should send a quote within a set time

limit, and the quoted price should be within a reason-

able bound. It is desirable to check conformance of

such constraints besides the correctness of task exe-

cution order.

Therefore, we propose a method for checking con-

formance between process models with the time at-

tribute and timed traces (a trace is an execution of a

process). The reason why we only focus on the time

attribute is that almost all event logs contain times-

tamps. For the formalism of process models, we adopt

the timed automaton. We regard locations of a timed

Ito, S. and Hamae, K.

Conformance Checking on Timed Automaton Process Models.

DOI: 10.5220/0012548800003690

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 26th International Conference on Enterprise Information Systems (ICEIS 2024) - Volume 2, pages 545-556

ISBN: 978-989-758-692-7; ISSN: 2184-4992

545

automaton as activities. Traces are sequences of pairs

of an activity and a timestamp (i.e. completion time

of the activity), that is, an event log consists of timed

traces. Since an execution of a timed automaton is

a sequence of pairs of locations and times, we can

naturally regard timed traces as executions of a timed

automaton.

Our proposed method of conformance checking

consists of two steps. The ﬁrst step is to evaluate con-

formance based only on the order of activities. We

call this the order ﬁtness, which takes a value be-

tween 0 and 1. For this, we adjust an alignment-based

conformance checking proposed for Petri net models

(Adriansyah et al., 2011b) to ﬁnite automaton mod-

els. This method ﬁnds a matching between an model

execution and a trace. The next step is to evaluate

the time ﬁtness (also takes a value between 0 and 1)

of the matching. The time ﬁtness, which we newly

deﬁne, evaluates how well the timestamps in a trace

conform to the constraints given in the model.

The alignment-based method searches the optimal

model execution (the execution having the smallest

difference from the trace) to compute ﬁtness values.

Although there are several such optimal executions in

general, they all have the same order ﬁtness value.

However, as we see later, such optimal executions

possibly have different time ﬁtness values. Therefore,

if one wants to ﬁnd the best time ﬁtness value, one

needs to search all possible optimal executions. Such

exhaustive search may be computationally expensive

if a model is large. Therefore, we implement A* algo-

rithm as a more efﬁcient algorithm, which is also used

in (Adriansyah et al., 2011b), as well as a naive ex-

haustive search algorithm and compare the difference

of performance and the obtained best ﬁtness values

using simple process models as an experiment.

This paper is organized as follows: Section 2 gives

a technical preliminary. Section 3 formally deﬁnes

the ﬁtness of our conformance checking on timed

automaton process models. Section 4 states the al-

gorithms to compute the ﬁtness values. Section 5

presents experimental results of the proposed method.

Section 6 gives related work. The ﬁnal section con-

cludes the paper.

2 PRELIMINARY

In this section, we formally deﬁne the event log and

the timed automaton process model. An event log is

a record or a history of executions of a process. An

event log consists of many cases. A case is an in-

stance of a process and corresponds to a sequence of

events (trace). An event consists of an activity and

several attributes. In this paper, the only attribute we

consider is the timestamp. Each event occurs in only

one case.

Let A be the set of activities.

Deﬁnition 1 (Event log). L

= (E,C,α,β,τ,≻) is an

event log over the set A of activities, where E is a

set of events, C is a ﬁnite set of cases, α : E → A is a

function that assigns an activity to each event, β : E →

C is a function that relates events to cases, τ : E →

≥0

is a function that gives the timestamp of an event,

and ≻⊆ E ×E is a strict total order on E. Let ℓ ∈ C be

a case identiﬁer. We write E

ℓ

for the trace of ℓ, which

is a sequence of events ⟨e

,.. .,e

ℓ

⟩, where β(e

) =

ℓ ⇔ e

∈ E

ℓ

for all 1 ≤ i ≤ |E

ℓ

| and e

≻ e

for all

1 ≤ i < j ≤ |E

ℓ

|. We extend α to a sequence of events,

i.e., α(E

ℓ

) = ⟨α(e

),.. .,α(e

ℓ

)⟩ is the sequence of

activities obtained from E

ℓ

. We write last(E

ℓ

) for the

last event of E

ℓ

, namely e

ℓ

The process model is formally deﬁned as a timed

automaton.

Deﬁnition 2 (TA-model). A timed automaton pro-

cess model (TA-model in short) is given as a tuple

(L,l

,z,A,t,T,γ) where L is a ﬁnite set of locations,

∈ L is the initial location, z ∈ L is the ﬁnal lo-

cation, A is a ﬁnite set of activities, t is a clock,

T ⊆ L × B(V ) × L is a set of transitions, B(V ) is a

set of clock constraints (guards) given as an interval

< t < d

∈ R

≥0

), and γ : L → A is a function

that assigns an activity to each location. For a transi-

tion (p,g,q) ∈ T , we denote G(p, q) = g. There is no

s ∈ L and g ∈ B(V ) such that (z,g,s) ∈ T , i.e., there is

no successor location of z.

We give an example process model in Figure 1.

0 < t < 3 1 < t < 5

2 < t < 7

5 < t < 10

Figure 1: An example process model. Locations are rep-

resented as circles, where location names are written above

and activity names are written below. The guards of transi-

tions are written above arrows.

Deﬁnition 3 (Execution). An execution of

a TA-model (L,l

,z,A,t,T,γ) is a sequence

⟨(l

),(l

),.. .,(l

)⟩, where l

is the ini-

tial location, l

= z (i.e. the ﬁnal location), and for

all 1 ≤ i < n, (l

i+1

) ∈ T and t

satisﬁes g

For example, ⟨(s

,1),(s

,2),(s

,6),(s

,8)⟩ is an

execution of the model in Figure 1.

An execution ⟨...(l

),(l

i+1

),.. .⟩ means

that the process ﬁnishes the activity of l

at time t

and

moves to location l

i+1

. Therefore, the timestamp of

ICEIS 2024 - 26th International Conference on Enterprise Information Systems

546

the ﬁnal location is not constrained by any guard (be-

cause there is no transition from it). One may regard

the activity in the ﬁnal location as just a mark of the

end of the process.

For a TA-model M = (L,l

,z,A,t,T,γ), we can ob-

tain an ordinary ﬁnite automaton model (called FA-

model) M

′

= (L,l

,z,A, T

′

,γ) by forgetting the clock

and guards. That is, T

′

⊆ L × L is obtained from T by

ignoring guards.

Let M = (L,l

,z,A, T, γ) be a FA-model. A se-

quence σ = ⟨s

,...,s

⟩ is said to be an execution

of M if s

= l

, s

= z, and for all i ∈ {0,..., n − 1},

i+1

) ∈ T . We write exe(M) for the set of execu-

tions of M.

Before concluding this section, we give some re-

marks about our deﬁnitions. In the standard deﬁnition

of the timed automaton, it has possibly many clocks,

and a transition has a set of clocks to be reset. This

means that when a transition takes place, the clocks

in the set are reset to 0 (in general, they can be as-

signed arbitrary values). We could include the reset

of clocks in our deﬁnition of the TA-model. In our

setting, however, reset is not important because we

are not interested in executing the model but in eval-

uating ﬁtness between the model and the execution,

for which only guards on transitions matter. With the

reset of clocks, the values of timestamps in an exe-

cution do not necessarily increase: for example, the

trace ⟨(s

,5),(s

,3),. ..⟩ is completely ﬁne as an ex-

ecution of TA-model in Figure 1. We can interpret

such execution that the clock was reset between the

activity a and b.

Another device that the standard timed automaton

has is the invariant. Each location has an invariant,

which is a condition for the system to stay in the lo-

cation. For example, if the location s

in Figure 1 has

the invariant t < 5, the system can stay at s

as long as

t < 5 (and thus if t ≥ 5, the system must exit s

). For

evaluating ﬁtness, one may also be interested in how

much the invariants are satisﬁed during the execution.

For simplicity, however, we omit the invariants be-

cause they can be treated similarly to the guards.

The deﬁnition of executions of a TA-model also

differs from the standard deﬁnition of runs of a timed

automaton. In the standard deﬁnition, runs are just

a sequence of the pair of locations and valuations

of clock ⟨(l

),(l

),.. .⟩, where (l

i+1

) can

be obtained from (l

) by two possible transitions:

the delay transition and the action transition. The

delay transition represents that the system stays at

the same location for some time (thus, l

i+1

= l

On the other hand, the action transition makes the

system to change its location according to the tran-

sition T and does not cause a time lapse. Thus,

i+1

is one of the successors of l

in the automa-

ton. Therefore, ⟨(s

,0),(s

,1.5),(s

,4),. ..⟩

is a run of the timed automaton in Figure 1,

but ⟨(s

,1),(s

,2),(s

,6),(s

,8)⟩ is not because

,1) → (s

,2) is neither the delay transition nor the

action transition. In our setting, we regard a trace

in an event log as an execution of a process model,

which is a sequence of events ⟨e

,.. .⟩ and each

event e

is a pair (a

), where a

is an activity and

is a timestamp. Therefore, we adopt such traces as

executions of a TA-model.

3 CONFORMANCE CHECKING

ON TIMED AUTOMATON

PROCESS MODELS

Conformance checking is a method for evaluating the

difference between an event log and a process model.

The difference is evaluated by the ﬁtness, which is

expressed as a value between 0 and 1. If the event

log and the process model do not match at all, the

ﬁtness value is 0, and if they match perfectly, the ﬁt-

ness value is 1. If the ﬁnesses is greater than 0 and

less than 1, there are two possible interpretations. (1)

There is a problem on the process model side. The

actual business process is not correctly modeled, i.e.,

there is room for improvement in the process model.

(2) There is a problem on the event log side. The ac-

tual execution of the process contains some kind of

violation, i.e., the operations are not being performed

as assumed in the process model. In this case, it may

lead to the discovery of inefﬁcient operations.

In this section, we give a method for evaluating

the ﬁtness between a TA-model M = (L,l

,z,A,t,T,γ)

and a trace E

ℓ

in an event log L

= (E,C,α,β, τ,≻).

The steps for this is as follows:

1. Find an optimal alignment between M

′

(FA-model

obtained from M) and α(E

ℓ

) (the sequence of ac-

tivities obtained from E

ℓ

), then compute the ﬁt-

ness value of the alignment (we call it the order

ﬁtness).

2. For the alignment obtained in Step 1, we com-

pute the time ﬁtness by evaluating how much the

guards are satisﬁed in it.

3. We take the average of the order and time ﬁtness

values obtained in Step 1 and 2, respectively, as

the ﬁtness value between M and E

ℓ

The order ﬁtness can be obtained by adjusting the

deﬁnition of the ﬁtness based on alignments of Petri

net models proposed in (Adriansyah et al., 2011b).

We will deﬁne the time ﬁtness by quantitatively eval-

Conformance Checking on Timed Automaton Process Models

547

uate how much the timestamps deviate from the inter-

vals given as guards in Section 3.2.

For the ﬁtness between M and L

(the entire event

log), we take average of the ﬁtness between M and E

ℓ

for all ℓ ∈ C, as usual.

3.1 Order Fitness

In this section, we formally deﬁne the order ﬁtness

between a FA-model and a trace.

First, we introduce instances of FA-models. An

instance is a straight line automaton that corresponds

to an execution of an automaton.

Deﬁnition 4. Let M = (L,l

,z,A, T, γ) be a FA-model

over the activity set A. An instance I = (LI,TI,ρ) of

M is deﬁned as:

• LI is a set of location instances,

• TI ⊆ LI × LI is a set of transition instances,

• ρ : LI → L assigns location instances to locations

in L,

where I satisﬁes the following:

1. for all (x, y) ∈ TI, (ρ(x),ρ(y)) ∈ T,

2. for all x ∈ LI, |succ(x)| ≤ 1,

3. for all x ∈ LI, if |pred(x)| = 0 then ρ(x) = l

where succ(x) = {x

′

| (x,x

′

) ∈ T }, pred(x) =

′

| (x

′

,x) ∈ T }.

Example 1. Let I = (LI, TI, ρ),

where LI = {s

′

′′

′

}, TI =

{(s

′

),(s

′

),(s

′

′′

),(s

′′

),(s

′′

′

)}, ρ = [s

′

7→

′

7→ s

′′

7→ s

′

7→ s

′′

7→ s

′

7→ s

]. Then,

I is an instance of the FA-model of Figure 1, which

corresponds to the execution ⟨s

⟩.

Note that instances may correspond to partial ex-

ecutions, which do not end at the ﬁnal location.

If an instance of a FA-model matches a trace, we

call it a matching instance, which is formally deﬁned

as:

Deﬁnition 5 (Matching instance). Let L

(E,C,α, β,τ,≻) be an event log over the activ-

ity set A and ℓ ∈ C. Let E

′

be a preﬁx of E

ℓ

. Let

M = (L,l

,z,A, T, γ) be a FA-model and I = (LI,TI,ρ)

be an instance of M. Let µ : E

′

⇁ LI be a partial

function that assigns events to location instances,

and µ induces the bijection from dom(µ) ⊆ E

′

rng(µ) ⊆ LI. If the following two conditions hold,

I is said to match E

′

by µ and is called a matching

instance:

1. for all e

∈ dom(µ), if there is a path from

µ(e

) to µ(e

) in I, then e

≻ e

2. for all e ∈ dom(µ), ρ(µ(e)) ∈ {s ∈ L | γ(s) =

α(e)}.

For an event e, we denote loc(e) = ρ(µ(e)). This

means that in the matching instance, the execution of

the event e is regarded as the execution of the activity

of the location loc(e) in the model. For p

′

∈ LI, we

write next(p

′

) for the unique q

′

such that (p

′

) ∈ TI

if it exists.

The condition 1 says that the order of events in

the preﬁx is preserved in the instance. The condition

2 says that an event in the preﬁx and its corresponding

location (related through maps µ and ρ) must have the

same activity.

We write (I

′

,µ) for a matching instance that

matches the trace E

′

by µ (I

′

is an automaton in-

stance), and write J

′

for the set of all such instances.

Example 2. Let I = (LI,TI,ρ) be the automaton in-

stance in Example 1. Let E

= ⟨e

⟩,

where α(e

) = a, α(e

) = b, α(e

) = c, α(e

) = b

and α(e

) = d. Let µ

= [e

7→ s

′

7→ s

′

7→

′

7→ s

′

]. Then, (I,µ

) is a matching instance. Let

= ⟨e

⟩ and µ

= [e

7→ s

′

7→ s

′

7→ s

′

Then, (I, µ

) is also a matching instance.

In Example 2, we can see e

/∈ dom(µ

). This

is interpreted that the event e

is inserted in the ex-

ecution of the process, i.e., e

should not have been

executed. On the other hand, s

′

̸∈ rng(µ

). This is

interpreted that the activity c (related to the location

′′

) is skipped in the execution of the process, i.e., c

should have been executed. Therefore, matching in-

stances can represent the difference between a trace

and a model execution, which is quantitatively evalu-

ated as the order ﬁtness.

Deﬁnition 6 (Order ﬁtness). Let M = (L, l

,z,A, T, γ)

be a FA-model over the activity set A. Let E

ℓ

be a

trace from an event log L

= (E,C, α,β,τ, ≻). Let I =

(LI, TI, ρ) be an automaton instance of M and (I,µ)

be a matching instance. Let LI

= LI − rng(µ) and

ℓ

= E

ℓ

− dom(µ). Furthermore, let κ

: A → N

and κ

: A → N

be functions that give the skip costs

and the insert costs of activities, respectively. Then,

the order ﬁtness of (I, µ) is deﬁned as:

order

= 1 −

cost

base

where

cost =

∑

′

∈LI

(γ(ρ(s

′

))) +

∑

e∈E

ℓ

(α(e)),

base = min

σ∈exe(M)

∑

s∈σ

(γ(s)) +

∑

e∈E

ℓ

(α(e)).

In this deﬁnition, the set LI

represents the set

of skipped activities in the trace E

ℓ

that should have

been executed according to the model, and the set

ℓ

represents the set of inserted events in the trace

ICEIS 2024 - 26th International Conference on Enterprise Information Systems

548

ℓ

that should not have been executed according to

the model. We call such mismatches of the model

execution and the trace execution as misalignments.

To each activity the costs representing the penalty of

skipping and inserting are assigned by functions κ

and κ

, respectively. The value base is the sum of the

minimal skip cost of model executions (regarded as

all model activities are skipped) and the insert cost

of the trace (regarded as all trace activities are in-

serted). This is the worst cost among the possible

alignments between the model and the trace. The

value cost take weighted sum for each misalignment,

where each weight is either the skip cost or the insert

cost. Therefore, the order ﬁtness is 1 minus the ra-

tio of the cost of misalignments to the worst cost. If

there is no misalignment, the order ﬁtness is 1, and

if the model does not match the trace at all, the order

ﬁtness is 0. Therefore, the order ﬁtness necessarily

takes a value between 0 and 1.

3.2 Time Fitness

In this section, we formally deﬁne the time ﬁtness be-

tween a TA-model and a trace. We quantitatively eval-

uate how much a given matching instance satisﬁes the

time constraints speciﬁed in the model.

As in the deﬁnition of the TA-model, we only con-

sider guards of the form l < t < u. For the guard g of

the form l < t < u, we deﬁne g = l and g = u.

Deﬁnition 7 (Time ﬁtness). Let M =

(L,l

,z,A,t,T,γ) be a TA-model over the activ-

ity set A. Let E

ℓ

be a trace from an event log

= (E,C, α,β,τ, ≻). Let I = (LI,TI,ρ) be an

automaton instance of M

′

(the FA-model obtained

from M) and (I,µ) be a matching instance. Let

D = dom(µ) −{last(E

ℓ

)}. If D is non-empty, the time

ﬁtness of (I, µ) for M is deﬁned as:

time

|D|

∑

e∈D

f (e)

F(e)

where

f (e) = G(loc(e), loc(next(e))

− G(loc(e),loc(next(e))

F(e) = max(τ(e),G(loc(e), loc(next(e))),

− min(τ(e),G(loc(e),loc(next(e))).

If D is empty, f

time

= 1.

We give an intuitive explanation of this deﬁnition.

Suppose the execution of the event e in the trace corre-

sponds to the execution of location p in the model and

the guard of the corresponding transition is l < t < u

(note that although there are possibly multiple tran-

sitions from p, the location corresponding to the next

event next(e) in the matching instance uniquely deter-

mines the transition). Then, the timestamp recorded

in e is τ(e). If l < τ(e) < u, the guard of this tran-

sition is satisﬁed. In this case, f (e) = u − l and

F(e) = max(τ(e), u) − min(τ(e),l) = u − l. Hence,

we have

f (e)

F(e)

= 1, that is, the execution of e perfectly

conforms to the model. On the other hand, if τ(e) < l,

then F(e) = u −τ(e), and thus

f (e)

F(e)

u−l

u−τ(e)

< 1. The

smaller τ(e) becomes than l, the smaller the value

f (e)

F(e)

is, which results in smaller f

time

. For exam-

ple, suppose l = 10 and u = 20. If τ(e) = 5 then

20−10

20−5

. If τ(e) = 0, then

20−10

20−0

Therefore, simply speaking, the value

f (e)

F(e)

is the ratio

of the length of the interval to the sum of the length

of the interval and the distance between τ(e) and the

interval.

The average of this value for each event in the

trace is the time ﬁtness f

time

of the matching instance.

Example 3. We consider the TA-model in Figure 1

and the trace ⟨(a, 2),(b,6), (c,7),(b,9), (d,10)⟩.

Let the matching instance ((LI,TI, ρ),µ)

be as follows: LI = {a

′

′′

′

TI = {(a

′

),(b

′

),(c

′

′′

),(b

′′

),(c

′′

′

)},

ρ(a

′

) = s

, ρ(b

′

) = ρ(b

′′

) = s

, ρ(c

′

) = ρ(c

′′

) = s

ρ(d

′

) = s

. µ((a,2)) = a

′

,µ((b,6)) = b

′

µ((c,7)) = c

′

, µ((b,9)) = b

′′

, µ((d, 10)) = d

′

. There

is no activity corresponding to c

′′

in LI; the activity

c is skipped once in the trace. Then, we have D =

dom(µ) − {last(E)} = {(a,2),(b, 6),(c,7), (b, 9)}.

The value of the time ﬁtness of this instance is:



max(0,3) − min(0,3)

max(2,3) − min(2,0)

max(1,5) − min(1,5)

max(6,5) − min(6,1)

max(2,7) − min(2,7)

max(7,7) − min(7,2)

max(1,5) − min(1,5)

max(9,5) − min(9,1)



(1 + 0.8 +1 +0.5) = 0.825

In the above example, the activity c is skipped in

the trace, which is not taken account in the computa-

tion of the time ﬁtness value. In general, misaligning

events and activities in the matching instance are not

taken into account in the computation of the time ﬁt-

ness value. This is because such misalignments are

taken into account in the order ﬁtness. Another reason

is that we cannot give reasonable timestamp values to

such misalignments due to lack of corresponding tran-

sitions. Our treatment of misalignments is similar to

Conformance Checking on Timed Automaton Process Models

549

Leoni et al.’s conformance checking (de Leoni et al.,

2012), which compares attribute values speciﬁed in

the model with recorded values in the trace.

When a timestamp takes the value precisely equal

to a boundary value of a guard, the time ﬁtness value

for such event is evaluated to 1. In the above exam-

ple, for the third event (c,7) in the trace, its time ﬁt-

ness value is

max(2,7)−min(2,7)

max(7,7)−min(7,2)

= 1. Since the guard

is 2 < t < 7 and the timestamp is 7, this event does

not logically satisfy the guard. In practice, however,

the probability that the timestamp precisely takes a

boundary value can be negligible. Moreover, al-

though both cases t = 7 and t = 7 + 10

−100

are log-

ically false, we can think that both cases conform to

the model almost equally. Therefore, we deﬁned that

if the timestamp takes a boundary value of a guard,

the corresponding ﬁtness value is 1.

3.3 Total Fitness

The total ﬁtness of a matching instance is the average

of the order ﬁtness value and the time ﬁtness value of

the instance.

Deﬁnition 8 (Total ﬁtness). Let M =

(L,l

,z,A,t,T,γ) be a TA-model over the activ-

ity set A, M

′

= (L,l

,z,A, T

′

,γ) be the FA-model

obtained from M. Let L

= (E,C, α,β,τ, ≻) be an

event log and E

ℓ

be a trace of a case ℓ ∈ C. Let (I,µ)

be a matching instance of E

ℓ

and M

′

. Let f

order

and

time

be the order ﬁtness value and the time ﬁtness

value of (I, µ), respectively. Then the total ﬁtness (or

simply ﬁtness) of (I, µ) is deﬁned as:

ﬁtness =

order

+ f

time

4 COMPUTATION OF FITNESS

VALUES

The previous section deﬁned the ﬁtness of a match-

ing instance. However, there are possibly many

matching instances for a single trace. For exam-

ple, if the process model has a loop, there is a

matching instance for each number of iteration of

the loop. Let us consider the model in Figure 1.

There are automaton instances corresponding to exe-

cution ⟨a,b,c, d⟩, ⟨a, b, c,b,c, d⟩, ⟨a, b, c,b,c, b,c,d⟩,

and so on. Each automaton instance yields differ-

ent matching instance. When checking conformance

of a trace to the model, which execution should we

choose for evaluating the ﬁtness? The answer is an

optimal matching instance. For example, if the trace

is ⟨a,b,d⟩, the execution of the model in Figure 1

most similar to it is ⟨a, b,c,d⟩. Thus, it is natural to

think that the trace intended to execute this path in the

model, but unfortunately a mistake happened. It is not

reasonable to think that the trace intended to execute

⟨a,b,c, b,c,d⟩ nor ⟨a,b,c, b,c,b, c,d⟩, because if the

trace really intended to such executions (i.e., loop it-

erations), at least b or c should occur more than once.

Therefore, we have to ﬁnd the most similar execution

to the trace for evaluating the ﬁtness, i.e. an optimal

matching instance. In other words, an optimal match-

ing instance represents the most similar execution of

the model to reality (the trace recorded in the event

log).

This section articulates the computation of the ﬁt-

ness values between a trace and a process model. For

this, we need to deﬁne the notion of optimal match-

ing instances. Furthermore, we show how we can ﬁnd

such optimal matching instances efﬁciently using A*

algorithm.

4.1 Optimal Matching Instance

We deﬁned the order ﬁtness in Deﬁnition 6. Here we

deﬁne the cost of a matching instance, and based on it

we deﬁne optimal matching instances.

Deﬁnition 9 (Cost of matching instance, optimal

matching instance). Let M = (L,l

,z,A, T, γ) be a

FA-model model over the activity set A. Let L

(E,C,α, β,τ,≻) be an event log over A and E

ℓ

be the

trace of a case ℓ ∈ C. Let E

′

be a preﬁx of E

ℓ

. Further-

more, let κ

: A → N

and κ

: A → N

be functions

that give the skip costs and the insert costs of activ-

ities, respectively. Then, the cost δ

: J

′

→ N of a

matching instance is deﬁned by:

((I

′

,µ)) =

∑

∈LI

(γ(ρ(s

))) +

∑

e∈E

′i

(α(e))

where I

′

= (LI, TI, ρ), LI

= LI − rng(µ) and E

′i

′

− dom(µ).

An optimal matching instance of E

′

for M is a

matching instance in J

′

that has the minimum cost.

Note that the cost of a matching instance appears

as cost in the deﬁnition of the order ﬁtness f

order

1 −

cost

base

in Deﬁnition 6. Since the value base is con-

stant (i.e., does not depend on a matching instance),

optimal matching instances have the maximum value

of the order ﬁtness.

We deﬁne the order ﬁtness of a trace E

ℓ

to be the

order ﬁtness of an optimal matching instance in J

ℓ

Note that there are possibly many optimal match-

ing instances for the same trace. Consider the trace

⟨a,b,c, b,d⟩ for the process model in Figure 1, and

assume that every activity has the same skip cost and

the insert cost. Then, there are two possible optimal

ICEIS 2024 - 26th International Conference on Enterprise Information Systems

550

matching instances: one corresponding to the model

execution ⟨a, b,c,d⟩ (the second b in the trace is in-

serted) and one corresponding to the model execution

⟨a,b,c, b,c,d⟩ (the second c in the model execution is

skipped in the trace). To compute the order ﬁtness of

a trace, we need to ﬁnd at least one optimal matching

instance.

4.2 Search for an Optimal Matching

Instance

To ﬁnd an optimal matching instance for a given trace

and a process model, we deﬁne the search space graph

whose vertices are matching instances. For this, we

ﬁrst deﬁne the transition relation and the distance be-

tween matching instances.

For an automaton instance I = (LI,TI, ρ) and S ⊆

LI, We write I ∩ S for the automaton instance (LI ∩

S,TI ↾

,ρ ↾

), where TI ↾

= {(l

) ∈ TI | l

∈ S ∧

∈ S}, and ρ ↾

is the restriction of ρ to S.

Deﬁnition 10 (Transition relation between matching

instances). Let M = (L, l

,z,A, T, γ) be a FA-model

over the activity set A. Let L

= (E,C, α, β,τ,≻) be

an event log over A and E

ℓ

be the trace of a case ℓ ∈C.

Let E

and E

be preﬁxes of E

ℓ

. Let I

= (LI

,TI

,ρ

)

and I

= (LI

,TI

,ρ

) be automaton instances of M,

and let (I

,µ

) ∈ J

and (I

,µ

) ∈ J

be matching

instances. Then, (I

,µ

) ▶ (I

,µ

) if and only if one

of the following hold:

• E

= E

· e and there is s

∈ LI

− LI

such that

= LI

∪ {s

}, µ

(e) = s

, ∀e

′

∈ E

.µ

′

) =

′

), and I

= I

∩ LI

. In other words, E

obtained from E

by appending the event e, and

a corresponding activity execution in the model is

also added to I

. This means that the trace execu-

tion and the model execution coincide.

• E

= E

and there is s

∈ LI

−LI

such that LI

∪ {s

}, ∀e

′

∈ E

.µ

′

) = µ

′

), and I

= I

∩

. In other words, an activity corresponding to

is added to I

. This means that an activity of the

model is skipped in the trace E

• E

= E

·e and ∀e

′

∈ E

.µ

′

) = µ

′

) and µ

(e)

is undeﬁned. In other words, E

is obtained from

by appending the event e, but no corresponding

activity is added to I

. This means that an event is

inserted to the trace E

If (I

,µ

) ▶ (I

,µ

), then (I

,µ

) is obtained by ex-

ecuting the same activity in the trace and the model,

or only the model executes an activity (and thus the

automaton instance grows) and the trace does not

change (skip), or only the trace executes an activity

(insert) and the automaton instance does not change.

We deﬁne the distance for such transitions be-

tween matching instances (technically, it is deﬁned

for every pair of matching instances).

Deﬁnition 11 (Distance between matching instances).

Let M = (L, l

,z,A, T, γ) be a FA-model over the ac-

tivity set A. Let L

= (E,C,α, β,τ,≻) be an event log

over A and E

ℓ

be the trace of a case ℓ ∈ C. Let E

and E

be preﬁxes of E

ℓ

. Let I

and I

be automaton

instances of M, and let (I

,µ

) ∈ J

and (I

,µ

) ∈

be matching instances. We deﬁne the distance

δ((I

,µ

),(I

,µ

)) between (I

,µ

) and (I

,µ

) as:

δ((I

,µ

),(I

,µ

)) = δ

((I

,µ

)) − δ

((I

,µ

))

+ |E

| − |E

Now we deﬁne the search space graph of matching

instances based on the above deﬁnitions. Here, we

write σ < σ

′

to mean that the sequence σ is a preﬁx

of the sequence σ

′

Deﬁnition 12 (Search space graph). Let M =

(L,l

,z,A, T, γ) be a FA-model over the activity set A.

Let L

= (E,C, α,β,τ, ≻) be an event log over A and

ℓ

be the trace of a case ℓ ∈ C. The search space graph

of matching instances of E

ℓ

for M is G = (V,W,ζ)

where

• V =

′

ℓ

′

is the set of vertices,

• W = {(v

) ∈ V × V | v

▶ v

} is the set of

edges, and

• ζ is a weight of edges, and deﬁned as ζ((v

)) =

δ(v

) for every (v

) ∈ W .

The sequence v

,.. .,v

is called a path of G if v

▶

i+1

for all 1 ≤ i < n. For a path π = v

,.. .,v

G, the length of π is deﬁned as:

len(π) =

∑

i=1

δ(v

Then, the optimal matching instance search prob-

lem is deﬁned as:

Deﬁnition 13 (Optimal matching instance search

problem). Let G = (V,W,ζ) be the search space

graph of E

ℓ

for M = (L,l

,z,A, T, γ). Let v

src

((

0,ρ

),µ

) ∈ J

⟨⟩

(here ρ

and µ

are the

empty maps) be the initial vertex. Let V

trg

{((LI, TI, ρ),µ) ∈ J

ℓ

| ρ(last((LI, TI,ρ))) = z} be the

set of target vertices, where last((LI, TI,ρ)) is the lo-

cation instance l such that succ(l) =

0 in (LI,TI,ρ).

Then, the optimal matching instance search problem

is a problem to ﬁnd the shortest path v

src

,...,v

goal

where v

goal

∈ V

trg

Remark 1. Adriansyah et al.’s deﬁnition of the target

vertices (Adriansyah et al., 2011b) includes automa-

ton instances that do not end with the ﬁnal location

z. In this case, if a trace partially executes the model

Conformance Checking on Timed Automaton Process Models

551

correctly, its order ﬁtness value is 1. On the other

hand, our target vertices are only those that execute

the model till the ﬁnal location. In our deﬁnition, the

order ﬁtness value of a trace that correctly executes

the model but not to the end is less than 1. Since traces

in an event log are regarded as executions of the pro-

cess from the initial activity to the ﬁnal activity, our

deﬁnition is more natural.

Theorem 1. If v

src

,...,v

goal

be the shortest path in the

search space graph of Deﬁnition 13, then v

goal

is an

optimal matching instance.

Proof. Let Π be the set of all paths from v

src

to some vertex in V

trg

in the search space graph.

Let π ∈ Π be a path ⟨(I

,µ

),...,(I

,µ

)⟩, where

,µ

) ∈ J

, E

< E

ℓ

for all i < n and E

ℓ

. Since δ((I

,µ

),(I

i+1

,µ

i+1

)) = δ

((I

i+1

,µ

i+1

)) −

((I

,µ

)) + |E

i+1

| − |E

|, the length of π is

len(π) =

n−1

∑

k=1

δ((I

,µ

),(I

k+1

,µ

k+1

))

=δ

((I

,µ

)) − δ

((I

,µ

)) + |E

| − |E

Here we have δ((I

,µ

)) = 0 = |E

| since (I

,µ

) =

src

. Therefore, len(π) = δ

((I

,µ

)) + |E

| =

(last(π)) + |E

ℓ

|. Hence,

argmin

π∈Π

len(π) =argmin

π∈Π

(δ

(last(π)) + |E

ℓ

=argmin

π∈Π

(last(π)),

because |E

ℓ

| is a constant. Assume that π is a match-

ing instance that gives the minimum len(π), that is,

π = ⟨(I

,µ

),...,(I

,µ

)⟩ is the shortest path. Clearly,

for all v ∈ V

trg

, there is a path from v

src

in the

search space graph. Therefore, min

π∈Π

(last(π)) =

min

v∈V

trg

(v). Then, from the above formula, its last

matching instance last(π) = v

goal

takes the minimum

cost δ

goal

) among the vertices in V

trg

, which is

equal to the value of cost in the deﬁnition of the or-

der ﬁtness (Deﬁnition 6). Therefore, v

goal

takes the

maximum order ﬁtness, i.e., it is an optimal matching

instance.

4.3 Search Algorithm

If we are only interested in the order ﬁtness, it is

sufﬁcient to ﬁnd one optimal matching instance, be-

cause every optimal matching instance has the same

order ﬁtness value. In this research, however, we are

also interested in the time ﬁtness, and the total ﬁtness

value is the average of the order ﬁtness value and the

time ﬁtness value. Since each optimal instance may

have different time ﬁtness values, each optimal in-

stance has a different total ﬁtness value. As we men-

tioned in Section 3, when checking conformance, we

need to ﬁnd the model execution most similar to the

trace (reality). Therefore, to ﬁnd the best total ﬁtness

value, we need to ﬁnd all possible optimal matching

instances.

Remark 2. The matching instance that has the best

total ﬁtness value among all matching instances might

not be optimal. In our deﬁnition, however, the order

ﬁtness of a trace is deﬁned as the order ﬁtness of an

optimal matching instance. Therefore, even if there

may be a matching instance that is not optimal but

has a better total ﬁtness value (due to the better time

ﬁtness value), it is not regarded as the ﬁtness value of

the trace.

In general, the set of vertices of a search space

graph is inﬁnite. For example, if a process model has

a loop, we can iterate the loop arbitrarily many times.

That is, we can skip the activities in the loop as many

times as possible. However, since we assume that the

skip cost (given by the function κ

) of activities are

positive, such arbitrary number of iteration just dete-

riorate the order ﬁtness. Thus, we can ﬁnd an optimal

matching instance in ﬁnite steps by a suitable search

algorithm.

As we mentioned above, we need to ﬁnd all pos-

sible optimal matching instances when we are to ﬁnd

the best ﬁtness value for a given trace and a process

model. Therefore, we need to perform the exhaustive

search. We can do this by breadth-ﬁrst search (BFS)

algorithm. To use BFS in ﬁnding all possible opti-

mal matching instances, we ﬁrst do usual BFS on the

search space graph and ﬁnd one optimal matching in-

stance. Then, we ﬁnd the minimum length of the path

to the target nodes. Using this value, we exhaustively

search all possible paths shorter than or equal to this

value (recall that the length of the path corresponds to

the cost of the matching instance of the ﬁnal vertex of

the path). We call this method the exhaustive search.

Clearly, the exhaustive search is not efﬁcient. As

the size of a process model or the length of a trace

grows, computation of the ﬁtness value will eventu-

ally be intractable. Therefore, we utilize A* algorithm

as a more efﬁcient algorithm, which is also used in

alignment-based conformance checking (Adriansyah

et al., 2011b). This algorithm ﬁnds an arbitrary opti-

mal matching instance and compute the ﬁtness value

for it. Of course, it may not give the best total ﬁtness

value, that is, it approximately computes the best total

ﬁtness value for a given trace and a process model.

To utilize A* algorithm in searching an opti-

mal matching instance, we need to deﬁne a suitable

heuristic function. For a search space graph (V,W,ζ)

ICEIS 2024 - 26th International Conference on Enterprise Information Systems

552

of Deﬁnition 12, we deﬁne the heuristic function h :

V → N as h(v) = |E

ℓ

| − |E

′

| for v ∈ J

′

. h(v) under-

estimates the distance from the vertex v to some ver-

tex in V

trg

. That is, for all v

trg

∈ V

trg

, h(v) ≤ ζ(v,v

trg

)

holds (Adriansyah et al., 2011b). With this h, we de-

ﬁne the evaluation function f as f (v) = g(v) + h(v),

where g(v) returns the minimum cost from v

src

to v,

which is the current position in the search.

To ensure that A* algorithm ﬁnds one of the target

vertices, we need to prove the following:

1. At least one target vertex is reachable,

2. The heuristic function actually gives an underes-

timation of the distance to the target vertices, and

3. The evaluation function is monotonously increas-

ing.

These claims are true as in (Adriansyah et al., 2011b).

5 EXPERIMENTAL RESULTS

AND DISCUSSION

This section shows experimental results of the pro-

posed conformance checking algorithms for some

simple TA-models and traces. We give the compar-

ison of the exhaustive search algorithm and A* algo-

rithm with respect to the obtained matching instance,

the order and time ﬁtness values, and the number of

the searched vertices and the computation time.

5.1 Experiment

We implemented both algorithm in Python. In our im-

plementation, a timed automaton is given in .xml for-

mat used in UPPAAL

(Larsen et al., 1997), a model

checker for timed automata, and a trace is given as a

text ﬁle consisting of a sequence of pairs of alphabets

(activities) and numerals (timestamps). For simplic-

ity, the skip cost and insert cost of every activity are

set to 1. We performed the experiment on the com-

puter with Core i9-13900 32GB RAM.

We gave three TA-models in this experiment.

The ﬁrst model contains only one loop (Figure 2).

For this model, we checked the conformance against

the trace ⟨(a,10),(b, 15),(c,25), (b, 15),(d,0)⟩. The

result is presented in Table 1.

The second model has a loop that contains a

branch (Figure 3). For this model, we checked the

conformance against the trace ⟨(a,5),(b,10), (c, 5),

(e,15),(b,10),(e,15)⟩. The result is presented in Ta-

ble 2.

https://uppaal.org/

The third model has a branch followed by a loop

(Figure 4). For this model, we checked the con-

formance against the trace ⟨(a, 10), (d,15), (e,10),

(d, 10),( f , 0)⟩. The result is presented in Table 3.

Note that in this trace the activities inside the branch

(b and c) are skipped.

5.2 Discussion

The results of the three experiments show that the or-

der ﬁtness is the same for each optimal instance found

by the exhaustive search algorithm, but the time ﬁt-

ness is different for each optimal instance. In other

words, the experiments conﬁrmed that even the op-

timal matching instances have different time ﬁtness

values. Since A* algorithm approximately ﬁnds the

total ﬁtness value, it fails to ﬁnd the best values in the

ﬁrst and third experiments, as shown in Table 1 and 3.

Therefore, we conﬁrmed that A* algorithm does not

necessarily ﬁnd the best ﬁtness value.

We analyze the third experiment a bit deeper. For

this model and the trace, the order ﬁtness value is

the same whether the activity b or c is interpreted as

skipped. However, when we consider the timestamp,

since the timestamp of a is 10, if the activity c is in-

terpreted as skipped, this does not give penalty by the

guard on the transition from a to c. On the other hand,

interpreting b as skipped gives penalty by the guard on

the transition from a to b. Hence, the interpretation of

c as skipped gives better ﬁtness value. We can see

this fact from Table 3. In the optimal instances found

by the exhaustive search, the c-skipped interpretation

(the second and the forth instances) give better time

ﬁtness values than the b-skipped interpretation (the

ﬁrst and the third instances).

The result of conformance checking can be in-

terpreted in two ways: either the process model is

normative and the trace (what happened in reality) is

wrong, or the trace is valid and the process model is

incomplete. In the former interpretation, the execu-

tion path in the process model with the best ﬁtness

value is the intended execution of the trace (reality).

The latter interpretation would suggest that the path

with the best ﬁtness value gives a hint to improve the

process model. In either case, the optimal path, which

was difﬁcult to identify only by the order ﬁtness, can

be identiﬁed with our proposed conformance check-

ing method, enabling effective analysis of identifying

errors in the trace or parts in the model deviating from

reality.

As for the computation time, A* algorithm is

about 15-200 times faster than the exhaustive search

algorithm. Since real business processes are generally

much more complex than the models used in these

Conformance Checking on Timed Automaton Process Models

553

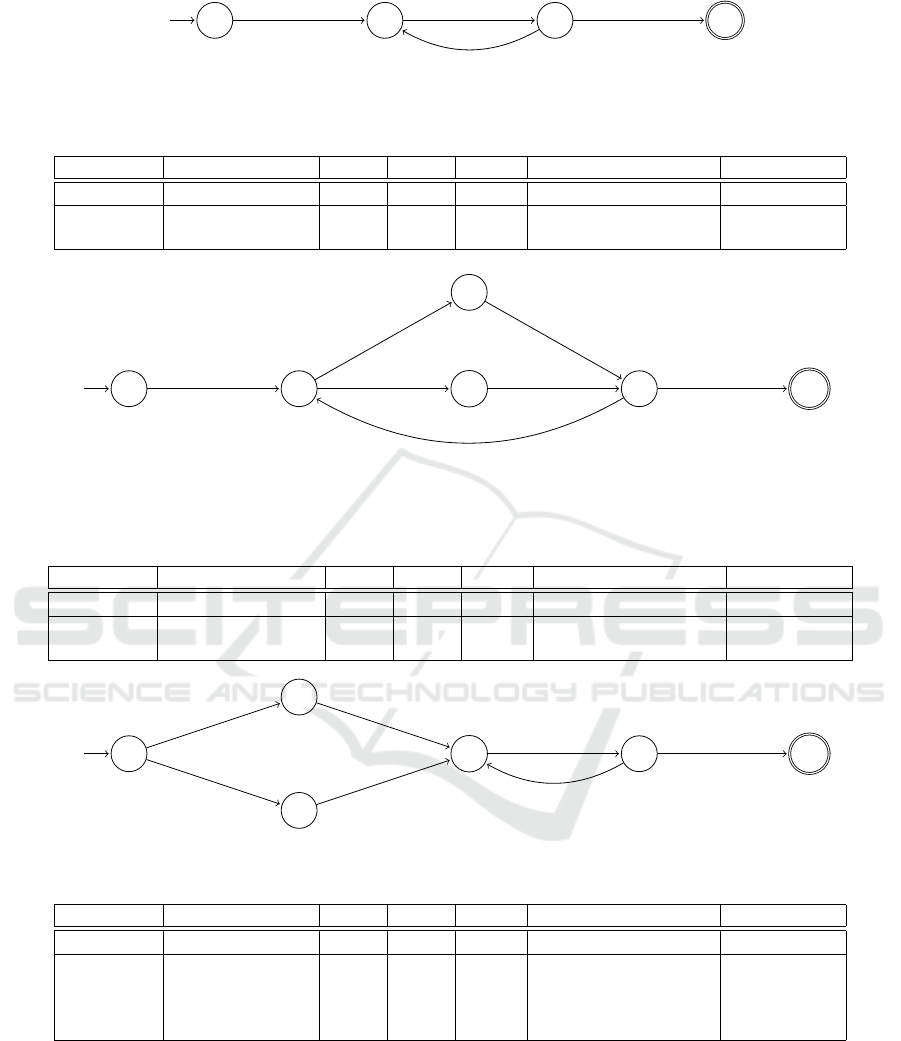
5 < t < 10 10 < t < 20

15 < t < 25

10 < t < 15

Figure 2: The ﬁrst TA-model. The location names designate the activity names.

Table 1: The result of conformance checking for the model in Figure 2 and the trace ⟨(a,10),(b, 15), (c, 25), (b, 15), (d,0)⟩.

Algorithm Optimal instance f

order

time

ﬁtness # of searched vertices Time

A* ⟨a,b,c,d⟩ 0.889 0.778 0.883 40 5.174 × 10

−4

Exhaustive

⟨a,b,c,d⟩ 0.889 0.778 0.833

355

8.066 × 10

−3

⟨a,b,c,b, c, d⟩ 0.889 1.000 0.944

5 < t < 10

10 < t < 15

20 < t < 30

5 < t < 10

10 < t < 20

Figure 3: The second TA-model. The location names designate the activity names.

Table 2: The result of conformance checking for the model in Figure 3 and the trace ⟨(a, 5), (b,10),(c,5),

(e,15), (b,10),(e,15)⟩.

Algorithm Optimal instance f

order

time

ﬁtness # of searched vertices Time

A* ⟨a,b,c,e,b,c,e, f ⟩ 0.818 0.917 0.867 147 2.562 × 10

−3

Exhaustive

⟨a,b,c,e,b,c, e, f ⟩ 0.818 0.917 0.867

3478

5.435 × 10

−1

⟨a,b,c,e,b,d,e, f ⟩ 0.818 0.833 0.826

25 < t < 35

10 < t < 20

5 < t < 10

15 < t < 25

5 < t < 15

15 < t < 25

Figure 4: The third TA-model. The location names designate the activity names.

Table 3: The result of conformance checking for the model in Figure 4 and the trace ⟨(a,10),(d,15), (e,10), (d,10),( f ,0)⟩.

Algorithm Optimal instance f

order

time

ﬁtness # of searched vertices Time

A* ⟨a,b,d, e, f ⟩ 0.800 0.689 0.744 99 1.428 ×10

−3

Exhaustive

⟨a,b,d,e, f ⟩ 0.800 0.689 0.744

988

5.105 × 10

−2

⟨a,c,d,e, f ⟩ 0.800 0.889 0.845

⟨a,b,d,e,d,e, f ⟩ 0.800 0.767 0.783

⟨a,c,d,e,d,e, f ⟩ 0.800 0.917 0.858

experiments, we need an efﬁcient algorithm like A*

that also takes the time ﬁtness into account to ﬁnd the

best matching instance. Since the problem of ﬁnding

optimal matching instances is known to be NP-hard

(de Leoni and van der Aalst, 2013), some approxima-

tive algorithm is desired even for computing the order

ﬁtness.

6 RELATED WORK

As we mentioned in Section 1, most conformance

checking method only consider the order of activities.

Only a few researches considering attributes or times-

tamps are known.

ICEIS 2024 - 26th International Conference on Enterprise Information Systems

554

Leoni et al. proposed a method for conformance

checking considering attributes of events (de Leoni

et al., 2012). In their research, a process model has

assignments of constants to variables (attributes), and

when activities are executed, the value of the variables

are updated according to the assignments. The align-

ment of a trace to a model is deﬁned as usual. The

ﬁtness is evaluated based on the number of activities

that are not misaligned but their attribute values do not

coincide with each other. That is, their method only

uses the number of discrepancies of attribute values.

On the other hand, our proposed method evaluate the

degree of discrepancy, not just the number of discrep-

ancies.

Leoni et al.’s approach is later extended to handle

inﬁnite data domains and customizable balance be-

tween the control-ﬂow perspective and the data per-

spective (Mannhardt et al., 2016). Our approach ﬁrst

considers the control-ﬂow perspective, then evaluate

the data perspective. Therefore, one possible future

direction is to enable such balancing in our proposed

method.

Giacomo et al. proposed a method for aligning

timed traces to a formula of Metric Temporal Logic

(MTL

) (Giacomo et al., 2021). For a given timed

trace and MTL

formula where the trace does not sat-

isfy the formula, their method ﬁnds the trace obtained

by editing the original trace with the lowest editing

cost to satisfy the formula. Their research does not

focus on computing the ﬁtness values. If one deﬁnes

it, it is necessarily based on the number of deletion

and insertion. Thus, the ﬁtness essentially equal to

the order ﬁtness. Furthermore, their method demands

NONELEMENTARY time for computation, making

it difﬁcult to put into practice.

Grohs and Rehse (Grohs and Rehse, 2023) pro-

posed a method for correlating process conformance

with trace attributes in order to explain the potential

cause of deviations. They creates a regression tree to

ﬁnd which attributes contribute to lower and higher

ﬁtness values. The purpose of utilizing attribute val-

ues is, thus, different from our approach.

7 CONCLUSIONS

In this paper, we proposed a conformance check-

ing on timed automaton process models, which takes

time attributes of events into account. Our proposed

method ﬁrst ﬁnds an optimal matching instance (i.e.,

alignment between a model and a trace). In the ob-

tained matching instance, we evaluate how much each

timestamp deviates from the interval represented by

the corresponding guard. Therefore, the ﬁtness is

given by the order ﬁtness, which is evaluated based

on the number of misalignments, and the time ﬁtness,

which is evaluated based on how much the times-

tamps satisfy the guards.

We implemented our method using the exhaustive

search algorithm and A* algorithm. The exhaustive

search algorithm ﬁnds the best ﬁtness value at the cost

of performance. A* algorithm runs faster than the ex-

haustive search but ﬁnds an arbitrary optimal match-

ing instance to compute the ﬁtness value, thus may

not give the best ﬁtness value.

By considering time attributes, we demonstrated

that we can uniquely determine the most similar exe-

cution of a model to a given trace, which is indistin-

guishable from other optimal executions in terms of

the order ﬁtness. Thus, our proposed method is useful

for identifying an error in the trace or in the process

model.

There are several future directions for extending

our method. In this paper, we only consider the time

attribute. It is natural to include other numerical at-

tributes such as the amount of a resource consumed

at the event (in a manufacturing process), or the price

of a quote (in a negotiation process). By including

such attributes, we can evaluate more precise ﬁtness

of traces and event logs.

Another direction is to extend our guard expres-

sions; we only have the form d

< t < d

. In general,

a guard is given as a conjunction of such intervals.

Therefore, we need to modify Deﬁnition 6 to handle

such formulas.

We also need to develop an efﬁcient search algo-

rithm in computing the ﬁtness value considering the

time ﬁtness.

Finally, we are to carry out extensive experiments

using real-life event logs and process models. The

problem is, however, the lack of timed automaton

process models in real-life examples. One attempt

is to discover a skeleton of the model using well-

established model discovery algorithm, then manu-

ally modify and annotate necessary information to it

(Ito et al., 2021). It is strongly desired to develop

some process discovery algorithm that constructs ap-

propriate timed automaton process models from event

logs.

ACKNOWLEDGMENTS

This work was supported by JSPS KAKENHI Grant

Number JP21K11756. The authors thank Atsushi

Takayanagi for helpful comments.

Conformance Checking on Timed Automaton Process Models

555

REFERENCES

Adriansyah, A. (2014). Aligning Observed and Modeled

Behavior. PhD thesis, Technische Universiteit Eind-

hoven.

Adriansyah, A., Sidorova, N., and van Dongen, B. F.

(2011a). Cost-based ﬁtness in conformance check-

ing. In 11th International Conference on Application

of Concurrency to System Design, ACSD 2011, New-

castle Upon Tyne, UK, June 20-24, 2011, pages 57–

66.

Adriansyah, A., van der Aalst, W. M. P., and van Don-

gen, B. F. (2011b). Conformance checking using

cost-based ﬁtness analysis. In 15th IEEE Inter-

national Enterprise Computing Conference, EDOC

2011, Helsinki, Finland, August 29-Spetember 2,

2011, pages 55–64.

de Leoni, M. and van der Aalst, W. M. P. (2013). Aligning

event logs and process models for multi-perspective

conformance checking: An approach based on integer

linear programming. In Daniel, F., Wang, J., and We-

ber, B., editors, Business Process Management - 11th

International Conference, BPM 2013, Beijing, China,

August 26-30, 2013. Proceedings, volume 8094 of

Lecture Notes in Computer Science, pages 113–129.

Springer.

de Leoni, M., van der Aalst, W. M. P., and van Dongen,

B. F. (2012). Data- and resource-aware conformance

checking of business processes. In Abramowicz, W.,

Kriksciuniene, D., and Sakalauskas, V., editors, Busi-

ness Information Systems - 15th International Confer-

ence, BIS 2012, Vilnius, Lithuania, May 21-23, 2012.

Proceedings, volume 117 of Lecture Notes in Business

Information Processing, pages 48–59. Springer.

Giacomo, G. D., Murano, A., Patrizi, F., and Perelli, G.

(2021). Timed trace alignment with metric tempo-

ral logic over ﬁnite traces. In Bienvenu, M., Lake-

meyer, G., and Erdem, E., editors, Proceedings of

the 18th International Conference on Principles of

Knowledge Representation and Reasoning, KR 2021,

Online event, November 3-12, 2021, pages 227–236.

Grohs, M. and Rehse, J.-R. (2023). Attribute-based

conformance diagnosis: Correlating trace attributes

with process conformance. In Montali, M.,

Senderovich, A., and Weidlich, M., editors, Process

Mining Workshops, pages 203–215, Cham. Springer

Nature Switzerland.

Ito, S., Vym

etal, D., and

Sperka, R. (2021). Process mining

approach to formal business process modelling and

veriﬁcation: a case study. Journal of Modelling in

Management, 16(2):602–622.

Ito, S., Vym

etal, D.,

Sperka, R., and Hala

ska, M. (2018).

Process mining of a multi-agent business simulator.

Computational & Mathematical Organization Theory,

24(4):500–531.

Larsen, K. G., Petterson, P., and Yi, W. (1997). UPPAAL

in a nutshell. International Journal on Software Tools

for Technology Transfer, 1(1/2):134–152.

Mannhardt, F., de Leoni, M., Reijers, H. A., and van der

Aalst, W. M. P. (2016). Balanced multi-perspective

checking of process conformance. Computing,

98(4):407–437.

Polyvyanyy, A., Weidlich, M., Conforti, R., Rosa, M. L.,

and ter Hofstede, A. H. (2014). The 4c spectrum of

fundamental behavioral relations for concurrent sys-

tems. In 32th International Conference in Application

and Theory of Petri Nets and Concurrency, PETRI

NETS 2014, Tunis, Tunisia, June 23-27, 2014. Volume

8489 of Lecture Notes in Computer Science, pages

210–232. Springer.

Rozinat, A. (2010). Process Mining Conformance and Ex-

tension. PhD thesis, Technische Universiteit Eind-

hoven.

van der Aalst, W. M. (2016). Process Mining: Data Science

in Action. Springer.

van der Aalst, W. M. P., Adriansyah, A., and van Dongen,

B. F. (2012). Replaying history on process models

for conformance checking and performance analysis.

Wiley Interdisc. Rew.: Data Mining and Knowledge

Discovery, 2(2):182–192.

vanden Broucke, S. K. L. M., Munoz-Gama, J., Carmona,

J., Baesens, B., and Vantheienen, J. (2014a). Event-

based real-time decomposed conformance analysis. In

On the Move to Meaningful Internet Systems, OTM

2014, Amantea, Italy, October 27-31, 2014, pages

345–363.

vanden Broucke, S. K. L. M., Weerdt, J. D., Vantheienen,

J., and Baesens, B. (2014b). Determining process

model precision and generalization with weighted ar-

tiﬁcial negative events. IEEE Trans. Knowl. Data

Eng., 26(8):1877–1889.

Weidlich, M., Polyvyanyy, A., Desai, N., Mendling, J.,

and Weske, M. (2011a). Process compliance analysis

based on behavioural proﬁles. Inf. Syst., 36(7):1009–

1025.

Weidlich, M., Polyvyanyy, A., Mendling, J., and Weske,

M. (2011b). Causal behavioural proﬁles – Efﬁcient

computation, applications, and evaluation. Fundam.

Inform., 113(3–4):399–435.

Zha, H., Wang, J., Wen, L., Wang, C., and Sun, J. (2010).

A workﬂow net similarity measure based on tran-

sition adjacency relations. Computers in Industry,

61(5):463–471.

ICEIS 2024 - 26th International Conference on Enterprise Information Systems

556