Muli-Quay Combined Berth and Quay Crane Allocation Using the

Cuckoo Search Algorithm

Sheraz Aslam

, Michalis P. Michaelides

and Herodotos Herodotou

Department of Electrical Engineering, Computer Engineering and Informatics, Cyprus University of Technology, Cyprus

Keywords:

Port Efﬁciency, Berth and Quay Crane Allocation Problem, Metaheuristic, Cuckoo Search Algorithm.

Abstract:

This study investigates the combined berth allocation problem (BAP) and quay crane allocation problem

(QCAP) while considering a multi-quay setting. First, a mixed integer linear programming mathematical

model is developed based on various constraints and real port settings. Then, the multi-quay combined BAP

and QCAP is solved using both the exact method and a metaheuristic optimization method, namely, the cuckoo

search algorithm (CSA). This analysis pertains to a one-week planning scenario, utilizing data from a real

port. The results of the comparative analysis show that the proposed CSA can provide a near-optimal solution

(<1.02% from the optimal) at a fraction of the computational time (10 times faster), as compared to the exact

solution. This makes it suitable for solving larger instances of the combined BAP and QCAP for bigger termi-

nals and extended planning horizons.

1 INTRODUCTION

International maritime trade plays a pivotal role in

the global economy, accounting for over 80% of

the transportation of goods around the globe. Sea-

ports play a crucial role in managing this substan-

tial volume of goods, encountering various oper-

ational challenges such as berth allocation (BAP),

truck scheduling, storage allocation, quay crane allo-

cation (QCAP), and optimization of straddle carriers.

To satisfy the increasing demand, it is essential for ter-

minals to enhance their operations through the utiliza-

tion of contemporary technologies and optimization-

driven methodologies. Given this imperative require-

ment, there has been signiﬁcant interest from both

academia and industry in devising innovative and ef-

fective approaches to optimize terminal operations

(Lind et al., 2020). At the terminals, berths and

quay cranes (QCs) are considered two of the basic

resources, and their efﬁcient use can help to reduce

the total turnaround time of vessels (Li et al., 2020).

Hence, BAP and QCAP have been the most con-

cerned optimization problems in port planning and

operations (Aslam et al., 2020; Zheng et al., 2019).

https://orcid.org/0000-0003-4305-0908

https://orcid.org/0000-0002-0549-704X

https://orcid.org/0000-0002-8717-1691

The primary operations of marine ports are cate-

gorized into three main areas: marshaling yard, sea-

side, and landside. The ﬁrst involves loading and un-

loading containers from incoming vessels using quay

cranes and other terminal resources. Inbound contain-

ers are stored in the marshaling yard. Finally, land-

side operations include activities related to dispatch-

ing containers to their ﬁnal destinations using trucks

or trains (Aslam et al., 2022a). Berths and quay cranes

(QCs) are bottleneck resources in ports due to the lim-

ited coastal environment and complexity of port ac-

tivities (Li et al., 2020). Single or multiple berth lines

are used to berth arriving vessels, and QCs are used

to perform loading and unloading operations. All

vessels arriving at the port may wait at the anchor-

age, then enter the port and moor at their assigned

berth section to perform loading and discharging op-

erations. Since available berths and QCs are limited,

good planning and proper coordination between them

can improve terminal productivity. The BAP identi-

ﬁes berthing positions and berthing times for arriving

vessels based on a variety of factors, such as expected

time of arrival (ETA), handling time or total load, re-

quested time of departure (RTD), etc. In addition, the

QCAP deals with the appropriate allocation of cranes

based on the BAP solution and availability of cranes,

since BAP and QCAP are interdependent problems

(Yu et al., 2019).

220

Aslam, S., Michaelides, M. and Herodotou, H.

Muli-Quay Combined Berth and Quay Crane Allocation Using the Cuckoo Search Algorithm.

DOI: 10.5220/0012553400003702

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 10th International Conference on Vehicle Technology and Intelligent Transport Systems (VEHITS 2024), pages 220-227

ISBN: 978-989-758-703-0; ISSN: 2184-495X

In the current literature, there are many studies

dealing with stand-alone BAP (Aslam et al., 2022a,

2021; Bierwirth and Meisel, 2015; Theofanis et al.,

2007; Ernst et al., 2017; Golias et al., 2009a,b; Al-

souﬁ et al., 2016). For instance, the authors of Theo-

fanis et al. (2007) solve a BAP with the objective of

reducing the number of late departures at the port of

Shahid Rajaee Shallow, Iran. Another study (Ernst

et al., 2017) also addresses the BAP to optimize the

departure times of vessels. The authors of Golias et al.

(2009a,b) also address BAP with the goal of optimal

berth allocation and propose heuristic-based solutions

to solve the problem. The work presented in Alsouﬁ

et al. (2016) also solves the BAP intending to reduce

the late departure of vessels by efﬁciently allocating

berths using a hybrid of genetic algorithm (GA) and

branch-and-cut (B&C) methods. Currently, there is

a growing tendency to address both BAP and QCAP

concurrently, since the number of cranes (and which

cranes in case of different handling productivity) as-

signed to a ship determines the berthing time of the

vessels (Xiang and Liu, 2021; Rodrigues and Agra,

2022). Most of the current studies consider only a

single quay, while they look at stand-alone BAP or

combined BAP-QCAP (Rodrigues and Agra, 2022).

There are only a few studies dealing with termi-

nals with multiple quays. For example, in a study

presented in Frojan et al. (2015), a solution for multi-

ple quays is proposed for BAP; however, in this study,

the total length of the quay is divided equally between

two quays and random data are used for the experi-

ments. In addition, practical constraints are not con-

sidered. A recent study in Krimi et al. (2020), also

solves the multi-quay BAP and concludes that the

proposed method does not always provide an optimal

solution and is sometimes 40% away from the opti-

mal solution. In another work, Gutierrez et al. (2019)

propose a fuzzy-based solution, but as the authors ac-

knowledge, the proposed method provides an optimal

solution when only up to 10 vessels are considered.

In our own previous work, we have explored using

metaheuristics, and in particular the cuckoo search al-

gorithm, for addressing the multi-quay scenario with

more practical settings but only for the standalone

BAP Aslam et al. (2022b, 2023). We have found only

a single research paper that addresses the combined

BAP and QCAP while considering multiple quays,

which employs fuzzy logic to solve the problem (Lu-

jan et al., 2021). However, the authors of that study

conclude that their approach is feasible only for small

instances and suggest the use of metaheuristics for

solving medium and large-size problems.

In this study, we explore the utilization of the

cuckoo search algorithm (CSA) to address the multi-

Time (hour)

v10

Quay length (m)

Quay 1 (with 2 cranes) Quay 2 (with 3 cranes)

Quay length (m)

c1, c2

c2, c3

Figure 1: Combined BAP and QCAP solution with two

berthing quays (both are continuous) and 10 arriving ships.

quay combined BAP and QCAP to alleviate the over-

all service cost of ships, encompassing handling cost,

waiting costs, penalties for late departure, and penal-

ties due to non-optimal berth/quay assignment. Fur-

thermore, an appropriate mixed integer linear pro-

gramming model is established for this problem,

which is subsequently solved using both the exact

mathematical approach and the proposed CSA. Pre-

liminary results employing a real dataset from the

Port of Limassol, Cyprus demonstrate the efﬁcacy of

the proposed CSA method, as compared to the exact

method.

The rest of the paper is organized as follows. Sec-

tion 2 provides the problem description and mathe-

matical formulation. Section 3 presents the developed

CSA method, while Section 4 shows the simulation

results from the case study at the Port of Limassol,

Cyprus. Section 5 concludes the study.

2 PROBLEM FORMULATION

The considered problem is discussed in this section

along with the main assumptions, followed by the

mathematical formulation of the problem.

2.1 Problem Explanation

The combined BAP and QCAP is an optimization

problem in which the objective is to allocate available

berths and available quay cranes (QCs) across time to

incoming ships to perform unloading/loading opera-

tions. An example of the solution of the problem for

two quays and 10 arriving ships is shown in Fig. 1. In

this research, we examine a practical conﬁguration of

a port featuring multiple quays, each equipped with

a speciﬁc number of cranes. Additionally, all quays

adhere to a continuous style berthing layout, allowing

arriving vessels to be docked at any location along

the quay. Vessels are arriving in a dynamic fash-

Muli-Quay Combined Berth and Quay Crane Allocation Using the Cuckoo Search Algorithm

221

Table 1: Nomenclature and notations.

Name Explanation

Notations

Alternative quay for vessel v

Expected arrival time of vessel v

Planned berthing position of vessel v

Planned berthing time of vessel v

Per hour handling cost of vessel v

Per hour waiting cost of vessel v

Per hour late departure cost of vessel v

nob

Penalty for non-optimal berthing position

of v

noq

Penalty for non-optimal berthing quay of v

min

Minimum berthing position served by

crane c

max

Maximum berthing position served by

crane c

Expected departure time of vessel v

Set of cranes assigned to vessel v (encoded

in binary form)

Handling time of vessel v

Handling productivity of crane c located on

quay q

Length of vessel v

Length of quay q

LDT

Late departure time of vessel v

Load

Total load of vessel v

Planned berthing quay of vessel v

Service cost per hour of crane c located on

quay q

PBP

Preferred berthing position of vessel v

PBQ

Preferred quay of vessel v

SD Safety distance between the berthing posi-

tions of two ships

SE Safety port entrance time between consec-

utive berthings

ST Safety time between the berthing times of

two ships

W T

Waiting time of vessel v

Sets and Indices

V Set of arriving vessels; v ∈ V a vessel

Q Set of quays; q ∈ Q a quay

B(q) Set of available berth positions on quay q ∈

Q; b ∈ B(q) a berth position

C(q) Set of quay cranes on quay q ∈ Q; c ∈ C(q)

a crane

K(q) Power set of cranes set C(q); k ∈ K(q) rep-

resents a subset of cranes from C(q) en-

coded in a binary form

T Set of time periods (planing horizon); t ∈ T

a time period

ion; however, their expected arrival times are known

in advance. The installed QCs perform loading and

unloading operations with some average productivity,

which can be different for each QC.

This study considers that the following informa-

tion is known in advance: number of ships, quays,

and lengths of quays; estimated times of arrival and

departure for each vessel; preferred berthing quay and

position for each vessel; the planning horizon (which

is divided into equal time intervals); and all costs and

penalties. In addition, the vessels cannot change their

berthing position during loading/unloading (i.e., berth

shifting is not considered).

2.2 Mathematical Formulation for

Multi-Quay Combined BAP and

QCAP

The primary objective of the multi-quay combined

BAP and QCAP is to allocate optimal berthing posi-

tions at the preferred quays, berthing times, and QCs

to arriving vessels in order to reduce the total service

cost (that is the combination of handling cost, waiting

costs, and several penalties), as shown in the below

cost function:

Cost (v, Q

, BP

, k

, BT

) = HT

· [C

+ f (v, Q

, BP

)]

+W T

·C

+ LDT

·C

(1)

The ﬁrst term of the cost function calculates the to-

tal handling cost based on the handling time HT

(in

hours), the handling cost per hour C

, and a penalty

function f (.) for assigning additional cost to non-

optimal quay and/or berth assignments. In this study,

the handling time is calculated based on the total load

of the vessel v and the handling productivity of the

cranes assigned to v. The second term in (1) calcu-

lates the total waiting cost and it depends on the total

waiting time W T

of vessel v and the per hour waiting

cost C

. The waiting time W T

of any vessel v is the

difference between berthing time BT

and arrival time

. The last term in (1) calculates the penalty cost

due to late departures, which is based on the late de-

parture time LDT

and the per hour penalty for late de-

parture C

. The late departure time is non-zero when

the berthing time BT

plus the handling time HT

ex-

ceeds the planned departure time DT

The primary goal of this work is to address the com-

bined BAP and QCAP within a multi-quay setting,

aiming to minimize the overall cost encompassing

handling costs, waiting costs, and various penalties.

The objective function is expressed by the following

VEHITS 2024 - 10th International Conference on Vehicle Technology and Intelligent Transport Systems

222

equation,

minimize

∑

v ∈ V

∑

q ∈ Q

∑

b ∈ B(q)

∑

k ∈ K(q)

∑

t ∈ T

Cost(v, q, b, k,t) · x

vqbkt

(2)

subject to the following constraints:

vqbkt

∈ {0, 1}, ∀ v ∈ V, q ∈ Q, b ∈ B(q), k ∈ K(q),t ∈ T

(3)

∑

q ∈ Q

∑

b ∈ B(q)

∑

k ∈ K(q)

∑

t ∈ T

vqbkt

= 1, ∀ v ∈ V (4)

≥ AT

, ∀ v ∈ V (5)

− BT

≥ SE ∀ v ̸= u ∈ V (6)

+ L

≤ L

, ∀ v ∈ V, q = Q

(7)

∑

v̸=u ∈V

+SD

∑

b=BP

−L

−SD

∑

k ∈ K(q)

+HT

+ST −1

∑

t=BT

−HT

−ST +1

uqbkt

= 0,

∀ v ̸= u ∈ V, q = Q

= Q

(8)

∑

v̸=u ∈V

∑

b ∈B(q)

∑

k ∈ K(q)

k & k

̸= 0

+HT

+ST −1

∑

t=BT

−HT

−ST +1

uqbkt

= 0,

∀ v ̸= u ∈ V, q = Q

= Q

(9)

min

< BP

+ L

& BP

< c

max

, ∀ v ∈ V, c ∈ k

(10)

The variable x

vqbkt

mentioned in constraint (3) takes

a value of 1 if vessel v is moored at berthing position

b of quay q at time t to be served by cranes k, and

0 otherwise. Constraint (4) ensures that each arriving

vessel is docked only once. In constraint (5), it is stip-

ulated that the scheduled berthing time BT

for a ves-

sel v must always be equal to or greater than its arrival

time AT

. The constraint (6) guarantees a minimum

safety entrance time (SE) between any two consec-

utive berthing operations. Constraint (7) ensures the

length of vessel v plus its berthing position does not

exceed the length of quay q, where it is moored. Con-

straint (8) restricts two vessels from overlapping dur-

ing mooring, both in terms of berthing positions, as

well as berthing times. Furthermore, it also ensures a

safety time (ST ) and safety distance (SD) between the

berthing of two ships. Constraint (9) restricts the set

of cranes k that is assigned to vessel u to not contain

any of the cranes allocated to another vessel v during

the same time period. Finally, constraint (10) ensures

that any crane c assigned to vessel v can reach the ves-

sel by checking that there is an overlap between the

minimum and maximum berthing positions served by

c and the quay positions occupied by v.

3 CUCKOO SEARCH

ALGORITHM

The cuckoo search algorithm is a relatively new

nature-inspired optimization method proposed by

Yang and Deb (2009) that has proven efﬁcient in solv-

ing several global optimization problems. CSA is

based on the basic rules of breeding parasitism of

some cuckoo species and then extended by the so-

called Levy ﬂights Yang and Deb (2009) instead of a

simple isotropic random walk (Yang and Deb, 2014).

Some cuckoo birds follow an aggressive production

strategy of laying eggs in communal nests and pos-

sibly removing eggs from other birds (host birds) to

maximize the probability of hatching for their own

eggs. When host birds discover the cuckoo eggs,

hosts either discard or abandon the eggs and build

new nests. Overall, the CSA operates on the basis of

cuckoo reproductive behavior by following three key

rules (Yang and Deb, 2009; Aslam et al., 2023):

1. one egg is dumped at a time by each cuckoo into

a randomly chosen nest;

2. the nests with high-quality eggs are retained and

utilized for the subsequent generation;

3. the quantity of host nests remains constant, and a

host bird detects an egg laid by a cuckoo with a

probability p

∈ (0, 1).

The correspondence between CSA and the multi-quay

combined BAP and QCAP is outlined as follows. A

single nest represents a collection of potential solu-

tions that include berthing times, quays, positions,

and a potential set of assigned cranes for all arriv-

ing ships, as illustrated in Fig. 2. Each egg within

a nest signiﬁes either a berthing time, berthing quay,

berthing position in a quay for an arriving ship, or a

potential set of cranes (using binary representation).

Meanwhile, a cuckoo egg represents a new or im-

proved solution (representing either a berthing time,

berthing quay, berthing position, or set of cranes).

In Fig.3, the operational ﬂow of CSA for the

multi-quay combined BAP and QCAP is depicted.

Muli-Quay Combined Berth and Quay Crane Allocation Using the Cuckoo Search Algorithm

223

7 10 33 49 54 3

8 11 30 46 57 2

9 10 30 47 57 1

. . .

Berthing times by CSA for 5 ships

1 2 1 5 70 133 68 333 220

{00000}

{00011}

{00111}

4 2 1 1 99 310 75 310 211

{00100}

2 2 1 5 155 88

Berthing quays by CSA for 5 ships

66 332 222

{10000}

{00111}

{01000}

Berthing positions by CSA for 5 ships

{00011}

Nest i

Nest i+1

Nest k

{00000}

{11000}

{00000}

{00110}

Cranes assigned by CSA for 5 ships

{00000}

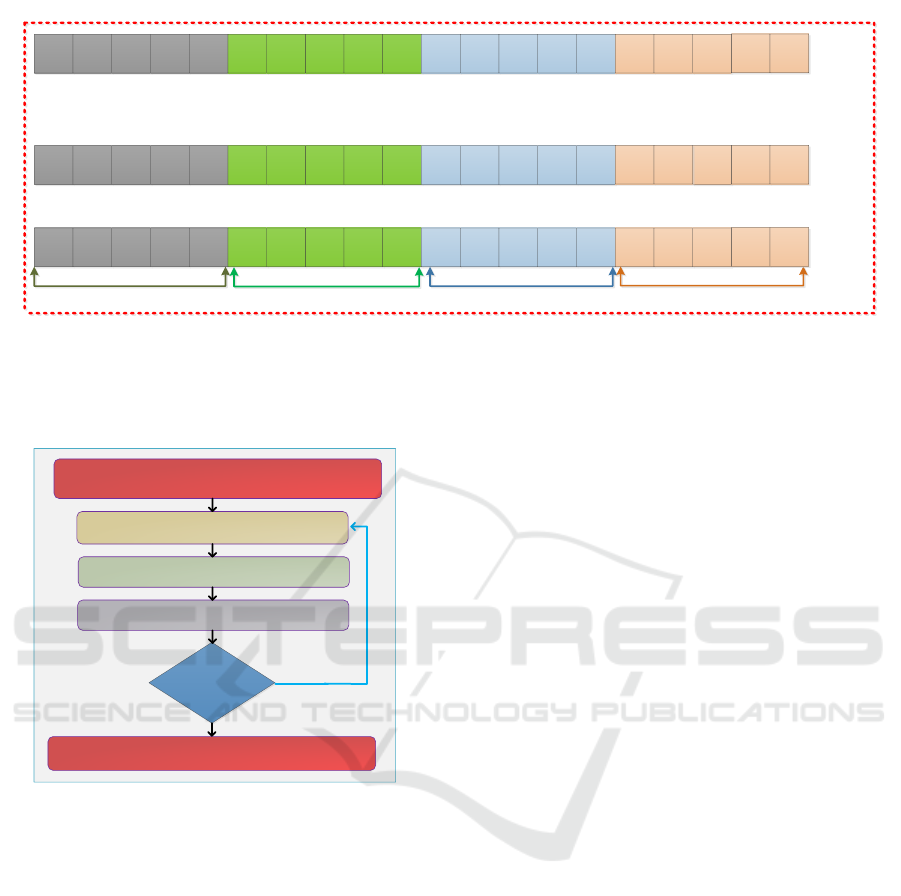
Figure 2: The representation of solutions by CSA with ﬁve ships. Each nest forms a full solution to the problem and contains

ﬁve berthing times, berthing quays, berthing positions, and crane assignments, one for each ship. The binary representation

of each crane assignment value denotes the set of cranes assigned to the ship.

Initial population of host nests and eggs

Get cuckoo with eggs by Levy flights

Fitness evaluation and store the best nest

with good solution

Termination

criteria?

Find best nest with minimum objective value and

terminate algorithm

Yes

Discard worst nests and build new ones

with new solutions

Figure 3: Flow chart of Cuckoo Search Algorithm.

The total number of host nests shows each iteration’s

search space, which remains constant (assuming 100

in our work). During each iteration, 100 solutions

(nests) are generated, and the size of each solution

is four times the total number of ships, as illustrated

in Fig.2. All the solutions are compared at each it-

eration and the best solution (nest) is considered the

local best. At the next step, some low-quality solu-

tions (nests) are discarded and new ones are built to

avoid getting stuck at local optima. Then, the ﬁtness

of new solutions is calculated and the best nest with

high quality solutions is selected. All the steps are re-

peated until termination criteria are met (as depicted

in Fig. 3).

4 CASE STUDY: PORT OF

LIMASSOL, CYPRUS

A real-world case study from the Port of Limassol,

Cyprus, is used to test the performance of the pro-

posed CSA-based approach for combined berth and

quay crane allocation to ships arriving during the ﬁrst

week of March 2018 (some example data for 10 of the

ships is presented in Table 2). In the Port of Limassol,

there are ﬁve commercial berthing quays, all of which

are continuous. All quays are of different lengths;

Container Quay: 800m; Ro-Ro Quay: 450m; West

Quay: 770m; North Quay: 430m; and East Quay:

480m. There are only two container quays, i.e., the

Container Quay and the Ro-Ro Quay, and a total of

seven cranes are installed at both quays (5 at the Con-

tainer Quay and 2 at Ro-Ro Quay). In addition, the

Container Quay is further divided into two parts; two

cranes operate on the left side, while the remaining

three cranes operate on the right side; note there is a

dead space in between the two parts of the container

quay. It should also be noted that the cranes can only

move within a certain range from their location. Fur-

thermore, the cranes cannot cross each other and all

have different handling productivity rates which are

known.

The newly developed methods for multi-quay

combined BAP and QCAP have been implemented in

MATLAB R2021b. All experiments are performed

using a Windows 10 computer system with a 3.4 GHz

Core i7 and 16 GB RAM.

Fig. 4 and Fig. 5 show the solutions proposed by

CSA and MILP, respectively, for the allocation of

berths and quay cranes. The rectangles in the ﬁg-

ures show each vessel, designating the berthing time

VEHITS 2024 - 10th International Conference on Vehicle Technology and Intelligent Transport Systems

224

Table 2: Example dataset for 10 out of 28 ships that arrived at the Port of Limassol, Cyprus during the ﬁrst week of March

2018.

Ship # ETA (day\time) HT (min.) ETD (day\time) PBQ ABQ PBP LoS (m)

1 1\04:00 919 1\22:30 Ro-Ro Quay Container Quay 240 194

2 1\05:30 1490 2\06:50 East Quay – 276 139

3 1\14:00 1285 2\12:50 West Quay North Quay 84 84

4 1\15:00 5700 5\14:03 East Quay – 51 89

5 1\17:00 5970 5\21:00 West Quay North Quay 314 190

6 2\04:30 470 2\13:50 Ro-Ro Quay Container Quay 138 159

7 2\05:00 168 2\09:30 Container Quay Ro-Ro Quay 571 196

8 2\08:00 440 2\15:55 North Quay West Quay 53 155

9 3\04:00 905 3\20:50 Ro-Ro Quay Container Quay 31 175

10 3\03:30 1331 4\06:15 Container Quay Ro-Ro Quay 389 277

at the x-axis, and the berthing position of each ves-

sel at the y-axis. The number in front of the rectan-

gle shows the ship index and the text in green color

shows the assigned set of cranes to each vessel. In

addition, ships with blue rectangles indicate that they

are moored at their preferred berthing quay (PBQ),

while ships moored in their alternate berthing quay

(ABQ) are colored red. Vessels are moored in the

ABQ typically when there is a long waiting time be-

fore the optimal berth assignment, which may result

in delayed departures and increased cost. From Fig. 5

it can be seen that vessel 23 is moored at the North

Quay (ABQ) instead of the West Quay (PBQ) when

MILP is used. On the other hand, CSA places vessel

23 at its PBQ but at the expense of placing both ves-

sels 21 and 23 far from their preferred berthing posi-

tion (PBP), thereby increasing the total service cost.

It is also important to note that there are only two

quays where QCs are installed and assigned; the re-

maining quays are passenger/general cargo quays and

no cranes are installed on these quays. For container

quays, the total operating time of the vessels is cal-

culated based on the number of cranes used and their

productivity. However, in the case of the other three

quays, the total operating time of the vessels is pro-

vided as an input. In a week, four ships arrive at the

Container Quay and six ships at the Ro-Ro Quay, all

of which are assigned the optimal number of cranes

using both implemented algorithms.

An in-depth comparison of the proposed method

CSA with the exact MILP method is provided in Table

3 in terms of the different costs and computation time

for the one-week tested scenario. Waiting costs are in-

curred when a vessel v has to wait before the optimal

berth allocation, while NOB costs are included in the

total service cost when a vessel v is berthed at a place

other than its PBP or at the ABQ instead of the PBQ.

NOB is calculated by determining the absolute differ-

ence between the optimal and the assigned berthing

positions, as determined by any algorithm. However,

Figure 4: Solution by CSA.

Figure 5: Solution by MILP.

a ﬁxed penalty is added in case of berth allocation

at the ABQ. Furthermore, to avoid the berthing of

vessels to quays other than the ABQ or the PBQ, a

penalty of inﬁnity is added. From this table, it can

be seen that MILP has a minimum total cost (10090)

with 0 waiting cost and 120 cost for late departures.

However, it provides an optimal solution at the ex-

Muli-Quay Combined Berth and Quay Crane Allocation Using the Cuckoo Search Algorithm

225

Table 3: Comparative analysis of CSA and MILP.

Algorithms: CSA MILP

Waiting cost (C) 50 0

NOB cost (C) 250 100

Normal handling cost (C) 9870 9870

Late departure cost (C) 140 120

Total service cost (C) 10320 10090

Computation time (sec) 84.73 912.55

pense of increased computation time, which is 912.55

seconds (more than 15 minutes) for the one-week sce-

nario. On the other hand, the total service cost for

CSA is near-optimal (10320) and closely resembles

MILP. However, CSA solves the problem in just 84.73

seconds, a 10× performance improvement. Note that

for larger problem instances (i.e., more ships or in-

creased planning horizon) using MILP becomes pro-

hibitive due to the exponentially growing complexity

of the problem. Based on the aforementioned compar-

ative analysis and discussion, it can be inferred that

the recently developed CSA-based approach for the

multi-quay combined BAP and QCAP is highly effec-

tive and capable of delivering a solution that is close

to optimal within a reasonable computation time.

5 CONCLUSIONS

This study investigates the multi-quay combined

berth allocation problem (BAP) and quay crane allo-

cation problem (QCAP) with the objective of mini-

mizing the total service cost for arriving vessels. To

solve the multi-quay combined BAP and QCAP, a

MILP model is formulated and solved using both an

exact method and our developed metaheuristic solu-

tion based on the cuckoo search algorithm (CSA).

Evaluation results using real data from the Port of Li-

massol, Cyprus, conﬁrmed the efﬁciency of the CSA,

as compared to the exact method (MILP), since it

was able to provide near-optimal results for the tested

scenario at a fraction of the computation time. The

MILP takes too much time (912.55 seconds) to solve

the problem; however, the CSA method solves the

same problem in only 84.73 seconds and the achieved

objective value (10320) is only 1.02% away from

the optimal solution (10090 euro). This makes the

CSA method more suitable for addressing real-world

problems with increased complexity where using the

MILP becomes prohibitive.

The future plan is to further evaluate CSA’s per-

formance for larger problem instances of the multi-

quay combined BAP and QCAP (with a larger num-

ber of ships and/or planning horizon). We also plan to

implement and compare other popular computational

intelligence methods such as genetic algorithm and

particle swarm optimization.

ACKNOWLEDGEMENTS

This work was supported by the European Union’s

Horizon Europe program for Research and In-

novation through the aerOS project under Grant

No. 101069732 as well as by the European

Regional Development Fund and the Republic of

Cyprus through the Cyprus Research and Innovation

Foundation (MDigi-I: STRATEGIC INFRASTRUC-

TURES/1222/0113).

REFERENCES

Alsouﬁ, G., Yang, X., and Salhi, A. (2016). Robust berth

allocation using a hybrid approach combining branch-

and-cut and the genetic algorithm. In International

workshop on hybrid metaheuristics, pages 187–201.

Springer.

Aslam, S., Michaelides, M. P., and Herodotou, H. (2020).

Internet of ships: A survey on architectures, emerging

applications, and challenges. IEEE Internet of Things

Journal, 7:9714–9727.

Aslam, S., Michaelides, M. P., and Herodotou, H.

(2021). Dynamic and continuous berth allocation us-

ing cuckoo search optimization. In International Con-

ference on Vehicle Technology and Intelligent Trans-

port Systems (VEHITS), pages 72–81.

Aslam, S., Michaelides, M. P., and Herodotou, H. (2022a).

Enhanced berth allocation using the cuckoo search al-

gorithm. SN Computer Science, 3(4):1–15.

Aslam, S., Michaelides, M. P., and Herodotou, H. (2022b).

Optimizing multi-quay berth allocation using the

cuckoo search algorithm. In Proceedings of the 8th

International Conference on Vehicle Technology and

Intelligent Transport Systems (VEHITS), pages 124–

133.

Aslam, S., Michaelides, M. P., and Herodotou, H. (2023).

Berth allocation considering multiple quays: A practi-

cal approach using cuckoo search optimization. Jour-

nal of Marine Science and Engineering, 11(7):1280.

Bierwirth, C. and Meisel, F. (2015). A follow-up survey of

berth allocation and quay crane scheduling problems

in container terminals. European Journal of Opera-

tional Research, 244(3):675–689.

Ernst, A. T., O

guz, C., Singh, G., and Taherkhani, G.

(2017). Mathematical models for the berth allocation

problem in dry bulk terminals. Journal of Scheduling,

20(5):459–473.

Frojan, P., Correcher, J. F., Alvarez-Valdes, R., Koulouris,

G., and Tamarit, J. M. (2015). The continuous

VEHITS 2024 - 10th International Conference on Vehicle Technology and Intelligent Transport Systems

226

berth allocation problem in a container terminal with

multiple quays. Expert Systems with Applications,

42(21):7356–7366.

Golias, M. M., Boile, M., and Theofanis, S. (2009a).

Berth scheduling by customer service differentia-

tion: A multi-objective approach. Transportation Re-

search Part E: Logistics and Transportation Review,

45(6):878–892.

Golias, M. M., Saharidis, G. K., Boile, M., Theofanis, S.,

and Ierapetritou, M. G. (2009b). The berth allocation

problem: Optimizing vessel arrival time. Maritime

Economics & Logistics, 11(4):358–377.

Gutierrez, F., Lujan, E., Asmat, R., and Vergara, E. (2019).

Fully fuzzy linear programming model for the berth

allocation problem with two quays. In Uncertainty

Management with Fuzzy and Rough Sets, pages 87–

113. Springer.

Krimi, I., Todosijevi

c, R., Benmansour, R., Ratli, M.,

El Cadi, A. A., and Aloullal, A. (2020). Modelling and

solving the multi-quays berth allocation and crane as-

signment problem with availability constraints. Jour-

nal of Global Optimization, 78(2):349–373.

Li, Y., Chu, F., Zheng, F., and Liu, M. (2020). A bi-

objective optimization for integrated berth allocation

and quay crane assignment with preventive mainte-

nance activities. IEEE Transactions on Intelligent

Transportation Systems.

Lind, M., Michaelides, M. P., Robert, W., and Richard,

W. T. (2020). Maritime informatics. Springer.

Lujan, E., Vergara, E., Rodriguez-Melquiades, J., Jim

enez-

Carri

on, M., Sabino-Escobar, C., and Gutierrez, F.

(2021). A fuzzy optimization model for the berth al-

location problem and quay crane allocation problem

(bap+ qcap) with n quays. Journal of Marine Science

and Engineering, 9(2):152.

Rodrigues, F. and Agra, A. (2022). Berth allocation and

quay crane assignment/scheduling problem under un-

certainty: a survey. European Journal of Operational

Research.

Theofanis, S., Boile, M., and Golias, M. (2007). An op-

timization based genetic algorithm heuristic for the

berth allocation problem. In 2007 IEEE Congress on

Evolutionary Computation, pages 4439–4445. IEEE.

Xiang, X. and Liu, C. (2021). An almost robust optimiza-

tion model for integrated berth allocation and quay

crane assignment problem. Omega, 104:102455.

Yang, X.-S. and Deb, S. (2009). Cuckoo Search via L

evy

Flights. In World Congress on Nature & Biologically

Inspired Computing (NaBIC), pages 210–214. IEEE.

Yang, X.-S. and Deb, S. (2014). Cuckoo search: recent ad-

vances and applications. Neural Computing and ap-

plications, 24(1):169–174.

Yu, T., Qiang, Z., and Benfei, Z. (2019). A genetic

algorithm based on spatiotemporal conﬂict between

continuous berth-allocation and time-varying spe-

ciﬁc crane assignment. Engineering Optimization,

51(3):390–411.

Zheng, F., Li, Y., Chu, F., Liu, M., and Xu, Y. (2019). In-

tegrated berth allocation and quay crane assignment

with maintenance activities. International Journal of

Production Research, 57(11):3478–3503.

Muli-Quay Combined Berth and Quay Crane Allocation Using the Cuckoo Search Algorithm

227