Sign Language Recognition Based on Subspace Representations in the

Spatio-Temporal Frequency Domain

Ryota Sato

, Suzana Rita Alves Beleza

1 a

, Erica K. Shimomoto

2 b

, Matheus Silva de Lima

Nobuko Kato

3 c

and Kazuhiro Fukui

1 d

University of Tsukuba, Department of Computer Science, Tsukuba, Ibaraki, Japan

National Institute of Advanced Industrial Science and Technology (AIST), Tokyo, Japan

Tsukuba University of Technology, Faculty of Industrial Technology, Tsukuba, Ibaraki, Japan

Keywords:

Sign Language Recognition, 3D Fast Fourier Transform, Product Grassmann Manifold, Subspace-Based

Methods.

Abstract:

This paper proposes a subspace-based method for sign language recognition in videos. Typical subspace-based

methods represent a video as a low-dimensional subspace generated by applying principal component analysis

(PCA) to a set of images from the video. Such representation is compact and practical for motion recognition

under few learning data. However, given the complex motion and structure in sign languages, subspace-based

methods need to improve performance as they do not consider temporal information like the order of frames.

To address this issue, we propose processing time-domain information on the frequency-domain by applying

the three-dimensional fast Fourier transform (3D-FFT) to sign videos, where a sign video is represented as a

3D amplitude spectrum tensor, which is invariant to deviations in the spatial and temporal directions of target

objects. Further, a 3D amplitude spectral tensor is regarded as one point on the Product Grassmann Manifold

(PGM). By unfolding the tensor in all three dimensions, PGM can account for the temporal information.

Finally, we calculate video similarity by using the distances between two corresponding points on the PGM.

The effectiveness of the proposed method is demonstrated on private and public sign language recognition

datasets, showing a signiﬁcant performance improvement over conventional subspace-based methods.

1 INTRODUCTION

Sign languages consist of visual and movement-based

languages primarily used by deaf and hard-of-hearing

communities worldwide. As with any language, they

have a rich grammatical structure and allow the com-

munication of complex information. However, sign

languages are often restricted to being used within

these minority groups and are not widely spoken by

the average member of society. This restriction intro-

duces a signiﬁcant challenge in integrating deaf and

hard-of-hearing individuals into public systems.

Developing sign language recognition systems is

an essential step towards overcoming this challenge.

Since sign languages are primarily visual-based, the

task of sign language recognition is often seen as a

task in action recognition. In this context, several

methods have been proposed to solve action recog-

nition, using classical methods, such as the subspace-

https://orcid.org/0000-0003-3200-8501

https://orcid.org/0000-0001-7838-8285

https://orcid.org/0000-0003-0657-6740

https://orcid.org/0000-0002-4201-1096

based methods (Tanaka et al., 2016; Peris and Fukui,

2012), and deep learning methods, such as (Tufek

et al., 2019; Jaouedi et al., 2020).

Subspace-based methods are attractive due to their

robustness in performance and require low computa-

tional resources, being suitable for embedded appli-

cations. They have also been shown to achieve good

performance using few data. This situation is typi-

cal in sign language recognition, where datasets are

scarce. Such methods represent videos as linear sub-

spaces modeled by applying the principal components

analysis (PCA) to the set of the video’s frames. This

representation is invariant to operating speed changes,

i.e., the same action performed at different speeds

will lead to similar subspace representations. Thus, a

typical subspace can represent simple human actions,

such as gait (Iwashita et al., 2015; Iwashita et al.,

2017; Sakai et al., 2019).

However, since each frame does not explicitly

carry temporal information, PCA by itself cannot ac-

count for the order of the frames. Therefore, they may

not be suitable for complex human actions such as

sign language.

152

Sato, R., Beleza, S., Shimomoto, E., Silva de Lima, M., Kato, N. and Fukui, K.

Sign Language Recognition Based on Subspace Representations in the Spatio-Temporal Frequency Domain.

DOI: 10.5220/0012577000003654

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 13th International Conference on Pattern Recognition Applications and Methods (ICPRAM 2024), pages 152-159

ISBN: 978-989-758-684-2; ISSN: 2184-4313

!"#$$%

&'()* +,-.)/

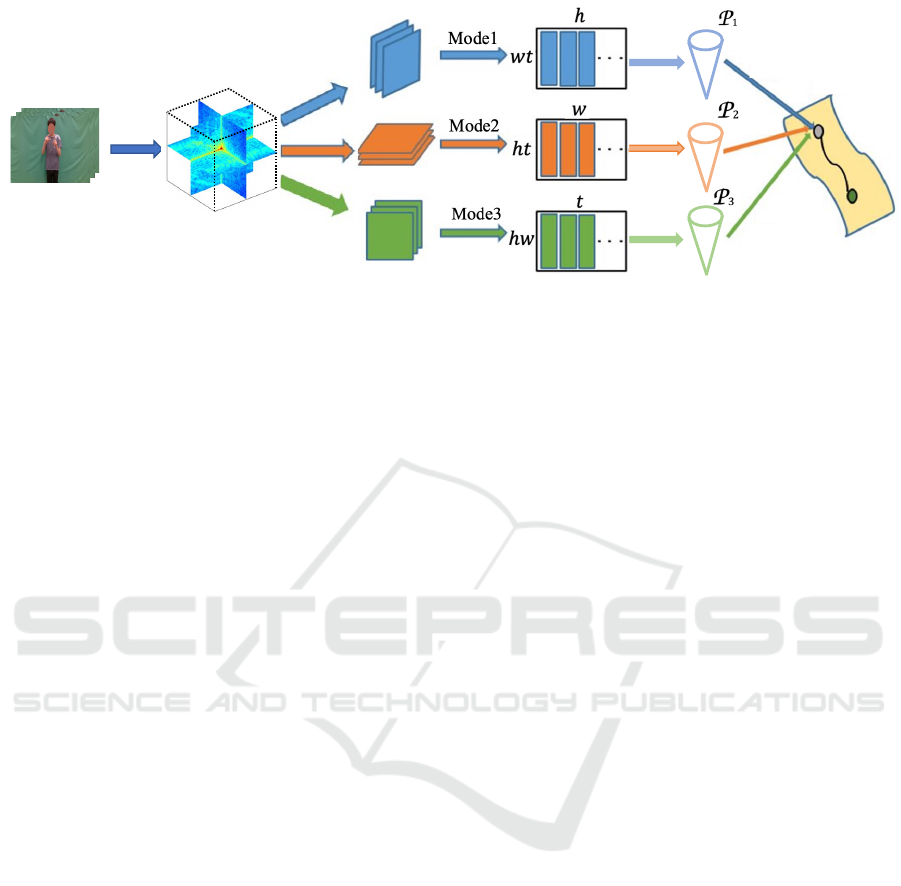
012

!"3-.45'67()3

/4)86,7.36)9/*,

:7;/4-8)

:5'8)3'93!3

(',)86'*9/

! " # " $

!"#

Figure 1: Overview of our method. We generate a 3D amplitude spectrum tensor A ∈ R

h×w×t

from set of frames of the input

video {V

}

i=1

∈ R

h×w

by applying the 3D-FFT. This 3D tensor is unfolded along the three dimensions resulting in the set

of modes A = {A

∈ R

(wt)×h

, A

∈ R

(ht)×w

, A

∈ R

(wh)×t

}. Then, we apply PCA to each mode matrix, resulting in three

mode subspaces {P

}

j=1

. Finally, the 3D tensor is regarded as a single point on the product Grassmann manifold (PGM).

The similarity between two 3D tensors is calculated as the distance between two corresponding points on the PGM.

Other subspace representations have been pro-

posed to overcome such naive subspaces’ lack of time

representation. For example, the randomized time

warping (RTW) (Suryanto et al., 2016) can ﬂexibly

represent such changes in speed by representing a

video as a subspace from its time-elastic features. The

RTW-based subspace is robust against internal varia-

tions in the video data. However, RTW requires con-

catenating feature vectors to account for temporal or-

dering. This operation leads to a signiﬁcant increase

in memory consumption when high-dimensional fea-

ture vectors are used. As another example, slow fea-

ture subspace (SFS) (Beleza et al., 2023) generated by

applying the Slow Feature Analysis (SFA) (Wiskott

and Sejnowski, 2002) to a video can also handle the

issue by selectively extracting slow temporal features.

However, two new hyper-parameters need to be con-

sidered to generate the SFS. They can be set to a ﬁxed

number, but extra experiments are needed to deter-

mine their values.

We propose an effective method based on the

three-dimensional fast Fourier transform (3D-FFT),

where each video is represented as a 3D tensor. Fig-

ure 1 shows a conceptual diagram of the proposed

method. Our method has been motivated by the posi-

tion invariance of 2D-FFT (Modler and Myatt, 2007;

Mahbub et al., 2013) in image recognition. The 3D

amplitude spectral tensor is invariant to spatial and

temporal shifts, so the proposed method is robust to

hand motion shifts.

By representing videos as 3D tensors, we con-

vert the problem of measuring the similarity between

two videos to measuring the similarity between the

3D amplitude spectrum tensors of the spatio-temporal

spectrum of the videos in the frequency domain. One

could simply vectorize the tensors and perform cosine

similarity; however, this approach could lead to loss

of the data structure within the tensors.

To avoid this issue, we apply the product Grass-

mann manifold (PGM) (Lui, 2012; Lui et al., 2010;

Batalo et al., 2022) that can effectively compare and

classify multiple 3D tensors. In our setting, we gen-

erate three subspaces from the unfolded vectors of

the modes of the 3D tensor using PCA, where sub-

spaces for each mode lie in a different Grassmann

manifold (Wong, 1967). PGM is then deﬁned as the

Cartesian product space of each mode’s correspond-

ing manifold. While PGM also uses PCA, due to

the unfolding operation in all three directions, re-

sulting unfolded vectors still carry temporal informa-

tion, making this subspace representation aware of the

frame orders.

Comparison between two 3D tensors is possible

by measuring the geodesic distance between their two

respective representations in PGM. Such similarity

measure relies on the subspace similarity (Yamaguchi

et al., 1998; Fukui, 2014; Fukui and Maki, 2015) and

can account for the unique structure present in each

mode.

Unlike other subspace representations, the pro-

posed method does not require the concatenation of

feature vectors or additional experiments to determine

parameters. Therefore, the proposed method can ef-

ﬁciently represent subspaces with a small computa-

tional cost.

The effectiveness of the proposed method is eval-

uated on two datasets: Tsukuba New Signs Dataset

(TNSD) that we created for this research and the

Chinese Sign Language Dataset (CSLD) (Liu et al.,

2016), showing signiﬁcant improvement in perfor-

mance against the conventional subspace-based meth-

ods.

Sign Language Recognition Based on Subspace Representations in the Spatio-Temporal Frequency Domain

153

The rest of the paper is organized as follows. In

Section 2, we formulate the problem of sign language

recognition and describe our method. In Section

3, we demonstrate the effectiveness of our method

through experimental evaluation on private and public

sign language datasets. Finally, Section 4 concludes

the paper.

2 PROPOSED METHOD

In this section, we describe our method for sign lan-

guage recognition. We formulate the sign recognition

task as follows: Let {(v

, y

)}

i=1

be a set of n reference

videos of hand signs from sign languages. Each video

is paired with a respective label y

corresponding

to its class, which describes the meaning of the hand

sign. Given an input video v

, the goal is to correctly

classify it into the corresponding class.

In the following, we ﬁrst explain our basic video

representation, obtained using 3D-FFT. Then, we

elaborate on how to compare the obtained 3D ampli-

tude tensors using the product Grassmann manifold.

Finally, we describe the identiﬁcation framework for

sign language recognition using our method.

2.1 3D-FFT Based Video

Representation

To effectively capture complex internal variations in

videos, we propose representing them as 3D ampli-

tude spectrum tensors in the frequency domain by ap-

plying the 3D-FFT. Our motivation comes from the

object position invariance property of 2D amplitude

spectrum image obtained with 2D-FFT. 3D ampli-

tude spectrum tensors obtained from the 3D-FFT are

invariant not only to changes in space, but also to

changes in time. This property is depicted in Figure 2.

Therefore, in our method, we apply the 3D-FFT

to each video v

, deﬁned as a set of video frames

{ f

i j

}

j=1

, f

i j

∈ R

h×w

, resulting in a 3D amplitude

spectrum A

∈ R

h×w×t

2.2 Product Grassmann Manifold

In sign language recognition, it is necessary to com-

pare 3D amplitude tensors effectively. In this com-

parison, it is essential to consider the data structure

within the tensor and keep the computational cost rea-

sonable, as larger tensors lead to an increase in mem-

ory consumption.

In this context, we incorporate the concept of the

product Grassmann manifold (PGM) (Lui, 2012; Lui

!"#$$%

!"&'"

!"#$$%

'"#$$%

'"()*+,-./01(

2+13.4/*(.15264

!"()*+,-./01(

2+13.4/*(-*)71

Figure 2: Process of 3D-FTT. Just as the 2D amplitude

spectrum image obtained from 2D-FFT is the same between

images of the same object in different positions, applying

3D-FFT to videos that perform similar motion yields a sim-

ilar 3D amplitude spectrum tensor.

et al., 2010) in our method. PGM is deﬁned as the

space of products of multiple Grassmann manifolds

and is a way to effectively represent tensors that hold

multiple dimensions or modes as a single data set.

Let A ∈ R

h×w×t

be a 3D amplitude spectrum video

tensor, where h, w, and t denote height, width, and

number of frames, respectively. Unfolding this tensor

along each dimension generates a set of mode matri-

ces A = {A

∈ R

(wt)×h

, A

∈ R

(ht)×w

, A

∈ R

(hw)×t

where each sliced matrix retains distinctive features

along its direction.

Then, we apply PCA to each mode matrix to com-

pactly represent them as low-dimensional subspaces

}

j=1

, with dimension m

in a d

-dimensional

space. Formally, each subspace is represented as a

matrix S

∈ R

×m

, which has the orthonormal basis

vectors of the subspace as its column vectors.

While the subspaces in PGM are also modeled

through simple PCA, the unfolded vectors in modes 1

and 2, along the directions of the height and width of

the video frames, contain temporal information and,

therefore, the representation on PGM can compactly

account for the order of the frames.

Each subspace S

is a point on the Grassmann

manifold M

, d

). A uniﬁed representation is con-

structed on product Grassmann manifold from a set of

factor manifolds {M

}

j=1

as follows:

M = M

× M

= (S

, S

), (1)

where × denotes Cartesian product. Consequently,

each tensor is represented as a single point on M.

Comparison on the PGM M is possible by mea-

suring the geodesic distance between two points on

M. Given the tensors X and Y , represented by sets

ICPRAM 2024 - 13th International Conference on Pattern Recognition Applications and Methods

154

!"#$% &'()$*

+,-./01"#$%0&'()$*

!"#$$%

234

560()-7"/.#$0

*-$8/'.)0/$,*%'

9(78.7(/$0

:$%#$*"80#"*/(,8$0

Figure 3: Conceptual ﬁgure of comparison between two 3D

amplitude tensors on PGM. Each tensor is represented as a

point on the PGM.

of subspaces {P

}

j=1

and {Q

}

j=1

, the similarity be-

tween them is deﬁned as follows:

ρ(X , Y ) =

∑

j=1

sim(P

, Q

)

, (2)

where sim(P

, Q

) denotes the structual similarity be-

tween subspaces P

and Q

The similarity sim(P

, Q

) can be measured with

the canonical angles {θ} between them in the mu-

tual subspace method (MSM) framework (Yamaguchi

et al., 1998; Fukui, 2014; Fukui and Maki, 2015).

Within the PGM context, this similarity allows the

comparison between tensor modes while considering

the unique structure information contained in each

mode.

Let P

P ∈ R

d×m

and Q

Q ∈ R

d×m

be the orthonormal

basis vectors of the two subspaces P and Q , with m

and m

dimensions respectively, and m

≤ m

. We

ﬁrst calculate the SVD P

⊤

Q = U

UΣ

ΣV

⊤

, where Σ

Σ =

diag(κ

, . . . , κ

), {κ

}

i=1

represents the set of singular

values(=cos θ

), and κ

≥ . . . ≥ κ

. The similarity

can then be calculated as follows:

sim(P , Q ) =

∑

i=1

, (3)

where 1 ≤ r ≤ m

The representation of the 3D amplitude tensors on

PGM allows their comparison without compromising

their essential structural information. This process is

depicted in Figure 3.

2.3 Algorithm for Sign Recognition

In this section, we describe the identiﬁcation frame-

work for sign language recognition using the pro-

posed method, shown in Figure 4. Given a set of n

training examples {(v

, y

)}

i=1

, where each video v

paired with a respective label y

∈ C which describes

the meaning of the hand sign, We perform recognition

of a given input video v

, according to the following

phases:

In the training phase, there are three steps:

1. For each training video v

, apply 3D-FFT to obtain

the 3D amplitude spectrum tensors {A

}

i=1

2. Unfold each tensor along the three dimen-

sions, resulting in the sets of mode matrices

, A

, }

i=1

3. Apply PCA to each mode matrix, yielding one set

of subspaces {S

, S

} for each video, where

each mode subspace S

lies in the manifold M

Next, the recognition phase consists of the following

four steps:

1. Apply 3D-FFT to the input video v

to generate

an 3D amplitude spectrum tensor A

2. Unfold the obtained tensor in all three directions,

obtaining the set of mode matrices {A

, A

3. Apply PCA to each mode matrix, yielding the set

of input subspaces {S

, S

4. Calculate the similarity between the input video

and each training video in the PGM using Equa-

tion 2. The class of the most similar training video

is considered the identiﬁcation result.

3 EVALUATION

This section compares our results to baseline methods

in our new Tsukuba New Signs Dataset (TNSD) and

Chinese Sign Language Dataset (CSLD) (Liu et al.,

2016). We evaluated the performance of the meth-

ods on the action recognition task using video frames

without pre-processing (i.e., raw images) and CNN

features.

3.1 Baseline Methods

We consider recent baseline methods that propose

different subspace types to represent video temporal

data. As they are all subspace-based methods, they

use the subspace similarity deﬁned in Equation 3 to

perform recognition. In the following, we brieﬂy ex-

plain each one and refer the reader to the original pa-

pers for details.

PCA: The subspace is obtained by applying PCA di-

rectly to the video data. Therefore, no time repre-

sentation is considered.

RTW (Suryanto et al., 2016): features are ran-

domly sampled from multiple video frames

Sign Language Recognition Based on Subspace Representations in the Spatio-Temporal Frequency Domain

155

!!!

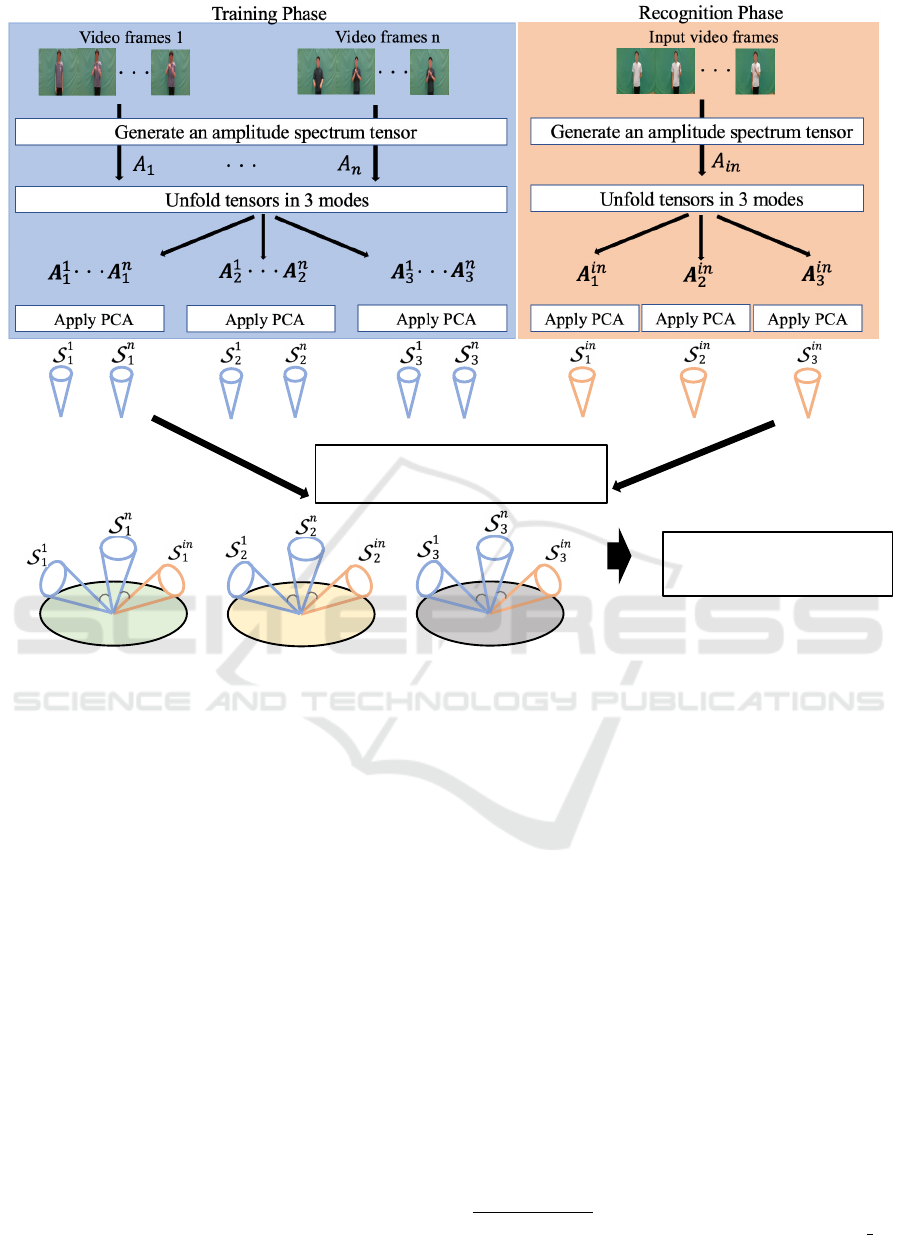
!"#$%#"&'(&)'(*+,+#"-+&.(/'&0''1(

*%/*2"$'*(+1 '"$)(,34'

!"#$%&'('$&)*+,"-)$&

+."/+%"),'0'1+/'(2)

534'6 534'7 534'8

Figure 4: The overview of the proposed framework. It consists of two phases: 1) In the training phase, a 3D amplitude tensor

in the training set is obtained by applying the 3D-FFT. Each tensor is unfolded into three mode matrices {A

}

j=1

. PCA is

applied to each mode matrix yielding one set of subspaces {S

, S

} for each video, where each mode subspace S

lies in

the manifold M

.; 2) In the recognition phase, we apply the 3D-FFT to the input video v

, obtaining its 3D tensor A

. This

tensor is unfolded into three mode matrices, which are modeled as mode subspaces {S

, S

} by PCA. Recognition is

then performed based on the geodesic distance on the PGM.

while maintaining the original temporal order.

By applying PCA to this feature set, a compact

subspace that considers sequential information is

computed.

Slow Feature Subspace (SFS) (Beleza et al., 2023):

This subspace is obtained by applying PCA to the

weight vectors extracted from the video data by

the slow feature analysis (SFA). Thus, the SFS

can represent the video characteristics with slow

temporal variation and is considered robust to

temporal ﬂuctuations and noise.

3D-FFT: the subspace is obtained by applying 3D-

FFT to the input data.

CNN+baseline: We also compare our results to the

baseline methods using CNN features. In this ap-

proach, we ﬁrst extract the CNN features of each

video using a VGG19 model pre-trained on Ima-

geNet

and then build the subspace as previously

explained in each baseline method.

3.2 Datasets

In our experiments, we used two different datasets:

Tsukuba New Signs Dataset. We created a new

dataset, called Tsukuba New Signs Dataset (TNSD),

for this research. TNSD consists of 31 signs cap-

tured from nine Japanese sign language native indi-

viduals in a controlled environment. These signs in-

clude terms from the IT area considered common to

daily use by the Japan Institute for Sign Language

Studies. In this dataset, the individuals performed

https://www.robots.ox.ac.uk/

∼

vgg/research/very dee

ICPRAM 2024 - 13th International Conference on Pattern Recognition Applications and Methods

156

!"#$%&'

()*+,

-)./

0,1'.,'1

2#+&

!"3'&

4&#55

67(

-'8

933):,1

Figure 5: Examples of the Tsukuba New Signs Dataset.

each sign three times, generating a total of 837 short

videos (=9 subjects×31 classes×3 shots). All videos

have the same structure, starting with the individ-

ual’s arms lowered, followed by a sign, and then their

arms lowered again. The fps of each video is 30,

and the number of frames ranges from 40 to 144.

Therefore, the dimension {d

}

j=1

of each mode is

{72 × 40, 128 × 40, 72 × 128}. For videos with more

than 40 frames, the ﬁrst 40 frames of the amplitude

spectral tensor are extracted. A dataset sample can be

seen in Figure 5.

This dataset contains three types of data: Un-

masked, where the face of the subjects is visible; eye-

masked, where the eye region is masked; and face-

masked, where the whole face is masked. We pro-

cessed the videos by converting them into gray-scale

images with dimensions of 72×128 pixels.

Chinese Sign Language Dataset. The Chinese

Sign Language Dataset (CSLD) (Liu et al., 2016) con-

sists of 500 different Chinese Sign Languages, per-

formed by 50 subjects in each class, amounting to

25,000 videos. Each video consists of 50 frames.

In the experiment, 10 signs were randomly sampled

from the entire dataset to create a subset of 500

videos. Figure 6 shows a sample of the CSLD.

3.3 Experiments on TNSD

For this dataset, we ran experiments with all three

types of data, i.e., unmasked, eye-masked and face-

masked to assess the inﬂuence of masking in our

framework’s performance. Furthermore, we consid-

ered two different experimental settings, described in

the following:

Experimental Setting 1. We considered the same

subjects for training and testing. Since there are three

videos for each class, one was used as training data

and two as test data. We consider 3-fold cross vali-

Goal

Clue

Development

Composition

Short

Swell

Brother

Grandmother

Soda

Class Example Class Example

Tag

Public welfare

Figure 6: Examples of Chinese Sign Language dataset. Fig-

ure taken from (Beleza and Fukui, 2021).

dation and report the average accuracy and the macro

F1-score obtained across all folds. The same process

was performed by swapping the training and test data

to reduce the inﬂuence of data bias. Across all of the

experiments, we set the dimension m of the subspaces

to 10. The value of r in Eq.(3) also was set to 10.

Experimental Setting 2. To understand how much

the subjects’ face inﬂuence in the sign recognition re-

sult, we chose eight subjects for training data and one

subject for test data. To generate the reference sub-

spaces in the training phase, we randomly selected

one video from each individual. For the recognition

phase, we performed classiﬁcation on the three videos

performed by each test individual. We performed 9-

fold cross validation by rotating the subjects in each

fold and report the average accuracy and the macro

F1-score obtained in these folds. We set the dimen-

sion m of the subspaces for all the experiments to 10.

The value of r also was set to 10.

Results and Discussions. Results for both experi-

mental settings are shown in Table 1 and Table 2.

Our method consistently outperformed all other ap-

proaches, except for the masked-eye region in setting

1, where PCA performed the best. This result indi-

cates that hand occlusion, which happens when the

hand overlaps the masked region, will likely not af-

fect the performance of any of the methods.

In setting 2, involving different subjects, our

method demonstrated signiﬁcantly higher perfor-

mance than other methods, achieving over twice the

accuracy and F1-score of methods that did not apply

3D-FFT. This result highlights the effectiveness of an-

alyzing videos in the frequency domain and extract-

ing only the amplitude spectrum as a robust feature

in handling temporal variations. Moreover, the inte-

gration of PGM with 3D-FFT in our method resulted

in a 7.2% accuracy improvement compared to solely

applying 3D-FFT. This result indicates that PGM can

preserve essential information and avoid the loss of

temporal information in the tensor structure.

Sign Language Recognition Based on Subspace Representations in the Spatio-Temporal Frequency Domain

157

Table 1: TNSL Dataset experimental results. We report the

recognition accuracy (%) in both settings. The best results

for each type of data in each setting are highlighted in bold.

Method

Accuracy (%)

Raw Eye Face Average

PCA 88.7 ± 9.3 88.9 ± 9.5 88.9 ± 9.5 88.8 ± 9.4

RTW 86.9 ± 8.9 85.8 ± 9.5 86.4 ± 8.8 86.4 ± 9.1

Setting 1 SFS 88.7 ± 8.8 88.7 ± 8.9 89.3 ± 9.0 88.9 ± 8.9

3D-FFT 88.7 ± 10.3 88.0 ± 10.1 88.0 ± 10.2 88.2 ± 10.2

Ours 89.8 ± 8.6 88.7 ± 9.2 90.1 ± 7.9 89.5 ± 8.6

PCA 12.2 ± 5.6 12.1 ± 6.3 11.5 ± 6.5 11.9 ± 6.1

RTW 11.2 ± 6.1 11.6 ± 4.9 10.6 ± 5.4 11.1 ± 5.5

Setting 2 SFS 12.7 ± 4.9 12.7 ± 5.2 12.7 ± 5.5 12.7 ± 5.2

3D-FFT 22.0 ± 11.7 23.1 ± 12.0 22.6 ± 11.8 22.6 ± 11.8

Ours 30.2 ± 14.3 29.8 ± 14.5 29.3 ± 13.8 29.8 ± 14.2

Table 2: TNSL Dataset experimental results. We report the

macro F1-score (%) in both settings. The best results for

each type of data in each setting are highlighted in bold.

Method

Macro F1-score (%)

Raw Eye Face Average

PCA 88.8 89.1 89.1 89.0

RTW 87.1 87.0 86.8 87.0

Setting 1 SFS 88.9 88.9 89.5 89.1

3D-FFT 88.8 88.1 88.2 88.4

Ours 90.0 88.9 90.3 89.7

PCA 11.4 11.3 10.7 11.1

RTW 11.3 11.2 11.3 11.3

Setting 2 SFS 12.1 12.2 12.1 12.1

3D-FFT 21.1 21.3 20.7 21.0

Ours 30.2 30.0 29.2 29.8

Furthermore, the large difference in results from

setting 1 and setting 2 indicates that most methods

rely on subject-speciﬁc characteristics for recogni-

tion. While our method still faced a decrease in per-

formance in setting 1, the gap was smaller than the

other methods.

In addition, while there is the possibility of data

imbalance, as there are differences in the number of

frames per class in this dataset, we observe a differ-

ence between the accuracy and F1-score values, indi-

cating that the learning is equally distributed among

all the methods.

3.4 Experiments on CSLD

Experimental Setting. In this dataset, each gray-

scale video was resized to 38×24 pixels. Therefore,

the dimension {d

}

j=1

of each mode is {38×50, 24×

50, 38 × 24}, respectively. Furthermore, out of the

500 videos, 300 were considered as the training set,

100 as the validation set, and 100 as the test set. We

performed 10-fold cross-validation and reported the

average accuracy and the macro F1-score across all

folds.

In addition, we also performed experiments us-

ing CNN features from the pre-trained VGG19 (Si-

Table 3: CSL Dataset experimental results. We report the

recognition accuracy (%) on the baseline methods with raw

features and CNN features, and compare with our method.

As the data form of the CNN features is not a 3D tensor,

we report only results with raw features on methods using

3D-FFT. The best performance is highlighted in bold.

Method

Accuracy (%)

Raw CNN

PCA 49.0 ± 4.2 54.5 ± 4.2

RTW 47.4 ± 4.0 60.8 ± 1.5

SFS 47.4 ± 5.0 57.5 ± 3.9

3D-FFT 59.5 ± 5.5 -

Ours 72.2 ± 8.2 -

Table 4: CSL Dataset experimental results. We report the

macro F1-score (%) on the baseline methods with raw fea-

tures and CNN features, and compare with our method. As

the data form of the CNN features is not a 3D tensor, we

report only results with raw features on methods using 3D-

FFT. The best performance is highlighted in bold.

Method

Macro F1-score (%)

Raw CNN

PCA 49.3 53.4

RTW 47.7 60.7

SFS 47.6 56.1

3D-FFT 59.5 -

Ours 71.7 -

monyan and Zisserman, 2014) speciﬁed in Sec-

tion 3.1. We extracted the features after the global

mean pooling for the ﬁfth hidden layer of VGG-19,

resulting in a vector of 512 dimensions to each frame.

Therefore, we hypothesize that these features include

local information from each sign and should improve

results. The obtained features are represented in their

respective subspace representations and are classiﬁed

using MSM-based methods. We varied the subspace

m from 2 to 10 with interval of 2 and performed

the test using the hyper-parameters that obtained the

highest classiﬁcation accuracy in the validation set.

In this case, since the CNN features are vectors, we

cannot apply 3D-FFT to them.

Results and Discussion. Results for this dataset can

be found in Table 3 and Table 4. We can see that

our method outperforms all other methods, including

the ones using CNN features. This result shows that

although CNNs can generate discriminative features,

they are extracted without considering any relation-

ship between frames and thus fail to capture complex

movements such as sign languages. our method can

account for temporal information and thus can obtain

a higher accuracy rate than CNN-based classiﬁcation

methods. There is small difference in the accuracy

and macro F1-score for any of the methods, indicat-

ing that the learning is consistent in all classes.

ICPRAM 2024 - 13th International Conference on Pattern Recognition Applications and Methods

158

4 CONCLUSIONS

In this paper, we proposed a new method for sign

language recognition that processes time-domain in-

formation on the frequency-domain by representing

videos as 3D amplitude tensors using the 3D Fast

Fourier Transform (3D-FFT) and effectively compar-

ing them in the Product Grassmann Manifold (PGM).

Focusing only on the amplitude spectrum, we ob-

tain features robust to time deviations. Furthermore,

PGM can effectively represent and compare the ten-

sor structures as subspaces generated from each ten-

sor mode while preserving the temporal information

due to the unfolding operation. Therefore, we estab-

lished a simple yet powerful subspace representation

that considers temporal information. Experimental

results showed that our method can signiﬁcantly im-

prove performance over other subspace-based meth-

ods. In the future, we are interested in verifying the

efﬁcacy of our method in other action recognition

tasks.

ACKNOWLEDGMENTS

This work was supported by JSPS KAKENHI Grant

Number 21K18481. The authors thank the Tsukuba

University of Technology students for their help in

collecting our TNSD data set.

REFERENCES

Batalo, B., Souza, L. S., Gatto, B. B., Sogi, N., and Fukui,

K. (2022). Temporal-stochastic tensor features for

action recognition. Machine Learning with Applica-

tions, 10:100407.

Beleza, S. R. and Fukui, K. (2021). Slow feature sub-

space for action recognition. In Pattern Recognition.

ICPR International Workshops and Challenges: Vir-

tual Event, January 10–15, 2021, Proceedings, Part

III, pages 702–716.

Beleza, S. R. A., Shimomoto, E. K., Souza, L. S., and

Fukui, K. (2023). Slow feature subspace: A video

representation based on slow feature analysis for ac-

tion recognition. Machine Learning with Applica-

tions, 14:100493.

Fukui, K. (2014). Subspace methods. In Computer Vision,

A Reference Guide, pages 777–781.

Fukui, K. and Maki, A. (2015). Difference subspace and

its generalization for subspace-based methods. IEEE

Transactions on Pattern Analysis and Machine Intel-

ligence, 37(11):2164–2177.

Iwashita, Y., Kakeshita, M., Sakano, H., and Kurazume,

R. (2017). Making gait recognition robust to speed

changes using mutual subspace method. In 2017 IEEE

International Conference on Robotics and Automation

(ICRA), pages 2273–2278.

Iwashita, Y., Sakano, H., and Kurazume, R. (2015). Gait

recognition robust to speed transition using mutual

subspace method. In International Conference on Im-

age Analysis and Processing, pages 141–149.

Jaouedi, N., Boujnah, N., and Bouhlel, M. S. (2020). A new

hybrid deep learning model for human action recogni-

tion. Journal of King Saud University-Computer and

Information Sciences, 32(4):447–453.

Liu, T., Zhou, W., and Li, H. (2016). Sign language recog-

nition with long short-term memory. In 2016 IEEE

international conference on image processing (ICIP),

pages 2871–2875.

Lui, Man, Y., Beveridge, Ross, J., Kirby, and Michael

(2010). Action classiﬁcation on product manifolds.

In 2010 IEEE Computer Society Conference on Com-

puter Vision and Pattern Recognition, pages 833–839.

Lui, Y. M. (2012). Human gesture recognition on prod-

uct manifolds. The Journal of Machine Learning Re-

search, 13(1):3297–3321.

Mahbub, U., Imtiaz, H., Roy, T., Rahman, M. S., and Ahad,

M. A. R. (2013). A template matching approach of

one-shot-learning gesture recognition. Pattern Recog-

nition Letters, 34(15):1780–1788.

Modler, P. and Myatt, T. (2007). Image features based on

two-dimensional fft for gesture analysis and recogni-

tion. SMC07, Leykada, Greece.

Peris, M. and Fukui, K. (2012). Both-hand gesture recogni-

tion based on komsm with volume subspaces for robot

teleoperation. In 2012 IEEE International Conference

on Cyber Technology in Automation, Control, and In-

telligent Systems (CYBER), pages 191–196.

Sakai, A., Sogi, N., and Fukui, K. (2019). Gait recognition

based on constrained mutual subspace method with

cnn features. In 2019 16th international conference

on machine vision applications (MVA), pages 1–6.

Simonyan, K. and Zisserman, A. (2014). Very deep con-

volutional networks for large-scale image recognition.

arXiv preprint arXiv:1409.1556.

Suryanto, C. H., Xue, J.-H., and Fukui, K. (2016). Random-

ized time warping for motion recognition. Image and

Vision Computing, 54:1–11.

Tanaka, S., Okazaki, A., Kato, N., Hino, H., and Fukui,

K. (2016). Spotting ﬁngerspelled words from sign

language video by temporally regularized canonical

component analysis. In 2016 IEEE International Con-

ference on Identity, Security and Behavior Analysis

(ISBA), pages 1–7.

Tufek, N., Yalcin, M., Altintas, M., Kalaoglu, F., Li, Y.,

and Bahadir, S. K. (2019). Human action recognition

using deep learning methods on limited sensory data.

IEEE Sensors Journal, 20(6):3101–3112.

Wiskott, L. and Sejnowski, T. J. (2002). Slow feature anal-

ysis: Unsupervised learning of invariances. Neural

computation, 14(4):715–770.

Wong, Y.-C. (1967). Differential geometry of grassmann

manifolds. Proceedings of the National Academy of

Sciences, 57(3):589–594.

Yamaguchi, O., Fukui, K., and Maeda, K. (1998). Face

recognition using temporal image sequence. In Pro-

ceedings third IEEE international conference on au-

tomatic face and gesture recognition, pages 318–323.

Sign Language Recognition Based on Subspace Representations in the Spatio-Temporal Frequency Domain

159