KluSIM: Speeding up K-Medoids Clustering over Dimensional Data with

Metric Access Method

Larissa R. Teixeira

1 a

, Igor A. R. Eleut

erio

1 b

, Mirela T. Cazzolato

1,2 c

, Marco A. Gutierrez

2 d

Agma J. M. Traina

1 e

and Caetano Traina-Jr.

1 f

Institute of Mathematics and Computer Science (ICMC), University of S

ao Paulo (USP), S

ao Carlos, Brazil

The Heart Institute (InCor), University of S

ao Paulo (USP), S

ao Paulo, Brazil

Keywords:

Dimensional Data, k-medoids, Clustering, Indexing, Metric Access Method.

Abstract:

Clustering algorithms are powerful data mining techniques, responsible for identifying patterns and extracting

information from datasets. Scalable algorithms have become crucial to enable data mining techniques on large

datasets. In literature, k-medoid-based clustering algorithms stand out as one of the most used approaches.

However, these methods face scalability challenges when applied to massive datasets and high dimensional

vector spaces, mainly due to the high computational cost in the swap step. In this paper, we propose the KluSIM

method to improve the computational efﬁciency of the swap step in the k-medoids clustering process. KluSIM

leverages Metric Access Methods (MAMs) to prune the search space, speeding up the swap step. Additionally,

KluSIM eliminates the need of maintaining a distance matrix in memory, successfully overcoming memory

limitations in existing methodologies. Experiments over real and synthetic data show that KluSIM outperforms

the baseline FasterPAM, with a speed up of up to 881 times, requiring up to 3,500 times fewer distance

calculations, and maintaining a comparable clustering quality. KluSIM is well-suited for big data analysis,

being effective and scalable for clustering large datasets.

1 INTRODUCTION

Clustering is a data mining task applied across differ-

ent applications, such as bio-informatics, image pro-

cessing, pattern recognition, ﬁnancial risk analysis,

and more (Qaddoura et al., 2020). Clustering is the

process of identifying patterns in a dataset through

grouping into clusters. Objects within the same clus-

ter have higher similarity to each other compared to

objects in different clusters. Among several clus-

tering algorithms in the literature, the most popular

are k-means and k-medoids, whereas the most em-

ployed variant of the latter is the Partitioning Around

Medoids (PAM) (Kaufman, 1990). The k-means al-

gorithm is based on deﬁning a centroid, which is the

arithmetic mean of all objects within a cluster. On the

https://orcid.org/0009-0007-9917-4404

https://orcid.org/0009-0007-3987-8880

https://orcid.org/0000-0002-4364-010X

https://orcid.org/0000-0003-0964-6222

https://orcid.org/0000-0003-4929-7258

https://orcid.org/0000-0002-6625-6047

other hand, k-medoids are algorithms that seek for a

medoid, an actual object within a cluster that have the

smallest distance sum to all other objects.

One of the advantages of k-medoids over k-means

algorithm is the results interpretability (Kenger et al.,

2023). By assigning actual objects as cluster rep-

resentatives, k-medoids results can provide insights

into the dataset based on the characteristics of the

medoids.

Medoid-based approaches have shown high clus-

tering quality. However, these methods show many

difﬁculties when running over large amounts of

data and high dimensional vector spaces. The k-

medoid-based algorithms rely on accurate initializa-

tion heuristics to preselect initial medoids as seed be-

fore the swap step. Good seeds can accelerate the

convergence of the algorithm and avoid distance cal-

culations during the swap step. The swap step iterates

over the entire dataset to ﬁnd the best combination of

non-medoid and medoid that minimizes a objective

function. This step is computationally costly and is

the bottleneck of the algorithm. Several approaches

maintain a in-memory distance matrix to speed up

Teixeira, L., Eleutério, I., Cazzolato, M., Gutierrez, M., Traina, A. and Traina-Jr., C.

KluSIM: Speeding up K-Medoids Clustering over Dimensional Data with Metric Access Method.

DOI: 10.5220/0012599900003690

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 26th International Conference on Enterprise Information Systems (ICEIS 2024) - Volume 1, pages 73-84

ISBN: 978-989-758-692-7; ISSN: 2184-4992

swap and avoid recomputing the distance between the

same objects. However, this option is unfeasible for

large datasets, due to limited memory.

We focus on clustering dimensional data over

large datasets. We propose KluSIM, a method

that speeds up the swap step of medoid-based ap-

proaches by taking advantage of Metric Access Meth-

ods (MAMs) to index and prune the search space,

without trading the semantic meaning of generated

clusters for performance. Thus, KluSIM avoids the

need for maintaining a distance matrix and reduces

the number of distance calculations. The key contri-

butions of our work are:

• MAM-Based Space Pruning. We strategically

take advantage of MAMs for search space prun-

ing during swap, drastically reducing the num-

ber of distance calculations. We also eliminate

the need for precomputing and keeping a in-

memory distance matrix. The MAM allows per-

forming a range query over the candidates of

medoid objects, even over large high-dimensional

datasets. The range query operation associates

each non-medoid object to the cluster with its

nearest medoid. KluSIM computes the minimum

distance, for each medoid, among other medoids,

and uses it to prune the search space.

• Centroid-Guided Candidate Selection. KluSIM

computes the centroid of each cluster and se-

lects its nearest objects through a k-NN query

to the centroid. The answers are the candi-

dates to be tested as medoid objects during swap.

Thus, unlike existing methods, KluSIM reduces

the medoids candidates to be evaluated at each it-

eration, also reducing the number of distance cal-

culations needed in the overall clustering process.

• KluSIM is Fast and Effective. Our method is up

to 881 faster than FasterPAM, the medoid-based

clustering approach baseline, while maintaining

comparable cluster quality.

KluSIM combines both k-NN and range queries

during clustering. Our experimental evaluation shows

a signiﬁcant improvement in the execution time, with

comparable quality. KluSIM improves efﬁciency,

captures spatial relationships, and enhances the over-

all clustering process.

Paper Outline. Section 2 gives the background.

Section 3 reviews the related work. Section 4 in-

troduces the proposed method KluSIM. Section 5

presents the experimental evaluation and discussion.

Finally, Section 6 concludes this work.

2 BACKGROUND

We present the relevant background on clustering al-

gorithms, k-medoids approaches, and metric access

methods. Table 1 shows the symbols and acronyms.

2.1 Clustering Algorithms

Clustering, as a data mining technique, partitions

a dataset into k groups, where objects within the

same group have high similarity among themselves,

while maintaining dissimilarity with objects from

other groups (Han et al., 2011). The literature

presents several clustering algorithms, mainly cate-

gorized into hierarchical and partitioning methods,

sometimes also including density-based approaches

(Ran et al., 2023). Hierarchical clustering builds a

cluster tree structure, also called dendrogram. The

objects are organized into a hierarchy of clusters by

iteratively merging (agglomerative approach) or di-

viding (divisive approach) them based on a distance

measure (Ran et al., 2023). Despite the dendrograms

being effective for small datasets, they do not provide

a ﬂat partitioning of the data. Therefore, simpler alter-

natives are generally preferred by users, such as par-

titioning methods (Schubert and Rousseeuw, 2021).

Partitioning methods assign each object to one of

a predeﬁned number of clusters (Han et al., 2011).

The goal is to optimize a certain objective function,

such as minimizing the within-cluster variance or

maximizing inter-cluster distances. Examples include

k-means and k-medoids (Kaufman, 1990). Given

the better results interpretability of clusters achieved

by k-medoid-based algorithms compared to k-means,

this paper focuses on the former.

2.1.1 k-medoids Algorithms

The Partitioning Around Medoids (PAM) (Kaufman,

1990) was one of the ﬁrst k-medoid-based algorithms

introduced in the literature. PAM has two main steps:

• build: Select k objects as initial medoids with a

greedy search.

• swap: Based on the initial medoids, PAM repeat-

edly performs the swap step to improve the clus-

tering quality until convergence. At each iteration,

a non-medoid object is evaluated to improve the

clustering quality by replacing one of the current

medoids with the non-medoid object.

2.1.2 Cluster Quality Measure

As part of the cluster quality assessment, many tech-

niques have been proposed in the literature. The clus-

ICEIS 2024 - 26th International Conference on Enterprise Information Systems

Table 1: Summary of symbols and deﬁnitions.

Symbol Description

k Number of clusters

n Number of objects in the dataset

S Set of objects

, s

Objects ∈ S

δ Dissimilarity (distance) measure

M Set of medoids

A medoid object ∈ M

C Set of k clusters

C A cluster

An object ∈ C

p Number of nearest neighbors

Set of objects returned from kNNq

TD The total deviation of cluster quality

SS Silhouette score

DBI Davies Bouldin Index

ξ Range query radius

tering quality of k-medoids is evaluated using the ab-

solute error criterion denoted as total deviation (TD),

deﬁned as:

TD =

∑

i=1

∑

∈C

δ(x

) (1)

which is the sum of distances from each object x

∈

to the medoid m

of its cluster (Schubert and

Rousseeuw, 2021).

The Silhouette Score (SS) is another popular mea-

sure to evaluate clustering quality (Lenssen and Schu-

bert, 2024). For each object, the Silhouette Score con-

siders two key metrics: i. The average distance of a

object i to other objects in the same cluster. ii. The

average distance of a object i to other objects in the

nearest neighbor cluster. The overall SS is the av-

erage of individual SS across all objects. The score

ranges from −1 to 1, where a higher score means

better-deﬁned and well-separated clusters.

Another cluster quality metric is the Davies-

Bouldin Index (DBI) (Davies and Bouldin, 1979).

The index considers both intra-cluster similarity and

inter-cluster dissimilarity to calculate the average

similarity of each cluster with all others. The DBI

index is obtained as the sum of average similarity val-

ues of all clusters, divided by the number of clusters.

Lower DBI indicates a better clustering result (mini-

mum index is zero).

2.2 Metric Access Methods

Metric Access Methods (MAMs) are built on top of

indexing structures designed to optimize the search

for nearest neighbors within a dataset. These meth-

ods take advantage of the inherent properties of met-

ric spaces, such as the triangular inequality, to prune

subsets of the search space, thus speeding up query

processing. Examples of MAMs include the VP-Tree

(Yianilos, 1993), Ball-Tree (Omohundro, 1989) and

KD-Tree (Bentley, 1975).

A metric space is represented as a domain of

objects and a distance function δ between two ob-

jects s

and s

from the domain that satisfy the fol-

lowing properties of a metric space (Zezula et al.,

2006): i. non-negativity: s

̸= s

→ δ(s

) > 0;

ii. identity: δ(s

) = 0 ⇔ s

= s

; iii. symme-

try: δ(s

) = δ(s

); iv. triangle inequality:

δ(s

) ≤ δ(s

) + δ(s

There are two main elementary similarity queries

in a metric space (Zezula et al., 2006):

i. Range Query (Rq): given a query object s

, a

distance function δ and a radius ξ, the operation

retrieves all objects that differ from s

by at most

the distance ξ.

ii. k-Nearest Neighbors (kNNq): retrieves the k ob-

jects closest to the query object s

∈ S considering

the distance function δ.

2.3 Vantage Point Tree

One notable MAM is the Vantage Point Tree (VP-

Tree) introduced by (Yianilos, 1993). Using a ball

partitioning approach, VP-Tree selects a vantage point

(vp) to partition a dataset S into two subsets S

⊂ S

and S

⊂ S. This partitioning is based on the me-

dian distance ˜x between the chosen vp to all other

objects. The objects are distributed to S

or S

as:

← {s

|δ(vp,s

) ≤ ˜x} and S

← {s

|δ(vp,s

) > ˜x}

where vp ∈ S. After this, the same process is recur-

sively applied to each subset, creating a hierarchy.

3 RELATED WORK

In this work, we focus on improving the efﬁciency of

k-medoids. Table 2 summarizes related studies. Here

we compare our proposal KluSIM with related meth-

ods considering the following aspects:

• Memory Optimization: most algorithms require

precomputing a distance matrix, which is a bot-

tleneck for large datasets. This aspect informs

whether the algorithm can perform without an in-

memory matrix, showing a signiﬁcant advantage

for the speciﬁc approach.

• Large Datasets: this aspect informs whether the

algorithm runs over the entire dataset within a fea-

sible time frame.

KluSIM: Speeding up K-Medoids Clustering over Dimensional Data with Metric Access Method

Table 2: KluSIM optimizes the usage of memory when performing clustering through a space-pruning technique.Comparison

of state-of-art algorithms with our proposed.

Works

Memory

optimization

Executes with

whole dataset

Main memory

Space-pruning

SWAP

optimization

PAM-SLIM Ë é é é

SFKM é Ë Ë é

FastPAM1 é Ë Ë é

FasterPAM é Ë Ë é

(Proposal) KluSIM Ë Ë Ë Ë

• Main Memory: this aspect informs whether the

algorithm runs in main memory, which is faster

than algorithms operating in secondary memory.

• Space-Pruning swap Optimization: whether

the algorithm takes advantage of space-pruning

heuristics, which can signiﬁcantly enhance the ef-

ﬁciency of the swap step in k-medoids algorithms

by avoiding many distance calculations.

The discussion of the related works is organized

into two parts, each addressing key aspects of en-

hancing the efﬁciency of k-medoid algorithms. Sub-

section 3.1 explores alternative approaches for k-

medoids initialization. Subsection 3.2 discusses tech-

niques related to k-medoids swap optimization.

This organization provides a comprehensive com-

parison of the proposed KluSIM method with existing

methodologies.

3.1 k-medoids Initialization Methods

PAM’s build step is well known for being state-of-

the-art heuristic for initializing k-medoids. However,

alternative approaches for initialization have been ex-

plored in the literature, such as the random selection

of initial medoids (Schubert and Rousseeuw, 2021).

In (Arthur and Vassilvitskii, 2007) the authors

propose a seeding strategy to improve the k-means

initialization, denoted as k-means++. The algorithm

randomly selects the ﬁrst centroid from the dataset.

Then, k-means++ selects the next centroids with the

probability proportional to their squared distance to

the nearest centroid. New centroid are likely to be far

from the previously chosen ones.

In (Barioni et al., 2008) the authors present a vari-

ation of PAM called PAM-SLIM. The algorithm uses

the Slim-Tree MAM (Traina et al., 2002), stored in

secondary memory, to assist the selection of initial

medoids. The algorithm leverages the tree structure to

choose the initial medoids, selecting objects located

at the middle level of the tree as possible medoids.

Unfortunately, as this method does not consider the

entire dataset when selecting the initial medoids, it

may affect the clustering quality. Additionally, PAM-

SLIM does not take advantage of the beneﬁts of

MAM to optimize the k-medoids swap step. It only

leverages the advantage of how the tree is organized,

focusing to select a subset of the dataset rather than

considering the whole dataset.

In (Park and Jun, 2009) the authors propose the

Simple and Fast k-medoids (SFKM), an initializa-

tion method for k-medoids that operates like k-means.

SFKM computes a distance matrix between all ob-

jects, aiming at ﬁnding new medoids in each iteration.

The algorithm selects the k-medoids with the small-

est normalized sum of distances within the dataset.

SFKM signiﬁcantly reduces the computation time and

shows performance comparable to PAM, but it is not

effective in improving cluster quality. Also, SFKM

tends to perform worse than randomly selecting ini-

tial medoids, as reported in (Schubert and Rousseeuw,

2021). SFKM lacks memory optimization as it re-

quires the creation of a distance matrix in memory for

the entire dataset.

3.2 k-medoids Swap Optimization

One of the main challenges of k-medoids for large

datasets is the high computational cost, leading to

long execution times and memory limitations. The

swap step contributes the most to the computational

cost of PAM, since it seeks for the best pair of medoid

and non-medoid objects, among all possible k × (n −

k) pairs, which can improve the clustering quality.

Our proposal does not rely on existing methods.

Many methods include techniques for parallel cluster-

ing algorithms, such as (Vandanov et al., 2023). Sta-

tistical estimation techniques have also improved the

performance of k-medoids, such as BanditPAM (Ti-

wari et al., 2020), an algorithm inspired by multi-

armed bandits. Despite the potential advantages of

existing approaches, our proposal concentrates on op-

timizing the clustering algorithm in its original form

without changing the overall problem-solving strat-

ICEIS 2024 - 26th International Conference on Enterprise Information Systems

egy. Parallel clustering algorithms and statistical esti-

mation techniques have proven beneﬁcial in overcom-

ing computational challenges. However, they often

introduce complexities or modiﬁcations to the meth-

ods. Our goal is to enhance the efﬁciency and perfor-

mance of the clustering algorithm while preserving its

intrinsic structure and characteristics.

Additionally, other techniques have been intro-

duced to enhance existing approaches, such as faster

k-medoids (Schubert and Rousseeuw, 2021). The

work proposes FastPAM1 and FasterPAM algorithms,

both bringing an enhancement to the PAM algorithm.

FastPAM1 ensures the same output as PAM, while

FasterPAM does not, although maintains equivalent

quality. Both approaches improve the k-medoids

complexity in a factor of O(k). However, when the

number of objects in the dataset n is much larger than

the number of medoids k, the improvement may not

be advantageous, as also observed by (Tiwari et al.,

2020). Based on experimental results, FasterPAM is

faster than FastPAM1. Both approaches lack memory

optimization, as require a distance matrix as an input,

and lack space pruning optimization.

3.3 Open Issues

There is a gap in the existing literature concerning the

k-medoids strategy to employ MAMs in main mem-

ory. Such a strategy should not require a distance ma-

trix to enhance the swap step of the algorithm, which

would be beneﬁcial for large datasets. Our proposed

KluSIM method ﬁlls this gap. The baseline competi-

tor is FasterPAM, which has a speciﬁc focus on im-

proving the swap step. In contrast, other related stud-

ies have mainly focused on developing new strategies

for selecting initial medoids.

We propose a method to improve the swap of

PAM, incorporating a space pruning optimization ap-

proach. We aim to optimize memory usage enabling

working with large datasets, exchanging the distance

matrix with a much smaller distance indexing MAM.

We detail our proposal in the next section.

4 THE KluSIM METHOD

In this work, we propose the k-medoids clustering

Swap Improvement with Metric Access Method

(KluSIM) method, designed to enhance the efﬁciency

of the swap step of k-medoids clustering. KluSIM

clusters objects in a vector space, satisﬁes the metric

space constraints (see Section 2.2), and takes advan-

tage of MAMs for space pruning.

Algorithm 1 presents the pseudocode of KluSIM.

It takes as input: the set of objects; the number of

clusters; the number of nearest neighbors of medoid

candidates during the swap step; and the initialization

method. The outputs are the set of k medoids, and the

produced clusters.

Roman numbers in parentheses indicate the steps

of the algorithm. In line 2, the algorithm starts in-

stantiating a MAM with the objects in S, and then

selects the initial set of k medoids (line 3). Line 4

performs the ASq operation, which computes overall

cluster quality TD and the current cluster assignment

Cusing the initial set of medoids M (line 4). Then,

KluSIM repeats the following steps for each cluster

(lines 6-17): Computes cluster centroids (line 7); Per-

forms k-NN search (line 8); Executes ASq operation

for each object o

within the set S

of nearest objects

of the centroid (line 12); Measures cluster quality im-

provement (line 13). The loop repeats while TD de-

creases, i.e. the cluster quality improves.

Algorithm 1: KluSIM (S,k, p, initMethod).

input : S: Set of objects

input : k: Number of clusters

input : p: Number of nearest neighbors of

medoid candidate

input : initMethod: Initialization method (e.g.,

build, k-means++)

output : M: Set of k medoids

output : C: Set of clusters

1 begin

2 mam ← CreateMAM(S) ; (i)

3 M ← InitializeMedoids(k, initMethod) ; (ii)

4 TD, C← mam.ASq(M) ; (iii)

5 while TD decreases do

6 for cluster C

∈ C do

7 µ

← ComputeCentroid(C

) ; (iv)

8 S

← mam.kNNq(µ

, p) ; (v)

9 for o

∈ S

/* Check if object o

improves

cluster quality */

10 M

′

← M ;

11 m

′

← o

; m

′

∈ M

′

12 TD

′

← mam.ASq(M

′

) ; (iii)

13 if TD

′

< TD then (vi)

14 TD ← TD

′

;

15 C ← C

′

;

16 swap m

with o

;

Figure 1 illustrates the workﬂow of KluSIM. It di-

vides the algorithm into six steps, as detailed next.

The step numbering is the same as indicated in Algo-

rithm 1.

The initial step (i) of KluSIM instantiates a MAM

with all objects in the dataset. In step (ii), the algo-

rithm initializes by selecting k initial medoids using

KluSIM: Speeding up K-Medoids Clustering over Dimensional Data with Metric Access Method

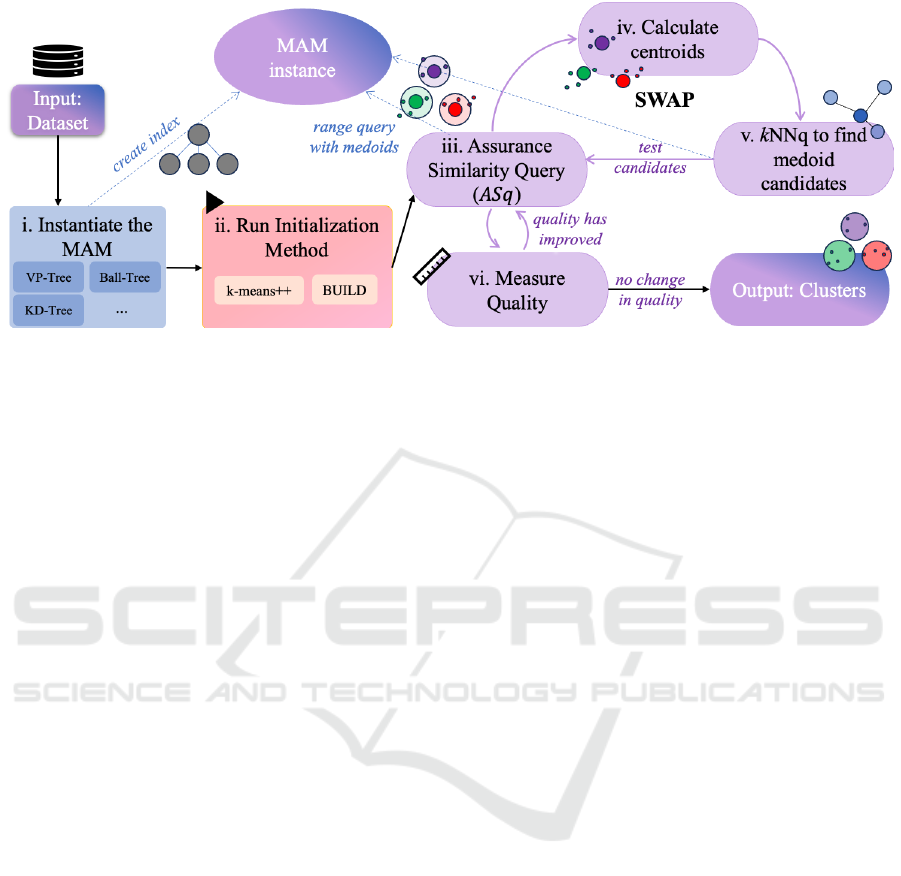
Figure 1: The KluSIM algorithm. i. Create a MAM with input objects. ii. Select k initial medoids using a given initialization

method. iii. Perform the Assurance Similarity Query (ASq). iv. Calculate the centroid for each cluster. v. Find the p nearest

objects from each centroid. vi. Calculate TD. Repeat the process while TD decreases.

an initialization method such as build or k-means++.

Step (iii) executes a search operation, referred to as

Assurance Similarity Query (ASq), using the MAM

instance. Then, following steps are executed itera-

tively until convergence:

• Compute Cluster Centroids (step iv): For each

cluster, compute the centroid object.

• Perform a k-NN Search to Find Medoid Can-

didates (step v): Based on the centroid of each

cluster, select the p nearest objects to the centroid

employing a MAM. In this step, parameter p is

the number of nearest neighbors. Taking advan-

tage of MAMs data organization allows to efﬁ-

ciently prune the search space when performing

query operations. During the kNNq, the MAM

discards regions, as they are unlikely to contain

nearest neighbors, avoiding unnecessary distance

calculations.

• Execute the assurance similarity query opera-

tion ASq (step iii): Analyze each object o

∈

returned from the kNNq as a potential new

medoid within a cluster C

∈ C (line 9). For each

candidate, we replace the current medoid m

to o

(lines 10-11). Function ASq returns the clustering

quality TD and k clusters (line 12).

• Measure Cluster Quality Improvement (step

6): If the non-medoid object o

decreases TD,

then execute a swap operation between m

and o

In this work, we evaluate our algorithm using the

VP-Tree MAM. However, other MAMs that rely on

using representative objects to partition the data space

can be employed.

4.1 Assurance Similarity Query (ASq)

This operation is designed to easy creating k groups,

based on medoid objects. Function ASq gets as in-

put the set of medoids. It assures that each object is

assigned to the cluster with the most similar medoid.

The operation involves three steps: (1) Deﬁnition of

coverage radius; (2) Assignment of nearest objects;

(3) Association of remaining objects.

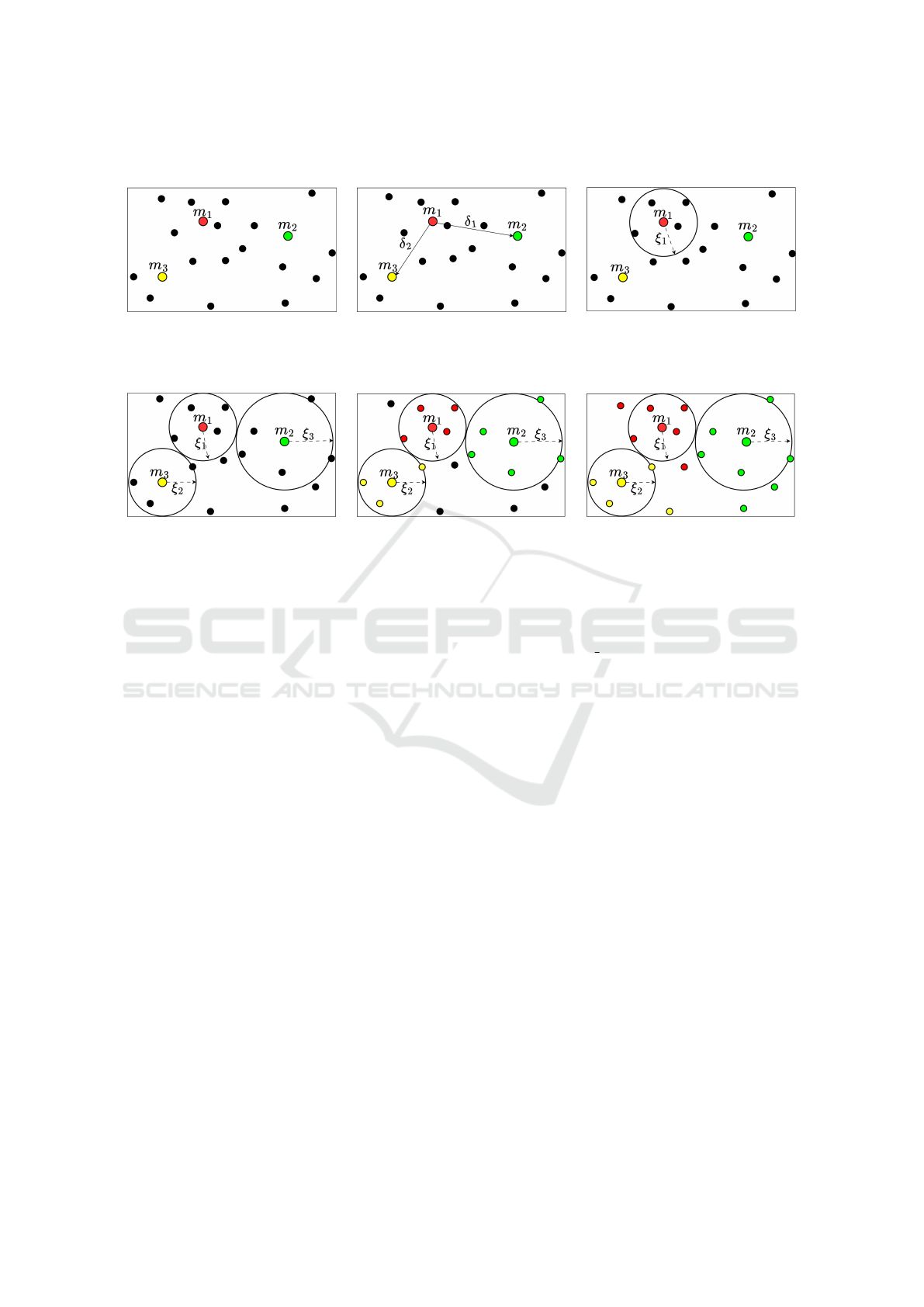
4.1.1 Deﬁnition of Coverage Radius

For each medoid m

∈ M, |M| = k, calculate the dis-

tance δ(m

), where 1 ≤ j ≤ k and i ̸= j. The cover-

age radius ξ

for medoid m

is deﬁned as

min

/2, where

min

represents the smallest distance obtained from

the distance of m

to all other medoids.

Figure 2 illustrates the process to deﬁne the cov-

erage radius ξ of the medoid m

. Considering k = 3

(a), the ﬁrst step computes the distance (b) from the

medoid m

to m

and m

. Then, in (c) the coverage

radius ξ of m

is determined as

min

/2. This process

repeats for the remaining medoids in (a).

4.1.2 Assignment of Nearest Objects

Figure 3(a) shows the coverage radius of each

medoid. For each medoid m

∈ M, a range query us-

ing MAM is conducted with the coverage radius ξ

as in (b). The objects covered by ξ

from medoid m

will form an initial cluster. Then, KluSIM employs

the instantiated MAM to prune the search space and

efﬁciently identify regions within the speciﬁed radius.

ICEIS 2024 - 26th International Conference on Enterprise Information Systems

(a) Initial medoids m

e m

(b) Computing distance from m

and m

medoids.

min

/2 for medoid m

Figure 2: Finding the coverage radius ξ of medoid m

, for k = 3.

(a) Coverage radius ξ of each medoid.

(b) Assigning objects to the group

covered by radius ξ of each medoid.

the nearest medoid.

Figure 3: Assigning each object to the nearest medoid, for k = 3.

4.1.3 Association of Remaining Objects

Objects outside the covering radius from any medoid

are treated as exceptions. In Figure 3(c), the algorithm

calculates the distance from each non-covered object

to all medoids. Then, each object is assigned to the

group of the nearest medoid.

4.2 Aspects and Advantages of KluSIM

KluSIM employs a clever heuristic that relies on prun-

ing the search space to signiﬁcantly reduce the dis-

tance calculations. The swap step considers only a

subset of objects near the cluster centroid to be con-

sidered as better medoids during clustering iterations.

The swap step is the bottleneck of k-medoid-based

approaches, and KluSIM reduces the computational

cost of such approaches. The proposed approach ben-

eﬁts clustering tasks over large datasets, since it ex-

changes the distance matrix of the objects with locally

based subsets of distances maintained by MAM. Fol-

lowing, we experimentally evaluate the improvements

obtained by KluSIM.

5 EXPERIMENTS

In this section, we evaluate the efﬁciency (execution

time and number of distance calculations) and effec-

tiveness (cluster quality) of the KluSIM.

5.1 Datasets and Setup

The experiments were conducted on several datasets:

• Synthetic Datasets: All synthetic datasets are

from the make blobs generator (Pedregosa et al.,

2011). A total of 48 datasets were created, with

dimensions (8, 64, and 128), number of samples

(5,000, 25,000, 50,000, and 100,000), and num-

bers of clusters k (5, 20, 50, and 100).

• Real Datasets: We selected the image datasets

ds-Mammoset (3457 tuples, 2 clusters) (Oliveira

et al., 2017), ds-DeepLesion (33334 tuples, 5 clus-

ters) (Yan et al., 2017) and ds-MNIST (70000 tu-

ples, 10 clusters)(Lecun et al., 1998). We em-

ployed the feature vectors provided by (Cazzolato

et al., 2022), generated with descriptors Texture

Spectrum (TS, 8 dimensions), Normalized Color

Histogram (NCH64, 64 dimensions), and Color

Structure (CS, 128 dimensions).

The choice of an optimal initialization method

is crucial. We evaluate two initialization strategies:

the build method and k-means++. The results re-

ported for each dataset are the average performance

across 10 iterations. In all experiments, our proposed

algorithm was compared against the state-of-the-art

FasterPAM algorithm, our baseline.

All experiments were performed on an Intel®

Core

i5-7300U (2.60Ghz) with 16GB of RAM and

Ubuntu 20.04 LTS (64-Bit) GNU/ Linux OS. All al-

gorithms are implemented in Cython with the same

KluSIM: Speeding up K-Medoids Clustering over Dimensional Data with Metric Access Method

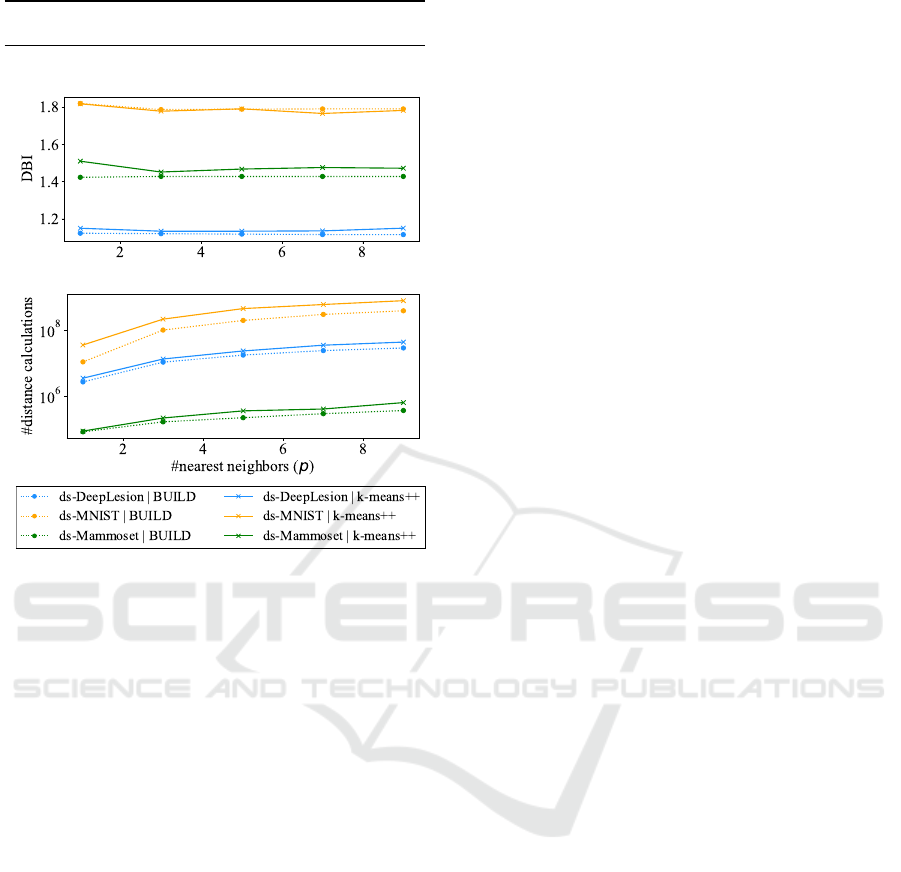
Real Datasets: Cluster quality and #distance

calculations (log scale)

(a) Cluster Quality by p value (DBI: the lower the

better)

(b) Number of distance calculations by p value

Figure 4: The plots show the cluster quality and number of

distance calculations varying p value. For p ≥ 3, the cluster

quality does not improve signiﬁcantly, but the number of

distance calculation increases.

conﬁguration, and none of them utilizes a distance

matrix in memory, ensuring a fair comparison.

Reproducibility. Our codes are available at https://

github.com/teixeiralari/KluSIM.

5.2 Estimating the Best Value for p

In step (v) (k-NN to ﬁnd medoids candidates) of

KluSIM (see Figure 1), we perform a kNNq opera-

tion to ﬁnd the p objects nearest to the centroid. We

evaluate the inﬂuence of p in the cluster quality. We

tested KluSIM with p values set to 1, 3, 5, 7, and 9,

analyzing the effect on both cluster quality and num-

ber of distance calculations. Figure 4 shows (a) the

cluster quality and (b) the number of distance calcu-

lations across different k values for real datasets. No

signiﬁcant improvement occured in the cluster quality

for the number of nearest neighbors p ≥ 3, although

there is an almost linear increase in the number of dis-

tance calculations. Thus, the remaining experiments

were conducted using p = 3.

5.3 Evaluating the Execution Time

The efﬁciency of clustering algorithms is critical for

large-scale datasets. We evaluate execution time for

KluSIM against FasterPAM. The primary focus here

is to understand how the execution time varies regard-

ing the number of samples and clusters.

Figure 5 shows the experiments over synthetic

datasets with the number of samples from 5,000 to

100,000, and the average run time with build and

k-means++ initialization. All results are averaged

across each dimension (8, 64,128), for each dataset.

We compared the results of KluSIM and FasterPAM.

In (a), the scenario with a small number of clusters

(k = 5) and a large number of samples (S = 100, 000)

using build initialization, FasterPAM’s swap run time

was 5,144 seconds, and KluSIM took 5.96 sec-

onds, being approximately 863 times faster. With k-

means++ initialization, KluSIM outperformed Faster-

PAM by a speedup factor of 881 times. As the num-

ber of clusters increased to k = 100 with large sam-

ple size of S = 100,000 using build (Figure 5-d), a

speedup of about 35 times was observed. Similarly,

with k-means++, KluSIM exhibited still a substantial

speedup of about 16 times compared to FasterPAM.

Figure 6 shows the results for real datasets.

Speciﬁcally, for ds-Mammoset with a dimension of 8

(a), there is an approximate 21-fold acceleration in the

swap step with the build initialization and roughly 35

times using k-means++ when compared to FasterPAM

under the same conditions. On the other hand, for ds-

MNIST dataset, our algorithm achieved a speedup of

approximately 99 times with build initialization and

123 times with k-means++ in comparison to Faster-

PAM in the same scenarios. Furthermore, consider-

ing a higher dimension (c), the gain of our method is

nearly 40 times using build or k-means++ initializa-

tion for ds-Mammoset, and 275 times for ds-MNIST

dataset using build initialization.

5.4 Evaluating the Number of Distance

Calculations

We evaluated the number of distance calculations re-

quired in the clustering process for both KluSIM and

FasterPAM, varying the number of samples and clus-

ters. This analysis aims to understand the computa-

tional cost associated with KluSIM when compared

with the baseline FasterPAM approach. Given that

one of the goals of KluSIM is to provide efﬁciency

and scalability when clustering large datasets, as well

as reducing potential computational overhead in en-

vironments with limited memory, we conducted the

experiments, for both KluSIM and FasterPAM, with-

ICEIS 2024 - 26th International Conference on Enterprise Information Systems

Synthetic Datasets - Execution time

(a) Number of clusters (k) = 5

(b) Number of clusters (k) = 20

(d) Number of clusters (k) = 100

Figure 5: KluSIM outperforms the main competitor by up to

881 times on synthetic datasets of different sizes. In nearly

all cases, KluSIM achieves faster times.

out storing a distance matrix in memory. All required

distances were calculated on the ﬂy.

Figure 7 displays the total number of distance

calculations taken by the algorithms in the cluster-

ing process, for both build and k-means++ initializa-

tion. The results are averaged across all dimensions

(8,64,128) for each dataset. With a large number of

samples (S = 100, 000) and a small number of clusters

(k = 5) (a), our proposed algorithm KluSIM converges

with approximately 3,500 times fewer distance calcu-

lations than FasterPAM, using build or k-means++.

Real Datasets - Execution time

(a) 8 dimensions

(b) 64 dimensions

Figure 6: KluSIM is consistently faster than the main com-

petitor for real datasets. The plots shows the run time

of KluSIM and FasterPAM on real datasets. In all cases,

KluSIM speeds up clustering.

As the number of clusters increases to k = 100 (d),

there is a notable reduction of roughly 39 times for

build initialization and 15 times for k-means++ ini-

tialization in the number of distance calculations in

comparison with the baseline FasterPAM.

Figure 8 presents the results for real datasets.

With 8 dimensions (a), our method exhibits a sig-

niﬁcant reduction in the number of distance calcu-

lations. Speciﬁcally, there is a 184-fold reduction

when opting for the build initialization, compared to a

151-fold reduction with k-means++ initialization for

a smaller dataset (ds-Mammoset). In contrast, for

a larger dataset (ds-MNIST), there is a reduction of

59 times in the number of distance calculations with

build, and 56 times with k-means++. All these im-

provements are observed in comparison to FasterPAM

under same conditions. Considering a highest dimen-

sionality (c), KluSIM reduces by 62 times the num-

ber of distance calculations with build initialization,

and 54 times with k-means++ initialization for the ds-

KluSIM: Speeding up K-Medoids Clustering over Dimensional Data with Metric Access Method

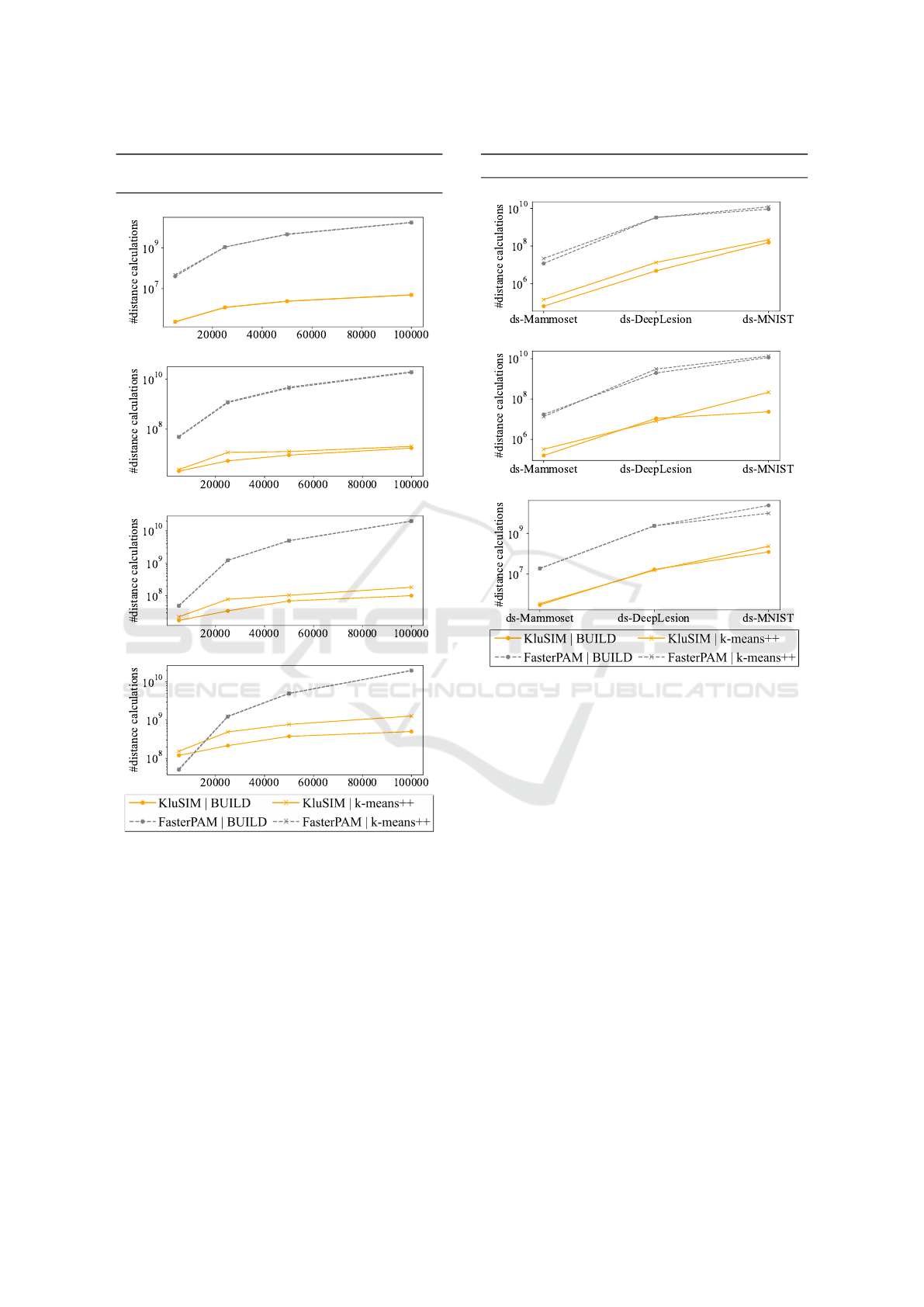
Synthetic Datasets - #distance calculations (log

scale)

(a) Number of clusters (k) = 5

(b) Number of clusters (k) = 20

(d) Number of clusters (k) = 100

Figure 7: KluSIM reduces the number of distance calcula-

tions by up to 3,500 times when compared to FasterPAM.

The plots show the number of distance calculations on syn-

thetic datasets for KluSIM and FasterPAM.

Mammoset. For the ds-MNIST dataset, KluSIM needs

193 times fewer distance calculations with build ini-

tialization when compared with FasterPAM.

5.5 Evaluating Cluster Quality

Finally, we evaluated the cluster quality. Enhancing

the speed of clustering algorithms is essential for han-

dling large datasets, while maintaining or even im-

proving the quality of the results. We investigate how

our proposal KluSIM strikes a balance between time

Real Datasets - #distance calculations (log scale)

(a) Dimension= 8

(b) Dimension= 64

Figure 8: KluSIM shows a reduction in the number of dis-

tance calculations in the clustering process when compared

to FasterPAM. The plots shows the number of distance cal-

culations on real datasets for KluSIM and FasterPAM.

efﬁciency and cluster quality in comparison to Faster-

PAM employing synthetic and real datasets.

Figure 9 displays the average silhouette score (SS)

across all dimensions categorized by the number of

clusters and samples over synthetic datasets. The re-

sults show that KluSIM exhibits comparable cluster

quality to FasterPAM. Figure 10 illustrates the clus-

ter quality over real datasets. Similar to the synthetic

datasets, we observed an equivalent quality between

our method KluSIM and FasterPAM.

5.6 Discussion

The choice of the initialization method is a crucial as-

pect that inﬂuences our method KluSIM convergence

and overall cluster quality. Our experiments show the

build initialization method outperforming k-means++

in terms of quality, time efﬁciency, and number of dis-

tance calculations required for convergence. This su-

periority appears because build chooses each medoid

ICEIS 2024 - 26th International Conference on Enterprise Information Systems

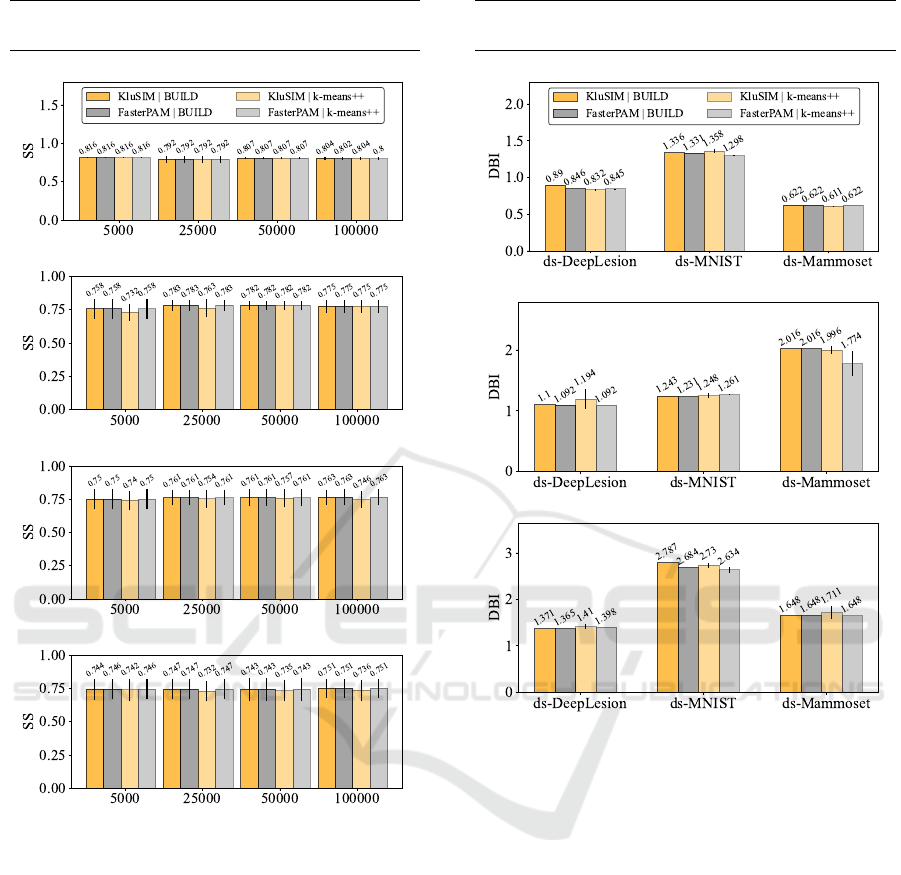
Synthetic Datasets - Cluster quality (SS: the

higher the better)

(a) Number of clusters (k) = 5

(b) Number of clusters (k) = 20

(d) Number of clusters (k) = 100

Figure 9: KluSIM quality of clustering is equivalent to the

quality of main competitor. Cluster quality over synthetic

datasets.

with an optimal quality (i.e. less TD). On the other

hand, k-means++ randomly selects the ﬁrst and sub-

sequent objects that are likely to be far from each

other, without a focus on minimizing TD. Notably,

using build showcased a substantial speed-up of up

to 881 times. The improvement was particularly high

in scenarios where the number of clusters k was sub-

stantially smaller than the number of objects in the

dataset S (k ≪ n).

All in all, KluSIM has shown a signiﬁcant reduc-

tion in the number of distance calculations, speeding

up existing approaches, and maintaining comparable

quality results.

Real Datasets - Cluster quality (DBI: the lower the

better)

(a) = 8 dimensions

(b) 64 dimensions

Figure 10: KluSIM quality of clustering is equivalent to the

quality of the main competitor. Cluster quality over real

datasets.

6 CONCLUSION

This paper introduced the KluSIM approach, designed

to improve the efﬁciency of k-medoids algorithms by

incorporating a metric access methods to speed up

clustering. KluSIM focuses on the swap step pro-

cess, exhibiting signiﬁcant improvements. Through

experimentation, KluSIM was compared to the base-

line FasterPAM, signiﬁcantly reducing time in clus-

tering processing.

Our algorithm exhibited an average speedup of up

to 881 times when compared with the baseline Faster-

PAM, and a reduction of up to 3,500 times in distance

calculations, whereas maintaining a comparable clus-

tering quality. Unlike several methods in the litera-

ture, our algorithm does not store a distance matrix in

memory, eliminating a potential bottleneck faced by

other methods when clustering large datasets.

KluSIM: Speeding up K-Medoids Clustering over Dimensional Data with Metric Access Method

Our KluSIM proposal stands out as an efﬁcient

and scalable solution for k-medoids clustering tasks.

The combination of metric access methods, opti-

mized initialization heuristics, and the elimination

of the need for a distance matrix in memory col-

lectively contribute to the outstanding performance

gains. Thus, KluSIM is a powerful tool for scalable

and high-performance clustering tasks, particularly

in scenarios with limited computational resources or

large datasets.

In future work, we intend to explore MAM-based

initialization heuristics to leverage the index structure

in the entire clustering process. We also want to eval-

uate KluSIM with other distance functions.

ACKNOWLEDGEMENT

This research was ﬁnanced in part by the

Coordenac¸

ao de Aperfeic¸oamento de Pessoal de

ıvel Superior - Brasil (CAPES) - Finance Code 001

and 12620352/M, by the S

ao Paulo Research Founda-

tion (FAPESP, grants 2016/17078-0, 2020/11258-2),

the National Council for Scientiﬁc and Technological

Development (CNPq) and JIT Educac¸

ao.

REFERENCES

Arthur, D. and Vassilvitskii, S. (2007). K-means++ the ad-

vantages of careful seeding. In Proceedings of the

eighteenth annual ACM-SIAM symposium on Discrete

algorithms, pages 1027–1035.

Barioni, M. C. N., Razente, H. L., Traina, A. J., and

Traina Jr, C. (2008). Accelerating k-medoid-based al-

gorithms through metric access methods. Journal of

Systems and Software, 81(3):343–355.

Bentley, J. L. (1975). Multidimensional binary search trees

used for associative searching. Communications of the

ACM, 18(9):509–517.

Cazzolato, M. T., Scabora, L. C., Zabot, G. F., Gutier-

rez, M. A., Traina Jr, C., and Traina, A. J. (2022).

Featset+: Visual features extracted from public image

datasets. Journal of Information and Data Manage-

ment, 13(1).

Davies, D. L. and Bouldin, D. W. (1979). A cluster separa-

tion measure. IEEE Transactions on Pattern Analysis

and Machine Intelligence, PAMI-1(2):224–227.

Han, J., Kamber, M., and Pei, J. (2011). Data Mining: Con-

cepts and Techniques, 3rd edition. Morgan Kaufmann.

Kaufman, L. (1990). Rousseeuw, pj: Finding groups in

data: An introduction to cluster analysis. Applied

Probability and Statistics, New York, Wiley Series in

Probability and Mathematical Statistics.

Kenger, O. N., Kenger, Z. D.,

Ozceylan, E., and Mru-

galska, B. (2023). Clustering of cities based on

their smart performances: A comparative approach of

fuzzy c-means, k-means, and k-medoids. IEEE Ac-

cess, 11:134446–134459.

Lecun, Y., Bottou, L., Bengio, Y., and Haffner, P. (1998).

Gradient-based learning applied to document recogni-

tion. Proceedings of the IEEE, 86(11):2278–2324.

Lenssen, L. and Schubert, E. (2024). Medoid silhouette

clustering with automatic cluster number selection.

Information Systems, 120:102290.

Oliveira, P. H., Scabora, L. C., Cazzolato, M. T., Bedo,

M. V., Traina, A. J., and Traina-Jr, C. (2017). Mam-

moset: An enhanced dataset of mammograms. In

Satellite Events of the Brazilian Symp. on Databases.

SBC, pages 256–266.

Omohundro, S. M. (1989). Five balltree construction al-

gorithms. International Computer Science Institute

Berkeley.

Park, H.-S. and Jun, C.-H. (2009). A simple and fast algo-

rithm for k-medoids clustering. Expert systems with

applications, 36(2):3336–3341.

Pedregosa, F., Varoquaux, G., Gramfort, A., Michel, V.,

Thirion, B., Grisel, O., Blondel, M., Prettenhofer, P.,

Weiss, R., Dubourg, V., et al. (2011). Scikit-learn:

Machine learning in python. the Journal of machine

Learning research, 12:2825–2830.

Qaddoura, R., Faris, H., and Aljarah, I. (2020). An efﬁcient

clustering algorithm based on the k-nearest neighbors

with an indexing ratio. International Journal of Ma-

chine Learning and Cybernetics, 11(3):675–714.

Ran, X., Xi, Y., Lu, Y., Wang, X., and Lu, Z. (2023).

Comprehensive survey on hierarchical clustering al-

gorithms and the recent developments. Artiﬁcial In-

telligence Review, 56(8):8219–8264.

Schubert, E. and Rousseeuw, P. J. (2021). Fast and eager

k-medoids clustering: O (k) runtime improvement of

the pam, clara, and clarans algorithms. Information

Systems, 101:101804.

Tiwari, M., Zhang, M. J., Mayclin, J., Thrun, S., Piech, C.,

and Shomorony, I. (2020). Banditpam: Almost linear

time k-medoids clustering via multi-armed bandits. In

NeurIPS.

Traina, C., Traina, A., Faloutsos, C., and Seeger, B. (2002).

Fast indexing and visualization of metric data sets us-

ing slim-trees. IEEE Transactions on Knowledge and

Data Engineering, 14(2):244–260.

Vandanov, S., Plyasunov, A., and Ushakov, A. (2023). Par-

allel clustering algorithm for the k-medoids problem

in high-dimensional space for large-scale datasets.

In 2023 19th International Asian School-Seminar on

Optimization Problems of Complex Systems (OPCS),

pages 119–124.

Yan, K., Wang, X., Lu, L., and Summers, R. M. (2017).

Deeplesion: Automated deep mining, categorization

and detection of signiﬁcant radiology image ﬁndings

using large-scale clinical lesion annotations. arXiv

preprint arXiv:1710.01766.

Yianilos, P. N. (1993). Data structures and algorithms for

nearest neighbor. In Proceedings of the fourth annual

ACM-SIAM Symposium on Discrete algorithms, vol-

ume 66, page 311. SIAM.

Zezula, P., Amato, G., Dohnal, V., and Batko, M. (2006).

Similarity search: the metric space approach, vol-

ume 32. Springer Science & Business Media.

ICEIS 2024 - 26th International Conference on Enterprise Information Systems