On the Formal Robustness Evaluation for AI-based Industrial Systems
Mohamed Ibn Khedher
1
, Afef Awadid
1
, Augustin Lemesle
2
and Zakaria Chihani
2
1
IRT - SystemX, 2 Bd Thomas Gibert, 91120 Palaiseau, France
2
CEA, The French Alternative Energies and Atomic Energy Commission, France
Keywords:
Uncertainty in AI, AI Verification, AI Robustness, Adversarial Attacks, Formal Evaluation, Industrial
Application.
Abstract:
The paper introduces a three-stage evaluation pipeline for ensuring the robustness of AI models, particularly
neural networks, against adversarial attacks. The first stage involves formal evaluation, which may not always
be feasible. For such cases, the second stage focuses on evaluating the model’s robustness against intelligent
adversarial attacks. If the model proves vulnerable, the third stage proposes techniques to improve its robust-
ness. The paper outlines the details of each stage and the proposed solutions. Moreover, the proposal aims
to help developers build reliable and trustworthy AI systems that can operate effectively in critical domains,
where the use of AI models can pose significant risks to human safety.
1 INTRODUCTION
Over the last decade, there has been a significant
advancement in Artificial Intelligence (AI) and, no-
tably, Machine Learning (ML) has shown remarkable
progress in various critical tasks. Specifically, Deep
Neural Networks (DNN) have played a transforma-
tive role in machine learning, demonstrating excep-
tional performance in complex applications such as
cybersecurity (Jmila and Khedher, 2022) and robotics
(Khedher et al., 2021).
Despite the capacity of Deep Neural Networks to
handle high-dimensional inputs and address complex
challenges in critical applications, recent evidence in-
dicates that small perturbations in the input space
can lead to incorrect decisions (Bunel et al., 2018).
Specifically, it has been observed that DNNs can be
easily misled, causing their predictions to change with
slight modifications to the inputs. These carefully
chosen modifications result in what are known as ad-
versarial examples. These discoveries underscore the
critical challenge of ensuring that machine learning
systems, especially deep neural networks, function as
intended when confronted with perturbed inputs.
Adversarial examples are specially crafted inputs
that are designed to fool a machine learning model
into making a wrong prediction. These examples are
not randomly generated but created with precise cal-
culations. There are various methods for generating
adversarial examples, but most of them focus on min-
imizing the difference between the distorted input and
the original one while ensuring the prediction is in-
correct. Some techniques require access to the en-
tire classifier model (white-box attacks), while others
only need the prediction function (black-box attacks).
Adversarial attacks pose a significant threat to
critical industrial applications, particularly in sectors
such as manufacturing, energy, and infrastructure,
where precision and reliability are paramount. These
attacks, carefully crafted to exploit vulnerabilities in
machine learning models, introduce subtle modifica-
tions to input data. In critical industrial processes, the
consequences of misclassification or data manipula-
tion by adversarial attacks can result in operational
failures, compromised safety, and potentially catas-
trophic outcomes.
To illustrate the severity of adversarial attacks in
crucial applications like anomaly detection in the cy-
bersecurity domain, consider Figure 1. An attacker,
possessing malicious traffic, can manipulate the traf-
fic by adding imperceptible perturbations, making it
appear benign to the cybersecurity system, allowing
it to pass undetected. Such attacks can severely com-
promise the system’s ability to identify and mitigate
threats, posing significant security risks.
In this paper, we recommend a three-stage
pipeline (Khedher et al., 2023) to industrialists to in-
vestigate the robustness of their models and, if possi-
Khedher, M., Awadid, A., Lemesle, A. and Chihani, Z.
On the Formal Robustness Evaluation for AI-based Industrial Systems.
DOI: 10.5220/0012618100003645
Paper published under CC license (CC BY-NC-ND 4.0)
In Proceedings of the 12th International Conference on Model-Based Software and Systems Engineering (MODELSWARD 2024), pages 311-321
ISBN: 978-989-758-682-8; ISSN: 2184-4348
Proceedings Copyright © 2024 by SCITEPRESS – Science and Technology Publications, Lda.
311

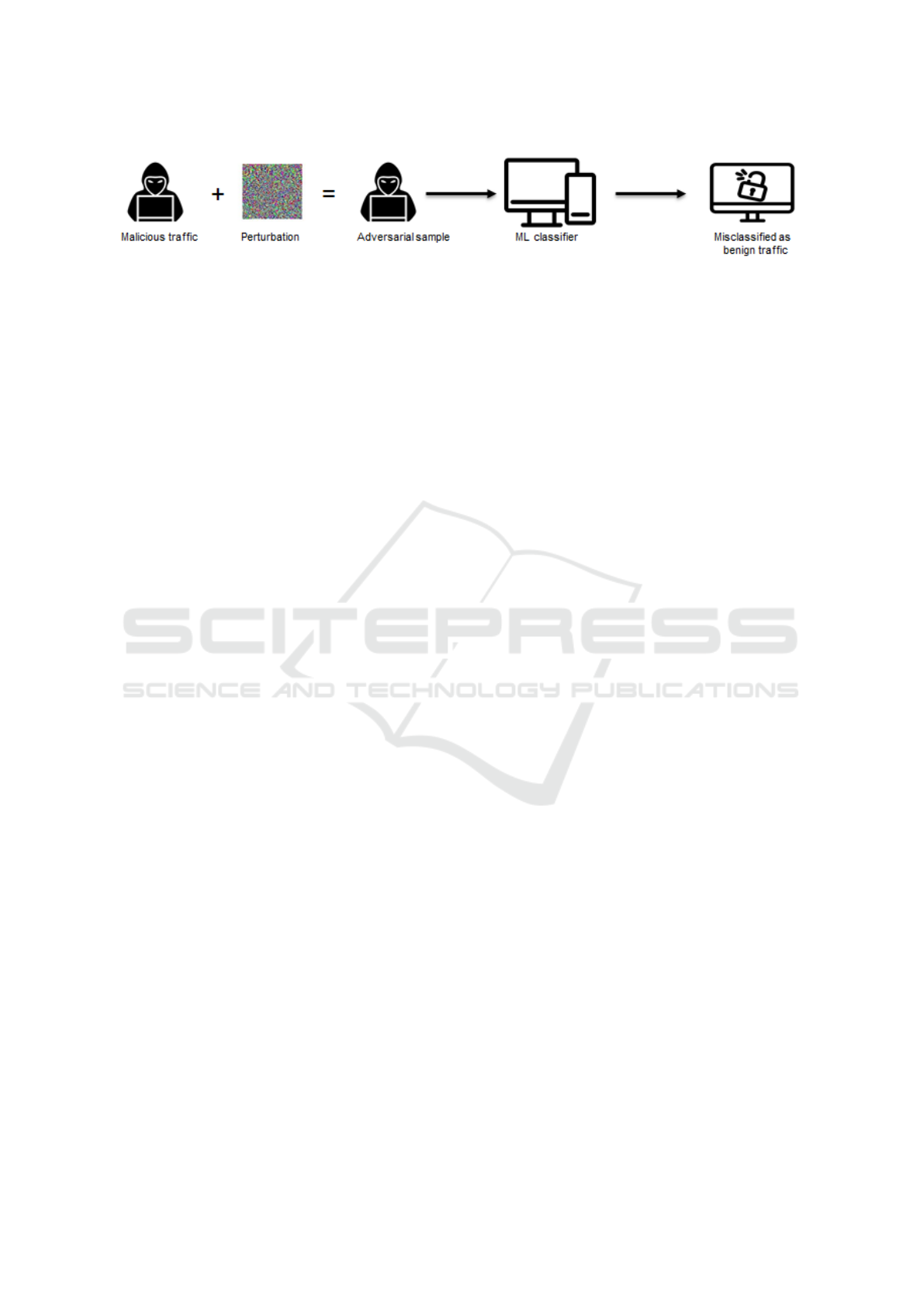
Figure 1: Adversarial attack generation in Network Intrusion Detection System (NIDS) (Jmila and Khedher, 2022).
An adverse sample is generated by adding a small perturbation to the original sample. Thus, malicious perturbed
traffic can be misclassified as benign and thus bypass the intrusion detection system. This can have serious
consequences for the system (Jmila and Khedher, 2022).
ble, obtain a formal guarantee of robustness. The first
stage is formal evaluation, which consists of evalu-
ating all possible inputs of the model and formally
verifying its output. This stage is very complex, or
even impossible, if the model is complex or the data
is of very high dimensionality. In this last case, we
propose a second stage that consists of evaluating the
robustness of the AI model against a set of adversarial
attacks. If the model fails against adversarial attacks,
we recommend the third stage, which consists of im-
proving robustness using techniques called defenses
or adversarial training.
In the rest of the paper, in section 2, the need of
Formal methods for AI-based critical systems is de-
tailed. Then, in sections 3, 4 and 5, we describe each
of the three stages of robustness evaluation pipeline
and describe the popular solutions proposed in the
state of the art. Finally, the section 6 concludes the
paper.
2 THE NEED FOR
TRUSTWORTHY AI-BASED
CRITICAL SYSTEMS
The use of Artificial Intelligence techniques is be-
coming increasingly popular in various applications
(Miglani and Kumar, 2019), as the technologies ma-
ture and become more affordable (Boardman and
Butcher, 2019). These techniques can be physically
embodied as in the case of safety-critical systems
such as electricity grids or on-board aircraft networks
or exist only as software agents that autonomously
process data at speeds or for durations that humans
are not capable of.
Applying AI techniques can confer a compet-
itive advantage to the industry by providing both
high value-added products and services and support
to decision-makers (Mattioli et al., 2023). In this
sense, production efficiency, product quality, and ser-
vice level will be improved by artificial intelligence
(Li et al., 2017). However, while AI has much poten-
tial for innovative applications (advanced automation
and autonomous systems), it raises several concerns
such as security and safety (El-Sherif et al., 2022).
These concerns are even more salient when it comes
to AI-based critical systems, where the integration of
AI technologies can pose significant risks to human
safety.
AI-based critical systems are defined as those sys-
tems containing AI-based components alongside tra-
ditional software components and whose failure leads
to unacceptable circumstances such as loss of hu-
man lives (Mwadulo, 2016). Such systems are not
only safety-critical but also complex. Consequently,
they impose strict certification requirements and high
safety standards (Ferrari and Beek, 2022). In this
sense, the integration of AI technologies in those sys-
tems is constrained by the need for verification, ex-
tensive testing, and certification.
When employing verification in the engineering
process, trust in the safety of the resulting system will
to a large extent be deduced from trust in the inte-
grated AI/ ML models. Therefore, such models need
to be robust and the results of the verification process
need to be trustworthy. To achieve the highest lev-
els of trustworthiness, one might proceed by formally
verifying the robustness of AI/ ML models. Indeed,
formal robustness evaluation helps developers build
reliable and trustworthy AI systems that can operate
effectively in critical domains. Thus, it is essential for
AI safety-critical systems for several reasons includ-
ing:
• Identifying vulnerabilities: AI systems are sus-
ceptible to various vulnerabilities, including ad-
versarial attacks, data distribution shifts, and
model biases. Formal robustness evaluation helps
identify these vulnerabilities by subjecting the
system to rigorous testing and analysis. By under-
standing the system’s weaknesses, developers can
take appropriate measures to mitigate risks and
improve the system’s robustness.
• Safety assurance: AI systems are increasingly
being deployed in safety-critical domains such
MBSE-AI Integration 2024 - Workshop on Model-based System Engineering and Artificial Intelligence
312

as autonomous vehicles, healthcare, and finance.
These systems must operate reliably and safely, as
failures can have severe consequences, including
loss of life or significant financial losses. Formal
robustness evaluation helps ensure that the system
behaves as intended and can handle unexpected
scenarios or adversarial attacks.
• Adversarial robustness: Adversarial attacks in-
volve intentionally manipulating inputs to deceive
or mislead AI systems. Formal robustness evalu-
ation helps assess the system’s resilience against
such attacks. By analyzing the system’s response
to adversarial inputs, developers can identify vul-
nerabilities and develop defenses to ensure the
system remains robust in the face of potential at-
tacks.
• Compliance with regulations and standards:
Many safety-critical domains have regulations
and standards that govern the deployment of AI
systems. Formal robustness evaluation helps
demonstrate compliance with these requirements
by providing evidence of the system’s reliability,
safety, and ability to handle unexpected situations.
It allows developers to provide a rigorous and sys-
tematic assessment of the system’s performance,
which is crucial for gaining regulatory approvals
and ensuring public trust.
• Handling edge cases: AI systems often en-
counter edge cases or scenarios that are not well-
represented in the training data. These cases can
lead to unexpected behavior or errors. Formal
robustness evaluation involves testing the system
with a wide range of inputs, including edge cases,
to ensure it can handle them appropriately. By
identifying and addressing potential issues in edge
cases, developers can improve the system’s over-
all reliability and safety.
3 FORMAL METHODS FOR
NEURAL NETWORK
VERIFICATION
Formal methods are a set of techniques that use
logic and mathematics to rigorously prove that soft-
ware meets specific requirements. These methods
were initially developed in the 1960s and involved
hand-written proofs for small programs (Floyd, 1967;
Hoare, 1969). However, recent advancements have
led to the creation of automated software verification
tools.
These tools focus on the semantic properties of
programs, which are concerned with how the pro-
gram behaves when it runs. Unlike syntactic prop-
erties, which can be determined by simply looking
at the code, semantic properties cannot be fully au-
tomated due to the undecidability of Rice’s theorem.
This means that verification tools must make some
trade-offs between automation, generality, and com-
pleteness. While they cannot always provide a com-
plete answer, formal methods ensure that any property
proven by a tool is indeed true.
Formal methods are widely used in the hardware
and software industries, and are mandated by safety
standards for critical embedded systems like avion-
ics software. Their adoption is expanding into less
critical domains, such as Facebook and Amazon’s use
cases (Newcombe et al., 2015). This demonstrates the
maturity and scalability of formal methods for soft-
ware verification.
3.1 Formal Methods Categories
Different approaches to verify neural networks can be
categorized into three categories based on the formu-
lation of the problem :
• Reachability: This method aims to identify in-
puts that lead to specific states or properties within
the network. It approximates around selected rep-
resentative inputs, propagates the over approxi-
mation along the layers.
• Optimization: This method employs optimiza-
tion techniques to find instances that violate the
given property. The network’s function is incor-
porated as a constraint in the optimization pro-
cess. Due to the non-convex nature of the opti-
mization problem, various techniques have been
developed to represent nonlinear activation func-
tions as linear constraints.
• Search: This method systematically explores the
input space to find inputs that contradict the prop-
erty. It often utilizes heuristics or probabilistic
search strategies to guide the exploration.
In the following sections, we will discuss formal
methods for verifying neural networks. We will
present a variety of solutions that have been proposed
in the literature.
3.2 Reachability Approaches
In the verification of neural networks, the Reachabil-
ity approach involves computing the reachable set for
a specific output, meaning finding the set X such that
every element in that set produces a predefined output
y when propagated through the network:
On the Formal Robustness Evaluation for AI-based Industrial Systems
313

R (X , f ) := y : y = f (x), ∀x ∈ X (1)
The straightforward task of verifying all outputs
produced by a set of inputs can already be expensive,
depending on the size of the input set. This indicates
that the reverse problem of finding the sets for which
a property on the output holds is not scalable and is
infeasible in practice. For this reason, most work in
this domain uses over-approximations of the sets, for
example, employing abstract domains instead of exact
sets, as defined in Abstract Interpretation.
Two main approaches to reachability analysis for
neural networks are proposed in the literature : exact
and approximate reachability. Below, we outline for-
mal methods associated with each type of reachabil-
ity approach. The choice between exact and approxi-
mate reachability depends on the specific application
and the desired balance between accuracy and com-
putational efficiency. For safety-critical applications
where precise results are required, exact reachability
may be the preferred method. However, for applica-
tions where speed is more critical, approximate reach-
ability can be a valuable alternative.
3.2.1 Exact Reachability
This approach aims to determine the precise set of
outputs associated with a given set of neural network
inputs. It is particularly well-suited for piece-wise lin-
ear networks, where the reachable set can be com-
puted by dividing the network into smaller segments
and analyzing each segment individually. However,
this method becomes computationally demanding as
the network grows in size due to the exponential
growth of linear segments.
ExactReach. Exact reachability analysis for neural
networks using either linear or ReLU activations is
achieved in (Xiang et al., 2017b) by precisely rep-
resenting input sets as unions of polyhedra. Exac-
tReach, a specialized tool designed for this purpose,
utilizes polyhedron manipulation tools for computing
the reachable set at each network layer. For ReLU
activation functions, ExactReach demonstrates a key
property: the reachable set of outputs can also be rep-
resented as a union of polyhedra if the input set is rep-
resented in the same manner. This property enables
ExactReach to thoroughly explore the reachable set
for networks with ReLU activations, ensuring precise
determination of the exact boundaries of the reach-
able set, considering all possible combinations of in-
put values and activation functions. As a result, Exac-
tReach provides comprehensive insights into the net-
work’s behavior and helps identify output ranges as-
sociated with specific input regions.
3.2.2 Approximate Reachability
Approximate reachability provides an over-
approximation of the reachable set, meaning that
it estimates the set that is guaranteed to contain all
possible outputs, even if it may not be the exact set.
This method is more efficient than exact reachability
as it does not require dividing the reachable set into
smaller pieces, but it sacrifices some accuracy.
Abstract Interpretation. Abstract interpretation
(Cousot and Cousot, 1977) is a powerful technique
for computing sound approximations of the reach-
able set of a given function, expressed as specific sets
of properties that can be automatically determined.
Originally developed for analyzing program seman-
tics, abstract interpretation provides a systematic ap-
proach to relating an often-intractable concrete func-
tion with a more manageable abstract function, also
known as an abstract transformer. This abstraction en-
ables conservative over-approximations of the reach-
able set, allowing for efficient reasoning about com-
plex functions. Crucially, proving that the computed
over-approximation is safe implies that the concrete
reachable set is also safe.
An abstract transformer operates on abstract ele-
ments, which are typically logical properties rep-
resenting sets of corresponding concrete elements
within the actual function. These abstract elements
collectively form an abstract domain. The design
of effective abstract transformers and domains in-
volves a delicate balance between accuracy and ef-
ficiency. These abstractions must be sufficiently pre-
cise to identify erroneous cases as unreachable while
maintaining computational tractability and scalability
to handle large and complex functions.
Abstract interpretation, a technique for analyzing
program semantics, has found a new application in
analyzing neural networks. In the paper (Gehr et al.,
2018), the authors introduce a method for proving
properties of neural networks using abstract trans-
formers constructed from CAT (Conditional Affine
Transformation) functions. This approach offers a
promising avenue for formally verifying the behavior
of neural networks.
MaxSens. In (Xiang et al., 2017a), the authors con-
ducted a study on the estimation of reachable sets
by focusing on the computation of maximal sensi-
tivity in neural networks. They treated this problem
as a series of convex optimization problems within
a simulation-based framework that utilizes interval
arithmetic. This approach is scalable and supports
monotonic activation functions, making it applicable
MBSE-AI Integration 2024 - Workshop on Model-based System Engineering and Artificial Intelligence
314

Figure 2: Abstract Interpretation for Neural Network Verification (Gehr et al., 2018).
to a wide range of scenarios. However, it is impor-
tant to note that this method is incomplete and prone
to high over-approximations, particularly as the num-
ber of layers in the network increases. The authors
initially provide a description of how to calculate
the maximum sensitivity of a Multi-Layer Perceptron
(MLP) network. The sensitivity refers to the Lipschitz
constant of the network’s function, which measures
the output deviation resulting from a bounded distur-
bance around an input. The maximum sensitivity, on
the other hand, represents the maximum variation in
output for a robustness ball defined by the `
∞
norm.
3.3 Optimization Approaches
Optimization techniques are applied to challenge
the assertion, treating the neural network’s function
as a constraint in the optimization process. Con-
sequently, the optimization problem becomes non-
convex. In primal optimization, several approaches
have emerged to represent nonlinear activation func-
tions as linear constraints. Methods like NSVerify
(Lomuscio and Maganti, 2017a), MIPVerify (Tjeng
et al., 2019), Big-M (Ibn-Khedher et al., 2021), and
ILP (Bastani et al., 2016) are instances of techniques
that simplify constraints through primal optimiza-
tion. Alternatively, dual optimization techniques pro-
vide another avenue for simplifying constraints. La-
grangian dual methods, including Duality (Dvijotham
et al., 2018) and ConvDual (Kolter and Wong, 2017),
as well as semidefinite programming methods such as
Certify (Raghunathan et al., 2018) and SDP (Fazlyab
et al., 2022), represent representative approaches for
dual optimization.
3.3.1 Primal Optimization
Primal optimization methods tackle the verification
task by embedding the network structure as a con-
straint in the optimization problem. However, these
methods are currently limited to networks with ReLU
(Rectified Linear Unit) activations. To address this,
researchers have developed techniques to encode the
network using linear or mixed integer linear con-
straints, taking advantage of the piece-wise linear-
ity of ReLU activations. This approach allows for
a more focused exploration of optimization solutions
tailored to the specific characteristics of ReLU-based
networks.
Big-M. In the work presented in (Ibn-Khedher
et al., 2021), the authors advocate for utilizing the
bigM technique as an automated encoder for lin-
earizing the ReLU, a non-linear activation function.
This technique involves a mixed-integer linear pro-
gramming transformation that precisely converts non-
linear constraints into linear inequalities.
To illustrate, considering the example depicted in
Eq.2 where neurons H
1
and H
2
are activated with
ReLU, employing Big-M for the verification problem
results in formulating it as a maximization problem:
max Z = Constant, subject to a set of constraints that
delineate the relationships between neurons across
different layers. The core of this approach lies in the
linearization of the ReLU function, achieved by re-
placing it with a set of constraints. For instance, the
relationship between neuron H
1
and inputs x
1
and x
2
is expressed as the following system of equations.
On the Formal Robustness Evaluation for AI-based Industrial Systems
315

a
out
(H
1
) ≥ (θ
1
− 1)M + (x
1
+ x
2
)
a
out
(H
1
) ≤ (1 − θ
1
)M + (x
1
+ x
2
)
a
out
(H
1
) ≤ θ
1
× M
x
1
+ x
2
≥ (θ
1
− 1) × M
x
1
+ x
2
≤ θ
1
× M
θ
1
∈ {0, 1}
(2)
MIPVerify. The authors of (Tjeng et al., 2019) sim-
ilarly encode the neural network using mixed inte-
ger linear constraints. However, there are two key
distinctions between MIPVerify and NSVerify (Lo-
muscio and Maganti, 2017b). Firstly, MIPVerify em-
ploys node bounds to refine the constraints. Secondly,
MIPVerify addresses an adversarial problem that aims
to estimate the maximum permissible perturbation on
the input side. Like NSVerify, MIPVerify is also rec-
ognized as a complete method, ensuring that it can
successfully handle and analyze all feasible scenarios.
Formally, MIPVerify computes maximum allowable
disturbance using mixed integer linear programming.
Mathematically, MIPVerify optimizes for the adver-
sarial bound (min
x,y
||x − x
0
||
p
,s.t.y 6∈ Y , y = f (x)) us-
ing mixed integer encoding (with lower and upper
bounds) and returns adversarial bounds.
ILP. The authors of ILP (Iterative Linear Program-
ming) (Bastani et al., 2016) represents the neural net-
work as a series of linear constraints by linearizing
it around a reference point. In ILP, the optimization
problem addresses an adversarial scenario aiming to
determine the maximum permissible perturbation on
the input side. The optimization is performed itera-
tively. However, it is important to note that ILP is not
considered a complete method as it only considers a
single linear segment of the network, thus potentially
overlooking certain aspects of the overall network be-
havior.
3.3.2 Dual Optimization
While various techniques have been developed for en-
coding constraints in primal optimization methods,
dual optimization offers an alternative approach by
simplifying the constraints within the primal problem.
This simplification typically leads to fewer and more
manageable constraints in the dual problem. How-
ever, the corresponding objectives in dual optimiza-
tion tend to be more complex than those in the primal
problem. The construction of the dual problem often
involves incorporating relaxations, which means that
these approaches are considered incomplete due to the
approximation inherent in the relaxation process.
Duality. (Dvijotham et al., 2018) addressed vari-
ous challenges associated with SMT-based, branch-
and-bound, or mixed-integer programming methods,
particularly concerning scalability and restrictions
linked to specific piece-wise linear activation func-
tions. They introduced a universal approach capable
of accommodating any activation function and spec-
ification type. The key concept involves formulat-
ing the verification property as an optimization prob-
lem, aiming to identify the most substantial violation
of the specification. Their strategy entails solving a
Lagrangian relaxation of the optimization problem to
derive an upper bound on the maximum potential vi-
olation of the specification. While the approach is
sound, indicating that if the largest violation is less
than or equal to zero, the property holds, it is also
incomplete. A positive largest violation does not con-
clusively establish that the property does not hold in
reality. Moreover, the process can be halted at any
point to obtain the current valid bound on the maxi-
mum violation.
ConvDual. ConvDual (Wong and Kolter, 2018) fol-
lows a dual approach to estimate output bounds. It be-
gins by performing a convex relaxation of the network
within the primal optimization framework to simplify
the dual problem. Unlike explicit optimization, Con-
vDual heuristically computes the bounds by selecting
a fixed, dual feasible solution. This heuristic approach
allows ConvDual to achieve computational efficiency
compared to Duality. While the original ConvDual
approach utilizes the obtained bounds for robust net-
work training, this survey primarily concentrates on
the method’s capability to compute these bounds ac-
curately.
3.4 Search Approaches
Reluplex. In (Katz et al., 2017), the authors propose
Reluplex. Reluplex is the abbreviation of ReLU for
the simplex algorithm. The simplex algorithm is an
algorithm for solving linear optimization problems.
Its objective is to minimize a function on a set defined
by inequalities. Reluplex’s principle consists in for-
malizing the neural network by a set of equations. To
solve this system of equations, starting from an initial
assignment, it tries to correct some constraints vio-
lated at each step. The specification of this approach
is that, from one iteration to another, the constraints
between the variables can be violated.
PLANET. In (Ehlers, 2017), the authors propose
PLANET, "a Piece-wise LineAr feed-forward NEural
network verification Tool". Its principle consists first
MBSE-AI Integration 2024 - Workshop on Model-based System Engineering and Artificial Intelligence
316

of replacing non-linear neural network functions by a
set of linear equations. It tries then to find a solution
to the system of equations. The approach supports
both types of nodes: ReLU and Max Pooling.
BaB. BaB (Bunel et al., 2017) employs the branch
and bound technique to calculate the output bounds
of a network. Its modular design allows it to function
as a comprehensive framework that can accommodate
other methods like Reluplex and Planet. This versa-
tility enables BaB to serve as a unified platform for
various approaches within the field.
Fast-Lin. Fast-Lin (Weng et al., 2018) adopts a
layer-by-layer approach and utilizes binary search
within the input domain to determine a certified lower
bound on the allowable input disturbance for ReLU
networks. This methodology enables efficient compu-
tation and offers a dependable estimation of the max-
imum permissible input perturbation.
Fast-Lip. Fast-Lip (Weng et al., 2018) builds upon
the foundation of Fast-Lin for calculating activation
function bounds while also estimating the local Lip-
schitz constant of the network. Fast-Lin excels in
terms of scalability, being more efficient in this re-
gard. However, Fast-Lip provides enhanced solutions
specifically for ’L1 bounds,’ offering improved per-
formance in that specific context.
While we present a rough overview of the differ-
ent techniques developed in each field, it is impor-
tant to note that more often than not, state of the art
tools leverage more than one kind of method. They
rely on reachability approaches for their scalability,
adding some optimization to improve the precision
and make their tool complete through search based
approaches. One can look at the performances of state
of the art approaches through the VNN-COMP (Brix
et al., 2023), which brings together and evaluate tools
such as α-β-CROWN (Zhang et al., 2018), Marabou
(Katz et al., 2019), nnenum (Bak et al., 2020) or
PyRAT (Lemesle et al., 2023).
4 ROBUSTNESS TESTING
In some cases the formal evaluation of a neural net-
work is costly in terms of computation time. To get an
idea about the new robustness of the neural network,
it is recommended to start by analyzing the behavior
of the neural network in front of adversary attacks. A
network that is already vulnerable to adversarial at-
tacks needs to improve its robustness using state-of-
the-art adversarial training techniques and it is very
early to formally evaluate its robustness.
4.1 Adversarial Attacks Types
There are two main types of adversarial attacks
(White-box attacks and Black-box attacks) that aim
to fool neural networks into making incorrect predic-
tions. The key difference between the two lies in the
amount of knowledge the attacker has about the target
neural network.
White-box Attacks assume that the attacker has
full knowledge of the neural network, including its
architecture, weights, and training data. This al-
lows the attacker to comprehensively analyze the net-
work’s vulnerabilities and design targeted adversarial
attacks that exploit its specific weaknesses. In con-
trast, Black-box Attacks operate with limited or no
knowledge of the target network’s internal structure
or parameters. The attacker can only interact with the
network by making input queries and observing the
corresponding output predictions. This poses a sig-
nificant challenge, as the attacker must infer the net-
work’s vulnerabilities and design attacks without di-
rect access to its inner workings.
In the industrial context, the two type of attacks
serve distinct purposes. Organizations typically em-
ploy white-box Attacks internally to enhance their
systems and detect potential vulnerabilities before
they can be exploited by external actors. By gain-
ing comprehensive knowledge of their neural net-
works’ architectures, weights, and training data, orga-
nizations can thoroughly analyze their networks’ ro-
bustness and identify areas where adversarial attacks
could be successful. This proactive approach helps
organizations to detect the weakness of their models
and mitigate risks.
On the other hand, Black-Box Attacks play a cru-
cial role in testing and evaluating neural networks be-
fore they are deployed in real-world applications. By
simulating the actions of an external attacker, Black-
Box Attacks assess the network’s resilience against
unknown or obfuscated threats. This helps organiza-
tions identify potential vulnerabilities that may arise
from limited knowledge of the network’s internals.
4.2 Adversarial White-Box Attacks
Fast Gradient Sign Method (FGSM). (Goodfel-
low et al., 2015) have developed a method for gen-
erating adverse sample based on the gradient descent
method. Each component of the original sample x is
modified by adding or subtracting a small perturba-
tion ε. The adverse function ψ is expressed as fol-
On the Formal Robustness Evaluation for AI-based Industrial Systems
317

lows:
ψ : X ×Y −→ X
(x, y) 7−→ −ε∇
x
L(x, y)
Thus, the loss function of the classifier will decrease
when the class of the adverse sample is chosen as y.
We then wish to find x
0
adverse sample of x such as:
kx
0
− xk
p
≤ ε.
It is clear that the previous formulation of FGSM is
related to targeted attack case where y corresponds to
the target class that we wish to impose on the original
input sample. However, this attack can be applied in
the case of untargeted attack, by considering the fol-
lowing perturbation:
ρ : X −→ X
x 7−→ −ψ(x, C(x))
Thus, the original input x is modified in order to
increase the loss function L when the classifier re-
tains the same class C(x). This attack only requires
the computation of the loss function gradient, which
makes it a very efficient method. On the other hand, ε
is a hyperparameter that affects the x
0
class: if ε is too
small, the ρ(x) perturbation may have little impact on
the x
0
class.
Basic Iterative Method (BIM). (Kurabin et al.,
2017) proposed an extension of the FGSM attack by
iteratively applying FGSM. At each iteration i, the ad-
verse sample is generated by applying FGSM on the
generated sample at the (i − 1)
th
iteration. The BIM
attack is generated as the following:
(
x
0
0
= x
x
0
i+1
= x
0
i
+ ψ(x
0
i
,y)
where y represents, in the case of a targeted attack,
the class of the adverse sample and y = C(x
0
N
) in the
case of an untargeted attack. Moreover, ψ is the same
function defined in the case of FGSM attack.
Projected Gradient Descent (PGD). The PGD
(Madry et al., 2017) attack is also an extension of
the FGSM and similar to BIM. It consists in applying
FGSM several times. The major difference from BIM
is that at each iteration, the generated attack is pro-
jected on the ball B(x, ε) =
{
z ∈ X : kx − zk
p
≤ ε
}
.
The adverse sample x
0
associated with the original one
x is then constructed as follows:
(
x
0
0
= x
x
0
i+1
= Π
ε
(x
0
i
+ ψ(x
0
i
,y))
where Π
ε
is the projection on the ball B(x, ε) and ψ is
the perturbation function as defined in FGSM. Like-
wise, y refers to the target label you wish to reach, in
the case of targeted attack, or it refers to C(x
0
N
) in the
case of an untargeted attack.
DeepFool. DeepFool is a non-targeted attack pro-
posed by (Moosavi-Dezfooli et al., 2015). The main
idea of DeepFool is to find the closest distance from
the original input to the decision boundary. To over-
come the non-linearity in high dimension, they per-
formed an iterative attack with a linear approxima-
tion. For an affine classifier f (x) = wT x + b, where
w is the weight of the affine classifier and b is the
bias, the minimal perturbation of an affine classifier
is the distance to the separating affine hyperplane
F = x : wT x + b = 0. Given the example of a linear
binary classifier, the robustness of the classifier f for
an input x
0
is equal to the distance of x
0
to the hyper-
plane separating the two classes. In fact, the minimal
perturbation to change the classifier’s decision corre-
sponds to the orthogonal projection of x
0
onto the hy-
perplane, given by: η
∗
(x) = −
f (x)
kwk
2
2
∗ w.
For a general differentiable classifier, DeepFool
assumes that f is linear around x
i
at each iteration.
The minimal perturbation is expressed as follows:
argmin
η
i
kη
i
k
2
subject to f (x
i
) + ∇ f (x
i
)
T
η
i
= 0.
This process runs until f (x
i
) 6= f (x), and the mini-
mum perturbation is eventually approximated by the
sum of η
i
. This technique can also be extended to
a multi-class classifier by finding the closest hyper-
planes. It can also be extended to a more general
`
p
norm, p ∈ [0, ∞). As mentioned in (Yuan et al.,
2019), DeepFool provides less perturbation compared
to FGSM.
4.3 Adversarial Black-Box Attacks
ZOO. Zeroth Order Optimization (ZOO) is pro-
posed by (Chen et al., 2017) to estimate the gradients
of target DNN in order to produce an adversarial in-
put. ZOO is suitable for problems where gradients
are unavailable, uncomputable or private. The threat
model assumed by the authors is that the target model
can only be queried to obtain the probability scores of
all the classes. The authors then use symmetric differ-
ence quotient method to estimate the gradient
∂ f (x)
∂x
i
,
where f is the loss function:
ˆg :=
∂ f (x)
∂x
i
≈
f (x + he
i
)
f (x − he
i
)
(3)
The naive solution above requires querying the
model 2p times, where p is the dimension of the in-
MBSE-AI Integration 2024 - Workshop on Model-based System Engineering and Artificial Intelligence
318

put. So the authors propose two stochastic coordinate
methods: ZOO-Adam and ZOO-Newton in which a
gradient is estimated for a random coordinate and the
update formula is obtained using ADAM and New-
ton’s Method until it reaches convergence. The au-
thors also discuss the generation of noise in a lower
dimension to improve efficiency and specify its ad-
vantages and disadvantages (Bhambri et al., 2019).
Boundary. Boundary Attacks are decision-based
adversarial attacks that are based on a model’s de-
cision. This was the first time that decision-based
attacks were introduced that focus on deep learning
models using real-life data sets such as ImageNet.
The proposed algorithm initializes by taking a ran-
dom distribution of pixels for an image in the range
of [0, 255]. Using this image, the algorithm traverses
the decision boundary of the class to which the sam-
ple input image belongs to. The initialized image is
then able to reduce its distance w.r.t. the input image
besides staying inside the adversarial region.
5 DEFENSE TECHNIQUE FOR
IMPROVING ROBUSTNESS
Defense techniques aim to strengthen a model’s re-
silience against adversarial attacks. The literature
distinguishes three categories of defense techniques,
specifically those based on: i) Modifying the input
data, ii) Modifying the classifier, and iii) Adding an
external model. These categories are elaborated upon
below.
5.1 Modifying the Input Data
Instead of directly altering the network architecture
or training process, data modification techniques fo-
cus on manipulating the input data itself. These tech-
niques aim to make the input data less susceptible to
adversarial perturbations, thereby improving the net-
work’s overall robustness. One such technique, Gaus-
sian data augmentation (Zantedeschi et al., 2017), in-
volves adding copies of the original data points with
Gaussian noise. This approach trains the network to
recognize the same class for both the original instance
and its slightly perturbed version, enhancing its abil-
ity to generalize and withstand adversarial modifica-
tions. The simplicity, ease of implementation, and ef-
fectiveness of Gaussian data augmentation have made
it a widely adopted technique for mitigating adversar-
ial attacks.
5.2 Modifying the Classifier
Classifier modifications involve altering the neural
network architecture or training process to enhance its
resilience to adversarial attacks. One such approach is
gradient masking, which aims to conceal or mask the
network’s gradient information from potential attack-
ers. While many adversarial attacks rely on knowl-
edge of the gradient, gradient masking aims to ob-
scure this information, making it more difficult for at-
tackers to manipulate the network.
Gradient masking techniques work by manipulat-
ing the gradients during the training process, effec-
tively hiding the network’s internal workings from ex-
ternal observers. This makes it challenging for attack-
ers to craft effective adversarial examples based on
gradient information.
5.3 Adding an External Model
Instead of directly modifying the primary network,
external model integration utilizes additional models
to augment the system’s defenses against adversarial
attacks. This approach introduces an extra layer of
protection, making it more challenging for attackers
to manipulate the network’s output.
One such technique, introduced in (Lee et al.,
2017), employs generative adversarial networks
(GANs) to enhance the network’s resilience. A sepa-
rate generator network actively generates adversarial
perturbations that aim to fool the primary network.
By incorporating this adversarial training process, the
system becomes more adept at identifying and coun-
teracting adversarial inputs. The integration of exter-
nal models alongside the primary network during test-
ing provides a robust and effective defense strategy.
This approach demonstrates the potential of combin-
ing different models and techniques to strengthen the
overall security of neural networks against adversarial
attacks.
6 CONCLUSION AND
PERSPECTIVES
Machine learning models are, ultimately, software
artefacts. And as such, there must be adequate consid-
eration and effort devoted to the characterization of its
safety and robustness aspects when it is used in sensi-
tive environments, particularly critical systems. How-
ever, ML models come with their own challenges, de-
manding new methods and tools to be devised. While
this task seems arduous, the goal of this paper is to of-
fer a broad range of avenues for trust, to show the first
On the Formal Robustness Evaluation for AI-based Industrial Systems
319

steps in these paths, and to inspire the conviction that
the research community is advancing on this topic and
making greater strides every year, expanding the tool-
box needed by the industrial sector to enforce trust in
their models.
In future work, we propose the application of the
suggested pipeline in real industrial use cases. Given
that the methods mentioned in this survey depend on
types of data (images, time series, tabular data), we
have observed that the approaches proposed for time
series are not sufficiently advanced. Therefore, we
suggest investigating the adaptability of this pipeline
for temporal data.
ACKNOWLEDGMENT
This work has been supported by the French govern-
ment under the "France 2030" program, as part of the
SystemX Technological Research Institute within the
Confiance.ai programme.
REFERENCES
Bak, S., Tran, H.-D., Hobbs, K., and Johnson, T. T. (2020).
Improved geometric path enumeration for verifying
relu neural networks. In Proceedings of the 32nd In-
ternational Conference on Computer Aided Verifica-
tion. Springer.
Bastani, O., Ioannou, Y., Lampropoulos, L., Vytiniotis,
D., Nori, A. V., and Criminisi, A. (2016). Measur-
ing neural net robustness with constraints. CoRR,
abs/1605.07262.
Bhambri, S., Muku, S., Tulasi, A., and Buduru, A. B.
(2019). A study of black box adversarial attacks in
computer vision. CoRR, abs/1912.01667.
Boardman, M. and Butcher, F. (2019). An exploration
of maintaining human control in ai enabled systems
and the challenges of achieving it. In Workshop on
Big Data Challenge-Situation Awareness and Deci-
sion Support. Brussels: North Atlantic Treaty Organi-
zation Science and Technology Organization. Porton
Down: Dstl Porton Down.
Brix, C., Bak, S., Liu, C., and Johnson, T. T. (2023). The
fourth international verification of neural networks
competition (vnn-comp 2023): Summary and results.
Bunel, R., Turkaslan, I., Torr, P. H., Kohli, P., and Kumar,
M. P. (2018). A unified view of piecewise linear neu-
ral network verification. In Proceedings of the 32Nd
International Conference on Neural Information Pro-
cessing Systems, NIPS’18, pages 4795–4804, USA.
Curran Associates Inc.
Bunel, R., Turkaslan, I., Torr, P. H. S., Kohli, P., and Kumar,
M. P. (2017). Piecewise linear neural network verifi-
cation: A comparative study. CoRR, abs/1711.00455.
Chen, P.-Y., Zhang, H., Sharma, Y., Yi, J., and Hsieh, C.-
J. (2017). ZOO: Zeroth Order Optimization based
Black-box Attacks to Deep Neural Networks without
Training Substitute Models. Proceedings of the 10th
ACM Workshop on Artificial Intelligence and Security,
pages 15–26. arXiv: 1708.03999.
Cousot, P. and Cousot, R. (1977). Abstract interpretation:
A unified lattice model for static analysis of programs
by construction or approximation of fixpoints. In
Conference Record of the 4th Annual ACM SIGACT-
SIGPLAN Symposium on Principles of Programming
Languages (POPL), Los Angeles, CA, pages 238–252.
ACM.
Dvijotham, K., Stanforth, R., Gowal, S., Mann, T. A., and
Kohli, P. (2018). A Dual Approach to Scalable Ver-
ification of Deep Networks. In Proceedings of the
Thirty-Fourth Conference on Uncertainty in Artificial
Intelligence, UAI 2018, Monterey, California, USA,
August 6-10, 2018, pages 550–559.
Ehlers, R. (2017). Formal verification of piece-
wise linear feed-forward neural networks. CoRR,
abs/1705.01320.
El-Sherif, D. M., Abouzid, M., Elzarif, M. T., Ahmed,
A. A., Albakri, A., and Alshehri, M. M. (2022). Tele-
health and artificial intelligence insights into health-
care during the covid-19 pandemic. In Healthcare,
volume 10, page 385. MDPI.
Fazlyab, M., Morari, M., and Pappas, G. J. (2022). Safety
verification and robustness analysis of neural net-
works via quadratic constraints and semidefinite pro-
gramming. IEEE Transactions on Automatic Control,
67(1):1–15.
Ferrari, A. and Beek, M. H. T. (2022). Formal methods in
railways: a systematic mapping study. ACM Comput-
ing Surveys, 55(4):1–37.
Floyd, R. W. (1967). Assigning meanings to programs.
Proceedings of Symposium on Applied Mathematics,
19:19–32.
Gehr, T., Mirman, M., Drachsler-Cohen, D., Tsankov, P.,
Chaudhuri, S., and Vechev, M. (2018). Ai2: Safety
and robustness certification of neural networks with
abstract interpretation. In 2018 IEEE Symposium on
Security and Privacy (SP), pages 3–18.
Gehr, T., Mirman, M., Drachsler-Cohen, D., Tsankov, P.,
Chaudhuri, S., and Vechev, M. (2018). AI2: Safety
and Robustness Certification of Neural Networks with
Abstract Interpretation. In 2018 IEEE Symposium on
Security and Privacy (SP), pages 3–18. ISSN: 2375-
1207.
Goodfellow, I. J., Shlens, J., and Szegedy, C. (2015). Ex-
plaining and Harnessing Adversarial Examples. In In-
ternational Conference on Learning Representations.
Hoare, C. A. R. (1969). An axiomatic basis for computer
programming. Commun. ACM, 12(10):576–580.
Ibn-Khedher, H., Khedher, M. I., and Hadji, M. (2021).
Mathematical programming approach for adversarial
attack modelling. In Rocha, A. P., Steels, L., and
van den Herik, H. J., editors, International Conference
on Agents and Artificial Intelligence, pages 343–350.
MBSE-AI Integration 2024 - Workshop on Model-based System Engineering and Artificial Intelligence
320

Jmila, H. and Khedher, M. I. (2022). Adversarial machine
learning for network intrusion detection: A compara-
tive study. Comput. Networks, 214:109073.
Katz, G., Barrett, C. W., Dill, D. L., Julian, K., and Kochen-
derfer, M. J. (2017). Reluplex: An efficient SMT
solver for verifying deep neural networks. CoRR,
abs/1702.01135.
Katz, G., Huang, D. A., Ibeling, D., Julian, K., Lazarus, C.,
Lim, R., Shah, P., Thakoor, S., Wu, H., Zeljic, A., Dill,
D. L., Kochenderfer, M. J., and Barrett, C. W. (2019).
The marabou framework for verification and analysis
of deep neural networks. In Dillig, I. and Tasiran,
S., editors, Computer Aided Verification - 31st Inter-
national Conference, CAV 2019, New York City, NY,
USA, July 15-18, 2019, Proceedings, Part I, volume
11561 of Lecture Notes in Computer Science, pages
443–452. Springer.
Khedher, M. I., Jmila, H., and El-Yacoubi, M. A. (2023).
On the formal evaluation of the robustness of neural
networks and its pivotal relevance for ai-based safety-
critical domains. International Journal of Network
Dynamics and Intelligence, page 100018.
Khedher, M. I., Mziou-Sallami, M., and Hadji, M. (2021).
Improving decision-making-process for robot naviga-
tion under uncertainty. In International Conference on
Agents and Artificial Intelligence, pages 1105–1113.
Kolter, J. Z. and Wong, E. (2017). Provable defenses against
adversarial examples via the convex outer adversarial
polytope. CoRR, abs/1711.00851.
Kurabin, A., Goodfellow, I. J., and Bengio, S. (2017).
Adversarial examples in the physical world. ICLR,
1607.02533v4.
Lee, H., Han, S., and Lee, J. (2017). Generative adversarial
trainer: Defense to adversarial perturbations with gan.
arXiv preprint arXiv:1705.03387.
Lemesle, A., Chihani, Z., Lehmann, J., and Durand,
S. (2023). PyRAT Analyzer website. https://
pyrat-analyzer.com/. Accessed: December 15th,
2023.
Li, B.-h., Hou, B.-c., Yu, W.-t., Lu, X.-b., and Yang, C.-w.
(2017). Applications of artificial intelligence in intel-
ligent manufacturing: a review. Frontiers of Informa-
tion Technology & Electronic Engineering, 18:86–96.
Lomuscio, A. and Maganti, L. (2017a). An approach to
reachability analysis for feed-forward relu neural net-
works. CoRR, abs/1706.07351.
Lomuscio, A. and Maganti, L. (2017b). An approach to
reachability analysis for feed-forward relu neural net-
works. CoRR, abs/1706.07351.
Madry, A., Makelov, A., Schmidt, L., Tsipras, D., and
Vladu, A. (2017). Towards deep learning mod-
els resistant to adversarial attacks. arXiv preprint
arXiv:1706.06083.
Mattioli, J., Le Roux, X., Braunschweig, B., Cantat, L.,
Tschirhart, F., Robert, B., Gelin, R., and Nicolas, Y.
(2023). Ai engineering to deploy reliable ai in indus-
try. In AI4I.
Miglani, A. and Kumar, N. (2019). Deep learning models
for traffic flow prediction in autonomous vehicles: A
review, solutions, and challenges. Vehicular Commu-
nications, 20:100184.
Moosavi-Dezfooli, S.-M., Fawzi, A., and Frossard, P.
(2015). Deepfool : a simple and accurate method to
fool deep neural networks. CoRR, 1511.04599.
Mwadulo, M. W. (2016). Suitability of agile methods for
safety-critical systems development: a survey of liter-
ature. International Journal of Computer Applications
Technology and Research, 5(7):465–471.
Newcombe, C., Rath, T., Zhang, F., Munteanu, B., Brooker,
M., and Deardeuff, M. (2015). How amazon web ser-
vices uses formal methods. Communications of the
ACM.
Raghunathan, A., Steinhardt, J., and Liang, P. (2018).
Certified defenses against adversarial examples. In
6th International Conference on Learning Represen-
tations, ICLR 2018, Vancouver, BC, Canada, April 30
- May 3, 2018, Conference Track Proceedings. Open-
Review.net.
Tjeng, V., Xiao, K. Y., and Tedrake, R. (2019). Evaluating
robustness of neural networks with mixed integer pro-
gramming. In 7th International Conference on Learn-
ing Representations, ICLR 2019, New Orleans, LA,
USA, May 6-9, 2019. OpenReview.net.
Weng, T., Zhang, H., Chen, H., Song, Z., Hsieh, C.,
Daniel, L., Boning, D. S., and Dhillon, I. S. (2018).
Towards fast computation of certified robustness for
relu networks. In Dy, J. G. and Krause, A., edi-
tors, Proceedings of the 35th International Conference
on Machine Learning, ICML 2018, Stockholmsmäs-
san, Stockholm, Sweden, July 10-15, 2018, volume 80
of Proceedings of Machine Learning Research, pages
5273–5282.
Wong, E. and Kolter, J. Z. (2018). Provable defenses against
adversarial examples via the convex outer adversar-
ial polytope. In Dy, J. G. and Krause, A., editors,
Proceedings of the 35th International Conference on
Machine Learning, ICML 2018, Stockholmsmässan,
Stockholm, Sweden, July 10-15, 2018, volume 80 of
Proceedings of Machine Learning Research, pages
5283–5292. PMLR.
Xiang, W., Tran, H., and Johnson, T. T. (2017a). Out-
put reachable set estimation and verification for multi-
layer neural networks. CoRR, abs/1708.03322.
Xiang, W., Tran, H., and Johnson, T. T. (2017b). Reachable
set computation and safety verification for neural net-
works with relu activations. CoRR, abs/1712.08163.
Yuan, X., He, P., Zhu, Q., and Li, X. (2019). Adversar-
ial examples: Attacks and defenses for deep learning.
IEEE transactions on neural networks and learning
systems, 30(9):2805–2824.
Zantedeschi, V., Nicolae, M.-I., and Rawat, A. (2017).
Efficient defenses against adversarial attacks. In
ACM Workshop on Artificial Intelligence and Security,
pages 39–49.
Zhang, H., Weng, T.-W., Chen, P.-Y., Hsieh, C.-J., and
Daniel, L. (2018). Efficient neural network robust-
ness certification with general activation functions.
Advances in Neural Information Processing Systems,
31:4939–4948.
On the Formal Robustness Evaluation for AI-based Industrial Systems
321