Steady-State Energy Consumption Evaluation in BaseBand Units Pool in

Cloud Radio Access Network

Maroua Idi

1 a

, Sana Younes

1 b

and Riadh Robbana

2 c

Faculty of Sciences of Tunis, University of Tunis El Manar, Tunis 2092, Tunisia

National Institute of Applied Sciences and Technology, University of Carthage, Tunis 1080, Tunisia

Keywords:

C-RAN, Energy Efﬁciency, Hysteresis, MRM, CTMC, CSRL.

Abstract:

Cloud Radio Access Network (C-RAN) have been proposed as a ﬁfth-generation (5G) cellular network so-

lution for high spectral and energy efﬁciency. In the C-RAN architecture, which leverages cloud computing

technology, the baseband processing is performed in the cloud. In fact, the BaseBand Units (BBUs) are located

in the cloud and generate Virtual Machines (VMs) to serve User Equipment (UE) calls. This paper performs

a quantitative analysis of the energy consumption computed over two schemes named Virtual Machine Hys-

teresis Allocation Strategy (VMHAS) and Virtual Machine Allocation Strategy (VMAS) for 5G C-RAN. The

ﬁrst, VMHAS, uses the hysteresis mechanism to minimize energy consumption by adjusting the number of

VMs in BBUs according to the trafﬁc load. It consists of switching the idle VMs to sleep mode to save energy.

The second, VMAS, allocates VMs without considering the sleep mode. We use the Markov Reward Model

(MRM) to evaluate measures related to energy consumption in the proposed schemes. Modeling and per-

formance measures speciﬁcation are achieved by Continuous-Time Markov chains (CTMCs) and Continuous

Stochastic Reward Logic (CSRL). We quantify the steady-state performance measures by checking CSRL for-

mulas using the PRISM model checker. The obtained results demonstrate that the scheme with the hysteresis

mechanism, VMHAS, achieves an enhanced energy performance compared to VMAS.

1 INTRODUCTION

Cloud Radio Access Network (C-RAN) architecture

(Checko et al., 2014) has been proposed as a one of

the ﬁfth generation (5G) cellular networks for pro-

viding high spectral efﬁciency and conserving en-

ergy. By leveraging cloud computing technology, C-

RAN implements the functional separation of tradi-

tional Base Station into two parts: the BaseBand Unit

(BBU) and the Remote Radio Head (RRH). C-RAN

moved all the BBUs to a central unit called the BBU

pool. Meanwhile, the RRHs are left off on the cell

sites. The connection between the BBUs and RRHs,

respectively responsible for baseband and radio func-

tionalities, is referred to as the fronthaul links and is

done via an optical transport network.

Several researchers have focused on improving

the energy efﬁciency of C-RAN using the ON-OFF

switching (also known as sleep mode) technique.

https://orcid.org/0000-0002-6467-8887

https://orcid.org/0000-0002-4883-3381

https://orcid.org/0000-0001-5736-4137

Considering that the RRHs only solely function as

transmitters/receivers with minimal energy consump-

tion, the energy conservation achieved by deactivat-

ing (sleep mode) RRHs would be restricted (Feng

et al., 2017). Therefore, it is highly appealing to in-

vestigate the ON-OFF switching for BBUs. Many

works (Sigwele et al., 2017) (Aldaeabool and Abbod,

2017) (Sahu et al., 2017) have studied the deactivating

mechanism for BBUs in C-RAN. Nonetheless, deacti-

vating a BBU affects all its associated RRHs and User

Equipment (UE) connected to those RRHs. Hence,

the activation and deactivation conditions of BBUs

are interconnected with the mappings between BBU-

RRH and RRH-UE. Since, in the C-RAN architec-

ture, all BBU functions are implemented on standard

hardware and executed on Virtual Machines (VMs)

(Yu et al., 2017) which serve UEs. Therefore, a more

accurate adjustment of the number of VMs in a BBU

that can support would improve the network capacity

and the energy efﬁciency which is the target for this

paper.

This paper continues the work proposed in (Idi

et al., 2022), in which a new Call Admission Con-

Idi, M., Younes, S. and Robbana, R.

Steady-State Energy Consumption Evaluation in BaseBand Units Pool in Cloud Radio Access Network.

DOI: 10.5220/0012629400003687

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 19th International Conference on Evaluation of Novel Approaches to Software Engineering (ENASE 2024), pages 99-109

ISBN: 978-989-758-696-5; ISSN: 2184-4895

trol (CAC) scheme was proposed. This scheme,

called Virtual Machine Hysteresis Allocation Strategy

(VMHAS), aims to adjust the number of active VMs

in BBUs by making non-used VMs in sleep mode. To

achieve this, VMHAS utilizes the hysteresis mecha-

nism by dividing the VMs of BBUs into levels. Each

level will be activated when the number of used VMs

attains an activated threshold. Similarly, the level is

deactivated when the number of used VMs is less than

a deactivation threshold. Only the call-blocking prob-

ability was evaluated without considering the main

performance measure related to the energy consump-

tion that the scheme should enhance. It is the main

contribution of this paper in which we focus on evalu-

ating energy consumption. To show the effectiveness

of the VMHAS scheme, we compare the system’s en-

ergy consumption under this allocation strategy with

a new traditional scheme, called Virtual Machine Al-

location Strategy (VMAS), that does not consider the

VM sleep mode.

We use the Markov Reward Model (MRM) to

evaluate energy consumption measures in this work’s

proposed schemes. MRM (Katoen et al., 2005)

is a mathematical model used to describe and ana-

lyze the behavior of a system over time. It com-

bines a continuous-time Markov model and a set

of reward functions. We model CAC schemes by

Continuous-Time Markov Chains (CTMCs) (Kulka-

rni, 2016) and specify performance measures by Con-

tinuous Stochastic Reward Logic (CSRL) (Haverkort

et al., 2002). We quantify the steady-state perfor-

mance measures by checking CSRL formulas using

the PRISM model checker.

The work contains the following contributions:

1. We perform a quantitative analysis of the en-

ergy consumption computed over an MRM of the

hysteresis-based CAC scheme VMHAS.

2. We model a new traditional scheme VMAS with

an MRM and quantify the energy consumption

relative to this scheme.

3. We use the PRISM model checker to perform

modeling, speciﬁcation, and quantiﬁcation of the

steady-state reward measures of CAC schemes

(VMHAS and VMAS) by checking CSRL formu-

las.

4. We perform a comparative analysis of the en-

ergy consumption between VMHAS and VMAS

schemes. Results show that the VMHAS scheme

performs better than VMAS in saving energy un-

der low and medium trafﬁc.

The remainder of this paper is organized as fol-

lows. Section 2 is devoted to the related work. In sec-

tion 3, we introduce the MRM and CSRL logic. Sec-

tion 4 provides a formal modeling of CAC schemes.

Section 5 presents a formal speciﬁcation of steady-

state reward requirements. Section 6 gives numerical

results. Finally, section 7 concludes the paper.

2 RELATED WORK

Several works are related to the energy efﬁciency in

C-RAN. In (Sigwele et al., 2015), authors proposed a

green intelligent Trafﬁc and Resource Elastic Energy

CAC scheme called iTREE. In iTREE, the number

of used BBUs is reduced to equal the correct amount

of the trafﬁc load (Idle BBUs can then turn to sleep

mode). To minimize the energy consumption in C-

RAN, the authors proposed an approximation heuris-

tic bin-packing algorithm. The work in (Sigwele

et al., 2017) is an extension of (Sigwele et al., 2015),

in which authors proposed an energy reduction model

for C-RAN architecture that considers workload con-

solidation of BBUs located in the cloud. The idea of

the model is to act with a ﬁxed amount of BBUs and,

according to the demand, deactivate the idle BBUs

and reactivate them only in case of overloading. The

proposed model reduces the total consumption of en-

ergy and saves resources. In (Aldaeabool and Ab-

bod, 2017), authors proposed a strategy for switching

a BBU between On/Off modes according to the traf-

ﬁc load in the associated RRH. In fact, they proposed

a host server in the BBU pool that hosts a Modiﬁed

Best Fit Decreasing (MBFD) algorithm. They formu-

lated an optimization problem of reducing the num-

ber of BBUs with low loads by transferring them to

neighboring BBUs with the available capacity. Simu-

lation results demonstrated that the MBFD algorithm

performs better than traditional ones by minimizing

the number of active BBUs and the power consump-

tion for normalized trafﬁc load. The authors studied

in (Zhang et al., 2016) the BBU pool energy con-

sumption problem under a tidal trafﬁc scenario. By

developing heuristic algorithms, the number of active

BBUs is minimized. In (Sahu et al., 2017), a scheme

based on the graph method to reduce the energy con-

sumption in the BBU pool is proposed. Simulation

results show that the proposed algorithm reduces en-

ergy consumption by about 20%. In (Alhumaima

et al., 2018), authors introduced the problem of allo-

cating an optimal number of VMs to the cloud server.

They used Monte Carlo-based evolutionary algorithm

to reach the suboptimal number of VMs that opti-

mizes C-RAN energy efﬁciency. In (Mai et al., 2023),

the authors proposed an optimization model for sys-

tem energy efﬁciency that jointly allocates multiple

resources for C-RAN downlink transmission.

ENASE 2024 - 19th International Conference on Evaluation of Novel Approaches to Software Engineering

100

3 MARKOV REWARD MODEL

MRM (Katoen et al., 2005) is a mathematical model

used to describe and analyze the behavior of a sys-

tem over time. It combines the principles of Markov

chains and rewards to quantify the expected rewards

associated with different states in the system. In this

work, we consider a continuous-time Markov reward

model, which is a combination of a CTMC with a re-

ward function associated with states of the chain. For-

mally, a CTMC M is a tuple (S, R) where S is a set of

states and R : S × S → R

is the rate matrix (Kulka-

rni, 2016).

For a CTMC, there are two types of state proba-

bilities: transient probabilities, where the system is

considered at time t, and steady-state probabilities,

when the system reaches an equilibrium if it exists.

Let Π

′

) be the steady-state probability to be in

state s

′

starting from the initial state s. If M is er-

godic, Π

′

) exists, and it is independent of the ini-

tial distribution that we will denote by Π

′

). Let

be the steady-state probability vector. For S

′

⊆ S,

we denote Π

′

) the steady-state probability to be

in states of S

′

, Π

′

) =

∑

′

∈S

′

In order to specify and check performance re-

quirements over a RMM, we use CSRL (Haverkort

et al., 2002), which is an extension of Continu-

ous Stochastic Logic (CSL) (Aziz et al., 2000) by

adding constraints over rewards. CSL is a tempo-

ral logic that provides ample means to specify state

and path-based performance measures for CTMC but

does not support reward formulas. Therefore, we use

the CSRL, which contains reward operators that re-

fer to the stationary and transient behavior of the sys-

tem under consideration. This paper concentrates on

model-checking procedures for steady-state perfor-

mance measures. Indeed, we will use the steady-state

reward formula E

(φ), which asserts that the long run

reward rate in S

(States that satisfy the formula φ)

lies in J (J is an interval of real numbers).

Let ρ : S → R

be a reward structure that assigns

to each state s ∈ S a reward value ρ(s). The veriﬁca-

tion of this reward formula E

(φ) requires the compu-

tation of the steady-state distribution Π

of the con-

sidered M .

s |= E

(φ) iff

∑

′

∈S

′

) · ρ(s

′

) ∈ J

(1)

4 FORMAL MODELING OF THE

CONSIDERED CAC SCHEMES

This paper considers a C-RAN system with a cell con-

taining a certain number of RRHs and a centralized

BBU pool of K BBUs. Each BBU comprises a set of

VMs; it could serve each UE by generating a VM. We

suppose that each UE has its corresponding VM i.e. a

VM can only serve one UE. We also assume that all

BBUs are identical: They have the same performance

and they support the same number of VMs.

In the following, we will formally describe and

model the two CAC schemes (VMHAS and VMAS).

4.1 Formal Model of VMHAS Scheme

In this subsection, we recall from (Idi et al., 2022) the

basic concept of VMHAS and give its corresponding

Markov chain rate matrix.

4.1.1 VMHAS Description

The VMHAS scheme uses the hysteresis mechanism

to save energy in the C-RAN system. In fact, since

the energy consumption of an idle VM (activated VM

waiting for a call) is 60 to 80 percent of that of a

busy VM (VM occupied by a call) (Duan et al., 2015).

Therefore we use the hysteresis mechanism to divide

each BBU into three levels of VMs. A VM can be in

three modes: sleep, idle, or busy, as shown in Fig.1. A

VM in sleep mode is a deactivated VM and consumes

the lowest energy compared to its consumption in the

other modes.

Active

Idle BusySleep

Figure 1: VM modes.

Initially, for all BBUs, we suppose that VMs in

the ﬁrst level are activated and are in idle mode, while

the remaining VMs belonging to the other levels are

in sleep mode. When a call arrives, it will be assigned

to the available VM in the least-load BBU; there-

fore, it passes from idle to busy mode. By default,

when the current trafﬁc load is the same in all BBUs,

the ﬁrst BBU will serve the incoming call. When

the number of VMs in busy mode reaches the ﬁrst

hysteresis-activated threshold (V m

), the second level

will be activated (VMs of the second level pass from

sleep mode to idle mode). Similarly, the third level in

all BBUs will be activated when the number of busy

VMs reaches the second hysteresis-activated thresh-

old (V m

). The hysteresis mechanism supposes that

the deactivation thresholds differ from the activation

thresholds to avoid redundant activation/deactivation

of levels containing only VMs in idle mode. These

Steady-State Energy Consumption Evaluation in BaseBand Units Pool in Cloud Radio Access Network

101

thresholds: T

for the deactivation of the second level

and T

for the deactivation of the third level, are

respectively less than their corresponding activation

levels (V m

and V m

Let us recall that V

max

is the maximum number of

VMs in a BBU, and K is the total number of BBUs.

We assume that the call arrival process follows the

Poisson distribution with the following mean rates:

λ. We suppose that the holding time of VM is expo-

nentially distributed with mean 1/µ and independent

from the arrival process.

Based on these assumptions, the VMHAS scheme

(Idi et al., 2022) is modeled by a multidimen-

sional homogeneous CTMC. In the case of K-BBUs,

a state of the CTMC is represented by the tuple

.··· , i

,··· , i

,l), where i

represents the num-

ber of VMs in the busy mode in the k

BBU, where

1 ≤ k ≤ K. l represents the activated level of VMs

which can be equal to 1, 2, or 3.

4.1.2 Markov Chain for Two BBUs

To represent the VMHAS model, we use a labeled

Markov model in the case of two BBUs (K = 2), as

VMHAS is modeled by CTMC consisting of a large

number of components, where each dimension rep-

resents the number of active VMs in the BBU. We

recall from (Idi et al., 2022) the Markov state space

of VMHAS. We then present their rate matrix in the

particular case of two BBUs.

Markov Chain State Space. In the case of two

BBUs, the VMHAS scheme is modeled by a three-

dimensional CTMC. The obtained CTMC is com-

posed of three blocks relative to the number of lev-

els in the hysteresis mechanism. Therefore, the state

space S

′

is composed of three subsets: S

′

, S

′

and S

′

The subset S

′

(resp. S

′

) (see Eq.2 and Eq.3) contains

states relatives to the activation of the ﬁrst (resp. the

second) level of VMs. S

′

(see Eq.4) contains states

relatives to the activated VMs of the third block.

Therefore, the whole state space is given by:

′

= S

′

∪ S

′

∪ S

′

In state (i, j,l), i (resp. j) represents the number

of busy VMs in BBU

(resp. BBU

), and l represents

the activate level of VMs (1, 2 or 3):

′

= {(i, j,1);1 ≤ i ≤ V m

and 0 ≤ j ≤ i − 1}

∪ {(i, j,1);0 ≤ j ≤ V m

− 1 and 0 ≤ i ≤ j}

(2)

′

= {(i, j,2);T

≤ i ≤ V m

and 0 ≤ j ≤ i − 1}

∪ {(i, j,2);T

≤ j ≤ V m

− 1 and 0 ≤ i ≤ j}

(3)

′

= {(i, j,3);T

≤ i ≤ V

max

and 0 ≤ j ≤ i − 1}

∪ {(i, j,3);T

≤ j ≤ V

max

and 0 ≤ i ≤ j}

(4)

Markov Chain Rate Matrix. Transition rates

′

(s;(

l)) from the state s = (i, j, l) to the state

(

l) are deﬁned as:

• Markov Rates due only to the arrival of calls.

– Rates when the ﬁrst level is activated.

A call arrives and assigned to a VM in the ﬁrst

BBU.

′

(s = (i, j,1);(i + 1, j, 1)) = λ if

{

0 ≤ i ≤ j ≤ V m

− 1

}

A call arrives and assigned to a VM in the sec-

ond BBU.

′

(s = (i, j,1);(i, j + 1, 1)) = λ if

{

1 ≤ i ≤ V m

− 1; 0 ≤ j ≤ i − 1

}

{

i = V m

;0 ≤ j ≤ V m

− 2

}

A call arrives and assigned to a VM in the sec-

ond BBU and the second level of VMs is acti-

vated.

′

(s = (i, j,1);(i, j + 1, 2)) = λ if

{

i = V m

; j = V m

− 1

}

– Rates when the ﬁrst and the second level are

activated.

A call arrives and assigned to a VM in the ﬁrst

BBU.

′

(s = (i, j,2);(i + 1, j, 2)) = λ if

{

0 ≤ i ≤ j; T

≤ j ≤ V m

− 1

}

A call arrives and assigned to a VM in the sec-

ond BBU.

′

(s = (i, j,2);(i, j + 1, 2)) = λ if

{

≤ i ≤ V m

− 1; 0 ≤ j ≤ i − 1

}

{

i = V m

;0 ≤ j < V m

− 2

}

A call arrives and assigned to a VM in the sec-

ond BBU and the third level of VMs is acti-

vated.

′

(s = (i, j,2);(i, j + 1, 3)) = λ if

{

i = V m

; j = V m

− 1

}

– Rates when all levels are activated.

A call arrives and assigned to a VM in the ﬁrst

BBU.

′

(s = (i, j,3);(i + 1, j, 3)) = λ if

{

0 ≤ i ≤ j; T

≤ j ≤ V

max

}

ENASE 2024 - 19th International Conference on Evaluation of Novel Approaches to Software Engineering

102

A call arrives and assigned to a VM in the sec-

ond BBU.

′

(s = (i, j,3);(i, j + 1, 3)) = λ if

{

≤ i ≤ V

max

;0 ≤ j ≤ i − 1

}

{

i = V

max

;0 ≤ j < V

max

− 1

}

• Markov Rate due only to the departure of calls.

– Rates when the ﬁrst level is activated.

A VM is released from the ﬁrst BBU.

′

(s = (i, j,1);(i − 1, j, 1)) = iµ if

{

0 < i ≤ V m

;0 ≤ j ≤ V m

− 1

}

A VM is released from the second BBU.

′

(s = (i, j,1);(i, j − 1, 1)) = jµ if

{

0 < i ≤ V m

;0 ≤ j ≤ V m

− 1

}

– Rates when the second level is activated.

A VM is released from the ﬁrst BBU.

′

(s = (i, j,2);(i − 1, j, 2)) = iµ if

{

0 < i ≤ j; T

≤ j ≤ V m

− 1)

}

{

< i ≤ V m

;0 ≤ j ≤ i − 1

}

A VM is released from the second BBU.

′

(s = (i, j,2);(i, j − 1, 2)) = jµ if

{

≤ i ≤ V m

;0 < j ≤ i − 1

}

{

0 ≤ i ≤ j; T

< j ≤ V m

− 1

}

{

i = T

; j = T

}

Following the departure of a call, the second

level of VMs is deactivated.

′

(s = (i, j,2);(i, j − 1, 1)) = jµ if

{

0 ≤ i < T

; j = T

}

′

(s = (i, j,2);(i − 1, j, 1)) = iµ if

{

i = T

;0 ≤ j < T

}

– Rates when all levels are activated.

A VM is released from the ﬁrst BBU.

′

(s = (i, j,3);(i − 1, j, 3)) = iµ if

{

0 < i ≤ j; T

≤ j ≤ V

max

}

{

< i ≤ V

max

;0 ≤ j ≤ i − 1

}

A VM is released from the second BBU.

′

(s = (i, j,3);(i, j − 1, 3)) = jµ if

{

i = T

; j = T

}

{

≤ i ≤ V

max

;0 < j ≤ i − 1

}

{

0 ≤ i ≤ j; T

< j ≤ V

max

}

Following the departure of a call, the third

level of VMs is deactivated.

′

(s = (i, j,3);(i, j − 1, 2)) = jµ if

{

0 ≤ i < T

; j = T

}

′

(s = (i, j,3);(i − 1, j, 2)) = iµ if

{

i = T

;0 ≤ j < T

}

4.2 Formal Model of VMAS Scheme

In order to assess the effectiveness of the VMHAS

scheme, we have chosen to compare it with the

VMAS model, which does not consider VM sleep

mode. Indeed, in the VMAS scheme, all the VMs in

all BBUs are always activated. Therefore, when a call

arrives, it will be assigned to the available VM in the

least-load BBU. By default, when the current trafﬁc

load is the same in all BBUs, the ﬁrst BBU will serve

the incoming call.

4.2.1 Algorithmic Description

The algorithmic description of the VMAS scheme in

the case general of K-BBUs is presented in Algorithm

1. Notes that the arrival of different calls and the de-

parture of ongoing calls cannot trigger simultaneously

due to the Markovian hypothesis.

4.2.2 Markov Chain of VMAS

In the case of K-BBUs, a state of the CTMC is rep-

resented by (i

.··· , i

,··· , i

), where i

represents

the number of VMs in the busy mode in the k

BBU,

1 ≤ k ≤ K. Let us remark that a state in VMAS does

not contain the l component (as for VHMAS) because

a BBU is considered with one level of VMs that are

always activated.

Similarly to the VMHAS scheme, we formally

present the Markov chain of the VMAS in the case of

two BBUs. It is presented in Fig.2 and deﬁned with

the following state space:

′

= {(i, j); 1 ≤ i ≤ V

max

and 0 ≤ j ≤ i − 1}

∪ {(i, j); 0 ≤ j ≤ V

max

and 0 ≤ i ≤ j}

(5)

For VMAS, the transition rates R

′

(s;(

j)) from

the state s = (i, j) to the state (

j) are deﬁned as:

• A call arrives and assigned to a VM in the ﬁrst

BBU.

′

((i, j); (i + 1, j)) = λ if

{

0 ≤ i ≤ j < V

max

}

• A call arrives and assigned to a VM in the second

BBU.

′

((i, j); (i, j + 1)) = λ if

{

1 ≤ i ≤ V

max

;0 ≤ j ≤ i − 1

}

• A VM is released from the ﬁrst BBU.

′

((i, j); (i − 1, j)) = iµ if

{

0 < i ≤ V

max

;0 ≤ j ≤ V

max

}

• A VM is released from the second BBU.

′

((i, j); (i, j − 1)) = jµ if

{

0 ≤ i ≤ V

max

;0 < j ≤ V

max

}

Steady-State Energy Consumption Evaluation in BaseBand Units Pool in Cloud Radio Access Network

103

Algorithm 1: Proposed algorithm of VMAS scheme in

the case of K-BBUs.

K: Total number of BBUs;

max

: Max number of VMs in a BBU;

: Number of VMs in busy mode in the k

BBU where ( 1 ≤ k ≤ K);

/* All BBUs are empty. */

for (1 ≤ k ≤ K) do

= 0

/* Two call verification methods:

arrival and departure. */

CallA = CallArrived();

CallD = CallDeparture();

while (CallA or CallD) do

if CallA then

/* Put the call in the first

BBU. */

if (∀ 1 ≤ k ≤ K,V

= V

... = V

) then

= V

+ 1;

else

/* Put the call in the

least loaded BBU. */

if (∀ 1 ≤ k ≤ K,V

< V

max

) then

= min V

;

= V

+ 1;

else

/* Call rejected: all VMs

in all BBUs occupied

(∀ 1 ≤ k ≤ K,V

= V

max

Reject call ;

if CallD then

/* Function returning a BBU from

which a call departed. */

k = departedcall();

= V

− 1;

CallA = CallArrived();

CallD = CallDeparture();

0,0

1,0

1,1 0,1

2µ

2,1 2,0

2µ

Vmax,Vmax-1

Vmax,Vmax-2 Vmax,0

(Vmax-2)µ

Vmax-1,Vmax

0,Vmax

Vmaxµ

(Vmax-1)µ

Vmaxµ

Vmax,Vmax

Vmaxµ

Figure 2: CTMC of the proposed VMAS.

5 FORMAL SPECIFICATION OF

STEADY-STATE REWARD

REQUIREMENTS

We use E

(true) formula, which belongs to CSRL

logic (Haverkort et al., 2002), to express QoS require-

ments. Hence, we enrich CTMC models that we de-

veloped on PRISM with reward functions. The veriﬁ-

cation of the reward formula E

(φ) requires the com-

putation of the steady-state distribution Π

of the

considered CTMC (see Eq.1).

5.1 Speciﬁcation for VMHAS Scheme

In order to check steady-state reward formulas to

quantify the steady-state energy consumption (for

BBU

, BBU

, and the whole system), the mean num-

ber of idle VMs, and the mean number of sleep VMs:

we enrich PRISM with the following reward func-

tions. These reward functions are written for K-BBUs

and 2-BBUs.

5.1.1 Energy Consumption

We note by E

the energy consumption of a sleepy

VM, E

the energy consumption of an idle VM, E

the energy consumption of a busy VM, and E

the

additional energy consumption of a VM caused by its

activation.

In the case of K-BBUs, the energy consump-

tion function E for the proposed VMHAS is deﬁned

by: E : S → R

≥0

,∀s = (i

.··· , i

,··· , i

,l) → E(s),

where E(s) associated to s is equal to:

E(s) =











∑

k=1

+ E

(KV m

−

∑

k=1

)

+ E

K(V

max

−V m

) if l = 1

∑

k=1

+ E

(KV m

−

∑

k=1

)

+ E

K(V

max

−V m

) if l = 2

∑

k=1

+ E

(KV

max

−

∑

k=1

) if l = 3

In order to evaluate the effect of activating VMs

in each level, we associate the activation transitions

of level 2 and level 3 with the cost in terms of energy.

For the activation transition of level 2, we associate

(V m

−V m

), and for the activation transition of

level 3, we associate KE

max

−V m

). These addi-

tional costs are counted when evaluating the energy

consumption.

In the case of 2-BBUs, the energy consumption

′

of the proposed VMHAS is given as follows: E

′

→ R

≥0

,∀s = (i, j, l) → E

′

(s) where E

′

(s) is associ-

ENASE 2024 - 19th International Conference on Evaluation of Novel Approaches to Software Engineering

104

ated to the state s deﬁned by:

′

(s) =











(i + j) + E

(2V m

− (i + j))

+ E

2(V

max

−V m

) if l = 1

(i + j) + E

(2V m

− (i + j))

+ E

2(V

max

−V m

) if l = 2

(i + j) + E

(2V

max

− (i + j)) if l = 3

(6)

We associate the cost 2E

(V m

− V m

) (resp.

max

−Vm

)) for the activation transition of level

2 (resp. level 3).

Additionally, we are interested in evaluating the

energy consumption in each BBU. Therefore we de-

ﬁne two functions E

′

and E

′

. E

′

: S

′

→ R

≥0

,∀s =

(i, j, l) → E

′

(s) which associates to each state s the

energy consumption of BBU

in this state. Similarly,

′

: S

′

→ R

≥0

,∀s = (i, j,l) → E

′

(s) which associates

to each state s the consumption energy of BBU

in s.

These values E

′

(s) and E

′

(s) are deﬁned as follow-

ing:

′

(s) =











i + E

(V m

− i) + E

max

−V m

)

if l = 1

i + E

(V m

− i) + E

max

−V m

)

if l = 2

i + E

max

− i)

if l = 3

(7)

′

(s) =











j + E

(V m

− j) + E

max

−V m

)

if l = 1

j + E

(V m

− j) + E

max

−V m

)

if l = 2

j + E

max

− j)

if l = 3

(8)

5.1.2 Number of Idle VMs

In order to evaluate the number of idle VMs, we de-

ﬁne the reward function related to this measure. We

ﬁrst give this function in the case of K-BBUs, I. Then

we write the function in the case of 2-BBU, I

′

For K-BBU, I : S → R

≥0

, ∀s =

.··· ,i

,··· ,i

,l) → I(s). I(s) is deﬁned as

following:

I(s) =







KV m

−

∑

k=1

if l = 1

KV m

−

∑

k=1

if l = 2

max

−

∑

k=1

if l = 3

For 2-BBUs, I

′

: S

′

→ R

≥0

,∀s = (i, j, l) → I

′

(s).

′

(s) is deﬁned as following:

′

(s) =







2V m

− (i + j) if l = 1

2V m

− (i + j) if l = 2

max

− (i + j) if l = 3

(9)

5.1.3 Number of Sleep VMs

To evaluate the mean number of sleep VMs, we deﬁne

the reward function related to this measure. We give

the formal deﬁnition of this function in the case of

K-BBUs (L) and in the case of 2-BBUs (L

′

In the case of K-BBUs, L is deﬁned by: L :

S → R

≥0

, ∀s → L(s) that associates to each state

s = (i

.··· ,i

,··· ,i

,l), the number of sleep VMs

in s:

L(s) =







K(V

max

−V m

) if l = 1

K(V

max

−V m

) if l = 2

0 if l = 3

For 2-BBUs and by replacing K by 2, L

′

: S

′

→

≥0

,∀s = (i, j, l) → L

′

(s). L

′

(s) is deﬁned by:

′

(s) =







2(V

max

−V m

) if l = 1

2(V

max

−V m

) if l = 2

0 if l = 3

(10)

5.2 Speciﬁcation for VMAS Scheme

To check the steady-state reward formulas to evalu-

ate the mean energy consumption and the mean num-

ber of idle VMs for the VMAS scheme, we enrich

the model of VMAS, implemented in PRISM, with

the following reward functions. We deﬁne these func-

tions for K-BBUs and 2-BBUs.

5.2.1 Energy Consumption

The function related to the energy consumption for

VMAS scheme in the case of K-BBUs is deﬁned by:

E : S → R

≥0

, ∀s → E(s) where E(s) is associated

to s = (i

,··· ,i

) as following:

E(s) = E

∑

k=1

+ E

(KV

max

−

∑

k=1

)

In the case of 2-BBUs the reward function is:

′

: S

′

→ R

≥0

, ∀s → E

′

(s) where E

′

(s) is associ-

ated to s = (i, j):

′

(s) = E

(i + j) + E

(2V

max

− (i + j)) (11)

Steady-State Energy Consumption Evaluation in BaseBand Units Pool in Cloud Radio Access Network

105

5.2.2 Number of Idle VMs

The reward function associated to the evaluation of

the mean number of idle VMs is deﬁned for K-BBUs

and 2-BBUs as following.

We deﬁne, for K-BBUs, the reward function I :

S → R

≥0

, ∀s → I(s) that associates to each state s =

,··· ,i

) the number of idle VMs:

I(s) = KV

max

−

∑

k=1

For 2-BBUs, the reward function is I

′

: S

′

→ R

≥0

∀s → I

′

(s) that associates to each state s = (i, j) the

number of idle VMs:

′

(s) = 2V

max

− (i + j) (12)

6 NUMERICAL RESULTS

In this section, we present numerical results to show

the effectiveness of VMHAS scheme. These results

are obtained by verifying CSRL formulas under the

VMHAS model and compared with VMAS (a model

which does not consider the sleep mode). In order to

construct and solve the studied models, we use the

probabilistic model checker PRISM (Kwiatkowska

et al., 2011). This tool is a high-level modeling lan-

guage, and formulas are checked automatically. The

numerical results in this section are obtained with the

parameters presented in Table 1.

6.1 VMHAS Performance

This subsection is devoted to evaluating the perfor-

mance of VMHAS scheme in terms of the steady-

state number of sleep VMs and the steady-state en-

ergy consumption of each BBU.

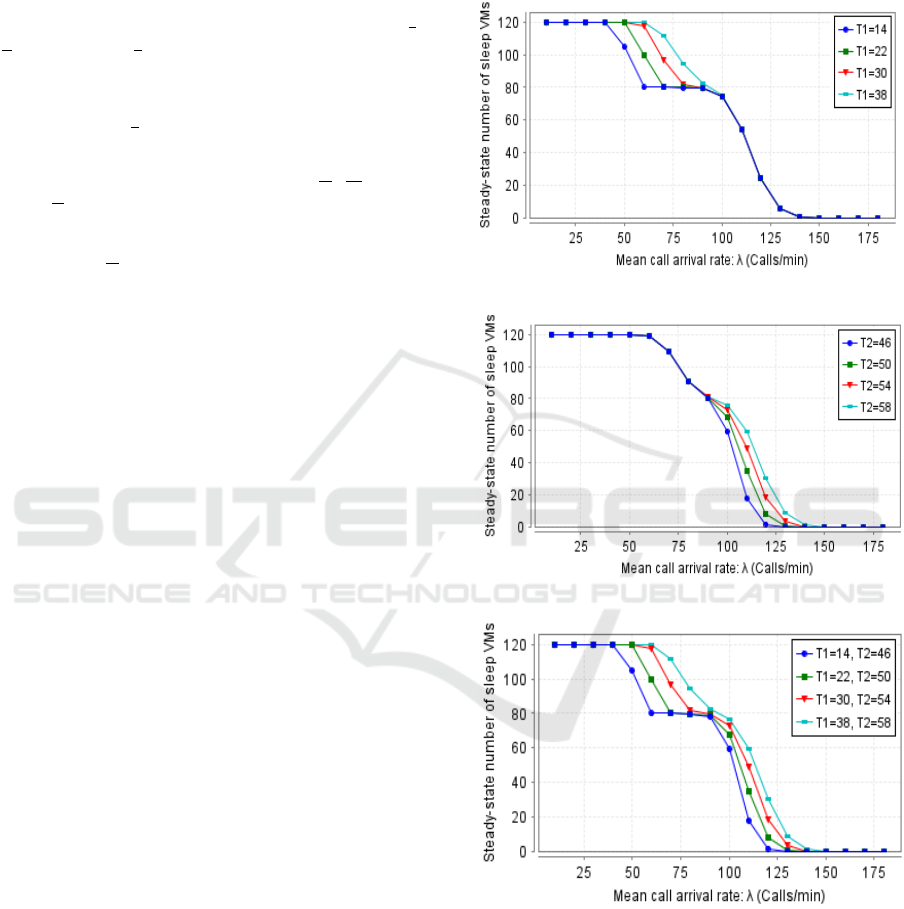
Fig.3 shows the steady-state number of sleep VMs

depending on the hysteresis deactivating thresholds

and T

) and the trafﬁc load λ. The correspond-

ing reward function to this measure is L

′

, presented in

Eq.10.

We can ﬁrst remark that all curves are decreasing

because when the arrival of calls increases, VMs pass

from sleep mode to an activated mode to serve calls,

and therefore the number of sleep VMs decreases. In

Fig.3(a), we can observe that the highest curve cor-

responds to the highest value of T

. This result is

explained by the fact that when we increase T

(be-

comes near to V m

), the second level will close fre-

quently, and therefore VMs of the second level fre-

quently pass to the sleep mode. The same results can

be seen through Fig.3(b) when varying T

. In Fig.3(c),

we illustrate the mean number of sleep VMs when we

vary T

and T

. We can observe that the highest curve

is related to the highest values of T

and T

, which

conﬁrms the results of Fig.3(a) and Fig.3(b).

(a) Varying T

(b) Varying T

and T

Figure 3: Steady-state number of sleep VMs.

In order to evaluate the steady-state energy con-

sumption in BBU

and in BBU

by considering dif-

ferent trafﬁc loads, we vary the arrival rate λ of calls

from 10 to 180 calls/min. The corresponding reward

function to these measures are E

′

for BBU

(see Eq.7)

and E

′

for BBU

(see Eq.8).

ENASE 2024 - 19th International Conference on Evaluation of Novel Approaches to Software Engineering

106

Table 1: Experimental Parameters.

Parameters Value

K: Total number of BBUs. 2

V max: Max number of VMs in a BBU. 100

V m

: Hysteresis Level 3 activating threshold. 60

V m

: Hysteresis Level 2 activating threshold. 40

: Hysteresis Level 3 deactivating threshold. 56

: Hysteresis Level 2 deactivating threshold. 36

1/µ: Mean VM holding time (per minute). 1

: Energy consumption of a sleeping VM(per mJ). 0.2

: Energy consumption of an idle VM (per mJ). 0.4

: Energy consumption of a busy VM (per mJ). 0.5

: Additional energy consumption of a VM caused by activation (per mJ). 2

Table 2: Steady-state energy consumption in each BBU.

Steady-state energy consumption (mJ)

Call arrival rate: λ (calls/min) BBU

BBU

10.0 28.521550765802747 28.478449234200447

20.0 29.022981186839626 28.977018814554246

30.0 29.52356702449307 29.476432992294825

40.0 30.023902006144166 29.976125945301177

50.0 30.550625554609844 30.502443296489755

60.0 32.77501023996112 32.72654758056934

70.0 42.53185589385637 42.48318793333326

80.0 45.26724652233278 45.21842171268469

90.0 40.17329401118137 40.12434544337346

100.0 47.250198654799775 47.20114993720736

110.0 67.23262000827796 67.18348857666923

120.0 71.25853230740609 71.20933140571053

130.0 57.790673358614654 57.74141328345368

140.0 49.39830475913209 49.34899371437636

150.0 47.79158282943648 47.74222902769638

160.0 48.04006386928369 47.99069960088592

170.0 48.5055002528775 48.45631940730138

180.0 48.931289400383555 48.882897731887205

It can be observable through Table 2 that when

λ does not exceed 60 calls, the energy consumption

increases slightly in each BBU. This is expected be-

cause only the ﬁrst level of VMs in two BBUs is acti-

vated to accept calls. However, the remaining two lev-

els are deactivated because they are not needed. When

λ = 70, the energy consumption shows a remarkable

increase; this is explained by the energy consumption

due to the opening of the second level of VMs (see

the ﬁrst two boxes: λ = 70 and λ = 80). In addition,

each BBU consumes the maximum energy when the

VMs of the third level are activated (see the second

two boxes: λ = 110 and λ = 120).

As observed, the energy consumption of BBU

slightly lower than the energy consumption of BBU

This slight difference is explained by the fact that

when the call arrives, it will be assigned to the avail-

able VM in the least-load BBU. By default, when the

current trafﬁc load is the same in the two BBUs, the

ﬁrst BBU will serve the incoming call. All that shows

that VMHAS schemes ensures the load balancing be-

tween BBUs.

6.2 Performance Comparison Between

VMHAS and VMAS

In this subsection, we perform a comparative analysis

of the steady-state number of idle VMs and the energy

consumption between VMHAS and VMAS schemes.

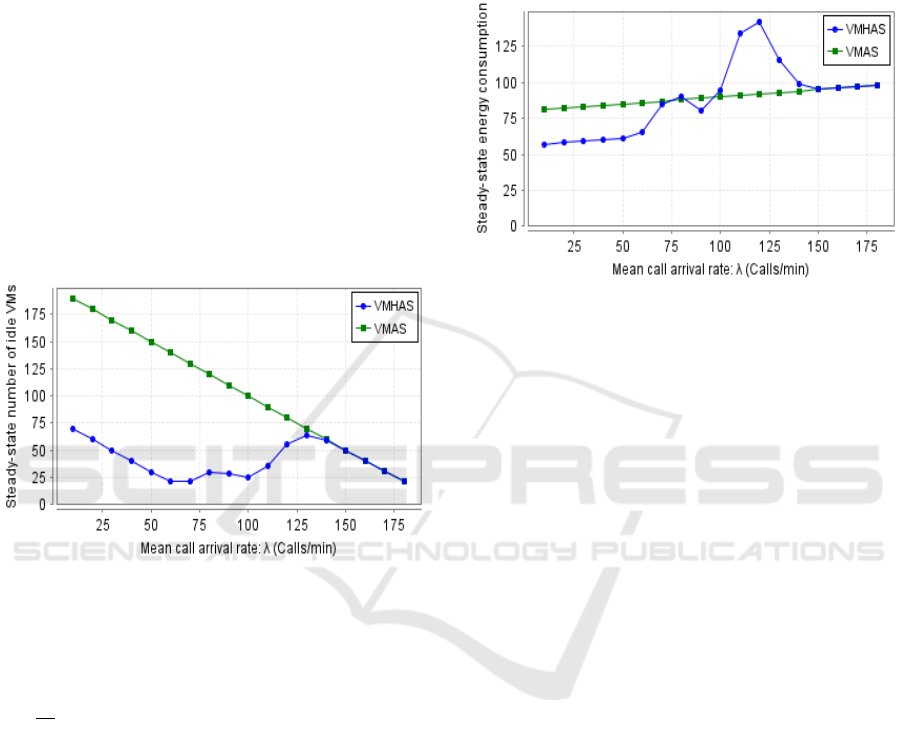
Fig.4 illustrates the steady-state number of idle

VMs (activated VMs waiting for calls) in VMHAS

and VMAS schemes under different trafﬁc loads.

Their corresponding reward functions are deﬁned re-

spectively by I

′

(see Eq.9) and I

′

(see Eq.12). It can

be seen that the curve of VMAS is always higher

Steady-State Energy Consumption Evaluation in BaseBand Units Pool in Cloud Radio Access Network

107

than that of VMHAS and is decreasing because it is a

model that does not consider sleep mode. VMAS is

a scheme in which VMs can be only in two modes:

busy (VMs occupied by calls) or idle; therefore, this

explains the negative slope of its corresponding linear

curve.

For VMHAS, we can see that when the trafﬁc load

in the system does not exceed 60 calls/min, we ob-

tain a decreasing curve because one level of VMs in

two BBUs can support all UEs. The increase of idle

VMs twice (see the two peaks) is caused by the ac-

tivation of VMs of the second (resp. the third level).

Once level three is activated, the two CAC schemes

will have the same number of idle VMs because there

are no VMs in sleep mode in VMHAS. Clearly, the

VMHAS scheme outperforms VMAS because it ad-

justs the number of VMs needed to support the trafﬁc

load in the system.

Figure 4: Steady-state number of idle VMs.

We compare the steady-state energy consumption

between VMHAS and VMAS schemes by consider-

ing different trafﬁc loads. Their corresponding reward

functions are respectively deﬁned by E

′

(see Eq.6)

and E

′

(see Eq.11). It can be observable through Fig.

5 that when the trafﬁc load increases, the mean energy

consumption for both VMHAS and VMAS schemes

increases. This is trivial because when the number

of calls increases, the number of busy VMs increases

too. The VMHAS scheme consumes less energy than

the VMAS scheme due to the utilization of fewer

number of VMs during the low-trafﬁc periods (λ of

calls from 10 to 65 calls per minute). On the other

hand, the VMAS scheme consumes more energy than

expected because all VMs in the two BBUs are always

active. It is also remarkable that in the curve of the

VMHAS scheme, the ﬁrst peak of energy consump-

tion is shown when the second level of VMs activated;

its energy consumption stays better than the VMAS

scheme. Nevertheless, as the offered trafﬁc increases

(arrival rate λ of calls is from 110 to 120), the second

peak of energy consumption is shown. As a result,

the curve of VMHAS becomes above that of VMAS;

this is justiﬁable by the additional energy caused by

the activation of 80 VMs. Then, from λ = 150, both

schemes have the same energy consumption because

all VMs are activated.

Figure 5: Steady-state energy consumption.

7 CONCLUSION

In this paper, we have performed a quantitative anal-

ysis of the energy consumption computed over two

schemes named Virtual Machine Hysteresis Alloca-

tion Strategy (VMHAS) and Virtual Machine Allo-

cation Strategy (VMAS) for C-RAN. The VMHAS

scheme consists of switching the idle VMs to sleep

mode to save energy, but the VMAS scheme allocates

VMs without considering the sleep mode. We mod-

eled schemes with MRMs to evaluate measures re-

lated to energy consumption. We used the PRISM

model checker to perform modeling, speciﬁcation,

and quantiﬁcation of the steady-state reward measures

of VMHAS and VMAS schemes by checking CSRL

formulas. Results show that the VMHAS scheme per-

forms better than the VMAS scheme in saving en-

ergy under low and medium trafﬁc. Furthermore, it

allowed load balancing between the BBUs. In the fu-

ture, we will extend this work by using Discrete-Time

Markov Decision Processes (MDPs) to enhance the

performance and energy efﬁciency in the resource al-

location scheme using the hysteresis and the migra-

tion mechanisms.

REFERENCES

Aldaeabool, S. R. and Abbod, M. F. (2017). Reducing

power consumption by dynamic BBUS-RRHS alloca-

tion in C-RAN. In 25th Telecommunication Forum

(TELFOR), pages 1–4. IEEE.

ENASE 2024 - 19th International Conference on Evaluation of Novel Approaches to Software Engineering

108

Alhumaima, R. S., Ahmed, R. K., and Al-Raweshidy, H. S.

(2018). Maximizing the energy efﬁciency of virtual-

ized C-RAN via optimizing the number of virtual ma-

chines. IEEE Transactions on Green Communications

and Networking, 2(4):992–1001.

Aziz, A., Sanwal, K., Singhal, V., and Brayton, R.

(2000). Model-checking continuous-time markov

chains. ACM Transactions on Computational Logic

(TOCL), 1(1):162–170.

Checko, A., Christiansen, H. L., Yan, Y., Scolari, L., Kar-

daras, G., Berger, M. S., and Dittmann, L. (2014).

Cloud RAN for mobile networks—A technology

overview. IEEE Communications surveys & tutorials,

17(1):405–426.

Duan, L., Zhan, D., and Hohnerlein, J. (2015). Optimiz-

ing cloud data center energy efﬁciency via dynamic

prediction of CPU idle intervals. In IEEE 8th Interna-

tional Conference on Cloud Computing, pages 985–

988. IEEE.

Feng, M., Mao, S., and Jiang, T. (2017). Base station

ON-OFF switching in 5G wireless networks: Ap-

proaches and challenges. IEEE Wireless Communi-

cations, 24(4):46–54.

Haverkort, B., Cloth, L., Hermanns, H., Katoen, J.-P., and

Baier, C. (2002). Model checking performability

properties. In Proceedings International Conference

on Dependable Systems and Networks, pages 103–

112. IEEE.

Idi, M., Youn

es, S., and Robbana, R. (2022). Performance

evaluation of call admission control strategy in cloud

radio access network using formal methods. In Inter-

national Conference on Software and Data Technolo-

gies.

Katoen, J.-P., Khattri, M., and Zapreevt, I. (2005). A

markov reward model checker. In Second Interna-

tional Conference on the Quantitative Evaluation of

Systems (QEST’05), pages 243–244. IEEE.

Kulkarni, V. G. (2016). Modeling and analysis of stochastic

systems. Chapman and Hall/CRC.

Kwiatkowska, M., Norman, G., and Parker, D. (2011).

PRISM 4.0: Veriﬁcation of probabilistic real-time sys-

tems. In International conference on computer aided

veriﬁcation, pages 585–591. Springer.

Mai, Z., Chen, Y., Xie, Y., and Chen, G. (2023). An en-

ergy efﬁciency optimization jointing resource alloca-

tion for delay-aware trafﬁc in fronthaul constrained C-

RAN. Wireless Networks, 29(1):353–368.

Sahu, B. J., Dash, S., Saxena, N., and Roy, A. (2017).

Energy-efﬁcient BBU allocation for green C-RAN.

IEEE Communications Letters, 21(7):1637–1640.

Sigwele, T., Alam, A. S., Pillai, P., and Hu, Y. F. (2017).

Energy-efﬁcient cloud radio access networks by cloud

based workload consolidation for 5G. Journal of Net-

work and Computer Applications, 78:1–8.

Sigwele, T., Pillai, P., and Hu, Y. F. (2015). iTREE: In-

telligent trafﬁc and resource elastic energy scheme for

Cloud-RAN. In 2015 3rd International Conference on

Future Internet of Things and Cloud, pages 282–288.

IEEE.

Yu, N., Song, Z., Du, H., Huang, H., and Jia, X. (2017).

Multi-resource allocation in cloud radio access net-

works. In IEEE International Conference on Com-

munications (ICC), pages 1–6. IEEE.

Zhang, J., Ji, Y., Xu, X., Li, H., Zhao, Y., and Zhang, J.

(2016). Energy efﬁcient baseband unit aggregation in

cloud radio and optical access networks. Journal of

Optical Communications and Networking, 8(11):893–

901.

Steady-State Energy Consumption Evaluation in BaseBand Units Pool in Cloud Radio Access Network

109