Tail-Latency Aware and Resource-Efficient Bin Pack Autoscaling for

Distributed Event Queues

Mazen Ezzeddine

1,2

, Françoise Baude

and Fabrice Huet

Université Côte d’Azur, CNRS, I3S Nice, France

HighTech Payment Systems, HPS, Aix en Provence, France

Keywords: Distributed Queue, Bin Pack, Tail Latency, Dynamic Resource Provisioning, Autoscaler, Rebalancing, Kafka,

Event Consumer Group, Message Broker.

Abstract: Distributed event queues are currently the backbone for many large-scale real-time cloud applications

including smart grids, intelligent transportation, and health care monitoring. Applications (event consumers)

that process events from distributed event queue are latency-sensitive. They require that a high percentile of

events be served in less than a desired latency. Meeting such desired latency must be accomplished at low

cost in terms of resources used. In this research, we first express the problem of targeting resource-efficient

and latency-aware event consuming from distributed event queues as a bin pack problem. This bin pack

depends on the arrival rate of events, the number of events in the queue backlog, and the maximum

consumption rate of event consumers. We show that the proposed bin pack solution outperforms a linear

autoscaling solution by 3.5% up to 10% in terms of latency SLA. Furthermore, we discuss how dynamic event

consumers provisioning in distributed event queues necessitates a blocking synchronization protocol. We

show that this blocking synchronization protocol is at conflict with meeting a desired latency for high

percentile of events. Hence, we propose an extension to the bin pack autoscaler logic in order to reduce the

tail latency caused by the events accumulated during the blocking synchronisation protocol.

1 INTRODUCTION

Distributed event queues have emerged as a central

component in building large scale and real time cloud

applications. They are currently being used in many

latency-sensitive cloud applications such as recording

and analyzing web accesses for recommendations and

ad placement (Goodhope et al., 2014), health care

monitoring (Al-Aubidy et al., 2017), fraud detection

(Mohammadi et al., 2018), smart grids (Albano et al.,

2015) and intelligent transportation (Fernández-

Rodríguez et al., 2017). Furthermore, distributed

event queues are the backbone for the event driven

microservices software architectural style where an

application is composed of several small services

communicating by exchanging events across a

distributed event queue (Laigner et al., 2020;

Pallewatta et al., 2022; Xiang et al., 2021). As such,

many cloud providers already offer event queue as a

service (Amazon Kinesis, 2023; Azure Event Hub,

2023; Google Cloud Pub/Sub, 2023).

A distributed event queue is composed of several

partitions or sub-queues deployed over a cluster of

servers. Applications (event consumers) that pull and

process events from distributed queues are latency-

sensitive. They require that a high percentile of events

is processed in less than a desired latency. Otherwise,

providing end-users with experience beyond such

desired latency might result in million dollars

reduction in revenues as indicated by several tech

giants (Eaton, 2012). Overprovisioning of resources

to meet the desired latency is not the optimal solution

since it incurs large monetary cost for the service

provider. Therefore, architecting solutions for

resource-efficient and latency-aware event

consumers from distributed event queues is of

paramount importance. As we describe throughout

this paper, latency-aware and cost-efficient (cost-

efficient and resource-efficient will be used

interchangeably) event consumers denotes two

simultaneous objectives to be met by the designed

architecture : (1) ensuring that the latency for a high

percentile of events served by event consumers is less

than a desired latency, that is, reduce tail latency

(Dean and Barroso, 2013) and (2) the designed

architecture is able to dynamically provision and

Ezzeddine, M., Baude, F. and Huet, F.

Tail-Latency Aware and Resource-Efﬁcient Bin Pack Autoscaling for Distributed Event Queues.

DOI: 10.5220/0012630100003711

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 14th International Conference on Cloud Computing and Services Science (CLOSER 2024), pages 50-64

ISBN: 978-989-758-701-6; ISSN: 2184-5042

deprovision resources (event consumers replicas) so

that the usage of resources is minimized while

guaranteeing (1).

Solutions offered by cloud providers and by on-

premises cluster orchestrators such as Kubernetes

(KEDA, 2023) to scale event consumer replicas when

a certain metric reaches a certain threshold are not

satisfactory. In essence, these autoscalers assume a

linear relationship between the current value of a

monitored metric and the desired value of that metric

to compute the needed number of replicas. Hence, a

linear autoscaler for event queues emulating cloud

autoscalers will use the ratio of the arrival rate of

events to the maximum consumption rate per replica

to get the needed number of replicas. However, the

number of needed replicas meets a bin pack solution

rather than a linear one as we describe throughout this

paper. Furthermore, Kubernetes and cloud

autoscalers are not middleware/platform aware. As

such, they do not recommend or participate in the

assignment of the provisioned event consumer

replicas to partitions. Rather, they rely on the

distributed event queue middleware logic for

assigning partitions to event consumers. This might

result in scenarios where event consumer replicas

might not be assigned to partitions in a latency-aware

manner, even if enough replicas are provisioned by

such autoscalers. A latency-aware and resource-

efficient autoscaler for distributed event queue must

provision just enough replicas to achieve the desired

latency, and it must recommend to the distributed

event queue middleware the assignment of partitions

to the provisioned event consumer replicas in order to

guarantee the desired latency.

As we discuss throughout this paper, in distributed

event queues aiming at high percentile latency SLA

is not straightforward even in the presence of a

dynamic resource provisioning mechanism. This is

because reducing the percentage of events that exhibit

a latency beyond the desired latency (that is, the tail

latency) while at the same time dynamically

provisioning and deprovisioning of resources (event

consumer replicas) are two objectives which are at

conflict in distributed event queues. This stems from

the fact that scaling up or down event consumers

necessitates a blocking synchronization protocol to

distribute the load of the events waiting in queues

among the provisioned event consumer replicas.

During this synchronization protocol, which is also

called rebalancing or assignment (Blee-Goldman,

2020; Narkhede et al., 2017) all the event consumer

replicas will stop processing events, thus eventually

contribute to a larger tail latency and less percentile

of latency SLA guarantee. The increase in the tail

latency results from the fact that all the events

arriving during the synchronization protocol

execution will exhibit a relatively higher latency as

compared to the latency of events processed during

normal operation of the system. Clearly, the relation

between the desired latency SLA and the time of the

blocking rebalancing protocol dictates if there is some

space for regularly and dynamically modifying or not

the number of event consumers. If the rebalancing

time is very high compared to the desired latency

SLA, obviously the only deployment that can ensure

the desired latency SLA for a high percentile of

events is one where all replicas would be provisioned

from start-up time (an overprovisioned solution).

Even if this is at a cost considered to be non-optimal

as some of the ready replicas may not operate all the

time. But if the ratio of the desired latency SLA to the

rebalancing time is greater than 1, a good tradeoff can

be sought: a just-needed number of replicas deployed

while ensuring a small tail-latency. Our research

contributes a solution towards finding such a tradeoff,

still prioritizing the latency SLA guarantee over cost

reduction.

To achieve this, we first formulate the problem of

autoscaling event consumers from distributed event

queues to meet a desired latency as a bin pack

problem: it depends on the arrival rate of events into

queues which can even be skewed, the number of

events in the queues backlog, and the maximum

consumption rate of the event consumers. We

propose an appropriate heuristic (Least Loaded) to

solve the bin pack problem in polynomial time and to

maintain a balanced load in terms of events served by

each event consumer replica. As the synchronization

protocol upon consumer replica (un-)provisioning is

blocking, we extend our initial bin pack solution by

taking into account new events that will accumulate

during the autoscaling. We also propose several

recommendations on the configurations of the

rebalancing protocol that contribute to a lower tail

latency. We first experimentally show that on some

selected workloads, our bin pack solution

outperforms a linear autoscaling solution by 3.5% up

to 10% in terms of latency guarantee in a first system

setting where rebalancing time overhead is way

smaller than the desired latency SLA. Then, under

other and less favourable system settings regarding

rebalancing overhead, we show that the proposed bin

pack extension applied to the same workloads results

in a lower tail latency, and thus better latency SLA,

but at higher resource utilization cost.

To our knowledge, latency-aware and dynamic

resource provisioning for distributed event queues in

the presence of a blocking resource synchronization/

Tail-Latency Aware and Resource-Efﬁcient Bin Pack Autoscaling for Distributed Event Queues

rebalancing protocol has not yet been addressed in the

literature.

2 CONTEXT - BACKGROUND

We target a general event driven architecture where

applications (that is, event consumers) pull and

process events from distributed event queues. As

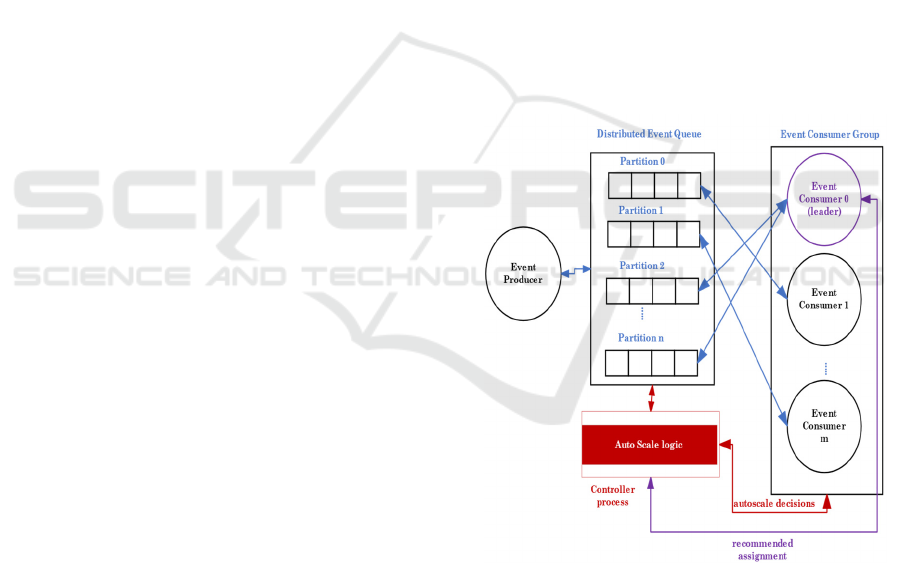
shown in Figure 1, a distributed event queue is

composed of several partitions (sub-queues)

deployed over a cluster of servers. A producer

application generates events and writes them into a

certain partition of the distributed queue according to

a partitioning strategy. An event consumer group is a

set of event consumers that jointly and cooperatively

consume events from the partitions of the distributed

queue. Generally, for a distributed event queue, we

have n partitions and m consumers that read and

process events. The (re-) assignment of the m

consumers to the n partitions (or inversely) is

performed through a blocking synchronization

protocol. This synchronization protocol is called

rebalancing (or assignment). The terms

synchronization, rebalancing and assignment will be

used interchangeably thereafter. As stated earlier, the

rebalancing protocol represents a short time of

unavailability during which all event consumers will

stop processing events. Rebalancing might happen

several times during the lifetime of an event

consumer group such as when the group is initiated,

or when a consumer leaves or joins the group. Hence,

every scale action to add or remove event consumers

to/from the consumer group will trigger a rebalancing

process. The rebalancing duration is among the

metrics exposed by the distributed event queue

middleware, and hence, it can be measured

dynamically. As shown in Figure 1, each partition of

the distributed event queue must be assigned to

exactly one event consumer. Consumers, on the other

hand, can be assigned several partitions.

Event consumers operate in group. The

management of the event consumer group is

performed by a special process called consumer

group coordinator. The coordinator process is a part

of the distributed event queue middleware. It

appropriately handles requests sent by event

consumers to join or leave the group. Once registered

with the group, event consumers keep membership in

the group by sending periodic heartbeats to the

coordinator.

Moreover, the consumer group coordinator is

responsible of the execution of the

assignment/rebalancing protocol. As part of the

protocol execution, the coordinator offloads the

assignment logic to one of the event consumers

namely the leader. Next, the coordinator takes the

assignment proposed by the leader and inform each

member (event consumer replica) of the group about

its assigned partitions. Figure 1 shows the added

Controller process which runs periodically the

proposed bin pack dynamic scale logic to add or

remove event consumer replicas. Also, as part of our

proposed autoscaling logic, notice in Figure 1 how the

leader consumer calls the Controller for its

recommended latency-aware consumers-partitions

assignment as per the result of the bin pack.

Finally, it is noteworthy that we use Kafka

(Narkhede et al., 2017) as a distributed event queue.

Kafka is by far one of the most used distributed event

queues in the industry. Nevertheless, we believe that

the discussion and techniques used in this work are to

a broad extent generalizable to other distributed event

queues and not limited to Kafka. In this context, the

experimental use case employed in this research is a

simplified version of a Kafka-based payment

authorization system used in production.

Figure 1: A distributed event queue with an event producer

and event consumer group. Notice the assignment of

partitions to consumers. Shown also in red the Controller

process which runs the bin pack based autoscale logic and

recommends the resulting bin pack partitions-consumers

assignment to the consumer group leader.

CLOSER 2024 - 14th International Conference on Cloud Computing and Services Science

3 RELATED WORK

Performance SLAs are hard to guarantee. Cloud

providers rarely offer end-to-end performance

guarantee or focus on overprovisioning of resources

and isolation of services to meet a desired

performance SLA (Baset et al., 2012; Qu et al., 2018).

To our knowledge none of the cloud providers

offering distributed queue as a service provides

performance SLA (e.g., latency) guarantee for events

consuming and processing. Furthermore, none of the

existing, widely used event queues, such as MQTT

ActiveMQ

, RabbitMQ

and Kafka (Narkhede et al.,

2017), provides an SLA latency guarantee for event

processing.

Nevertheless, cloud providers offering distributed

event queues as a service provide autoscalers to add

or remove event consumer replicas depending on the

value of a monitored metric. In essence, these

autoscalers assume a linear relationship between the

current value of the monitored metric and the desired

value of that metric to compute the needed number of

replicas. Hence, as previously mentioned, a linear

autoscaler for event queues emulating cloud

autoscalers will compute the ratio of the event arrival

rate to the maximum consumption rate per replica to

get the needed number of event consumer replicas.

Unfortunately, this neither guarantees that the arrival

rate into each event consumer replica is less than its

maximum consumption rate, nor it associates a

maximum load of events to each consumer replica to

maintain a desired latency. Furthermore, cloud

autoscalers are not platform/middleware aware. As

such, when the arrival rate of events into partitions of

the distributed queue is not uniform, cloud

autoscalers and similar on-premises solutions

(KEDA, 2023) do not perform a load-aware

assignment of partitions to event consumer replicas.

Thus, leading to a situation where a subset of event

consumers replicas is assigned much higher load as

compared to the remaining replicas. In fact, recent

research (Wang et al, 2022) has shown that cloud

autoscalers for distributed event queues are not cost

efficient, and hence, clients are over-charged for

under-utilized resources. Also, these autoscalers may

rely on misleading metrics. For example, Amazon

Kinesis is not always capable of accurately

identifying bottlenecks as relying on CPU policy can

be misleading (Wang et al, 2022). As opposed to

relying on the CPU utilization metric, the research

http://mqtt.org/

http://activemq.apache.org/.

https://www.rabbitmq.com/

work of (Chindanonda et al, 2020) uses the ratio of

the total arrival rate to event consumption rate per

replica to estimate the required number of consumer

replicas. Nevertheless, similarly to cloud autoscalers,

(Chindanonda et al, 2020) do not consider the

assignment of partitions to consumer replicas in a

load-aware manner, neither it associates a desired

latency to a minimal number of replicas. Rather, it

aims at keeping the total consumption rate greater

than the total arrival rate into the distributed event

queue.

On the other hand, the impact of the blocking

synchronization protocol on the overall latency SLA

during dynamic provisioning is rarely addressed in

the literature. In this context, Kafka recently

introduced the cooperative incremental rebalancing

protocol (Blee-Goldman, 2020) that promotes

sticking partitions to their assigned consumers. The

benefit is that if a partition is not reassigned to a

different event consumer, consumption from it will

not be blocked. But this solution promotes stickiness

and data locality rather than load-awareness. For

example, given 3 partitions with different loads

assigned to 2 consumers, triggering the cooperative

incremental rebalancing protocol will privilege the

current assignment even if an event consumer is

assigned the 2 higher load partitions, and the other

consumer is assigned the lower loaded one. This

makes the incremental rebalancing protocol not

suitable for latency-awareness which requires that

partitions be freely (re-)assigned to maintain the

desired latency, rather than sticking them to their

assigned consumers at the cost of violating the

desired latency. To our knowledge, tail-latency

awareness of distributed event queues in face of a

blocking synchronization protocol is not yet

addressed in the literature.

4 MATHEMATICAL MODEL

FOR LATENCY-AWARE

BINPACK AUTOSCALING OF

AN EVENT CONSUMER

GROUP

The aim of this research is to provide an autonomic

event consumer replica provisioner so that a high

percentile of events is served in less than a desired

latency, while simultaneously minimizing the

Tail-Latency Aware and Resource-Efﬁcient Bin Pack Autoscaling for Distributed Event Queues

Table 1: Notations used in the mathematical description of

the tail latency-aware autoscaling model.

Notation Description

m An event consumer group m

𝑝



A partition of the distributed event queue

𝑤



Maximum event processing latency for m.

(latency for a high percentile of events

served by m shall be ≤ 𝑤



)

𝑙𝑎𝑔







Number of events waiting in the partition

𝑝



at time t.

𝜆







Partition 𝑝



event arrival rate at time t.

𝑙𝑎𝑔



Set of existing lag at time t for all

partitions.

𝑙𝑎𝑔



= {𝑙𝑎𝑔







,𝑙𝑎𝑔







,…, 𝑙𝑎𝑔







}

𝜆



Set of arrival rates at time t for all

partitions.



={𝜆







,𝜆







, ….,𝜆







}

𝑚



replica of the event consumer group.

𝜇





Maximum consumption rate per single

replica of m.

𝑙𝑎𝑔







Lag of the j

replica of the consumer

group 𝑚 at time t.

𝜆







Arrival rate into the j

replica of the

consumer group 𝑚 at time t.

𝐺





Set of replicas for the consumer group m

needed at time t to guarantee 𝑤



𝐺



Available set of replicas in m.

decision

interval

Interval of time between two successive

scale decisions.

𝑡



Time to complete a rebalance.

𝑙𝑎𝑔







Number of events accumulated in the

partition 𝑝



due to a rebalance.

𝑡𝑜𝑡𝑎𝑙𝐿𝑎𝑔



Total lag of a partition (existing lag plus

rebalancing lag)

𝑙𝑎g





Set of total lag at time t for all partitions.

𝑙𝑎g





= {𝑡𝑜𝑡𝑎𝑙𝐿𝑎𝑔



,𝑡𝑜𝑡𝑎𝑙𝐿𝑎𝑔



,…}

𝑓



Scale up threshold

𝑓



Scale down threshold

desired latency, while simultaneously minimizing the

number of replicas used. The autonomic replica

provisioning logic is executed at each decision

interval by the Controller process as shown in Figure

1. A decision interval is a configurable interval of

time between 2 successive scale decisions as

indicated in Table 1 where all notations used

throughout this section are summarized.

This section is designed to develop the

mathematical model we use for the logic of the

autonomic event consumer provisioner/autoscaler. It

is modelled as a two-dimensional bin pack problem

where event consumer replicas are the bins and

partitions are the items. In this work, we use

homogenous event consumers, that is, all event

consumer replicas have the same event processing

rate, an extension to heterogeneous consumers is in

progress.

Given a distributed event queue with n partitions,

𝑙𝑎𝑔







is the number of events waiting in the partition

𝑝



at time t. Similarly, 𝜆







denotes the event arrival

rate into the partition 𝑝



at time t. The set of arrival

rates into each partition at time t is denoted as λ



{𝜆







,𝜆







, ….,𝜆







}. The set of existing lag for each

partition at time t is denoted as

𝑙𝑎𝑔



= {𝑙𝑎𝑔







,𝑙𝑎𝑔







,…, 𝑙𝑎𝑔







𝑚



denotes a j

replica of the event consumer

group m. Recall from section 2 that a partition 𝑝



can

be assigned to exactly one event consumer 𝑚



, while

an event consumer can be assigned many partitions.

The maximum consumption rate per any replica of m

𝜇





is calculated as the number of events polled by the

replica divided by their processing time as shown in

equation 1.

𝜇





# 𝑒𝑣𝑒𝑛𝑡𝑠 𝑝𝑜𝑙𝑙𝑒𝑑 𝑝𝑒𝑟 𝑎 𝑟𝑒𝑝𝑙𝑖𝑐𝑎

𝑗

𝑜𝑓 𝑚

𝑃𝑟𝑜𝑐𝑒𝑠𝑠𝑖𝑛

𝑔

𝑇𝑖𝑚𝑒 𝑜

𝑓

𝑒𝑣𝑒𝑛𝑡𝑠

(1)

𝑙𝑎𝑔







is the lag of the j

replica of the consumer

group 𝑚 at time t. It is defined as the sum of lags of

each partition assigned to 𝑚



as shown in equation 2.

𝑙𝑎𝑔







=𝑙𝑎𝑔











∈



(2)

𝜆







=𝜆











∈



(3)

Similarly, 𝜆







is the arrival rate into 𝑚



at time t. It

is defined as the sum of arrival rates of each partition

assigned to 𝑚



as shown in equation 3.

Notice that in case a certain partition features an

arrival rate greater than the maximum consumption

rate, the controller logic, better described below, will

suggest the only possible solution: have this partition

be the only one associated to a given consumer.

However, this case should not happen if one assumes

that the topic is partitioned in a way that guarantees

that 𝜆







< 𝜇





∀ 𝑡. Otherwise, solving the problem

of latency SLA guarantee would require dynamic

topic repartitioning, which is out of scope of this

work.

If later on, the arrival rate decreases below the

maximum consumption rate, the system will have an

opportunity to scale down and assign that partition to

another consumer holding some other partitions. This

CLOSER 2024 - 14th International Conference on Cloud Computing and Services Science

dynamicity due to arrival rate of workload being

dynamic is the key advantage of our proposition

compared to a system overprovisioned from the initial

stage.

𝑤



is the desired maximum total event processing

latency for the event consumer group m. That is, a

high percentile of events served by any replica of m

shall exhibit a latency ≤ 𝑤



. Now consider a time

t where a decision on the minimal set of replicas for

the consumer group m (we call it 𝐺





) must be made.

In this context, to increase the percentile of latency

SLA among the arriving events, we must ensure the

following:

∀ 𝑚



∈𝐺





𝑙𝑎𝑔







< 𝜇





× 𝑤



𝐴𝑁𝐷 𝜆







< 𝜇





(4)

Equation 4 states the following: at time t, ensure

that: (1) each event consumer replica 𝑚



can absorb

its existing lag ( 𝑙𝑎𝑔







) in less than 𝑤



. This will

contribute towards maintaining the waiting time of

the newly arrived events less than 𝑤



, and thus

increasing their chance of respecting the latency SLA.

(2) each event consumer replica has the measured

arrival rate into its assigned partitions less than its

maximum consumption rate. Nevertheless, it is

noteworthy that as a partition can be assigned to

exactly one consumer (and not to many consumers),

equation 4 can sometimes be violated, so does not

guarantee that there won’t be any latency violation.

For instance, it is possible that a partition has its lag

greater than 𝜇





×𝑤



because during the

preceding interval some partitions assigned to the

same consumer exhibited an increase in their arrival

rate. In such case the best possible solution consists

now of assigning a dedicated consumer to that

partition. However, this single dedicated consumer

will not be able to process the existing lag in less than

𝑤



and consequently some events will violate the

latency SLA.

Let 𝐺





= {𝑚



,𝑚



,…, 𝑚



} denotes the set of

event consumer replicas needed at time t to preserve

the latency requirements of the event consumer group

m as per equation 4. The aim now is to decide on the

minimum number of event consumer replicas for m,

that is, the cardinality of 𝐺





to satisfy equation 4.

This can be mathematically expressed as per equation

5 below:

𝑚𝑖𝑛

𝐺





𝑠𝑢𝑐ℎ 𝑡ℎ𝑎𝑡

∀ 𝑚



∈𝐺





(5)

𝑙𝑎𝑔







< 𝜇





×𝑤



𝐴

𝑁𝐷 𝜆







< 𝜇





The optimization problem in 5 can be formulated as

an Integer Linear Programming (ILP) model. In the

formulation below 𝑔



and 𝑝



are binary variables

indicating respectively whether a j

event consumer

replica is used at time t, and whether partition i is

assigned to replica j at time t.

𝑚𝑖𝑛 |𝐺

𝑚

𝑡

|= 𝑔

𝑗

such that

∑

𝑝



= 1 ∀ 𝑖 ;

(

𝑎

)

∑

𝑝



𝑙𝑎𝑔









≤ 𝑔



× 𝜇





×𝑤



∀ 𝑗

(b)

∑

𝑝



𝜆









≤ 𝑔



×𝜇





∀ 𝑗

(c)

∑

𝑔



≤ 𝑛𝑏 𝑜𝑓 𝑝𝑎𝑟𝑡𝑖𝑡𝑖𝑜𝑛𝑠 (d)

𝑔



, 𝑝



𝑏𝑖𝑛𝑎𝑟𝑦 𝑣𝑎𝑟𝑖𝑎𝑏𝑙𝑒𝑠,𝑡 > 0

(a) ensures that each partition is assigned to only one

event consumer replica, (b) ensures that the sum of

lags of the partitions assigned to each event consumer

replica is less than the lag that can be served in 𝑤



which is equivalent to 𝜇





×𝑤



. Similarly, (c)

ensures that the sum of arrival rates of the partitions

assigned to each event consumer replica is less than

the maximum consumer consumption rate 𝜇





Finally, (d) ensures that the number of event

consumers used is less or equal to the number of

partitions.

The ILP formulation shows that the problem of

assigning partitions to event consumers while

guaranteeing the 𝑤



latency requirement is NP-

complete. This assignment problem is equivalent to a

two-dimensional bin packing where, at time t, the

items are the partitions described by their arrival rates

𝜆



and by their lags 𝑙𝑎𝑔



. The bins, on the other hand,

are the event consumer replicas described by their

maximum consumption rate 𝜇





and by their

maximum consumption rate multiplied by 𝑤



i.e.,

𝜇





×𝑤



As this assignment problem must be solved

online, we resorted to an approximation algorithm

that can solve the problem in polynomial time.

Furthermore, to ensure a balanced load to each event

consumer replica we used the Least-Loaded bin pack

heuristic. It was proposed by (Ajiro and Tanaka,

2007) for packing VMs in a datacenter into a minimal

number of physical servers, while guaranteeing a fair

(load-balanced) assignment of VMs across the

physical servers.

Tail-Latency Aware and Resource-Efﬁcient Bin Pack Autoscaling for Distributed Event Queues

scaleEventConsumer (𝝀

𝒕

, 𝒍𝒂𝒈

𝒕

, 𝝁

𝒎

𝒋

, 𝒘

𝒔𝒍𝒂

, 𝒇

𝒖𝒑

𝒇

𝒅𝒐𝒘𝒏

)

1 Set 𝐺



to the current set of replicas of m

2 Set 𝐺





= Least-Loaded (𝜆



, 𝑙𝑎g



, 𝑤



, 𝜇





×𝑓



)

3 IF |𝐺





| > |𝐺



//Current nb of consumers violates the latency SLA,

scale up

4 Scale up by 𝐺





\ 𝐺



5 ELSE

𝐺







= 𝐺





𝐺





= Least-Loaded (𝜆



, 𝑙𝑎𝑔



, 𝑤



, 𝜇





×𝑓



)

8 IF |𝐺





|< |𝐺



//We can scale down without violating the latency SLA

9 Scale down by 𝐺



/ 𝐺





10 ELSE

//Current partitions-consumers assignment violates the

latency?

11 IF assignmentViolatesTheSLA(𝑓



)

//A reassignment is needed, we reassign as per 𝑮

𝒓𝒆𝒂𝒔𝒔𝒊

𝒈

𝒏

12 Trigger a rebalance (𝐺







)

13 END IF

14 END IF

15 END IF

Algorithm 1: The latency-aware bin pack autoscaler.

We have introduced two additional parameters to

the original Least-Loaded bin pack heuristic namely

𝑓



and 𝑓



with 0< 𝑓



< 𝑓



<1. For

scaling-up, the Least-Loaded heuristic performs the

packing into µ





×𝑓



(instead of µ





). In essence,

using a value for 𝑓



smaller than 1 ensures that the

bin (event consumer) will not be used at its full

capacity, and hence, the controller will have margin

to scale up slightly before 𝑤



is reached. Example

of values for 𝑓



include 0.9, 0.8 and 0.7. An 𝑓



0.7 will provide earlier scale up as compared to an 𝑓



of 0.8 or 0.9. This will generally provide a better

latency SLA but at a higher cost in terms of replica-

minutes (that is, the number of minutes during which

a single event consumer replica is used and the client

is billed for its usage) as compared to an 𝑓



of 0.8 or

0.9. On the other hand, for scaling-down, the bin pack

heuristic performs the packing into µ





×𝑓



(instead of µ





). 𝑓



controls the frequency of

scale down. Example of values for 𝑓



include 0.5,

0.4 and 0.3. For a constant value of 𝑓



, an 𝑓



0.3 will result in a smaller number of scale down

actions as compared to an 𝑓



of 0.4 or 0.5 but at a

higher cost in terms of replica-minutes.

The logic of the bin pack autoscaler is shown in

the Algorithm scaleEventConsumer above. In the

algorithm, 𝐺



refers to the already existing set of

replicas of m. At time t, the algorithm calculates 𝐺





by packing the partitions into 𝜇





×𝑓



(line 2). If

|𝐺





|>|𝐺



|, then a scale up is needed (line 3-4). The

set 𝐺





\𝐺



denotes the set of the replicas to be added.

If a scale up action is not necessary, 𝐺





is computed

again using 𝜇





×𝑓



(lines 6-8). If |𝐺





|𝐺



|, then a scale down is needed and the set

𝐺



\𝐺





denotes the set of the replicas to be removed.

If neither a scale up nor a scale down is performed,

the logic checks if the current assignment of partitions

to existing event consumer replicas violates the

latency SLA. If so (line 11), we trigger a

rebalance/reassignment so that the replicas-partitions

assignment as per 𝐺



takes place. The

assignment is performed as per 𝐺



because

checking whether the current replicas-partitions

assignment violates the latency SLA is parametrized

by 𝑓



as shown in line 11. The parametrization by

𝑓



is selected because the assignment resulting from

packing the partitions into 𝜇





×𝑓



(larger bins)

will result in a more balanced load across the event

consumer replicas as compared to packing the

partitions into 𝜇





×𝑓



(smaller bins). Finally, if

there is no violation of the latency SLA, the algorithm

terminates without action. The logic for the

procedure assignmentViolatesTheSLA(𝑓



) is shown

below. On the other hand, the Least-Loaded bin pack

heuristic is discussed in detail in (Ajiro and Tanaka,

2007). We do not show its pseudocode in this paper

due to space limitation.

assignmentViolatesTheSLA (𝒇

𝒖

𝒑

)

1 Set 𝐺



to the existing set of event consumers

2 FOR each 𝑚



in 𝐺



//Equation 4 of the model is violated

IF 𝑙𝑎𝑔







>𝜇





×𝑤



×𝑓



OR 𝜆







> 𝜇





×𝑓



4 RETURN TRUE

5 END IF

6 END FOR

7 RETURN FALSE

4.1 Event Consumer Replica

Provisioning with Planning for the

Events Accumulated during

Rebalancing (Tail Latency Aware

Autoscaling)

As stated before, upon a scale action, event

consumers will be blocked, and hence events arriving

during the rebalancing will be accumulated and

lagged in the partitions of the distributed queue until

the end of the rebalancing process. The accumulated

lag per partition 𝑙𝑎g







is equal to the arrival rate into

that partition multiplied by the rebalancing time (𝑡



)

as shown in equation 8 below. Note that the

CLOSER 2024 - 14th International Conference on Cloud Computing and Services Science

rebalancing time (𝑡



) is among the metrics exposed

by the distributed event queue middleware.

𝑙𝑎g







= 𝜆







×𝑡



(6)

The case of event consumer replica provisioning

while planning for the number of events that will be

lagged during rebalancing consists as well of packing

the partitions into event consumers. However, in this

case the lag of each partition consists of the existing

lag in the partition plus the prospective lag that will

be accumulated upon a scale action. This is denoted

as 𝑡𝑜𝑡𝑎𝑙𝐿𝑎𝑔



as described in Table 1. 𝑡𝑜𝑡𝑎𝑙𝐿𝑎𝑔



can be calculated as per equation 9 below where 𝑙𝑎g







is the lag resulting from a rebalance/assignment and

𝑙𝑎𝑔







is the existing lag in the partition.

𝑡𝑜𝑡𝑎𝑙𝐿𝑎𝑔



= 𝑙𝑎g







+ 𝑙𝑎𝑔







(7)

scaleEventConsumer2 (𝝀

𝒕

, 𝒍𝒂𝒈

𝒕

, 𝒍𝒂𝐠

𝒕𝒐𝒕𝒂𝒍

𝒕

, 𝝁

𝒎

𝒋

, 𝒘

𝒔𝒍𝒂

𝒇

𝒖

𝒑

, 𝒇

𝒅𝒐𝒘𝒏

)

1 action = null

2 action = scaleNeeded(𝜆



, 𝑙𝑎𝑔



, 𝜇





,𝑤

𝑠𝑙𝑎

, 𝑓



, 𝑓



)

3 IF action != null

doScale(𝜆



, 𝑙𝑎g





, 𝜇

𝑚

𝑗

, 𝑤

𝑠𝑙𝑎

, 𝑓



, 𝑓



)

4 END IF

Algorithm 2: The tail latency-aware bin pack autoscaler

logic executed by the Controller at each decision interval

(planning for the lag accumulated during rebalancing).

In this context, the set of total lag (existing and

rebalancing) for all the partitions is denoted as

𝑙𝑎g





= {𝑡𝑜𝑡𝑎𝑙𝐿𝑎𝑔



,𝑡𝑜𝑡𝑎𝑙𝐿𝑎𝑔



,… } as

indicated in Table 1.

As shown in Algorithm 2

(scaleEventConsumer2), event consumer replica

provisioning while planning for the rebalancing lag

requires a slight modification into Algorithm 1

(scaleEventConsumer). This modification is

performed in two phases. In the first phase, Algorithm

2 calls the procedure scaleNeeded shown below.

scaleNeeded performs the exact logic of Algorithm 1

using the set of partitions existing lag 𝑙𝑎𝑔



and

without performing any scale action. Instead,

scaleNeeded returns an “UP”, “DOWN” or “REASS”

flag depending on the scale action recommended. In

the second phase, the procedure doScale shown

below is called. doScale performs the scale action

recommended in the first phase while considering the

lag that will accumulate during the prospective

rebalancing. To this end, the set of total partitions lag

(existing and rebalancing)

𝑙𝑎g





and the

recommended scale action

are passed as argument to

doScale. Depending on the action passed, doScale

performs the appropriate Least Loaded bin pack using

𝑙𝑎g





. It then performs the appropriate scale action

and provide the required replicas accordingly.

scaleNeeded (𝝀

𝒕

, 𝒍𝒂𝒈

𝒕

, 𝝁

𝒎

𝒋

, 𝒘

𝒔𝒍𝒂

, 𝒇

𝒖𝒑

, 𝒇

𝒅𝒐𝒘𝒏

)

1 Set 𝐺



to the current set of replicas of m

2 Set 𝐺





= Least-Loaded (𝜆



, 𝑙𝑎g



, 𝑤



, 𝜇





×𝑓



)

3 IF |𝐺





| > |𝐺



4 RETURN “UP”

5 ELSE

𝐺







=𝐺





𝐺





= Least-Loaded(𝜆



, 𝑙𝑎𝑔



, 𝑤



, 𝜇





×𝑓



)

8 IF |𝐺





|<|𝐺



9 RETURN “DOWN”

10 ELSE

11 IF assignmentViolatesTheSLA(𝑓



)

12 RETURN “REASS”

13 END IF

14 END IF

15 END IF

Procedure 1: A function that performs Least-Loaded bin

pack and returns the action needed without performing any

scale action.

doScale (𝝀

𝒕

, 𝒍𝒂𝒈

𝒕𝒐𝒕𝒂𝒍

𝒕

, 𝝁

𝒎

𝒋

, 𝒘

𝒔𝒍𝒂

, 𝒇

𝒖𝒑

, 𝒇

𝒅𝒐𝒘𝒏

, action)

1 Set 𝐺



to the current set of replicas of m

2 IF action == “UP” OR “REASS”

3 𝐺





= Least-Loaded (𝜆



, 𝑙𝑎g





, 𝑤



, 𝜇





×𝑓

𝑢𝑝

)

4 IF |𝐺





| > |𝐺



5 Scale up by 𝐺





\𝐺



6 ELSE

7 Trigger a rebalance(𝐺





)

8 END IF

9 ELSE //action = down

10 𝐺





= Least-Loaded (𝜆



, 𝑙𝑎g





, 𝑤



, 𝜇





𝑓

𝑑𝑜𝑤𝑛

)

11 IF |𝐺





| < |𝐺



12 Scale down by G



\ G





13 END IF

14 END IF

Procedure 2: A procedure that performs the required scale

action while taking the rebalancing lag into account.

5 EXPERIMENTAL WORK

In this section we report some of the experiments we

performed using Algorithm 2

(scaleEventConsumer2) described in the previous

section. As discussed previously, this algorithm

performs bin pack replica provisioning with planning

for the events that will be lagged during rebalancing.

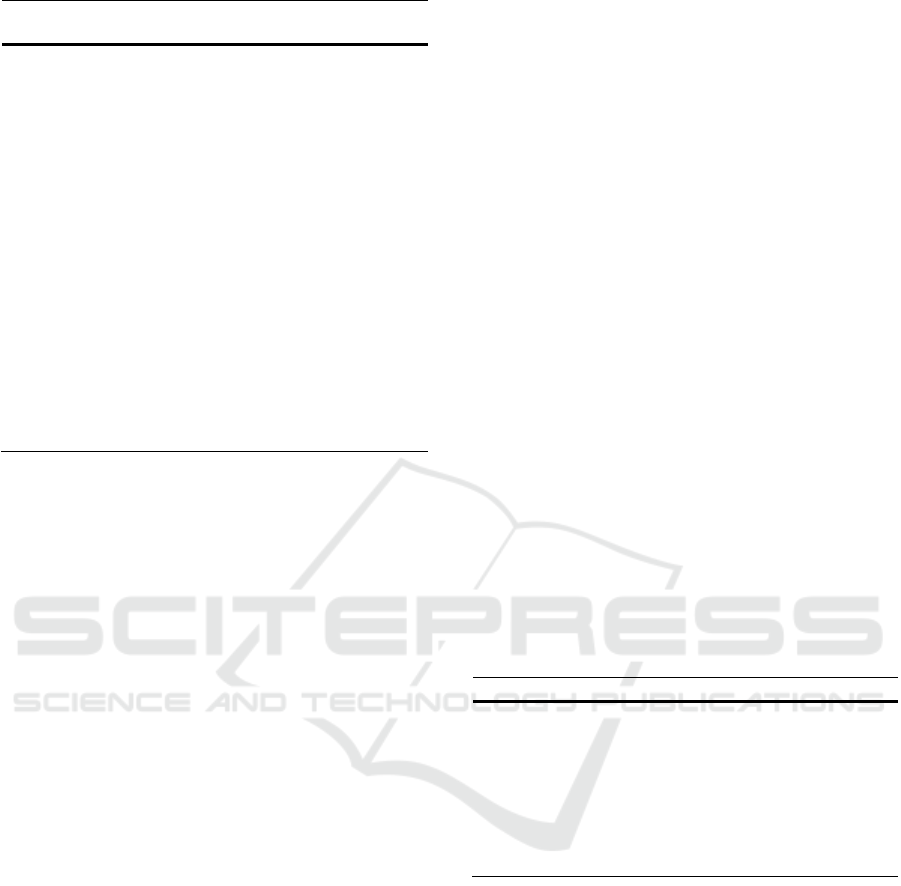
For the experiments we used two workloads. The

first is adapted from (Chindanonda et al, 2020). It is a

10-minutes workload with a total of around 109k

events. The arrival rate per second of the 109K events

Tail-Latency Aware and Resource-Efﬁcient Bin Pack Autoscaling for Distributed Event Queues

is distributed over the 10 minutes interval as shown

in Figure 2. The second workload, see Figure 3,

corresponds to a two-hours trace from the New York

City Taxi Trip dataset (Donovan and Work, 2016).

This dataset contains records for four years (2010 -

2014) of taxi trips in New York City. We used a 2h

long trace from January 2013 trips. To construct the

trace, we employed a speed factor of 40. This means

that 40 seconds of real-world events are replayed in 1

second in the experiments. The trace contains around

1.35M events with arrival rate distributed over the 2h

interval as shown in Figure 3. Each batch of events

sent to the distributed queue is uniformly distributed

across the partitions unless otherwise stated.

As a business use case, we used a simplified

payment authorization application (adapted from real

payment authorization system used in production). In

our experimental setup, a producer application

generates payment events with a rate per second

corresponding to the employed workload. The

payment events are written into the distributed event

queue. An event consumer group pulls the payment

events out of the distributed queue and either declines

or accepts the payment. We set

𝑤



to 500 ms as per

the business requirement. The processing time per

payment event was set to 5 ms. This processing time

was used since it corresponds to the 100-percentile

(worst case) processing latency for a payment event.

Hence, the maximum consumption rate µ used

throughout the experiments is equal to 200

events/seconds.

Figure 2: First workload used in the experiments.

All the experiments were performed on Google

Cloud Platform GCP using a Kubernetes cluster

(version 1.20.6-gke.1400) composed of 5 virtual

machines each with 4 vcpu and 16GB of RAM.

Throughout the experiments we used a distributed

event queue with 5 partitions unless otherwise stated.

The distributed event queue is based on Kafka version

Figure 3: Second workload used in the experiments: 2h

trace from the NYC taxi driver dataset.

Figure 4: Event latencies for Algorithm 2 with the first

workload.

2.7. The decision interval is set to 1 second. The

couple (fup, fdown) was set to (0.9, 0.4). Finally, we

note that 99-percentile rebalancing time in our

deployment setup was equivalent to 50 ms. This value

was used as the rebalancing time (tr) to compute the

lag accumulated on a rebalancing process as per

equation 8.

5.1 Performance of the Proposed

Least-Loaded Binpack (Algorithm

Now we report the performance of Algorithm 2 that

uses the Least-Loaded bin pack to provision and

deprovision event consumer replicas. As discussed in

section 3, this algorithm aims at maintaining the event

total latency at less than the desired latency (500 ms)

while simultaneously aiming at minimizing the

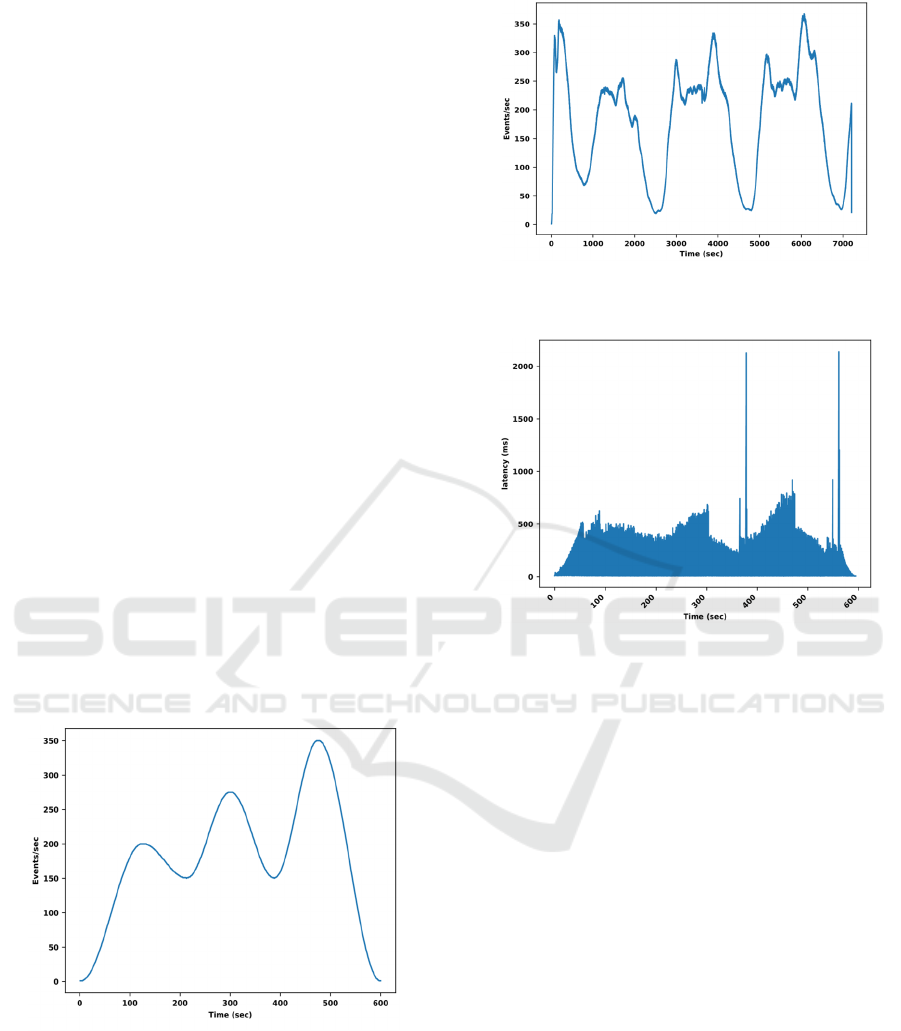
number of replicas used. Figure 4 shows the event

latencies for Algorithm 2 under the first workload.

Also, Figure 5 shows the event latency per each of the

provisioned event consumer replica over the lifetime

of the experiment. Notice in Figure 5 the provisioning

and deprovisioning time for the 7 event consumer

CLOSER 2024 - 14th International Conference on Cloud Computing and Services Science

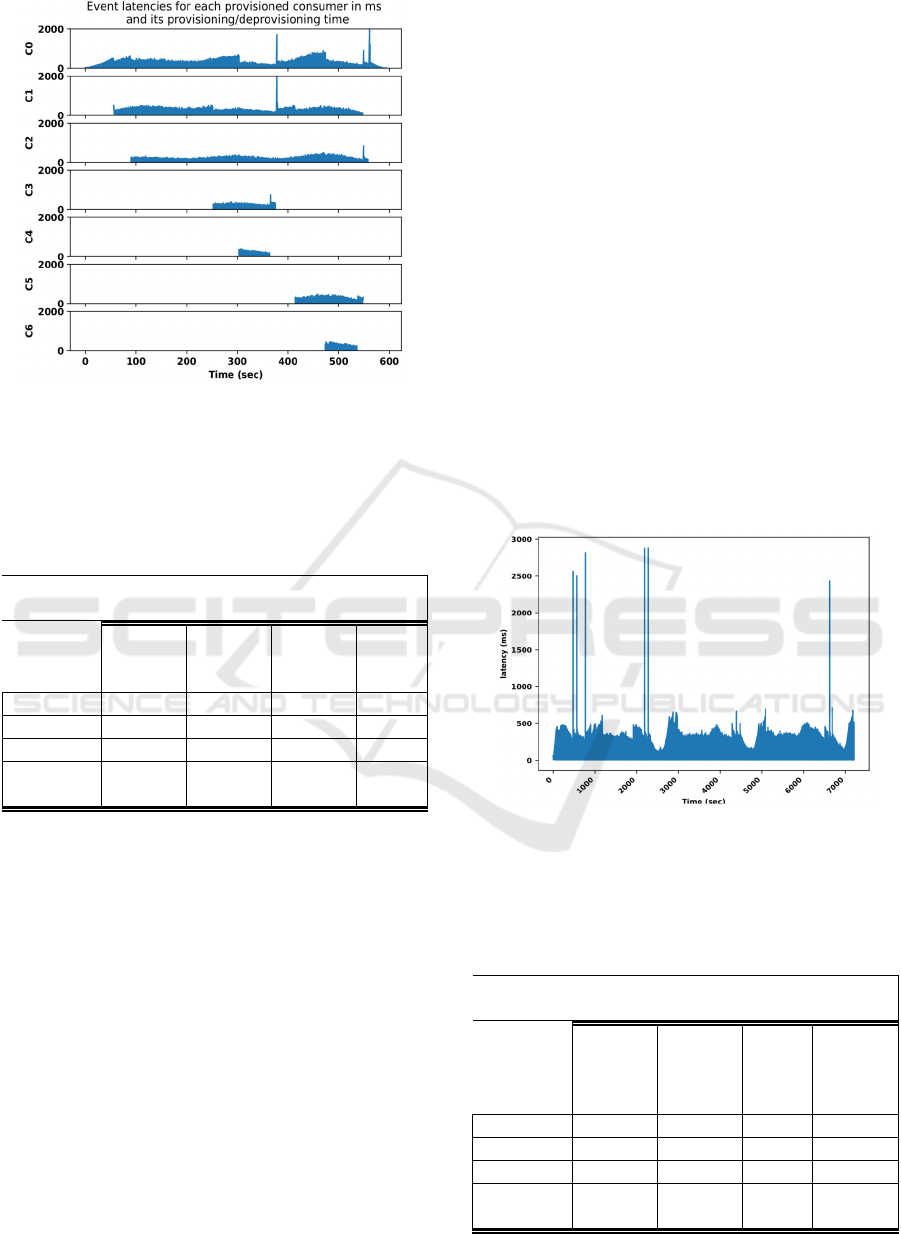
Figure 5: Event latency for each of the 7 event consumers

used by Algorithm 2 with the first workload. Ci on the y-

axis denotes the ith consumer.

Table 2: Latency SLA and replica-minutes of Algorithm 2

(with the first workload) compared to an overprovisioning

solution and an optimal autoscaler. Also shown the results

for the Linear autoscaling solution.

wsla = 500 ms, decision interval = 1 second, µ= 200

events/sec

First

Workload

latency

SLA

Cost

replica-

minutes

Nb of

Scale

Nb of

Scale

Down

Alg. 2 97.4 30.21 6 6

Linear 94.7 25.5 6 6

Optimal 100 32.7 6 6

Overpro-

visioning

100 50 0 0

replicas provisioned over the lifetime of the

experiment. Figure 6 shows the event latencies for

Algorithm 2 under the NYC Taxi workload. We do

not show the event latency per each provisioned

replica over the time interval of the NYC workload

due to space limitation. The results for the first and

second workload are shown in Table 2 and 3

respectively. For instance, as shown in Table 2, with

the first workload, the latency-aware bin pack

autoscaler (Algorithm 2) scored 97.4% latency SLA

at 30.21 replica-minutes. On the other hand, an

optimal autoscaler scored 32.7 replica-minutes at

100% latency guarantee. Note that the results for the

optimal autoscaler were obtained using a python

simulator where event consumer replicas are

provisioned when the rate of event arrivals reaches

the latency-violating number of events (that is,

𝜇





×𝑤



), and deprovisioned otherwise. Also, with

the optimal autoscaler, replicas are provisioned

instantaneously, and the rebalancing/synchronization

time is set to zero. The overprovisioning solution

scored 100% latency SLA at the cost of 50 replica-

minutes. Implementing overprovisioning

experiments means: the number of event consumers

is resulting from Algorithm 2 (Least-Loaded bin

pack) but when the partitions are considered to be

filled at their maximum arrival rate as per the input

workload. That is, it considers the partitions arrival

rate is equal to the peak arrival rate of the input

workload divided by the number of partitions. For

each case, notice the number of scale up and down

actions. Later in this section we compare our bin pack

autoscaler with a Linear autoscaler solution under

non-skewed and skewed workloads.

Table 3 summarizes results obtained using the

second workload. Therefore, the proposed bin pack

autoscaler provided 31% reduction in cost as

compared to an overprovisioning solution

(overprovisioning is largely used by cloud providers

for performance SLAs) at around 1% decrease in

latency guarantee.

Figure 6: Event latencies for Algorithm 2 under the second

workload.

Table 3: Latency SLA and replica-minutes of Algorithm 2

(with the second workload) compared to an

overprovisioning solution and optimal autoscaler. Also

shown the results for the Linear autoscaling solution.

wsla = 500 ms, Decision interval = 1 second, µ= 200

events/sec

Second

(NYC

Taxi)

Workload

latency

SLA

Cost

replica-

minutes

Nb of

Scale

Nb of

Scale

Down

Alg. 2 98.9 402.9 20 16

Linear 95.4 325.7 23 20

Optimal 100 414.11 20 16

Overpro-

visioning

100 600 0 0

Tail-Latency Aware and Resource-Efﬁcient Bin Pack Autoscaling for Distributed Event Queues

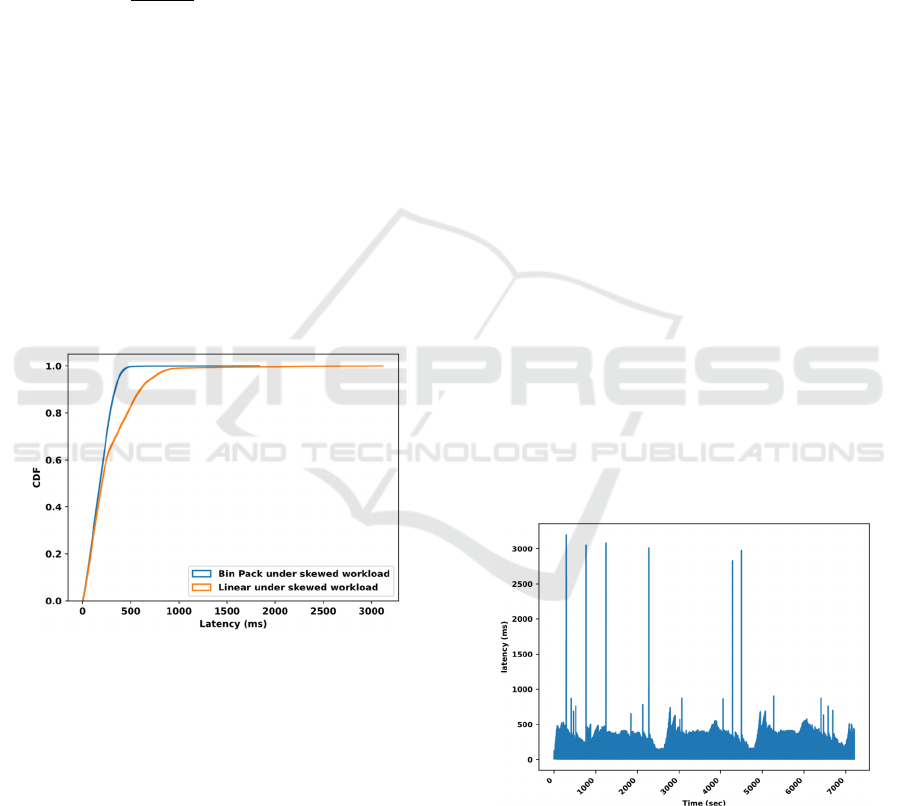
Comparison with a Linear Autoscaling Solution.

We have also tested and compared Algorithm 2 with

a linear autoscaler. As stated before, a linear

autoscaler might miss the exact number of replicas

needed to maintain the desired latency. This will lead

to a non-latency-aware partitions-consumers

assignment performed by Kafka as the load assigned

to certain consumers might bypass the latency-

violating load. To experiment with linear autoscaler,

we configured the newly designed Controller with the

linear formula (

×



×



) using (fup, fdown) of (0.9,

0.4) to compute the needed number of replicas. As

shown in Table 2, with the first workload the bin pack

based autoscaler scored 97.4% latency guarantee at

30.21 replica-minutes while the linear autoscaler

scored 93.9% at 25.5 replica-minutes. This represents

a 3.7% improvement in the latency SLA. As shown

in Table 3, similar results were obtained with the

NYC Taxi dataset workload where the bin pack

autoscaler reached 3.

% increase in latency SLA as

compared to the linear autoscaling solution. This

shows that the proposed bin pack autoscaler

(Algorithm 2) achieved a better latency SLA on a

regular non skewed workload as compared to a linear

autoscaler.

Figure 7: CDFs for the bin pack solution and Linear

solution under the first workload with skewness introduced.

Comparison with a Linear Autoscaling Solution

when the Workload is Skewed. As stated before,

linear autoscalers are not middleware-aware. That is,

they only decide to request addition or removal of

replicas to the underlying cluster manager (e.g.

Kubernetes), but they do not consider the assignment

of event consumer replicas to partitions upon adding

or removing new replicas. Rather, these autoscalers

rely on standard Kafka non-load-aware assignment

strategy for assigning partitions to consumers. This

might result in unbalanced load among the event

consumers replicas when the partitions have non

uniform arrival rate. In this context, recall that as per

Algorithm 2, partitions-consumers assignment is

load-aware. It is performed as per the result of the bin

pack assignment accomplished by the Controller.

Upon rebalancing, the consumer group leader

contacts the Controller for its recommended latency-

aware assignment and performs the assignment

accordingly. Hence, to show the advantage of

Algorithm 2 when the partitions arrival rate is non-

uniform, we have introduced skewness into our two

workloads by sending 0.5 of the event rate into the

first two partitions and the remaining 0.5 into the

other partitions. Note that in order to keep the arrival

rate into a single partition less than latency-violating

arrival rate (that is, the arrival rate at which 𝑤



reached), we have used a distributed queue with 9

partitions in this experiment. With the first workload,

the bin pack autoscaler scored 98.9% latency SLA at

29.8 replica-minutes while the linear autoscaler

scored 84.7 at 25.5 replica-minutes. Figure 7 shows

the CDF (cumulative distribution function) of event

latencies in both cases.

Similar results were obtained with the second

workload (NYC taxi dataset). Figure 8 shows the

event latencies when running the second workload

with skewness introduced using the bin pack

autoscaler. With our proposed bin pack autoscaler the

latency guarantee reached 99.08% at 392.15 replica-

minutes. On the other hand, the linear autoscaling

solution scored 85.9% at 329.7 replica-minutes.

These results represent more than 10% improvement

in terms of latency SLA for the bin pack autoscaler

(Algorithm 2) as compared to a linear autoscaler

when the workload is skewed.

Figure 8: Event latency of the bin pack solution under the

NYC taxi workload with skewness introduced.

5.2 Interpretation of the Resulting Tail

Latency

The results shown and discussed in the previous

section intentionally delayed a major interpretation.

CLOSER 2024 - 14th International Conference on Cloud Computing and Services Science

What is the cause of this variable peak latency

appearing few times in Figures 4, 6 and 8. Also, this

peak latency manifested as a tailed CDF in Figure 7.

A major observation from Figure 5 (notice the

provisioning and deprovisioning time of event

consumers) is that this peak latency is not due to scale

up action and its associated rebalancing overhead as

it does not manifest upon upscaling. Therefore, the

synchronization upon scale-up hypothesis was

eliminated. Nevertheless, one can clearly see from

Figure 5 that this peak latency appears timely with a

scale down action. Hence, it is most likely caused by

a complementary action of the synchronization

protocol that is exclusive to a scale down action.

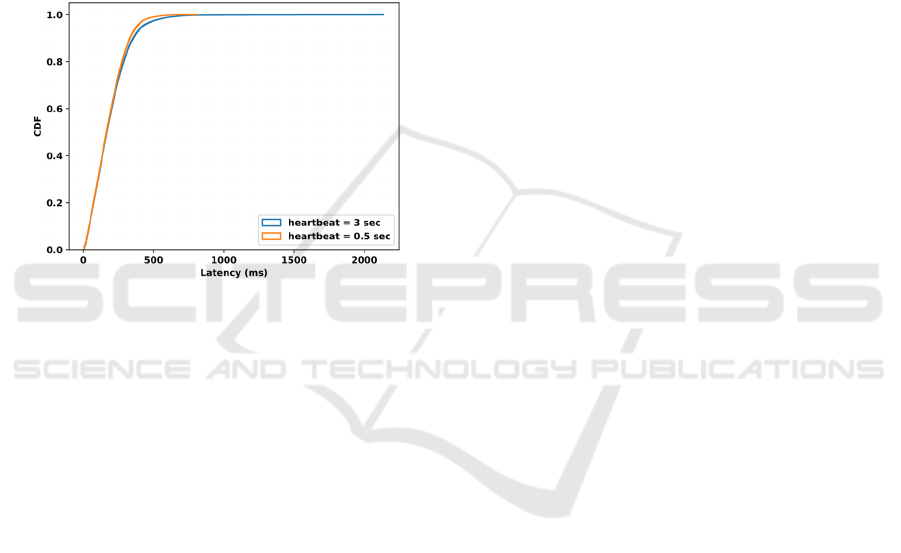
Figure 9: CDF for Algorithm 2 with the first workload

under 500 ms and 3 seconds heartbeat.

As stated in section 2, the event consumer replicas

operate in group managed by the consumer group CG

coordinator. Upon a scale action, the replicas to be

removed/added will inform CG coordinator about

their intention to leave/join the group so that the CG

starts a synchronization/assignment process. This

duration is not blocking during a scale up as the

newly added replicas do not have any assigned

partitions. However, this time is partially blocking in

case of scale down as the leaving consumers are

already assigned partitions from which they will stop

consuming as soon as they inform the coordinator

about their intention to leave. Still, even with that in

mind, a latency of up to few seconds on a scale down

is not justifiable as it will take the CG coordinator an

order of few milliseconds to inform the other event

consumers to revoke their partitions for reassignment.

Unfortunately, however, it turns out that the CG

coordinator does not instantaneously send request to

other event consumers in the group to revoke their

partitions for reassignment. In contrast, it will wait to

receive a heartbeat from the existing consumers, and

it will ask them to revoke their partitions as part of the

heartbeat response. As the default Kafka heartbeat

interval is equal to 3 seconds, the relatively high tail

latency upon a scale down is now justifiable. To

further confirm our hypothesis and eventually aiming

at reduced tail latency, we reran the bin pack

autoscaler logic (Algorithm 2) with a heartbeat

interval of 500 ms. For instance, Figure 9 shows a

CDF comparison when running Algorithm 2 under

the first workload with a heartbeat of 3 seconds and

500 ms. Notice how the 100-percentile tail latency

dropped to less than one second with a heartbeat of

500ms in the first workload. Furthermore, the

percentile of latency SLA increased from 97.4% to

98.1%. With a heartbeat of 500ms, similar results

were observed for the NYC Taxi workload where the

100-percentile tail latency dropped to less than 1

second (alas was around 3 seconds, see Figure 6, with

default value) and the percentile of latency guarantee

increased from 98.9 to 99.07 percentile.

5.3 Impact of the Rebalancing Time on

the Tail Latency

In our deployment and experimental setup, the 99

percentile of the synchronization/rebalancing time

was less than 50 ms which is lower than the desired

target latency 𝑤



. Hence, the synchronization time

did not have a large impact on the latency guarantee,

neither it did result in a large tail latency. To this end,

this section is designed to show the negative impact

of a large synchronization duration for the event

consumer group on the overall percentile of latency

guarantee. In other words, this section shows the

resulting high tail latency observed when a relatively

high rebalancing time governs the event consumer

group synchronization. In particular, the first

subsection shows the observed tail latency when

higher rebalancing time is set while no action is taken

to reduce the effect of the tail latency, that is, using

Algorithm 1. The next subsection shows how

Algorithm 2 that accounts for the rebalancing lag

upon autoscaling, can reduce the impact of the

observed tail latency at higher cost in terms of replica-

minutes. Due to space limitations, and without loss of

generality, we restrict the experiments of this section

to the first workload.

Higher Tail Latency Resulting from Higher

Rebalancing/Synchronization Time. As stated

above, the synchronization time of the event

consumer group might take up to few seconds in some

cases (e.g., when the event consumers are stateful and

state migration to remote servers is needed). Hence,

to show the impact of a larger synchronization time

on the latency guarantee, we set this latter to 500 ms

and 2 seconds. The aim is to quantify the resulting tail

Tail-Latency Aware and Resource-Efﬁcient Bin Pack Autoscaling for Distributed Event Queues

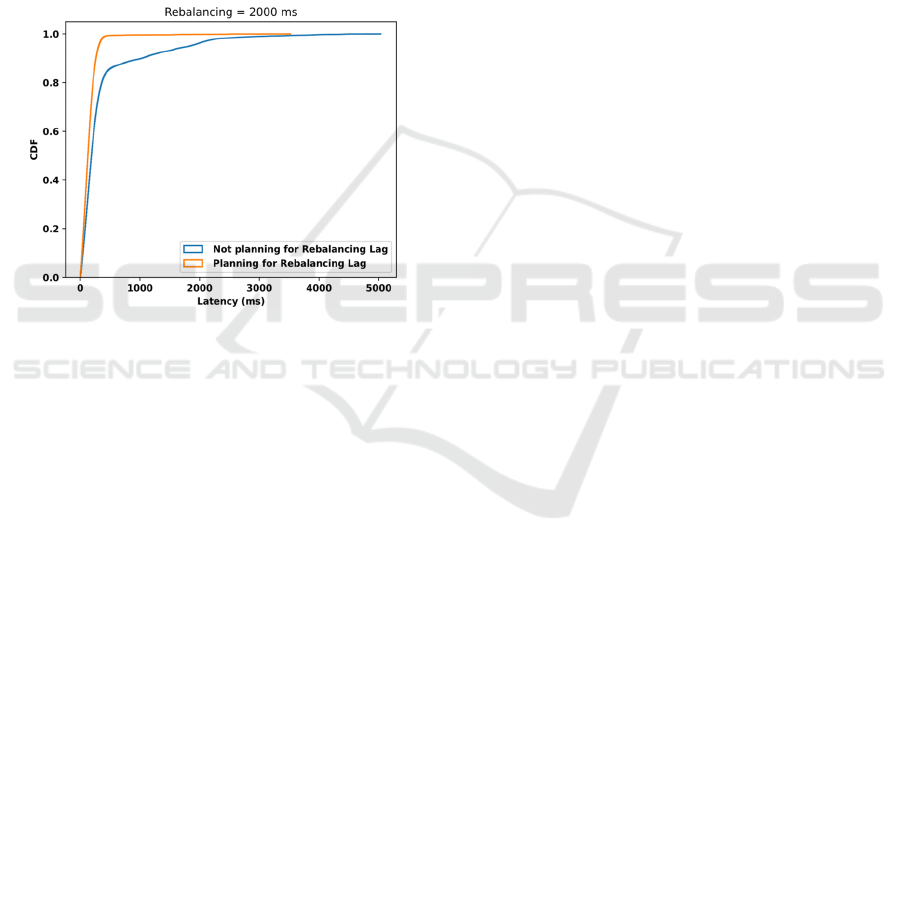
Figure 10: Resulting tail latency under different rebalancing

time when not accounting for the rebalancing lag (that is,

using Algorithm 1 instead of Algorithm2).

latency with 500 ms and 2 seconds synchronization

(rebalancing) time as to less than 50 ms. To this end,

we ran Algorithm 1 driven by the first workload in

these scenarios. Recall that, as compared to

Algorithm 2, Algorithm 1 does not account for the

rebalancing lag while planning for the number of

replicas upon autoscaling, and hence it is less resilient

to the resulting tail on rebalancing. The resulting

CDFs are shown in Figure 10: notice how the higher

rebalancing time of 2 seconds resulted in the worst-

case tail latency. Also, this tail latency was higher

with a rebalancing time of 500 ms as compared to the

default rebalancing time. For instance, the latency

SLA on a rebalancing time of 2 seconds scored 85.4%

as compared to 90.1% for the case of 500 ms

rebalancing time, and to 97.4% in the default setup

case. In the next subsection, we show how Algorithm

2 contributes to a reduction in the tail latency at higher

replica-minutes.

Before completing this section, it is worth noting

that when 𝑤



is higher than the rebalancing time 𝑡



that is, the fraction









is greater than 1, the

rebalancing/synchronization protocol won’t have a

large negative impact on the final percentile of

latency guarantee. On the other hand, when 𝑤



smaller or equal to the rebalancing time, that is, the

fraction









is smaller or equal to 1, the final

percentile of latency guarantee will be affected by the

rebalancing process. The more the fraction









low, the more achieving high percentile of latency

guarantee becomes costly in terms of replica-minutes.

For instance,









=0.1 means that the rebalancing

time is 10x the 𝑤



. Hence, the rebalancing process

will result in more events violating the latency SLA.

In such scenarios, Algorithm 2, will result in a higher

cost in terms of replica-minutes to maintain a low tail

latency. This is because Algorithm 2 will plan (take

into account) the relatively high number of events that

will be lagged during the rebalancing upon a scale up.

It will further restrict scale down actions till lower

arrival of events, where the lagged events upon

rebalancing become smaller thus resulting in less

latency SLA violations.

Tail Latency Reduction Using Algorithm 2

(Planning for the Events Lagged during

Rebalancing). As discussed in section 3, Algorithm

2 complements Algorithm 1 by planning for the

rebalancing lag upon replica-provisioning. This has

the benefit of better resilience in face of tail latency

resulting from rebalancing. To this aim, we repeated

the same experiments with higher rebalancing time (2

seconds, 500 ms and default) driven by Algorithm 2

instead of Algorithm 1. In essence, under a

rebalancing of 500ms, the percentile latency SLA

increased to around 98.2% with Algorithm 2 at 34.61

replica-minutes as compared to 90.1% at 33.85

replica-minutes with Algorithm 1. These results show

an increase of around 8% in the percentile latency

guarantee at 2.2% increase in replica-minutes.

Figure 11: Resulting tail latency under a rebalancing time

of 500ms when not accounting for the rebalancing lag

(Algorithm 1) vs. when accounting for the rebalancing lag

(Algorithm 2).

For the case when the rebalancing time was set to

2 seconds (that is, rebalancing =4×𝑤



), the

percentile latency guarantee increased to 99.4% at

44.7 replica-minutes with Algorithm 2 as compared

to 85.6% at 34.16 replica-minutes using Algorithm 1.

This represents around 14% increase in the latency

SLA at 30.8% increase in the cost in terms of replica-

minutes. As compared to the case when the

rebalancing time was 500 ms, notice the higher values

of both replica-minutes and latency SLA. This is

because higher rebalancing time generates higher

rebalancing lag, and thus more replicas are

provisioned to accommodate for the resulting lag

CLOSER 2024 - 14th International Conference on Cloud Computing and Services Science

upon a scale up. Furthermore, with higher rebalancing

time, Algorithm 2 becomes more restrictive on scale

down, as a scaling down at high arrival rates will

generate latency-violating lag. Thus, deferring

scaling down to lower arrival rates in such a way that

scale down actions would result in non-latency-

violating lag. This behaviour is desired as lower

arrival rates of events typically corresponds to

nonpeak business times which is most likely the best

time to handle the non-availability of the event

consumer group caused by rebalancing. Scale down

deferring is a default technique used in many cloud

autoscalers such as Amazon Kinesis as indicated by

in (Wang et al, 2023).

Figure 12: Resulting tail latency under a rebalancing time

of 2 seconds when not accounting for the rebalancing lag

(Algorithm 1) vs. when accounting for the rebalancing lag

(Algorithm 2).

6 CONCLUSION

We proposed a latency-aware and resource-efficient

dynamic event consumer provisioning in distributed

event queues. The dynamic event consumer replica

provisioner was modelled as a two-dimensional bin

pack problem with the Least-Loaded heuristic.

Experimental work has shown that the bin pack

solution outperforms a linear autoscaler by up to 10%

in terms of latency SLA when the workload is

skewed. Furthermore, we discussed the negative

impact of the blocking event consumer group

synchronization protocol on the tail latency. We then

proposed an extension to the bin pack autoscaler to

reduce the tail latency caused by the events

accumulated during rebalancing.

The case of dynamic event consumer

provisioning when consumer replicas have different

processing capacities, and the case of dynamic event

consumer provisioning for an event driven

microservices architecture is currently a work in

progress.

ACKNOWLEDGEMENTS

This research is funded by the enterprise HighTech

Payment Systems HPS and ANRT through a PhD

CIFRE collaboration with UniCA and CNRS I3S

laboratory.

REFERENCES

Goodhope, K., Koshy, J., Kreps, J., Narkhede, N., Park, R.,

Rao, J., & Ye, V. Y. (2012). Building LinkedIn's Real-

time Activity Data Pipeline. IEEE Data Eng. Bull.,

35(2), 33-45.

Mohammadi, M., Al-Fuqaha, A., Sorour, S., & Guizani, M.

(2018). Deep learning for IoT big data and streaming

analytics: A survey. IEEE Communications Surveys &

Tutorials, 20(4), 2923-2960.

Al-Aubidy, K. M., Derbas, A. M., & Al-Mutairi, A. W.

(2017). Real-time healthcare monitoring system using

wireless sensor network. International Journal of

Digital Signals and Smart Systems, 1(1), 26-42.

Albano, M., Ferreira, L. L., Pinho, L. M., & Alkhawaja, A.

R. (2015). Message-oriented middleware for smart

grids. Computer Standards & Interfaces, 38, 133-143.

Fernández-Rodríguez, J. Y., Álvarez-García, J. A., Fisteus,

J. A., Luaces, M. R., & Magaña, V. C. (2017).

Benchmarking real-time vehicle data streaming models

for a smart city. Information Systems, 72, 62-76.

Laigner, R., Kalinowski, M., Diniz, P., Barros, L., Cassino,

C., Lemos, M., ... & Zhou, Y. (2020, August). From a

monolithic big data system to a microservices event-

driven architecture. In 2020 46th Euromicro conference

on software engineering and advanced applications

(SEAA) (pp. 213-220). IEEE.

Xiang, Q., Peng, X., He, C., Wang, H., Xie, T., Liu, D., &

Cai, Y. (2021). No free lunch: Microservice practices

reconsidered in industry. arXiv preprint arXiv:

2106.07321.

Pallewatta, S., Kostakos, V., & Buyya, R. (2022).

Microservices-based IoT applications scheduling in

edge and fog computing: A taxonomy and future

directions. arXiv preprint arXiv:2207.05399.

Amazon Kinesis. https://aws.amazon.com/kinesis/. (2023).

Google Cloud Pub/Sub., https://cloud.google.com/pubsub/

(2023).

Microsoft Event Hubs., https://azure.microsoft.com/en-us/

services/event-hubs/ (2023).

Eaton, K., (2012.) How One Second Could Cost Amazon

$1.6 Billion In Sales. https://www.fastcompany.com/

1825005/how-one-second-could-cost-amazon-16-

billion-sales

Dean, J., & Barroso, L. A. (2013). The tail at scale.

Communications of the ACM, 56(2), 74-80.

Tail-Latency Aware and Resource-Efﬁcient Bin Pack Autoscaling for Distributed Event Queues

KEDA, (2023) Kubernetes-based event-driven autoscaling,

https://keda.sh/.

Narkhede, N., Shapira, G., & Palino, T. (2017). Kafka: the

definitive guide: real-time data and stream processing

at scale. " O'Reilly Media, Inc.".

Blee-Goldman, S., (2020) From Eager to Smarter in

Apache Kafka Consumer Rebalances. Confluent,.

[Online]. Available: https://www.confluent.io/blog/

cooperative-rebalancing-in-kafkastreamsconsumer-

ksqldb/.

Ajiro, Y., & Tanaka, A. (2007, December). Improving

packing algorithms for server consolidation. In int.

CMG Conference Vol. 253, pp. 399-406).

Chindanonda, P., Podolskiy, V., & Gerndt, M. (2020). Self-

Adaptive Data Processing to Improve SLOs for

Dynamic IoT Workloads. Computers, 9(1), 12.

Qu, C., Calheiros, R. N., & Buyya, R. (2018). Auto-scaling

web applications in clouds: A taxonomy and survey.

ACM Computing Surveys (CSUR), 51(4), 1-33.

Baset, S. A. (2012). Cloud SLAs: present and future. ACM

SIGOPS Operating Systems Review, 46(2), 57-66.

Wang, Y., Lyu, B., & Kalavri, V. (2022, June). The non-

expert tax: quantifying the cost of auto-scaling in cloud-

based data stream analytics. In Proceedings of The

International Workshop on Big Data in Emergent

Distributed Environments (pp. 1-7).

Donovan, B., & Work, D. (2016). New York City taxi trip

data (2010-2013). University of Illinois at Urbana-

Champaign, 10, J8PN93H8.

CLOSER 2024 - 14th International Conference on Cloud Computing and Services Science