A Code Distance Approach to Measure Originality in Computer

Programming

Elijah Chou

1 a

, Davide Fossati

1 b

and Arnon Hershkovitz

2 c

Computer Science Department, Emory University, Atlanta, GA, U.S.A.

Science and Technology Education Department, Tel Aviv University, Tel Aviv, Israel

Keywords:

Originality, Creativity, Educational Data Mining, Tree Edit Distance, Computer Science Education.

Abstract:

We propose a novel approach to measure student originality in computer programming. We collected two

sets of programming problems in Java and Python, and their solutions submitted by multiple students. We

parsed the students’ code into abstract syntax trees, and calculated the distance among code submissions

within problem groups using a tree edit distance algorithm. We estimated each student’s originality as the

normalized average distance between their code and the other students’ codes. Pearson correlation analysis

revealed a negative correlation between students’ coding performance (i.e., the degree of correctness of their

code) and students’ programming originality. Further analysis comparing state (features of the problem set)

and trait (features of the students) for this measure revealed a correlation with trait and no correlation with

state. This suggests that we are likely measuring some trait that a student has, possibly originality, and not

some coincidental feature of our problem set. We also examined the validity of our proposed measure by

observing the agreement between human graders and our measure in ranking the originality of pairs of code.

1 INTRODUCTION AND

RELATED WORK

Creativity is an important quality that has been widely

studied in education (Kupers et al., 2019; Donovan

et al., 2014). However, there is no established way

of measuring creativity in the context of computer

programming. In this study, we propose a method

to quantitatively measure originality, which is one

of the fundamental dimensions of creativity, by com-

paring code written by students with code written by

their peers. Moreover, we evaluate the relationships

between our originality measure and students’ out-

comes. With a consistent, objective measurement of

originality, we could potentially use it to improve pro-

gramming curricula and help people learn this impor-

tant skill.

Creativity Dimensions. Creativity has been rec-

ognized as an important skill for modern citizens

(Said Metwaly et al., 2017) that people can train start-

ing at a young age (Beghetto, 2010; Vygotsky, 2004).

https://orcid.org/0000-0002-6272-9601

https://orcid.org/0000-0003-3587-8860

https://orcid.org/0000-0003-1568-2238

It was suggested to promote academic achievement,

and motivate students in engaging more with learning

in the classroom (Anthony and Frazier, 2009; Davies

et al., 2013). Researchers have studied creativity

extensively through different perspectives (Kaufman

and Beghetto, 2009). Creativity was studied as a pro-

cess (Guilford, 1950), and as a personal trait (Parsons,

1971). It has been assessed through the products of

creativity themselves (Martindale, 1989). While cre-

ativity is widely considered an important trait, there

is still a lot of debate about the deﬁnition of creativity

and how it can be measured (Kilgour, 2006).

The general consensus is that creativity is a mul-

tidimensional concept that is composed of four key

characteristics. The ﬁrst is ﬂuency – the ability to gen-

erate a large number of ideas and directions of thought

for a particular problem. The second is ﬂexibility – the

ability to think about as many uses and classiﬁcations

as possible for a particular item or subject. The third

is originality – the ability to think of ideas that are

not self-evident or banal or statistically ordinary, but

rather those that are unusual and even refuted. The

last is elaboration – the ability to expand an existing

idea and to develop and improve it by integrating ex-

isting schemes with new ideas (Martindale, 1989).

Our goal is to explore how creativity is expressed

Chou, E., Fossati, D. and Hershkovitz, A.

A Code Distance Approach to Measure Originality in Computer Programming.

DOI: 10.5220/0012632100003693

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 16th International Conference on Computer Supported Education (CSEDU 2024) - Volume 2, pages 541-548

ISBN: 978-989-758-697-2; ISSN: 2184-5026

541

through the learning process, and create a measure

that can accurately capture one’s creativity. Partic-

ularly, we are trying to quantify students’ creativity

through the key characteristic of originality by ana-

lyzing their code (which can be considered as prod-

ucts of their creativity) for ideas that are not statisti-

cally ordinary.

Creativity and Computer Programming. In re-

cent years, creativity was shown to have a signiﬁ-

cant correlation with computational thinking, and it

was acknowledged to have a positive impact on all

ﬁelds of study (Romeike, 2007). Studies indicated

that computational problem solving helped inspire

creativity in producing art (Lau and Lee, 2015; Seo

and Kim, 2016), and it was suggested that creativ-

ity can help facilitate the process of solving compu-

tational problems (Kong, 2019). It was also indi-

cated that standardized creativity tests were able to

predict the creativity of computer programming so-

lutions (Liu and Lu, 2002). The reason behind the

strong correlation between creativity and computer

programming was suggested to be that the two share

a set of thinking tools, such as observation, imagina-

tion, visualization, abstraction, and creation (Yadav

and Cooper, 2017). Hershkovitz et al. found positive

associations between computational creativity and the

ﬂuency and ﬂexibility dimensions of creative think-

ing (Hershkovitz et al., 2019), but signiﬁcant nega-

tive correlations between computational thinking and

the ﬂexibility and originality dimensions of creativity

(Israel-Fishelson et al., 2021).

Previous studies tried to use machine learning and

artiﬁcial intelligence to predict creativity scores in

computer programming (Manske and Hoppe, 2014;

Kovalkov et al., 2021b; Kovalkov et al., 2021a). For

example, Kovalkov et al. attempted to predict the

creativity scores of Scratch programs by training a

machine learning model. However, like many of the

other cited studies, their study did not have conclusive

results due to a discrepancy among human experts

when grading the same Scratch programs for creativ-

ity (Kovalkov et al., 2021b). Thus, our ultimate goal

is to deﬁne and implement a creativity measure that

does not depend on training data annotated for cre-

ativity by human judges. As different dimensions of

creativity might require different measures, we will

now narrow our focus on the originality dimension of

creativity.

Tree Edit Distance. In order to deﬁne a com-

putational approach to assessing student originality

through students’ computer programs, we need to be

able to calculate differences between programs. For-

tunately, computer programs are written with a for-

mal syntax which enables them to be represented in

structures such as abstract syntax trees (ASTs). Rep-

resenting programs with ASTs allows us to quantify

their differences by calculating their tree edit dis-

tance. Tree edit distance is deﬁned as the minimum-

cost sequence of node edit operations that transform

one tree into another. Edit operations are node dele-

tions, node insertion, and label renaming (Zhang and

Shasha, 1989). Tree edit distance was shown to be

useful for applications such as computing text simi-

larities (Sidorov et al., 2015). Zhang and Shasha pro-

posed a recursive solution for calculating tree edit dis-

tance in 1989 (Zhang and Shasha, 1989). Their solu-

tion recursively decomposes trees into smaller sub-

forests. The new subforests are created by either

deleting the leftmost or the rightmost root node of a

given subforest. Algorithms that implement Zhang

and Shasha’s recursive approach are referred to as

Zhang decompositions (Schwarz et al., 2017).

2 MEASURING ORIGINALITY

We propose a practical, data driven deﬁnition of orig-

inality in computer programming. We will measure

the amount of originality of a computer programmer

as a function of how much, on average, the code writ-

ten by that programmer differs from the code written

by other programmers to solve the same set of prob-

lems. We tested our approach on two collections of

computer programs written by college students en-

rolled in introductory courses in two major universi-

ties. We calculated code distance measures on those

programs, and then used those distances to calculate

originality scores for each student.

Data Sets. The primary dataset used in this study

includes Java programs written by undergraduate

students in an introductory computer programming

course at Emory University. The dataset includes

ﬁve semesters of anonymized code submissions from

2016 to 2018. These programs were originally sub-

mitted as part of proctored quizzes, and had been

manually scored for correctness by the teaching as-

sistants of the course. We have a total of 19,284

unique student programs, each written by one of 867

students. Excluding incorrect programs, there is a

total of 12,475 student submitted programs. These

12,475 programs are those that the teaching assistants

deemed to fulﬁll all the requirements of their respec-

tive question. Since this data was taken from an intro-

ductory course, the efﬁciency and elegance of student

code was not considered when grading.

CSEDU 2024 - 16th International Conference on Computer Supported Education

542

We also analyzed a smaller dataset of similar pro-

grams written in Python. These programs were writ-

ten by students in an introductory computer program-

ming course at Carnegie Mellon University in Qatar

between 2013 and 2014. The Python dataset includes

a total of 1,724 anonymized student programs, and a

total of 931 programs after the exclusion of incorrect

ones.

Besides the difference in size, our Python and Java

datasets are quite comparable, as the programs were

written during proctored exams by students of similar

level, in similar courses, taught by the same instructor.

Using two different datasets will allows us to validate

the stability of our originality measure across differ-

ent coding languages.

Data Preprocessing. Student programs were ﬁrst

exported from their original source as text ﬁles that

included all student source codes. These were then

converted into Java ﬁles in preparation for JavaParser

processing into abstract syntax trees (ASTs). Once

converted, the Java programs were sorted into sepa-

rate folders according to which coding problem the

program was written to solve.

Within the collection of student code, some pro-

grams were written to correct, or debug, “wrong”

code. For these questions, students were given a com-

mon piece of code that contained a few errors that

students were asked to ﬁx. Since all students would

ultimately submit code that may not differ from one

another that much, we deemed it necessary to exclude

these programs from our analysis.

Another subset of code that was excluded from the

analysis were questions that asked students to answer

theoretical questions in addition to writing code. This

is because students may have earned full points on

the theoretical component of the question, but may

have earned no points on the coding aspect. The origi-

nality measure calculated from these programs would

most likely not have the same correlation with the

ﬁnal assignment score compared to other code-only

questions.

Due to the implementation of JavaParser, student

code that had any issues with compiling or other syn-

tactical issues were also excluded from the ﬁnal anal-

ysis. We would not be able to use these programs

especially if ASTs cannot be created for them.

For the Python dataset, we built a Python imple-

mentation with the same logic and calculations used

in the Java implementation of the originality compu-

tation. As such, we did not convert Python code into

Java code. However, the same preprocessing steps

that were outlined above were done on the Python

dataset as well, including the exclusion of programs

that students debugged, programs that included the-

oretical components, and programs that could not be

converted to abstract syntax trees.

Tree Edit Distance Calculation. To compute the

tree edit distance between two ASTs, we used the

Zhang-Shasha algorithm(Zhang and Shasha, 1989),

with some modiﬁcations to account for superﬁcial dif-

ferences between programs (such as variable names)

that we want to ignore. For each computer program

in every folder, a tree edit distance was calculated be-

tween the AST of the program and the AST of one

other program in the folder. This was added to a to-

tal distance sum for each computer program, and once

this was repeated for every other computer program in

the folder, a ﬁnal average is calculated for each com-

puter program. Once these averages were computed,

a comma-separated values (CSV) ﬁle was written for

each problem folder, with each row containing meta

data about a computer program and its calculated av-

erage distance. This process was completed for both

Java and Python programs with their respective im-

plementations.

As discussed previously, we needed to normalize

the average distances between programs because dif-

ferent programming problems require varying lengths

of code. Longer code tends to have a greater dis-

tance than shorter code, so directly comparing aver-

ages across different coding problems would not be

accurate. The z-scores of the average tree edit dis-

tances were calculated for each computer program

within their respective coding problem groups. The

CSV ﬁles were imported into a Jupyter notebook us-

ing Python and the pandas library, and the z-scores

were calculated using the statistical functions of the

SciPy library. For the purpose of exploring the ef-

fect of including or excluding non-perfect computer

programs from the originality measure for a student,

the above steps were repeated twice: once including

all computer programs available in the data, and the

second including only solutions that earned the maxi-

mum number of points possible.

Aggregate by Student. The z-scores were aggre-

gated according to their corresponding student to ﬁnd

the average z-score per student. The sum of all points

earned by each student on every computer program

they submitted was also calculated, along with the

sum of all possible points each student could have

earned for each submitted program. With this infor-

mation, a programming performance per student was

derived by dividing the student’s total earned points

by the total maximum points the student could have

earned. We found that there was a total of 867 unique

A Code Distance Approach to Measure Originality in Computer Programming

543

students in the Java dataset. Among these students,

there were 816 students who had at least one submit-

ted program in which they scored the maximum pos-

sible points. This subset of students was used for the

second part of the Pearson correlation analysis.

3 ANALYSIS AND EVALUATION

In this section we present three different types of anal-

ysis and evaluation of our originality measure. First,

we show a negative correlation between our original-

ity measure and the scores reﬂecting students’ pro-

gramming ability. Second, we show a state-vs-trait

analysis that indicates that our originality measure

likely detects some student’s trait, and not some con-

cidental feature of our problem sets. Third, we show a

comparison between our automated originality mea-

sure and the intuitive judgments of expert program-

mers: here we observed very low agreement among

human judges, but much better agreement between

the automated system and the majority vote of human

judges.

Originality vs. Programming Performance. To

explore the relationship between our originality mea-

sure and the students’ academic performance, we

calculated the Pearson correlation between students’

originality and the average scores earned by the stu-

dents for all the problem they submitted (a very good

indicator of their coding performance in the course).

In our ﬁrst analysis, all the data that was included af-

ter the initial screening (excluding non-parseable and

theoretical answers) was used in the correlation cal-

culation. This included a total of 867 students in the

Java dataset, and 160 students in the Python dataset.

The results are shown in Table 1 and Figure 1.

To better understand the effect of the inclusion of

programs that did not receive full score on the orig-

inality measure, we repeated the above analysis, but

using only the submissions that earned the maximum

score to calculate originality. Of course, the program-

ming performance score still included all the submis-

sions. We dropped 50 students from the Java dataset

and 10 students from the Python dataset because they

had no submissions that earned the maximum score.

Thus, we recalculated the Pearson correlation using

the originality measures and programming scores of

817 students from the Java dataset and 150 students

from the Python dataset. The results are in Table 1

and Figure 1.

From the table and ﬁgures, we can observe a sta-

tistically signiﬁcant negative correlation between the

students’ originality measure and their coding perfor-

mance score. The negative correlation and statistical

signiﬁcance persisted both with and without the in-

clusion of incorrect programs in the Java dataset, but

lost signiﬁcance in the Python dataset after the exclu-

sion of the incorrect programs, possibly because of

the smaller sample size, or possibly because the mea-

sure might not be stable across coding languages – we

will discuss this topic further in the next two sections.

We suggest a couple of possible preliminary inter-

pretations for the negative correlation between origi-

nality and coding performance. On the one hand, it

could be explained by the time-constrained environ-

ment of proctored exams, where students that pursue

more original approaches in one question could have

less time overall to work on other questions. With

less time, students could perform worse on exams

overall compared to other students who submit more

canonical solutions that may be simpler and/or may

take less time to write. On the other hand, we also

observed that several of the more creative solutions,

although technically correct, were more complicated

and/or less elegant solutions, which makes us think

that the students writing them were indeed less pro-

ﬁcient programmers. Both these interpretations have

practical pedagogical implications that warrant future

investigation.

State vs. Trait Analysis. We performed a state vs.

trait analysis (Baker, 2007) to determine whether our

originality measure for each student can be better pre-

dicted by state or trait explanations. State explana-

tions, which in our context are represented by the

speciﬁc coding problems, are ones that would sug-

gest that some aspect of a student’s current situation

guided the student to write the solution as they did.

Trait explanations, which are represented by the stu-

dents as nominal variables in our experiment, are ones

that would suggest that speciﬁc traits that a student

has (which could be originality) guided a student to

write the solution as they did. If our originality mea-

sure is better explained by traits than state, this would

be a good indication that our measure does indeed

quantitatively assess some trait of a student, and it

may suggest that originality could be one of the traits

it measures.

To create a regression model for the trait explana-

tions of our originality measure, we ﬁrst consolidated

all results of the tree edit distance calculations to one

location. The total number of computer programs we

had after the preprocessing steps and distance calcu-

lations was 19,284. From here, we generated two

new datasets: one that treated students as nominal

variables and another that treated coding problems as

nominal variables. In both sets, the calculated origi-

CSEDU 2024 - 16th International Conference on Computer Supported Education

544

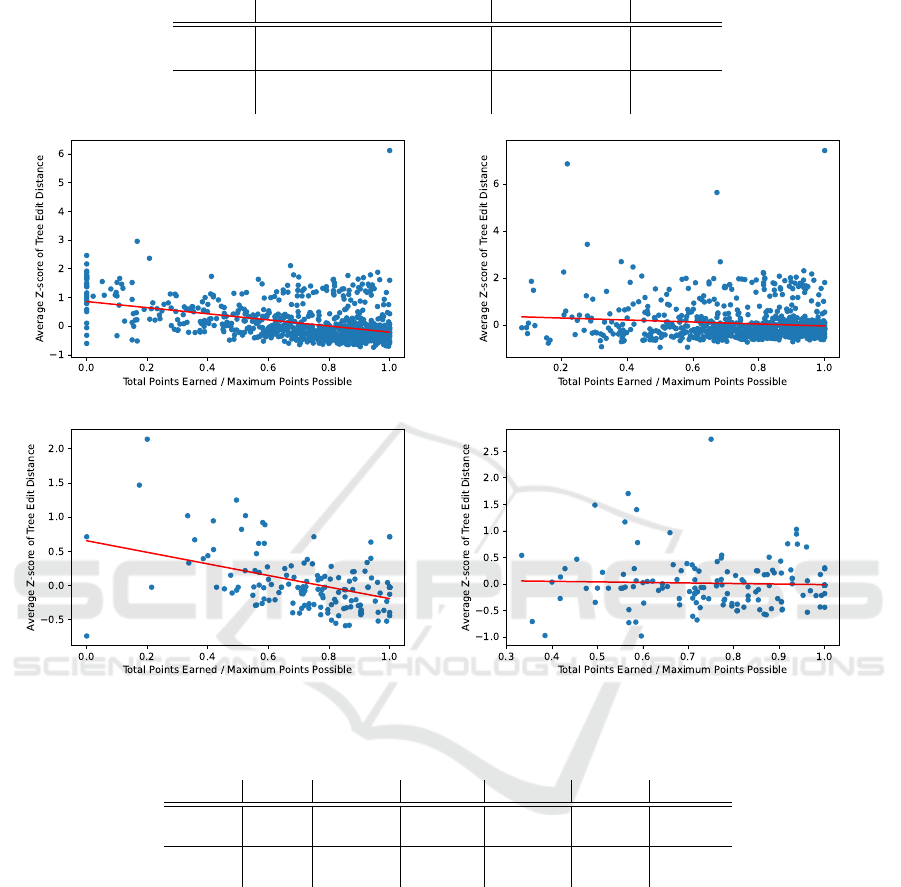
Table 1: Correlation between student originality and coding performance.

Dataset Inclusion Criteria Pearson Coeff. P-value

Java All Programs -0.42 3.44e-38

Only Full-scored Programs -0.11 2.45e-3

Python All Programs -0.43 1.28e-08

Only Full-scored Programs -0.04 0.66

Figure 1: Student originality vs coding performance. Top: Java dataset; bottom: Python dataset. Left: all programs; right:

only full-scored programs.

Table 2: State vs. trait analysis.

Dataset Model R

Adj. R

F-stat P-val BiC

Java State 1.32e-31 -5.27e-3 2.51e-29 1 55732.1

Trait 0.29 0.26 8.78 2.2e-16 56616.6

Python State 5.30e-31 -0.02 2.56e-29 1 5160.79

Trait 0.15 0.07 1.76 8.92e-8 5807.17

nality scores assigned to each computer program were

included.

In the student dataset, we created a column for ev-

ery unique student ID. If a program was associated

with one student ID, the column corresponding to the

student ID would be given the value of 1, and all other

student ID columns would be set to 0. Essentially, we

one-hot encoded for the student ID variable. The cod-

ing problem dataset was prepared in a similar fash-

ion. This resulted with the student dataset having a

total of 867 predictor columns for the 867 unique stu-

dents and the coding problem dataset having a total

of 101 predictor columns for the 101 unique coding

problems.

Once the datasets were ready, we trained two mul-

tiple regression models using the linear regression

models in R. The R

, adjusted R

, F-statistic, p-value,

and BiC values were calculated and are summarized

in Table 2.

In this experiment, we observed that the state ex-

planations model failed to ﬁt the data with an ad-

justed R

value of -5.27e-3 and had a p-value of 1.

On the other hand, we found that the trait explana-

tions model ﬁt the model better with an adjusted R

0.26 and a p-value of 2.2e-16. This indicates that the

trait explanations explained our proposed originality

measure better than state explanations and suggests

that the measure assessed a trait (or multiple traits) of

A Code Distance Approach to Measure Originality in Computer Programming

545

the students. Since originality could be one of these

traits, it would be interesting to further evaluate this

originality measure to examine whether it does indeed

measure a student’s originality or some other student

traits.

We repeated this analysis with the Python dataset,

and achieved similar results (Table 2): traits explained

originality better than state. This result suggests that

our originality measure is stable across different pro-

gramming languages.

Validation with Human Judges. For this particular

experiment, we wanted to demonstrate two particular

notions. First, that it is difﬁcult for human judges to

consistently agree on assessing originality. This was

shown in previous works when originality experts had

trouble agreeing with each other on rating the orig-

inality of several Scratch programs (Kovalkov et al.,

2021b); thus we expect to ﬁnd signiﬁcant discrepancy

among human judges in our experiment as well. Sec-

ond, we want to check if our proposed automatic com-

putational method agrees (at least in part) with the (al-

beit imperfect) human judgement. If we can observe

a reasonable agreement with human judges, we be-

lieve that our proposed originality measure would be

promising for further experimentation in the future.

We randomly selected 30 separate pairs of pro-

grams, each pair from a different coding problem, and

organized them into a survey for human judges to read

and decide which of each pair was more creative. To

isolate correctness of the program from biasing the

judges, only programs that scored full points were

considered for random selection. 30 coding problems

were randomly selected from the 101 problems we

had in our data, and programs were separated into

three equally sized bins based on their z-score of the

distance measure. From those bins, one program was

randomly selected from the lower group and another

from the higher group to form the pair. Through ran-

dom selection from high and low clusters, we would

more likely select programs with more apparent dif-

ferences to potentially aid and simplify the human

judges’ decisions. If a program with the maximum or

minimum z-score of the coding problem group was

selected, we would randomly re-sample the cluster

again to avoid using an outlier in this experiment.

The chosen pairs of programs were copied onto a

Google Forms survey. Each pair was presented into

a separate section, and the coding question was listed

prior to the two programs. The judges were asked to

choose which student’s program solved the problem

more creatively. The judges were informed that only

programs that earned full points were displayed.

Three experienced human judges (the instructor of

the course, an undergraduate teaching assistant, and

an undergraduate computer science student) submit-

ted their originality rankings for each of the 30 pairs

of programs. We then calculated Fleiss’ kappa inter-

rater agreement coefﬁcient to evaluate the agreement

level among our human raters. We did this using the

“irr” R package. Our ﬁndings of this analysis is ar-

ranged in Table 3. Such extremely low kappa value

shows that, even among humans, it is difﬁcult to de-

termine which programs are more creative than oth-

ers. This is similar to the issues that were discussed in

Kovalkov et al.’s works where conclusive evidence of

predicting originality with machine learning models

could not be obtained due to human expert disagree-

ment (Kovalkov et al., 2021b).

In addition, we wanted to evaluate how well our

originality measure agreed with our human judges.

Instead of simply adding the measure’s ranking of

the same 30 program pairs to the previous analysis,

we deemed it more interesting to evaluate the agree-

ment between our proposed measure and the major-

ity vote of the three human judges. We aggregated

the rankings of all human graders to one choice for

every pair, and calculated Cohen’s kappa inter-rater

agreement coefﬁcient to evaluate the level of agree-

ment between our originality measure and the human

judgement as represented by their majority vote. The

results of this analysis is also summarized in Table

3. As discussed in McHugh’s discussion of inter-rater

reliability, we can interpret the 0.533 kappa statistic

value as indicating moderate agreement between our

proposed originality measure and the majority vote

of human graders (McHugh, 2012). This is already

better than the inter-rater agreement found among the

human graders themselves, and this suggests that our

measure, while imperfect, has the potential to be a

good representation of a group’s opinion when rank-

ing programs in programming originality.

4 DISCUSSION AND

CONCLUSIONS

We observed that the originality measure was better

explained through trait explanations rather than state

explanations. In other words, our data showed that

the variation in the originality measure is better under-

stood through the differences in students’ characteris-

tics or traits rather than the differences among the quiz

coding problems that the students needed to solve.

While this ﬁnding is derived from a very high-level

view of state or trait explanations, we believe that our

proposed originality measure could indeed measure

student originality.

CSEDU 2024 - 16th International Conference on Computer Supported Education

546

Table 3: Kappa coefﬁcients of agreement between human judges and originality measure.

Experiment Kappa Statistic P-value

Human vs. Human vs. Human -0.0714 0.498

Human (Majority) vs. Originality Measure 0.533 0.00341

Our results reinforced the notion that original-

ity, even in programming, is an intricate, complex

concept that is not easily agreed upon between two

or more humans. We observed that there was poor

agreement among three different human graders when

they were tasked with ranking one program of two

programs as more creative for 30 different pairs of

program code. However, when we transformed the

rankings of the three graders into one majority vote

ranking and compared that to the originality mea-

sure’s ranking, we found that there was a statisti-

cally signiﬁcant, moderate agreement between the

two. Even though it is difﬁcult for human graders

to agree among themselves, we demonstrated that the

originality measure has the potential to represent the

collective opinion of a group of graders through ma-

jority vote in ranking originality in programming.

When replicating our experiments on the Python

data, we observed results similar to those from the

Java data. We still found that the trait explanations

better explained our originality measure compared to

the state explanations. This provides some support

to the stability of our originality measure across pro-

gramming languages.

Overall, our results indicate that our originality

measure, which uses abstract syntax trees and tree

edit distance, is a good candidate for computationally

assessing a student’s originality through their code.

While further experimentation is needed to bolster the

measure’s validity of accurately assessing originality,

this study acts as a starting point for computational

originality research to start conducting extensive stud-

ies on the use of abstract syntax trees and tree edit dis-

tances as a standardized method of assessing student

originality in the classroom. Our results also suggest

that this study can be replicated on datasets of differ-

ent coding languages as well. If future work continues

to show promise for our proposed measure, it could

help instructors better adapt their computing courses

to their students’ originality levels.

5 LIMITATIONS AND FUTURE

WORK

A limitation of our study is that our data was taken

from two university courses’ quizzes. Replicating

this study with data from either other courses of dif-

ferent education levels, or simply just from different

contexts (such as homework assignments, which tend

to have longer code submissions) will be crucial in

showing that this computational method is trustwor-

thy and generalizable.

Another limitation is the possibility that our mea-

sure could simply assign higher values to programs

that are longer and less efﬁcient than others. To check

that this was not necessarily the case, we found in our

data examples of programs that, despite having the

same length, resulted in largely different originality

scores. Despite this reassuring ﬁnding, we did not

completely rule out the possibility that our measure

may be heavily inﬂuenced by the length of code. Fu-

ture reﬁnements can attempt to penalize longer code

to reduce the effect of length on the originality mea-

sure.

In the future, it would be interesting to explore

clustering of the data based on the originality mea-

sure and other variables such as quiz scores. By clus-

tering the data, we might be able to observe patterns

of more “canonical” versus “original” code, and pos-

sibly detect different structures of originality in dif-

ferent groups of students.

An important experiment that should follow up on

this study is further validation of our originality mea-

sure. There should be a larger pool of human judges

than we had in this study, and a more complex ranking

of multiple programs should be conducted, instead of

our simple ranking between two programs at a time.

Even though it has been a challenge to do so in the

past due to disagreement among human graders (Ko-

valkov et al., 2021b; Kovalkov et al., 2021a), it will

still be necessary to complete these studies in order

for the proposed computational method to be more

dependable as a measure.

REFERENCES

Anthony, K. and Frazier, W. (2009). Teaching students to

create undiscovered ideas. Science Scope.

Baker, R. (2007). Is gaming the system state-or-trait? edu-

cational data mining through the multi-contextual ap-

plication of a validated behavioral model.

Beghetto, R. A. (2010). Creativity in the Classroom,

page 447–464. Cambridge Handbooks in Psychology.

Cambridge University Press.

Davies, D., Jindal-Snape, D., Collier, C., Digby, R., Hay, P.,

and Howe, A. (2013). Creative learning environments

A Code Distance Approach to Measure Originality in Computer Programming

547

in education—a systematic literature review. Thinking

Skills and Creativity, 8:80–91.

Donovan, L., Green, T. D., and Mason, C. (2014). Exam-

ining the 21st century classroom: Developing an in-

novation conﬁguration map. Journal of Educational

Computing Research, 50(2):161–178.

Guilford, J. P. (1950). Creativity. American Psychologist,

5:444–454.

Hershkovitz, A., Sitman, R., Israel-Fishelson, R., Egu

ıluz,

A., Garaizar, P., and Guenaga, M. (2019). Creativity in

the acquisition of computational thinking. Interactive

Learning Environments, 27(5-6):628–644.

Israel-Fishelson, R., Hershkovitz, A., Egu

ıluz, A., Garaizar,

P., and Guenaga, M. (2021). The associations between

computational thinking and creativity: The role of per-

sonal characteristics. Journal of Educational Comput-

ing Research, 58(8):1415–1447.

Kaufman, J. C. and Beghetto, R. A. (2009). Beyond big

and little: The four c model of creativity. Review of

General Psychology, 13(1):1–12.

Kilgour, M. (2006). Improving the creative process: Anal-

ysis of the effects of divergent thinking techniques

and domain speciﬁc knowledge on creativity. Inter-

national Journal of Business and Society, 7.

Kong, S.-C. (2019). Components and Methods of Evalu-

ating Computational Thinking for Fostering Creative

Problem-Solvers in Senior Primary School Education,

pages 119–141. Springer Singapore, Singapore.

Kovalkov, A., Paassen, B., Segal, A., Gal, K., and Pinkwart,

N. (2021a). Modeling creativity in visual program-

ming: From theory to practice. In Proceedings of the

14th International Conference on Educational Data

Mining, EDM 2021, virtual, June 29 - July 2, 2021.

International Educational Data Mining Society.

Kovalkov, A., Paaßen, B., Segal, A., Pinkwart, N., and

Gal, K. (2021b). Automatic creativity measurement

in scratch programs across modalities. IEEE Transac-

tions on Learning Technologies, 14(6):740–753.

Kupers, E., Lehmann-Wermser, A., McPherson, G., and van

Geert, P. (2019). Children’s creativity: A theoretical

framework and systematic review. Review of Educa-

tional Research, 89(1):93–124.

Lau, K. W. and Lee, P. Y. (2015). The use of virtual reality

for creating unusual environmental stimulation to mo-

tivate students to explore creative ideas. Interactive

Learning Environments, 23(1):3–18.

Liu, M.-C. and Lu, H.-F. (2002). A study on the creative

problem-solving process in computer programming.

Manske, S. and Hoppe, H. U. (2014). Automated indicators

to assess the creativity of solutions to programming

exercises. In 2014 IEEE 14th International Confer-

ence on Advanced Learning Technologies, pages 497–

501.

Martindale, C. (1989). Personality, Situation, and Creativ-

ity, pages 211–232. Springer US, Boston, MA.

McHugh, M. L. (2012). Interrater reliability: the kappa

statistic. Biochem Med (Zagreb), 22(3):276–282.

Parsons, M. J. (1971). White and black and creativity.

British Journal of Educational Studies, 19(1):5–16.

Romeike, R. (2007). Three drivers for creativity in com-

puter science education.

Said Metwaly, S., Van den Noortgate, W., and Kyndt, E.

(2017). Methodological issues in measuring creativ-

ity: A systematic literature review. Creativity Theories

– Research – Applications, 4.

Schwarz, S., Pawlik, M., and Augsten, N. (2017). A new

perspective on the tree edit distance. In Beecks, C.,

Borutta, F., Kr

oger, P., and Seidl, T., editors, Similar-

ity Search and Applications, pages 156–170, Cham.

Springer International Publishing.

Seo, Y.-H. and Kim, J.-H. (2016). Analyzing the effects

of coding education through pair programming for the

computational thinking and creativity of elementary

school students. Indian Journal of Science and Tech-

nology, 9.

Sidorov, G., G

omez-Adorno, H., Markov, I., Pinto, D., and

Loya, N. (2015). Computing text similarity using

tree edit distance. In 2015 Annual Conference of the

North American Fuzzy Information Processing Soci-

ety (NAFIPS) held jointly with 2015 5th World Con-

ference on Soft Computing (WConSC), pages 1–4.

Vygotsky, L. S. (2004). Imagination and creativity in child-

hood. Journal of Russian & East European Psychol-

ogy, 42(1):7–97.

Yadav, A. and Cooper, S. (2017). Fostering creativity

through computing. Commun. ACM, 60(2):31–33.

Zhang, K. and Shasha, D. (1989). Simple fast algorithms for

the editing distance between trees and related prob-

lems. SIAM Journal on Computing, 18(6):1245–1262.

CSEDU 2024 - 16th International Conference on Computer Supported Education

548