A Machine Learning Workflow to Address Credit Default Prediction
Rambod Rahmani
a
, Marco Parola
b
and Mario G. C. A. Cimino
c
Dept. of Information Engineering, University of Pisa, Largo L. Lazzarino 1, Pisa, Italy
Keywords:
FinTech, Credit Scoring, Default Credit Prediction, Machine Learning, NSGA-II, Weight of Evidence.
Abstract:
Due to the recent increase in interest in Financial Technology (FinTech), applications like credit default pre-
diction (CDP) are gaining significant industrial and academic attention. In this regard, CDP plays a crucial
role in assessing the creditworthiness of individuals and businesses, enabling lenders to make informed deci-
sions regarding loan approvals and risk management. In this paper, we propose a workflow-based approach
to improve CDP, which refers to the task of assessing the probability that a borrower will default on his or
her credit obligations. The workflow consists of multiple steps, each designed to leverage the strengths of
different techniques featured in machine learning pipelines and, thus best solve the CDP task. We employ
a comprehensive and systematic approach starting with data preprocessing using Weight of Evidence encod-
ing, a technique that ensures in a single-shot data scaling by removing outliers, handling missing values, and
making data uniform for models working with different data types. Next, we train several families of learning
models, introducing ensemble techniques to build more robust models and hyperparameter optimization via
multi-objective genetic algorithms to consider both predictive accuracy and financial aspects. Our research
aims at contributing to the FinTech industry in providing a tool to move toward more accurate and reliable
credit risk assessment, benefiting both lenders and borrowers.
1 INTRODUCTION AND
BACKGROUND
In the financial sector, credit scoring is a crucial task
in which lenders must assess the creditworthiness of
potential borrowers. In order to determine credit risk,
several characteristics related to income, credit his-
tory, and other relevant aspects of the borrower must
be deeply investigated.
To manage financial risks and make critical deci-
sions about whether to lend money to their customers,
banks and other financial organizations must gather
consumer information to identify reliable borrowers
from those unable to repay debt. This results in solv-
ing a credit default prediction problem, or in other
words a binary classification problem (Moula et al.,
2017).
In order to address this challenge, over the years
several statistical techniques have been embedded in
a wide range of applications for the development
of financial services in credit scoring and risk as-
sessment (Sudjianto et al., 2010; Devi and Radhika,
a
https://orcid.org/0009-0009-2789-5397
b
https://orcid.org/0000-0003-4871-4902
c
https://orcid.org/0000-0002-1031-1959
2018). However, such models often struggle to repre-
sent complex financial patterns because they rely on
fixed functions and statistical assumptions (Luo et al.,
2017). While they have some advantages such as
transparency and interpretability, their performance
tends to suffer when faced with the challenges pre-
sented by the vast amounts of data and intricate rela-
tionships in credit prediction tasks.
On the contrary, Deep Learning (DL) approaches
have garnered significant attention across diverse do-
mains, including the financial sector. This is due
to their superior performance compared to traditional
statistical and Machine Learning (ML) models (Teles
et al., 2020). In particular, DL has made great strides
in several application areas, such as medical imaging
(Parola et al., 2023b), price forecasting (Lago et al.,
2018) (Cimino et al., 2018), and structural health
monitoring (Parola. et al., 2023) (Parola et al., 2023a)
(Cimino. et al., 2022) (Parola. et al., 2022), demon-
strating its versatility in handling complex data pat-
terns.
Besides developing classification strategies, a dis-
tinct approach to enhance the workflow is to focus on
preprocessing. A common data preprocessing tech-
nique in the credit scoring field is Weight of Evidence
714
Rahmani, R., Parola, M. and Cimino, M.
A Machine Learning Workflow to Address Credit Default Prediction.
DOI: 10.5220/0012640200003690
Paper published under CC license (CC BY-NC-ND 4.0)
In Proceedings of the 26th International Conference on Enterprise Information Systems (ICEIS 2024) - Volume 1, pages 714-720
ISBN: 978-989-758-692-7; ISSN: 2184-4992
Proceedings Copyright © 2024 by SCITEPRESS – Science and Technology Publications, Lda.

(WoE) data encoding, as it enjoys several properties
(Thomas et al., 2017). First, being a target-encoding
method, is able to capture nonlinear relationships be-
tween the features and the target variable. Second, it
can handle missing values; which often afflict credit
scoring datasets as borrowers may not provide all the
required information when applying for a loan. WoE
handles missing values by binning them separately.
Finally, WoE coding reduces data dimensionality by
scaling features (both numerical and categorical) into
a single continuous variable. This can be particu-
larly useful in statistic, ML and DL contexts, be-
cause models may have different intrinsic structures
and may only be able to work with a specific data type
(L’heureux et al., 2017).
The goal of this work is to combine different tech-
nologies and frameworks into an effective ML work-
flow to address the task of credit default prediction for
the financial sector. Besides the data preprocessing
via WoE coding, we introduce an ensemble strategy
to build a more robust model; a hyperparameter opti-
mization to maximize performance, and a loss func-
tion that focuses learning on hard-to-classify exam-
ples to overcome data imbalance problems.
To assess model performance and workflow
strength, we present results obtained on known and
publicly available benchmark datasets. These datasets
provide a common reference point and enable mean-
ingful comparisons between different models.
The paper is organized as follows. The material
and methodology are covered in Section 2, while the
experiment results and discussions are covered in Sec-
tion 3. Finally, Section 4 draws conclusions and out-
lines avenues for future research.
2 MATERIALS AND
METHODOLOGY
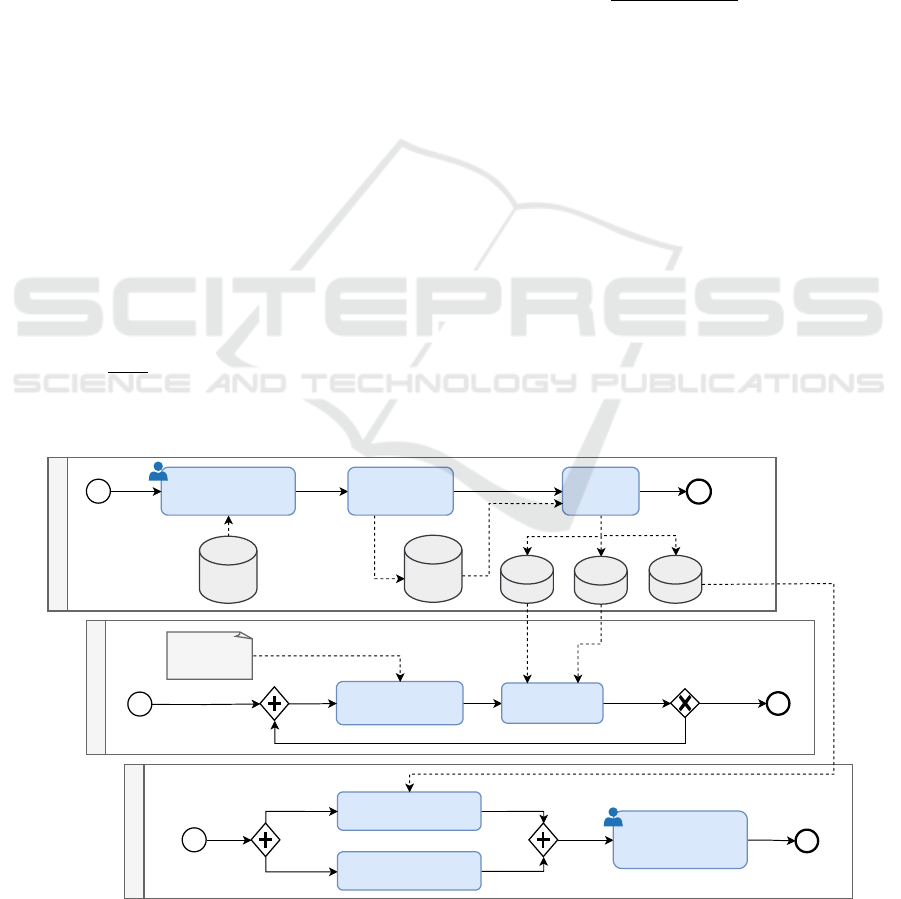
The proposed ML workflow is shown in Figure 1
by mean of a Business Process Model and Notation
(BPMN) diagram. BPMN is a formal graphical no-
tation that provides a visual representation of busi-
ness processes and workflows, allowing for efficient
interpretation and analysis of systems (Cimino and
Vaglini, 2014). BPMN was chosen due to its ability
to visually represent complex processes in a standard-
ized and easily understandable manner.
The diagram provides a comprehensive overview
of the ML workflow for credit scoring default predic-
tion task. The first lane focuses on data preprocess-
ing, where manual column removal and data encod-
ing through Weight of Evidence (WOE) techniques
are employed. The second lane is dedicated to model
training and optimization, exploring various learning
models described below. Finally, the third lane in-
volves computing evaluation metrics, while also in-
corporating the expertise of a financial expert to as-
sess the performance.
The second lane aims to solve a supervised ma-
chine learning problem where the goal is to predict
whether a borrower is likely to default on a loan
or not. Specifically, a binary classification model
(Dastile et al., 2020), trained on a dataset of historical
borrowers information with the final goal of finding
a model ψ
p
: R
n
⇒ {−1, +1} which maps a feature
vector x ∈ R
n
to an output class y ∈ {−1, +1}; where
x identifies the set of attributes describing a borrower,
y is the class label (non-default −1, default +1), and
p is the set of parameters describing the model ψ:
ψ
p
: x ⇒ y. (1)
To evaluate the classification performance of the
above problem, the Area Under the Curve (AUC)
metric is introduced:
AUC =
Z
1
0
ROC(u) du, (2)
where ROC(u) is the receiver operating characteris-
tic (ROC) curve at threshold u, defined as the ratio
between the true positive rate T PR(u) and the false
positive rate FPR(u) both at threshold u.
Another popular metric for evaluating perfor-
mance when dealing with unbalanced datasets is the
F-score, computed as the average of the well-known
precision and recall metrics.
The Brier score metric (Bequ
´
e et al., 2017) was
used to measure the mean squared difference be-
tween the predicted probability and the actual out-
come. Given a dataset D , composed of n samples,
BS metric is shown in Equation 3.
BS =
1
n
n
∑
i=1
(p
i
− o
i
)
2
, (3)
where p
i
is the (default) probability predicted by the
model and o
i
is the actual label.
Generally in the credit scoring literature, the cost
of incorrectly classifying a good applicant as a de-
faulter (i.e., c
0
, false positive) is not considered to be
as important as the cost of misclassifying a default
applicant as good (i.e., c
1
, false negative). Indeed,
when a bad borrower is misclassified as good, they
are granted a loan they are unlikely to repay, which
can lead to significant financial losses for the lender
(Hand, 2009). The c
0
cost is equal to the return on
investment (ROI) of the loan and we assume the ROI
(c
0
) to be constant for all loans, as is usually the case
in consumer credit scoring (Verbraken et al., 2014a).
A Machine Learning Workflow to Address Credit Default Prediction
715

It is worth noting that the above argument assumes
that there is no opportunity cost associated with not
granting a loan to a good credit borrower. However,
in reality, there may be some opportunity cost, as the
borrower may take their business elsewhere if they are
not granted a loan (Verbraken et al., 2014b).
Under this premise, we introduce the Expected
Maximum Profit (EMP) metric, since the metrics in-
troduced previously consider only minimizing credit
risk and not necessarily maximize the profit of the
lender. The EMP metric takes into account both the
probability of insolvency and the profit associated
with each loan decision (
´
Oskarsd
´
ottir et al., 2019).
To define the EMP metric we first introduce the
average classification profit metric per borrower in
Equation 4; it is determined based on the prior proba-
bilities of defaulters p
0
and non-defaulters p
1
, as well
as the cumulative density functions of defaulters F
0
and non-defaulters F
1
. Additionally, b
0
represents the
profit gained from correctly identifying a defaulter, c
1
denotes the cost incurred from erroneously classify-
ing a non-defaulter as a defaulter, while c∗ refers to
the cost associated with the action taken. Hence, EMP
can be defined as shown in Equation 5:
P(t; b
0
, b
1
, c∗) = (b
0
− c∗)π
0
F
0
(t) − (c
1
− c∗)π
1
F
1
(t)
(4)
EMP =
Z
b
0
Z
c
1
P(T (θ); b
0
, c
1
, c∗) · h(b
0
, c
1
) db
0
cd
1
(5)
where θ =
c
1
+c∗
b
0
−c∗
is the cost-benefit ratio, while
h(b
0
, c
1
) is the joint probability density function of
the classification costs. Finally, the best cut-off value
is T as shown in Equation 6; and, the average cut-off-
dependent classification profit is optimized to produce
the highest profit.
T = argmax
∀t
P(t; b
0
, b
1
, c∗) (6)
2.1 Learning Models
According to (Dastile et al., 2020), in this section we
introduce three categories of learning models: statis-
tical models, machine learning, and deep learning.
Logistic regression (LR) is a popular statistical
model in binary classification defined by the formu-
las P(y = 1|x) =
1
1+exp(−(α
0
+α
T
x))
and P(y = −1|x) =
1−P(y = 1|x); where P(y = 1|x) and P(y = −1|x) are
the probabilities of classifying the observation x as a
good or bad borrower, respectively. Once the model
parameters α
0
and α are trained, the decision rule to
classify an input feature vector x as the output value y
is
y =
(
+1 when exp(α
0
+ α
T
x) < 1
−1 otherwise.
(7)
Another category of models introduced is the ML
ones. A Classification Tree (CT) is a popular algo-
rithm used as a classifier in ML. It is a flowchart-like
structure, where each internal node represents a fea-
ture, each branch represents a decision rule, and each
leaf node represents the classification. The algorithm
works by recursively partitioning the dataset, based
on the feature that best splits the data at each node,
until a stopping criterion is reached.
Preprocessing
Manual feature
removal
WoE data
encodiding
Split
Raw
data
Test
Proce.
data
Val
Train
Risk evaluation
Testing
Financial expert
evalutation
Compute metrics
NSGA-II optimization
Generate genes Training
Yes
No
Reach max
generations?
Initial
hyper-param
Figure 1: Workflow design of the proposed method.
ICEIS 2024 - 26th International Conference on Enterprise Information Systems
716

The last model category introduced is DL, which
through neural networks outperformed in several ar-
eas compared to traditional models. This is due to
DL’s ability to learn hierarchical representations and
complex patterns of input data.
Each learning model can be enhanced with the en-
semble technique. This approach combines the pre-
dictions of multiple models to improve the overall
classification performance. Specifically, a weight-
based voting strategy is implemented to combine the
predictions. The decision function of the ensemble
models can be expressed as:
y = argmax
n
∑
i=1
a
i
· w
i
(8)
where a
i
is the predicted class probability by the i-th
individual model, and w
i
is the weight assigned to the
i-th model.
In the case of ensemble of different CT, a model
called Random Forrest (RF) is obtained; while in the
case of the DL ensemble, it is referred to as Ensemble
Multi-Layer Perceptron (EMLP).
2.2 Data Encoding
The Weight of Evidence (WoE) encoding was used
as a data encoding method to preprocess the datasets
(Raymaekers et al., 2022). The WoE value of each
categorical variable is computed as:
WoE
i
= ln

P
i,0
P
i,1

(9)
where WoE
i
is the WoE value for category i, P
i,1
is the
probability of a borrower defaulting on a loan within
category i, and P
i,0
is the probability of a borrower not
defaulting on a loan.
WoE encoding can also be applied to numerical
variables, by first discretizing them through binning
process. It does not embed a binning strategy, hence
it must be explicitly defined and integrated within the
data encoding. Several binning techniques have been
devised, such as equal-width or equal-size, however,
not all of them guarantee the necessary conditions for
good binning in credit scoring (Zeng, 2014):
• missing values are binned separately,
• a minimum of 5% of the observations per bin,
• for either good or bad, no bins have 0 accounts.
In the proposed workflow, we integrated the opti-
mal binning method proposed by Palencia; his im-
plementation is publicly available at (Navas-Palencia,
2020a). The optimal binning algorithm involves two
steps: A prebinning procedure generating an initial
granular discretization and further fine-tuning to sat-
isfy the enforced constraints.
The implementation proposed by Palencia is
based on the formulation of a mathematical optimiza-
tion problem solvable by mixed-integer programming
in (Navas-Palencia, 2020b). The formulation was
provided for a binary, continuous, and multi-class tar-
get type and guaranteed an optimal solution for a
given set of input parameters. Moreover, the math-
ematical formulation of the problem is convex, result-
ing that there is only one optimal solution that can
be obtained efficiently by standard optimization meth-
ods.
2.3 Hyperparameter Optimization
Non-dominated Sorting Genetic Algorithm II
(NSGA-II) was introduced in the workflow to
perform the hyperparameter optimization of credit
scoring models (Verma et al., 2021). NSGA-II is a
well-known multi-objective optimization algorithm
widely used in various domains. In the workflow,
we used NSGA-II to optimize the hyperparameters
of the models, by considering two distinct objective
functions: the Area Under the Receiver Operating
Characteristic curve (AUC) as a classification metric,
and the Expected Maximum Profit (EMP) as a
financial metric. By incorporating EMP, we aim
to optimize the credit scoring models not only for
classification accuracy but also for their financial
impact. The proposed approach enables us to find
a set of non-dominated solutions which provide the
best trade-off between AUC and EMP and allows
us to select the best model for a particular financial
institution based on their specific requirements.
2.4 Focal Loss
It has been shown that class imbalance impedes
classification. However, we refrain from balancing
classes for two reasons. First, our objective is to ex-
amine relative performance differences across differ-
ent classifiers. If class imbalance hurts all classifiers
in the same way, it would affect the absolute level
of observed performance but not the relative perfor-
mance differences among classifiers. Second, if some
classifiers are particularly robust toward class imbal-
ance, then such a trait is a relevant indicator of the
classifier’s merit. Equation 10 presents the rate
de f
in-
dicator used to evaluate the dataset unbalance.
rate
de f
=
De f ault cases
Total cases
(10)
To mitigate the problem, a loss function called
f ocalloss (Mukhoti et al., 2020) was used; Equation
A Machine Learning Workflow to Address Credit Default Prediction
717

11 shows its formulation.
Focal loss is a modification of the cross-entropy
loss function, which assigns a higher weight to hard
examples that are misclassified. The focal loss also
introduces the focusing parameter, which tunes the
emphasis degree on misclassified samples.
FL(p
t
) = −α
t
(1 − p
t
)
γ
ln(p
t
) (11)
where p
t
is the predicted probability of the true class,
α
t
∈ [0, 1] is a weighting factor for class t and γ is the
focusing parameter.
3 EXPERIMENTS AND RESULTS
The described experiments were performed in Python
programming language on a Jupyter Lab server run-
ning Arch Linux operating system. Hardware re-
sources used included AMD Ryzen 9 5950x CPU,
Nvidia RTX A5000 GPU and 128 GiB of RAM. To
ensure reproducibility and transparency, we publicly
released the code and results of the experiments on
GitHub.
Four datasets well-known in the literature and
publicly available were used to implement and test the
proposed methodology. Table 1 presents the datasets
indicating the amount of samples and the rate
de f
.
Table 1: Dataset details.
Name Cases rate
def
GermanCreditData-GER 1000 0.3
HomeEquityLoans-HEL 5960 0.19
HomeEquityCreditLine-HECL 10460 0.52
PolishBankruptcyData-PBD 43405 0.04
The GER and PBD datasets are popular credit
scoring data accessible through the UCI Machine
Learning repository
1
. The HEL dataset was re-
leased publicly in 2020 with (Do et al., 2020). The
HELC dataset was provided by Fair Isaac Corporation
(FICO) as part of the Explainable Machine Learning
challenge
2
.
To ensure that good estimates of the performance
of each classifier are obtained, Optuna (Akiba et al.,
2019), an open source hyperparameter optimization
software framework, was used. Optuna enables effi-
cient hyperparameter optimization by adopting state-
of-the-art algorithms for sampling hyperparameters
and pruning efficiently unpromising trials. The pro-
vided NSGA-II implementation with default parame-
1
https:archive.ics.uci.edu
2
https:community.fico.comsexplainable-machine-
learning-challenge
ters was used to continually narrow down the search
space leading to better objective values.
Figure 2 illustrates an example of hyperparame-
ter optimization processes and highlights the pareto
front, represented by the red points in the scatter plot.
The pareto front is composed of the non-dominated
solutions that refer to the best sets of hyperparame-
ters, capturing the trade-off between EMP and AUC
performance metrics (Hua et al., 2021). The models
whose results are shown in Tables 2, 3, 4 and 5 were
manually chosen from those on the pareto front by
observing the values of the performance metrics.
We can see how the DL models outperformed the
statistical and ML models for each dataset; in fact, the
best results are consistently found in the last rows of
the tables for the MLP and EMLP models. In addi-
tion, the ensemble models introduce an enhancement
over the corresponding non-ensemble models.
300μ
200μ
100μ
0
0.5 0.51 0.52
80k
60k
40k
20k
100k
60k
50k
40k
30k
20k
10k
ROC AUC
Trial Best Trial
EMP
Figure 2: Scatter plot of the random forrest hyperparameter
optimization process.
Table 2: Performance metrics on GER dataset.
Model AUC F1 BS EMP
LR .800 .627 .255 .051
CT .701 .546 .341 .041
RF .792 .558 .236 .037
MLP .799 .616 .273 .050
EMLP .801 .632 .249 .053
Table 3: Performance metrics on HEL dataset.
Model AUC F1 BS EMP
LR .869 .580 .151 .017
CT .820 .671 .152 .025
RF .940 .693 .114 .023
MLP .864 .604 .210 .022
EMLP .866 .636 .136 .024
ICEIS 2024 - 26th International Conference on Enterprise Information Systems
718

Table 4: Performance metrics on HECL dataset.
Model AUC F1 BS EMP
LR .801 .610 .251 .054
CT .812 .631 .242 .060
RF .863 .703 .214 .063
MLP .892 .717 .198 .068
EMLP .906 .748 .136 .070
Table 5: Performance metrics on PBD dataset.
Model AUC F1 BS EMP
LR .781 .516 .359 .051
CT .793 .538 .342 .059
RF .824 .609 .317 .060
MLP .841 .612 .296 .062
EMLP .883 .648 .233 .069
4 CONCLUSION
In this paper, we proposed a novel ML workflow
for assessing the risk evaluation in the credit scor-
ing context that combines WoE-based preprocessing,
ensemble strategies of different learning models, and
NSGA-II hyperparameter optimization.
The proposed workflow has been tested on dif-
ferent public datasets, and we have presented bench-
marks. The experiments indicate the methodology
succeeds in effectively combining the strengths of the
different technologies and frameworks that constitute
the workflow to improve the robustness and reliabil-
ity of the risk assessment support tools in the financial
industry.
Future work could explore the applicability of
our approach in real-world scenarios by integrating
the classification models into enterprise software sys-
tems, thereby enhancing usability for bank employees
and financial consultants. This integration has the po-
tential to streamline and optimize financial processes,
providing a practical solution for the challenges faced
in the banking and financial consulting domains. In
addition, the applicability of this approach can be ex-
tended to corporate credit scoring, beyond the cus-
tomer.
ACKNOWLEDGEMENTS
Work partially supported by: (i) the University of
Pisa, in the framework of the PRA 2022 101 project
“Decision Support Systems for territorial networks
for managing ecosystem services”; (ii) the European
Commission under the NextGenerationEU program,
Partenariato Esteso PNRR PE1 - ”FAIR - Future Ar-
tificial Intelligence Research” - Spoke 1 ”Human-
centered AI”; (iii) the Italian Ministry of Educa-
tion and Research (MIUR) in the framework of the
FoReLab project (Departments of Excellence) and of
the ”Reasoning” project, PRIN 2020 LS Programme,
Project number 2493 04-11-2021.
REFERENCES
Akiba, T., Sano, S., Yanase, T., Ohta, T., and Koyama, M.
(2019). Optuna: A next-generation hyperparameter
optimization framework. In Proceedings of the 25th
ACM SIGKDD international conference on knowl-
edge discovery & data mining, pages 2623–2631.
Bequ
´
e, A., Coussement, K., Gayler, R., and Lessmann, S.
(2017). Approaches for credit scorecard calibration:
An empirical analysis. Knowledge-Based Systems,
134:213–227.
Cimino., M., Galatolo., F., Parola., M., Perilli., N., and
Squeglia., N. (2022). Deep learning of structural
changes in historical buildings: The case study of
the pisa tower. In Proceedings of the 14th Inter-
national Joint Conference on Computational Intel-
ligence (IJCCI 2022) - NCTA, pages 396–403. IN-
STICC, SciTePress.
Cimino, M. G. and Vaglini, G. (2014). An interval-
valued approach to business process simulation based
on genetic algorithms and the bpmn. Information,
5(2):319–356.
Cimino, M. G. C. A., Dalla Bona, F., Foglia, P., Monaco,
M., Prete, C. A., and Vaglini, G. (2018). Stock price
forecasting over adaptive timescale using supervised
learning and receptive fields. In Groza, A. and Prasath,
R., editors, Mining Intelligence and Knowledge Ex-
ploration, pages 279–288, Cham. Springer Interna-
tional Publishing.
Dastile, X., Celik, T., and Potsane, M. (2020). Statisti-
cal and machine learning models in credit scoring: A
systematic literature survey. Applied Soft Computing,
91:106263.
Devi, S. S. and Radhika, Y. (2018). A survey on machine
learning and statistical techniques in bankruptcy pre-
diction. International Journal of Machine Learning
and Computing, 8(2):133–139.
Do, H. X., R
¨
osch, D., and Scheule, H. (2020). Liquid-
ity constraints, home equity and residential mortgage
losses. The Journal of Real Estate Finance and Eco-
nomics, 61:208–246.
Hand, D. J. (2009). Measuring classifier performance: a
coherent alternative to the area under the roc curve.
Machine learning, 77(1):103–123.
Hua, Y., Liu, Q., Hao, K., and Jin, Y. (2021). A survey of
evolutionary algorithms for multi-objective optimiza-
tion problems with irregular pareto fronts. IEEE/CAA
Journal of Automatica Sinica, 8(2):303–318.
Lago, J., De Ridder, F., and De Schutter, B. (2018). Fore-
casting spot electricity prices: Deep learning ap-
A Machine Learning Workflow to Address Credit Default Prediction
719

proaches and empirical comparison of traditional al-
gorithms. Applied Energy, 221:386–405.
Luo, C., Wu, D., and Wu, D. (2017). A deep learn-
ing approach for credit scoring using credit default
swaps. Engineering Applications of Artificial Intel-
ligence, 65:465–470.
L’heureux, A., Grolinger, K., Elyamany, H. F., and Capretz,
M. A. (2017). Machine learning with big data: Chal-
lenges and approaches. Ieee Access, 5:7776–7797.
Moula, F. E., Guotai, C., and Abedin, M. Z. (2017). Credit
default prediction modeling: an application of support
vector machine. Risk Management, 19:158–187.
Mukhoti, J., Kulharia, V., Sanyal, A., Golodetz, S., Torr,
P., and Dokania, P. (2020). Calibrating deep neural
networks using focal loss. Advances in Neural Infor-
mation Processing Systems, 33:15288–15299.
Navas-Palencia, G. (2020a). Github optbinning
repository, https://github.com/guillermo-navas-
palencia/optbinning.
Navas-Palencia, G. (2020b). Optimal binning: mathemati-
cal programming formulation. abs/2001.08025.
´
Oskarsd
´
ottir, M., Bravo, C., Sarraute, C., Vanthienen, J.,
and Baesens, B. (2019). The value of big data for
credit scoring: Enhancing financial inclusion using
mobile phone data and social network analytics. Ap-
plied Soft Computing, 74:26–39.
Parola., M., Dirrhami., H., Cimino., M., and Squeglia.,
N. (2023). Effects of environmental conditions on
historic buildings: Interpretable versus accurate ex-
ploratory data analysis. In Proceedings of the 12th In-
ternational Conference on Data Science, Technology
and Applications - DATA, pages 429–435. INSTICC,
SciTePress.
Parola, M., Galatolo, F. A., Torzoni, M., and Cimino, M.
G. C. A. (2023a). Convolutional neural networks
for structural damage localization on digital twins.
In Fred, A., Sansone, C., Gusikhin, O., and Madani,
K., editors, Deep Learning Theory and Applications,
pages 78–97, Cham. Springer Nature Switzerland.
Parola., M., Galatolo., F. A., Torzoni., M., Cimino., M. G.
C. A., and Vaglini., G. (2022). Structural damage
localization via deep learning and iot enabled digital
twin. In Proceedings of the 3rd International Con-
ference on Deep Learning Theory and Applications -
DeLTA, pages 199–206. INSTICC, SciTePress.
Parola, M., Mantia, G. L., Galatolo, F., Cimino, M. G.,
Campisi, G., and Di Fede, O. (2023b). Image-based
screening of oral cancer via deep ensemble architec-
ture. In 2023 IEEE Symposium Series on Computa-
tional Intelligence (SSCI), pages 1572–1578.
Raymaekers, J., Verbeke, W., and Verdonck, T. (2022).
Weight-of-evidence through shrinkage and spline bin-
ning for interpretable nonlinear classification. Applied
Soft Computing, 115:108160.
Sudjianto, A., Nair, S., Yuan, M., Zhang, A., Kern, D., and
Cela-D
´
ıaz, F. (2010). Statistical methods for fighting
financial crimes. Technometrics, 52(1):5–19.
Teles, G., Rodrigues, J. J., Saleem, K., Kozlov, S., and
Rab
ˆ
elo, R. A. (2020). Machine learning and decision
support system on credit scoring. Neural Computing
and Applications, 32:9809–9826.
Thomas, L., Crook, J., and Edelman, D. (2017). Credit
scoring and its applications. SIAM.
Verbraken, T., Bravo, C., Weber, R., and Baesens, B.
(2014a). Development and application of consumer
credit scoring models using profit-based classifica-
tion measures. European Journal of Operational Re-
search, 238(2):505–513.
Verbraken, T., Bravo, C., Weber, R., and Baesens, B.
(2014b). Development and application of consumer
credit scoring models using profit-based classifica-
tion measures. European Journal of Operational Re-
search, 238(2):505–513.
Verma, S., Pant, M., and Snasel, V. (2021). A comprehen-
sive review on nsga-ii for multi-objective combina-
torial optimization problems. Ieee Access, 9:57757–
57791.
Zeng, G. (2014). A necessary condition for a good bin-
ning algorithm in credit scoring. Applied Mathemati-
cal Sciences, 8(65):3229–3242.
ICEIS 2024 - 26th International Conference on Enterprise Information Systems
720