Stochastic Simulation Agent for Unknown Inventory Demands

in Healthcare Supply Management

Rafael Marin Machado de Souza

1,2,5 a

, Leandro Nunes de Castro

1,4,5 b

, Marcio Biczyk

Marcos dos Santos

2,3 d

and Eder Costa Cassettari

Hospital das Clínicas da Faculdade de Medicina da Universidade de São Paulo (HCFMUSP), InLab,

Rua Doutor Ovídio Pires de Campos 75 (Portaria 1), São Paulo, SP, Brazil

Universidade de São Paulo (USP), Campus Piracicaba – Luiz de Queiroz,

Rua Alexandre Herculano, 143 – Monteiro, Piracicaba, SP, Brazil

Ministério da Defesa - Comando da Marinha, Centro de Análises de Sistemas Navais – CASNAV,

Praça Barão de Ladário S/N° - Ed. 23, Centro, Rio de Janeiro, RJ, Brazil

Florida Gulf Coast University (FGCU), 10501 Fgcu Blvd S, Fort Myers, FL 33965, U.S.A.

Universidade Estadual de Campinas (UNICAMP), Faculdade de Tecnologia,

R. Paschoal Marmo, 1888 - Jd. Nova Itália, Limeira, SP, Brazil

Keywords: Software Agent, Simulation, Monte Carlo, Inventory Theory.

Abstract: The acquisition of innovative items or those without historical demand data considerably increases the com-

plexity of the routine of buyers, who among the daily challenges are keeping stocks up to date, with quantities

that provide maximum profitability or maximum use of the purchased items. Seeking to provide a tool to

assist in these goals, this study implements a Python-based software agent employing the Monte Carlo method

for stochastic simulation and proposes a solution for uncertain inventory demands, providing a decision-mak-

ing tool in the absence of historical data, thereby optimizing inventory levels and maximizing profitability.

Experiments conducted across both local and cloud server configurations, with a comparative analysis of CPU

and GPU performance, demonstrates the agent's capacity to generate random scenarios with a statistical tol-

erance margin of 1% from 10,000 simulations. Scalability tests underscore the agent's adaptability to diverse

scenarios, effectively harnessing GPU capabilities for processing extensive data.

1 INTRODUCTION

The pandemic scenario brought to light latent

difficulties in managing stocks in both the private and

public areas, such as a lack of materials and vaccines,

in all instances. The main question of all professionals

in the area was: “How much medicine and supplies

should be bought in a situation never experienced

before?”

The lack of historical data is one of the challenges

among the many experienced by healthcare supply

chain managers and discussed globally in the

scientific literature (Privett and Gonsalvez, 2014;

https://orcid.org/0000−0002−7939−6030

https://orcid.org/0000−0003−3409−4589

https://orcid.org/0000−0003−1862−712X

https://orcid.org/0000−0003−1533−5535

https://orcid.org/0000−0001−9177−9520

Shang et. al. 2022; Kok, 2018), that listed the ten most

common problems in supply chain management,

which are:

▪ Lack of Orchestration: Fragmented data across

separated data lakes.

▪ Inventory Management: Control of inventory

levels, such as allocations and quantities.

▪ Demand Information: Due to the previous item,

the demands are unknown or sparse.

▪ Dependency on Human Resources: As this is an

area with high employee turnover, lack of

professional experience is a risk factor

and constant training, and qualification are

Marin Machado de Souza, R., Nunes de Castro, L., Biczyk, M., dos Santos, M. and Cassettari, E.

Stochastic Simulation Agent for Unknown Inventory Demands in Healthcare Supply Management.

DOI: 10.5220/0012674700003756

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 13th International Conference on Data Science, Technology and Applications (DATA 2024), pages 211-217

ISBN: 978-989-758-707-8; ISSN: 2184-285X

211

challenges to be considered.

▪ Request Management: Planning, requesting,

and tracking purchases.

▪ Shortage: The lack of preventive control of

stock levels generates replacements conducted

with the urgency of the shortage that tend to be

more expensive.

▪ Expirations: Control the output order based on

the expiration date.

▪ Warehouse Management: Logistic organization.

▪ Temperature Control: Including transport and

storage.

▪ Movement Visibility: Control of delivery times,

delays, and material arrivals.

Enterprise Resource Planning (ERP)

management systems help in the evaluation and

control of the discussed problems. The combination

of decision-making techniques, such as those present

in operational research, for example, together with

this type of system is making it possible for all these

problems to be overcome (ElMadany et al., 2022).

Inventory control aims to meet customer demands

and maximize profit from operations (when it comes

to companies). For this, it must meet three main

criteria: the frequency of measuring the stock level;

the timing of replacement, and the amount of that

replacement (Ma et al., 2019; Silver, 1981).

The question that motivates this work is: How to

carry out purchases of multiple items for storage and

distribution, when none of these previous indicators

are known? This is common in a scenario where there

is no data about previous demands (for the evaluation

of time series), as was the case with vaccines and

materials to combat COVID-19, for example.

The literature on stochastic inventory control

underscores storage space as a prevailing constraint

in this domain, as emphasized by Franco et al. (2019).

Particularly for smaller distributors and resellers, the

permissible quantity for storage per item is also

linked to the budget allocated for supply, as

elucidated by Zhen et al. (2021) and Boulaksil et al.

(2018). Notably, the profitability indicator emerges as

a crucial decision-making parameter, navigating

among the various quantities that align with the

previously mentioned constraints, as posited by

Candan et al. (2016). This connection of factors

highlights the multifaceted nature of decision-making

in inventory control, where considerations of storage

capacity, budgetary constraints, and profitability

collectively shape strategic choices for supply chain

management.

In the domain of agents and simulation, studies

have explored the application of software agents to

enhance decision-making processes. Ma et al. (2019)

delved into stochastic inventory control, emphasizing

the importance of incorporating randomness in

demand scenarios. Marin et al. (2019) proposed the

integration of an Association Rule Mining Agent in

an ERP system, showcasing the potential of agent-

based systems to augment computational scalability.

Mesbahi et al. (2015) introduced a cooperative multi-

agent approach-based clustering in Enterprise

Resource Planning (ERP), indicating the versatility of

agent-based models in addressing complex

organizational processes. Within this context, the

proposed software agent in this study contributes to

the existing literature by employing the Monte Carlo

method for stochastic simulation, offering a

specialized tool to simulate purchasing scenarios and

optimize inventory levels, particularly when

historical data is limited or non-existent, estimating

the quantity of items to be purchased without

historical data on stock or market movements. To do

so, it is proposed a stochastic simulation that meets

the constraints of storage space and costs, and which

calculates a profitability indicator to assist in decision

making. It aims to contribute to the area of data

science by using a simulation algorithm to generate

data that can be extracted in uncertain scenarios.

Monte Carlo Simulation (MCS) is a numerical

method that uses random sampling for massive

simulation of data, meeting certain constraints (Garg

et. al., 2019; Harrison, 2010). The use of the Monte

Carlo method in conjunction with inventory theory is

discussed in the literature for demand simulation as

the newsboy problem (Kevork, 2010). Jiao (2010)

synthesizes its use in four steps, starting with the

design of a probabilistic model, generating random

values respecting this model, then repeating the

process massively, and finally testing the results

statistically.

The main contributions of this article are:

1. Development of a Python-based software agent:

The article introduces a Python-based software

agent designed to handle complex inventory

management scenarios in the healthcare supply

chain. This agent is tailored to simulate various

scenarios and optimize decision-making

processes, attending to restrictions keys, and an

architecture where it is possible to integrate it in

other systems, like ERP systems.

2. Application of the Monte Carlo method for

inventory management: The software agent

employs the Monte Carlo method, a stochastic

simulation technique, to address the

unpredictability of inventory demands. This

method is particularly useful in situations where

DATA 2024 - 13th International Conference on Data Science, Technology and Applications

212

historical data is lacking, providing a robust

approach to simulate possible outcomes.

3. Generation of diverse scenarios for informed

decision-making: By leveraging the Monte

Carlo method, the agent generates a wide range

of scenarios, facilitating informed decision-

making aligned with organizational goals. This

diversity in simulation outcomes helps

organizations better prepare for dynamic and

unpredictable inventory requirements.

4. Detailed statistical analysis and performance

evaluation: The study provides a comprehensive

statistical analysis of the simulation results,

including measures such as mean, standard

deviation, error, confidence interval, and

tolerance.

5. Performance evaluation of different hardware

configurations, highlighting the processing

behavior on CPUs and GPUs: The research

compares the performance of the software agent

across different hardware configurations.

This paper is organized into three sections. In the

Materials and Methods section, a software agent

developed in Python, capable of integrating with ERP

systems, is presented, receiving constraints and items’

parameters, and returning simulations of quantities

that meet them. In the Results section, there is a

comparison between the usage of CPU (Central

Processing Unit) and GPU (Graphics Processing

Unit), using different quantities of scenarios with

simulated parameters and the values processed by the

tool are evaluated. Finally, in the Conclusions the

uses and potential future works are discussed.

2 MATERIALS AND METHODS

Software Agent (softbot) is a technique that aims to

componentize the processing responsibility, so that

the evaluation of its inputs and responses (outputs)

are autonomous and independent, being able to be

used as inputs of other software agents in a structure

known as multi-agent systems (Russell and Norvig,

2010, Marin et. al., 2019).

The proposed agent follows the PEAS

(Performance, Environment, Actuators, Sensors)

definition, as described in Table 1. The input structure

proposed to the agent, expects a communication with

an ERP system to make it possible to know the

restriction keys necessary for the evaluation of items

that have unknown demand, either because they are

new items on the market (innovative), as occurred

with vaccines against the COVID-19 virus, or by

restricting access to information from other sources

for demand comparisons, as occurs in the private

sector due to competition between companies.

Table 1: PEAS description of an agent.

Performance Environment Actuators Sensors

Profitability

Healthcare

Storages

Purchasing

Scenarios

Costs and

Storage

Space

In order to evaluate demands, the Inventory

Theory uses two types of models: i) deterministic,

when the demand is known; and ii) stochastic, for

unknown or random demands (Chopra and Meindl,

2015; Hillier and Lieberman, 2013; Bowersox et. al.,

2013; Ballou, 2005). As this work deals with

unknown demands, a stochastic model is necessary to

simulate scenarios.

This paper seeks a first-purchase approach, where

there are no previous quantities in inventory, nor

previous data to be used with deterministic or

machine learning methods, performing the

calculations in GPU (Graphics Processing Unit).

There is not a single Monte Carlo method, but the

several that exist follow some specific patterns. They

start by modelling the system as a data series that

meets a probability density function, then create

random samples that meet this function, and finish by

calculating statistics from simulated data (Harrison,

2010).

The internal processing structure of the agent uses

a Monte Carlo simulation to create random scenarios

based on inventory space constraints and budget cost

for the set of items determined in the input

configuration, which has the following parameters:

▪ Number of simulations required.

▪ Total budget cost.

▪ Total cubed space available for items.

▪ Support, used to validate simulations so that the

total simulated cost remains above a configured

factor in percentage terms (set at 95% statistical

confidence by default);

▪ Number of threads, enabling parallel

processing (for CPU comparisons).

As it is a CSV file, each subsequent line deals

separately with an item to be simulated, and therefore

has configuration parameters per item as follows:

▪ Item identifier, code that the agent uses to refer

to the item in simulations.

▪ Unit cost.

▪ Cubed space per unit.

▪ Estimated sale value.

As an output structure, the agent processes the input

parameters using space and cost as constraints, and

Stochastic Simulation Agent for Unknown Inventory Demands in Healthcare Supply Management

213

the estimated sales value parameter to calculate an

estimate of profitability and use it as an index for

decision making. Other outputs calculated by the

agent are statistical indicators of average profitability,

standard deviation, lower and upper intervals, error,

and tolerance.

The distribution of values among the items is also

performed randomly, and the support parameter is

used to assess the final total cost of the proposed

scenario. The total cost and total space variables are

independent of each other, and both are dependent on

the quantity variable.

Although it seems controversial to calculate

statistical data using random data, this method was

used to develop a software agent in the Python

language, capable of using input data provided by an

ERP system and, as a result, deliver the possible

simulated scenarios.

3 EXPERIMENTS AND RESULTS

The software agent was developed in python, using

Pandas (Pandas, 2023) and Numpy (NumPy, 2023)

for the tests in CPU, and CuDF and CuPy (Nvidia,

2023) for the tests in GPU, receives an input data

matrix to parametrize the simulation. In the first line

it determines the global parameters to be used,

starting with a file validation string, the number of

resulting simulations, the total cost that will be used

for distribution, a support parameter, and the number

of threads. To validate the results, the input file is

described in Figure 1.

Figure 1: Configuration of simulated items.

Three different experiments were performed: Sets

with ten thousand, one hundred thousand and one

million simulations to compare between CPU and

GPU in two different configurations. The first one

uses a Google cloud server (using Google Collab

interface), with a 64-bit Intel Xeon CPU with

2.20GHz (called here little Endian), 2 cores and 2

threads per core, 12 GB of RAM running Linux

Ubuntu Server 18.04 and Python 3.10 and an Nvidia

Tesla T4 GPU with 16GB RAM. The second

configuration uses a local (virtualized) server with

Intel Xeon Gold 6136 CPU with 3.00GHz (called

here Gold Endian), 8 cores and 1 thread per core, 16

GB RAM running Linux Ubuntu Server 20.04 and a

RTX Quadro 6000 GPU with 16 GB RAM.

Another test was conducted in RTX Quadro 6000

GPU starting from two million to ten million

simulated scenarios (with two million steps between

them) to evaluate the scalability of GPU usage. For

all these sets, hypothetical values were used and a

total budget of $120,131.22 and a total space for the

items of 12,198 cubic meters, the support factor was

0.95, and ten threads and twenty threads

configurations were used in tests.

The following lines of the parameter matrix are

the items that will be used for quantity distribution. It

can add as many lines as necessary, starting with an

item identifier parameter, followed by the unit cost of

the item and finally the maximization parameter that

is used. For private companies, the goal can be an

estimate of the unit sales value (to maximize profit)

and for the public area it can be the number of patients

treated per unit of the item, for example. For the

experiments performed here, 5 (five) items were

configured, according to Figure 1.

The agent run in 3 steps: At the first step, creates

random samples with 10 times the size of the set

requested in the input file. At the second step, the

agent calculates the space and costs per items for each

simulated scenarios and summarize the lines in Stotal

and Ctotal columns, and evaluates the samples that

meet the constraint keys existing in the input file

(budget, total space and support) and eliminate the

others, and removes the duplicate simulations among

the selected ones, if the number of simulations are

below the requested, the process repeats until it

reaches the target, if it is above the requested, a

pruning is executed.

And, at the last step, the agent calculates the

values and the Profit for all selected scenarios and

returns two different outputs.

The first output (output.csv) contain all the

simulations that met the constraints. The second

output (stats.csv) returns the processing times and

statistical evaluations of the simulations developed,

analysing mean (1), standard deviation (2), error (3),

Confidence interval (4) and tolerance (5) for 95%

confidence (Favero & Belfiore, 2021), calculated as

follows:

DATA 2024 - 13th International Conference on Data Science, Technology and Applications

214

𝑋





∑

𝑋







𝑛

(1)

The mean ( 𝑋



) is the sum of maximization

parameter (Profitability) (X) divided by the number of

samples (n).

𝑆



∑



X













n1



(2)

Standard deviation (𝑆 is a statistical measure that

evaluates the dispersion between samples (𝑋



) and the

mean (𝑋



) and it is calculated by the Square Root of

the variance.

𝐸𝑟𝑟

𝑧𝑐∗S

√

(3)

The Error (𝐸rr is used to produce a confidence

interval based on a constant zc (also called standard

score or z-score), to determine the percentage of

confidence of the model, here it is used 1.96

equivalent to 95% of confidence (2 𝑆) and it is

calculated by selecting a zc confidence and multiplied

by the standard deviation (S) and divided by the

squared root of the number of samples (

√

𝑛

.

CIX



Err

(4)

Confidence interval (CI) calculates the lower and

upper interval based on mean (𝑋



) and the error (Err)

and tolerance (tol) is the absolute proportion of error

(Err) within the mean (𝑋



𝑡𝑜𝑙

𝐸𝑟𝑟

𝑋





(5)

All the three sets were evaluated for combinations

of five items, with a tolerance of 1%. Processing

times showed exponential behaviour for CPUs’ and a

linear behaviour for GPUs’, as can be seen in Figure

2. A point to highlight is the fact that the time

increases as the threads increase, which demonstrates

Figure 2: Simulation processing time.

the processing bottleneck due to the quantity of

processor cores.

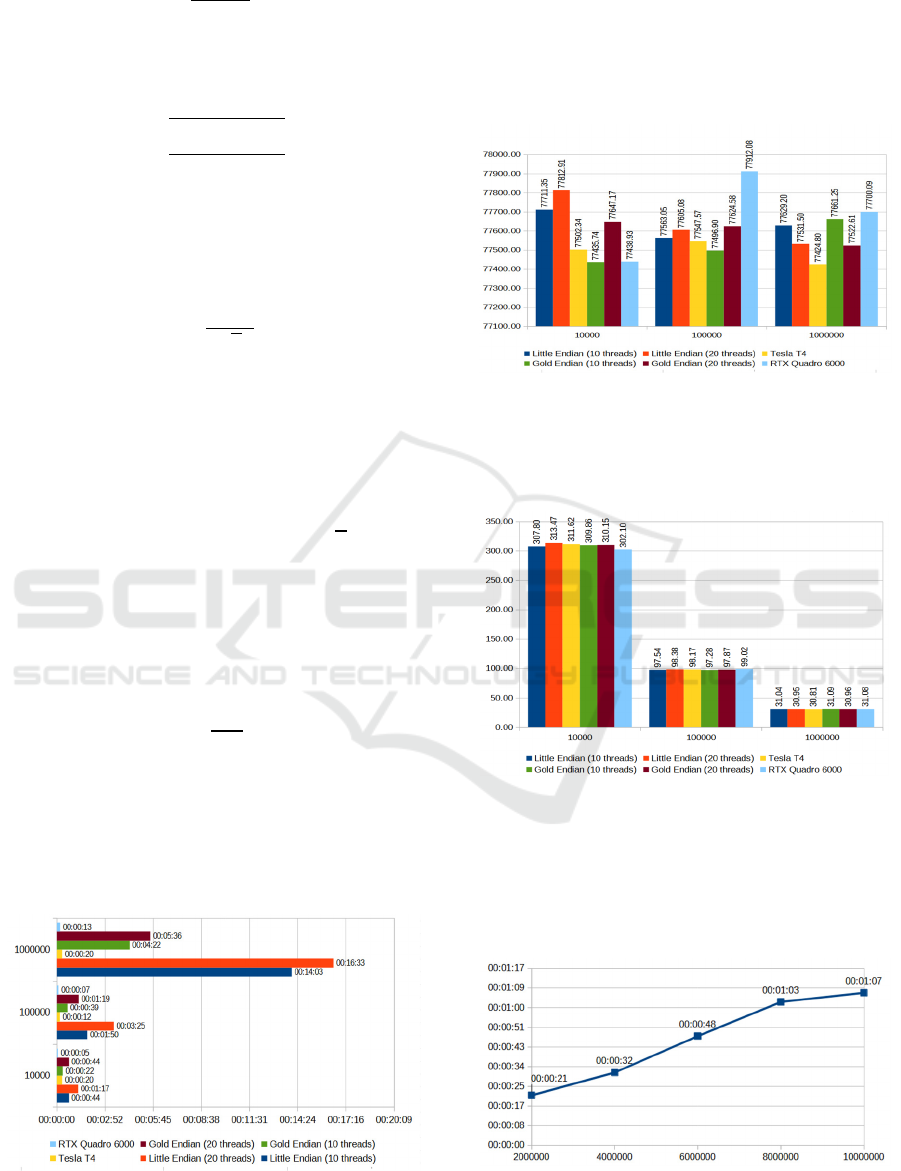
The averages stabilized around 77500 for all the

simulation sets, as can be seen in Figure 3. Which can

be explained by the law of large numbers (Chen et.

al., 2022; Dinov et. al., 2017).

Figure 3: Averages of profits.

And the error also decreased with exponential

behaviour as can be seen in figure 4, that shows a

reduction of dispersion in the simulated data.

Figure 4: Errors per set.

As the processing times of the GPUs did not show

significant variations for the initially proposed sets, new

sets were tested until the first minute of processing was

reached. To do this, new sets of 2, 4, 6, 8 and 10 million

scenarios were tested, as can be seen in Figure 5.

Figure 5: Simulation processing time on RTX Quadro 6000

GPU.

Stochastic Simulation Agent for Unknown Inventory Demands in Healthcare Supply Management

215

To reach the first minute of simulations’ processing,

an RTX Quadro 6000 GPU its needed 8 million valid

and exclusive random scenarios, also demonstrating

its linear behaviour.

4 CONCLUSIONS

The exploration within the domain of healthcare

supply chain management has shed light on substantial

challenges, especially in the unprecedented

circumstances introduced by the COVID-19 pandemic.

This study seeks to explore the complexities linked to

unknown inventory demands, particularly in scenarios

where historical data is unavailable. A Python-based

software agent (source code available in appendix

section), driven by the Monte Carlo method, is

proposed as a solution to address the multifaceted

issues encountered in multi-criteria decision-making

for inventory management. The computational

experiments carried out to validate the software agent

made it possible to demonstrate the efficiency and

effectiveness of the proposed solution. Despite the

inherent high computational cost associated with

stochastic simulations, the agent demonstrated its

ability to reach a statistically tolerable margin of 1%

after 10,000 simulations. The variety of scenarios

generated by the agent serves as a resource for

informed decision-making in alignment with an

organization's objectives. The experiments conducted

on different server configurations shown the agent's

potential across various technological landscapes. The

proposed software agent offers a pathway for

organizations to simulate different scenarios, for other

items and restriction keys, offering a solution to the

challenges posed by dynamic and unpredictable

scenarios. This work encourages further exploration

and refinement of simulation-based decision-making

tools, as the implementation of new restrictions,

fostering adaptability in the face of ever-evolving

healthcare landscapes.

ACKNOWLEDGEMENTS

This study was funded by FAPESP (grant number

2021/11.905-0 and process number 2023/13355-3).

REFERENCES

Ballou, R. H. (2005). Supply Chain Management / Business

Logistics. Bookman.

Boulaksil, Y., van Wijk, S. (2018). A cash-constrained sto-

chastic inventory model with consumer loans and sup-

plier credits: the case of nanostores in emerging markets.

International Journal of Production Research. 56. 1-22.

10.1080/00207543.2018.1424368.

Bowersox, D. J., Closs, D. J., Cooper, M. B., Bowersox, J.

C. (2013). Supply Chain Logistics Management.

AMGH.

Candan, G; Yazgan, H. (2016). A novel approach for inven-

tory problem in the pharmaceutical supply chain.

DARU Journal of Pharmaceutical Sciences. 24.

10.1186/s40199-016-0144-y.

Chen, B., Wu, Q. (2022). The laws of large numbers for

Pareto-type random variables under sub-linear expecta-

tion. Front. Math 17, 783–796. https://doi.org/

10.1007/s11464-022-1026-x

Chopra, S; Meindl, P. (2015). Supply Chain Management:

Strategy, Planning and Operations. Pearson.

Dinov, I. Christou, N. & Gould, R. (2017) Law of Large

Numbers: The Theory, Applications and Technology-

Based Education. Journal of Statistics Education, 17:1,

DOI: 10.1080/10691898.2009.11889499

Elmadany, H.; Alfonse, M.; Aref, M. (2022). Forecasting

in Enterprise Resource Planning (ERP) Systems: A Sur-

vey. 10.1007/978-981-16-2275-5_24.

Favero, L. P., Belfiore, P. (2017). Data Analysis Manual.

LTC. Ed. 1. ISBN 8535270876

Franco, C., Alfonso-Lizarazo, E. (2019). Optimization un-

der uncertainty of the pharmaceutical supply chain in

hospitals. Computers & Chemical Engineering. 135.

106689. 10.1016/j.compchemeng.2019.106689.

Garg, N., Yadav, S. & Aswal, D.K. (2019). Monte Carlo

Simulation in Uncertainty Evaluation: Strategy, Impli-

cations and Future Prospects. MAPAN 34, 299–304.

https://doi.org/10.1007/s12647-019-00345-5.

Harrison, R. L. (2010). Introduction to Monte Carlo Simu-

lation. AIP Publishing.

Hillier, F., Lieberman, G. (2013). Introduction to Opera-

tions Research. McGraw Hill.

Jiao, S and Du, S. (2010). Modeling for Random Inventory

System Based on Monte Carlo Theory and Its Simula-

tion. Third International Symposium on Information

Science and Engineering, Shanghai, China, 2010, pp.

396-399, doi: 10.1109/ISISE.2010.30.

Kevork, I. S. (2010). Estimating the optimal order quantity

and the maximum expected profit for single-period in-

ventory decisions. Elsevier: Omega, Volume 38 (3–4),

218-227, ISSN 0305-0483, https://doi.org/10.

1016/j.omega.2009.09.005.

Kok, T. Grob, C. Laumanns, M. Minner, S. Rambau, J.

Schade, K. (2018). A typology and literature review on

stochastic multi-echelon inventory models. European

Journal of Operational Research, 269 (3), 955-983.

Ma, X., Rossi, R., Archibald, T. (2019). Stochastic Inven-

tory Control: A Literature Review. IFAC-

PapersOnLine. 52. 1490-1495. 10.1016/j.ifacol.

2019.11.410.

Marin, R., Vilasbôas, F., Notargiacomo, P., de Castro, L.N.

(2019). Integrating an Association Rule Mining Agent

in an ERP System: A Proposal and a Computational

DATA 2024 - 13th International Conference on Data Science, Technology and Applications

216

Scalability Analysis. Proceedings of the 11th Interna-

tional Conference on Agents and Artificial Intelligence

(ICAART 2019), 778-786.

Mesbahi, N., Kazar, O., Benharzallah, S., Zoubeidi, M.

(2015). A Cooperative Multi-Agent Approach-Based

Clustering in Enterprise Resource Planning. Interna-

tional Journal of Knowledge and Systems Science

(IJKSS). 6. 34-45. 10.4018/ijkss.2015010103.

Nvidia. (2023). RAPIDS - GPU accelerated data science.

Available at: https://rapids.ai/ (Accessed: September 04

2023).

NumPy. (2023). NumPy - The fundamental package for sci-

entific computing with Python. Available at:

https://numpy.org/ (Accessed: August 12, 2023).

Pandas. (2023). Pandas. Available at: https://numpy.org/

(Accessed: August 12, 2023).

Privett, N., Gonsalves, D. (2014). The top ten global health

supply chain issues: Perspectives from the field. Oper-

ations Research for Health Care. 3. 226-230.

10.1016/j.orhc.2014.09.002.

Russell, S., Norvig, P. (2010). Artificial Intelligence A

Modern Approach. Prentice Hall.

Shang, X., Zhang, G. Jia, B. Almanaseer, M. (2022) The

healthcare supply location-inventory-routing problem:

A robust approach. Transportation Research Part E:

Logistics and Transportation Review, 158.

Silver, E.A. (1981). Operations research in inventory man-

agement: A review and critique. Operations Research,

29(4), 628–645.

Zhen, C., Rossi, R. (2021). A dynamic ordering policy for a

stochastic inventory problem with cash constraints.

Elsevier: Omega.

Stochastic Simulation Agent for Unknown Inventory Demands in Healthcare Supply Management

217