
Optimizing Traffic Adaptive Signal Control: A Multi-Objective
Simulation-Based Approach for Enhanced Transportation Efficiency
Sarah Salem
a
and Axel Leonhardt
b
Institute of Transport and Spatial Planning, University of the Bundeswehr Munich, Munich, Bavaria, Germany
Keywords: Multi-Objective Optimization, Simulation-Based Optimization, Traffic Signal Control.
Abstract: This research aims to improve traffic flow efficiency, reduce congestion, and enhance the overall performance
of the transportation system for different road users, while keeping in mind the ease of implementation of the
provided approach. That is achieved by optimizing the stage length parameter in the VAP files for VISSIM
using ParMOO, a powerful optimization tool. The VAP files contain crucial information about traffic signal
control logic, including signal timings, stage durations, and cycle lengths. The maximum stage length
parameter within VAP files represents the maximum allowable time for a particular traffic signal stage before
transitioning to the next stage. Optimizing this parameter can significantly impact traffic performance by
reducing delays and improving overall traffic flow efficiency. Average delays for passenger cars and
pedestrians are chosen as objective functions to be minimized. Sensitivity analysis is employed to validate
the optimized solutions. Comparing the traffic performance measures using the optimized VAP files with the
base case, we found that the optimized solutions consistently outperformed the observed performance. The
research contributes by utilizing the ParMOO algorithm and integrating it within VISSIM software, enabling
researchers to readily apply the methodology and advance the field of traffic signal control with practical and
industry-relevant solutions.
1 INTRODUCTION
The increasing demand for urban mobility
underscores the necessity of improving transportation
networks. However, congestion in urban areas
impedes efficiency, causing delays, increased fuel
consumption, and pollution. Construction of new
roads in densely populated urban areas is challenging
due to space constraints and environmental concerns.
Moreover, improving roads may exacerbate traffic by
attracting more vehicles. Innovative solutions
focusing on current infrastructure and efficient
transportation policies are essential to tackle these
challenges. Expanding road infrastructure is
impractical due to limited land resources and
socioeconomic factors. Research efforts now
prioritize effective traffic management,
transportation facility enhancements, and meeting
escalating traffic demands. Developing efficient
traffic management solutions offers a cost-effective
approach to alleviate congestion and address
a
https://orcid.org/0009-0004-5581-9192
b
https://orcid.org/0009-0000-1382-3231
optimization challenges in cities by enhancing
network performance.
Upgrading transportation systems to enhance
intelligence is a significant focus in transportation
research. The Intelligent Transportation System (ITS)
integrates technology into infrastructure to enhance
performance, efficiency, and safety. ITS targets
transportation issues such as safety, congestion,
efficiency, and environmental protection through
smarter highways and innovative technologies.
Traffic signal control systems play a crucial role in
urban traffic management and are a key area of study
in ITS. They regulate traffic at intersections, ensuring
the safety of all road users. Efficient operation of
these systems is vital for network performance and is
integral to ITS.
Two main strategies for optimizing traffic signal
timing exist: mathematical programming and
simulation-based methods. Mathematical
programming utilizes mathematical models to
optimize traffic management goals. However, these
344
Salem, S. and Leonhardt, A.
Optimizing Traffic Adaptive Signal Control: A Multi-Objective Simulation-Based Approach for Enhanced Transportation Efficiency.
DOI: 10.5220/0012682100003702
Paper published under CC license (CC BY-NC-ND 4.0)
In Proceedings of the 10th International Conference on Vehicle Technology and Intelligent Transport Systems (VEHITS 2024), pages 344-351
ISBN: 978-989-758-703-0; ISSN: 2184-495X
Proceedings Copyright © 2024 by SCITEPRESS – Science and Technology Publications, Lda.

models often entail complex computations, limiting
their real-time usability and accuracy in depicting
detailed traffic dynamics. Simulation-based methods
strive to accurately model interactions among various
traffic characteristics. Recent studies favor
simulation-based techniques, employing microscopic
traffic simulators to illustrate complex traffic patterns
in cities. Nevertheless, scarcity of simulation
resources presents a challenge for addressing large-
scale urban traffic management problems. Advanced
simulation models require further development to
tackle high-dimensional optimization challenges in
large metropolitan networks (Chen & Chang, 2014;
P. T. M. Nguyen, 2020; Papatzikou & Stathopoulos,
2015; Poole & Kotsialos, 2016).
Improvements in traffic signal management
systems have targeted multiple goals, including
reducing queue lengths, delays, travel time,
enhancing traffic flow, and minimizing traffic
exhaust emissions. Optimizing traffic signals can
achieve these goals simultaneously, leading to
reduced travel times and improved traffic flow.
However, optimization for different road users and
environmental goals may conflict with other priorities
and receive limited consideration. Transportation
management studies often focus on single-goal
issues, despite real-world situations involving
multiple objectives (Chen & Chang, 2014; P. T. M.
Nguyen, 2020; Papatzikou & Stathopoulos, 2015;
Poole & Kotsialos, 2016).
2 LITERATURE REVIEW
Traffic simulation models are classified into
macroscopic, microscopic, and mesoscopic models
based on their level of detail. Macroscopic models
represent traffic flow using aggregate measures,
while microscopic models simulate individual
vehicles in detail. Mesoscopic models strike a balance
between detail and efficiency. This study focuses on
microscopic and mesoscopic simulators like VISSIM
due to their ability to handle complex traffic
scenarios. Microscopic simulators offer detailed
modeling capabilities, while mesoscopic simulators
compromise between detail and computational
efficiency. They utilize driver behavior models to
simulate vehicle interactions based on perception and
response thresholds. (Qadri et al., 2020).
Multi-objective optimization problems (MOOPs)
are prevalent across scientific and engineering
domains, including product design and model fitting,
where multiple performance criteria must be
considered. The main goal of MOOPs is to identify
solutions that balance conflicting objectives, resulting
in a range of achievable values for each objective. This
range of solutions, known as the Pareto front or
tradeoff curve, illustrates inherent trade-offs within the
problem. Real-world MOOPs often include additional
constraints or rules that solutions must adhere to. In
multi-objective simulation-based optimization,
objectives are typically derived from costly
simulations, providing data to evaluate different
designs or strategies. By optimizing these objectives, a
set of Pareto-optimal solutions is revealed, offering
various trade-offs between conflicting objectives. In
essence, MOOPs provide a framework for decision-
making amid conflicting goals, facilitating the
exploration of trade-offs and the identification of
optimal solutions that align with specific requirements
and priorities (Červeňanská et al., 2020; Chang &
Wild, 2023; P. T. M. Nguyen, 2020).
There appears to be a research gap in
implementing multi-objective simulation-based
optimization for the traffic signal control problem
(Qadri et al., 2020). Most transportation management
optimization studies and implementations focus on
issues with a single goal; real-world situations, on the
other hand, frequently entail many goals.
Optimization for other road users such as transit
vehicles or pedestrians or optimization for
environmental goals sometimes clash with other
priorities, and as a result, they are given little
consideration. P. H. Nguyen et al. (2016), Hatri and
Boumhidi (2016), Zheng et al. (2019), and Zhang et
al. (2022) have been among the few researchers to
employ a multi-objective simulation-optimization
approach. Although this approach is relevant, there
appears to be a research gap when it comes to
implementing multi-objective Simulation
Optimization for the traffic signal control problem.
Nguyen et al. proposed a multi-objective
simulation-optimization approach for urban traffic
signal control. Their approach integrated a local
search algorithm with NSGA-II, outperforming other
algorithms and achieving good simulation results
during the optimization process. The study
demonstrated the effectiveness of the approach in
balancing multiple objectives and improving traffic
flow (P. H. Nguyen et al., 2016). Hatri et al. focused
on bi-objective optimization of traffic signal timings
using the NSGA-II algorithm with the Enhanced
Archive Memory (EAM) technique. The goal was to
find optimal signal timings that strike a balance
between traffic flow and delay. The results indicate
that the proposed approach effectively manages the
trade-off between these two objectives and achieves
improved performance compared to other methods.
Optimizing Traffic Adaptive Signal Control: A Multi-Objective Simulation-Based Approach for Enhanced Transportation Efficiency
345

By utilizing the EAM technique, the algorithm can
efficiently handle the optimization process (Hatri &
Boumhidi, 2016). Another study by Zheng et al.
presented a bi-objective stochastic simulation-
optimization approach for traffic signal optimization.
They incorporated surrogate models to capture the
mapping relationship between decision variables and
objectives, resulting in improved performance
compared to other approaches. The use of surrogate
models also enhanced the efficiency of the
optimization process (Zheng et al., 2019). Zhang et
al. utilized a multi-objective evolutionary algorithm
for the optimization of signal timing at intersections.
The algorithm addressed the challenge of
coordinating traffic signals to improve traffic flow
and reduce congestion. By simultaneously optimizing
multiple objectives, the algorithm identified a set of
Pareto-optimal solutions offering different trade-offs
between objectives. This approach provides decision-
makers with a range of options based on their
priorities (Zheng et al., 2019).
The research introduces a significant
advancement by utilizing ParMOO, an open-source
algorithm, for multi-objective optimization in traffic
signal control. This approach ensures accessibility
and ease of implementation for researchers, industry
experts, and municipalities involved in traffic
management. Additionally, the study incorporates
modifications within the VAP file of VISSIM, a
widely recognized software in transportation and
municipal planning. These modifications align the
proposed methodology with existing practices and
enable seamless integration into real-world traffic
management systems.
3 METHODOLOGY
This research utilizes VISSIM, a popular microscopic
traffic simulation software, and the ParMOO
algorithm for multi-objective optimization to tackle
the challenge of optimizing traffic signal timings.
VISSIM provides a realistic platform for modelling
and simulating complex traffic scenarios, allowing
researchers and practitioners to assess various traffic
management strategies' performance. Meanwhile,
ParMOO offers a comprehensive framework for
multi-objective optimization, facilitating
simultaneous optimization of conflicting objectives.
In the following section, we delve into the
functionalities and methodologies of VISSIM and
ParMOO, highlighting how their capabilities are
leveraged to enhance traffic flow and alleviate
congestion through signal timing optimization.
3.1 Traffic Simulation and VISSIM
VISSIM, developed by Company PTV AG, is the
chosen traffic modelling tool for this paper. Widely
used by traffic engineers and researchers, VISSIM
offers an intuitive graphical user interface (GUI) for
designing road networks and running simulations.
Additionally, the VISSIM-COM interface allows
programmers to control simulator functions and
parameters through various programming languages
like Matlab and Python. (PTV Vissim VisVAP User
Manual, 2021; VISSIM: Microscopic Multi-modal
Traffic Flow Simulation, 2021; Tettamanti &
Horváth, 2020; Yan et al., 2013).
The Vissig module of VISSIM determines signal
data, including stage and interstage definitions.
Control logic, governing traffic signal operations, is
defined using VAP (Vehicle Actuated Programming),
with VisVAP serving as a GUI to create flowchart-
based control logic stored in a .vap file. Static signal
base data can be defined in VISSIG, stored in a .pua
file, serving as main inputs for the VISSIM
simulation environment. (Figure 1).
Parameterizing maximum stage durations in VAP
files and simulating signal control schemes lets you
evaluate their effects. This iterative method explores
and optimizes traffic signal layouts to improve system
performance, lowering delays, boosting traffic flow
efficiency, and improving road user experiences.
3.2 Multi-Objective Optimization with
ParMOO
ParMOO, a strong multi-objective optimization
toolkit, is used in this section. Multi-objective
optimization is crucial to traffic signal timing
optimization, and ParMOO's features and capabilities
help (Chang & Wild, 2023). ParMOO is designed for
simulation-based multiobjective optimization. The
difference between simulations and objectives is
crucial to ParMOO. Simulations with ParMOO
require a lot of processing power and time. ParMOO
uses response surface methodology to solve this. This
method fits computationally simpler surrogate
models to simulation outputs. ParMOO optimizes
problem scalarizations using surrogate models
instead of expensive simulations. This method
efficiently explores and optimises the multiobjective
problem space while lowering computational costs
and execution time (Chang & Wild, 2023; ParMOO
Documentation, 2022). Main components of
ParMOO (Parallel Multi-Objective Optimization)
(ParMOO Documentation, 2022):
VEHITS 2024 - 10th International Conference on Vehicle Technology and Intelligent Transport Systems
346
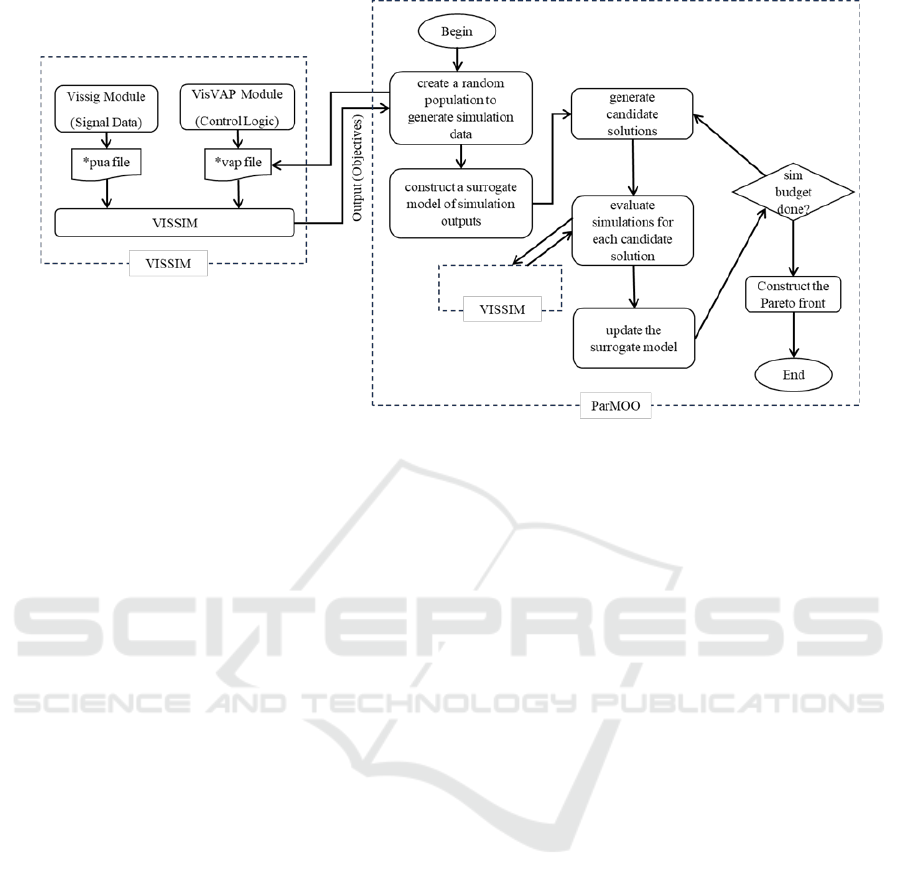
Figure 1: Framework of ParMOO and VISSIM Integration (Parmoo Documentation, 2022; VISSIM: Microscopic Multi-modal
Traffic Flow Simulation, 2021).
A MOOP object is a data structure that contains
essential information for a multi-objective
optimization problem. The problem is solved using a
multi-objective optimization technique.
Objective Functions. With ParMOO, define one or
more functions to represent the performance
measures to optimize. These functions measure
optimization aims. Traffic signal optimization
objectives may include decreasing delays,
maximizing throughput, reducing emissions, or
minimizing user class conflicts.
Decision Variables. Adjustable parameters or
variables that can be optimized to meet desired
outcomes. ParMOO can optimize traffic signal
decision variables like maximum stage length.
Pareto Front. ParMOO uses the concept of the Pareto
front, which represents the set of non-dominated
solutions in the multi-objective optimization
problem. The Pareto front consists of solutions that
cannot be improved in one objective without
worsening another objective.
Surrogate Functions. Incorporating a simulation
dictionary links each simulation in the MOOP object
to a surrogate model. This relationship uses solution
data to approximate the simulation's response surface.
The surrogate model estimates simulation behavior
and outcomes more efficiently and cheaply than the
actual simulation.
Search Techniques. Each simulation in the MOOP
object has a unique search technique assigned upon
inclusion. This method generates simulation data
before ParMOO's first iteration to fit initial surrogate
models.
Figure 1 demonstrates the ParMOO algorithm and
its components. More information on ParMOO can be
found at (Chang & Wild, 2023; ParMOO
Documentation, 2022).
3.3 Methodology for Traffic Signal
Timing Optimization
This section outlines the methodology for traffic
signal timing optimization. It provides a detailed step-
by-step explanation of how VISSIM and ParMOO are
integrated and employed to optimize traffic signal
timings. The methodology employed in this study
follows a scientific approach to optimize the
maximum stage length parameter using ParMOO and
subsequently incorporating the optimized values into
the VISSIM simulation environment. Figure 1 shows
how VISSIM and ParMOO interact.
The methodology begins by defining the design
variables that represent the maximum lengths of
different stages in the traffic signal cycle. These
design variables are carefully selected to capture the
key parameters that influence traffic flow and
congestion. The lower and upper limits are chosen as
5 and 40 seconds, respectively, for a three-stage
signal plan. To begin, the code implemented three
design variables representing the lengths of different
stages in the traffic signal cycle. These variables are
set within predefined ranges, allowing for flexibility
in optimizing signal timings while keeping the
allowable minimum and maximum stage lengths.
Optimizing Traffic Adaptive Signal Control: A Multi-Objective Simulation-Based Approach for Enhanced Transportation Efficiency
347
A simulation function is developed to simulate the
traffic scenario using VISSIM. This function takes
the design variables as input and modifies the VAP
file accordingly to update the maximum stage
lengths. The simulation function then runs the
VISSIM simulation and calculates the average delay
for passenger cars and pedestrians.
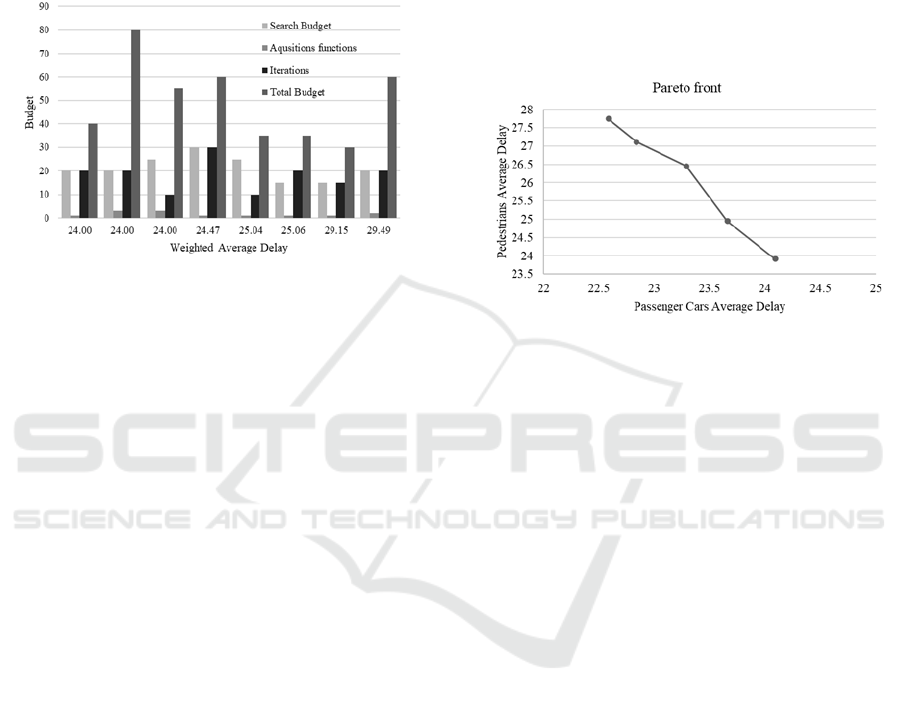
Figure 2: Different Budget Configurations with
Corresponding Weighted Average Delay Values.
The ParMOO algorithm is employed to search the
design space and identify Pareto-front solutions. The
algorithm iteratively explores different combinations
of the design variables to find optimal signal timings
that balance the conflicting objectives. A range of
budgets were tested, and ultimately, a budget
configuration of 20, 1, and 20 was selected (Figure 2).
This configuration represents the search budget,
number of acquisition functions, and maximum
iterations, respectively. By combining these values,
the final budget totalled 40 (Equation 1). The
surrogate model used is gaussian RBF, and the
acquisition function type is uniform weights. The
execution time of the algorithm ranges between 400
and 700 seconds using a PC with an 11th Gen Intel
(R) Core (TM) i7-1165G7 @ 2.80 GHz. These results
suggest that for practical applications and larger-scale
optimization problems, cloud computing or more
powerful processors may be necessary to achieve
acceptable processing times.
(1)
As mentioned before, ParMOO provides multiple
optimal solutions, known as the Pareto front, it presents
decision-makers with a range of alternatives to choose
from (Figure 3). Ultimately, the choice of the optimal
solution depends on a careful balance of technical
analysis, stakeholder input, and informed decision-
making. By considering multiple factors, objectives,
and perspectives, the solution that best aligns with
predefined goals and maximizes the desired outcomes
for your transportation system can be selected. In our
research, a weighted objective approach is chosen as a
decision criterion. The weight assigned to each
objective is 0.5. This approach allows you to prioritize
certain objectives over others and select the solution
with the minimum weighted sum. The optimized
maximum stage lengths are then incorporated into the
VAP files, which contain the traffic signal control logic
for the VISSIM simulation. The necessary
modifications are made to ensure that the optimized
values are used during the simulation runs.
Figure 3: Pareto front for one of the scenarios.
3.4 Experimental Setup
To evaluate the proposed methodology's
effectiveness and robustness, a simple four-legged
intersection is chosen from VISSIM examples.
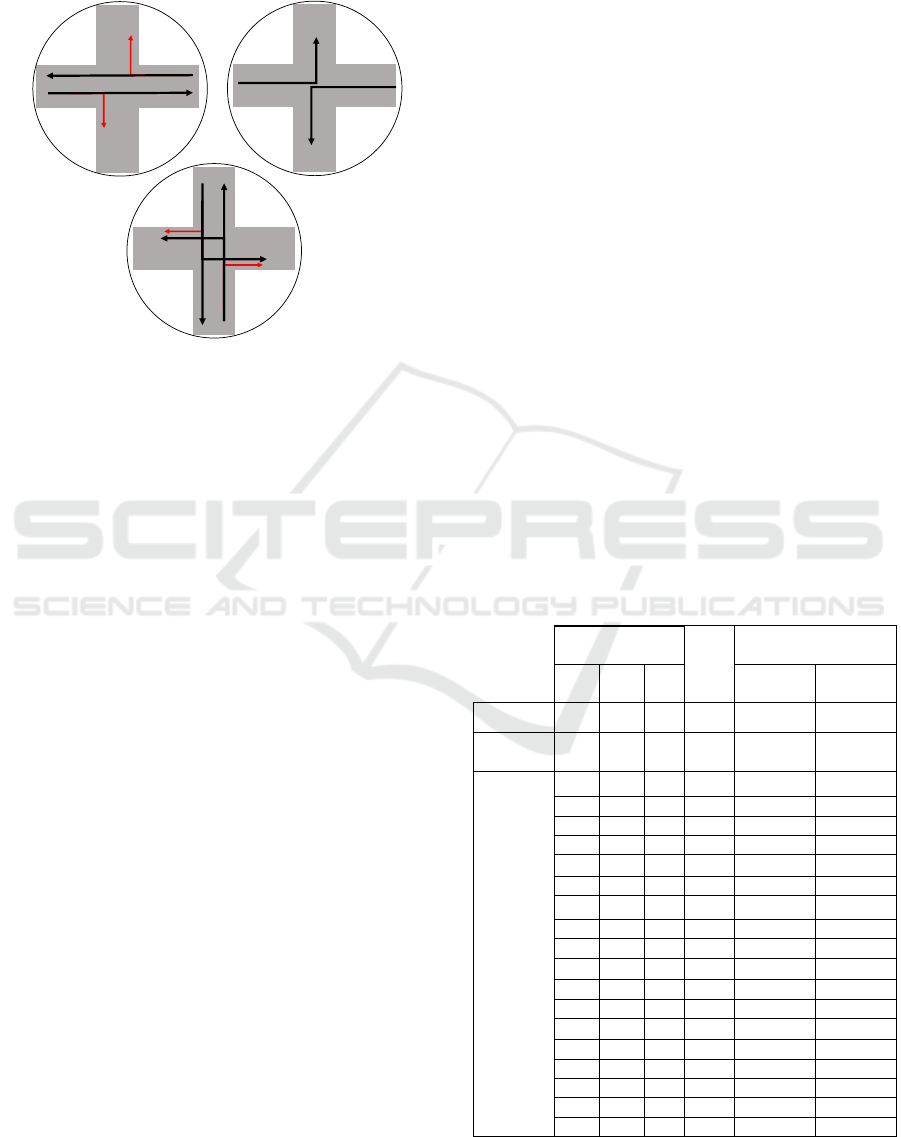
Examples of three-stage fixed-time control and three-
stage vehicle actuated control are provided with the
VISSIM installation, along with control logic files
created with VisVAP for reference, incorporating
pedestrian demands. Each scenario consists of three
stages (Figure 4), with lane widths ranging from 2.75
to 3.50 m and a vehicle composition of 5% heavy
goods vehicles (HGV) and 95% passenger cars, with
an average speed of 50 km/hr.
The proposed methodology is applied to each
traffic scenario by configuring design variables and
executing the optimization process using the
ParMOO algorithm. The objective is to identify
optimal signal timings minimizing average delay for
both passenger cars and pedestrians, accounting for
each scenario's specific characteristics and demands.
After the optimization process, resulting Pareto
front solutions are obtained for both traffic scenarios.
These solutions represent trade-offs between average
delays for different vehicle types, offering a
comprehensive view of achievable performance
improvements in each scenario. To assess the
methodology's performance, optimized signal
timings from Pareto front solutions are implemented
in respective traffic scenarios. Subsequently, VISSIM
VEHITS 2024 - 10th International Conference on Vehicle Technology and Intelligent Transport Systems
348
simulations are conducted using updated signal
timings to evaluate the optimization process's
effectiveness.
Figure 4: Traffic Stages.
4 RESULTS AND ANALYSIS
This section of the paper contains two components:
validation and sensitivity analysis. These analytical
approaches are employed to evaluate and validate the
optimized solutions obtained through the
optimization process.
4.1 Validation Analysis
In the validation analysis, the optimization algorithm
is tested by varying parameters to be optimized,
ensuring it can identify values leading to reduced
delays. Systematically varying these parameters, we
compare resulting objective values with optimized
solutions to evaluate effectiveness and robustness.
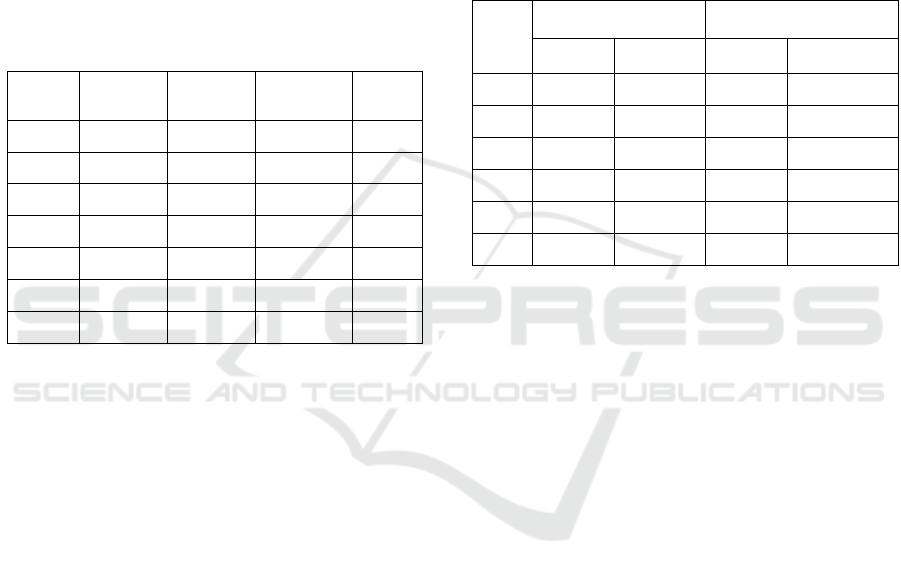
Table 1 presents the validation results of scenario
2 (actuated). The table provides the average delay
values (in seconds) for passenger cars and pedestrians
under different cases. For the fixed control scenario,
the optimization algorithm was highly effective in
finding the most optimized values for the three
parameters, specifically the maximum stage length,
which resulted in substantial reductions in delays.
This success in optimizing the parameters indicates
the algorithm's ability to efficiently balance the trade-
offs and find signal timings that significantly enhance
traffic performance in the fixed control setting (the
validation results for scenario 1(fixed) is not
presented because of space limitation).
On the other hand, in the vehicle actuated control
scenario, the optimization process also led to
reductions in delays. However, the validation analysis
revealed that only the maximum gap parameter
exhibited a strong response to optimization efforts.
This means that optimizing the maximum gap had a
substantial impact on reducing average delays in the
vehicle actuated control scenario.
These findings suggest that the vehicle actuated
control system already exhibits a higher level of
adaptability and responsiveness to changing traffic
conditions, making the optimization process less
influential for other parameters. Nevertheless, the
optimization of the maximum gap parameter
showcased the algorithm's capability to identify
critical adjustments that improve traffic performance
in this scenario.
Overall, the validation analysis provides valuable
insights into the performance of the optimization
algorithm in both control scenarios. It demonstrates
the algorithm's success in finding optimized
parameter values that effectively reduce delays in the
fixed control scenario. In the vehicle actuated control
scenario, the analysis highlights the significance of
the maximum gap parameter and its sensitivity to
optimization efforts, further solidifying the
algorithm's capability to fine-tune signal timings for
improved traffic flow.
Table 1: Validation Results of Traffic Scenario 2 (Vehicle
Actuated Control).
Max stage length
(sec.)
Max
Gap
Average Delay (sec.)
St. 1
St. 2
St.3
Passenger
Cars
Pedestrians
Base Values
20
5
10
3
16.75
19.90
Optimal
values
11
7
10
1
15.50
17.26
Random Values
5
5
5
1
17.15
17.56
7
5
5
1
15.95
17.47
7
5
5
2
16.15
19.14
20
20
20
1
15.96
17.62
20
20
20
1
17.14
20.15
11
10
7
1
15.47
17.79
19
20
11
1
15.44
17.34
19
20
11
2
16.67
19.69
8
8
8
2
16.97
18.71
8
8
8
1
15.50
17.52
8
8
8
3
16.84
19.97
11
7
11
1
15.50
17.31
12
6
11
1
15.49
17.34
11
7
10
2
16.63
19.84
11
8
10
1
15.50
17.26
10
7
10
1
15.56
17.29
9
7
10
1
15.57
17.33
9
7
9
1
15.52
17.40
Stage 1
Stage 2
Stage 3
Optimizing Traffic Adaptive Signal Control: A Multi-Objective Simulation-Based Approach for Enhanced Transportation Efficiency
349
4.2 Sensitivity Analysis
In the sensitivity analysis, the demands of vehicles
and pedestrians are systematically varied to evaluate
the robustness of the optimized solutions obtained
through traffic signal optimization. By modifying the
input parameters related to traffic demand, we aim to
examine the performance of the optimized solutions
under different scenarios. Several simulations are
conducted, each representing a specific variation in
the demand for vehicles (Table 2). Average delays for
personal cars and pedestrians are collected and
compared to those of the base case, where no
optimization was applied.
Table 2: Demand Variations for Sensitivity Analysis.
North-bound
East-bound
South-bound
West-
bound
Base
140
244
248
500
Case 1
1000
244
248
500
Case 2
140
1500
248
500
Case 3
140
244
248
2000
Case 4
1000
244
1200
500
Case 5
140
244
1200
500
Case 6
140
244
248
500
The results indicated that simulations with
optimized values significantly reduced the average
delay for both personal cars and pedestrians
compared to simulations with base values. These
outcomes highlight the effectiveness of the optimized
solutions in adapting to varying traffic demands,
leading to more efficient traffic flow and reduced
congestion. This finding underscores the importance
and benefits of conducting sensitivity analysis to
evaluate the impact of optimized values on traffic
flow and overall efficiency.
Table 3 shows the performance gain for different
scenarios and cases. The Performance Gain is
determined by comparing the reduction in average
delay achieved in the optimized scenario with respect
to the base case. This reduction is calculated as a
percentage of the average delay in the base case. The
table presents the average delay reduction percentage
for passenger cars and pedestrians in Scenario 1 and
Scenario 2. Each row represents a specific scenario,
and the corresponding values indicate the percentage
reduction in average delay for the given case and
scenario.
Furthermore, as a step towards real-world
applicability, our plan is to implement the approach
at an actual intersection. By deploying the optimized
signal timings in a live traffic environment, we can
assess the effectiveness and feasibility of our
methodology in a practical setting. This real-world
implementation will provide valuable insights into
the challenges and considerations involved in
translating optimization results into tangible
improvements in traffic operations. Additionally, it
will allow us to validate the performance of our
approach and gather empirical evidence of its impact
on various road users and the overall traffic system.
Table 3: Performance Gain.
Cases
Scenario 1 (Fixed-Time)
Scenario 2 (Vehicle-
Actuated)
Passenger
Cars
Pedestrians
Passenger
Cars
Pedestrians
1
13.78%
34.11%
7.44%
13.02%
2
14.77%
33.53%
14.89%
10.30%
3
6.88%
14.60%
5.24%
12.96%
4
5.41%
11.38%
1.42%
24.19%
5
3.12%
26.00%
3.06%
9.06%
6
22.27%
20.69%
28.93%
14.00%
5 CONCLUSIONS
Overall, the assessment of the methodology in the two
selected traffic scenarios (fixed-time control and
vehicle actuated control) has provided valuable
insights into its effectiveness in optimizing signal
timings and improving traffic performance. The
analysis of the results has allowed us to evaluate the
methodology's applicability in diverse traffic settings
and its potential for practical implementation in real-
world traffic management scenarios. ParMOO has
proven to be a valuable tool, facilitating the
identification of efficient and effective traffic signal
plans that enhance overall transportation system
performance.
In future work, our aim is to extend the
optimization approach to include the needs and
priorities of additional road users, such as cyclists and
public transit vehicles. We can work toward a more
comprehensive and all-inclusive approach to traffic
signal timing optimization by including these modes
of transportation in our framework. This expansion
will enable us to develop signal timings that enhance
the safety, efficiency, and overall travel experience of
cyclists and public transit users.
Furthermore, as a step towards real-world
applicability, our plan is to implement the approach
VEHITS 2024 - 10th International Conference on Vehicle Technology and Intelligent Transport Systems
350

at an actual intersection. By deploying the optimized
signal timings in a live traffic environment, we can
assess the effectiveness and feasibility of our
methodology in a practical setting. This real-world
implementation will provide valuable insights into
the challenges and considerations involved in
translating optimization results into tangible
improvements in traffic operations. Additionally, it
will allow us to validate the performance of our
approach and gather empirical evidence of its impact
on various road users and the overall traffic system.
ACKNOWLEDGMENTS
This research is part of the project MORE – Munich
Mobility Research Campus. The project is funded by
dtec.bw – Digitalization and Technology Research
Center of the Bundeswehr. dtec.bw is funded by the
European Union – NextGenerationEU.
REFERENCES
Červeňanská, Z., Kotianová, J., Važan, P., Juhásová, B., &
Juhás, M. (2020). Multi-Objective optimization of
production objectives based on surrogate model.
Applied Sciences, 10(21), 7870.
https://doi.org/10.3390/app10217870
Chang, T. H., & Wild, S. M. (2023). ParMOO: A Python
library for parallel multiobjective simulation
optimization. Journal of Open Source Software, 8(82),
4468. https://doi.org/10.21105/joss.04468
Chen, Y., & Chang, G. (2014). A Macroscopic Signal
Optimization Model for Arterials Under Heavy Mixed
Traffic Flows. IEEE Transactions on Intelligent
Transportation Systems, 15(2), 805–817.
https://doi.org/10.1109/tits.2013.2289961
Hatri, C. E., & Boumhidi, J. (2016). Q-learning based
intelligent multi-objective particle swarm optimization
of light control for traffic urban congestion
management. IEEE International Colloquium on
Information Science and Technology (CiSt), Tangier,
Morocco. https://doi.org/10.1109/cist.2016.7804996
Nguyen, P. H., Passow, B. N., & Yang, Y. (2016).
Improving anytime behavior for traffic signal control
optimization based on NSGA-II and local search.
International Joint Conference on Neural Networks
(IJCNN), Vancouver, BC, Cana.
https://doi.org/10.1109/ijcnn.2016.7727804
Nguyen, P. T. M. (2020). Multi-objective Optimization in
Traffic Signal Control. De Montfort University.
Papatzikou, E., & Stathopoulos, A. (2015). An optimization
method for sustainable traffic control in urban areas.
Transportation Research Part C: Emerging
Technologies, 55, 179–190.
https://doi.org/10.1016/j.trc.2015.02.006
ParMOO Documentation. (2022). Retrieved January 1,
2023, from
https://parmoo.readthedocs.io/en/latest/about.html
Poole, A., & Kotsialos, A. (2016). Swarm intelligence
algorithms for macroscopic traffic flow model
validation with automatic assignment of fundamental
diagrams. Applied Soft Computing, 38, 134–150.
https://doi.org/10.1016/j.asoc.2015.09.011
PTV Vissim VisVAP User Manual. (2021). PTV Group.
Qadri, S. S. S. M., Gökçe, M. A., & Öner, E. (2020). State-
of-art review of traffic signal control methods:
challenges and opportunities. European Transport
Research Review, 12(1).
https://doi.org/10.1186/s12544-020-00439-1
Tettamanti, T., & Horváth, M. T. (2020). A Practical
Manual for Vissim-COM Programming in Matlab and
Python 5 th edition for Vissim version 2020 and 2021.
ResearchGate.
https://www.researchgate.net/publication/355118337_
A_practical_manual_for_Vissim-
COM_programming_in_Matlab_and_Python_5_th_ed
ition_for_Vissim_version_2020_and_2021
VISSIM: Microscopic Multi-modal Traffic Flow
Simulation. (2021). PTV Group. Retrieved May 1,
2023, from
https://www.ptvgroup.com/en/solutions/products/ptv-
vissim/
Yan, L., Yu, L., Tao, S., & Chen, K. (2013). Multi-
Objective optimization of traffic signal timing for
oversaturated intersection. Mathematical Problems in
Engineering, 2013, 1–9.
https://doi.org/10.1155/2013/182643
Zhang, X., Fan, X., Yu, S., Shan, A., Fan, S., Yan, X., &
Dang, F. (2022). Intersection Signal Timing
Optimization: a Multi-Objective Evolutionary
Algorithm. Sustainability, 14(3), 1506.
https://doi.org/10.3390/su14031506
Zheng, L., Xu, C., Jin, P. J., & Ran, B. (2019). Network-
wide signal timing stochastic simulation optimization
with environmental concerns. Applied Soft Computing,
77, 678–687.
https://doi.org/10.1016/j.asoc.2019.01.046
Optimizing Traffic Adaptive Signal Control: A Multi-Objective Simulation-Based Approach for Enhanced Transportation Efficiency
351
