Enhancing Echo Processing Through the Integration of Support Vector

Machine and Weber’s Law Descriptors

Mehdia Hedir

1 a

, Fethi Demim

2 b

, Ali Zakaria Messaoui

3 c

, Aimen Abdelhak Messaoui

3 d

Hadjira Belaidi

4 e

, Abdenebi Rouigueb

5 f

and Abdelkrim Nemra

2 g

Faculty of Technology of M’Hamed BOUGARA University-Boumerdes (UMBB), Algeria

Laboratory of Guidance and Navigation, Ecole Militaire Polytechnique, Bordj El Bahri, Algiers, Algeria

Laboratory of Complex Systems Control and Simulators, Ecole Militaire Polytechnique, Bordj El Bahri, Algiers, Algeria

Signals and Systems Laboratory, Institute of Electrical and Electronic Engineering, University M’Hamed Bougara of

Boumerdes, Algeria

Laboratory of Artiﬁcial Intelligence and Virtual Reality, Ecole Militaire Polytechnique, Bordj El Bahri, Algiers, Algeria

Keywords:

Cloud, Tracking, Ground Echoes, SVM, WLD, WLBP.

Abstract:

Removing ground echoes from weather radar images is a topic of great importance due to their signiﬁcant

impact on the accuracy of processed data. To address this challenge, we aim to develop methods that effectively

eliminate ground echoes while preserving the precipitation, which is a crucial meteorological parameter. To

accomplish this, we propose to test Local Descriptors based on Weber’s law (WLD), as well as descriptors that

combine Weber’s law with Local Binary Pattern (WLBP), using Support Vector Machine (SVM) classiﬁers to

automate the recognition of both types of echoes. The proposed methods are rigorously tested at the sites of

Setif and Bordeaux to evaluate their effectiveness in accurately identifying the ground echoes and precipitation.

The results of our experiments demonstrate that the proposed techniques are highly effective in eliminating

ground echoes while preserving the precipitation, and can be considered satisfactory for practical applications

in meteorological data processing.

1 INTRODUCTION

The scientiﬁc community is compelled to proactively

address the complexities of the atmosphere and its

intricate energy exchanges. Weather radar, a pivotal

tool for national weather services, airports, and mete-

orological research departments, is employed to mon-

itor precipitation, necessitating the implementation of

various ﬁltering methods to eliminate false echoes.

Numerous studies have concentrated on reﬁning radar

data ﬁltering techniques within this domain.

In a seminal work, the authors of (Paixao et al.,

2015) devised a method speciﬁcally tailored for iden-

https://orcid.org/0000-0002-9089-8007

https://orcid.org/0000-0003-0687-0800

https://orcid.org/0000-0001-5753-5776

https://orcid.org/0000-0003-0687-0800

https://orcid.org/0000-0003-2424-626X

https://orcid.org/0000-0001-6530-2160

https://orcid.org/0000-0001-9237-9449

tifying areas of severe precipitation. Big data tech-

niques and technologies were proposed in (Fathi et al.,

2022) to effectively manage and analyze vast amounts

of meteorological data. Beyond its conventional ap-

plications, weather information has found relevance

in medical studies, exempliﬁed by research on virus

spread, such as COVID-19 (Malki et al., 2020). Nev-

ertheless, meteorological data faces contamination

challenges from unwanted echoes, including Anoma-

lous Propagation (APs) and ground echoes (Kaissas-

sou et al., 2015). AP occurrences, associated with

temperature inversions and high humidity gradients,

were modeled using Markov chains in ((Haddad et al.,

2000)). Textural features were effectively employed

in (Haddad et al., 2004) to mitigate APs and soil

echoes, while fuzzy logic strategies were explored in

(Cho et al., 2006), (Islam et al., 2012).

In preceding research, a combination of textu-

ral characteristics derived from co-occurrence matri-

ces, Support Vector Machines (SVM), and Convolu-

tional Neural Networks (CNN) were leveraged to dis-

Hedir, M., Demim, F., Messaoui, A., Messaoui, A., Belaidi, H., Rouigueb, A. and Nemra, A.

Enhancing Echo Processing Through the Integration of Support Vector Machine and Weber’s Law Descriptors.

DOI: 10.5220/0012682700003758

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 14th International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH 2024), pages 19-26

ISBN: 978-989-758-708-5; ISSN: 2184-2841

tinguish precipitation echoes from background noise

(Hedir and Haddad, 2016). Additionally, local bi-

nary models and their variations were investigated

for eliminating unwanted echoes (Hedir et al., 2018),

(Hedir et al., 2019).

In this study, we extend the descriptor repertoire

for echo characterization to incorporate Weber’s Law

Descriptor (WLD) (Chen et al., 2010) and Weber’s

Local Binary Model (WLBM) (Liu et al., 2013),

(Cortes and Vapnik, 1995). These features serve as

inputs to develop a robust SVM classiﬁer (Cervantes

et al., 2020), (Rouigueb et al., 2022), (Rouigueb et al.,

2023), capable of discerning various types of echoes.

The organization of this work unfolds as follows:

Section II details the descriptors utilized in this study,

while Section III focuses on the Support Vector Ma-

chine classiﬁer. Section IV provides insights into the

databases used for validating the proposed approach

and presents the obtained results. Lastly, Section V

offers concluding remarks and outlines potential fu-

ture directions.

2 LOCAL DESCRIPTORS

2.1 Local Binary Pattern

A proposed descriptor to characterize a local region is

part of the Local Binary Pattern (LBP) approach de-

scribed in (Ojala et al., 2002). LBP works by comput-

ing a binary code for each 3 × 3 neighborhood by di-

viding the values of the central pixel value (g

) by the

eight neighbors (g

), where the value 1 is assigned for

a positive outcome and the value 0 for a negative re-

sult (see Eq. (1). This standard basis of LBP produces

256 texture patterns. A result is a binary number that

represents the LBP code. The calculation of the afore-

mentioned code is illustrated in Figure 1. This ﬁgure

not only demonstrates the computational process but

also provides visual clarity to the methodology dis-

cussed.

Figure 1: Calculation of the LBP code.

LBP

P,R

P−1

∑

i=0

−g

= 159 with



1, x ≥ 0

0, x < 0

(1)

where g

is the central pixel and gi are the neighbors.

The 3 × 3 neighborhood size of LBP prevents it from

tracking large constructions. The operators are ex-

panded to encompass neighborhoods of various sizes

to address this issue. The LBP calculation can be ap-

plied to a symmetric circular neighborhood with ra-

dius R and P expressing the number of evenly spaced

samples. The following equations can be used to de-

termine the coordinates of g



= x

+ cos(

2πp

)

= y

− sin(

2πp

)

(2)

In image processing, interpolation is used to es-

tablish the gray level of a neighbor’s coordinates that

are not always found in the center of a pixel. The

multiscale Local Binary Pattern (LBP) was developed

based on this concept, and to enhance its characteri-

zation, two more ideas are included: uniformity and

non-uniformity. The uniform binary pattern incor-

porates a maximum of two transitions from 1 to 0

and vice versa, while non-uniform patterns have more

than two transitions. The LBP

P,R

operator is calcu-

lated using these concepts. This information is found

in (Ojala et al., 2002).

LBP

P,R

(x,y) =







I(LBP

P,R

(x,y))i fU(LBP

P,R

)

≤ 2, I(Z) ∈ [0, (P − 1)P + 1]

(P − 1)P + 2 Otherwise

(3)

The circular symmetry of the neighborhood facil-

itates the deﬁnition of a secondary pattern, LBP

P,R

which remains invariant not only to monotonic trans-

formations of the gray level scale but also to rota-

tions of the image. This second pattern, known as

the rotation-invariant LBP, is derived as follows:

LBP

P,R

= min{ROR(LBP

P,R

(x,y),i / i ∈ [0,P − 1])}

(4)

We conduct a thorough investigation by testing

different combinations of radius and the number of

neighbors to determine the optimal parameter values

for the Local Descriptors and the Local Binary Pat-

tern descriptors used in our proposed methods. The

value ROR(a, i) corresponds to the result of i succes-

sive circular shifts to the right of the bits of number a

(coded on P bits).

2.2 Weber Law Descriptor

The relationship between a mental sensation and the

physical size of a stimulus is described by Weber’s

law. The principle was initially observed by the Ger-

man physiologist E.H. Weber and ﬁnds application

across different stimuli, including the correlation be-

tween the perceived intensity of a sound and the asso-

ciated pressure wave. The modern technique involves

SIMULTECH 2024 - 14th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

two components, the excitation difference and the ori-

entation gradient, and is considered a robust descrip-

tor. Weber’s law is expressed as ∆I/I = K, where ∆I

is the threshold increment and I is the initial stimulus

intensity. Reference (Chen et al., 2010) is cited as the

source of Weber’s law.

Differential Excitation

This component is noted by ξ(xc) with x

the current

pixel, its intensity must be different from zero. It is

modeled by the arc tangent of the sum of the differ-

ences of intensities between the current pixel and its

neighbors divided by the intensity of the current pixel

as it is represented by Eq. (5):

ξ(x

) = arctan



∑

P−1

i=0

− x

)



(5)

with x

represents the i

neighboring pixel of the cur-

rent pixel, and the value of ξ(x

) lies within the range

of [−

]. When ξ(x

) is positive, it indicates that

the neighborhood is darker than the current pixel.

Orientation

The ratio between the change in the horizontal direc-

tion and the vertical direction of an image is used to

calculate the orientation gradient. Figure 3 offers a

summary of the calculation’s speciﬁcs. These mathe-

matical equations can be used to represent this calcu-

lation as can be seen in Eq. (6), where v

= x

− x

= x

−x

and x

are the neighbors of

pixel x

on 3 × 3 neighborhood as shown in Fig. 2.

θ = arctan(

) (6)

Figure 2: Demonstration of 3 × 3 neighborhood.

Weber Local Binary Pattern Descriptor

Since LBP can extract more information than the ori-

entation gradient, it was chosen as a part of the We-

ber descriptor. The Local Binary Pattern Descriptor

(LBP) is a robust descriptor that has been used in

many applications. The LBP vector is computed by

Figure 3: Example of gradient calculation based on excita-

tion for an image (Chen et al., 2010).

taking into account the eight adjacent pixels, mak-

ing it a discriminating descriptor. However, the ori-

entation gradient, which only considers four pixels,

preserves more information about the local structure.

The uniform LBP is preferred due to the prevalence

of uniform patterns, as shown in previous experi-

ments. The formula for calculating WLBP for an im-

age f (x,y) at position (x, y) is also provided.

g(x,y) = h(x,y) ⊗ f (x,y) (7)

h(x,y) = exp



−

+ y

2σ



(8)

where h(x, y) is the 2D Gaussian function and g(x,y)

is the convolution product of h(x,y) and f (x,y). Sub-

sequently, the estimation of ∆I is done by equation:

∆I = ∇

[h(x,y) ⊗ f (x,y)] =

πσ



+ y

2σ

− 1



exp



−

2σ

+ y

)



(9)

In the case of the differential excitation, it is pre-

sented by ξ(x

) = arctan(∆I/I), where I refers to the

current pixel x

’s gray level intensity. Theoretically,

WLBP ought to be more discriminating than LBP;

however, this is really due to the interaction between

LBP and the excitation difference, which contributes

signiﬁcantly to the information. The WLBP is more

illuminating and strong while yet maintaining the dis-

crimination.

Enhancing Echo Processing Through the Integration of Support Vector Machine and Weber’s Law Descriptors

3 SUPPORT VECTOR MACHINE

The Support Vector Machine (SVM) concept’s cen-

tral principle is the learning-based classiﬁcation or

recognition of data. The latter generates an output

y = f (x) from a set of inputs x

. The goal is to de-

termine a function f from the observation of numer-

ous input/output pairs (also known as training data),

where x

represents any item and y

represents a class

label. This function, which corresponds to model

(Cervantes et al., 2020), effectively categorizes each

input/output pair into its respective class with preci-

sion. The task is to ﬁnd a decision boundary that sep-

arates the space into two regions. Finding a decision

boundary that divides the space into two sections is

the problem at hand. The data is typically not linearly

separable, so a kernel function is utilized to increase

the distance between them. The data is represented in

a different place called feature space. The SVM train-

ing tool utilizes the LIBSVM library. Each sample

was split into two major groups (training and testing).

We employ the Radial Basis Function (RBF) kernel

for processing, which is presented as follows:

k(x

) = exp(−γ∥x

− x

∥

), γ > 0 (10)

γ acts as a parameter that determines the hyperplane

during model training, with x

representing a sample

of input data and x

denoting all other samples. Con-

sequently, the decision function can be formulated as:

f (x) =

∑

i=1

k(x, x

) + b (11)

denotes the Lagrange multipliers with values rang-

ing between 0 and C, where b stands for the bias, and

C represents a positive constant that regulates errors

and maximizes the margin.

4 DATABASE AND

METHODOLOGY BASED

APPROACH

The 5799 photos acquired in Setif in 1999 and the

10.052 photographs taken in Bordeaux in 1996 make

up the database used for this study. Two incoher-

ent pulsed radars captured the 512 × 512 pixel im-

ages with a resolution of 1 km per pixel, which were

then displayed using the Plan Position Indicator Mode

(PPIM). Bordeaux has a gray level coding of 64 and

Setif has a gray level of 16. The ﬁrst radar is situ-

ated close to Setif at the summit of Meghres Moun-

tain. The geography of the province of Setif is di-

vided into several regions: in the north, the Babors

Chain rises to a height of 2004 m. The Djurdjura and

Bibans Mountains, with peak elevations of 2300 m

and 1417 m, are located in the southwest. The altitude

at the region’s center ranges from 800 to 1300 m. Ev-

ery 15 minute, photos of Setif were captured as shown

in Fig. 4(a). The Bordeaux radar, which is situated

at Bordeaux M

A©rignac Airport, is a member of the

Meteo-France-run operational French weather radar

network. The Pyrenees Mountains, which rise to a

height of 3000 m in the south and are located 200 km

from the radar, as well as the industrial sector that

surrounds the radar, are only two of the challenges in

the Bordeaux region. The main reason for permanent

echoes in this area is the industrial area. Every day,

ﬁve minutes were spent gathering these photographs.

Fig. 4(b) displays an illustration from the Bordeaux

website. Initially, a database comprising two sets of

images is compiled. One set exclusively portrays pre-

cipitation echoes, selected from images where distin-

guishing between ground echoes and precipitation is

straightforward. The other set comprises images cap-

tured during clear weather conditions, devoid of pre-

cipitation, depicting solely ground echoes. In the clas-

siﬁcation process, training data for precipitation is as-

signed the label (−1), while training data for ground

echoes is labeled (1).

The model design involves two key processes:

learning and validation. The training data is parti-

tioned into two segments, one for model training and

the other for validating the optimal model. Subse-

quently, a separate set of labeled test data, previously

unseen during the learning phase, is employed to eval-

uate the classiﬁer’s robustness. The allocation of pix-

els for training and testing at both Setif and Bordeaux

sites is detailed in Table 1.

The SVM will be trained using the characteristic

vectors to identify the ideal parameters (γ,η). One of

these vectors is used to learn and create SVM mod-

els, and the other is utilized to validate just one model

out of the designed ones. With the introduction of

the nonlinear kernel, nonlinear data is taken into ac-

count. The selection of a suitable kernel function

and the modifying of its parameters form the foun-

dation of nonlinear SVM design. We use the Ra-

dial Basis Function kernel in our strategy. This ﬁ-

nal example displays positive test ﬁndings. We can

assess the effectiveness of the suggested strategy us-

ing the statistics in Table 2, where a and d represent

the correct identiﬁcation of precipitations and ground

echoes, while b and c represent the false identiﬁcation

in order.

For better visualization of the WLD vector param-

eters, we propose to design a new descriptor which

combines WLD’s component and LBP

8,1

.The LBP

SIMULTECH 2024 - 14th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

(a) Image from Setif site. (b) Image from Bordeaux site.

Figure 4: Example of images from Setif and Bordeaux sites.

Table 1: Number of pixels used in training and testing for both databases.

Sites Training data Test data

Precipitations Ground echoes Precipitations Ground echoes

Setif 6500 6500 88015 72590

Bordeaux 6500 6500 1378267 956738

consider the nine neighbors, the threshold lets the

LBP be more sensitive to small gray level variation.

This leads the descriptor to extract a maximum of lo-

cal structure and it is very discriminating. However,

WLD can perfectly extract the edges even in the pres-

ence of intense noise, this encourages us to use the

WLD-LBP combination. We observed during exper-

iments on the database that the uniform binary mo-

tif gives a percentage equal to 86% for images con-

taining precipitations and 80% for those with ground

echoes using R = 1 and P = 8, while for R = 2 and

P = 16, the percentage is 67% for precipitation and

60% for ground echoes. We can note that the major-

ity of the binary patterns are uniform, that’s why we

favored the LBP

8,1

4.1 Setif’s Results

We consider two situations for the Setif site : the

ﬁrst concerns the case where we distinguish ground

echoes from precipitations; the second describes the

situation where the precipitation is covered by clut-

ter. The results obtained in the ﬁrst case are sum-

marized in Table 3. The use of LBP

, LBP

and

LBP

riu2

shows an average efﬁciency in the treat-

ment of echoes. Indeed, more than 79.6% of echoes

are eliminated while the preservation of precipitation

does not exceed 64%. Considering PODE for WLD,

WLP and WLD-LBP, we notice that the second and

third cases exhibit a good suppression of undesirable

echoes with more than 92%, while WLD suppressed

only 84.69%. However, the percentage of correct

identiﬁcation reaches its best score 90.13% with the

WLD-LBP descriptor as well as the SR which deﬁnes

the positive identiﬁcation of ground echoes among

all the identiﬁcations with a rate equal to 94.93%.

This shows that the information added in the modi-

ﬁed WLD-LBP descriptor provided additional infor-

mation for the identiﬁcation of echoes. Fig. 5 shows

the obtained results when we ﬁlter an image of Fig.

5(a) with LBP

and Fig. 5(b) with D − LBP. The

second case is when the precipitations are coved by

ground echoes, the estimations of statistical parame-

ters are difﬁcult so only visual appreciation is possi-

ble. Fig. 6 and Fig. 7 illustrate this situation, and the

results are the same as for the ﬁrst case.

4.2 Bordeaux’s Results

The LBP variants exhibit a commendable rate of

ground echo elimination, with the highest score

achieved at 97.85% by LBP

riu2

, while PODP does not

exceed 75.89%. CIA remains acceptable across all

three variants, with the best score reaching 76.77%.

With WLBP and WLD-LBP, PODE stands at 92.08%

and 91.84% respectively, and PODP ranges between

80% and 82%. This highlights the effectiveness of our

proposed descriptor in preserving precipitation while

eliminating ground echoes.

Notably, the ratio of parameter b to c+d is consid-

erably higher, owing to the greater number of precip-

itation pixels compared to ground echoes. Misclas-

siﬁcation of 1% of precipitation echoes corresponds

to 13782 pixels, representing 15% of ground echoes,

signiﬁcantly impacting the SR and CSI. FARE varies

within the range of (73 − 84%), which is compara-

Enhancing Echo Processing Through the Integration of Support Vector Machine and Weber’s Law Descriptors

Table 2: Statistical parameters.

POD (Echoes) POD (Precipitations) FAR (Echoes) FAR(Precipitations)

PODE =

c+d

PODP =

a+b

FARE =

b+d

FARP =

c+a

Success Ratio Critical Success Index Correct Identiﬁcation

Accuracy

SR =

b+d

CSI =

a+b+c

CIA =

a+d

a+b+c+d

Table 3: Number of pixels used in training and testing for Setif databases.

Combination category PODE PODP FARE FARP SR CSI CIA

LBP

R1 83.74 62.48 35.19 17.66 64.80 57.56 72.09

LBP

R2 77.85 16.36 56.56 52.73 43.43 38.65 44.16

LBP

R3 85.56 11.79 55.55 50.23 44.44 41.34 45.13

LBP

R1 85.52 56.52 38.13 17.43 61.86 56.00 69.63

LBP

R2 67.81 57.18 43.36 31.70 56.63 44.63 61.98

LBP

R3 61.41 63.65 41.78 33.33 58.21 42.62 62.63

LBP

riu2

R1 79.60 63.45 35.76 20.95 64.23 55.15 70.75

LBP

riu2

R2 81.64 53.34 40.92 22.10 59.07 52.14 66.13

LBP

riu2

R3 72.66 65.69 45.54 19.017 54.45 45.19 68.21

WLD 84.69 94.15 7.71 11.82 92.28 79.09 89.88

WLBP 92.51 76.34 23.66 7.48 76.33 71.89 83.65

WLD-LBP 92.51 80.97 5.06 26.26 94.93 88.15 90.13

(a) Filtered image with LBP

. (b) Case of separated echos image

D − LBP.

Figure 5: Example of ﬁltered images.

(a) Filtered image with LBP

. (b) Filtered image with

W LD − LBP.

Figure 6: Example of two combination categories.

SIMULTECH 2024 - 14th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

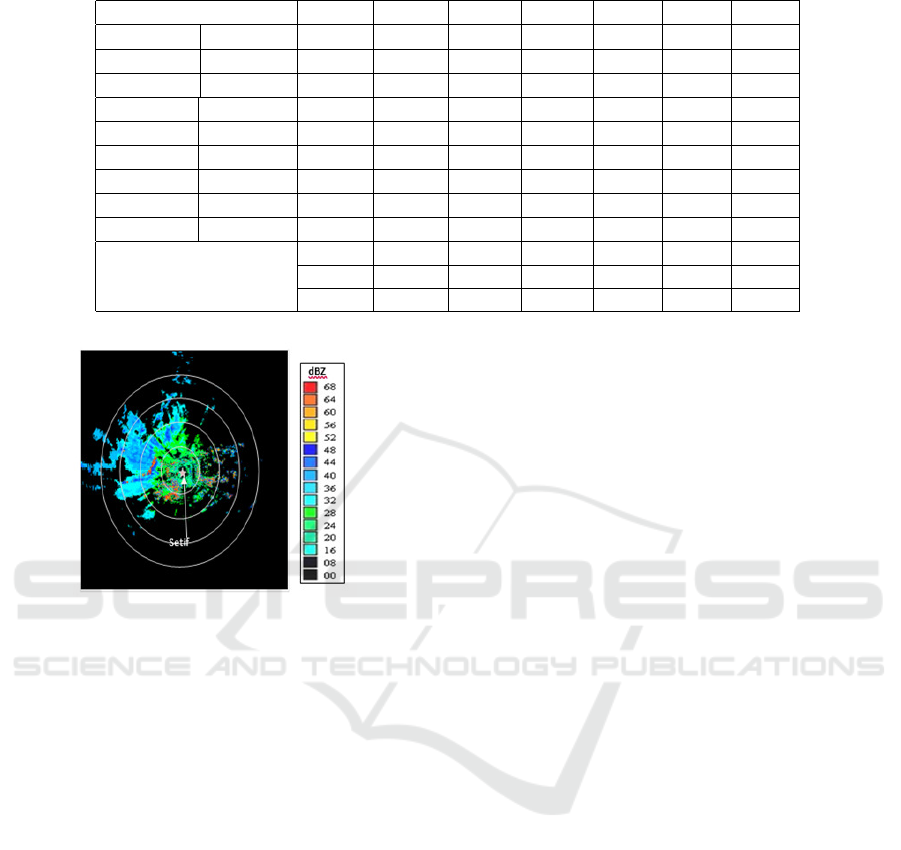
Table 4: Number of pixels used in training and testing for Bordeaux databases.

Combination category PODE PODP FARE FARP SR CSI CIA

LBP

R1 91.39 66.42 84.55 0.86 15.44 15.22 67.99

LBP

R2 93.23 48.57 89.70 0.87 10.29 10.21 51.23

LBP

R3 96.42 41.75 90.04 0.56 9.95 9.92 45.17

LBP

R1 89.73 75.89 79.77 0.91 20.22 19.76 76.77

LBP

R2 93.29 62.79 85.64 0.70 14.35 14.20 64.70

LBP

R3 70.85 56.9 90.08 3.30 9.9 9.5 57.81

LBP

riu2

R1 89.54 69.08 83.78 1.00 16.21 15.91 70.36

LBP

riu2

R2 95.60 49.39 88.78 0.59 11.21 11.15 52.28

LBP

riu2

R3 97.85 44.13 90.14 0.30 9.85 9.83 47.29

WLD 88.45 80.17 76.02 1.00 23.97 23.24 80.72

WLBP 92.08 66.07 84.64 0.79 15.35 15.15 67.70

WLD-LBP 91.84 82.76 73.74 0.65 26.25 25.66 83.33

Figure 7: Image with ground echoes cover precipitations.

tively high due to the extensive surface area of pre-

cipitations.

As for the reﬂectivity-SVM method, our ex-

periments yield the following performance met-

rics: PODE: 97.81%, FARE: 19.81%, SR: 80.19%,

CSI: 78.78%, and CIA: 88.40%. Conversely, the

reﬂectivity-NN method produces the following re-

sults: PODE: 88.40%, FARE: 19.81%, SR: 80.19%,

CSI: 78.78%, and CIA: 88.4%, consistent with ﬁnd-

ings reported in (Ojala et al., 2002).

Importantly, our approach demonstrates supe-

rior suppression of ground echoes compared to the

reﬂectivity-NN approach. Furthermore, our proposed

methods utilizing WLD and WLD-LBP, when evalu-

ated at the Setif site, outperform the techniques intro-

duced in (Islam et al., 2012).

5 CONCLUSION

In this study, we initiated on an exploration of various

descriptors aimed at effectively characterizing radar

echoes. Among these descriptors, we investigated

the Weber Law Descriptor (WLD), Local Binary Pat-

tern (LBP), and Weber-LBP (WLBP). The WLD fur-

nishes a comprehensive representation of each 3 × 3

region by capturing its excitation difference and ori-

entation components. Simultaneously, the LBP and

WLBP furnish complementary insights across differ-

ent scales, thereby enriching the descriptive power of

our approach.

By combining the strengths of these descriptors,

we developed the WLD-LBP method, employed for

training Support Vector Machine (SVM) classiﬁers.

These classiﬁers were assigned the task of distin-

guishing between different types of radar echoes.

While our preliminary ﬁndings are promising, there

is still signiﬁcant scope for improvement. This could

entail meticulous parameter tuning during training or

exploring alternative descriptors that may better cap-

ture the unique characteristics of our data.

Our research provides valuable insights into the

advancement of robust techniques aimed at ﬁltering

out ground echoes from weather radar images while

preserving vital precipitation information. This un-

dertaking represents a noteworthy stride towards im-

proving the precision and dependability of radar data

analysis in meteorological contexts. Moving forward,

our future work will focus on addressing challenges

such as optimizing the fusion of descriptors, enhanc-

ing the adaptability of classiﬁers to diverse weather

conditions, and exploring innovative methods for han-

dling complex radar data scenarios.

REFERENCES

Cervantes, J., Garcia-Lamont, F., Rodriguez-Mazahua, L.,

and Lopez, A. (2020). A comprehensive survey on

support vector machine classiﬁcation: Applications,

challenges and trends. pages 6189–215.

Chen, J., Shan, S., He, C., Zhao, G., Pietikainen, M., Chen,

Enhancing Echo Processing Through the Integration of Support Vector Machine and Weber’s Law Descriptors

X., and Gao, W. (2010). Wld: A robust local image

descriptor. In IEEE Transactions on Pattern Analysis

and Machine Intelligence, pages 1705–1720.

Cho, Y., Lee, G., Kim, K., and Zawadzki, I. (2006). Identi-

ﬁcation and removal of ground echoes and anomalous

propagation using the characteristics of radar echoes.

pages 1206–1222.

Cortes, C. and Vapnik, V. (1995). Support-vector networks.

pages 273–297.

Fathi, M., Kashani, M., Jameii, S., and Mahdipour, E.

(2022). Big data analytics in weather forecasting: A

systematic review. pages 1247–1275.

Haddad, B., Adane, A., Mesnard, F., and Sauvageot, H.

(2000). Modeling anomalous radar propagation using

ﬁrst-order two-state markov chains. pages 283–292.

Haddad, B., Adane, A., Sauvageot, H., Sadouki, L., and

Naili, R. (2004). Identiﬁcation and ﬁltering of rainfall

and ground radar echoes using textural features. pages

4641–4656.

Hedir, M., Demim, F., and Haddad, B. (2018). Radar echoes

classiﬁcation based on local descriptor. In IEEE In-

ternational Conference on Signal, Image, Vision and

their Applications, pages 1–6.

Hedir, M., Demim, F., and Haddad, B. (2019). A compara-

tive analysis of the ground clutter suppression on me-

teorological images. In IEEE 6th International Con-

ference on Image and Signal Processing and their Ap-

plications, Mostaganem, Algeria, pages 1–7.

Hedir, M. and Haddad, B. (2016). Automatic system for

radar echoes ﬁltering based on textural features and

artiﬁcial intelligence.

Islam, T., Rico-Ramirez, M., Han, D., and Srivastava, P.

(2012). Artiﬁcial intelligence techniques for clut-

ter identiﬁcation with polarimetric radar signatures.

pages 95–113.

Kaissassou, S., Lenouo, A., Tchawoua, C., Lopez, P., and

Gaye, A. (2015). Climatology of radar anomalous

propagation over west africa. pages 1–12.

Liu, F., Tang, Z., and Tang, J. (2013). Weber local binary

pattern for local image description. pages 325–335.

Malki, Z., Atlam, E., Hassanien, A., Dagnew, G., Elhos-

seini, M., and Gad, I. (2020). Association between

weather data and covid-19 pandemic predicting mor-

tality rate: Machine learning approaches. pages 110–

137.

Ojala, T., Pietikainen, M., and Maenpaa, T. (2002). Mul-

tiresolution grey-scale and rotation invariant texture

classiﬁcation with local binary patterns. pages 971–

987.

Paixao, E., Mirza, M., Shephard, M., Auld, H., Klaassen,

J., and Smith, G. (2015). An integrated approach

for identifying homogeneous regions of extreme rain-

fall events and estimating IDF curves in Southern On-

tario, Canada: Incorporating radar observations.

Rouigueb, A., Demim, F., Belaidi, H., Messaoui, A., Bena-

tia, M., and Djamaa, B. (2023). Improving the license

plate character segmentation using na

A¯ve bayesian

network. In Proceedings of the 20th International

Conference on Informatics in Control, Automation

and Robotics (ICINCO 2023), Rome, Italy, pages 61–

68. Giuseppina Gini; Henk Nijmeijer and Dimitar

Filev.

Rouigueb, A., Demim, F., Nemra, A., and Djamaa, B.

(2022). Gearbox fault diagnosis using the short-time

cepstral features. In Proceedings of the 2nd IEEE In-

ternational Conference on Advanced Electrical Engi-

neering (ICAEE), pages 1–8. IEEE.

SIMULTECH 2024 - 14th International Conference on Simulation and Modeling Methodologies, Technologies and Applications