Geodetic Fundamentals in the Development of a Voxel Model for the

Subsoil of the City of Sevilla (Spain)

Andreas Fuls

, Emilio J. Mascort-Albea

, Francisco M. Hidalgo-Sánchez

, Martin Kada

Cristina Soriano-Cuesta

, Rocío Romero-Hernández

and Antonio Jaramillo-Morilla

Institut für Geodäsie und Geoinformationstechnik, Methodik der Geoinformationstechnik,

Fakultät VI Planen Bauen Umwelt, Technische Universität Berlin, Berlin, Germany

Departamento de Estructuras de Edificación e Ingeniería del Terreno, Escuela Técnica Superior de Arquitectura,

Universidad de Sevilla, Sevilla, Spain

Keywords: Coordinate Reference System (CRS), Map Distortions, Digital Terrain Model (DTM), LiDAR, Vertical

Control Points.

Abstract: Current global challenges require a better understanding of the subsoil to optimise underground resources and

plan for sustainable development. This is a key issue in anthropised metropolitan environments, where the

high density of elements makes difficult to gain knowledge of this reality. The use of Geographic Information

Systems (GIS) enables spatial management and visualisation of the underground data obtained from

geotechnical surveys. The creation of 3D models in voxel format constitutes a pioneering and relevant line of

research. This paper evaluates the main factors resulting from the integration of different topographic sources

at a territorial level for the creation of surface models that efficiently adjust the geotechnical data collected,

which usually lacks global height values. This task involved designing a coordinate system and a reference

grid, as well as adjusting elevation data for the selected study case: the metropolitan area of Sevilla, Spain.

1 INTRODUCTION

The significance of understanding the underground

reality in highly anthropised urban and metropolitan

areas cannot be overstated. Accurate subsurface data

is crucial to the design of new constructions, the

conservation of existing ones and urban planning.

Nevertheless, current information techniques are

limited in their ability to provide detailed subsurface

data through the use of remote sensors that capture

information from the earth's surface on a massive

scale. To address this issue, efficient strategies are

required to collect data from geotechnical tests (such

as boreholes and soil penetrometer) for the precise

characterisation of the underground through the

generation of 2D cartographies and 3D models by

https://orcid.org/0000-0003-3633-7230

https://orcid.org/0000-0002-5737-9969

https://orcid.org/0000-0001-5310-1567

https://orcid.org/0000-0002-7490-7452

https://orcid.org/0000-0002-1814-7401

https://orcid.org/0000-0002-3468-4055

https://orcid.org/0000-0002-6075-5670

means of Geographic Information Systems (GIS).

Regarding this approach, proposals that use vector

and raster models to allow the visualisation of the

distribution of underground geotechnical strata in a

correlated way with the organisation of the urban

infrastructure should be considered (Nonogaki et al.,

2021; Soriano-Cuesta et al., 2023).

Given the interest of this line of work, the present

research raises the need to develop models that can

effectively manage detailed subsurface information

using the voxel format. The accurate correlation of

the subsurface information with the topographic

configuration of the surface is essential in all the cases

mentioned. Consequently, the current investigation

presents the geodetic fundamentals that allow a

rigorous adjustment of the relationship between

144

Fuls, A., Mascort-Albea, E., Hidalgo-Sánchez, F., Kada, M., Soriano-Cuesta, C., Romero-Hernández, R. and Jaramillo-Morilla, A.

Geodetic Fundamentals in the Development of a Voxel Model for the Subsoil of the City of Sevilla (Spain).

DOI: 10.5220/0012683000003696

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 10th International Conference on Geographical Information Systems Theory, Applications and Management (GISTAM 2024), pages 144-151

ISBN: 978-989-758-694-1; ISSN: 2184-500X

surface information from different sources and

subsurface data obtained from geotechnical tests of a

spot nature. The study area chosen for this purpose is

Sevilla, a city located in the south of Spain with a high

heritage value and a metropolitan population of

approximately one million inhabitants (Sanchez

Fuentes et al., 2021) has been taken as a

representative study area. The case study is based on

a database of geotechnical tests that mostly lack

geometric information on the absolute height of the

test points, since they usually referenced their depth

in relation to the surface level.

2 REFERENCE SYSTEM

The municipality of Sevilla covers an area of 142 km²

and is located between 5°49’W and 6°02’W of

Greenwich and between 37°18’N and 37°27’N of the

equator. Since September 2012 the urban

development department of Sevilla (Gerencia de

Urbanismo y Medioambiente, 2023) has been using

the "European Terrestrial Reference System 1989"

(ETRS89), which is based on the GRS80 ellipsoid

and in accordance with the INSPIRE guidelines.

Coordinates are represented in the Universal

Transverse Mercator projection (UTM), zone 30N.

However, Sevilla is located on the western

periphery of UTM zone 30N and on the eastern

periphery of the neighbouring zone 29N, causing

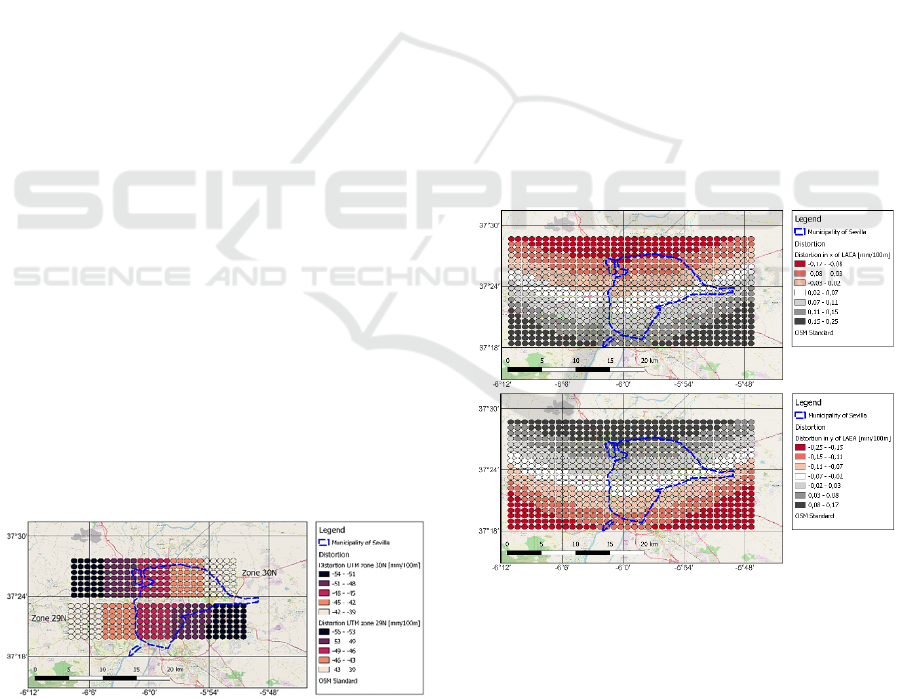
distortions in distances, both in x and y direction,

between 40 and 50mm per 100m (Figure 1). We

chose the coordinate system of UTM zone 30N

because the main part of the city falls east of the 6th

degree of longitude west of Greenwich and thus in

UTM zone 30N. The resulting distortions between

ellipsoidal and projected distances had to be accepted

to comply with Spain's official reference system,

which also uses ETRS89 in conjunction with

cartographic projections in UTM zones.

Figure 1: Distortion of UTM zones 29N and 30N at the city

of Sevilla. Distortion values are given in mm per 100m and

they are identical in x- and in y-direction at one location

because of the conformal Transverse Mercator projection.

The official Spanish cadastre states that:

“Cadastral mapping has a nominal precision of +/- 0.5

m in urban and +/- 2 meters in rustic. This precision

is sufficient in most cases” (Dirección General del

Catastro. Gobierno de España, 2023).

However, the development of a voxel model for

the subsurface of the city of Sevilla (Spain) raises the

question of whether such an accuracy requirement is

adequate for geotechnical concerns. Volume

calculations of the subsurface rely on the results of

the area calculations on the surface and the strata

depth data. Any distortions in distance measurements

will inevitably lead to inaccuracies in area

calculations. Furthermore, the depth values are

provided without such a scale, which can cause a

distortion between horizontal and vertical dimensions

in the voxel model. For these reasons, a specific

reference system was defined for the geotechnical

project.

To ensure accurate area and volume calculations,

an equal-area projection is necessary. The Lambert

azimuthal projection was used for this purpose. The

centre of the projection should be within the urban

territory and was set to 37°24’N and 6°00’W (Figure

2). The GRS80 ellipsoid was used as the reference

ellipsoid which aligns with Spain's official reference

system.

Figure 2: Distortion of the Lambert azimuthal equal-area

(LAEA) projection in a) x-coordinates, b) y-coordinates.

Distortion values are given in mm per 100m.

By using the Lambert azimuthal equal-area

(LAEA) projection, distortions are minimized to less

than 0.2mm per 100m distance (or 2mm per km)

within the territory of Sevilla (Figure 2). The chosen

projection therefore allows for the creation of an

inherently true scale voxel model for the city of

Sevilla.

Geodetic Fundamentals in the Development of a Voxel Model for the Subsoil of the City of Sevilla (Spain)

145

3 REGULAR ANALYSIS GRID

A regular grid is frequently utilized in geotechnical

analysis. In statistical analysis, for instance, point

density is based on statistical units of equal size.

Another application is the organization of tiles of a

digital terrain model with equal sizes.

Based on the coordinate reference system LAEA-

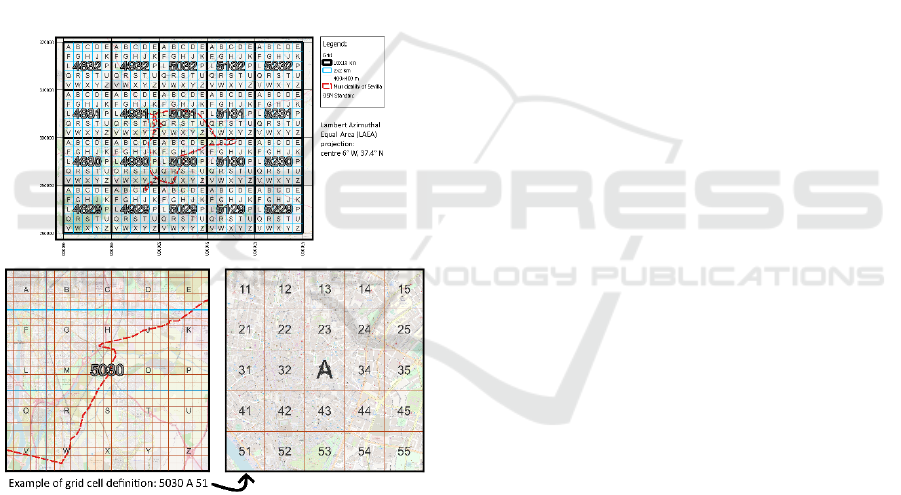
Sevilla described above, a regular grid with three

zoom levels is defined. Zoom level 1 uses a 10 x 10

km cell size starting each cell at rounded coordinates

(Figure 3: top). The numbering of each cell refers to

the coordinate values of the upper left corner, rounded

to 10 km. Grid cell 5030, for example, covers the

range in x between 500000m and 510000m and in y

from 290000m to 300000m. A coordinate-based

numbering system is the most flexible option, as a

10km grid can be extended, without the need to

rename existing cells if necessary.

Figure 3: Definition of a regular grid with three zoom

levels: Level 1 (10x10km), Level 2 (2x2km), Level 3 (400

x400m). The grid based on the coordinate reference system

LAEA-Sevilla.

Each cell of Zoom level 1 is subdivided into 25

cells with a size of 2km x 2km (Zoom level 2). The

cells labeled with characters starting with ‘A’ in the

NW corner and continuing row by row from north to

south until character ‘Z’. Character ‘I’ is not used to

avoid any confusion with character ‘J’ (Figure 3:

bottom left).

For large scale studies a third Zoom level 3 is used

with a cell size of 400x400m. The 25 cells are labelled

through numerical codes in such a way, that the first

number refers to the relative cell position in the y-

direction and the second number refers to the position

in x-direction. Therefore, labelling of Zoom level 3

starts with ‘11’ and ends with ‘55’ (Figure 3: bottom

right).

The combination of the label for each zoom level

provides the complete information about the position

of the cell. Grid cell 5030 A 51, for example, covers

the square area from point (500000.00, 298000.00) in

the SW corner to point (500400.00, 298400.00) in the

NE corner.

Per definition, locations falling exactly between

two cells are assigned to the eastern cell and the

southern cell, respectively. This means, for example,

that a point at location (500000.00, 300000.00) falls

into cell 5030 A 11.

4 ELEVATION DATA

There are two primary sources of altitude information

for the urban area of Sevilla and the surrounding

countryside: cadastral survey points and LiDAR

measurements taken from an airplane (Centro

Nacional de Información Geográfica, 2020). Based

on LiDAR measurements from 2012 to 2022

(containing UTM coordinates and ellipsoidal heights)

a DTM has been created by the National Geographic

Institute and the National Center for Geographic

Information in Spain (Instituto Geográfico Nacional

(IGN) / Centro Nacional de Información Geográfica

(CNIG) (Mº Fomento)). Only filtered ground points

have been used to calculate the DTM, interpolating

the elevation values of areas covered by non-ground

points. In addition, satellite measurements and the

digital surface models derived from them are also

available: SRTM (National Aeronautics and Space

Agency -NASA-, 2013), ALOS AW3D (Japan

Aerospace Exploration Agency -JAXA-, 2021) and

MERIT (Global Hydrology Group, 2018). These

measurements can be used to determine the elevation

of boreholes (Table 1).

The vertical accuracy of global Digital Elevation

Models (DEMs) is partially dependent on the slope

(Uuemaa et al., 2020). For this reason, the MERIT

DEM was also used as a data source, as it removes

multiple error components and a comparison of

global DEMs has shown that in flat terrain the

MERIT DEM is more accurate than SRTM

(Yamazaki et al., 2017) and AW3D (Uuemaa et al.,

2020, p. 9). Comparing the LiDAR based DTM with

MERIT DEM results into a standard deviation of

±3.2m (1-sigma range; total grid coverage); the range

GISTAM 2024 - 10th International Conference on Geographical Information Systems Theory, Applications and Management

146

Table 1: Data sources of elevation, their Coordinate Reference System (CRS) and reference ellipsoid, horizontal resolution,

and accuracy of elevation for the area of the grid as well as for the city of Sevilla and in the rural area.

Source (year) Type of geometry CRS Ellipsoid

Horizontal

resolution

Elevation accuracy

IDE Sevilla Redes

Topo (2009)

point UTM 30N GRS 1980

accuracy ca.

±0.001

accuracy ca. ±0.001m

Cadaster

surveying (2001 to

2017)

point UTM 29N, 30N GRS 1980

accuracy ca.

±0.01m

accuracy ca. ±0.01m

LiDAR (from

2001 to 2015)

point UTM 29N, 30N GRS 1980 2.00m

±0.15m

(max. error <=0.6m)

LiDAR (from

2015 to 2022

)

DTM based on

filtered

round

oints

UTM 29N, 30N GRS 1980 2.00m

±0.15m

(

max. error <=0.6m

)

SRTM GL1

(

2000

)

DEM EPSG 4326 WGS 84

1 arcsec

(

ca. 30m

)

±3.4m

(

cit

±3.7m, rural ±1.8m

)

AW3D30 (from

2006 to 2011)

DEM EPSG 4326 WGS 84

1 arcsec

(ca. 30m)

±3.1m

(city ±4.3m, rural ±1.5m)

MERIT DEM EPSG 4326 WGS 84

3 arcsec

(

ca. 90m

)

±3.2m

(

cit

±2.8m, rural ±1.6m

)

of the differences, however, falls between -206m

because of gravel pits constructed after DEM data

collection and +45m because of buildings not

removed in the DTM but constructed after DEM data

collection. The standard deviation inside the city of

Sevilla is approximately ±2.8m due to the presence of

the numerous buildings, but in the rural area the

standard deviation is much smaller, around ±1.6m.

The AW3D30 DEM is a digital surface model that

includes all buildings, bridges etc. This means, that

men made features have not been removed in the

DEM. As a result, its standard deviation is greater

than for MERIT, especially inside the city of Sevilla

(Table 1). The same observation can be made for

elevation data of SRTM (Nikolakopoulos, 2020, p.

45).

To determine the local elevation for each borehole

location, a terrain model of the same time the

borehole was measured is required. The most precise

elevation data come from altimeter points and LiDAR

measurements. However, it is important to note that

both sources of data are time-dependent.

Additionally, a few building heights not recognized

in the LiDAR based DTM as well as altimeter points

not representing the terrain should be eliminated.

4.1 Filtering LiDAR Points

Only LiDAR points that are classified as ground

should be used to calculate the terrain model.

However, some LiDAR points are misclassified as

ground although they represent other objects such as

buildings or bridges. To eliminate misclassified

ground points, the following filter operations can be

performed:

1. Select only LiDAR points that are not

located within water areas such as rivers,

canals, lakes, artificial water tanks and

pools. The elevation values of water have

been set to ‘no data’.

2. Only select LiDAR points that are not

located within huge buildings of unusual

shape and roof type that are misclassified as

ground points. There are 22 buildings that

have been manually identified in the terrain

model and their elevation values have been

set to ‘no data’.

The result is a terrain surface with 2m horizontal

resolution but only including the elevation of the

terrain at the time of the LiDAR measurements.

4.2 Filtering Altimeter Points

In this research 504,818 surveying points fall within

the above defined area of the grid, but not all of them

represent the terrain. In order to filter altimeter points

with correct values of the elevation of the terrain, the

following filter operations must be performed.

1. Only select altimeter points with TTGGSS

028112.

2. Eliminate points with unknown elevation

(height = 0).

3. Eliminate points with incorrect elevation

values at surrounding towns that are placed

very close to the city of Sevilla as Olivares

(constant height = 160m) and Villanueva del

Ariscal (constant height = 150m).

4. Eliminate surveying points on top of

buildings with an elevation much greater

Geodetic Fundamentals in the Development of a Voxel Model for the Subsoil of the City of Sevilla (Spain)

147

than the local trend surface based on filtered

LiDAR ground points. In this case, the

threshold equals 0.5m, which is about 2.5

times of the maximum elevation error of

LiDAR.

The elevation of the surveying points can be

checked for gross errors through the comparison with

the LiDAR based DTM. The standard deviation of the

height differences of 1,199 precise surveying points

equals ±0.32m. There are 24 points that have a height

difference greater than 1m. Most of these points are

located on highways and bridges.

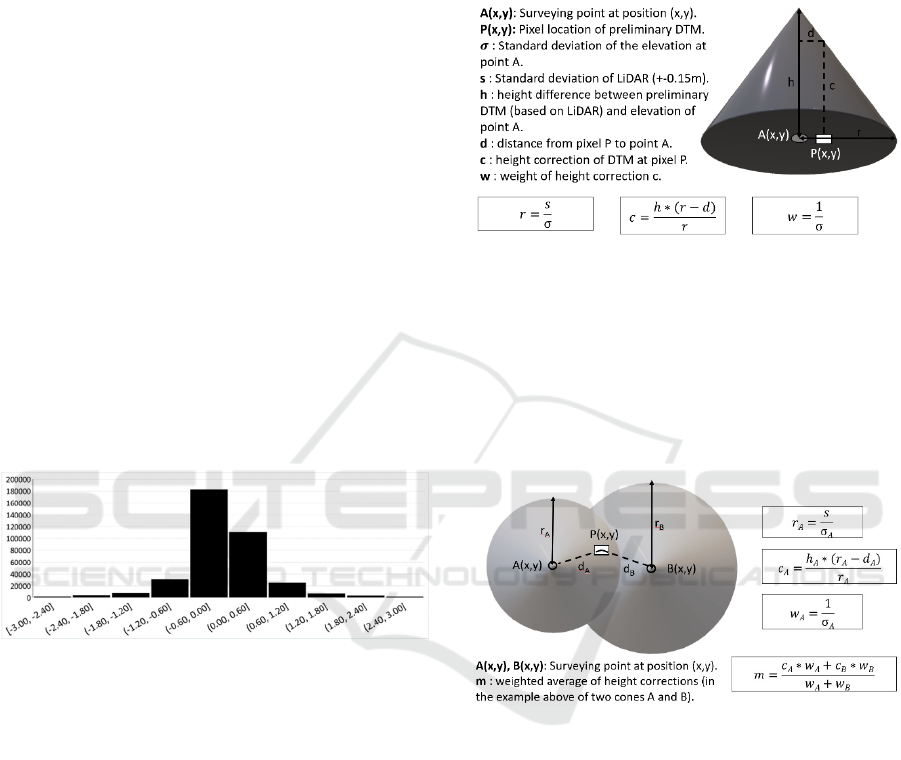
The standard deviation of the height differences

of 292,926 altimeter points with a supposed precision

of 1cm equals ±1.07m (Figure 4). This is due to

several points that exhibit a height difference of up to

21m in relation to the LiDAR based DTM. Taking the

time of measurement into account there seems to be a

trend that the accuracy in the years 2001 to 2003 and

2011 is about ±1m, but much greater in the years 2004

(±1.96m) and 2005 (±1.51m). Most precise are 14

points measured in 2012 with an accuracy of ±0.25m.

The reason for this is likely due to the fact that the

LiDAR measurements were performed closer to that

year than to other years.

Figure 4: Histogram of height differences between

surveying and altimeter points on one side and the LiDAR

based DTM on the other (range from -3m to +3m, excluding

outliers).

4.3 Correcting the LiDAR Based DTM

Finally, the filtered surveying and altimeter points

can be used to calculate a correction for each pixel of

the preliminary (LiDAR based) digital terrain surface.

Since the elevation values of surveying and altimeter

points are more precise than that of LiDAR points

(Table 1), we should base the DTM on these elevation

data. However, there are many areas without any

surveying and altimeter point, especially in the rural

areas outside of the city of Sevilla. In these “empty”

areas we must rely on the LiDAR points with third

highest vertical accuracy.

The cone model of DTM correction enables the

calculation of elevation correction at a pixel location

in the preliminary DTM using all exact elevation data

of the survey points from the surrounding area

(Figure 5a). The maximum sphere of influence is

described by a cone whose radius depends on the ratio

of the accuracy of the LiDAR heights (±15cm) to the

measurement accuracy (±1mm and ±1cm).

Figure 5a: Cone model of DTM correction describing the

method of calculating the DTM correction of a pixel

location in relation to a surveying point with a more precise

elevation of the terrain. The greater the distance d between

pixel and surveying point, the smaller is the correction c,

which also depends on the ratio r between both standard

deviations of the elevation values. The cone is defined

through height difference h and ratio r. At the centre of the

cone the correction equals h and is zero at the radius of the

cone.

Figure 5b: Overlap of two cones and calculation of the

weighted mean height correction m.

When cones from multiple survey points overlap,

correction values are weighted and averaged based on

the reciprocal of measurement accuracy of the

measurement and the distance between the pixel and

the survey point (Figure 5b). However, the

interpolation between a pixel and a survey point

should not be carried out across break lines. For this

reason, all areas with a slope greater than 30° have

been identified as potential breakline areas in the

preliminary DTM. The areas surrounding these have

been marked and vectorised as terrain zones. By

checking whether the interpolation takes place within

the same terrain zone and does not intersect any inner

breakline zone or the outer boundary, it was possible

to ensure that the interpolations do not take place

GISTAM 2024 - 10th International Conference on Geographical Information Systems Theory, Applications and Management

148

across artificial unevenness in the terrain, such as the

boundaries of rivers, lakes, bridges, ramps, docks,

and steep ditches. This also includes areas with

LiDAR points from buildings that were incorrectly

identified as ground points, such as buildings with

green roofs or unusual roof shapes.

Figure 6: Map of a test area representing the height

correction of the LiDAR based DTM.

In a final step the height corrections can be

applied to the elevation of the DTM (Figure 6). The

result is a digital terrain model with elevation values

of mixed accuracy. To address this, the estimated

accuracy of each elevation is stored in a second band

of the raster file.

4.4 Temporal Aspect of Elevation Data

The ground surface undergoes permanent changes,

especially in urban areas with numerous construction

projects. Therefore, it is necessity to take the temporal

aspect into account when developing a digital terrain

model (Figure 7).

Figure 7: Surveying points with a valid elevation until

present (year 2023).

However, the exact time of measurement is in most

cases unknown, and we can only provide a temporal

range at which measurements were performed.

LiDAR data are based on flights between 2015 and

2021, but the surveying work to obtain elevation data

was carried out between October 2001 and June 2022.

Most of the elevation points, however, were measured

from 2001 to 2005 and 2011, making them older than

the LiDAR data.

Most of the points at the old city center of Sevilla

were surveyed in 2001, but points at the modern part

of the city were measured as late as 2011. Surveying

points at the towns and villages outside of the

municipality of Sevilla were collected between 2001

and 2005. Any gaps without points must be filled up

with elevation data derived from LiDAR data to

calculate a continuous DTM. The temporal aspect,

however, has not been covered in this paper due to its

complexity which will be considered in future

analyses.

5 CONCLUSIONS

The paper presents a rigorous evaluation of the main

factors that affect the problems derived from the

creation of a voxel model at a territorial level based

on data from the primary sources of height

information. In this case, the paper has focused on

aspects related to topographic adjustment, but the

findings can be applied to future issues related to the

integration of subsurface information. In this sense,

the definition of a working grid at different scales

enables the evaluation of the quality and quantity of

the information collected by sector, and the

establishment of an efficient work plan. This

approach identifies areas with common

characteristics and problems that can be solved with

shared methods and strategies.

Regarding the creation of a voxel model of the

subsurface from the borehole data, an accurate Digital

Terrain Model (DTM) is required, which allows us to

determine the surface elevation of boreholes. Height

information of varying accuracy is available for the

area of Sevilla and its rural surroundings, which is

used to correct a DTM based on LiDAR

measurements. LiDAR data of bridges and buildings

often misidentified as ground points must be

eliminated in order to improve the preliminary DTM,

which is partially representing a Digital Surface

Model (DSM) instead of a Digital Terrain Model

(DTM) (Figure 8). The challenge here is to develop a

suitable method to determine DTM corrections from

Geodetic Fundamentals in the Development of a Voxel Model for the Subsoil of the City of Sevilla (Spain)

149

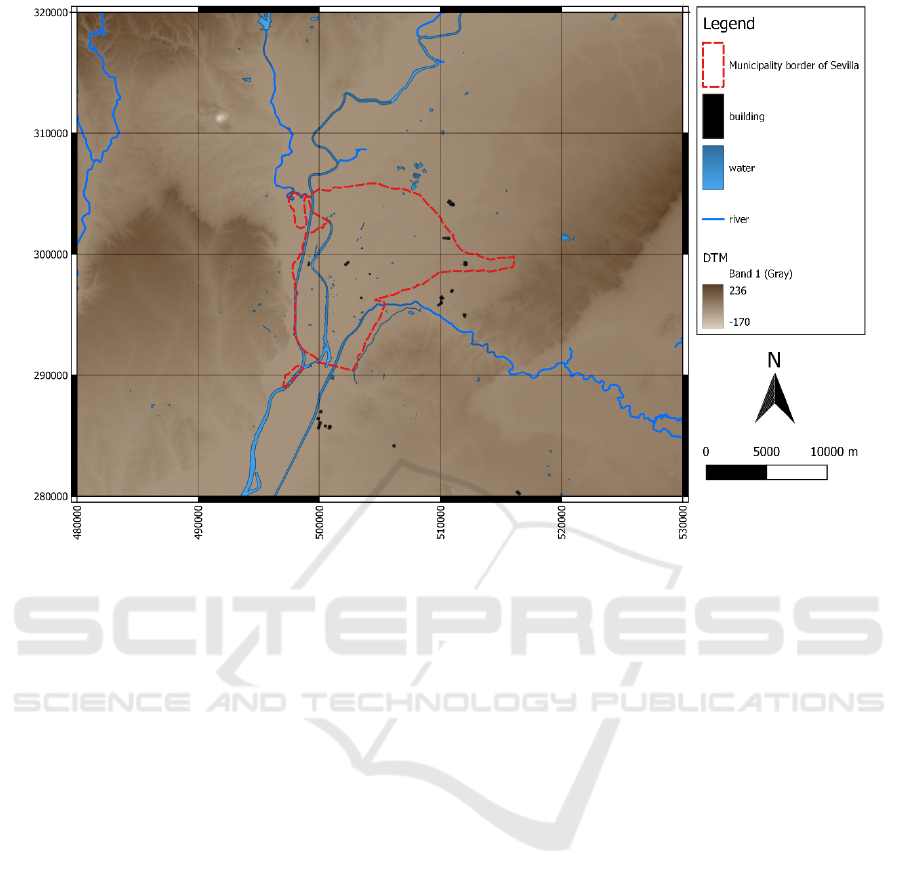
Figure 8: DTM of Sevilla. Water surfaces, rivers, and some buildings are marked as ‘no data’.

various height measurements with a different spatial

distribution and accuracy. The cone model of DTM

correction presented in this paper is a simplified

version of a local terrain correction. The method

analyses diverging height values from different

measurement points for each grid cell in the DTM.

However, further investigations are required in order

to combine the only punctual available height

measurements of high accuracy with the less accurate

but area-wide LiDAR data while preserving the

terrain profile. The correction of elevation data may

require a local trend surface to derive at a smooth

distribution of height corrections. Consequently, the

improvement of the methodology of incorporating

elevation data from various sources and accuracies

requires further research.

Finally, it is necessary to mention that the DTM

presented in this paper is based on the most recent

data valid until now (2023), but the test drillings

described in many reports were performed since 1970

until present (2023). Determining the exact elevation

of the surface above sea level for each location at the

time of the drilling is beyond the scope of the paper.

Not only has the terrain been modified over the years,

but also has undergone changes due to the

construction of basements, underground car parks and

metro lines. Therefore, the improvement of the

methodology of incorporating elevation data from

various sources and accuracies demands extensive

investigations.

ACKNOWLEDGEMENTS

The research and writing of this article were

supported by the following grants: (1) Grant for

Attendance and Participation in International

Scientific Conferences from the VII Research Plan of

the University of Sevilla for 2024 (VII PPI-US,

2024); (2) Grant for the International Mobility of

Research Staff from the VII Research Plan of the

University of Sevilla for 2022 (VII PPI-US, 2022).

Additionally, the authors would like to expressly

acknowledge the work of Julien Baerenzung

(Technische Universität Berlin) and M. Teresa

González-Silva (Universidad de Sevilla) for their

technical support.

SOFTWARE

The calculations and the cartographic outputs were

made with the help of QGIS (version 3.28.10) and a

PostgreSQL/PostGIS database.

GISTAM 2024 - 10th International Conference on Geographical Information Systems Theory, Applications and Management

150

REFERENCES

Centro Nacional de Información Geográfica. (2020).

Especificaciones Técnicas para la realización de vuelo

LIDAR que permita la obtención de información

altimétrica. In LIDAR 2

Cobertura (2015 -

Actualidad). https://pnoa.ign.es/resources/archivos/Esp

Tec/2020_Especificaciones_VL_Andalucía.pdf

Dirección General del Catastro. Gobierno de España.

(2023). Información básica sobre el servicio catastral

español. Registro Oficial Del Catastro. https://www.

catastro.minhap.es/esp/faqs_catastro_registro.asp#

Gerencia de Urbanismo y Medioambiente. (2023).

Servicios cartográficos básicos de la ciudad de Sevilla.

Infraestructura de Datos Espaciales de Sevilla

(IDE.Sevilla).

Global Hydrology Group. (2018). MERIT DEM: Multi-

Error-Removed Improved-Terrain DEM. https://

hydro.iis.u-tokyo.ac.jp/~yamadai/MERIT_DEM/

Japan Aerospace Exploration Agency -JAXA-. (2021).

ALOS Global Digital Surface Model (AW3D30).

https://portal.opentopography.org/raster?opentopoID=

OTALOS.112016.4326.2

National Aeronautics and Space Agency -NASA-. (2013).

NASA Shuttle Radar Topography Mission (SRTM).

Shuttle Radar Topography Mission. https://portal.open

topography.org/datasetMetadata?otCollectionID=OT.0

42013.4326.1

Nikolakopoulos, K. G. (2020). Accuracy assessment of

ALOS AW3D30 DSM and comparison to ALOS

PRISM DSM created with classical photogrammetric

techniques. European Journal of Remote Sensing,

53(sup2), 39–52. https://doi.org/10.1080/22797254.20

20.1774424

Nonogaki, S., Masumoto, S., Nemoto, T., Nakazawa, T.

(2021). Voxel modeling of geotechnical characteristics

in an urban area by natural neighbor interpolation using

a large number of borehole logs. Earth Science

Informatics 14, 871–882. https://doi.org/10.1007/s12

145-021-00600-x

Sanchez Fuentes, D., Mascort-Albea, E. J., Del Espino

Hidalgo, B., Hidalgo-Sánchez, F. M., & Gutiérrez, M.

A. (2021). Spatial data for the design of critical

cartographies in the metropolitan area of Sevilla

(Spain). In Reciprociudad: design diplomacy in Sevilla

design diplomacy in Sevilla (pp. 251–264).

Recolectores Urbanos. https://idus.us.es/handle/11441/

143692

Soriano-Cuesta, C., Romero-Hernández, R., Mascort-

Albea, E. J., Kada, M., Fuls, A., & Jaramillo-Morilla,

A. (2023). Evaluation of Open Geotechnical

Knowledge in Urban Environments for 3D Modelling

of the City of Sevilla (Spain). Remote Sensing, 16(1),

141. https://doi.org/10.3390/rs16010141

Uuemaa, E., Ahi, S., Montibeller, B., Muru, M., & Kmoch,

A. (2020). Vertical Accuracy of Freely Available

Global Digital Elevation Models (ASTER, AW3D30,

MERIT, TanDEM-X, SRTM, and NASADEM).

Remote Sensing, 12(21), 3482. https://doi.org/10.3390/

rs12213482

Yamazaki, D., Ikeshima, D., Tawatari, R., Yamaguchi, T.,

O’Loughlin, F., Neal, J. C., Sampson, C. C., Kanae, S.,

& Bates, P. D. (2017). A high‐accuracy map of global

terrain elevations. Geophysical Research Letters,

44(11), 5844–5853. https://doi.org/10.1002/2017GL07

2874

Geodetic Fundamentals in the Development of a Voxel Model for the Subsoil of the City of Sevilla (Spain)

151