A Regression Based Approach for Leishmaniasis Outbreak Detection

Ernie Baptista, Franco Vigil and Willy Ugarte

Universidad Peruana de Ciencias Aplicadas, Lima, Peru

Keywords:

Random Forest, Machine Learning, Leishmaniasis, NTDs, Outbreaks.

Abstract:

Leishmaniasis is part of a group of diseases called Neglected Tropical Diseases (NTDs) that affects poor and

forgotten communities and reports more than 5,000 cases in regions like Brazil, Peru, and Colombia being

categorized as endemic in these. In this study, we present a machine-learning model (Random Forest) to

predict cases in the future and predict possible outbreaks using meteorological and epidemiological data of the

province of la Convencion (Cusco - Peru). Understanding how climate variables affect leishmaniasis outbreaks

is an important problem to help people to perform prevention systems. We used several techniques to obtain

better metrics and improve our model performance such as synthetic data and hyperparameter optimization.

Results showed two important climate factors to analyze and no outbreaks.

1 INTRODUCTION

Neglected Tropical Diseases (NTDs) are a group of

diseases caused by a diverse group of pathogens such

as parasites, bacteria, and viruses. Affecting more

than 1 billion people worldwide, this group of dis-

eases mainly affects poor and forgotten communi-

ties leading to economic and social consequences

Leishmaniasis part of the NTDs, is a parasitic dis-

ease caused by a protozoa parasite and transmitted

to humans by the bite of infected sandﬂies. Cuta-

neous leishmaniasis (CL) is the most common form

of the disease with more than 700,000 new cases each

year

. Americas is one of the regions where leish-

maniasis had more impact, reporting cases of CL in

20 countries and categorizing 18 of them as endemic,

regions with the most cases of Cl are Brazil, Colom-

bia, and Peru with more than 5,000 cases reported

only in 2021

. According to the Peruvian Center for

disease control (CDC), 4,768 cases of CL were re-

ported with a cumulative incidence of 14.35 cases per

100,000, 847 and 529 of the total cases correspond

https://orcid.org/0000-0002-7510-618X

United States Agency for International Development

(USAiD) - https://www.usaid.gov/global-health/health-are

as/neglected-tropical-diseases

Centers for Disease Control and Prevention (CDC) -

https://www.cdc.gov/parasites/leishmaniasis/epi.html

World Health Organization (WHO) - https://www.wh

o.int/data/gho/data/themes/topics/topic-details/GHO/leish

maniasis

to the regions of Madre de Dios and Cusco

. In La

Convencion province located in the region of Cusco,

364 cases of CL were registered in 2022

. Covid-19

pandemic cause an impact on different programs es-

pecially those related to the detection of NTDs delay-

ing case detection and stopping some programs due

to the prioritization of the combat of the pandemic.

Identifying the elements that cause increases or out-

breaks of leishmaniasis cases is the main challenge

to creating models that predict those scenarios and

trying with them to help in creating early prevention

systems. Several studies are related to the study of

different diseases and their epidemics. In (Nejad and

Varathan, 2021) the authors use different ML mod-

els like Bayes net, Support Vector Machine, Naive

Bayes, and Decision Tables. Their main objective was

to identify climatic risk factors that cause dengue out-

breaks using techniques like the Pearson Correlation

Coefﬁcient (PCC). Then, they found an important fac-

tor that combines the average temperature of the last

5 weeks and the accumulative rainfall of the last 2

weeks.

In (Xu et al., 2020), authors use LSTM, a deep

learning model to compare it with regression mod-

els like SVR, GBM, or GAM. This approach uses as

well meteorological data but this time in a monthly

Peruvian Center for disease control - https://www.dge.

gob.pe/epipublic/uploads/boletin/boletin 202252 31 153

743.pdf

Cusco Regional Health Management - http://www.di

resacusco.gob.pe/inteligencia/epidemiologia/boletines.htm

204

Baptista, E., Vigil, F. and Ugarte, W.

A Regression Based Approach for Leishmaniasis Outbreak Detection.

DOI: 10.5220/0012683900003699

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 10th International Conference on Information and Communication Technologies for Ageing Well and e-Health (ICT4AWE 2024), pages 204-211

ISBN: 978-989-758-700-9; ISSN: 2184-4984

way. However, this process would not allow for bet-

ter disease tracking due to a monthly forecast and not

following the progress of the disease through days

or weeks. The key components of our approach are

mainly composed in the model of machine learning,

Random Forest, which is an ensemble method that

consists of the use of decision trees with the method

of bagging. Then, we train and test the model with

weekly data of conﬁrmed cases of leishmaniasis from

2017 to 2022, obtained through a request form to

the Cusco Regional Health Management (GERESA -

CUSCO)

and meteorological data obtained from the

ofﬁcial web app of the National Meteorological and

Hydrological Service of Peru (SENAMHI)

Our main contributions are as follows:

• We build an ML model for weekly prediction of

CL cases based on meteorological data and con-

ﬁrmed cases.

• We have identiﬁed meteorological risk factors and

possible cases in La Convencion through weekly

predictions from 1 to 4 weeks ahead in 2023 as

well as reporting possible outbreaks.

• We have conducted an experimental analysis to

show the feasibility of our approach.

This paper is distributed in the next sections: First,

we review in Section 2 studies related to the study

and prediction of epidemics of viral infections and

neglected tropical diseases, and their risks. In sec-

tion 3, we will discuss the main contribution of our

research, introduce background and overview related

to the prediction and forecast of epidemics, to ﬁnally

explain the method of our approach. Then, in Sec-

tion 4, we present all the experiments performed with

the model of ML their metrics, and how we improve

those metrics. Finally, in Section 5 conclusions of our

work will be presented.

2 RELATED WORKS

Epidemiological study has been showing a big growth

in different diseases in recent years. The covid-19

pandemic set a huge increase in different studies and

approaches in areas like machine learning and deep

learning. Therefore, this area has diverse methods to

detect, predict or forecast using models of ML and

DL applying techniques like classiﬁcation and regres-

sion. The next articles show a brief outlook on several

studies related to NTDs and the methods they used to

predict cases.

https://sites.google.com/view/geresacusco/inicio

https://www.senamhi.gob.pe/?&p=estaciones

In (Zhao et al., 2020), the authors propose a Ran-

dom Forest (RF) model that will compete against an

Artiﬁcial Neural Network (ANN), searching for the

best results at predicting dengue cases in Colombia,

with pooled national data and department data, this

data uses various predictors, like previous dengue

cases, air temperature, population counts and educa-

tion. Both models are evaluated with Mean Abso-

lute Error (MAE) and then compared using the Rel-

ative MAE. Instead, we are predicting cases of leish-

maniasis using RF, using data from a speciﬁc region

in Cusco called La Convencion, besides we don’t in-

clude data like population or socio-economic factors,

since we only look for a correlation between climate

data and its impact in the number of new cases.

In (Harvey et al., 2021), the authors use a combi-

nation of Gaussian Processes and Random Forest Re-

gressors to predict malaria cases over a period of 13

weeks in Burkina Faso, so it can validate a warning

system for a potential epidemic. They use data from

the Integrated e-Diagnostics Management of Child-

hood Illness (IeDA) for the conﬁrmed diagnosis of

malaria, and after a selective process, they decide to

use rainfall, because it improves the precision of the

algorithm. Instead, we use data of conﬁrmed cases

obtained from health organizations in Peru using it as

a target. The predictors that we use are: precipitation,

humidity, and temperature. And we only use Random

Forest for the prediction because, to the best of our

knowledge in the literature, we found that RF is the

most robust model for our scenario.

In (Elsheikh et al., 2021), the authors propose

an LSTM model to predict conﬁrmed cases, recov-

ered cases, and deaths of COVID-19 in Saudi Arabia

three weeks ahead. Also, they compare the proposed

model with a statistical model called AutoRegres-

sive Integrated Moving Average (ARIMA), and an

AI model called Nonlinear AutoRegresive Artiﬁcial

Neural Networks (NARANN). The data they utilize

to train the models are from the ofﬁcial report from

the Ministry of Health using the conﬁrmed cases, re-

covered cases, and deaths in three different periods of

time. The evaluation criteria, they use, for the models

are seven RMSE, R

, MAE, EC, OI, COV, and CRM.

On the other hand, our approach uses only conﬁrmed

cases, because mortality rates of CL in Peru are low

having 1 conﬁrmed death in 2022

, and data of recov-

ered cases are hard to obtain.

In (da Silva et al., 2021), the authors propose

a method that combines Ensemble Empirical Mode

Decomposition (EEMD) with Autoregressive Inte-

grated Average Exogenous inputs (ARIMAX), named

EEMD-ARIMAX to analyze the correlation between

human mobility and meteorological data with the

A Regression Based Approach for Leishmaniasis Outbreak Detection

205

number of COVID-19 cases in the capitals of Brazil.

For their data of COVID-19 cases, they use Brasil.io,

which is a website that compiles newsletters from the

State Health Secretariats of Brazil, for the meteoro-

logical data they use data from the Centro de Previsa o

de Tempo e Estudos Clim

aticos and used Minimum

and Maximum Temperature, Humidity, and Rainfall,

and the human mobility data they use the COVID-

19 Community Mobility Reports given by Google, it

shows the trends of mobility in certain places, like

Retail and recreation, Parks, Workplaces, etc. Us-

ing RMSE, ME, and MAE they evaluate the predic-

tions for their method, and they compare it with ARI-

MAX. They normalized their data, showing an im-

provement in their method in metrics like RMSEW.

In contrast, we use meteorological data and conﬁrmed

cases to ﬁnd correlations and predict the number of

cases weeks ahead, instead of ﬁnding patterns with

the trends of population or climate data using a time

series model like ARIMA.

In (Nguyen et al., 2022), the authors searched a

model that can accurately predict dengue cases in

Vietnam with meteorological factors, for this, they

compared Convolutional Neural Network (CNN),

Transformers, Long Short-Term Memory (LSTM),

and Attention-enhanced LSTM (LSTM-ATT) with

more traditional machine learning models like XG-

Boost, Super Vector Regressor (SVR), etc. Their

data was constituted with monthly incident conﬁrmed

cases and deaths for dengue and meteorological data

like average monthly temperature, maximum average

monthly temperature, monthly rainfall, monthly av-

erage relative humidity, monthly evaporation, total

monthly sunshine hours, etc.

For the evaluation of models in a time period of

one to three months, they use RMSE and MAE, they

also assessed the months between outbreaks or not

for the model LSTM-ATT, for this epidemic detec-

tion they used four metrics, which are: accuracy, pre-

cision, sensitivity, and speciﬁcity. In contrast, we use

weekly data, due to that type of format data gives us

an opportunity to follow and visualize if there are me-

teorological patterns that could increase the spread of

CL, since the granularity of weekly data may cause a

loss of patterns.

3 CONTRIBUTION

3.1 Preliminary Concepts

Deﬁnition 1 (Regression (Chandramouli et al.,

2018)). Regression is the process of ﬁnding an asso-

ciation or relation of a dependent variable, which is

Figure 1: Example of linear regression (Al-Mudhafar,

2020).

the variable that we want to predict, with independent

variables that are known as predictors.

Example 1 (Regression). Figure 1 represents the

structure of a linear regression model, showing the

relationship between two variables.

Deﬁnition 2 (Ensembled Models (Zhou, 2021; Sarkar

and Natarajan, 2019)). It’s a technique that combines

the outputs of different models of machine learning

to get a better result in comparison to each model on

their own, for this reason, they are usually built with

simpler models but it also applied to stronger models

so it can use less of them.

The ensemble has various techniques that include:

Averaging (taking the average of the outputs between

all the models to get its ﬁnal result), Boosting (using

weak learners and, through multiple iterations, con-

verts them into strong learners, focusing on the mis-

takes of the hypothesis), Bootstrapping (the model

obtains a sampling that will be used as an input for

the models and the output will be the most voted or

an average if the case is a regression), Bagging (based

on bootstrap sampling, it takes a dataset with a num-

ber of samples, takes a random sample, and copies it

in the sampling set, it keeps the sample so it can be

chosen again and repeats the process several times).

Deﬁnition 3 (Decision Trees (Zhou, 2021)). It’s a

representation of the choices and decisions a person

can make in each situation in the structure of a tree,

being the branches as the multiple decisions that a

person can take, and the leaves being nodes of the

outcomes or states of every decision, and the root is

the initial state of the situation.

Deﬁnition 4 (Random Forest (Zhou, 2021)). It works

as an extension of the bagging method, using the ran-

domness of bootstrapping to create decision trees so

they are different from each other, so it can reduce

overﬁtting and make the outcome more precise. It

ICT4AWE 2024 - 10th International Conference on Information and Communication Technologies for Ageing Well and e-Health

206

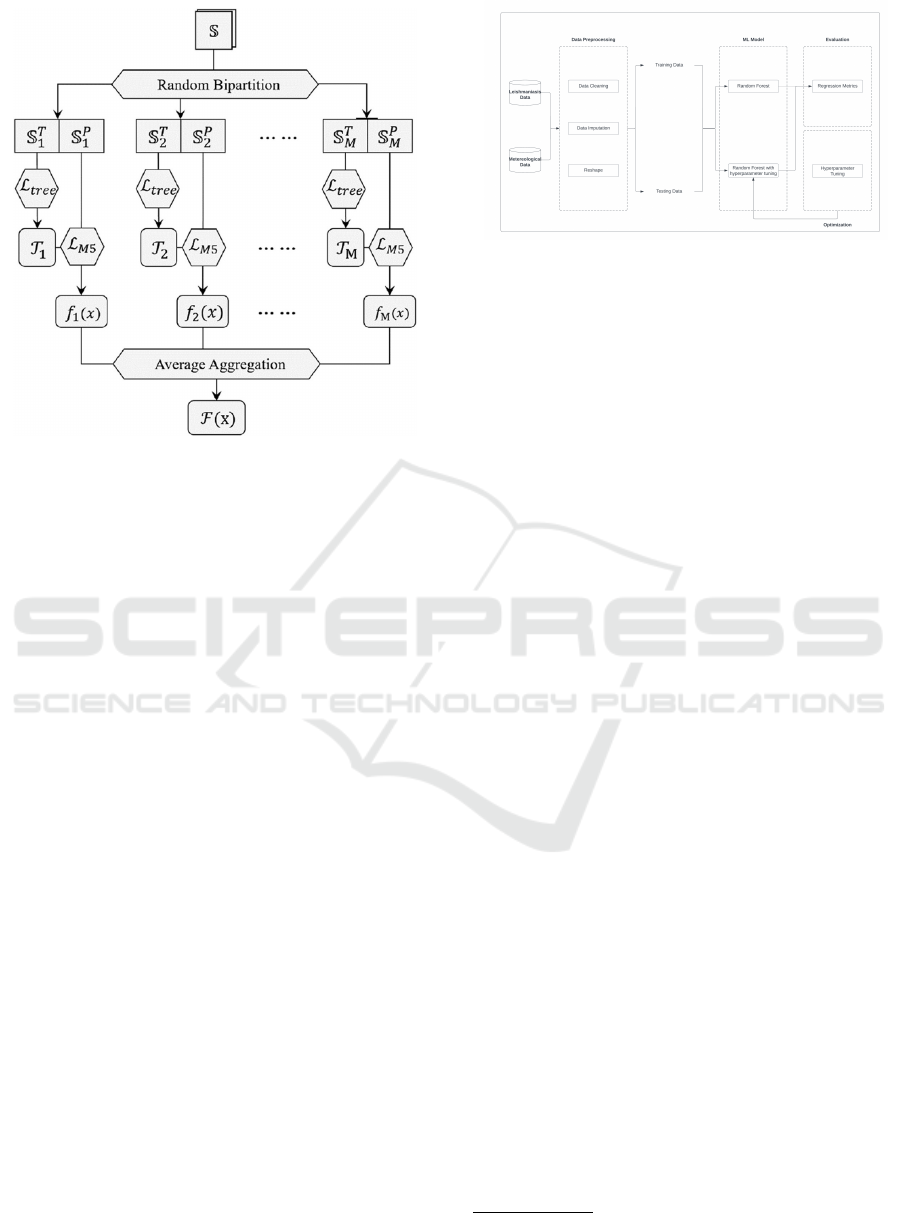
Figure 2: Structure of Random Forest (Ao et al., 2019).

usually starts with a lower performance with fewer

trees but with more learners it can get better perfor-

mance, also it has a low computational cost.

Example 2 (Random Forest). In Figure 2, we see the

structure of a Random Forest with the partitions of

samples for every decision tree, the outputs of these,

and the ﬁnal solution made with average aggregation.

3.2 Method

The method designed to predict leishmaniasis out-

breaks consists of a group of stages. The whole pro-

cess begins with collecting the data, then we con-

tinue with Data preprocessing, which is involved the

process of cleaning the data detecting missing values

and removing noisy data; Data resampling, where we

change the format of the dataset to weekly variables

and we also apply feature engineering in this process

to get new variables like the average temperature of

the week. After the preprocessing stage, we have the

model stage, where we start setting the partition of

our dataset for training and testing. This second stage

is made with the Random Forest Regressor, we train

and test the model and we analyze the ﬁrst results of

the model in the evaluation stage with regression met-

rics. The third stage corresponds to the optimization

process, different techniques will be used to get the

best parameters for our model and improve error pre-

dictions and improve our metrics (Figure 3).

Figure 3: Method Diagram.

3.2.1 Data Preprocessing

Two datasets were collected for this study, one of

them corresponds to meteorological data that was

obtained from the ofﬁcial website of the Meteoro-

logical Service of Peru

from 2017 to 2022. The

data was provided hourly, with attributes like tem-

perature, humidity, precipitation, wind direction, and

wind speed. Leishmaniasis data was obtained through

a request form to the Cusco Regional Health Man-

agement (GERESA - CUSCO)

, this dataset con-

tains only conﬁrmed cases of leishmaniasis from the

province of La Convencion in a weekly format.

Data cleaning is the ﬁrst technique used in this

stage, the meteorological dataset had a lot of miss-

ing values that were handled imputing those hours

and dates that were missing, then the meteorologi-

cal values were imputed with a linear interpolation

method. The percentage of missing values is pre-

sented in Table 1. The Leishmaniasis dataset had 28

weeks of missing data, to solve this problem we re-

moved those values in order to avoid noise. Clas-

sic imputation techniques can’t be applied directly to

this type of data due to the different behavior of the

disease through the weeks and its spread. Then, we

have the resampling process, due to the formats of the

datasets (hourly format and weekly format). This pro-

cess has two stages:

1. We resample the meteorological dataset in a daily

format here we also apply feature engineering to

get new variables: minimum, maximum, and av-

erage temperature and humidity of the day.

2. In the second stage, we resample the dataset to a

weekly format and we combine the whole dataset

with leishmaniasis cases.

After applying feature selection and considering epi-

demiological variables we found that wind direction

and wind speed won’t impact to the prediction of

the cases, due to their correlation coefﬁcients (0.045,

https://www.senamhi.gob.pe/?&p=estaciones

https://sites.google.com/view/geresacusco/inicio

A Regression Based Approach for Leishmaniasis Outbreak Detection

207

Table 1: Missing Values %.

Attribute

Missing Values (%)

1 Temperature 8.47%

2 Humidity 8.53%

3 Precipitation 21.36%

4 Wind Speed 8.68%

5 Wind Direction 8.68%

0.12). The ﬁnal dataset resulted in 233 rows, and

7 variables: mintemp, maxtemp, avgtemp, minhum,

maxhum, avghum and prec.

3.2.2 Synthetic Data

This technique consists in creating new artiﬁcial data

for the training set based on our existing dataset. We

propose this method due to a lack of data and its future

impact on the performance of the model. We use Syn-

thetic Data Vault (SDV) (Patki et al., 2016) to build

the new training dataset for our model. This process

consists in prepare the data for the training of the SDV

model, here we load the data and deﬁne the format of

each variable. Then we have the modeling stage, SDV

provides different models called synthesizers, for this

project FAST ML

was used. The model learns from

the existing data and then we sample new data based

on the number of new rows that we want.

3.2.3 Random Forest

RF is an ensemble model that uses decision trees with

a bagging method, so it can prevent overﬁtting. RF

has many decision trees that use different samples of

data and train separately from each other, each tree

produces different results that are ranked and select-

ing the best result. In this stage, we use the sklearn

library of the Random Forest Regressor

. For our

RF model, we deﬁne training and testing in a differ-

ent way, with our approach of using synthetic data

we cannot use all the original dataset to generate new

data, because while testing, the model will overﬁt, to

avoid this problem we split the original dataset having

only the 2022 data to testing and only generating new

data based on years 2017 - 2021.

3.2.4 Evaluation

The evaluation methods that will be used to evalu-

ate the regression model predictions are Mean Ab-

solute Error (MAE) and Root Mean Squared Error

https://docs.sdv.dev/sdv/single-table-data/modeling/s

ynthesizers/fast-ml-preset

https://scikit-learn.org/stable/modules/generated/skle

arn.ensemble.RandomForestRegressor.html

(RMSE). MAE calculates the sum of all the absolute

differences between the actual and the predicted value

and then divided by the total number of data points.

RMSE is the square root of MSE, and Mean Squared

Error (MSE) is basically the squared difference be-

tween actual and predicted value.

Both metrics represent similarities because they

determine how close is the prediction to the actual

values on average, even detecting large errors in the

case of RMSE. Low values of MAE and RMSE indi-

cate that de model is correctly predicting and larger

values represent poor prediction.

3.2.5 Optimization

In order to optimize our model and get better results in

our metrics we will use hyperparameter tuning. This

technique uses different methods to obtain the best

set of hyperparameter values that produce better re-

sults in the model’s performance. Random forest has

several hyperparameters that can be modiﬁed to get

better performance. Getting the best set of hyperpa-

rameters can be challenging if we do it manually, so

in this study, we will use different methods such as

random search, grid search, and Three-based Pipeline

Optimization (TPOT).

• Grid Search (GS). GS is one of the most common

techniques to optimize hyperparameters. Its func-

tionality is relatively simple, we create a grid of

different hyperparameters values then GS ﬁts in

every combination, saves every performance for

each set created, and selects the best performance

as output.

• Random Search (RS). This technique uses a

method that chooses random values of a prede-

ﬁned set of hyperparameters, then in each iter-

ation ﬁts the model with a set chosen and re-

turns the best set after several iterations. Ran-

dom Search performs better when we have a large

search space and also takes less time than GS to

show results.

• Three-Based Pipeline Optimization (TPOT) (Le

et al., 2020). It’s a machine learning tool that

uses genetic programming to help to ﬁnd the best

pipeline for a machine learning model. For this

study, we use TPOT to get the best set of hyper-

parameters for Random Forest.

ICT4AWE 2024 - 10th International Conference on Information and Communication Technologies for Ageing Well and e-Health

208

4 EXPERIMENTS

4.1 Experimental Protocol

All our was conducted with Google Colab, a free ver-

sion of a Python environment. Colab provides 12.7

GB of ram and 107.7 GB of disk to write and exe-

cute Python code and store ﬁles for up to 12 hours.

Dataset ﬁles were stored in google drive and imported

with a Python library gdown. For the optimization

stage, a dictionary of parameters was determined and

the possible values for each parameter are shown in

Table 2. Our code is publicly available in: https:

//github.com/RyzewitchChicken/LMR-Code.git

4.2 Results

The proposed work carried out several experiments in

order to get better metric values and reduce error pre-

diction. Those experiments are presented in different

scenarios where we deﬁned hypotheses and present

the results of them.

Scenario 1. The ﬁrst scenario performed is re-

lated to training and testing the model with the orig-

inal dataset. The experiment resulted in MAE and

RMSE values, 3.97 and 4.91 respectively.

Scenario 2. After several tests with synthetic data,

Table 2: Values for optimization.

Parameter Possible Value

Number of

estimators

100, 200, 300, 400, 500 - 1500

Max features sqrt, log2

Max depth 10, 20, 50, 65, 70, 90, 110, none

Min samples split 2, 5, 10

Min samples leaf 1, 2, 4

Table 3: Synthetic data values test.

Quantity of rows

MAE

1,500 3.91

4,500 3.90

7,500 3.91

10,500 3.77

13,500 3.89

Table 4: Result of Optimizers.

Optimizer

Quantity of

estimators

Min

samples

split

Min

samples

leaf

Max

features

Max

depth

Random

700 10 2 sqrt 10

Grid

1200 5 4 log2 90

TPOT 400 2 2 sqrt 65

we concluded by adding 10,500 new rows of data to

the original dataset based on the results of MAE val-

ues, see Table 3. In this experiment, we got better

value metrics in comparison with the original dataset,

3.77 in MAE and 4.56 in RMSE. The distribution of

new data in comparison with real data is shown in

Figure 4. Until this scenario, random forest hyper-

parameters were not modiﬁed, so settings were used

by default based on the sklearn library.

Scenario 3. Table 4 shows the optimizers’ best

results according to the values established in Table 2.

Random search performs slightly better in compari-

son to TPOT and grid search, having a better value in

RMSE with 4.42 (Table 5) and being faster than oth-

ers because of the random selection of hyperparam-

eters. On the other hand, grid search also has good

results but performs badly in RMSE getting 4.51, due

to its search space and all combinations evaluation,

grid search tends to be computationally slow.

Scenario 4. In order to get better metric values,

we propose a hypothesis that our model tends to per-

form badly due to the low case periods and according

to our research approach (predict outbreaks) we con-

sider that low case periods would be not necessary. In

this scenario, we performed two experiments: i) We

considered that cases lower than 5 cause low perfor-

mance. Our model struggles to predict minor values

causing large prediction errors and resulting in higher

MAE and RMSE values. We conducted an experi-

Figure 4: Distribution comparison between synthetic and

real data.

Table 5: Metric Results.

Experiment MAE RMSE

Random Forest (Original Dataset) 3.97 4.91

Synthetic Data 3.77 4.56

Random Forest + Random Search 3.65 4.42

Random Forest + Grid Search 3.67 4.51

Random Forest + TPOT 3.64 4.47

Random Forest + Cases > 5 2.79 3.48

Random Forest + Cases > 7 2.27 2.93

A Regression Based Approach for Leishmaniasis Outbreak Detection

209

(a) 8 weeks ahead.

(b) 16 weeks ahead.

Figure 5: Predicting Outbreaks.

ment where we deleted values lower than 5 and we

got better results, having 2.79 in MAE and 3.48 in

RMSE. And, ii) for the second experiment we tested

values higher than 7. In this case, we even got bet-

ter results in our metric error, MAE 2.27 and 2.93 in

RMSE, an improvement of 18.64% in MAE in com-

parison to the previous MAE value. Important to

mention that scenario 4 experiments were conducted

with our best model and the optimizer (Random For-

est + Random Search), a big improvement consider-

ing that MAE dropped from 3.65 to 2.27 and that our

model has problems predicting low values. All met-

ric values of the different experiments performed are

shown in Table 5.

Prediction. With our previous results in the fourth

scenario, we can ﬁnally generate predictions having

our best model. In Figure 5a and Figure 5b, we gen-

erate an 8-week and 16-week prediction, all these

predictions correspond to the ﬁrst 4 months of 2023

(January, February, March, and April). Both Figures

present the cases of 2022 and the predictions gener-

ated, in both, we can see that the province of La Con-

vencion won’t show outbreaks and the trend shows no

outbreaks for the incoming months. The way that we

detect an outbreak is by using the Z-score method if

we detect an outlier in our set of predictions we deﬁne

that as an outbreak.

4.3 Discussion

Metrics. In order to get better metric values and re-

duce MAE and RMSE we performed several exper-

iments (Table 5). Considering that the lowest MAE

and RMSE value we get is the better our model per-

forms, we proposed a few techniques to achieve. The

ﬁrst experiment gave us a perspective on how the

model is performing with the original dataset, we

found that missing values and zero values cause noise

and reduce our dataset size, therefore, our model per-

formed badly with high metric values and a higher

RMSE value of 4.91. Synthetic data helped us to get

more rows with a similar distribution to the original

dataset, showing that with this technique we can re-

duce error prediction going from 3.97 in MAE to 3.77

and 4.91 in RMSE to 4.56.

We compared three optimizer techniques where

Random Search performed a bit better than TPOT,

having similar results in MAE with 3.65 and 3.64 and

a slight difference in RMSE with 4.42 and 4.47. Grid

Search also performs similarly in MAE (3.67) but

struggles to get a good RMSE value getting 4.51. On

the other hand, we have Table 4 results. We put out at-

tention to the number of estimators and ”max depth”,

Grid Search costs a high computationally perfor-

mance due to the values in estimators 1200 and 90

in max depth, more estimators and higher depth for

a tree tend to have a higher training time. Random

Search and TPOT have different results, with more

estimators for RS with a lower depth tree but fewer

estimators for TPOT with a higher depth tree. Even

with more estimators RS performed a little faster than

TPOT, this is caused because of the depth. In RF,

max depth deﬁnes the number of splits for each de-

cision tree, so in the case of RS takes less time for

the model to train due to fewer splits. This experi-

ment shows that hyperparameter tuning was a good

approach because reduces signiﬁcantly error predic-

tion, we went from 3.77 with synthetic data without

modifying hyperparameters and using it based on the

setting of sklearn to 3.65 testing different combina-

tions of hyperparameters.

Our last experiment proposed a hypothesis based

on how our model was performing until the last sce-

nario. We have shown that zero values caused noise

in the model and produced bad performance, but go-

ing deeper into the experiments, we noticed that the

model was still struggling with low values. Two tests

were conducted with a similar approach, dropping

those values that may cause trouble for the model.

These two experiments showed that having cases val-

ues higher than 5 and 7 caused better metric values,

in MAE and RMSE improved error prediction from

3.65 to 2.79 and 2.27, in the case of RMSE from 4.42

to 3.48 and 2.93. These major changes helped us in

predicting larger values to detect outbreaks in the fu-

ture which makes our model better to predict larger

cases but worst to predict lower cases.

Model. Feature importance is an important technique

ICT4AWE 2024 - 10th International Conference on Information and Communication Technologies for Ageing Well and e-Health

210

to analyze our model and how our attributes are con-

tributing to predicting leishmaniasis cases. Based on

our analysis maximum humidity is the most important

feature in the prediction, representing 18%. Average

temperature and minimum humidity represent another

15% and 14% of contribution while precipitation rep-

resents the lowest importance with 11%. We can see

that humidity has a good correlation with leishmania-

sis cases while there is a low correlation between pre-

cipitation and our target variable (cases), but we no-

ticed that this might be related to the meteorological

dataset.

5 CONCLUSION

In this work, we used a Random Forest model to pre-

dict leishmaniasis cases and possible outbreaks in the

future. As an ensembling model, RF shows good

results in predicting cases. We performed several

tests to get a better model with less error prediction,

showing that our original dataset was really small and

caused problems for the model. Even with synthetic

data, our error prediction was high, so an optimization

process was necessary. Optimizers showed great re-

sults, Random Search and a genetic algorithm (TPOT)

performed better than an approach like Grid Search

reducing error prediction in metrics like MAE from

3.77 to 3.64-65.

Our ﬁrst approach was deleting 0 values due to the

noise that causes, but we noticed that low values cause

trouble. We proposed two experiments where we con-

sidered that low values won’t be necessary. After sev-

eral tests, we conclude that cases greater than 5 and 7

contribute to getting better metrics values with an im-

provement of 24% and 38% (MAE) respectively. That

experiment causes a model that is better at predicting

high values but worst at low values. Finally, we no-

ticed that humidity and temperature are the most im-

portant predictors.

As an extension of this work, a better and bigger

dataset is necessary to get a better model with the cor-

rect recollection of meteorological data and epidemi-

ological data. On the other hand, NTDs have several

diseases that cause problems in different parts of the

world.

REFERENCES

Al-Mudhafar, W. J. (2020). Integrating machine learning

and data analytics for geostatistical characterization of

clastic reservoirs. Journal of Petroleum Science and

Engineering, 195:107837.

Ao, Y., Li, H., Zhu, L., Ali, S., and Yang, Z. (2019). The

linear random forest algorithm and its advantages in

machine learning assisted logging regression model-

ing. Journal of Petroleum Science and Engineering,

174:776–789.

Chandramouli, S., Dutt, S., and Das, A. (2018). Machine

Learning. Pearson Education India, 1st edition.

da Silva, T. T., Francisquini, R., and Nascimento, M. C. V.

(2021). Meteorological and human mobility data on

predicting COVID-19 cases by a novel hybrid decom-

position method with anomaly detection analysis: A

case study in the capitals of brazil. Expert Syst. Appl.,

182:115190.

Elsheikh, A. H., Saba, A. I., Elaziz, M. A., Lu, S., Shan-

mugan, S., Muthuramalingam, T., Kumar, R., Mosleh,

A. O., Essa, F., and Shehabeldeen, T. A. (2021). Deep

learning-based forecasting model for covid-19 out-

break in saudi arabia. Process Safety and Environ-

mental Protection, 149:223–233.

Harvey, D., Valkenburg, W., and Amara, A. (2021). Predict-

ing malaria epidemics in burkina faso with machine

learning. PLOS ONE, 16(6):1–16.

Le, T. T., Fu, W., and Moore, J. H. (2020). Scaling tree-

based automated machine learning to biomedical big

data with a feature set selector. Bioinform., 36(1):250–

256.

Nejad, F. Y. and Varathan, K. D. (2021). Identiﬁcation of

signiﬁcant climatic risk factors and machine learning

models in dengue outbreak prediction. BMC Medical

Informatics Decis. Mak., 21(1):141.

Nguyen, V.-H., Tuyet-Hanh, T. T., Mulhall, J., Minh, H. V.,

Duong, T. Q., Chien, N. V., Nhung, N. T. T., Lan,

V. H., Minh, H. B., Cuong, D., Bich, N. N., Quyen,

N. H., Linh, T. N. Q., Tho, N. T., Nghia, N. D., Anh,

L. V. Q., Phan, D. T. M., Hung, N. Q. V., and Son,

M. T. (2022). Deep learning models for forecasting

dengue fever based on climate data in vietnam. PLOS

Neglected Tropical Diseases, 16(6):1–22.

Patki, N., Wedge, R., and Veeramachaneni, K. (2016). The

synthetic data vault. In DSAA, pages 399–410. IEEE.

Sarkar, D. and Natarajan, V. (2019). Ensemble Machine

Learning Cookbook. Packt Publishing, 1st edition.

Xu, J., Xu, K., Li, Z., Meng, F., Tu, T., Xu, L., and Liu,

Q. (2020). Forecast of dengue cases in 20 chinese

cities based on the deep learning method. Interna-

tional Journal of Environmental Research and Public

Health, 17(2):453.

Zhao, N., Charland, K., Carabali, M., Nsoesie, E. O.,

Maheu-Giroux, M., Rees, E., Yuan, M., Garcia Bal-

aguera, C., Jaramillo Ramirez, G., and Zinszer, K.

(2020). Machine learning and dengue forecasting:

Comparing random forests and artiﬁcial neural net-

works for predicting dengue burden at national and

sub-national scales in colombia. PLOS Neglected

Tropical Diseases, 14(9):1–16.

Zhou, Z.-H. (2021). Machine learning. Springer, Gateway

East, Singapore.

A Regression Based Approach for Leishmaniasis Outbreak Detection

211