Design of Interactive STACK Exercises Using JSXGraph for Online

Course: Exploring Strategies for Supporting Students with

Mathematical Challenges

Henry Lähteenmäki

, Jarkko Hurme

and Päivi Porras

Department of Civil and Energy Engineering, South-Eastern Finland University of Applied Sciences, Kotka, Finland

Department of Electrical, Automation and Mechanical Engineering, Oulu University of Applied Sciences, Oulu, Finland

Technology, LAB University of Applied Sciences, Lappeenranta, Finland

Keywords: STACK, JSXGraph, Interactive Digital Tasks, e-Assessment, Online Learning.

Abstract: The integration of technology into education has changed the way students learn and utilise course materials

in online courses. However, the effectiveness of online courses greatly depends on the quality of learning

materials, the ability to provide feedback and interactivity. With regard to mathematical exercises, the issue

of designing interactive tasks has not yet been adequately addressed. This article presents a model to support

the design of automatic interactive exercises using the Moodle STACK plugin and the JavaScript library

JSXGraph, with special attention paid to providing immediate feedback and supporting students with

mathematical challenges. We also delve into the technical aspects of the design of interactive exercises to

highlight the opportunities and challenges that open-source tools bring to the creation of digital tasks. We

argue that with careful exercise design and attention to specific technical considerations, interactive STACK

exercises created with JSXGraph can particularly enhance students’ understanding of conceptual aspects in

the mathematical sciences. A specific example exercise is given, and its design is discussed. In conclusion,

this article extensively discusses important factors to consider in the design of interactive exercises and

examines rarely addressed issues in the design of automatic digital tasks, such as accessibility, pedagogical

soundness, expanding the possibilities of immediate hints, dynamic guiding of students, feedback, and

students with mathematical challenges.

1 INTRODUCTION

Continuous learning is more and more popular

nowadays. In the changing world of work, updating

one's own competence is vital. This is especially

important for the unemployed and people who did not

finish school. The prospects for people without a

degree are poor, which may affect their self-esteem

and increase exclusion. In education, mathematical

skills are often emphasised from the application

phase. If a person has not studied for a long time or if

their schooling was interrupted due to poor

mathematical skills, it will be necessary for them to

repeat the basics. The educational background of the

disadvantaged is usually lower, suggesting that

traditional education may not have been the best

https://orcid.org/0009-0001-3626-8709

https://orcid.org/0009-0000-5148-6192

https://orcid.org/0000-0002-6098-1731

option for them. This paper introduces an online

course specifically aimed at helping the

disadvantaged improve their mathematical skills.

Learning in self-paced online course requires

motivation and self-direction. If students do not have

self-efficacy, meaning that they do not believe in their

own ability to learn, self-paced online courses may

not be the best option. Even with good self-efficacy,

students require a good reason (motivation) and

commitment to do well on self-paced online courses.

And still life may throw a spanner into the wheel and

make it difficult to study. This paper studies methods

of improving self-efficacy and commitment by giving

encouraging feedback interactively during problem

solving, not only after answers are submitted.

Dropping out of online courses is common and the

reasons for this have been extensively studied (Bawa,

Lähteenmäki, H., Hurme, J. and Porras, P.

Design of Interactive STACK Exercises Using JSXGraph for Online Course: Exploring Strategies for Supporting Students with Mathematical Challenges.

DOI: 10.5220/0012684600003693

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 16th International Conference on Computer Supported Education (CSEDU 2024) - Volume 2, pages 549-556

ISBN: 978-989-758-697-2; ISSN: 2184-5026

549

2016; Onah et al., 2014; Shaikh & Asif, 2022). Since

independent online courses lack teacher contact, the

structure of the course is crucial. A course which is

poorly implemented technically, and pedagogically

confusing will not motivate students to complete it. If

students receive feedback on their competence only

at the end, they do not have the opportunity to focus

on the topics they understand poorly. The

effectiveness of online courses greatly depends on the

quality of learning materials, the ability to provide

feedback and interactivity. It has been argued that the

major limitation of online courses is the lack of rich,

well supported activities as a framework for learning

by doing (Koedinger et al., 2015).

E-learning environments such as Moodle are

being used to host and deliver online activities and

assessments. A range of assessments and activity

types are available, from filling in the blanks to

multiple choice questions. The Moodle platform has

specific tools to enwiden the range of interactive

activities in mathematical sciences, namely the e-

assessment system STACK and the JavaScript library

JSXGraph for dynamic geometry.

This paper presents a model for designing

interactive exercises using STACK (STACK

Documentation, 2024) and JSXGraph (JSXGraph

Documentation, 2024), with a focus on providing

immediate feedback and accommodating students

with mathematical challenges. Technical aspects of

the design of interactive exercises are discussed. We

highlight the opportunities and challenges that open-

source tools bring to the creation of digital tasks.

The paper argues that interactive STACK

exercises created with JSXGraph can enhance

students’ understanding of conceptual aspects in the

mathematical sciences. The design of interactive

exercises should consider factors such as

accessibility, expanding the possibilities of

immediate hints, feedback, dynamic guiding of

students, a learner-centred approach and students

with mathematical challenges.

2 TECHNICAL ASPECTS OF

INTERACTIVE EXERCISE

DESIGN

STACK is a prominent open-source e-assessment

system which operate within the Moodle and

integrates effectively with other platforms. Utilising

an open-source Computer Algebraic System (CAS)

called Maxima (Maxima Documentation, 2024),

STACK tasks are programmed mainly using Maxima

syntax. Furthermore, STACK permits specific

functions which are absent in Maxima but are crucial

for the generation of STACK tasks. Responses to

STACK tasks can use mathematical formats such as

polynomials, matrices, integers and floating-point

numbers. Personalised versions of tasks are enabled

through randomisation of initial values, ensuring

unique renditions for each student. Traditional

STACK tasks, lacking the interactive interface,

commonly require answers to be typed into

designated answer fields. More advanced

interactivity, such as mouse interactions with

geometrical shapes, text objects or equations, can be

introduced via JSXGraph, a dynamic geometry

software that has been integrated into STACK.

The versatility of JSXGraph permits the creation

of diverse content by capitalising on JavaScript's

adaptability to construct interactive components,

limited only by the task creator's programming

expertise. The visualisation capacities of JSXGraph

offer numerous possibilities in digital task design,

such as visual prompts and responses.

In interactive tasks, hidden answer fields may

contain diverse data types, such as the coordinates of

interactively manipulatable objects, lists or Boolean

values. One fundamental principle in the coding of

interactive tasks is that the final state of JSXGraph

should be restored, meaning that the position of

objects as set by the student before checking the

answer can be restored and the final state shown

rather than the initial state. STACK provides object

binding functions tailored to JSXGraph but in more

complex situations storing the JSXGraph state as a

JSON string is a feasible method.

The realm of digital tasks offers both

opportunities and challenges, particularly concerning

the completion of STACK tasks. Amour (2023)

highlights the fact that developing proficient STACK

tasks is time-consuming and incorporating

interactivity with JSXGraph demands even more

time. Nonetheless, that meticulously designed digital

resources will be valuable for next several years is

undeniable. Mastery of coding skills is crucial,

including an in-depth understanding of Maxima

syntax and the commands and functions utilised in

STACK. Equally important is a thorough grasp of the

requirements for constructing a STACK task within the

Moodle environment. Moreover, integrating

interactive elements requires expertise in JSXGraph.

Proficiency in both the JSXGraph library and its

documentation, along with a wider comprehension of

JavaScript, is essential to incorporate interactive

elements into STACK tasks. The primary constraint

when developing interactive tasks is the coder's

CSEDU 2024 - 16th International Conference on Computer Supported Education

550

programming abilities. Although artificial intelligence

can aid in JSXGraph task creation, full integration of

interactive elements within STACK tasks is not yet

possible as JSXGraph works in a sandbox within

STACK, which requires special knowledge.

The benefits arising from interactive tasks can

permeate all levels of education. This paper seeks to

demonstrate the effectiveness of these tasks in

enhancing fundamental mathematical skills and

solidifying foundational mathematical concepts.

Although these aspects may not be the primary focus

in higher education institutions where it is assumed

students possess adequate competencies in

mathematical sciences, the decline in mathematical

skills has been steep in recent years. Consequently,

developing supportive measures with the aim of

strengthening basic mathematical skills to facilitate

successful higher education pursuits is now urgent.

3 MODEL FOR DESIGNING

INTERACTIVE EXERCISES

Several particular aspects must be considered in the

design of the assessment and learning environments

for online courses. Promotion of self-directed

learning skills, authenticity of exercises and well-

timed, appropriate feedback form the characteristics

of a powerful online learning model (Hurme et al.,

2023). Thus, concentrating on mindset and self-

directive learning skills may help disadvantaged

students complete a course. Shaikh and Asif (2022)

also remark that motivational incentives such as

financial outcomes may help with persistence.

Rasila et al. (2015) outlines how the presentation

of mathematics plays a pivotal role in the construction

of an agreeable user experience. The mathematical

content of online courses needs to be comprehensible

without a teacher's assistance, and the interaction

between the student and the computer should be as

seamless as possible. Furthermore, certain issues with

materials and systems may subsequently be identified

indirectly through students' exercise response data as

gathered by the e-learning environment. In every

instance, user feedback and ensuing revisions of both

the e-learning platform and study materials are

necessary to enhance the user experience.

Koedinger et al. (2015) showed that engaging in

interactive activities during online courses yields

more significant improvements in study outcomes

compared to simply watching videos or reading

theoretical material. Interactive activities foster active

learning which is more effective than passive

knowledge acquisition, and the learning-by-doing

method seems to be a reasonable foundation for the

design of an online course.

Paiva et al. (2015) argues that interactive learning

modules, including interactive multimedia books,

online quizzes and tutorial videos, create an effective

online learning environment for mathematics in higher

education. Students with initially lower basic maths

skills showed significant improvement after such

modules, highlighting the potential of the interactive

approach to bridge learning gaps in mathematics. The

study provided evidence that interactivity could be an

effective tool for enhancing learning outcomes.

Velichová (2021) sums up that learning by doing

enhances learners’ motivation, enthusiasm, interest,

attitude towards the entire learning process and desire

to acquire new knowledge.

Modern e-learning environments permit the

creation of more diverse mathematical tasks for

STEM courses compared to the era of textbook-

sourced tasks (Rasila et al., 2015). Traditional digital

tasks often resembled textbook problems and were

crafted similarly. However, dynamic geometry

software introducef an innovative dimension to

interactive tasks (Gerhäuser et al., 2011), and Bach et

al. (2021) confirmed that dynamic geometry

facilitates the development of challenging visual

conceptual tasks while enabling novel advancements

thanks to JavaScript's versatility.

Interactive tasks in higher education are

increasingly prevalent; however, effective design

frameworks remain scarce. It is crucial to

acknowledge that open-source tools can generate

impactful interactive tasks, and accessibility must be

considered to ensure compatibility with users' diverse

needs. Interactive tasks should adopt a learner-

centred approach, simplifying phenomena so that

interactivity aids comprehension of the underlying

principles. The technical design should not be overly

complex, and brief instructions should suffice in

order for task objectives to be understood.

3.1 Inclusive Design Approach

An inclusive design approach is essential when

crafting interactive tasks. This may involve dynamic

warning messages, guiding messages or hints to

create an engaging and motivating experience for

students. Moreover, usability must be addressed,

ensuring that interactive functions fulfil their

intended purpose efficiently and intuitively. The

model of Porras et al. (2023) for designing interactive

tasks to enhance the basic conceptualisation and skills

in mathematics draws on the work of Bloom (1984)

Design of Interactive STACK Exercises Using JSXGraph for Online Course: Exploring Strategies for Supporting Students with

Mathematical Challenges

551

and Pelkola (2018). This model emphasises the power

of automated assessment and feedback to provide the

seeds to support a growth in self-regulation and

learning for mastery of mathematical skills. It is

crucial to design interactive tasks and assessment in a

learner-centred way, thereby promoting active

student participation in a powerful learning

environment. Brown (2023) expanding on the

thoughts of Winne (1982), reasons that if the learning

environment is not inclusive there is a risk that

students who are less able to mediate or self-regulate

their learning will face barriers. Therefore, self-

regulation is a key characteristic in models of

powerful e-learning environments.

3.2 Feedback Is a Key Component of

the Learning Process

Feedback, whether associated with guidance or

assessment of activities, should be seen as an act

which will affect students’ future performance.

Coherent feedback requires explanations with three

informative components: why something is incorrect,

how the error should be construed and what may help

solve the problem (Brown, 2023; Shute, 2008;

Torrance, 2012). The third component of coherent

feedback involves providing the student with ideas to

strengthen their learning and information on which

areas are now under control, giving a positive impact

to learning.

Malecka et al. (2022) described some elements

which can help students better understand the function

of assessment and its role in the learning process: a

positive attitude towards feedback, improving

feedback literacy and constructing an understanding of

feedback cycles. This is challenging in fully online

courses, but it is necessary to put into practice when

giving feedback on activities and exams.

Assessment and feedback related to standard

exercises and activities will strongly influence students’

capacity to learn. The idea is to reveal and address issues

related to thinking, concepts, procedures and modelling.

Traditionally, when teachers carry out assessments they

interpret students’ outputs i.e. the representations of

their learning outcomes. Teachers use their professional

judgment based on what they have read. In blended

learning environments, although some automatic

evaluation is used in e-learning environments, teachers

have the possibility of explaining their assessment

policies at some level. On massive open online courses

(MOOC) this is not possible, and poorly designed tasks

increase difficulty in e-learning environments, therefore

a new form of assessment is required. System output

after an assessment should allow students to better

understand their learning progress and the outcomes of

the activities or exams in question. There is a quest for

assessment to be both personal and at the same time

general, equitable and fair, to include clear feedback,

and to fulfil classical evaluation criteria. In order to

ensure this, the central role of feedback and guidance

need to be understood and described accurately. A

conceptual re-thinking of the role of assessment in e-

learning environments is required to meet the

expectations of all stakeholders (namely students and

educators) in the learning process so that learning

outcomes can be evaluated in a coherent way

3.2.1 Feedback types

Feedback and guidance can be classified in terms of

the desired level of the student’s action:

- Instant and formative (right or wrong) (IF)

- Informative, process-oriented (address the gap

in knowledge) (IP)

- Informative, concept-oriented or subject-

oriented (IC)

- Selective, student can choose the amount and

type of feedback (S)

- Facilitative, meaning informative and

selective (FA)

- Immediate (I) or delayed (D)

An example of instant and informative (IF)

feedback can be seen in an activity which is scored

directly as either right or wrong. When solving. first

or second order polynomial equations, for example,

the process is clearly traceable, and any gaps are

addressable. This clarifies which feedback type (IC or

IP) is needed. Selective feedback is needed to define

the content of the facilitative form of assessment

(FA). Selectivity authorises the learner to decide the

level of support they desire. The most intrinsic new

approach is the facilitative form of assessment and

guidance (FA). In this the student’s role is the true

focus. Immediate feedback (I) is effective particularly

when learners lack some basic knowledge which is

essential for addressing questions or resolving

problems and prevents learners from grappling

incessantly without any prospect of success.

Therefore, immediate feedback is applied in this

context even though delayed feedback (D) has been

shown to reduce cognitive load and engender deeper

cognitive processing, as this applies only in cases

where students have basic knowledge of the matter at

hand. Trenholm et al. (2015) suggest that immediate

feedback promotes procedural learning, while

delayed feedback supports conceptual learning.

Optimal feedback focuses on learning tasks and

developing an understanding of the task's underlying

concepts. As mentioned above, in the context of a

CSEDU 2024 - 16th International Conference on Computer Supported Education

552

complete lack of basic mathematical skills, delayed

feedback is not a feasible option.

3.2.2 The Hint Matrix as a Tool for

Facilitative Feedback

An effective method for offering immediate support

to students without requiring a response is to employ

a hint matrix (refer to Figure 1). Hint matrices can be

incorporated into any STACK task using JSXGraph,

with the task designer determining when it is

appropriate for students to receive hints, potentially

from the beginning of the task. The main principle of

the hint matrix is that as the black dot is dragged

horizontally theoretical hints pertinent to the task

appear; concurrently, as the black dot is dragged

vertically, practical hints relevant to solving the task

appear. The students themselves are able to control the

number and quality of hints by dragging the black dot.

It is crucial to stress that students should

endeavour to progress independently in a task with

minimal hints. This is necessary in order to minimise

the chances of a student quickly moving the black dot

to the upper right corner of the hint matrix, revealing

all possible hints. Although this cannot be directly

prevented in an online course, efforts should be made

to inform students that solving tasks independently is

crucial to their learning and understanding, and

merely accessing all hints without personal reflection

is not recommended.

Various tools for offering hints can be devised to

enhance students' reflective and cognitive processes.

While not all tasks necessitate hints, in certain cases,

it may prove advantageous for students to begin tasks

with the assistance of hints, particularly in online

courses without direct teacher-student interaction.

The hint matrix exemplifies how students can actively

engage in constructing their understanding and

consider what level of support will best foster

development of problem-solving competency.

Open-source digital tools can be used to design

and implement various task frameworks for a range

of students and learners. Additionally, there are

diverse ways to provide hints. Owing to security

concerns surrounding the unrestricted incorporation

of JavaScript into STACK, it is likely that its

integration into STACK tasks will be restricted in the

foreseeable future. This will constrain the inclusion

of external content such as audio or video links within

STACK tasks. The multitude of possibilities presents

challenges regarding time management and the

identification of pedagogically efficacious methods,

thus necessitating a focus on task clarity and

coherence.

Figure 1: A hint matrix.

4 ENHANCING CONCEPTUAL

UNDERSTANDING IN THE

MATHEMATICAL SCIENCES

Rasila et al. (2015) posit that mathematical skills

comprise five interconnected components:

conceptual understanding, procedural fluency,

strategic competence, deductive abilities and interest.

They maintain that conceptual comprehension is the

critical element to render mathematical problem-

solving capabilities genuinely transferable.

Hooper and Jones (2023) recognise the challenges

in assessing conceptual understanding in online

courses, while procedural understanding can be

readily evaluated using automatic assessment

systems. Nonetheless, they demonstrated that

JSXGraph can address this issue, at least with simple

statistics. Students tend to perform better on

procedural tasks than conceptual ones, indicating an

ability to execute mechanical tasks without

necessarily grasping the underlying concepts (ibid).

This suggests that utilising interactive STACK tasks

may establish a foundation for improving students'

conceptual comprehension before they engage in

problem-solving activities which require an accurate

understanding of the subject matter.

Velichová (2021) contends that active student

participation facilitates improved understanding

through discovery and investigation rather than

memorisation of isolated facts. Conceptual

understanding entails not only identifying the correct

answer but also comprehending a step-by-step

solution. Interactive STACK tasks offer a potentially

infinite range of valid solution methods, which

requires students to grasp concepts and encourages

Design of Interactive STACK Exercises Using JSXGraph for Online Course: Exploring Strategies for Supporting Students with

Mathematical Challenges

553

independent inquiry. This independent exploration

facilitates development of in-depth comprehension of

mathematical tasks.

Before the development of interactive interfaces

for digital tasks, engaging with mathematical

concepts was challenging due to a lack of suitable

visual tools. The advent of interactive tasks presents

an opportunity to diversify the learning environment

within mathematical domains, fostering essential

skills required in mathematics and the natural

sciences. Consequently, it is reasonable to expect that

interactive tasks will substantially enhance these

foundational capabilities in the future.

Trenholm et al. (2015) highlight a discrepancy

between studies on e-assessment systems: some

demonstrate improved performance, while others

indicate a focus on procedural learning. Certain

students may adopt a trial-and-error approach,

reaching the correct answers but misunderstanding

concepts. This potential shortcoming of e-assignment

systems could be mitigated by incorporating

interactive tasks with graphical interfaces, as these

inherently involve conceptual rather than procedural

understanding.

Davies et al. (2022) noted that STACK tasks

employed in undergraduate mathematics courses

predominantly involved procedural tasks and lack

purely conceptual tasks. Recognising this limitation

of common STACK tasks, we will discuss one

example of how conceptual STACK tasks can be

developed using JSXGraph.

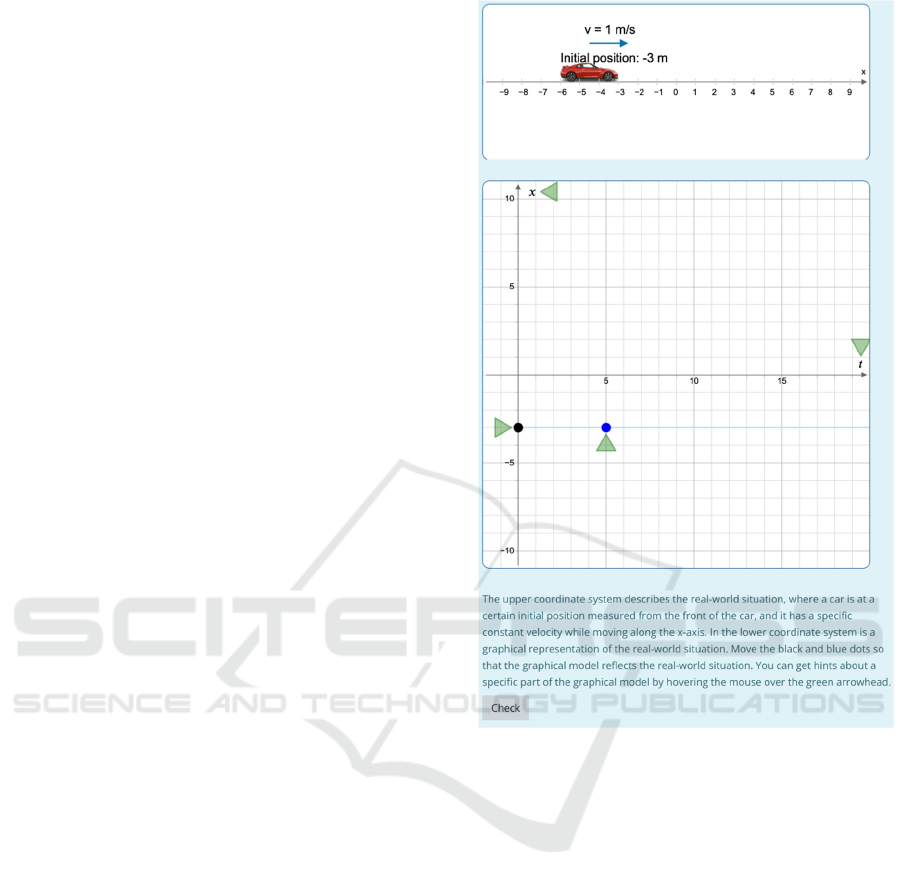
The exemplar task pertains to kinematics in

physics (refer to Figure 2) and involves analysing the

motion of a car with constant velocity. In the upper

coordinate system, the automobile is represented at a

distinct initial position with a specific constant

velocity. Objects within this coordinate system

remain unmovable; however, their positions and

values are randomised.

Velichová (2021) asserts that employing non-

linguistic representations during learning significantly

enhances brain activity, thereby facilitating the

formation of cognitive connections and promoting the

acquisition of knowledge and deeper comprehension

of fundamental principles and concepts.

In the lower coordinate system, students are

required to drag black and blue points to accurately

represent the real-world scenario depicted above. This

exercise aims to illustrate the correlation between real-

world situations and their corresponding graphical

models. Within the coordinate system, green

arrowheads indicate essential elements, and hovering

over them reveals dynamic guidance regarding their

significance.

Figure 2: Car moving with constant velocity and the

respective graphical model.

The incorporation of dynamic guidance proves

particularly advantageous in assisting students with a

weaker grasp of the subject to engage in problem-

solving. Following Bloom's Learning for Mastery

pedagogical method, subsequent tasks may replicate

the original one but omit the green directive

arrowheads. By incrementally increasing the

difficulty of the similar tasks, mastery in each subject

area can be attained. Interactive tasks offer several

benefits, including effortless modification from

simpler to more complex versions of similar tasks,

which is hypothesised to maintain higher student

engagement compared to solving nearly identical

calculations.

This interactive approach reinforces students'

understanding of how physical situations can be

examined from multiple perspectives: constructing a

graphical model based on real-world phenomena or

interpreting data from a physical event. Schaathun

CSEDU 2024 - 16th International Conference on Computer Supported Education

554

(2022) emphasises the importance of tasks being

relevant to students’ everyday lives and real-world

phenomena.

Creating the upper coordinate system follows a

relatively straightforward procedure. An image

within this system was converted to Base64 format.

Utilising Base64 ensures the image is included within

the task, eliminating the need for external links. The

initial position, vector length and numerical values

are derived from random variables within STACK.

The design of the lower coordinate system

employs scalability for different screen sizes and

event listeners facilitated by JavaScript. By hovering

over the green arrow tips, students can receive

dynamic guidance relevant to that specific object. If

this functionality is intended for touchscreens,

additional event listeners need to be coded for finger

and stylus events.

Both the black and blue points are movable. The

black dot moves along the position axis as it denotes

the initial position, while the blue point adjusts the

physical slope given as velocity from the upper

coordinate. When checking answers, restoration of

the coordinate system’s final state is achieved by

storing the coordinates in hidden input fields as JSON

strings. Additional hidden input fields store Boolean

variables referring to the initial position and slope.

The potential impact of interactive STACK

(2024) tasks crafted with JSXGraph (2024) is that

students can attain foundational understanding before

advancing to calculation-based tasks. Supported by

dynamic guidance tools and self-guided learning

mechanisms, interactive tasks offer diverse learning

experiences. Interactive tasks require not only

mechanical execution of solution steps but also

comprehensive grasp of the underlying issues and

recognising multiple correct solutions to a given

problem, which can potentially enhance students'

reasoning, problem-solving prowess, logical thinking

and analytical capacities.

An inherent advantage of interactive tasks is that

they allow students to independently investigate

mathematical concepts. This exploratory approach

enables students to discern mathematical patterns

autonomously. Fundamentally, interactive tasks

ought to incorporate intuitive interfaces, obviating the

need for extensive instructions. Interactive tasks with

immediate hints and feedback might be particularly

advantageous for students with weaker mathematical

abilities. Such tasks alleviate maths anxiety by

fostering mathematical thinking without resorting to

mechanical problem-solving.

5 CONCLUSIONS

Devlin (2008) posits that the forthcoming revolution

in mathematics will primarily alter the presentation of

mathematical content, as opposed to the content itself.

Advancements in e-assignment systems and feedback

mechanisms, such as the integration of adaptive

formats personalised for individual students, might

fuel this progression. However, substantial doubts

persist regarding the extent of the learning these

systems can facilitate. We presented a classification

of different types of feedback and considered the

challenges and opportunities of enhancing conceptual

understanding in mathematics using the open-source

tools STACK and JSXGraph. The hint matrix was

presented as a new way to enwiden learner-centred

assessment and promote learning outcomes. There is

a pressing need for additional research focused on

comprehending the dynamics of interactions with

online courses, especially concerning the learning

outcomes they produce. The developed model

provides proof of concept. Future research should

provide more evidence to report the results of this

approach in real scenarios with students.

ACKNOWLEDGEMENTS

We thank the European Social Fund for co-funding

this project (S30235).

REFERENCES

Amour, I. S. (2023). STACK for interactive online

numerical analysis tutorials: Development, competence

and performance. Journal of ICT Systems, 1(1), 1–18.

https://doi.org/10.56279/jicts.v1i1.17

Bach, S., & Altieri, M. (2021). Drawing Graphs of

Differentiable Functions with STACK and JSXGraph

using Hermite Splines. International Meeting of the

STACK Community 2021. https://doi.org/10.5281/

zenodo.4915954

Bawa, P. (2016). Retention in Online Courses: Exploring

Issues and Solutions—A Literature Review. Saga

Journals, 6(1). https://doi.org/10.1177/215824401562

1777

Bloom, B. (1984). The 2 Sigma Problem: The search for

Methods of Group Instruction as Effective as One-to-

One Tutoring. Educational Researcher, 13(6), 4–16.

Brown, K. (2023). eAssessment in engineering

mathematics: Gaps in perceptions of students and

academics [University of Glasgow].

https://theses.gla.ac.uk/

Design of Interactive STACK Exercises Using JSXGraph for Online Course: Exploring Strategies for Supporting Students with

Mathematical Challenges

555

Davies, B., Smart, T., Geraniou, E., & Crisan, C. (2022).

STACKification: Automating assessments in tertiary

mathematics. Proceedings of the Twelfth Congress of

the European Society for Research in Mathematics

Education.

Devlin, K.J. (2008). Proof and other Dilemmas: What Will

Count as Mathematics in 2100?

Fisher, M. J., & King, J. (2010). The self-directed learning

readiness scale for nursing education revisited: A

confirmatory factor analysis. Nurse Education Today,

30(1), 44–48. https://doi.org/10.1016/j.nedt.2009.05.0

Gerhäuser, M., Miller, C., Valentin, B., & Wassermann, A.

(2011). JSXGraph--Dynamic Mathematics Running on

(nearly) Every Device. Electronic Journal of

Mathematics & Technology, 5(1).

Hooper, C., & Jones, I. (2023). Conceptual Statistical

Assessment Using JSXGraph. International Journal of

Emerging Technologies in Learning (iJET), 18(01),

269–278. https://doi.org/10.3991/ijet.v18i01.36529

Hurme, J., Porras, P., & Lähteenmäki, H. (2023).

Enhancing Mathematical Skills for Vocational School

Students Pursuing Undergraduate Studies. 557–569.

https://doi.org/10.22492/issn.2435-9467.2023.43

JSXGraph Documentation. (2024). https://jsxgraph.org/

docs/index.html

Koedinger, K. R., Kim, J., Jia, J. Z., McLaughlin, E. A., &

Bier, N. L. (2015). Learning is Not a Spectator Sport:

Doing is Better than Watching for Learning from a

MOOC. Proceedings of the Second (2015) ACM

Conference on Learning @ Scale, 111–120.

https://doi.org/10.1145/2724660.2724681

Malecka, B., Boud, D., & Carless, D. (2022). Eliciting,

processing and enacting feedback: Mechanisms for

embedding student feedback literacy within the

curriculum. Teaching in Higher Education, 27(7), 908–

922. https://doi.org/10.1080/13562517.2020.1754784

Maxima Documentation. (2024). https://maxima.source

forge.io/docs/manual/maxima_singlepage.html

Onah, D., Sinclair, J., & Boyatt, R. (2014). Dropout Rates

of Massive Open Online Courses: Behavioural Patterns.

https://doi.org/10.13140/RG.2.1.2402.0009

Paiva, R. C., Ferreira, M. S., Mendes, A. G., & Eusébio, A.

M. J. (2015). Interactive and Multimedia Contents

Associated with a System for Computer-Aided

Assessment. Journal of Educational Computing

Research, 52(2), 224–256. https://doi.org/10.1177/

0735633115571305

Porras, P., Hurme, J., & Lähteenmäki, H. (2023).

Improving mathematical skills towards undergraduate

studies. The 21st SEFI Special Interest Group in

Mathematics – SIG in Mathematics, 120–125.

https://www.sefi.be/publication/mathematics-sig-semi

nar-2023-proceedings/

Pelkola, T., Rasila, A., & Sangwin, C. (2018). Investigating

Bloom’s Learning for Mastery in Mathematics with

Online Assessment. Informatics in Education, 17(2),

363–380. https://doi.org/10.15388/infedu.2018.19

Rasila, A., Malinen, J., & Tiitu, H. (2015). On automatic

assessment and conceptual understanding. Teaching

Mathematics and Its Applications, 34(3), 149–159.

https://doi.org/10.1093/teamat/hrv013

Schaathun, H. G. (2022). On Understanding in Mathematics.

Teaching Mathematics and Its Applications: An

International Journal of the IMA, 41(4), 318–328.

https://doi.org/10.1093/teamat/hrac016

Shaikh, U. U., & Asif, Z. (2022). Persistence and Dropout

in Higher Online Education: Review and

Categorization of Factors. Frontiers in Psychology, 13.

https://www.frontiersin.org/articles/10.3389/fpsyg.202

2.902070

Shute, V. (2008). Focus on Formative Feedback. Review of

Educational Research, 78(1), 153–189.

STACK Documentation. (2024). https://docs.stack-

assessment.org/en/

Torrance, H. (2012). Formative assessment at the

crossroads: Conformative, deformative and

transformative assessment.+. Oxford Review of

Education, 38(3), 323–342. https://doi.org/10.1080/03

054985.2012.689693

Trenholm, S., Alcock, L., & Robinson, C. (2015). An

investigation of assessment and feedback practices in

fully asynchronous online undergraduate mathematics

courses. International Journal of Mathematical

Education in Science and Technology, 46(8), 1197–

1221. https://doi.org/10.1080/0020739X.2015.10369

Velichová, D. (2021). The role of visualization in

mathematics. The 20th SEFI MWG Seminar on

Mathematics in Engineering Education, 63–68.

Winne, P. H. (1982). Minimizing the black box problem to

enhance the validity of theories about instructional

effects. Instructional Science, 11(1).

CSEDU 2024 - 16th International Conference on Computer Supported Education

556