Swarm Intelligence Path-Planning Pipeline and Algorithms for UAVs:

Simulation, Analysis and Recommendation

Wyatt Harris

, Sean Tseng

, Tabatha Viso

, Max Weissman

and Chun-Kit Ngan

Department of Robotics Engineering, Worcester Polytechnic Institute, 100 Institute Rd., Worcester, MA, U.S.A.

Data Science Program, Worcester Polytechnic Institute, 100 Institute Rd., Worcester, MA, U.S.A.

Keywords:

Artiﬁcial Intelligence, Artiﬁcial Potential Field, Bio-Inspired Optimization, Heuristic Search, Hybrid

Optimization Methods, Path Planning, Policy Gradient, Swarm Robotics, State-of-the-Art, UAV.

Abstract:

This research work aims to support domain experts in the selection of proper path planning algorithms for

UAVs to solve a domain business problem (i.e., the last mile delivery of goods). In-depth analysis, insight,

and recommendations of three promising approaches, including reinforcement learning-based, bio-inspired-

based, and physics-based are used to address the multi-agent UAV path planning problem. Speciﬁcally, the

contributions of this work are fourfold: First, we develop a uniﬁed pipeline to implement each approach to

conduct this analysis. Second, we build a 2D UAV path planning environment to simulate each approach.

Third, using this 2D environment, we run the 450 simulations in three different group sizes of swarm UAV

agents (i.e., 3, 5, and 10) within three environments of varying complexity (i.e., Easy, Intermediate, and Hard).

We aggregate the simulation data and compare their performance in terms of success rate, run-time, and path

length while using the classical A* Search as a baseline. Finally, based upon the performance of each approach

and our analytical investigations, we provide informed recommendations for the optimal use case of each UAV

path planning approach. The recommendations are presented using parameters for environmental complexity

and urgency of goods delivery.

1 INTRODUCTION

Swarm robotics is a ﬁeld that describes groups of in-

dividual agents that can act in a decentralized manner

through local decision making processes.

Initially, the ﬁeld of swarm robotics started as a

section of research focused on robot communications.

Now the ﬁeld has grown to house a variety of inter-

disciplinary applications and domains for both com-

mercial and military sectors (Theraulaz et al., 2021).

One of the main advantages of using swarm robotics

over individual robotic agents is that swarm robotics

may leverage smaller and cheaper robots to accom-

plish tasks as effectively, or in some cases, more ef-

fectively than individual agents. This is especially

clear in large environments with high time-cost ac-

tions such as search and rescue, path planning to tar-

gets, warehouse routines, and military engagements

(Tan and Zheng, 2013) (Zhen et al., 2020).

Unmanned Aerial Vehicles (UAVs) as members of

robotic swarms have gained popularity in recent years

as possible tools for last mile delivery of goods. Last

mile delivery, or ﬁnal mile delivery, is the movement

of goods from a warehouse to a customer’s house or

designated package area (DHL, 2023). This interest

stems from companies seeking solutions to higher de-

livery volumes, aging workforce, and on-time deliv-

ery. Several companies such as Alibaba, Alphabet,

Amazon, DHL, UPS and even Domino’s have experi-

mented with UAV delivery of groceries, medical sup-

plies and mail (Li and Kunze, 2023).

Amazon has developed a UAV targeting a 60

minute delivery time once a customer orders a med-

ication as a part of Amazon Pharmacy’s delivery op-

tions. The company is also increasing the range of

these drones from 5 km to 15 km, reducing the build

cost from $ 146,000 to $60,000 and increasing the

number of goods available to be shipped via UAVs

(Staff, 2023) (Kim and Long, 2022). Another notable

commercial use case of UAVs is the company Zipline

which effectively delivers important medical supplies

across remote and inaccessible regions in Ghana (Li

and Kunze, 2023).

However, operational research analyzing the cost

per shipment and cost per payload unit between un-

manned ground drones against UAVs found that the

factors “operator costs per hour” and “average beeline

service radius” in combination with “average cruis-

ing speed” were the most crucial cost driver variables

of delivery. The authors noted that in order to drive

Harris, W., Tseng, S., Viso, T., Weissman, M. and Ngan, C.

Swarm Intelligence Path-Planning Pipeline and Algorithms for UAVs: Simulation, Analysis and Recommendation.

DOI: 10.5220/0012686000003690

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 26th International Conference on Enterprise Information Systems (ICEIS 2024) - Volume 1, pages 747-758

ISBN: 978-989-758-692-7; ISSN: 2184-4992

747

down costs and make UAV’s competitive with regular

ground vans, the number of drones per human opera-

tor must increase (Li and Kunze, 2023).

The demand for UAVs is increasing, as noted in

a Statista report, 630,000 units were shipped in 2020

with an expectation of a four-fold increase in 2025

to 2.6 million units (Tractica, 2019). Peak demand

is heavily inﬂuenced by military and defense spend-

ing, with an expectation of the UAV market growing

from $25 billion in 2018 to nearly $70 billion in 2029

(BIS, 2019). This demonstrates that interest in UAVs

is only growing. In order to make UAV drones more

viable, larger groups of drones must be leveraged to

drive down costs, increase reliability and ultimately

be more effective than traditional vans. Swarm UAVs

leverages the growing global interest in UAV drones

and can potentially provide more effective last mile

delivery.

Multi-agent path planning for UAV drones last

mile delivery of goods encompasses three distinct cat-

egories of approaches, each offering unique perspec-

tives and methodologies. In reinforcement learning

(RL), artiﬁcial intelligence principles enable agents,

such as UAVs, to dynamically learn optimal paths

through trial and error, adapting their decision-

making over time based on feedback. Alternatively,

bio-inspired algorithms draw inspiration from nature,

replicating the decentralized and collaborative behav-

iors observed in social insects or ﬂocking birds. These

approaches excel in promoting adaptability and re-

silience within the swarm. Lastly, physics-based al-

gorithms ground themselves in principles of physics

and motion, modeling interactions and constraints

among agents and their environment. By consider-

ing factors such as collision avoidance and potential

ﬁelds, physics-based algorithms provide a foundation

for realistic and reliable path planning, particularly

in scenarios where precise control and adherence to

physical constraints are crucial. Together, these cat-

egories contribute diverse tools to address the chal-

lenges posed by complex and dynamic environments

in swarm multi-agent systems.

The reinforcement learning based algorithm stud-

ied in this work is the Multi-Agent Deterministic Pol-

icy Gradient (MADPG) for UAV path planning (Zhu

et al., 2023). The algorithm is a lighter version of

the Multi-Agent Deep Deterministic Policy Gradi-

ent (MADDPG) without neural networks to facilitate

faster computation speeds. UAV agents will choose

an action based on its value and then receive a reward

at the next state depending on the performance rela-

tive to the goal position. There is an actor and critic

system that updates the parameters of all agents based

on the swarm’s progress (Huang et al., 2020). In the

case of last mile deliveries, the algorithm can be used

for organizing a swarm of drones from different ware-

houses to converge to a customer’s home which pre-

vents the need for consecutive transport of goods from

warehouse to another. This method excels at ﬁnding

optimal policies to maximize rewards in dynamic en-

vironments (Wu et al., 2020b). One of the weaknesses

of reinforcement learning algorithms is that they seek

to ﬁnd a balance between exploration and exploitation

of the environment. Too much exploration can lead to

inefﬁciencies, and a ﬁxation on exploitation may yield

a non-optimal solution (Xue et al., 2023).

The bio-inspired approach studied in this work

is the promising Hybrid Simpliﬁed Grey Wolf Opti-

mization with Modiﬁed Symbiotic Organism Search

(HSGWO-MSOS) algorithm, which combines the

strengths of two relatively novel bio-inspired op-

timization algorithms proposed in 2014: Grey

Wolf Optimization (GWO) and Symbiotic Organisms

Search (SOS). Although this SOTA method was only

proposed for single-agent UAV path planning, it of-

fers great potential for multi-agent optimization, since

many comparable SOTA methods have successfully

utilized GWO for similar applications (Xu et al.,

2020). This algorithm is successful because it utilizes

the hierarchical structure of GWO to balance explo-

ration and exploitation, while also promoting coop-

eration and enabling effective local searches through

the commensal exploration method from SOS. By

combining these approaches, the proposed HSGWO-

MSOS has been shown to outperform classical al-

gorithms in UAV path planning, delivering efﬁcient

global searches and effective local reﬁnement (Qu

et al., 2020). In the context of last mile delivery, this

approach would function efﬁciently by continuously

identifying the most optimal route taken by a UAV

in a group of delivery agents, leveraging this path

to guide all agents, and simultaneously permitting

exploration of nearby alternative routes by remain-

ing agents. However, HSGWO-MSOS may strug-

gle with potential slow convergence and scalability is-

sues, which means it may not always ﬁnd the most op-

timal delivery routes or may not be well suited for op-

timizing a large number of delivery agents at a time.

Finally, a successful physics-based approach is

Improved Artiﬁcial Potential Field (APF) method,

which incorporates multiples advancements over the

traditional APF method. The algorithm incorporates

attractive and repulsive ﬁelds between UAV agents to

maintain an ideal distance for effective path planning.

APF is a widely-used algorithm for collision avoid-

ance in robotics path planning (Wu et al., 2020a). It

divides the environment into attractive and repulsive

forces, with goals exerting attractive forces and obsta-

ICEIS 2024 - 26th International Conference on Enterprise Information Systems

748

cles exerting repulsive forces on the UAV. By calcu-

lating these forces and taking their vector sum, the

direction of the UAV is determined. The simplic-

ity and efﬁciency of APF, along with its ability to

generate smooth trajectories, have made it a popular

choice in various applications, especially in dynamic

environments such as UAV delivery services for last

mile deliveries. Variations of the base APF algorithm

and similar physics-based approaches have been pro-

posed in the UAV delivery and UAV search and res-

cue domains (Zhao et al., 2020). The base APF al-

gorithm has limitations, such as convergence to local

minima and a jitter problem. The SOTA Improved

APF method overcomes many, but not all, of these

limitations, making it suitable for multi-UAV systems

where global optima and swarm compactness are cru-

cial (Zhang et al., 2022). While the Improved APF

algorithm has shown promising results in simulation

experiments, providing effective collision avoidance

and real-time performance, it still needs to maintain a

trade-off between speed and performance, and require

rigorous tuning of various parameters.

In this paper, we focus on swarm robotics and

its application to multi-agent path planning for UAVs

in unfamiliar environments and unknown static ob-

stacles. This work aims to support domain ex-

perts in the selection of proper path planning algo-

rithms for UAVs to solve a domain business prob-

lem (i.e., the last mile delivery of goods). In-

depth analysis, insight, and recommendations of

three promising approaches, including reinforcement

learning-based (i.e., Multi-Agent Deterministic Pol-

icy Gradient (MADPG)), bio-inspired-based (i.e., Hy-

brid Simpliﬁed Grey Wolf Optimization with Modi-

ﬁed Symbiotic Organism Search (HSGWO-MSOS)),

and physics-based (i.e., Improved Artiﬁcial Potential

Field (APF)) are used to address the multi-agent UAV

path planning problem. Speciﬁcally, the contributions

of this work are fourfold: First, we develop a uniﬁed

pipeline to implement each approach to conduct this

analysis. Second, we build a 2D UAV path planning

environment to simulate each approach. Third, using

this 2D environment, we run the 450 simulations in

three different group sizes of swarm UAV agents (i.e.,

3, 5, and 10) within three environments of varying

complexity (i.e., Easy, Intermediate, and Hard). We

aggregate the simulation data and compare their per-

formance in terms of success rate, run-time, and path

length while using the classical A* Search as a base-

line. Finally, based upon the performance of each ap-

proach and our analytical investigations, we provide

informed recommendations for the optimal use case

of each UAV path planning approach. The recom-

mendations are presented using parameters for envi-

ronmental complexity and urgency of goods delivery.

The remainder of the paper is organized as fol-

lows: Section 2 describes the development of the sim-

ulation environment and data ﬂow. Section 3 explains

the pipeline for implementing each approach, outlin-

ing the overall methodology, pseudo-code, and an ex-

ample. Section 4 details the experimental analysis

of all approaches within the bounds of our simula-

tion environment. Results of these simulations as well

as situational recommendations are included. Finally,

the results are summarized and future work is outlined

in Section 5.

2 SIMULATION ENVIRONMENT

To implement the three SOTA algorithms as well as

the baseline A* Search algorithm, a simulation en-

vironment was developed. Pygame, an open source

Python library typically used for multimedia applica-

tions, was leveraged to design the control environ-

ment. The pygame backbone allows for real-time

simulations of all methodologies included in this body

of work (Shinners, 2011).

The simulation environment was abstracted to

three main objects:

1. Agents

2. Obstacles

3. Goal State

Agents, which represent UAVs, are deﬁned with

a preset radius, identiﬁcation number, (x,y) tuple for

real time position, and more. Additional parameters

are included for tracking agent position over time.

Obstacles are static circles deﬁned with a (x,y) tu-

ple as well as radius. Their cylindrical shape ide-

ally represent avoidance areas around trees, poles and

tall buildings which UAVs commonly encounter and

need to avoid. Trees come in a variety of shapes and

widths, and the obstacle class can effectively repre-

sent that variance with custom sizes and overlap. The

goal state is a simple point with a static (x,y) tuple for

position. The superposition of these elements creates

unique simulation environments for implementation

of any path planning algorithm.

As shown in Figure 1, at simulation start, the user

is prompted to input the chosen algorithm, number of

agents in the swarm, and the environment difﬁculty.

This deﬁnes the problem. The start and end/goal po-

sitions of the agents are randomly selected. Then, the

inputs are used in the deﬁne algorithm, swarm size

and environment stage. The objects for all agents are

created along with instances of the three algorithms.

Then swarm sizes of 3, 5, and 10 are created. Pygame

Swarm Intelligence Path-Planning Pipeline and Algorithms for UAVs: Simulation, Analysis and Recommendation

749

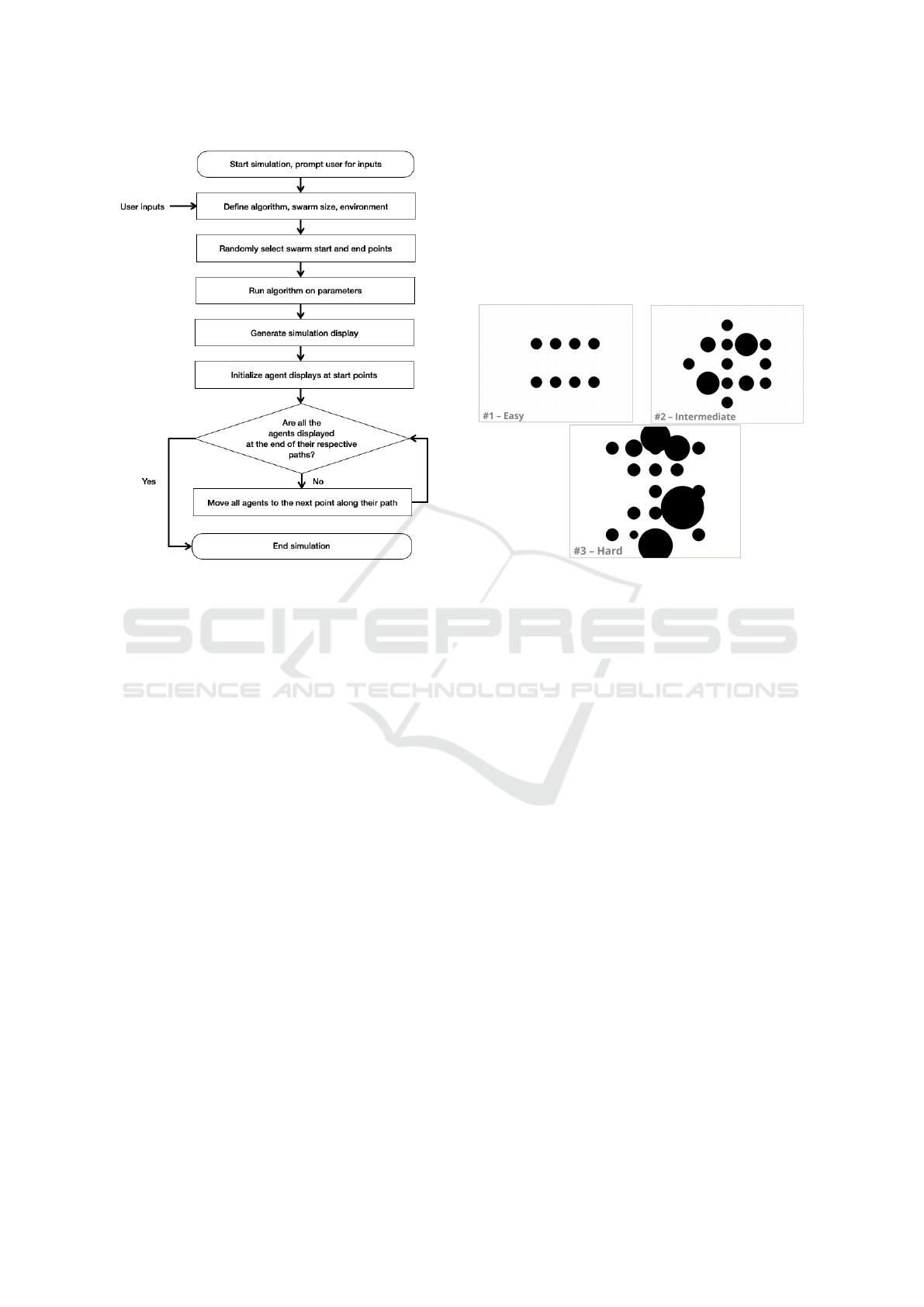
Figure 1: Simulation environment Workﬂow.

is used to create a simulation display with the environ-

ment obstacles. Next, the program generates random

initial start positions as well as the goal position for all

agents. All algorithms are run for all agents in the run

algorithms stage. The simulation display is created

to showcase the agents’ results which is followed by

plotting the agents’ initial positions. There is a loop

indicated at the diamond stage where every agent in

the group completes their movement until they have

reached the end of path planning. Lastly, once the

iteration count or goal position is reached, the simu-

lation is terminated.

While the structure of the environment can be ran-

domly generated, predetermined environments were

used to directly compare the performance of algo-

rithms. Three obstacle conﬁgurations of increasing

difﬁculty were developed, and are shown in Figure

2. The easy environment represents eight equal ob-

stacles of small diameter. In a last mile delivery ap-

plication, these obstacles might represent small trees,

lampposts, or other small structures, possibly orga-

nized in a structured way. The intermediate environ-

ment is more complex featuring a 5x5 grid of ob-

stacles of varying radii. Some cells in this environ-

ment are left empty to give the UAVs ample room

to navigate. This environment represents a slightly

more complex last mile delivery scenario, where there

might be a combination of trees of varying sizes and

infrastructure such as an electrical tower or lamp-

posts. The hard environment is also on a 5x5 grid,

but some obstacles are signiﬁcantly larger than in the

intermediate environment. The lack of free space in

the hard environment makes it more difﬁcult for the

UAVs to traverse without collisions. This represents a

tough delivery scenario with trees, infrastructure, and

other structures such as water towers, silos, or wind-

mills.

Figure 2: Simulation environments of increasing complex-

ity.

Using the developed environments, the simulation

was run for each algorithm, environment, and number

of agents (3, 5, and 10). Each of these unique conﬁg-

urations was run 50 times. For example, the MADPG

algorithm with ﬁve agents was run in the hard envi-

ronment 50 times. In total, each algorithm was run

450 times. The data collected was formatted and an-

alyzed to determine the characteristics of the imple-

mented algorithms.

3 PROPOSED PIPELINE AND

ALGORITHM

IMPLEMENTATION

The three different algorithms will have their own

classes in their own ﬁles and the main RunSim script

will call upon those classes to implement the different

methods. A* search algorithm will also be simulated

for each iteration of the script. Altogether, the algo-

rithms were run 450 times and produced results used

for analysis in Section 4.

In Figure 3, the user determines inputs such as

number of agents and which environment. This feeds

the script to run the algorithms with those param-

eters.The agents’ display is generated and then the

agents enter the loop where they keep moving until

ICEIS 2024 - 26th International Conference on Enterprise Information Systems

750

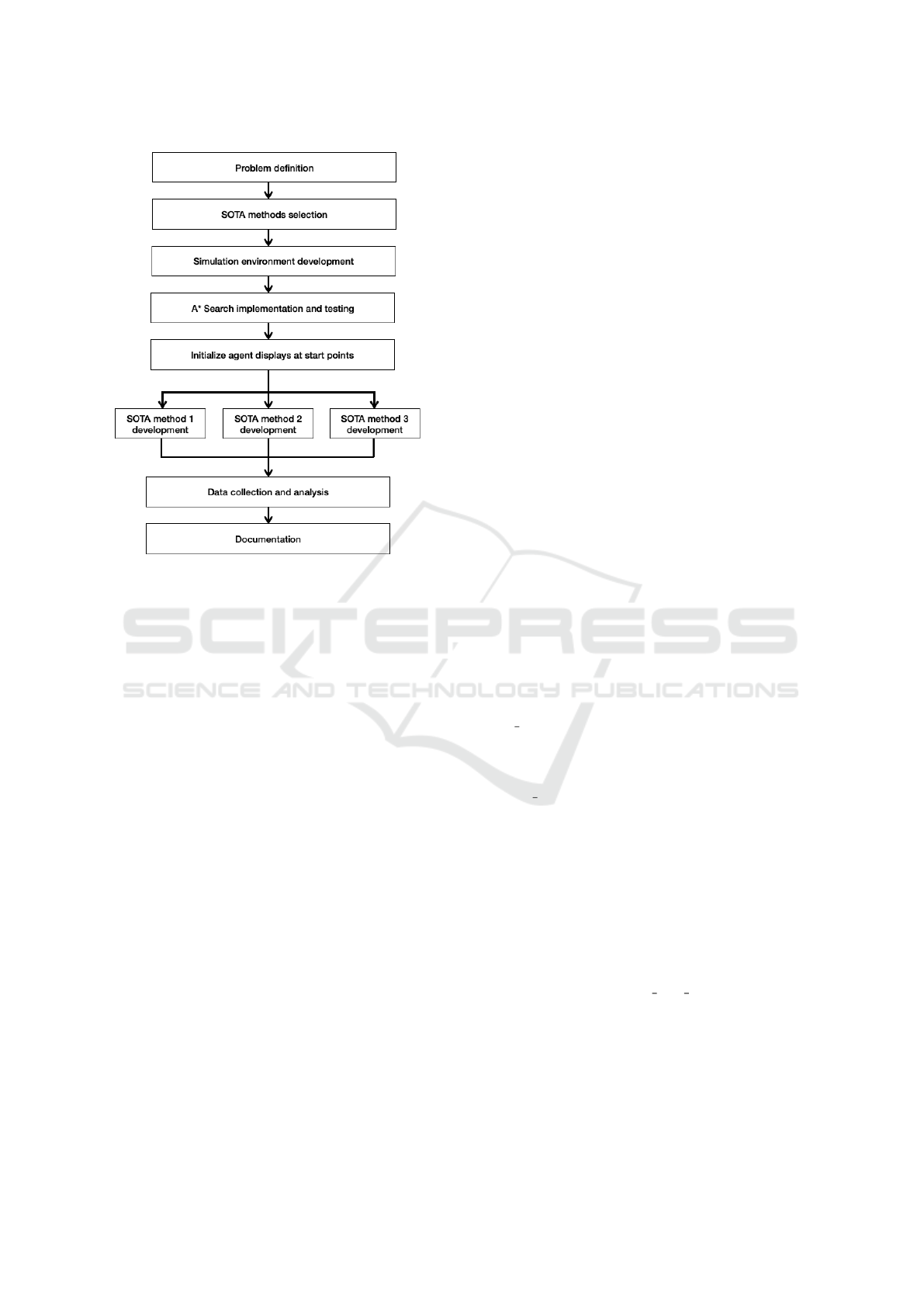
Figure 3: Proposed pipeline of simulation and general ﬂow

logic.

all of them reach the goal or the simulation time ex-

pires. Lastly, the data from the simulations is saved

and compiled for analysis.

3.1 MADPG Algorithm

3.1.1 Approach

The MADPG algorithm iterates through all agents’

set of policies which themselves contain ﬁve states.

Afterwards, the policies are evaluated based on the

value function Bellman equation from Markov Deci-

sion Process. The gradient of these results are calcu-

lated and then compared. If a lower gradient is de-

tected, the main critic will push an update to all actors

or agents to become more forgiving of lower reward

policies, with the opposite case leading to stricter

thresholds for acceptable polices.

Inside each agent are a couple methods, including

state validator, action, reward and critic update func-

tions. The action method generates a policy based

on the simulated annealing search algorithm, where

the agents have a certain initial searching tempera-

ture that is cooled over time as the agents approach

the goal position. Each move is determined through

calculating the probability of a future move bringing

the agent closer to the goal. Each navigation episode

consists of ﬁve transitions, which are the transitions

from ﬁve different states or in this case positions. The

algorithm checks if the goal is reached within the pre-

deﬁned movement speed; if so, the current position is

set to the goal position. Otherwise, the algorithm adds

a random angle between -30 to 30 degrees to generate

new potential destinations en route to the goal.

The policy path is evaluated for validity in the

state space. If the policy is acceptable with respect

to the boundaries according to the validator, the algo-

rithm then evaluates the energy cost for that transition

using the “reward” function. This is then used to cal-

culate the probability for approaching the goal state

using the aforementioned thermal equilibrium prob-

ability equation. The reward function calculates the

agent’s reward for a given state based on the maxi-

mum possible distance from the target position sub-

tracted by the current Euclidean distance to the goal.

There are any obstacles nearby within 12 units, a

penalty is applied to reward through subtraction from

the reward. This means the higher the reward, the

closer the agents are to the goal, while a lower number

indicates a large distance to the goal and encountering

many obstacles.

The critic update method takes signals from the

overarching critic to then update the parameters of the

agents. As agents complete the goal, the remaining

agents will be retrained differently as the algorithm

continuously updates the parameters. This is to simu-

late encouragement from other completed agents.

3.1.2 Pseudo-Code

First, obstacles, MADPG agent object, dis-

count factor, gradient, and paths must be initial-

ized. The positions, sizes and quantity of obstacles

are determined by the script. This will be used

by agents to determine if collisions happen. The

discount factor is hard coded in the program; it is a

decimal coefﬁcient that changes the balance between

exploration of the environment against exploitation

of gathered information. Gradient and paths are

container lists for future data regarding the agents’

paths and performance.

The action method is an epsilon greedy method

that uses simulated annealing to enable random explo-

ration. Epsilon greedy ﬁnds the highest reward action

and proceeds with it for ﬁve steps. The simulated an-

nealing probability triggers a random action and helps

with exploration. For agent next reward, the method

searches the whole list of state-action values for the

agent and ﬁnds the one with largest reward.

In Step 1, there is a loop for each agent to call the

action method and move position. The outputs of this

are agents’ paths, path length and reward. In Step 2,

the value of each agent’s value function is calculated

according to the reward and argmax of a future action

Swarm Intelligence Path-Planning Pipeline and Algorithms for UAVs: Simulation, Analysis and Recommendation

751

Initialize Obstacles, MADPG agent object,

discount factor, gradient, paths, goal

Methods

action: Moves agent using epsilon greedy and

simulated annealing decision making

agent next reward: Calculates max of agent’s

next reward

for each episode do

for each agent do

(1) Call action method for ﬁve

iterations and store path, length

(2) Calculate reward from current state

against obstacles object, distance to

goal

(3) V (S) = reward + discount factor ×

agent next reward

end

(4) Calculate gradient for given state and

append to local memory

(5) Compare gradient to change critic

networks of all agents

(6) Append state to agent memory for

plotting

(7) Append local path data to expected path

list for plotting

if All agents reach goal then

End loop

end

return Executed paths for all agents

Algorithm 1: Reinforcement Learning Approach:

MADPG Pseudo Code.

reward, the discount value was set to be 0.5 to bal-

ance exploration and exploitation. The gradient of all

the agents’ reward functions is taken for the current

iteration in Step 3, which is simply the slope of cur-

rent reward values from the previous episodes. This

is then used to inform Step 4, which is to compare the

change in the gradient and then subsequently send an

update to all agents. If the gradient becomes negative,

an update is sent to make the agents more exploratory

and if the gradient is positive the update makes the

agents more focused. This tuning is accomplished via

increasing and decreasing the threshold of accepting

higher or lower quality values. Lastly in Step 5, the

state history of each agent is appended to help with

plotting. Steps 6, and 7 store the state and path history

of the agents for future analysis. The ﬁnal if statement

ends the episode loop once all agents reach the goal

position.

For the example of ﬁve UAV delivery drones in the

swarm, each UAV will start at different random po-

sitions, representing different warehouses or distribu-

tion centers. The exploratory initial policy and similar

reward values near the initial starting position guides

them to make exploratory moves in the environment.

As the simulation iterates, the collective states from

the past ﬁve iterations are stored and analyzed for up-

dating the critic. The environment has obstacles and

some agents will enter the nearby boundary radius of

those regions. This triggers punitive rewards to dis-

incentive the agents. Instead agents pick locations

that circumvent obstacle and gain higher rewards the

closer they are to the goal. The episode ends after the

speciﬁed number of iterations are complete or after all

UAV agents reach the delivery goal.

3.2 HSGWO-MSOS Algorithm

3.2.1 Approach

As part of a broader agent-based simulation frame-

work, the Wolf class inherits from the Agent class,

allowing it to beneﬁt from generic functionalities

shared among different agents in the simulation.

However, each Wolf object is also initialized with ad-

ditional crucial attributes such as ﬁtness, which repre-

sents the ﬁtness of the Wolf’s current position in the

optimization process, and is-alpha, a boolean ﬂag des-

ignating whether the agent is responsible for guiding

the optimization process.

Moreover, the class includes two heuristic func-

tions that calculate Euclidean distances between

points in the search space and enable agents to nav-

igate and evaluate distances effectively. The up-

date ﬁtness method plays a vital role in evaluating the

ﬁtness of the Wolf’s current position in the optimiza-

tion process. It combines the Euclidean distance to

the goal (J fuel) and the threat posed by nearby obsta-

cles (J threat) into a weighted ﬁtness value (J cost).

The update position method governs the updating of

the Wolf’s position based on its designation, either

Alpha or Omega. If the Wolf is an Alpha, it moves

towards the goal by normalizing the direction vector,

while Omega Wolves adjust their positions based on

a strength value that determines the attraction towards

the Alpha Wolf. The new position is veriﬁed for va-

lidity before updating, and the Wolf’s path and tem-

porary path are recorded accordingly.

During the exploration phase, commensal agents

utilize the explore method to randomly explore the

search space by moving in different directions. This

method generates a random angle and calculates a

new destination point, attempting to strike a bal-

ance between exploration and obstacle avoidance

while remaining in a commensal state. The make-

alpha, make-omega, make-commensal, and i-already-

explored methods manage the designation of the

ICEIS 2024 - 26th International Conference on Enterprise Information Systems

752

Wolf, allowing it to take on different roles as Alpha,

Omega, or commensal explorer, depending on the op-

timization stage.

3.2.2 Pseudo-Code

Initialize Obstacles, Wolf agent object, Alpha

strength factor (constant), goal position, paths

Methods

update hierarchy Evaluates and compares the

ﬁtness of all agents, designates Alpha,

Omegas, and commensal explorers

evaluate ﬁtness Combines the Euclidean

distance to the goal (J

f uel

) and the threat

posed by nearby Obstacles (J

threat

) into a

weighted ﬁtness value (J

cost

)

update position Updates agent position based

on Alpha/Omega designation and Alpha

strength factor

for each iteration do

(1) Update Wolf hierarchy for each Wolf

(2) Update agent position

if Wolf is a commensal explorer then

(3) Evaluate 5 random nearby

locations

if Explored location is better than

current position then

(4) Update agent position

end

;

(5) Append new position to paths

end

return Executed paths for all agents

Algorithm 2: Bio-Inspired Approach: HSGWO-MSOS

Pseudo Code.

After initializing the multi-agent HSGWO-MSOS

swarm, the ﬁrst step of the algorithm is to deﬁne the

ﬁtness of all Wolves and create a hierarchy by iden-

tifying the Alpha (best individual), Omegas (all other

agents), and commensal explorers (randomly selected

Omega Wolves). At each iteration, the Alpha Wolf

evaluates (Step 2) the next best position based on its

position, nearby obstacles, and the desired goal. Each

Omega Wolf consequently evaluates their next best

position based on the Alpha’s location. In Step 3, the

commensal explorer randomly searches ﬁve nearby

locations and evaluates the potential ﬁtness of these

positions. If it ﬁnds a location that is better than its

current position, it moves to this new spot (Step 4).

Otherwise it remains in its current position. After

each wolf has updated its position, it appends the new

position to its path (Step 5). This process is iteratively

repeated from the beginning (Step 1), where the ﬁt-

ness of all Wolves is evaluated once again and a new

hierarchy is deﬁned. The agent with the best ﬁtness

is deﬁned at the new Alpha. All other Wolves are la-

beled as Omegas and a new commensal explorer is

chosen for the next iteration.

For example, in a swarm of ﬁve UAV agents, each

UAV’s ﬁtness is evaluated at initialization with re-

spect to the goal position and nearby obstacles. The

best scoring UAV is designated as the Alpha, while

the remaining four UAV are designated as Omegas.

One of the Omegas is randomly selected to be the

commensal explorer. The Alpha UAV updates its po-

sition ﬁrst, by moving towards the goal position along

the normalized direction vector. The four Omega

UAVs then update their positions by taking into con-

sideration both the Alpha’s new position, as well as a

constant strength factor. Finally, the commensal ex-

plorer UAV considers ﬁve randomly chosen nearby

locations and evaluates them. If any of those loca-

tions is better than its current position, it moves to it.

After all ﬁve agents have moved to their positions, the

ﬁtness of each UAV is re-evaluated and the hierarchy

is updated. The UAV with the best scoring ﬁtness is

now considered the Alpha, while the rest are consid-

ered Omegas, and a new commensal exploring Omega

is also selected. This process is repeated until the al-

gorithm returns the completed paths for the UAV.

3.3 Improved APF Algorithm

3.3.1 Approach

The Improved APF algorithm provides a robust and

adaptive framework for modeling multi-UAV sys-

tems. While there are multiple iterations of Improved

APF algorithms, this work will focus on leveraging

SOTA methodology described in Dongcheng (2020)

and Zhang (2022). In these methods, there is a com-

mon focus of modeling interactive repulsive forces

between UAVs.

To properly implement this algorithm, all repre-

sentative forces are considered for each agent, indi-

vidually. These forces are derived from the attractive

and repulsive potential ﬁelds throughout the environ-

ment. The attractive force created by the goal coun-

teracts the repulsive forces acting on each agent. Re-

pulsive forces for each obstacle in the environment are

implemented as well as repulsive forces between each

agent. For each agent, the total force is calculated and

broken down into component form, then later vector

summed together in order to move the agent forward

at each iteration.

Swarm Intelligence Path-Planning Pipeline and Algorithms for UAVs: Simulation, Analysis and Recommendation

753

It is necessary to include a solution to the jitter

problem as an aspect of the Improved APF implemen-

tation (Dongcheng and Jiyang, 2020). For each step

in the simulation, each agent is tested to analyze if it

is in a state of jitter. More speciﬁcally, this jitter state

occurs when the change in the angle of the resultant

force is between 180

◦

and a speciﬁed threshold value

between the current state and the previous state. If

this jitter condition is met, a dynamic step adjustment

is included when calculating the next position of each

agent. The dynamic step adjustment allows for each

agent to alter its step size to smoothly escape from

jitter scenarios.

A simpliﬁed approach for the Improved APF al-

gorithm is included in the Section 3.3.2 Pseudo-code.

3.3.2 Pseudo-Code

Initialize Obstacle set O, UAV agent set A,

Goal State g, paths

Methods

dynamicStepAd justment: Adjusts step size

updatePosition: Updates the position of the

agent

for each agent a in A do

(1) Calculate attractive force F

att

(a, g)

(2) Calculate repulsive force F

rep

(a, O)

(3) Calculate repulsive force F

rep

(a, A)

from each other agent in A

(4) Calculate F

tot

∑

att

∑

rep

if agent is in jitter state then

(5) dynamicStepAd justment

end

else

(6) updatePosition of a in direction of

tot

end

;

(7) Append new position to paths

end

return Executed paths for all agents

Algorithm 3: Physics-Based Approach: Improved APF

Pseudo Code.

To begin, the obstacle set, goal state, path variables,

and agent sets are initialized. All agents in the multi-

agent swarm are conﬁgured to run the Improved APF

algorithm. Inside each agent are a set of methods nec-

essary to execute the algorithm. Methods for calcu-

lating the attractive force between the agent and the

goal, F

att

(a, g), the repulsive force between the agent

and obstacles, F

rep

(a, O), and the repulsive force be-

tween the agents and all other agents in the swarm,

rep

(a, A). Another method is used to calculate the

total force, F

tot

, from all acting forces. A dynamic

step adjustment method is embedded in this imple-

mentation to solve assist the agent in escaping a jitter

state. Lastly, an update position function is included

to update the position of the agent at the end of each

loop. This position is appended to the agent’s path for

plotting within the simulation. For each agent in the

swarm, Steps 1-3 are used to calculate the component

forces acting on the agent. Step 4 takes the vector sum

of these forces to calculate the total force. A check is

made to ensure the agent is not in a jitter state. If the

agent falls into a jitter state, Step 5 is executed using

the dynamic step adjustment function. If the agent is

not in jitter state, Step 6 is executed using the update

position function.

Take a ﬁve-agent swarm, where all agents are run-

ning the Improved APF algorithm. They start in ﬁve

different positions, and need to avoid obstacles as well

as each other to reach the goal state. The pseudo-

code deﬁned in Algorithm 3, describes the behavior of

these agents at each iteration of the simulation. The

algorithm is run until all agents reach the goal state

or the iteration limit is reached. At the ﬁrst iteration,

each agent calculates the resultant force by ﬁrst ﬁnd-

ing all attractive and repulsive forces acting on the

agent. The agent updates its position with regard to

this resultant force. The positions of each other agent

are paramount to calculating the new position of the

current agent, as those repulsive forces affect the re-

sultant force for the given agent. In this example, an

assumption is made that the agent closest to the goal

gets stuck in a local minima near two obstacles. The

subsequent agents behind the furthest agent are able

to ”push” the stuck agent out of the local minima, al-

lowing for it to reach the goal. Each agent in this

swarm will help guide the further agent out of these

local minima. It is, however, possible for the last

agent to get stuck in this same local minima. If this

local minima causes the agent to jitter, the improved

APF algorithm leverages dynamic step adjustments to

guide the last agent to the goal.

4 SIMULATION RESULTS,

ANALYSIS, AND

RECOMMENDATIONS

4.1 Success Rate Results

Figure 4 shows the success rate results for each al-

gorithm in each environment. After analyzing the re-

sults, MADPG stands out with a high success rate in

complex environments. The randomization in the al-

gorithm leads to a high probability of success as the

ICEIS 2024 - 26th International Conference on Enterprise Information Systems

754

Figure 4: Average swarm success per environment.

number of iterations increases. HSGWO-MSOS and

Improved APF seem to have lower success rate, as

they are less reliant on randomization to escape local

minima, and may become stuck. Improved APF has

lower success rates than HSGWO-MSOS due to the

likelihood of some agents getting stuck to help other

Figure 5: Average algorithm run-time per environment.

agents. MADPG by far is the best algorithm devel-

oped if the goal is to solely increase success rate. This

is not considering A* Search, which has a perfect suc-

cess rate across the environments due to the informed

nature of the algorithm.

Swarm Intelligence Path-Planning Pipeline and Algorithms for UAVs: Simulation, Analysis and Recommendation

755

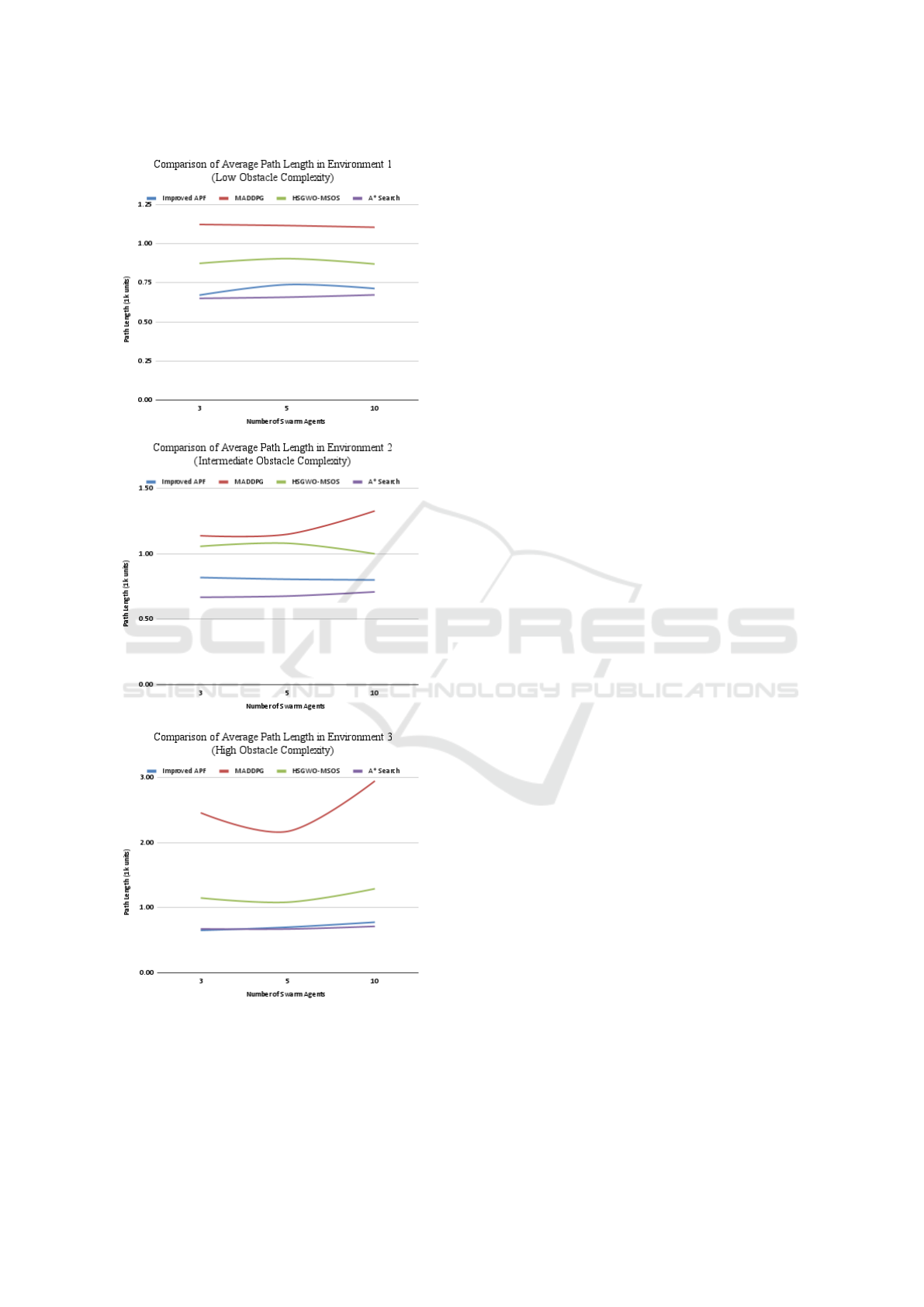
Figure 6: Average algorithm path length per environment.

4.2 Runtime Results

Figure 5 shows the runtime results for each algorithm

in each environment. The runtime of Improved APF

and HSGWO-MSOS are lower than the runtime of

MADPG by a fair margin. This is exasperated in high

complexity, large swarm situations. When Improved

APF and HSGWO-MSOS agents end up stuck in lo-

cal minima, an iteration cap may end the program as

they are not as reliant on randomization to escape lo-

cal minima. The MADPG algorithm will sacriﬁce

runtime to escape a local minima using randomiza-

tion. Improved APF and HSGWO-MSOS sacriﬁce

success rate for a decreased runtime. A* Search in

all three environments is a scale of magnitude greater

than the runtime of the three SOTA algorithms.

4.3 Path Length Results

Figure 7 shows the path length results for each algo-

rithm in each environment. The average generated

path lengths of the algorithms are compared against

A* as a baseline. The A* Search algorithm conducts

an informed search on the environment instead of a

partially informed search, and in turn has a perfect

success rate, increased runtime, and also ﬁnds the

shortest possible path from the start point to the end

point. Paths that ended up being incomplete were

not included in averages. Improved APF generated

path lengths that were very similar to A*, especially

in high complexity environments. However, this is

partially due to selection bias. As Improved APF’s

success rate decreases, the path lengths that are gen-

erated are more likely to be simple, straight paths to

the end goal. HSGWO-MSOS also generated path

lengths similar to that of A* and Improved APF. It

also was affected by this selection bias of results.

MADPG maintained a high success rate across all en-

vironments, and was not subject to this selection bias.

In high complexity environments, the algorithm cre-

ated path lengths over three times the length of other

algorithms. Even in low complexity environments,

it produced the longest path lengths of all the algo-

rithms. In Environment 3, the increased difference

of path lengths is likely related to selection bias, but

the results of Environment 1 do show that MADPG

generated the longest paths, Improved APF generated

the shortest paths, and HSGWO-MSOS generated the

middlemost paths.

4.4 Recommendations

The code effectively implemented all three SOTA

methods: MADPG, HSGWO-MSOS, and Improved

APF. Our work completed development of a 2D simu-

lation environment that effectively tested these meth-

ods. In addition, a data pipeline was designed to ef-

fectively run algorithms for path planning of multi-

agent swarms. The average results for each method

ICEIS 2024 - 26th International Conference on Enterprise Information Systems

756

are summarized in Table 1.

Table 1: Average results by swarm intelligence path-

planning method.

Approa-

Classi-

cal

Bio-

Inspired

Physics-

Based

Algori-

thm

MAD-

HSGWO-

MSOS

Improv-

APF

Swarm

Suc-

cess

Rate

[%]

100.0 99.8 88.4 48.4

Runtime

[sec-

onds]

26.67 1.03 0.11 0.09

Path

Length

[1k

units]

677.5 2725.8 1034.6 742.1

MADPG exhibits a high average swarm success

rate regardless of swarm size or environment com-

plexity. It is an ideal choice for longer distance de-

liveries where shipping completion and reliability is

paramount. Given that its runtimes and paths are

longer on average than the other methods, this re-

inforcement learning approach is more suitable for

scenarios where real-time decision-making or efﬁ-

cient path lengths is not a strict requirement. Alter-

natively, HSGWO-MSOS provides a reasonable av-

erage swarm success rate with lower runtimes and

path lengths. This bio-inspired method provides a

good balance of success rate and efﬁciency for sce-

narios where reliable, timely responses are needed

and resources like UAV battery-life may be limited.

It would most useful in urban last mile deliveries.

Lastly, Improved APF has a lower success rate, but

the fastest runtimes and shortest path lengths on av-

erage, making this physics-based approach suitable

for scenarios where package recovery is more eas-

ily attainable, and minimizing distances and rapid

decision-making take precedence.

Table 2 summarizes the ﬁndings for each algo-

rithm in each environment with respect to the ur-

gency of transported goods. The urgency of goods

can be directly correlated to the path length and run-

time of the algorithms. Since Improved APF and

HSGWO-MSOS exhibit faster runtimes and overall

shorter path lengths, they are more suitable for deliv-

ery of urgent goods. However, for non-urgent goods,

reliability may be prioritized over speed. In this sce-

nario, MADPG is recommended due to its high relia-

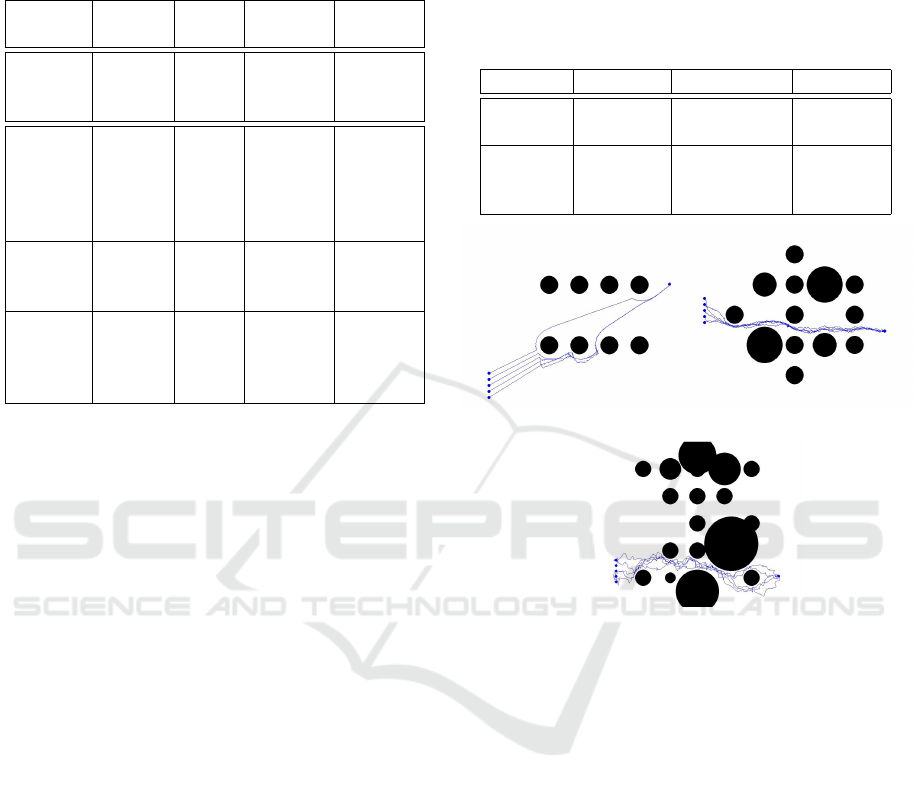
bility in complex environments. Figure 7 shows com-

pleted simulations and paths for ﬁve-agent swarms.

Each algorithm is showcased in its optimal and rec-

ommended environment.

Table 2: Recommended Algorithm depending on environ-

ment complexity and urgency of goods.

Environ. Easy Intermediate Hard

Urgent

Goods

Improved

APF

HSGWO-

MSOS

HSGWO-

MSOS

Non-

urgent

Goods

HSGWO-

MSOS

MADPG MADPG

(a) (b)

(c)

Figure 7: Sample algorithm performance in recommended

Environments.

(a) Easy environment with Improved APF.

(b) Intermediate environment with HSGWO-MSOS.

5 CONCLUSIONS AND FUTURE

WORK

In this paper, we focus on swarm robotics and its

application to multi-agent path planning for UAVs

in unfamiliar environments and unknown static ob-

stacles. This work aims to support domain ex-

perts in the selection of proper path planning algo-

rithms for UAVs to solve a domain business prob-

lem (i.e., the last mile delivery of goods). In-

depth analysis, insight, and recommendations of

three promising approaches, including reinforcement

learning-based (i.e., Multi-Agent Deterministic Pol-

icy Gradient (MADPG)), bio-inspired-based (i.e., Hy-

brid Simpliﬁed Grey Wolf Optimization with Modi-

Swarm Intelligence Path-Planning Pipeline and Algorithms for UAVs: Simulation, Analysis and Recommendation

757

ﬁed Symbiotic Organism Search (HSGWO-MSOS)),

and physics-based (i.e., Improved Artiﬁcial Potential

Field (APF)) are used to address the multi-agent UAV

path planning problem. Speciﬁcally, the contributions

of this work are fourfold: First, we develop a uniﬁed

pipeline to implement each approach to conduct this

analysis. Second, we build a 2D UAV path planning

environment to simulate each approach. Third, using

this 2D environment, we run the 450 simulations in

three different group sizes of swarm UAV agents (i.e.,

3, 5, and 10) within three environments of varying

complexity (i.e., Easy, Intermediate, and Hard). We

aggregate the simulation data and compare their per-

formance in terms of success rate, run-time, and path

length while using the classical A* Search as a base-

line. Finally, based upon the performance of each ap-

proach and our analytical investigations, we provide

informed recommendations for the optimal use case

of each UAV path planning approach. The recom-

mendations are presented using parameters for envi-

ronmental complexity and urgency of goods delivery.

While these recommendations are relevant in the do-

main of last mile delivery, further research is needed

to investigate elements of the problem not covered in

this work. Further research includes, but is not limited

to, inter-agent collisions, dynamic obstacles, 3D path

ﬁnding, and novel algorithms for solving multi-agent

path planning more efﬁciently and effectively.

ACKNOWLEDGEMENTS

The authors would like to acknowledge and thank

Professor Chun-Kit Ngan for his support and advice

during this project.

REFERENCES

BIS (2019). Global uav market value in 2018 and 2029 (in

billion u.s. dollars). Technical report, Statista.

DHL (2023). 4 ways to improve your last-mile delivery

performance. DHL.

Dongcheng, L. and Jiyang, D. (2020). Research on multi-

uav path planning and obstacle avoidance based on

improved artiﬁcial potential ﬁeld method. 2020 3rd

International Conference on Mechatronics, Robotics

and Automation (ICMRA).

Huang, Y., Wu, S., Mu, Z., Long, X., Chu, S., and Zhao, G.

(2020). A multi-agent reinforcement learning method

for swarm robots in space collaborative exploration.

2020 6th International Conference on Control, Au-

tomation and Robotics (ICCAR).

Kim, E. and Long, K. (2022). Amazon will pay a whopping

63 dollars per package for drone delivery in 2025 and

it shows just how the company is still grappling with

cost issues for last-mile delivery. Business Insider.

Li, F. and Kunze, O. (2023). A comparative review of air

drones (uavs) and delivery bots (sugvs) for automated

last mile home delivery. Logistics.

Qu, C., Gai, W., Zhang, J., and Zhong, M. (2020). A novel

hybrid grey wolf optimizer algorithm for unmanned

aerial vehicle (uav) path planning. Knowledge-Based

Systems, 194, 105530.

Shinners, P. (2011). Pygame. http://pygame.org/.

Staff, A. (2023). Amazon announces 8 innovations to bet-

ter deliver for customers, support employees, and give

back to communities around the world. Technical re-

port, Amazon.

Tan, Y. and Zheng, Z. (2013). Research advance in swarm

robotics. Defence Technology.

Theraulaz, G., Dorigo, M., and Trianni, V. (2021). Swarm

robotics: Past, present, and future. In Proceedings of

the IEEE.

Tractica (2019). Projected commercial drone hardware unit

shipments worldwide from 2020 to 2025. Technical

report, Statista.

Wu, E., Sun, Y., Huang, J., Zhang, C., and Li, Z. (2020a).

Multi uav cluster control method based on virtual core

in improved artiﬁcial potential ﬁeld. IEEE Access, 8,

131647–131661.

Wu, S., Huang, Y., Mu, Z., Long, X., Chu, S., and Zhao,

G. (2020b). A multi-agent reinforcement learning

method for swarm robots in space collaborative ex-

ploration. 6th International Conference on Control,

Automation and Robotics.

Xu, C., Xu, M., and Yin, C. (2020). Optimized multi-

uav cooperative path planning under the complex con-

frontation environment. Computer Communications,

162, 196–203.

Xue, J., Zhu, J., Du, J., Kang, W., and Xiao, J. (2023).

Dynamic path planning for multiple uavs with incom-

plete information. Electronics, 12(4), 980.

Zhang, M., Liu, C., Wang, P., Yu, J., and Yuan, Q. (2022).

Uav swarm real-time path planning algorithm based

on improved artiﬁcial potential ﬁeld method. 2021

International Conference on Autonomous Unmanned

Systems (ICAUS 2021).

Zhao, Y., Liu, K., Lu, G., Hu, Y., and Yuan, S. (2020). Path

planning of uav delivery based on improved apf-rrt*

algorithm. Journal of Physics: Conference Series,

1624:042004.

Zhen, Z., Chen, Y., Wen, L., and Han, B. (2020). An in-

telligent cooperative mission planning scheme of uav

swarm in uncertain dynamic environment. Aerospace

Science and Technology, 100, 105826.

Zhu, J., Xue, J., Du, J., Kang, W., and Xiao, J. (2023).

Dynamic path planning for multiple uavs with incom-

plete information. Electronics.

ICEIS 2024 - 26th International Conference on Enterprise Information Systems

758