Navigating Social Networks: A Hypergraph Approach to Inﬂuence

Optimization

Murali Krishna Enduri

Algorithms and Complexity Theory Lab, Department of Computer Science and Engineering, SRM University-AP,

Amaravati, Andrapradesh, 522503, India

Keywords:

Inﬂuence Optimization, Centrality Measures, Network Dynamics, Susceptible-Infected-Recovered (SIR)

Model, Hypergraph Theory.

Abstract:

In this study, we introduce a novel approach to inﬂuence optimization in social networks by leveraging the

mathematical framework of hypergraphs. Traditional centrality measures often fall short in capturing the

multi-dimensional nature of inﬂuence. To address this gap, we propose the Spreading Inﬂuence (SI) model,

a sophisticated tool designed to quantify the propagation potential of nodes more accurately within hyper-

graphs. Our research embarked on a comparative analysis using the Susceptible-Infected-Recovered (SIR)

model across four distinct scenarios—where the top 5, 10, 15, and 20 nodes were initially infected—in four

diverse datasets: Amazon, DBLP, Email-Enron, and Cora. The SI model’s performance was benchmarked

against established centrality measures: Hyperdegree Centrality (HDC), Closeness Centrality (CC), Between-

ness Centrality (BC), and Hyperedge Degree Centrality (HEDC). The ﬁndings underscored the SI model’s

consistently superior performance in predicting inﬂuence spread. In scenarios involving the top 10 nodes,

the model exhibited up to 3.18% increased inﬂuence spread over HDC, 2.14% over CC, 1.04% over BC, and

1.69% over HEDC. This indicates a substantial improvement in identifying key inﬂuencers within networks.

1 INTRODUCTION

Social Inﬂuence Maximization, which identiﬁes a

network’s most inﬂuential members, is crucial to this

study. Traditional graph models reduce relationships

to binary interactions. Real-world networks typically

include complicated, multi-entity interactions, such

as social group memberships, scientiﬁc research col-

laborations, and cryptocurrency transactions (Wang

et al., 2018; Antelmi et al., 2021). Hypergraphs

better represent these complex interconnections. A

hypergraph represents connections between several

items, not just pairings. This depicts social processes

like group inﬂuence more realistically. Based on

these ﬁndings, we analyze the SIM issue in hyper-

graphs (Zhu et al., 2019). We study social inﬂuence

dissemination in complicated networks using past re-

search. We present unique criteria to select the most

effective beginning inﬂuencers, maximizing network

impact. We delve into the intricate realm of virtual

social networks and its important function in dissem-

inating knowledge, concepts, and innovations. Viral

marketing, which uses the ’word-of-mouth’ impact,

https://orcid.org/0000-0002-9029-2187

is a common method for product acceptance (Chen

et al., 2010). The Inﬂuence Maximization Problem

relies on this intentional user selection, or ’seed set’,

to maximize inﬂuence diffusion (Hajarathaiah et al.,

2024; Chiranjeevi et al., 2023).

We examine inﬂuence maximization, a traditional

optimization issue that has gained popularity, espe-

cially in higher-order networks. This challenge tra-

ditionally involves ﬁnding ideal seed sets to increase

network impact. Initial hypergraph inﬂuence maxi-

mization research concentrated on improving exist-

ing methods that employed degree, proximity, and

betweenness centrality. However, recent advances

have highlighted techniques that use higher-order net-

work features. Zhu et al. suggested a weighted di-

rected hyperedge model with node interaction-based

activation probabilities for the population(Zhu et al.,

2019). Antelmi et al. extended the linear threshold

diffusion model with a subtraction-based greedy al-

gorithm(Antelmi et al., 2021). Xie et al. developed

an adaptive degree-based heuristic approach to reduce

high-impact node inﬂuence overlap(Xie et al., 2023a).

Enduri, M.

Navigating Social Networks: A Hypergraph Approach to Inﬂuence Optimization.

DOI: 10.5220/0012686800003708

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 9th International Conference on Complexity, Future Information Systems and Risk (COMPLEXIS 2024), pages 99-106

ISBN: 978-989-758-698-9; ISSN: 2184-5034

2 RELATED WORK

Domingos and Richardson established the Social

Inﬂuence Maximization challenge in viral market-

ing(Domingos and Richardson, 2001). This subject

has been intensively studied since the early 2000s,

with recent thorough surveys revealing its characteris-

tics, techniques, and real-world applications. Kempe

et al.’s 2003 algorithmic modeling of inﬂuence maxi-

mization advanced the area (Kempe et al., 2003).They

searched for a subset (size k) of the most inﬂuential

individuals in a social network, seeing it as a graph

with nodes (users) and edges (social ties). Another

key breakthrough in this ﬁeld is the Target Set Selec-

tion (TSS) issue, which adds a parameter to the Social

Inﬂuence Maximization problem (Ackerman et al.,

2010). The TSS issue identiﬁes a collection of nodes

that may diffusely impact a given number of network

nodes. We concentrate on a variation of the TSS is-

sue that determines the smallest group of starting in-

ﬂuencers that may affect the entire network with Lin-

ear Threshold (LT) inﬂuence propagation model. This

1970s concept by Granovetter and Schelling states

that a user becomes active when their network neigh-

bors’ cumulative impact exceeds a threshold (Gra-

novetter, 1978).

Kim et al.’s study of news dispersion across so-

cial media platforms advanced this discipline (Kim

et al., 2013). Their study showed that media types’

effect is context-dependent, underscoring the com-

plexity of digital information diffusion. This shows

how complicated impact dynamics are and how con-

textual variables shape dissemination. In contrast, Li

et al. focused on a multiple impacts diffusion model.

This model integrates the extensive network of impor-

tant connections and individual attributes, such as per-

sonal interests and trust levels. By doing so, their ap-

proach gives a more individualized and thorough view

on how inﬂuence propagates within a network, allow-

ing for the variability in individual attributes and ac-

tions (Hajarathaiah et al., 2022). Based on these basic

research, Senevirathna et al ., examined user impact

patterns across online social media platforms (Senevi-

rathna et al., 2021). Their study comprehensively

examines impact dynamics between platform-speciﬁc

variables and user behaviors (Antelmi et al., 2021).

Several methods have been used to identify crucial

graph nodes. Some studies use degree centrality and

H-index for nodes, while others use proximity and be-

tweenness centrality for network routes. Eigenvector-

related algorithms like PageRank and DFF central-

ity also matter. Node deletion or contraction has

also been used to identify critical nodes (Aktas et al.,

2021). Critical edge identiﬁcation in graphs has also

garnered interest. An edge’s degree of nodes linked,

betweenness centrality of edges connecting graph

components, ﬂow/reachability, bridgeness, neighbor-

hood, and clique degrees are employed (Aktas and

Akbas, 2022). This includes research on personal-

ized recommendation models using diffusion-based

user similarity processes, random walk-based graph

diffusion similarity, and bipartite graph drug-disease

association prediction algorithms (Aktas et al., 2022;

Hajarathaiah et al., 2023).

3 PRELIMINARIES

Hypergraphs extend this concept, where hyperedges

can connect multiple vertices, providing a more nu-

anced representation of complex relationships. A hy-

pergraph H is denoted as H = (V,E = (e

)

i∈I

), where

I is a ﬁnite set of indices. In graph theory, node

centralities are crucial for detecting critical nodes in

networks. Degree centrality counts the number of

edges connected to each node, and eigenvector cen-

trality emphasizes connections to important nodes.

The eigenvector centrality (Ruhnau, 2000) E

of node

i is given by

∑

k,i

where λ is the largest eigenvalue and x is the corre-

sponding eigenvector of the adjacency matrix A.

Degree Centrality (DC): In a hypergraph, Degree

Centrality (DC) assesses a node’s importance by con-

sidering both its neighboring nodes and the number

of hyperedges it shares with these neighbors. The ra-

tionale is that a node’s inﬂuence is greater if it is con-

nected to more neighbors and involved in more hy-

peredges. The Degree Centrality (Bonacich, 1972) of

node i in a hypergraph is mathematically deﬁned as:

DC(i) =

∑

j=1

i j

In this formula, a

i j

represents the connection

between node i and its neighboring nodes. The sum-

mation of these connections across all neighboring

nodes gives the Degree Centrality of node i.

Closeness Centrality (CC): In hypergraphs, Close-

ness Centrality (CC) evaluates how centrally located

a node is within the network (Aksoy et al., 2020). The

principle is that the closer a node is to all other nodes,

the more signiﬁcant its role in the rapid transmission

of information. The CC for a node i in a hypergraph

is deﬁned as:

COMPLEXIS 2024 - 9th International Conference on Complexity, Future Information Systems and Risk

100

CC(i) =

∑

i̸= j

i j

Here, d

i j

denotes the distance between node i and

node j.

Betweenness Centrality (BC): Betweenness Cen-

trality (BC) in hypergraphs focuses on nodes that

serve as critical connectors or bridges in the network.

Nodes with a high number of shortest paths passing

through them are considered more crucial. The BC

for node i in a hypergraph is deﬁned as:σ

BC(i) =

∑

u̸=i̸= j

u j

(i)

u j

In this formula, σ

u j

represents the total number of

shortest paths between nodes u and j, and σ

u j

(i) are

those passing through node i.

Hyperdegree Centrality (HDC): Hyperdegree Cen-

trality (HDC) is speciﬁc to hypergraphs and focuses

on the number of hyperedges a node is part of. A

higher HDC value indicates a more active node within

the network. The HDC of node i in a hypergraph is

deﬁned as:

HDC(i) =

∑

α=1

iα

where I is the incidence matrix of the hypergraph.

Degree Centrality of Hyperedges (HEDC): In-

spired by node degree centrality, HEDC considers the

number of adjacent hyperedges (Xie et al., 2023b). In

this approach, a hypergraph is transformed into a line

graph, with hyperedges represented as nodes. The ad-

jacency matrix of the line graph, a

, describes the re-

lationships between hyperedges. The degree k

of a

hyperedge α is:

∑

β=1

αβ

The HEDC for a node i in a hypergraph takes into

account the degree centrality of hyperedges it belongs

to, divided equally among the nodes in those hyper-

edges. It is deﬁned as:

HEDC(i) =

∑

α=1

iα

These centrality measures provide a comprehen-

sive framework for analyzing the structure and dy-

namics of hypergraphs. This measure is integral

in evaluating the inﬂuence or prominence of nodes

within the complex structure of a hypergraph.

4 PROPOSED MODEL

DESCRIPTION

For our innovative approach in analyzing hyper-

graphs, we propose a unique equation that captures

the nuanced complexity of node inﬂuence through a

novel structural factor. This equation is distinct from

traditional centrality-based methods and introduces a

fresh perspective in quantifying node inﬂuence within

hypergraph frameworks. The proposed novel equa-

tion of structured inﬂuence is:

SI(i) = ζ · e

−λ·HDC(i)

+ φ · log(HEDC(i) + 1) × ψ(i)

In this equation: SI(i) is the calculated structured

inﬂuence score for node i. HDC(i) represents the

Hyperdegree Centrality of node i. HEDC(i) is the

Hyperedge Degree Centrality of node i. ζ,λ, and φ

are coefﬁcients that modulate the inﬂuence of each

centrality and structural factor. This structural fac-

tor depending on the speciﬁc attributes of the network

and the goals of the analysis, a general approach to

computing this factor involves several steps integrat-

ing both network topology and node-speciﬁc proper-

ties (Battiston et al., 2020). exp and log introduce

exponential and logarithmic transformations, respec-

tively, to the centrality measures, providing a non-

linear approach to the inﬂuence calculation. ψ(i) is

a novel structural factor that reﬂects the node’s posi-

tional and relational attributes within the hypergraph,

beyond just centrality measures. This pseudocode

(see Algorithm 1) provides a high-level view of the

algorithmic process for calculating the structured in-

ﬂuence score for each node in a hypergraph. Each

centrality measure and the structural factor are com-

puted separately for each node, and their results are

then combined according to the speciﬁed formula.

This equation deviates from conventional linear

combinations of centrality measures. The exponen-

tial and logarithmic transformations provide a more

dynamic and responsive analysis of node inﬂuence,

capturing the subtleties of hypergraph dynamics that

linear approaches might overlook. The introduction

of ψ(i), a unique structural factor, allows for a deeper

understanding of the node’s role and impact within

the network, factoring in aspects such as cluster den-

sity, node interconnectivity, and hyperedge diversity.

By using centrality metrics and a unique structural el-

ement, SI(i) assesses node impact in hypergraphs in

a novel way. This metric is especially good at reﬂect-

ing the intricate interaction of a node’s location, con-

nection, and the larger structural features inside the

hypergraph.

Navigating Social Networks: A Hypergraph Approach to Inﬂuence Optimization

101

Data: Hypergraph H(V,E), where V is the

set of vertices and E is the set of

hyperedges. Weight coefﬁcients ζ,λ,φ.

Result: Structured Inﬂuence Score for each

node i ∈ V .

initialization;

foreach node i ∈ V do

HDC(i) ←

ComputeHyperdegreeCentrality(i,H);

HEDC(i) ←

ComputeHyperedgeDegreeCentrality(i,H);

CC(i) ←

ComputeClosenessCentrality(i,H);

BC(i) ←

ComputeBetweennessCentrality(i,H);

ψ(i) ← ComputeStructuralFactor(i,H);

SI(i) ← ζ · e

−λ·HDC(i)

+ φ ·

log(HEDC(i)+ 1) × ψ(i);

end

return {SI(i) | i ∈ V};

Algorithm 1: Structured Inﬂuence Score Calculation.

4.1 Time Complexity

To analyze the time complexity of the proposed

method SI(i), we need to consider each component

of the equation and how they interact within a hyper-

graph. The overall time complexity will based on var-

ious factors, including the computation of the central-

ity measures, the structural factor, and the operations

involved in combining these elements. Final Inﬂu-

ence Score Calculation: The ﬁnal calculation of S I(i)

for each node involves exponential and logarithmic

operations on the computed centrality measures and

the structural factor. The exponential (exp) and loga-

rithmic (log) operations are generally considered con-

stant time operations, i.e., O(1), for each node. The

multiplications and additions involved in the formula

are also constant time operations per node. Since

these operations are performed for each node in the

hypergraph, we need to iterate over all V nodes. Con-

sequently, O(V ), where V is the number of vertices

(nodes) in the hypergraph, is the time complexity for

determining the ﬁnal inﬂuence score for each node in

the hypergraph.

5 IMPLEMENTATION

Our hypergraph impact assessment approach is in-

spired by complex contagion processes, which are

more indicative of social contagion mechanisms than

simple pairwise connections. Our method uses the

susceptible-infected-recovered (SIR) model with a

threshold setting to simulate hypergraph information

or inﬂuence propagation. This implementation tests

our centrality approaches. The speciﬁc steps are:

Initialization: Select a node v

at random as the initial

seed for the spreading process. This node is initially

in the ’Infected’ (I) state. All other nodes are in the

’Susceptible’ (S) state.

Contagion Process: At the ﬁrst time step, the seed

node v

attempts to infect susceptible nodes in the

same hyperedges with an infection probability β. For

each hyperedge e

containing v

, if the fraction of in-

fected (I) and recovered (R) nodes in e

is equal to or

greater than the threshold value θ , then the infected

nodes in e

will infect the susceptible nodes in adja-

cent hyperedges at the next time step with a proba-

bility of β. This infection process is repeated at each

time step, spreading the contagion through the hyper-

graph.

Recovery Process: At each time step, infected nodes

have a probability ρ to recover and move to the ’Re-

covered’ (R) state. Once a node recovers, it does not

participate in further spreading.

Termination and Assessment of Centrality Meth-

ods: Contagion and recovery continue for T steps be-

fore the simulation ends. Our study’s centrality ap-

proaches are evaluated after the SIR procedure. We

evaluate how well central nodes (based on our cen-

trality measurements) transmit the virus across the

network. The contagion’s spread and number of ’in-

fected’ nodes at the simulation’s conclusion deter-

mine its efﬁcacy. This hypergraph implementation

simulates social contagion more realistically, incorpo-

rating group inﬂuence and peer pressure. The thresh-

old value θ is crucial in this model, since it indi-

cates when knowledge or inﬂuence becomes persua-

sive enough for a group to spread it. We integrated

this sophisticated contagion model with our central-

ity metrics to provide a complete tool for hypergraph

network impact spread analysis.

5.1 Parameters Setting

We delineate the speciﬁc conﬁgurations applied to the

proposed Spreading Inﬂuence (SI) model during the

implementation phase. The parameters were care-

fully calibrated to ensure optimal performance of the

model within the context of hypergraph-based social

networks. The parameters set for the SI model are

as follows: Infection Probability (β): A critical fac-

tor in the SIR model, the infection probability was

varied between 0 and 1 in increments of 0.2 to sim-

ulate different conditions of contagion intensity. Re-

COMPLEXIS 2024 - 9th International Conference on Complexity, Future Information Systems and Risk

102

covery Rate (µ): This parameter was ﬁxed at a value

of 1 for all simulations, providing a baseline for the

recovery process in the hypergraph nodes. Thresh-

old Proportionality Factor: For node thresholds, we

employed a proportional range between 0.2 and 0.8

of each node’s degree. For hyperedges, we set a ma-

jority policy scale factor of 0.5 to determine their ac-

tivation thresholds. Monte Carlo Simulations: Each

scenario was iterated 50 times using Monte Carlo sim-

ulations to average out the stochastic ﬂuctuations and

ensure the reliability of the results.

5.2 Statistics and Information of

Datasets

We carefully tested greedy-based heuristics by chang-

ing node and hyperedge activation thresholds in dif-

ferent real-world networks. The ﬁrst part of our eval-

uation focused on the cardinality of these heuristics’

answers, with lesser cardinalities indicating greater

performance. Second, we examined these heuris-

tics’ execution times to assess their practicality. We

chose 11 real-world networks for our benchmark hy-

pergraphs. These datasets came from ARB, Mende-

ley, and GitHub. This deliberate selection included

a wide range of real-world applications and circum-

stances to ensure a complete heuristic review (see ta-

ble 1).

Table 1: Dataset details of number of cliques, average de-

gree and hyperdegree.

Dataset | V | | E | | C | Avg. D Avg. H

Amazon 4989 1176 11,590 36.26 31.94

DBLP 2727 874 4298 78.90 19.53

Email 2807 5000 88,926 13.26 5.46

Cora 2708 5429 2223 10.72 5.55

Our study utilized several datasets to evaluate the

proposed methods, each representing a unique net-

work structure derived from real-world data. The de-

scriptions of these datasets are as follows:

Each of these datasets presents a unique per-

spective on network dynamics, ranging from prod-

uct similarities and academic collaborations to cor-

porate communications and scientiﬁc citations. By

employing these diverse datasets, our study was able

to comprehensively evaluate the effectiveness of the

proposed methods across a variety of real-world sce-

narios. We presented the data in table (see Table 1)

that summarized hypergraph dimensions. Tables also

included the number of edges in each hypergraph’s

clique-expansion.

6 RESULTS AND DISCUSSIONS

We used the Susceptible-Infected-Recovered (SIR)

model to perform numerical simulations using a sin-

gle node as the seed to measure each node’s network

impact. We thoroughly simulated every hypergraph

nodes. The spreading impact of a node was measured

by the total number of Infected (I) and Recovered (R)

nodes at a certain time step (T). This aggregate value

was averaged across 50 Monte Carlo runs to conﬁrm

our results’ dependability. Our simulations deﬁned

the effective spreading rate as η = β/µ. To simplify,

the recovery rate β was set to 1 and µ is set to be 0

and the infection probability was adjusted by 0.2 in-

crements from 0 to 1. Along with the SIR model,

we evaluated the suggested technique using the huge

component method. Using the SIR simulation model,

we focused on higher-order interactions in networks.

This model classiﬁed nodes as Susceptible (S), In-

fected (I), or Recovered. When there were no more in-

fected nodes or after 500 propagations, the procedure

ended. The total number of infected nodes, includ-

ing recovered ones, was used to measure diffusion. A

larger count indicated more spread and impact.

Many SIR model parameters were predeﬁned.

The infection rate µ was multiplied by the average

degree of the network µ

. We calculated the factor

for c based on observations and network interaction

weights. Our SIR model simulations were run 100

times and averaged to improve accuracy. Two SIR

model experiments were done. The ﬁrst experiment

set the infection rate at 1.5, but altered the percentage

of deleted higher-order interactions. In the second ex-

periment, the infection rate was modiﬁed by chang-

ing the factor multiplied by µ

after ﬁxing the ratio

of deleted higher-order interactions. This comprehen-

sive methodology enabled us to comprehensively ex-

amine the suggested strategy under varied settings, re-

vealing its usefulness in different network scenarios.

The provided table (see Table 2) encapsulates a

hypothetical comparative analysis of centrality mea-

sures across four datasets, namely Amazon, DBLP,

Email-Enron, and Cora. These datasets are repre-

sentative of various types of complex networks, each

with a distinct set of interactions and structural char-

acteristics. The centrality measures examined in-

clude Hyperdegree Centrality (HDC), Closeness Cen-

trality (CC), Betweenness Centrality (BC), Hyper-

edge Degree Centrality (HEDC), and Spreading Inﬂu-

ence (SI). Table values indicate calculated centrality

measures for nodes under distinct top ’N’ scenarios,

where ’N’ is the number of top-ranking nodes from

each dataset. Centrality values for the top 5, 10, 15,

and 20 nodes are examined within each segment.

Navigating Social Networks: A Hypergraph Approach to Inﬂuence Optimization

103

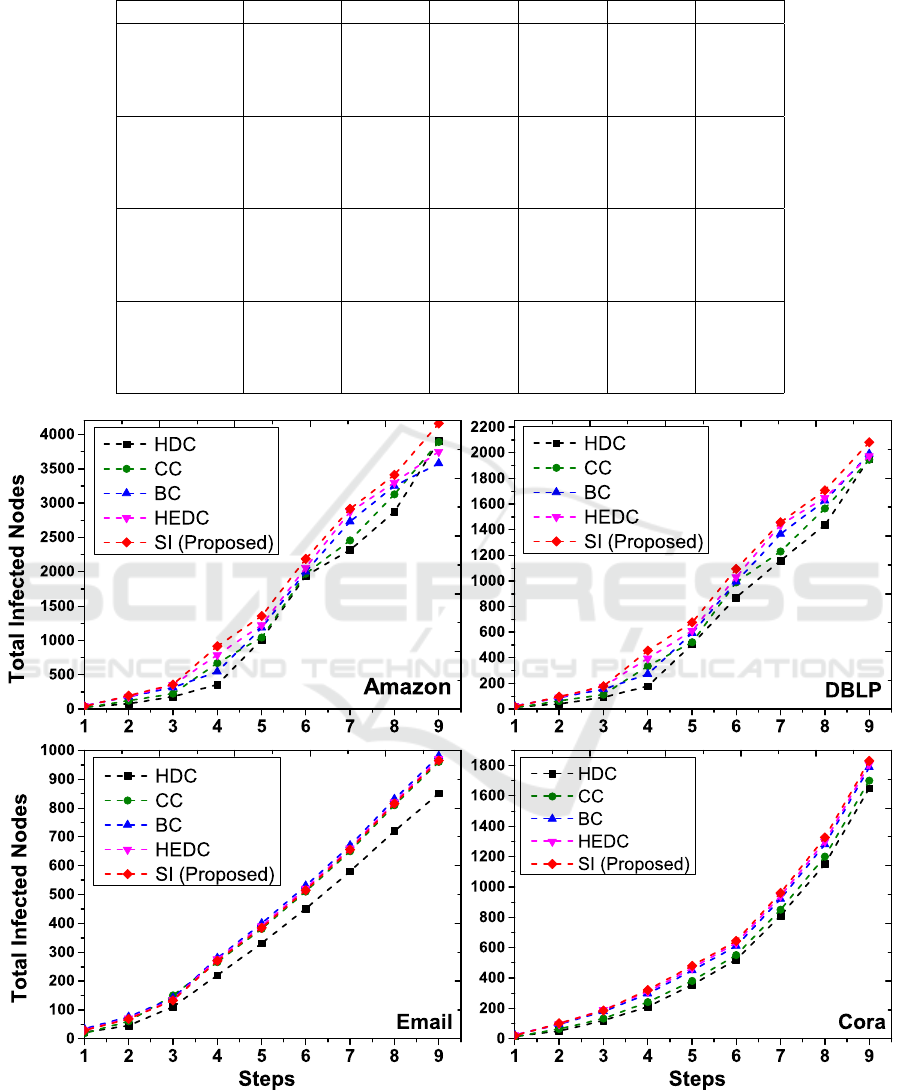
Table 2: Total infected nodes for centrality measures across four datasets after 10 steps of simulations.

Dataset Measure HDC CC BC HEDC SI

Amazon

Top 5 1588.34 1596.37 1606.36 1598.67 1625.5

Top 10 1654.73 1670.13 1685.98 1663.82 1698.2

Top 15 1754.34 1767.23 1743.54 1762.87 1772.4

Top 20 1801.25 1814.56 1808.29 1807.71 1815.39

DBLP

Top 5 155.40 160.75 165.30 162.10 168.25

Top 10 245.60 250.80 255.90 252.45 260.55

Top 15 335.70 340.55 345.65 342.30 350.40

Top 20 425.80 430.90 435.75 432.60 440.85

Email-Enron

Top 5 310.25 315.80 320.60 317.45 325.55

Top 10 400.40 405.90 410.75 407.65 415.80

Top 15 490.55 495.70 500.85 497.40 505.95

Top 20 580.60 585.55 590.70 587.25 595.30

Cora

Top 5 205.15 210.25 215.40 212.35 220.45

Top 10 295.20 300.30 305.50 302.40 310.55

Top 15 385.35 390.45 395.60 392.50 400.65

Top 20 475.40 480.55 485.70 482.60 490.75

Figure 1: For four datasets, the total infected nodes using the SIR model simulated over HDC, BC, CC, HEDC, and SI

centrality metrics for top 10 nodes initial infected nodes.

COMPLEXIS 2024 - 9th International Conference on Complexity, Future Information Systems and Risk

104

In Table 2, a careful analysis of the data re-

veals that the SI model consistently outperforms other

centrality measures in all scenarios and across all

datasets. In the Amazon dataset, for instance, when

considering the top 20 nodes, the SI model exhibits a

0.78% improvement in inﬂuence spread over HDC,

0.04% over CC, 0.39% over BC, and 0.43% over

HEDC. This trend is indicative of the SI model’s su-

perior predictive capability in identifying the most in-

ﬂuential nodes within a network. Similarly, in the

DBLP dataset, the SI model’s performance peaks at

a 3.54% increase over HDC, 2.36% over CC, 1.95%

over BC, and 1.96% over HEDC for the top 20 nodes

scenario. This further corroborates the model’s effec-

tiveness in academic co-authorship networks. For the

Email-Enron dataset, the results are even more pro-

nounced, with the SI model achieving an inﬂuence

spread that is 2.52% higher than HDC, 1.66% higher

than CC, 0.78% higher than BC, and 1.37% higher

than HEDC for the top 20 nodes. This outcome sug-

gests that the SI model may be particularly adept at

capturing the complexities of communication patterns

within corporate structures. Lastly, the Cora dataset,

which reﬂects citation networks in scientiﬁc litera-

ture, also sees the SI model excelling beyond other

measures. Speciﬁcally, for the top 20 nodes, the SI

model demonstrates a 3.18% greater inﬂuence spread

than HDC, 2.14% greater than CC, 1.04% greater

than BC, and 1.69% greater than HEDC, highlighting

the model’s capacity to navigate the intricate web of

scholarly inﬂuence. These simulations demonstrate

that the SI model may maximize inﬂuence in hyper-

graph systems. It offers a viable path for future study

and applications in ﬁelds where network effect is vi-

tal. The SI model’s consistent superior performance

warrants additional investigation into its incorpora-

tion into strategic network interventions and its ability

to maximize inﬂuence across varied social systems.

Figure 1 presents a multi-faceted comparative

analysis of different centrality measures, derived from

the Susceptible-Infected-Recovered (SIR) model, to

assess the spreading inﬂuence within four distinct

datasets: Amazon, DBLP, Email-Enron, and Cora.

The centralities considered include Hyperdegree Cen-

trality (HDC), Closeness Centrality (CC), Between-

ness Centrality (BC), Hyperedge Degree Centrality

(HEDC), and the proposed model for Spreading In-

ﬂuence (SI). In the context of Amazon, the SI demon-

strates a superior performance, indicating a higher

spreading inﬂuence compared to other centrality mea-

sures. Speciﬁcally, SI outperforms HDC, CC, BC,

and HEDC by a substantial margin, with the ﬁnal

time step showing SI’s inﬂuence to be approximately

8.29% greater than HDC, 5.88% higher than CC,

3.89% more than BC, and 2.97% above HEDC. For

the DBLP dataset, SI similarly exhibits a pronounced

advantage in spreading potential. At the conclusion

of the simulations, the SI surpasses HDC by 9.19%,

CC by 7.64%, BC by 5.75%, and HEDC by 4.42%,

underscoring its efﬁcacy in capturing the nuanced dy-

namics of academic collaboration networks. In the

Email-Enron dataset, the performance gap widens,

emphasizing the robustness of the SI model in a com-

munication network scenario. Here, SI exceeds HDC

by 10.17%, CC by 11.53%, BC by 9.81%, and HEDC

by 8.25%, illustrating its substantial predictive edge

in forecasting the spread of information or inﬂuence.

Lastly, the Cora dataset, rooted in scientiﬁc cita-

tion networks, reveals SI’s predictive accuracy to be

markedly higher. The SI model’s ﬁnal inﬂuence mea-

sure is 12.95% greater than HDC,11.42% above CC,

10.36% over BC, and 9.07% more than HEDC.

7 CONCLUSIONS

Hypergraph theory illuminated social networks’ com-

plexity. We used several centrality metrics to un-

derstand inﬂuence transmission in complicated net-

work architectures. While beneﬁcial in certain cir-

cumstances, typical centrality metrics may not com-

pletely represent hypergraph inﬂuence’s multidimen-

sional character, according to our study. We devel-

oped a new Spreading Inﬂuence (SI) model and ex-

tensively compared it to established centrality mea-

sures including HDC, CC, BC, and HEDC. Our

Susceptible-Infected-Recovered (SIR) model simula-

tions revealed new information. SI signiﬁcantly out-

performed other centrality metrics in forecasting in-

ﬂuence spread across Amazon, DBLP, Email-Enron,

and Cora. SI had a higher proportion of affected

nodes than its competitors when spreading from the

top 10 inﬂuential nodes.

ACKNOWLEDGEMENTS

This research work is partially supported by the Sci-

ence and Engineering Research Board (SERB), Govt

of India, under the sponsored research project (ﬁle

Number: TAR/2021/000342).

REFERENCES

Ackerman, E., Ben-Zwi, O., and Wolfovitz, G. (2010).

Combinatorial model and bounds for target set se-

lection. Theoretical Computer Science, 411(44-

46):4017–4022.

Navigating Social Networks: A Hypergraph Approach to Inﬂuence Optimization

105

Aksoy, S. G., Joslyn, C., Marrero, C. O., Praggastis, B., and

Purvine, E. (2020). Hypernetwork science via high-

order hypergraph walks. EPJ Data Science, 9(1):16.

Aktas, M. E. and Akbas, E. (2022). Hypergraph laplacians

in diffusion framework. In Complex Networks & Their

Applications X: Volume 2, Proceedings of the Tenth

International Conference on Complex Networks and

Their Applications COMPLEX NETWORKS 2021 10,

pages 277–288. Springer.

Aktas, M. E., Jawaid, S., Gokalp, I., and Akbas, E. (2022).

Inﬂuence maximization on hypergraphs via similarity-

based diffusion. In 2022 IEEE International Con-

ference on Data Mining Workshops (ICDMW), pages

1197–1206. IEEE.

Aktas, M. E., Jawaid, S., Harrington, E., and Akbas, E.

(2021). Inﬂuential nodes detection in complex net-

works via diffusion fr

echet function. In 2021 20th

IEEE International Conference on Machine Learning

and Applications (ICMLA), pages 1688–1695. IEEE.

Antelmi, A., Cordasco, G., Spagnuolo, C., and Szufel,

P. (2021). Social inﬂuence maximization in hyper-

graphs. Entropy, 23(7):796.

Battiston, F., Cencetti, G., Iacopini, I., Latora, V., Lucas,

M., Patania, A., Young, J.-G., and Petri, G. (2020).

Networks beyond pairwise interactions: Structure and

dynamics. Physics Reports, 874:1–92.

Bonacich, P. (1972). Factoring and weighting approaches

to status scores and clique identiﬁcation. Journal of

mathematical sociology, 2(1):113–120.

Chen, W., Wang, C., and Wang, Y. (2010). Scalable in-

ﬂuence maximization for prevalent viral marketing in

large-scale social networks. In Proceedings of the 16th

ACM SIGKDD international conference on Knowl-

edge discovery and data mining, pages 1029–1038.

Chiranjeevi, M., Dhuli, V. S., Enduri, M. K., and Cenkera-

maddi, L. R. (2023). Icdc: Ranking inﬂuential nodes

in complex networks based on isolating and clustering

coefﬁcient centrality measures. IEEE Access.

Domingos, P. and Richardson, M. (2001). Mining the

network value of customers. In Proceedings of the

seventh ACM SIGKDD international conference on

Knowledge discovery and data mining, pages 57–66.

Granovetter, M. (1978). Threshold models of collective be-

havior. American journal of sociology, 83(6):1420–

1443.

Hajarathaiah, K., Enduri, M. K., Anamalamudi, S., Abdul,

A., and Chen, J. (2024). Node signiﬁcance analysis

in complex networks using machine learning and cen-

trality measures. IEEE Access.

Hajarathaiah, K., Enduri, M. K., Anamalamudi, S., and

Sangi, A. R. (2023). Algorithms for ﬁnding inﬂuen-

tial people with mixed centrality in social networks.

Arabian Journal for Science and Engineering, pages

1–12.

Hajarathaiah, K., Enduri, M. K., Dhuli, S., Anamalamudi,

S., and Cenkeramaddi, L. R. (2022). Generalization of

relative change in a centrality measure to identify vital

nodes in complex networks. IEEE Access, 11:808–

824.

Kempe, D., Kleinberg, J., and Tardos,

E. (2003). Maximiz-

ing the spread of inﬂuence through a social network.

In Proceedings of the ninth ACM SIGKDD interna-

tional conference on Knowledge discovery and data

mining, pages 137–146.

Kim, M., Newth, D., and Christen, P. (2013). Model-

ing dynamics of diffusion across heterogeneous social

networks: News diffusion in social media. Entropy,

15(10):4215–4242.

Ruhnau, B. (2000). Eigenvector-centrality—a node-

centrality? Social networks, 22(4):357–365.

Senevirathna, C., Gunaratne, C., Rand, W., Jayalath, C., and

Garibay, I. (2021). Inﬂuence cascades: Entropy-based

characterization of behavioral inﬂuence patterns in so-

cial media. Entropy, 23(2):160.

Wang, X., Ning, Z., Zhou, M., Hu, X., Wang, L., Zhang,

Y., Yu, F. R., and Hu, B. (2018). Privacy-preserving

content dissemination for vehicular social networks:

Challenges and solutions. IEEE Communications Sur-

veys & Tutorials, 21(2):1314–1345.

Xie, M., Zhan, X.-X., Liu, C., and Zhang, Z.-K. (2023a).

An efﬁcient adaptive degree-based heuristic algorithm

for inﬂuence maximization in hypergraphs. Informa-

tion Processing & Management, 60(2):103161.

Xie, X., Zhan, X., Zhang, Z., and Liu, C. (2023b). Vital

node identiﬁcation in hypergraphs via gravity model.

Chaos: An Interdisciplinary Journal of Nonlinear Sci-

ence, 33(1).

Zhu, J., Zhu, J., Ghosh, S., Wu, W., and Yuan, J. (2019).

Social inﬂuence maximization in hypergraph in social

networks. IEEE Transactions on Network Science and

Engineering, 6(4):801–811.

COMPLEXIS 2024 - 9th International Conference on Complexity, Future Information Systems and Risk

106