On the Robustness of Correlation Network Models in Predicting the

Safety of Bridges

Prasad Chetti

and Hesham Ali

Northwest Missouri State University, U.S.A.

University of Nebraska at Omaha, U.S.A.

Keywords: Bridge Safety, National Bridge Inventory, Correlation Network Model, Deterioration Rates, Risk Management.

Abstract: The problem of assessing the safety of bridges and predicting potential unacceptable deterioration levels

remains one of the major problems in civil engineering. This work provides a comprehensive evaluation of

the Correlation Network Model (CNM) in safety assessment and the prediction of potential safety hazards of

bridges. The study applies a population analysis approach to compare individual or cluster performance

against a larger set of peers. The CNM outcomes were validated using a linear regression model and a

robustness analysis, resulting in a high level of consistency in identifying bridge clusters with different

deterioration rates, and thereby identifying clusters with high- risk and low risk bridges. This process allows

for the detection of significant parameters affecting bridge deterioration. The findings affirm the CNM's

capability in capturing complex relationships between input parameters and bridge deck conditions, which

exceeds the capabilities of simple linear regression models. Furthermore, the CNM's robustness, under various

conditions and assumptions, is confirmed. The study demonstrates the potential of CNM as an effective tool

for strategic planning and for efficient resource allocation, enabling focused maintenance and repair

interventions on bridge infrastructures that could potentially extend their service life.

1 INTRODUCTION

Every year, the U.S. Federal Highway

Administration (FHWA) collects data on the

condition ratings of more than 600,000 bridges. The

data document over 100 parameters for each bridge

in the National Bridge Inventory (NBI) database

(FHWA ASCII format, 2023) and the definitions of

these parameters are given in the "Recording and

Coding Guide for the Structure Inventory and

Appraisal of the Nation's Bridges" (FHWA coding

guide, 2023). This wealth of data presents a

significant big data challenge, requiring effective

analysis techniques. One essential parameter is the

condition rating, which is represented by a numerical

value ranging from 0 to 9. A rating of 9 signifies

excellent bridge condition, while a rating of 0

indicates that the bridge has failed. Ensuring public

safety and promoting economic growth are crucial

drivers for governments to prioritize the maintenance

and safety of transportation infrastructure,

particularly bridges. However, the current state of

bridges in the United States has raised concerns.

According to the American Society for Civil

Engineers (ASCE, 2021) report card, U.S. bridges

received a 'C' grade, indicating the need for sufficient

funds to ensure safety and optimal distribution of

those funds to address critical bridges first (ASCE

report card, 2021). With 42% of bridges being 50

years or older, 7.5% are classified as structurally

deficient, and an estimated $125 billion is required

for backlog bridge repairs, making it essential to

allocate funds effectively. To achieve this, a

comprehensive understanding of factors influencing

bridge safety is necessary, including structural

condition, age, materials used, design, exposure to

environmental factors (e.g., corrosion, weathering),

vulnerability to natural hazards (e.g., earthquakes,

floods), maintenance needs, traffic volume,

functional importance, socio-economic impacts,

available resources, budget constraints, stakeholder

preferences, and decision-making tools.

Additionally, accounting for geographical, material,

and design effects on bridge deterioration rates is

crucial. Various bridge deterioration models were

developed in the past to assess bridge performance

(Hatami & Morcous, 2011). However new data

driven approaches, such as the correlation network

Chetti, P. and Ali, H.

On the Robustness of Correlation Network Models in Predicting the Safety of Bridges.

DOI: 10.5220/0012692800003708

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 9th International Conference on Complexity, Future Information Systems and Risk (COMPLEXIS 2024), pages 107-113

ISBN: 978-989-758-698-9; ISSN: 2184-5034

107

models, have recently been developed by researchers

to identify the similarities in the bridge deteriorations

with respect to various bridge parameters (Chetti &

Ali, 2020; Chetti & Ali, 2019; Fuchsberger & Ali,

2017; Chetti et al., 2021).

Correlation network models (CNM) have

demonstrated their effectiveness in various domains

such as social networks and finance. In the context of

social networks, CNM has been used to identify early

opinion leaders on platforms like Twitter during the

COVID-19 pandemic (Hatami et al., 2021).

Similarly, in finance, correlation networks, combined

with population analysis, have been employed to

analyze the impact of crises on different sectors

(Hatami et al., 2023). In recent years, several

researchers have leveraged CNM and population

analysis to highlight the advantages of using

population analysis for identifying enriched

parameters and estimating inspection frequencies of

bridges within specific clusters parameters (Chetti &

Ali, 2020; Chetti & Ali, 2019; Fuchsberger & Ali,

2017). Additionally, it has been emphasized that

smart big data pipelines are necessary to tackle the

challenges associated with civil infrastructure in the

United States (Gandhi et al., 2018). Existing literature

indicates that the combination of CNM and

population analysis serves as a robust, big data model

for visualizing clusters of bridges and their

deterioration rates parameters (Chetti & Ali, 2020;

Chetti & Ali, 2019; Fuchsberger & Ali, 2017; Chetti

et al., 2021).

CNM was introduced by Chetti et al., (Chetti et

al., 2021) for analyzing safety and performance

factors in civil infrastructures, specifically focused on

highway bridges from the United States. The study

utilized correlation network models within

population analysis to understand the impact of

various parameters on bridge safety and deterioration

rates. In their study, Chetti et al. proposed a

population analysis approach, which involves

assessing the performance of an individual element or

community/cluster in comparison to a group of peers

or communities. The methodology they proposed

includes identifying significantly enriched

parameters for different bridge communities, as

illustrated in Fig. 1. The process consists of three

main steps: dataset preparation, population analysis,

and validation. Within the population analysis, three

specific steps are involved, namely creating a

similarity/correlation network, identifying candidate

clusters (CCs), and applying enrichment analysis.

Using a Spearman ranking correlation coefficient

of at least 0.90, a correlation network was created for

the condition ratings data, with bridges as nodes and

condition rating relationships as edges. The threshold

of correlation coefficient .90 is taken to capture the

clusters with bridges that have very high similarity in

their deterioration behavior. The Markov clustering

(Dongen, 2000) method was used to discern CCs, and

an inflation value of 1.9 was chosen for its modularity

and average deck condition rating differences. Of the

initial 17 clusters, 10, with a median size of 10 or

above, were viewed as CCs, constituting 233 out of

268 bridges as shown in Fig.2. Enrichment analysis

revealed a significant overrepresentation of input

parameters in seven CCs, as shown in Table 1. These

clusters were further divided into above-average and

below-average groups, each associated with

geographical regions, materials used, and factors

indicating high traffic usage and maintenance

effectiveness. However, a common limitation of

CNM for civil infrastructures is its validity. This

current study extends the work done in (Chetti et al.,

2021)

with a validation step, where the validation is

done by comparing CNM produced results with a

linear regression model and through a robustness

analysis.

2 METHODOLOGY

The verification of outcomes from a CNM, using a

population analysis strategy, can be undertaken in

three distinct ways. Initially, it can be accomplished

by scrutinizing existing scholarly works to identify

recurring themes or corroborating evidence. The

second technique contrasts the findings generated by

the CNM against those obtained from a linear

regression model by looking for alignment between

the two. Finally, implementing a robustness analysis

provides a means to assess the consistency and

reliability of the results under various conditions or

presumptions. This article primarily concentrates on

the latter two techniques, as the results were validated

using the existing literature about the durability of

concrete decks using the study done by Chyad et. al.

(Chyad et al., 2018).

2.1 Validation Using Simple Linear

Regression Model

Simple linear regression model can also be used to

validate the deterioration patterns of the candidate

clusters. The dependent variable (Y) is the condition

rating, and the independent variable (Age) is the time

in years. So, the regression equation is:

Y = b0 + b1 * Age (1)

COMPLEXIS 2024 - 9th International Conference on Complexity, Future Information Systems and Risk

108

Using the extrapolation from the regression equation,

one can estimate how a bridge could go to a structural

deficiency status (deck condition rating that is <=4 is

said to be structurally deficient (ASCE report card,

2021).

Figure 1: Methodological Steps of Population Analysis

with Correlation Network Model.

2.2 Validation Through Robustness

Analysis

Robustness analysis tests a model's stability by

evaluating its performance under data perturbations

or variations (Watts & Strogatz, 1998). It ensures that

significantly enriched parameters aren't overly reliant

on selected correlation coefficients. The analysis was

conducted by randomly selecting a percentage of

bridges (90% in this case) to identify the significant

input parameters. This robustness underscores CNM's

reliability in predicting bridge deterioration and

identifying clusters requiring maintenance and repair,

irrespective of differing correlation coefficients.

3 RESULTS

This section examines the outcomes obtained from

the application of the CNM, and its validation using

simple linear regression models, and robustness

analysis. These results highlight the capability of

CNM in predicting future bridge deterioration and

informing effective maintenance planning.

Table 1: Significant parameters of candidate clusters for the Robustness Analysis with 90% bridges selected and with >= .90

correlation.

Parameter CC pair End Avg. Condition Rating

Steel * Midwestern CC24 5.714

hPlains CC64 6.333

Prestr'CncrtCon

CC6 6.5

BxBm

GrdrSn

lSpr

CC23 6.555

Prestr'CncrtCon

* BxBm

GrdrSn

lSpr

CC23 6.555

hPlains CC23 6.555

ortheas

CC51 6.576

Prestr'Conc *

ortheas

* ADT

C CC51 6.576

Prestr'Conc * Southern CC3 6.933

Southern CC1 7

Prestr'Conc * St

Ml'bm

Grd

CC4 7

Prestr'Conc * Southeas

CC4 7

StateTollAuthorit

CC4 7

CncrtCont's * Southeas

* ADT

D CC4 7

Prestr'Conc * Southeas

* ADT

D CC4 7

CncrtCont's * Slab * ADT

D CC4 7

Prestr'Conc * St

Ml'bm

Grd

* ADT

D CC4 7

Prestr'Conc * St

Ml'bm

Grd

* Southeas

CC4 7

CncrtCont's * Slab * Southeast * ADT_D

CC4 7

Prestr'Conc * Stgr_Ml'bm_Grdr * Southeast * ADT_D

CC4 7

On the Robustness of Correlation Network Models in Predicting the Safety of Bridges

109

Figure 2: Correlation network of 268 bridges. Clusters with different numbered labels are generated using MCL clustering

algorithm (Chetti, 2023).

The regression models for each significant cluster

gave specific coefficients and statistical measures that

helped understand the lifespan and maintenance

requirements of bridge decks within each cluster. As

seen in Table 2, the β0 coefficient was the mean

response or average deck rating at age zero, indicating

the baseline value of the dependent variable before

age-related changes. The β1 coefficient denoted the

mean response change or average deck rating when

age increased by one unit, suggesting the

relationship's direction and magnitude between

independent and dependent variables. The adjusted

R-Square value measured the regression model's

strength and predictive power and assessed the

model's data fit.

3.1 Validation Using Simple Linear

Regression Model

It is worth noting that all bridges in this study started

with an initial deck condition rating of 9, with the

rating scale being 0-9, and 4 indicating a structurally

deficient status. Thus, the study bridges were initially

in good shape, deteriorating over time. Fast

deteriorating clusters were identified as CC43 and

CC88, with CC43 expected to reach structural

deficiency within the next 12 years, and CC88 within

the next 14 years (as the data started 26 years ago

(Chetti et al., 2021). These bridges are classified as

high-risk bridges based on their deterioration rate.

This data is crucial for prioritizing maintenance and

repairs. Other clusters, like CC15, CC45, CC17, CC4,

and CC3, displayed negative relationships between

age and average deck rating, with varying strength

and predictive power. The predicted timelines for

these clusters to reach structural deficiency ranged

from 49 years to over 100 years. These bridges are

classified as low-risk bridges.

Fig. 3 displays the deterioration curves of

significant clusters using simple linear regression. It

illustrates the relationship between average deck

rating and age for each cluster. The x-axis denotes

COMPLEXIS 2024 - 9th International Conference on Complexity, Future Information Systems and Risk

110

bridge deck age in years, and the y-axis indicates the

average deck rating on a 0-9 scale. The figure

highlights the swift decline of CC43 and CC88 as

their average deck ratings decrease rapidly with the

age of the bridge deck. This finding aligns with earlier

predictions suggesting that these clusters will likely

reach structural deficiency status within the next 12

and 14 years, respectively. Other clusters present a

slower decline, demonstrating a more gradual

decrease in their average deck ratings.

3.2 Comparing CNM with Linear

Regression Model

The CNM results were validated by comparison with

linear regression outcomes. The significant input

parameters identified by the CNM were found

consistent with the significant coefficients of the

linear regression models. This consistency

underscored the utility of the CNM in predicting

bridge deterioration and recognizing clusters needing

maintenance and repair.

Both models identified swiftly deteriorating

candidate clusters, specifically CC43 and CC88,

predicted by the linear regression model to reach

structural deficiency within 12 and 14 years,

respectively. These clusters were also identified as

underperforming by the CNM, signifying their faster

deterioration, potentially due to certain enriched input

parameters. Additionally, prior literature affirmed

that certain geographic regions, like the Midwest,

suffer from inferior bridge deck conditions (Chyad et

al., 2018), reinforcing the need for specific

maintenance and repair interventions. Besides

validating CNM usage, the study illuminated several

CNM benefits over the linear regression model.

These include capturing complex relationships

between input parameters and bridge deck

deterioration, identifying aberrant performance

clusters, pinpointing significantly enriched input

parameters in clusters, and informing efficient

resource allocation for bridge owners and managers

by identifying key clusters and input parameters

contributing to deck deterioration. The robust

validation of the CNM's use in predicting future

bridge deterioration and pinpointing maintenance and

repair intervention clusters was further enhanced by

its comparison with other models and existing

literature.

3.3 Robustness Analysis

Robustness analysis is a technique used to check the

stability of a model by evaluating its performance

when subjected to perturbations or variations in the

data (Watts & Strogatz, 1998). In this study,

robustness analysis was performed on the same set of

deck condition ratings of bridges by taking 90% of

the existing set of bridges with a .90 and above

correlation. The resultant candidate clusters, the ones

with significant parameters, are shown in Table 1.

There are seven candidate clusters with significant

parameters, and the comparison of the main dataset

(the previous dataset with all the bridges) with the

dataset with 90% of the bridges considered for the

robustness analysis indicates that both have the same

number of candidate clusters and similar significant

parameters.

Furthermore, robustness analysis was also

performed by checking other correlation coefficients,

such as >=.70 and >=.80. with correlation coefficient

>=.70. It is observed that there are only two candidate

clusters, indicating that the Midwestern region is

significantly enriched in the low rating cluster

category, while Southern and Southeast bridges are

still in the high-performing candidate cluster

category.

Table 2: Years to get to structural deficiency status.

Cluster β0 coefficient β1 coefficient Adjusted R-Square

Structural Deficiency

Years

CC43 8.962 -0.131 0.899 38

CC88 9.147 -0.13 0.927 40

CC15 9.802 -0.107 0.643 54

CC45 8.63 -0.096 0.654 49

CC17 8.303 -0.071 0.502 61

CC4 7.868 -0.047 0.278 83

CC3 7.597 -0.033 0.181 >100

On the Robustness of Correlation Network Models in Predicting the Safety of Bridges

111

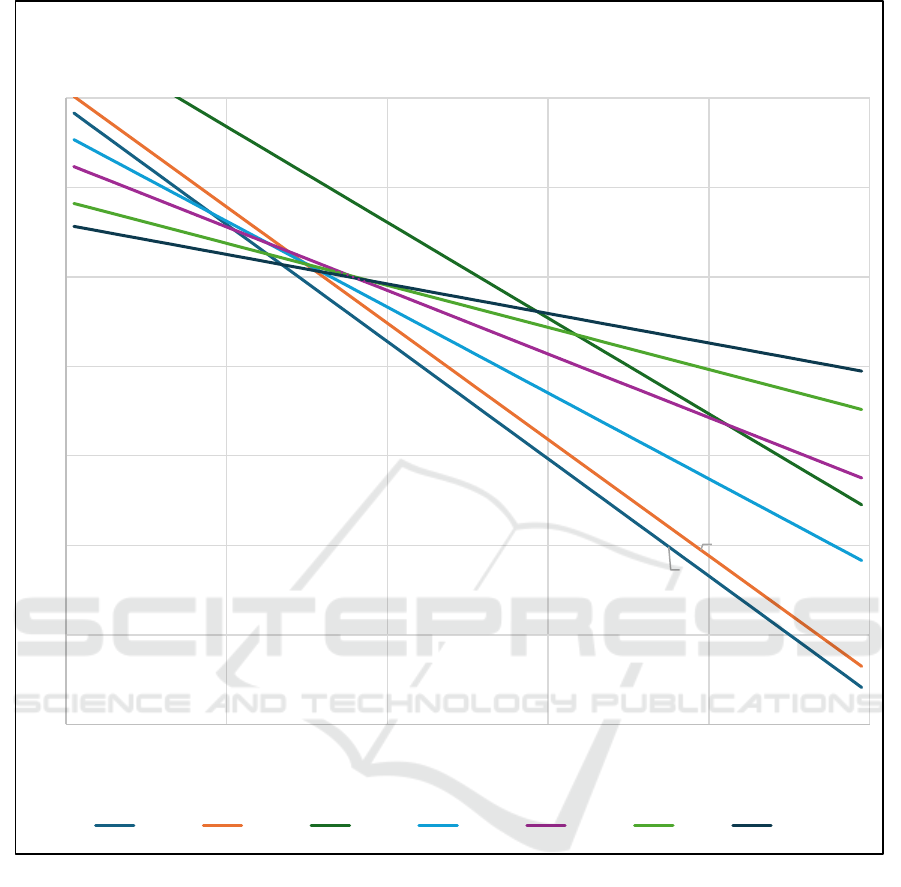
Figure 3: Deterioration curves of the significant clusters using simple linear regression.

Similar results were obtained with correlation

coefficient >=.80. The results show that there are four

candidate clusters with significant input parameters,

with the Steel parameter significantly enriched for the

low-performance cluster, such as CC20, while

Southern and Southeast bridges (along with other

parameters) are still in the high-performing candidate

cluster. These results suggest that the CNM is robust

and consistent in identifying candidate clusters with

significant parameters across different correlation

coefficients, and therefore demonstrating its

reliability in predicting future deterioration of bridges

and identifying clusters in need of maintenance and

repair interventions.

4 CONCLUSION

In conclusion, this research validates the

effectiveness of the CNM in predicting future

deterioration of bridges by using a population

analysis approach. Through the comparison with

linear regression models and robustness analysis, the

study has confirmed the CNM's ability to consistently

identify high and low risk bridge clusters with

different rates of deterioration. In addition, it has been

revealed that the CNM can detect significant

parameters influencing bridge deterioration and

outperforming simple linear regression models in this

3,984

3,947

3,926

1 11213141

Deck Rating

Age_Years

Deteriorations based on Regression Model

CC43 CC88 CC15 CC45 CC17 CC4 CC3

COMPLEXIS 2024 - 9th International Conference on Complexity, Future Information Systems and Risk

112

regard. Furthermore, the study has demonstrated the

CNM's robustness across different conditions and

assumptions. These findings have considerable

implications for strategic planning and resource

allocation in bridge infrastructure management. The

ability of the CNM to predict future bridge

deterioration, and highlight clusters that require

maintenance and repair interventions, could

potentially enhance the efficiency of these operations

and extend the service life of the bridges. This study

has thus underscored the value of the CNM as an

innovative tool for bridge infrastructure management,

deserving further exploration and application in this

field

REFERENCES

ASCE report card on US bridges. https://www.infrastru

cturereportcard.org/wp-content/uploads/2021/01/Bridg

es-Final.pdf (2023, August 15).

Chetti, P., & Ali, H. (2020). Estimating the inspection

frequencies of civil infrastructures using correlation

networks and population analysis. International Journal

on Advances in Intelligent Systems, 13(1&2), 151-162.

Chetti, P. (2023). Analyzing Structural Health of US

Bridges Using Correlation Networks and Population

Analysis (Doctoral dissertation, University of Nebraska

at Omaha).

Hatami, Z., Hall, M., & Thorne, N. (2021). Identifying early

opinion leaders on covid-19 on twitter. In HCI

International 2021-Late Breaking Papers: Design and

User Experience: 23rd HCI International Conference,

HCII 2021, Virtual Event, July 24–29, 2021,

Proceedings 23 (pp. 280-297). Springer International

Publishing.

Hatami, Z., Chetti, P., Ali, H., & Volkman, D. (2024). A

novel population analysis approach for analyzing

financial markets under crisis-a focus on excess returns

of the US stocks under 9/11 and COVID-19. Applied

Economics, 56(9), 1063-1076.

Chetti, P., & Ali, H. (2019). Analyzing the structural health

of civil infrastructures using correlation networks and

population analysis. In Proceedings of the Eighth

International Conference on Data Analytics, Porto,

Portugal.

Federal Highway Administration. (2023, August 15).

https://www.fhwa.dot.gov/bridge/nbi/ascii.cfm

Federal Highway Administration. (2023, August 15).

https://www.fhwa.dot.gov/bridge/mtguide.pdf

Hatami, A., & Morcous, G. (2011). Developing

deterioration models for Nebraska bridges (No. SPR-P1

(11) M302). Nebraska Transportation Center.

Dongen, S. (2000). A cluster algorithm for graphs. CWI

(Centre for Mathematics and Computer Science).

Fuchsberger, A., & Ali, H. (2017). A correlation network

model for structural health monitoring and analyzing

safety issues in civil infrastructures.

Chetti, P., Ali, H., Gandhi, R., Ricks, B., Ghersi, D., &

Najjar, L. (2021). A new approach for analyzing safety

and performance factors in civil infrastructures using

correlation networks and population analysis. Will be

Coming in the Proceedings of the 13th IWSHM.

Chyad, A. M., Abudayyeh, O., Zakhil, F., & Hakimi, O.

(2018, May). Deterioration rates of concrete bridge

decks in several climatic regions. In 2018 IEEE

International Conference on Electro/Information

Technology (EIT) (pp. 0065-0068). IEEE.

Gandhi, R. A., Khazanchi, D., Linzell, D., Ricks, B., & Sim,

C. (2018, May). The hidden crisis: Developing smart

big data pipelines to address grand challenges of bridge

infrastructure health in the United States. In

Proceedings of the... International ISCRAM

Conference.

Watts, D. J., & Strogatz S. H. (1998). Collective dynamics

of ‘small world’ networks. Nature, 393(6684), 440-442.

On the Robustness of Correlation Network Models in Predicting the Safety of Bridges

113