Interpolation-Based Learning for Bounded Model Checking

Anissa Kheireddine

, Etienne Renault

and Souheib Baarir

1,3

LIP6, Sorbonne Universit

e, Paris, France

SiPearl, Maisons-Lafﬁtte, France

Universit

e Paris-Nanterre, Nanterre, France

Keywords:

Bounded Model Checking, SAT, Craig Interpolation, Parallelism, Pre-Processing.

Abstract:

In this paper, we propose an interpolation-based learning approach to enhance the effectiveness of solving the

bounded model checking problem. Our method involves breaking down the formula into partitions, where

these partitions interact through a reconciliation scheme leveraging the power of the interpolation theorem to

derive relevant information. Our approach can seamlessly serve two primary purposes: (1) as a preprocessing

engine in sequential contexts or (2) as part of a parallel framework within a portfolio of CDCL solvers.

1 INTRODUCTION

Model checking (Clarke et al., 2009) is an automated

procedure that establishes the correctness of hardware

and software systems. In contrast to testing, it is a

complete and exhaustive method. Model checking is

therefore an essential industrial tool for eliminating

bugs and increasing conﬁdence in hardware designs

and software products. Usually, the studied program

(model) is expressed in a formal language whereas

the property to be checked is expressed as a formula

in some temporal logic (e.g., LTL (Rozier, 2011),

CTL (Clarke and Emerson, 1982)). A property is said

to be veriﬁed if no execution of the model can invali-

date it, otherwise, it is violated. To achieve this veri-

ﬁcation a (full) traversal of the state-space, represent-

ing the behaviors of the model, is required. Two ap-

proaches have been considered: explicit model check-

ing (Holzmann, 2018) and symbolic model check-

ing (Clarke et al., 1996). In symbolic model check-

ing, states of the studied system are represented im-

plicitly using Boolean functions. From that, mod-

ern satisﬁability (SAT) solvers have since become

one of the core technology of many model checkers,

greatly improving capacity when compared to Binary

Decision Diagrams-based model checkers (Biere and

oning, 2018). In particular, SAT procedures ﬁnd

extensive application in the bounded version of model

checking, speciﬁcally for verifying LTL speciﬁca-

tions. Bounded model checking (BMC) (Biere et al.,

2003) refers to a model checking approach where

the veriﬁcation of the property is performed using a

bounded traversal, i.e., a traversal of symbolic repre-

sentation of the state-space that is bounded by some

integer k. Such an approach does not require storing

state-space and hence, is found to be more scalable

and useful (Zarpas, 2004). Within this context, nu-

merous optimizations have been developed to guide

SAT procedures towards promising search spaces, ul-

timately reducing the solving times. One particularly

noteworthy optimization involves the generation and

utilization of high-quality (learnt) clauses from Con-

ﬂict Driven Clause Learning-like SAT solvers (Silva

and Sakallah, 1997; Moskewicz et al., 2001). The pri-

mary emphasis of this paper is to enhance the learn-

ing mechanisms within the realm of SAT-based BMC

problems. We explore a clause learning framework

that leverages Craig interpolation (Dreben, 1959).

Firstly, we introduce a novel decomposition method

tailored speciﬁcally for BMC problem-solving that

decomposes the SAT formula into independent sub-

parts. Secondly, we harness the interpolation mecha-

nism as a means to generate learnt clauses. To do so,

we took inspiration from the work in (Hamadi et al.,

2011). These learnt clauses are then used in two dis-

tinct dimensions:

• Interpolants as a Preprocessing Engine: within

a sequential context, our approach harnesses the

introduction of interpolants before the solving.

This enhances the efﬁciency of the SAT solving

process by introducing valuable clauses derived

from interpolation.

• Interpolants in a Parallel Environment: To fur-

ther leverage the wealth of information provided

Kheireddine, A., Renault, E. and Baarir, S.

Interpolation-Based Learning for Bounded Model Checking.

DOI: 10.5220/0012703500003687

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 19th International Conference on Evaluation of Novel Approaches to Software Engineering (ENASE 2024), pages 605-614

ISBN: 978-989-758-696-5; ISSN: 2184-4895

605

by interpolants, we extend the application of in-

terpolants into parallel environments by sharing

these interpolants to guide other CDCL solvers

towards promising search spaces. This collabo-

rative approach among solvers improves their col-

lective reasoning capabilities and ultimately leads

to more efﬁcient problem-solving.

The paper structure starts by reviewing important con-

cepts in Section 2 before positioning our work in Sec-

tion 3 to state-of-the-art approaches. Section 4 recalls

the random decomposition of (Hamadi et al., 2011)

and our BMC-based decomposition. Sections 5 and 6

study the effectiveness of interpolation-based learning

on both sequential and parallel settings, respectively.

2 PRELIMINARIES

2.1 SAT Procedures

The satisﬁability problem (SAT) is the canonical NP-

complete problem that aims to determine whether

there exists an assignment of values to the Boolean

variables of a propositional formula that makes the

formula true (Cook, 1971). Despite its theoretical

complexity, SAT has evolved into a widely embraced

methodology for tackling challenging problems, par-

ticularly in the realm of formal veriﬁcation.

Formally, a literal is a Boolean variables or its

negation. A clause c is a ﬁnite disjunction of liter-

als. A conjunctive normal form (CNF) propositional

formula F is a ﬁnite conjunction of clauses. For a

given F, the set of its variables is noted V . We use

V (c) to denotes the set of variables composing the

clause c. An assignment α of the variables of F is a

function α : V −→ {⊤, ⊥}. α is total (complete) when

all elements of V have an image by α, otherwise it is

partial. For a given formula F and an assignment α,

a clause of F is satisﬁed when it contains at least one

literal evaluated to true regarding α. F is satisﬁed by

α iff all clauses of F are satisﬁed. F is said to be SAT

if such an α exists. It is UNSAT otherwise.

In this work, we are interested in the CDCL al-

gorithm for solving F with signiﬁcant improvements

that considerably enhance its efﬁciency. CDCL

incorporates the concept of learning into the DPLL

algorithm (Davis et al., 1962)

, making it possible

to learn from conﬂicts (past errors) in order to avoid

similar decision errors in the future.

The overall concept of DPLL has been kept in modern

CDCL algorithms.

2.2 SAT-Based Bounded Model

Checking

The SAT-based BMC approach constructs a proposi-

tional formula that captures the interplay between the

system and the negation of the speciﬁcation to be ver-

iﬁed, both unrolled up to a given bound, denoted here

by k. When this propositional formula is proven to be

satisﬁable (SAT), it implies the presence of a property

violation within a maximum length of k. Conversely,

when the formula is unsatisﬁable (UNSAT), it afﬁrms

that the property holds up to length k.

Consider a Kripke structure denoted as M =

⟨S, T, I, AP, L⟩, which represents the system under

study where S is the set of states, T is the transition

relation over the states of S, I ∈ S represents the set of

initial states, AP is a set of atomic propositions, and L

is a labeling function. The negation of the property to

be checked on M is represented by an LTL formula ϕ.

The propositional formula [[M, ϕ]]

deﬁnes the BMC

problem for ϕ over M w.r.t. k:

[[M, ϕ]]

Initial states

z}|{

I(s

) ∧

k−1

i=0

transition relation

z }| {

T (s

, s

i+1

)

| {z }

Model

∧

j=0

[[ϕ]]

| {z }

Property

(1)

At time step i, s

encompasses truth value assignments

to the set of state variables. The expression [[ϕ]]

translates the property into its unrolled from up to k.

2.3 Craig Interpolation

The Craig interpolation theorem (Dreben, 1959) pro-

vides a powerful tool for analyzing the relationship

between two formulas A and B in the context of satis-

ﬁability. It guarantees the existence of an interpolant

when A ∧ B =⇒ ⊥, allowing us to extract additional

information about the logical structure of A and B.

Given an unsatisﬁable conjunction of formulas,

speciﬁcally A ∧ B, an interpolant, denoted by I, is a

formula that adheres to the following properties: (i)

A =⇒ I: This implies that if A holds true, then I must

also be true; (ii) B ∧ I =⇒ ⊥: The conjunction of B

and I is unsatisﬁable, indicating that there is no as-

signment of variables that simultaneously satisﬁes B

and I; (iii) I is deﬁned over the common language of

A and B: I is constructed using variables that appear

in both A and B, ensuring that it captures the relevant

information shared by both formulas. The interpolant

I provides an over-approximation of formula A while

still conﬂicting with formula B. It can be thought of

I as a logical abstraction of A that captures the essen-

tial features needed to demonstrate the conﬂict with

ENASE 2024 - 19th International Conference on Evaluation of Novel Approaches to Software Engineering

606

B. While the Craig interpolation theorem guarantees

the existence of an interpolant, it does not provide an

algorithm for ﬁnding it. However, there are known al-

gorithms for generating interpolants for various log-

ics. One common approach is to derive an interpolant

for A ∧ B from a proof of unsatisﬁability of the con-

junction. By analyzing the proof structure, it is possi-

ble to extract the necessary information to construct

the interpolant. In the context of SAT procedures,

McMillan’s interpolation (McMillan, 2003) has been

widely employed. It has been shown to be competi-

tive with SAT solving algorithms and can provide ef-

fective interpolants for model checking problems. To

gain a deeper understanding of McMillan’s interpola-

tion and other interpolation systems, a complete study

can be found in (D’Silva, 2010).

2.4 An Interpolant-Based Decision

Procedure

UNSAT

SAT

n−1

UNSAT

n−1

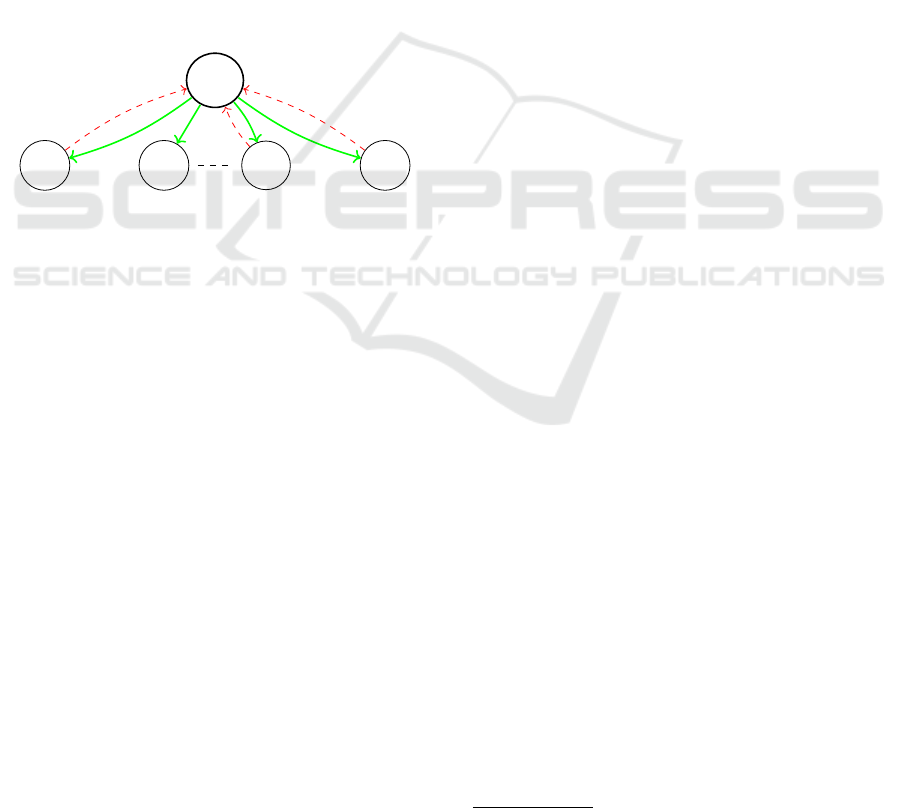
Figure 1: Reconciliation scheme.

The section outlines the framework proposed

in (Hamadi et al., 2011), describing an interpolation-

based decision procedure for SAT formulas. The

main idea is to compute partial solutions for different

parts of the formula at hand and then calculate a

global solution using interpolation mechanisms.

Indeed, they implemented the reconciliation schema

depicted in Figure 1, where partitions of the formula

are reconciled through the variables they share.

Let’s denote by ψ

for i = 1, . . . , n, the subfor-

mulas of the studied problem F. These subformulas

are solved by individual SAT solver units. However,

when the partitions happen to share variables (i.e.,

V (ψ

) ∩ V (ψ

) ̸=

0, for some j ̸= i), the resolutions

of the different partitions must be reconciled and syn-

thesized into a feasible global solution. To do so, an-

other solver is added to the schema. Named as the

manager G, it is responsible for reconciling the solu-

tions returned by each partition into a feasible global

solution that satisﬁes the entire formula F. The recon-

ciliation procedure is built using the following lemma:

Lemma 1. Let F = ψ

∧·· · ∧ψ

and let α be a partial

solution provided by G that covers the shared vari-

ables, V (G):

V (G) =

[

i, j=1,i̸= j

V (ψ

) ∩ V (ψ

If I is an interpolant between ¬ψ

and ¬α for any

1 ≤ i ≤ n, then F =⇒ I.

The resulting interpolants I

(red arrows in Fig. 1)

from ¬(ψ

∧ α) are added into G, effectively remov-

ing the partial solution α (green arrows in Fig. 1) in

future iterations.

Using the above lemma, the authors of (Hamadi et al.,

2011) present a reconciliation algorithm, for solving

SAT problems using any decomposition method. The

algorithm takes as input a CNF formula F and a num-

ber of partitions n.

The entire procedure has been implemented in a

framework called DESAT

. It integrates the McMil-

lan interpolation (McMillan, 2003) and the lazy de-

composition that will be detailed in Section 4.1. DE-

SAT uses MINISAT1.14P (E

en and S

orensson, 2003)

as a core engine. This older version of MINISAT has

the ability to provide a proof of unsatisﬁability.

3 RELATED WORKS

(Hamadi et al., 2011) used an interpolation-based

technique when treating formulas that are too large

to be handled by a single computing unit. To achieve

this, they propose decomposing the formulas into par-

titions that can be solved by individual computing

units. Once each partition is solved, the partial re-

sults are combined using Craig interpolation (Dreben,

1959) to obtain the overall result. However, the pro-

posed approach did not use any structural information

of the problem at hand.

Apart from the usage of interpolation mecha-

nisms in IC3 (Bradley, 2012), PDR (Een et al.,

2011) and some usage in the incremental SAT-based

BMC (Wieringa, 2011; Sery et al., 2012; Cabodi

et al., 2017), to the best of our knowledge, no one

has explored their usage on one single BMC instance.

The most closely work related to ours is (Ca-

bodi et al., 2017). This preliminary research pro-

poses to extract information from an interpolant-

based model-checking engine during the solving pro-

cess (in-processing). They manage to derive an over-

approximation of ﬁxed time frames with the aim

of early detecting invalid variable assignments at a

speciﬁc time frame. This initial study can provide

additional insights when integrated with our ongo-

ing work, where pre-processing and in-processing

interpolation procedures are simultaneously applied.

However, it’s worth noting that the effectiveness of

https://www.winterstiger.at/christoph/

Interpolation-Based Learning for Bounded Model Checking

607

this approach for various types of speciﬁcations is not

known, as their study was exclusively applied to in-

variant properties, while our approach is applied for

any type of LTL property.

In the context of parallel computing, the au-

thors of (Ganai et al., 2006) extended the concept

from (Zhao et al., 2001) to the domain of BMC. This

method involves distributed-SAT solving across a net-

work of workstations using a Master/Client model,

wherein each Client workstation holds an exclusive

partition of the SAT problem. The authors of (Ganai

et al., 2006) optimized the communication within the

context of BMC by introducing a structural partition-

ing approach. This strategy allocates each processor

a distinct set of consecutive BMC time frames. As

a result, when a Client workstation completes unit

propagation on its assigned clauses, it only broadcasts

the newly implied variables to speciﬁc Clients. This

allows for effective communication between Clients

and ensures that receiving Clients never need to pro-

cess a message not intended for them. Besides, the

works of (Kheireddine et al., 2023) provide a new

metric to identify relevant learnt clauses based on

the variable origins from BMC problems. The au-

thors propose some heuristics based on this measure

to tune the learnt clause databases of CDCL SAT

solver. They also employ these heuristics to redeﬁne

the clause exchange policy between multiple CDCL

solvers in a parallel context.

4 DECOMPOSITION-BASED

STRATEGIES

To formally explore the idea mentioned in Sec-

tion 2.4, we begin by examining how the formula is

decomposed. We ﬁrst study the initial decomposition

proposed in (Hamadi et al., 2011), and then we detail

our new splitting method tailored to the BMC prob-

lem.

Throughout this work, we maintain using the DE-

SAT framework (cited in Section 2.4) for all the pre-

sented experiments since the framework DESAT al-

ready has the interpolation algorithms and the rec-

onciliation mechanism in place. The integration of

a modern SAT solver, like CADICAL (Biere et al.,

2021), is in our perspective.

4.1 Lazy Decomposition (LZY-D)

The process of ﬁnding sparsely connected partitions

in a formula and eliminating connections to make

the partitions independent is not a straightforward

operation. Hamadi et al. (Hamadi et al., 2011) pro-

pose a computationally-free decomposition (LZY-D),

known as lazy decomposition:

Deﬁnition Lazy Decomposition (LZY-D). Let F be

in conjunctive normal form of q clauses, i.e., F =

∧ · ·· ∧ F

. A lazy decomposition of F into n par-

titions is an equivalent set of formulas ψ

, . . . , ψ

where each ψ

is equivalent to some conjunction of

clauses from F. In other words, there exist integers

a and b (with a < b ≤ q) such that ψ

= F

∧ ··· ∧ F

The lazy decomposition approach (LZY-D) does not

explicitly enforce independence among the partitions.

Instead, it divides the clauses of the problem into a

number of equally sized partitions. The clauses are

ordered as they appear in the input ﬁle, and each par-

tition ψ

is assigned the clauses numbered from i·⌊

⌋

to (i + 1) · ⌊

⌋.

4.2 BMC Decomposition (BMC-D)

Cutting the set of clauses randomly remains a generic

approach which does not require the knowledge of

the problem’s structure. Indeed, consider the spe-

ciﬁc structure of a BMC problem, characterized by

a ﬁnite state system. As the system operates on dis-

crete states, each state can be represented by a set of

variables and its corresponding constraints in the SAT

formula. It becomes evident that isolating each state

encoding from the SAT formula is a straightforward

task. By leveraging this inherent structure, we can

partition the SAT-based BMC formula into subformu-

las based on the k + 1 states of the system (k steps

+ initial state). This ﬁner decomposition will allow

us to create (relatively) more independent and smaller

subproblems. Moreover, it enables the prediction of

relevant information about the system’s behavior to

easily split potential error paths through the genera-

tion of precise interpolants.

In light of this observation, we propose a

decomposition-based BMC (BMC-D) approach that

takes advantage of the problem’s structure

From the encoding of BMC problem into proposi-

tional formula 1, the partitioning approach we pro-

pose is based on system states, where each partition

, i = 1 . . . n, is assigned a subset of adjacent states

of equal size t = ⌊

k+1

⌋:

i·t−2

j=(i−1)·t

T (s

, s

j+1

) ∧

i·t−1

j=(i−1)·t

[[ϕ]]

(2)

Each partition encompasses a segment of the transi-

tion unrolling as well as the constraints encoding a

Source code are available in: https://github.com/

akheireddine/DECOMP-BMC

ENASE 2024 - 19th International Conference on Evaluation of Novel Approaches to Software Engineering

608

portion of the property ϕ. The partitions on both ends,

and ψ

, contain more information than the internal

partitions that follow the above formula 2:

– ψ

includes constraints of the initial states

I(s

) .

– ψ

includes the

remaining last transition constraints .

Example. Consider a partitioning with n = 4 for a

BMC problem that has been unrolled up to bound k =

20 that veriﬁes an invariant property (e.g., G p for any

p ∈ AP). Each partition groups t = ⌊

⌋ = 5 frames.

V (ψ

) contains variables of steps s

to s

, implying

that:

• constraints assigned to ψ

are I(s

) ∧T (s

, s

) ∧

··· ∧ T (s

, s

) ∧ [[ϕ]]

∧ ··· ∧ [[ϕ]]

• ψ

encloses variables of s

to s

, i.e., T (s

, s

) ∧

··· ∧ T (s

, s

) ∧ [[ϕ]]

∧ ··· ∧ [[ϕ]]

• ψ

are T (s

, s

)∧··· ∧ T (s

, s

)∧[[ϕ]]

∧···∧

[[ϕ]]

, and,

• ψ

with T (s

, s

) ∧ · · ·∧ T (s

, s

) ∧[[ϕ]]

∧

··· ∧ [[ϕ]]

Two successive partitions ψ

and ψ

i+1

are con-

nected, respectively, through the last and ﬁrst states

of the partitions. In the example above, partitions ψ

and ψ

are connected through the transition T (s

, s

)

where state s

is included in the ﬁrst partition ψ

and

on ψ

. Thus, this transition involves variables from

both partitions. Due to the ambiguity of including

these frames in either ψ

or ψ

i+1

, it is reasonable

for the partition G to integrate them into its clause

database. This ensures consistent decisions across

different partitions and prevents conﬂicting decisions

regarding the shared variables.

This last observation leads to a modiﬁcation of the

reconciliation algorithm, where G is initialized with a

subset of the problem’s clauses corresponding to the

transitions linking the n partitions together. This ini-

tialization also encompasses a segment of the prop-

erty’s constraints. This adaptation proves particularly

relevant for certain types of formulas whose interpre-

tation involves adjacent time steps. For instance, con-

sider the speciﬁcation ”G X p” for any p ∈ AP. Its

propositional formula encoding implies variables at

time steps i and i + 1, which correspond to states s

and s

i+1

of the system’s automaton. This implies that

G incorporates the following constraints of the prob-

lem:

G =

i=1

T (s

i·t−1

, s

i·t

) ∧

n−1

j=1

j<l

[[ϕ]]

with N =

(

n if n mod k = 0

n − 1 otherwise

where

[[ϕ]]

represents the property’s constraints that

entail the j-th and l-th partitions, i.e., a state from ψ

is linked to a state in ψ

in the property formula.

Hence, G will be in charge of deciding on the follow-

ing shared variables:

V (G) =

n−1

[

i=1

V (ψ

) ∩ V (ψ

i+1

)

| {z }

common variables

between two partitions

[

|{z}

variables composing

G’s clauses

When solving G, the process involves the assign-

ing of values to a subset of the whole formula’s vari-

ables (V (G) ⊂ V (F)). This approach narrows down

the focus to a limited set of variables, thereby decreas-

ing the communication overhead with the partitions.

It’s worth noting that G has a partial view of the prob-

lem, incorporating the transitions between successive

partitions. Each partition can be seen as a represen-

tation of a portion of the paths connecting the initial

state s

(contained in ψ

) to the ﬁnal state s

(in ψ

Consequently, the generated partial assignments α are

constructed in a way that aligns the partitions in order

to identify a complete path that violates the property.

Where, in contrast, the manager G of LZY-D starts

with no initial constraints. This decomposition is con-

ducted randomly, distributing constraints encoding a

transition or property constraints at a ﬁxed depth un-

evenly among partitions. The following subsection

will allow a comparison of these two decomposition

methods.

4.3 Comparing LZY-D and BMC-D

Hamadi et al.’s approach was originally designed as

a complete decision procedure for satisﬁability prob-

lems. However, it heavily relies on computationally

intensive methods, with interpolation being the pri-

mary one. This characteristic diminishes its practical

feasibility for direct application. Nevertheless, it is

entirely conceivable to adapt and reuse this approach

for other purposes. One potential utility lies in using

it as a pre-processing tool or on a parallel context that

furnishes insights about the problem at hand, thereby

assisting classical SAT solvers in achieving more ef-

ﬁcient resolutions. Hence, the idea we will explore in

this paper is to leverage the interpolants generated by

a (potentially partial) execution of this approach as a

set of auxiliary information that can be incorporated

into the original problem.

Nevertheless, we initiated a preliminary series

of experiments with the intention of comparing

Interpolation-Based Learning for Bounded Model Checking

609

Table 1: Comparison of LZY-D and BMC-D decomp. for different partition sizes n.

part. n 5 10 20 30 40 50

#S P #S P #S P #S P #S P #S P

BMC-D 15 622h 28 586h 44 541h 35 561h 21 604h 49 534h

LZY-D 4 654h 6 649h 5 653h 9 642h 10 638h 9 642h

the aforementioned decomposition approaches when

used as complete solving procedures for BMC prob-

lems. This will shed light on the quality of the inter-

polants generated by each approach.

Benchmark Setup. Our BMC benchmark com-

prises SMV (McMillan, 1993) programs. These pro-

grams, along with their respective LTL properties,

have been sourced from a diverse range of bench-

marks, including the HWMC Competition (2017

and 2020

), hardware veriﬁcation problems (Cimatti

et al., 2002), the BEEM database, and the RERS

Challenge

. Additionally, certain LTL properties

have been generated using Spot

to ensure that each

category of the Manna & Pnueli hierarchy (Manna

and Pnueli, 1990) is represented. We utilized various

bounds k ranging in {60, 80, ..., 1000}. We excluded

trivial instances that executed in less than 1 second on

MINISAT1.14P (E

en and S

orensson, 2003).

Table 1 presents the results of 200 randomly

selected BMC problems from the aforementioned

benchmark (mainly composed of safety and persis-

tence properties). The partition sizes used were n =

5, 10, ..., 50, with a time limit of 6000 seconds. We re-

stricted the evaluation to these partition sizes, aligning

with the choices made in the original paper’s experi-

ments (Hamadi et al., 2011), employing the same in-

terpolation algorithm (McMillan (McMillan, 2003)).

The table highlights the number of solved instances

(#S) and the PAR-2

time (P).

We observe that BMC-D outperforms LZY-D

signiﬁcantly, especially when dealing with larger par-

tition sizes (e.g., n = 50). BMC-D successfully

solves 49 instances, leading to a noteworthy reduc-

tion of 108 hours in PAR-2 time compared to LZY-

D. These results seem to imply that the improvement

is attributed to concentrating the majority of clauses

in partition G, resulting in empty partitions within ψ

as n approaches the bound k of the considered prob-

lem. This brings us back to the scenario of a stan-

http://fmv.jku.at/hwmcc17/,http://fmv.jku.at/hwmcc20/

https://tinyurl.com/29a4jcme

https://spot.lre.epita.fr/

PAR-k is a measure used in SAT competitions that pe-

nalizes the average run-time, counting each timeout as k

times the running time cutoff

dard (ﬂat) resolution. However, our concrete obser-

vations invalidate this hypothesis, revealing that the

partitions do indeed encompass a fair portion of

the problem’s clauses. On the contrary, the BMC-D

strategy helps to separate independent subspaces pro-

viding better performances than LZY-D strategy.

Due to interpolation computation, neither of the

two approaches managed to surpass the performance

of a classical solver (MINISAT1.14P). This is in

contradiction with the reported results in (Hamadi

et al., 2011). Actually, LZY-D fails to outperform

MINISAT1.14P within a veriﬁcation benchmark con-

text. One potential explanation is that the benchmark,

as pointed out by the authors, is composed of fully

symmetrical problems, whereas the BMC benchmark

contains relatively fewer symmetries than expected:

the conversion of BMC problems into CNF format

disrupts symmetries, largely due to the introduction

of extra variables during the encoding that break out

the symmetry.

In light of these results, we draw two conclusions:

(1) the clauses produced by the interpolants appear

to provide valuable insights, and (2) the current ap-

proach is hindered by the computational complexity

of interpolation. This prompts the question: how

can we leverage these interpolants in an optimal

solving process? Our suggestions for addressing this

question are discussed in the following two sections.

5 INTERPOLATION-BASED

OFFLINE LEARNING

It is intriguing to thoroughly assess the relevance

and quality of information generated by interpola-

tion when compared to that naturally acquired by a

state-of-the-art SAT solver during its learning pro-

cess. Our intuition suggests that clauses derived from

interpolants could be highly beneﬁcial in aiding a

SAT solver, potentially leading to reduced solving

times.

To validate our intuitions and hypothesis, we con-

ducted an experiment employing LZY-D and BMC-

D as pre-processing steps for a CDCL SAT solver.

The primary objective here was to evaluate the infor-

ENASE 2024 - 19th International Conference on Evaluation of Novel Approaches to Software Engineering

610

Table 2: Impact of interpolants’ clauses on the solving.

part. n 5 10 20 30 40 50

#S P #S P #S P #S P #S P #S P

BMC-D-ITP 111 328h 110 333h 111 329h 111 329h 109 331h 110 329h

LZY-D-ITP 109 335h 107 338h 105 341h 110 327h 107 338h 107 338h

original inst. 107 337h

Table 3: Average rate of interpolants size.

part. n 5 10 20 30 40 50 Avg aug.

BMC-D 1.14 % 1.24 % 1.53 % 1.63 % 1.48 % 1.48 % 1.41 %

LZY-D 4.13 % 2.68 % 2.03 % 1.16 % 0.69 % 0.79 % 1.91 %

mation’s value provided by interpolants in contrast

to the information gathered by a conventional SAT

solver, all within the same time constraints. To be

more speciﬁc, each of the two algorithms was run

for a limited time period, with a particular partition

size. The interpolants generated during this period

were converted into clauses and added to the initial

instance. We refer to this process as “ofﬂine learn-

ing”. The augmented instance was then solved by a

CDCL-like SAT solver.

In this context, we randomly selected a set of 200

BMC instances from the benchmark setup described

in Section 4.3. Each instance underwent an enrich-

ment process involving the incorporation of interpo-

lation clauses generated through ofﬂine learning over

a period of 600 seconds. These instances were solved

by MINISAT1.14P within a timeout of 6000 seconds.

For reference, the original instances (without ad-

ditional clauses) were also solved by MINISAT1.14P

within a timeout of 6600 seconds to accommodate the

additional time required for ofﬂine learning.

Table 2 highlights the obtained results. BMC-D-

ITP (resp. LZY-D-ITP) indicates the line where in-

stances are augmented with BMC-D (resp. LZY-D)

interpolants. The line labeled as original inst refers to

the original instances without any additional clauses.

The rest of the reported information are the same as

in Table 1. Both decomposition approaches exhibit

improved solving times and succeed in resolving ad-

ditional instances that could not be tackled without

the ofﬂine learning. Notably, BMC-D interpolants

have enhanced the solving. It showcases superior per-

formance with a partition size of n = 5, solving 4 in-

stances more and reducing the PAR-2 time by up to

9 hours compared to solving the original problem.

LZY-D decomposition yields better outcomes with

n = 30, solving 3 instances more in 10 hours shorter

than solving the original instances.

These results conﬁrmed our initial intuition re-

garding the signiﬁcance of information acquired

through the interpolation process. It becomes evident

that the interpolants obtained from the structural de-

composition method BMC-D prove to be more valu-

able compared to those derived from LZY-D.

Indeed, Table 3 illustrates the average percentage

of the number of additional clauses added to the orig-

inal problems, that were learnt by the LZY-D and

BMC-D strategies during the ofﬂine learning phase,

and across various partitioning sizes n. The last col-

umn displays the average percentage increase across

all partition sizes.

..... BMC-D decomposition consistently generates

a stable and equivalent set of clauses across all par-

titioning sizes. The increase in the total number

of clauses remains limited, reaching a maximum of

1.63 % of additional clauses, with an average aug-

mentation of 1.41 %. Regardless of the chosen parti-

tion size, on the contrary, the LZY-D approach tends

to produce a larger number of clauses, including up

to 4.13 % of interpolation clauses with an average

augmentation of 1.91 %. We observe a decrease in

the number of generated interpolants relative to the

partition size. These two trends can be explained as

follows: the decomposition-based BMC strategy al-

lowed us to generate a relatively consistent amount

of information within the 600 seconds time frame.

This consistency arises from two related aspects: (a)

the distribution of shared variables between two par-

titions is homogeneous, with the exception of the ﬁrst

and last partitions, each containing more or less infor-

mation than the others (ψ

contains the initial state

I(s

) and ψ

the remaining states if any). These

shared variables are designed to connect the parti-

tions, thereby identifying a complete path that vio-

lates the property; (b) The partial assignment α, gen-

erated by G, consistently produces conﬂicts, i.e., in-

terpolants, regardless of the partition size. For in-

stance, when using a partitioning scheme with n = 5

Interpolation-Based Learning for Bounded Model Checking

611

(resp. n = 50), BMC-D generates an average of 4.40

(resp. 34.06) interpolants per round, where a round

signiﬁes when the manager G has traversed all parti-

tions ψ

over the current partial assignment α.

..... In contrast, the random partitioning approach

LZY-D generates fewer interpolants per round, with

an average of 1.81 interpolants for n = 5 and 2.86

for a partition size of n = 50. We observed that the

distribution of shared variables is less homogeneous

between partitions. This non-homogeneity arises be-

cause the partitioning is random, leading to some

partitions sharing many more variables than others.

Thus, due to this randomness in the shared variables,

it becomes challenging to produce many conﬂicts re-

gardless of the given assignment α. Additionally, the

manager G of the LZY-D approach starts with no

constraints in its database, which can result in the

generation of assignments α that do not differ signif-

icantly. Consequently, it becomes more challenging

for G to ﬁnd a model α that violates a majority of

the partitions, leading to a reduced number of inter-

polants.

..... Based on these measurements, this analysis

clearly underscores the competitive and efﬁcient na-

ture of a decomposition approach that takes into con-

sideration the structural aspects of the BMC problem,

in contrast to a randomized decomposition strategy.

6 INTERPOLATION-BASED

LEARNING IN PARALLEL

SOLVING

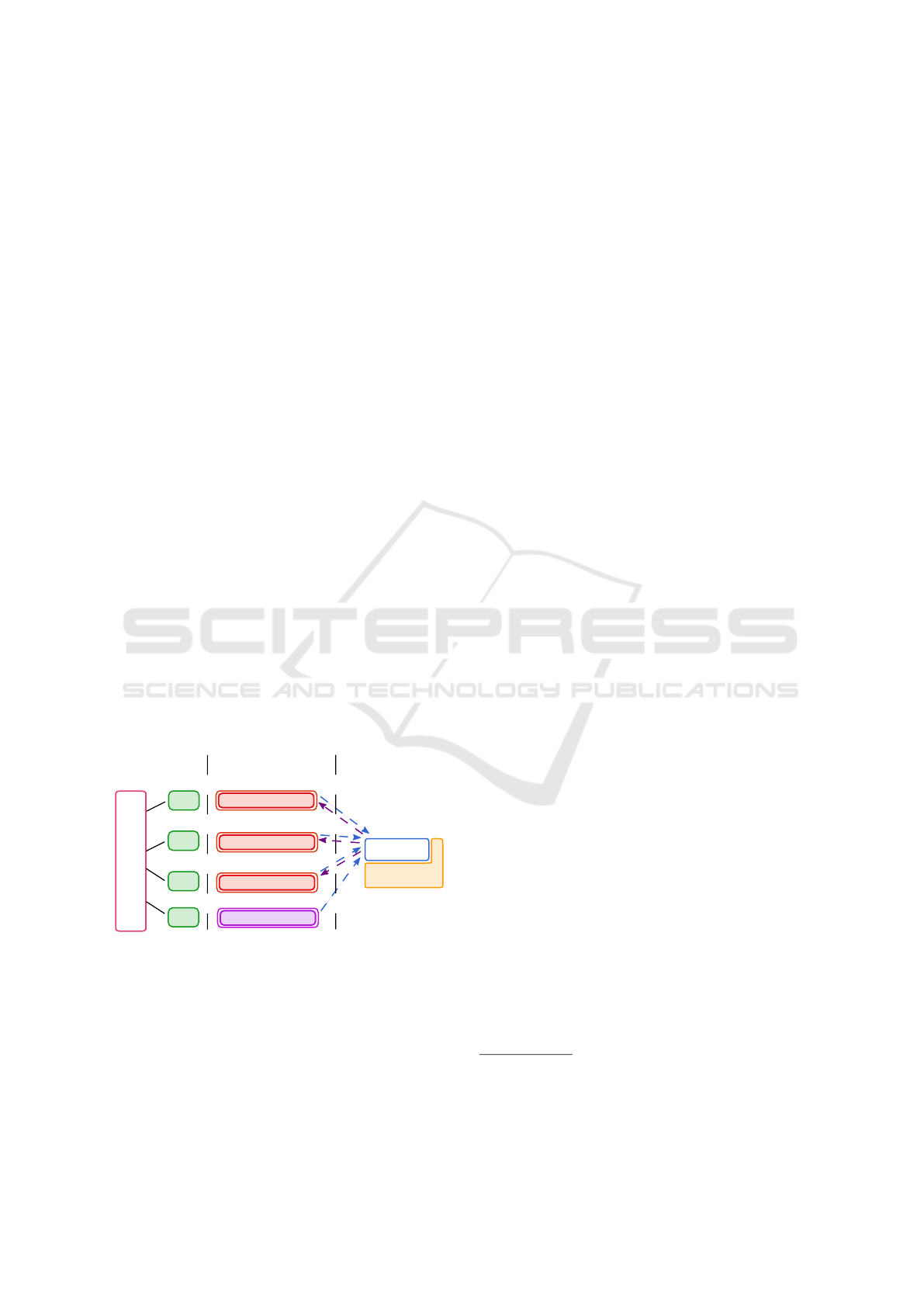
Sharing

Parallelization

...

ControlFlow

Sharer

Sequential

Engines

...

CDCL solver

...

CDCL solver

...

Decomposition-based

Interpolants

solver

Figure 2: Portfolio of solvers with sharing scheme using the

framework PaInleSS.

As demonstrated earlier, interpolation clauses have

a positive impact on the overall resolution time for

BMC problems (refer to Table 2). This ﬁnding un-

derscores the potential advantages of integrating our

concept within a parallel computing context. One of

the most effective strategies in parallel SAT solving

is the “portfolio” approach. In essence, a portfolio

consists of a set of sequential SAT solvers that run in

parallel and compete to solve a problem. These core

engine solvers vary in several ways, including the al-

gorithms they employ and their initialization parame-

ters. Moreover, they can exchange information to ex-

pedite problem-solving and avoid repeating the same

mistakes. This aspect forms the basis for the integra-

tion of the approaches discussed thus far. Indeed, we

incorporate our decomposition-based solver, along-

side multiple sequential CDCL engines into a portfo-

lio strategy (via the PAINLESS framework (Le Frioux

et al., 2017)), as illustrated in Figure 2. Three main

components arise when treating parallel SAT solvers:

(i) sequential engines. it can be any CDCL state-

of-the art solver; (ii) parallelization. is represented

by a tree-structure. The internal nodes of the tree rep-

resent parallelization strategies, and leaves are core

engines (SW), and; (iii) sharing. is in charge of re-

ceiving and exporting the set of clauses provided by

the sequential engines during the solving process.

In this integration, the interpolation-derived

clauses are shared among the CDCL solvers. This

aims to enhance the knowledge base of CDCL solvers

and support them throughout the solving process. In

this framework, the decomposition-based solver does

not import information from other solvers; instead, it

exclusively provides its interpolants to them. It func-

tions as a ”black-box”, serving as a specialized clause

generator designed for BMC problems.

For the sake of simplicity, the exchange phase

of the sharing component is to share clauses with a

limited LBD

value (Simon and Audemard, 2009).

Speciﬁcally, CDCL solvers export learnt clauses iden-

tiﬁed by an LBD ≤ 4, a threshold that has been em-

pirically proven to be effective in recent portfolios

Upon receiving the interpolants from the n parti-

tions, the manager G calculates their corresponding

LBD values and shares only those with LBD ≤ 4, fol-

lowing a similar approach as used for sharing conﬂict-

ing learnt clauses.

To encourage the solvers to explore diverse search

subspaces, it is essential to introduce some variation

in the solver’s parameters, such as the initial phase of

the variables. By ensuring that each solver runs with

a different initialization phase, they are more likely to

make distinct decisions, leading to exploration of dis-

tinct search subspaces. This diversiﬁcation approach

will be applied to all the portfolios evaluated in the

subsequent analysis.

LBD is a learnt clause quality metric used in almost all

competitive sequential CDCL-like SAT solvers and parallel

sharing strategies.

https://satcompetition.github.io/2023/

ENASE 2024 - 19th International Conference on Evaluation of Novel Approaches to Software Engineering

612

Table 4: Performance comparison between Portfolios.

Portfolio part. n SAT UNSAT Total PAR-2

P-BMC-D

5 186 115 301 356h05

50 186 119 305 345h40

P-LZY-D

5 184 113 297 371h09

50 185 113 298 367h20

P-MINISAT - 185 113 298 362h57

Experimental Evaluation

Table 5: Number of solved instances of P-BMC-D for dif-

ferent frame sizes t.

Portfolio

num. steps t

[1 , 7] [8 , 30] [31, 200]

P-LZY-D 0 +12 -1

P-MINISAT +3 +10 -1

The experiments were conducted on the same bench-

mark described in Section 4.3 with 200 additional

BMC instances (400 instances in total). Each in-

stance had a time limit of 6000 seconds for execution.

The portfolio setups comprised 10 threads, and the

solvers used in these portfolio conﬁgurations were as

follows: (i) P-MINISAT: The portfolio exclusively

employs the original MINISAT1.14P solver; (ii) P-

BMC-D: One MINISAT1.14P solver was replaced

with a decomposition-based solver using BMC-D de-

composition. (iii) P-LZY-D: Similar to P-BMC-D

portfolio, it incorporates LZY-D instead.

Table 4 presents the results for both smaller (n =

5) and larger (n = 50) partition sizes. The remaining

conﬁgurations yielded outcomes similar to those with

n = 5. The table provides information on the number

of solved SAT and UNSAT instances, along with the

total instances and the PAR-2 metrics.

Unsurprisingly, P-BMC-D outperforms the base-

line P-MINISAT by solving 6 more UNSAT instances

and 1 additional SAT instance, all within a remarkable

17 hours reduction in PAR-2 solving time. Further-

more, P-BMC-D exhibits a clear advantage over P-

LZY-D for both partitioning sizes (n = 5, 50), solving

up to 7 more instances and achieving a PAR-2 time re-

duction of up to 21 hours.

Given these results, we sought to examine the re-

lationship between the partitioning size and the un-

rolling depth k of the BMC problem. To do this, we

conducted an analysis in which we categorized the en-

tire benchmark of 400 BMC problems based on the

number of frames within a single partition ψ

, noted

t. This categorization was performed for various par-

tition sizes, n = 5, 10, 20, 30, 40, 50.

Table 5 provides an overview of the additional in-

stances solved (+) or lost (-) by P-BMC-D in com-

parison to the P-LZY-D and P-MINISAT portfolios,

indicated in the ﬁrst and second rows, respectively.

We categorized the BMC problems into three groups

based on the number of frames t contained within

a partition ψ

. The ﬁrst column ([1,7]) includes in-

stances where each partition contains at least one

frame and at most 7 frames (1 ≤ t ≤ 7). The next

column corresponds to instances where t falls within

the range of 8 to 30. Finally, the last column groups

the remaining values of t up to 200. The evaluated

benchmark bounds k varies from 10 to 1000 steps, we

have t =

1000

= 200 frames as a limit.

An interesting observation is that clustering a

large number of frames within a single partition (30 <

t ≤ 200) negatively impacts the performance of P-

BMC-D. This is evident from Table 5, where P-

BMC-D failed to solve one instance compared to the

other two portfolios. The most signiﬁcant improve-

ment is observed when t ∈ [8, 30], where P-BMC-D

solved 10 and 12 additional problems compared to P-

MINISAT and P-LZY-D, respectively. Furthermore,

grouping a small number of frames within a single

partition ([1,7]) only marginally enhances the perfor-

mance of P-BMC-D.

Based on the above analysis, it becomes evi-

dent that utilizing interpolation-based clause learning

through a BMC-based partitioning, which balances

the inclusion of a reasonable number of frames within

each partition (t ∈ [8, 30]), yields the most favorable

outcomes in terms of solving efﬁciency. This sug-

gests that the granularity of partitioning n and the to-

tal number of frames t within each partition play a key

role in computing relevant interpolants.

7 CONCLUSION

Our objective was to enhance the efﬁciency of SAT-

based BMC solving by leveraging the interpolation

mechanism to generate learned clauses. Our ongoing

research aims to extend this concept to more recent

solvers, such as CADICAL, which holds the potential

to furnish robust unsatisﬁable proofs, consequently

yielding more informative interpolants.

REFERENCES

Biere, A., Cimatti, A., Clarke, E. M., Strichman, O., and

Zhu, Y. (2003). Bounded model checking.

Biere, A., Fleury, M., and Heisinger, M. (2021). CaD-

iCaL, Kissat, Paracooba entering the SAT Competi-

tion 2021. In Balyo, T., Froleyks, N., Heule, M., Iser,

M., J

arvisalo, M., and Suda, M., editors, Proc. of SAT

Interpolation-Based Learning for Bounded Model Checking

613

Competition 2021 – Solver and Benchmark Descrip-

tions, volume B-2021-1 of Department of Computer

Science Report Series B. University of Helsinki.

Biere, A. and Kr

oning, D. (2018). SAT-Based Model Check-

ing, pages 277–303. Springer International Publish-

ing, Cham.

Bradley, A. R. (2012). Understanding IC3. In SAT, volume

7317 of Lecture Notes in Computer Science, pages 1–

14. Springer.

Cabodi, G., Camurati, P., Palena, M., Pasini, P., and Ven-

draminetto, D. (2017). Interpolation-based learning

as a mean to speed-up bounded model checking (short

paper). In Cimatti, A. and Sirjani, M., editors, Soft-

ware Engineering and Formal Methods, pages 382–

387, Cham. Springer International Publishing.

Cimatti, A., Clarke, E., Giunchiglia, E., Giunchiglia, F., Pi-

store, M., Roveri, M., Sebastiani, R., and Tacchella,

A. (2002). NuSMV Version 2: An OpenSource Tool

for Symbolic Model Checking. In CAV 2002, volume

2404 of LNCS, Copenhagen, Denmark. Springer.

Clarke, E., Emerson, E., and Sifakis, J. (2009). Model

checking. Communications of the ACM, 52.

Clarke, E., McMillan, K., Campos, S., and Hartonas-

Garmhausen, V. (1996). Symbolic model checking.

In Alur, R. and Henzinger, T. A., editors, Computer

Aided Veriﬁcation, pages 419–422, Berlin, Heidel-

berg. Springer Berlin Heidelberg.

Clarke, E. M. and Emerson, E. A. (1982). Design and syn-

thesis of synchronization skeletons using branching

time temporal logic. In Logics of Programs, Berlin,

Heidelberg. Springer Berlin Heidelberg.

Cook, S. A. (1971). The complexity of theorem proving

procedures. In Proceedings of the Third Annual ACM

Symposium, pages 151–158, New York. ACM.

Davis, M., Logemann, G., and Loveland, D. (1962). A ma-

chine program for theorem-proving. Commun. ACM.

Dreben, B. (1959). William craig. linear reasoning. a new

form of the herbrand-gentzen theorem. the journal of

symbolic logic, vol. 22 (1957), pp. 250–268. - william

craig. three uses of the herbrand-gentzen theorem in

relating model theory and proof theory. the journal of

symbolic logic, vol. 22 (1957), pp. 269–285. Journal

of Symbolic Logic, 24(3):243–244.

D’Silva, V. (2010). Propositional interpolation and abstract

interpretation. In Gordon, A. D., editor, Programming

Languages and Systems, pages 185–204, Berlin, Hei-

delberg. Springer Berlin Heidelberg.

Een, N., Mishchenko, A., and Brayton, R. (2011). Efﬁ-

cient implementation of property directed reachabil-

ity. In 2011 Formal Methods in Computer-Aided De-

sign (FMCAD), pages 125–134.

en, N. and S

orensson, N. (2003). An extensible sat-solver.

In International Conference on Theory and Applica-

tions of Satisﬁability Testing.

Ganai, M., Gupta, A., Yang, Z., and Ashar, P. (2006). Efﬁ-

cient distributed sat and sat-based distributed bounded

model checking. International Journal on Software

Tools for Technology Transfer, 8:387–396.

Hamadi, Y., Marques-Silva, J., and Wintersteiger, C.

(2011). Lazy decomposition for distributed decision

procedures. In Proceedings 10th International Work-

shop on Parallel and Distributed Methods in veriﬁCa-

tion (PDMC’11), volume 72, pages 43–54.

Holzmann, G. J. (2018). Explicit-state model checking. In

Clarke, E. M., Henzinger, T. A., Veith, H., and Bloem,

R., editors, Handbook of Model Checking, pages 153–

171, Cham. Springer International Publishing.

Kheireddine, A., Renault, E., and Baarir, S. (2023). To-

wards better heuristics for solving bounded model

checking problems. Constraints.

Le Frioux, L., Baarir, S., Sopena, J., and Kordon, F.

(2017). PaInleSS: a framework for parallel SAT solv-

ing. In Proceedings of the 20th International Con-

ference on Theory and Applications of Satisﬁability

Testing (SAT’17), volume 10491 of Lecture Notes in

Computer Science, pages 233–250. Springer, Cham.

Manna, Z. and Pnueli, A. (1990). A hierarchy of temporal

properties (invited paper, 1989). In PODC ’90.

McMillan, K. L. (1993). The SMV System, pages 61–85.

Springer US, Boston, MA.

McMillan, K. L. (2003). Interpolation and sat-based model

checking. In Hunt, W. A. and Somenzi, F., editors,

Computer Aided Veriﬁcation, pages 1–13, Berlin, Hei-

delberg. Springer Berlin Heidelberg.

Moskewicz, M. W., Madigan, C. F., Zhao, Y., Zhang, L.,

and Malik, S. (2001). Chaff: Engineering an efﬁcient

sat solver. In DAC, pages 530–535. ACM.

Rozier, K. Y. (2011). Survey: Linear temporal logic sym-

bolic model checking. Comput. Sci. Rev.

Sery, O., Fedyukovich, G., and Sharygina, N. (2012).

Interpolation-based function summaries in bounded

model checking. In Eder, K., Lourenc¸o, J., and She-

hory, O., editors, Hardware and Software: Veriﬁca-

tion and Testing, pages 160–175, Berlin, Heidelberg.

Springer Berlin Heidelberg.

Silva, J. a. P. M. and Sakallah, K. A. (1997). Grasp—a

new search algorithm for satisﬁability. In Proceedings

of the 1996 IEEE/ACM International Conference on

Computer-Aided Design, ICCAD ’96, page 220–227,

USA. IEEE Computer Society.

Simon, L. and Audemard, G. (2009). Predicting Learnt

Clauses Quality in Modern SAT Solver. In Twenty-

ﬁrst International Joint Conference on Artiﬁcial Intel-

ligence (IJCAI’09), Pasadena, United States.

Wieringa, S. (2011). On incremental satisﬁability and

bounded model checking. CEUR Workshop Proceed-

ings, 832:13–21.

Zarpas, E. (2004). Simple yet efﬁcient improvements of

sat based bounded model checking. In Hu, A. J. and

Martin, A. K., editors, Formal Methods in Computer-

Aided Design, pages 174–185, Berlin, Heidelberg.

Springer Berlin Heidelberg.

Zhao, Y., Malik, S., Moskewicz, M., and Madigan, C.

(2001). Accelerating boolean satisﬁability through ap-

plication speciﬁc processing. In Proceedings of the

14th International Symposium on Systems Synthesis,

ISSS ’01, page 244–249, New York, NY, USA. Asso-

ciation for Computing Machinery.

ENASE 2024 - 19th International Conference on Evaluation of Novel Approaches to Software Engineering

614