chiku: Efficient Probabilistic Polynomial Approximations Library
Devharsh Trivedi
1 a
, Nesrine Kaaniche
2 b
, Aymen Boudguiga
3 c
and Nikos Triandopoulos
1
1
Department of Computer Science, Stevens Institute of Technology, Hoboken, NJ 07030, U.S.A.
2
T
´
el
´
ecom SudParis, Institut Polytechnique de Paris, 91000, France
3
Universit
´
e Paris-Saclay, CEA-List, 91191 Gif-sur-Yvette, France
Keywords:
Python Library, Comparison Approximation, Private Machine Learning, Fully Homomorphic Encryption.
Abstract:
Fully Homomorphic Encryption (FHE) is a prime candidate to design privacy-preserving schemes due to its
cryptographic security guarantees. Bit-wise FHE (e.g., FHEW , T FHE) provides basic operations in logic
gates, thus supporting arbitrary functions presented as boolean circuits. While word-wise FHE (e.g., BFV,
CKKS) schemes offer additions and multiplications in the ciphertext (encrypted) domain, complex functions
(e.g., Sin, Sigmoid, TanH) must be approximated as polynomials. Existing approximation techniques (e.g.,
Taylor, Pade, Chebyshev) are deterministic, and this paper presents an Artificial Neural Networks (ANN)
based probabilistic polynomial approximation approach using a Perceptron with linear activation in our pub-
licly available Python library chiku. As ANNs are known for their ability to approximate arbitrary functions,
our approach can be used to generate a polynomial with desired degree terms. We further provide third and
seventh-degree approximations for univariate Sign(x) ∈ {−1,0,1} and Compare(a − b) ∈ {0,
1
2
,1} functions
in the intervals [−1,1] and [−5,−5]. Finally, we empirically prove that our probabilistic ANN polynomials
can improve up to 15% accuracy over deterministic Chebyshev’s.
1 INTRODUCTION
Fully Homomorphic Encryption (FHE) is a crypto-
graphic primitive that can perform arithmetic compu-
tations directly on encrypted data. This makes FHE a
preferred candidate for privacy-preserving computa-
tion and storage. FHE has received significant atten-
tion worldwide, which yielded many improvements
since (Gentry, 2009). As a result, FHE is used in
many applications (Angel et al., 2018; Bos et al.,
2017; Bourse et al., 2018; Kim and Lauter, 2015).
FHE can be classified as word-wise (Brakerski et al.,
2014; Cheon et al., 2017; Fan and Vercauteren, 2012;
Gentry et al., 2013) and bit-wise (Chillotti et al.,
2016; Ducas and Micciancio, 2015) schemes as per
the supported operations.
Word-wise FHE provides component-wise addi-
tion and multiplication of an encrypted array over Z
p
for a positive integer p > 2 (Brakerski et al., 2014;
Fan and Vercauteren, 2012) or the field of complex
numbers C (Cheon et al., 2017). These schemes al-
low for packing multiple data values into a single ci-
a
https://orcid.org/0000-0001-6374-7249
b
https://orcid.org/0000-0002-1045-6445
c
https://orcid.org/0000-0001-6717-8848
phertext and performing computations on these values
in a Single Instruction Multiple Data (SIMD) (Smart
and Vercauteren, 2014) manner. Encrypted inputs are
packed to different slots of ciphertext such that the
operations carried over a single ciphertext are carried
over each slot independently.
For word-wise FHE schemes, performing a non-
polynomial operation such as Sin, Sign(Signum), and
Compare becomes difficult. As a compromise, the ex-
isting approaches using these schemes either approx-
imate non-polynomial functions using a low-degree
polynomial (Gilad-Bachrach et al., 2016; Kim et al.,
2018) or avoid using them (Dathathri et al., 2019).
Contrary to word-wise FHE schemes, bit-wise
FHE provides basic operations in the forms of logic
gates such as NAND (Ducas and Micciancio, 2015)
and Look-Up Table (LUT) (Chillotti et al., 2016;
Chillotti et al., 2017). Bit-wise schemes encrypt their
input in a bit-wise fashion such that each bit of the
input is encrypted to a different ciphertext, and the
operations are carried over each bit separately. While
these schemes support arbitrary functions presented
by boolean circuits, they are impractical for large cir-
cuit depth (Cheon et al., 2019b; Chillotti et al., 2020).
This paper extends our ANN-based approach pre-
634
Trivedi, D., Kaaniche, N., Boudguiga, A. and Triandopoulos, N.
chiku: Efficient Probabilistic Polynomial Approximations Library.
DOI: 10.5220/0012716000003767
Paper published under CC license (CC BY-NC-ND 4.0)
In Proceedings of the 21st International Conference on Security and Cryptography (SECRYPT 2024), pages 634-641
ISBN: 978-989-758-709-2; ISSN: 2184-7711
Proceedings Copyright © 2024 by SCITEPRESS – Science and Technology Publications, Lda.

x
1
x
2
x
d
b
h
b
out
w
1
w
2
w
d
w
out
y
out
Linear
Activation
Linear
Activation
Back-propagation
(Loss minimization)
Input
Layer
Hidden
Layer
Output
Layer
x
Feed-forward
Figure 1: Polynomial approximation using ANN.
sented in (Trivedi, 2023a) and (Trivedi et al., 2023) to
detail our open-source Python approximation library
(Trivedi, 2023b). We refer readers to (Trivedi et al.,
2023) for background on polynomial approximations.
Our contributions in this paper can be summarized as:
• First, we propose to use Perceptron (basic block
of Artificial Neural Network (ANN)) with linear
activation for polynomial approximation of arbi-
trary functions and release the implementation as
chiku, an open-source Python library.
• We propose to calculate Compare(a,b) =
(Sign(a − b) + 1)/2 by approximating
Sign(Signum) as a parameterized TanH function
for a word-wise FHE using our ANN based
approximation scheme. We also approximate
Compare directly as a parameterized Sigmoid in
the intervals [−1,1] and [−5,5].
• Finally, we show that the polynomials generated
using our probabilistic ANN scheme have lower
estimation errors than deterministic Chebyshev
polynomials of the same order.
2 APPROXIMATION LIBRARY
Complex (non-linear) functions like Sigmoid (σ(x))
and Hyperbolic Tangent (tanhx) can be computed
with FHE in an encrypted domain using piecewise-
linear functions or polynomial approximations like
Taylor (George, 1985), Pade (Baker et al., 1996),
Chebyshev (Press et al., 1992), Remez (Remez,
1934), and Fourier (George, 1985) series. A linear
approximation of σ(x) = 0.5 + 0.25x can be derived
from the first two terms of Taylor series
1
2
+
1
4
x. These
deterministic approaches yield the same polynomial
for the same function. In contrast, we propose to use
Figure 2: Sign(x) approximation in the intervals [−1, 1]
(left) and [−5,5] (right).
ANN to derive the approximation polynomial prob-
abilistically, where the coefficients are based on the
initial weights and convergence of the ANN model.
Our scheme is publicly available as a Python pack-
age. Table 1 compares our library with other popular
Python packages for numerical analysis. While the
mpmath library provides Taylor, Pade, Fourier, and
Chebyshev approximations, a user has to transform
the functions to suit the mpmath datatypes (e.g., mp f
for real float and mpc for complex values). In con-
trast, our library requires no modifications and can ap-
proximate arbitrary functions. Additionally, we pro-
vide Remez approximation along with the other meth-
ods supported by the mpmath.
While ANNs are known for their universal func-
tion approximation properties, they are often treated
as a black box and used to calculate the output value.
We propose to use a basic 3-layer perceptron (Fig-
ure 1) consisting of an input layer, a hidden layer,
and an output layer; both hidden and output layers
having linear activations to generate the coefficients
for an approximation polynomial of a given order. In
this architecture, the input layer is dynamic, with the
input nodes corresponding to the desired polynomial
degrees. While having a variable number of hidden
layers is possible, we fix it to a single layer with a sin-
gle node to minimize the computation. Our scheme is
outlined in Algorithms 1 and 2.
We show coefficient calculations for a third-order
polynomial (d = 3) for a univariate function f (x) = y
for an input x, actual output y, and predicted output
y
out
. Input layer weights are
{w
1
,w
2
,..., w
d
} = {w
1
,w
2
,w
3
} = {x, x
2
,x
3
}
and biases are {b
1
,b
2
,b
3
} = b
h
. Thus, the output of
the hidden layer is
y
h
= w
1
x + w
2
x
2
+ w
3
x
3
+ b
h
The predicted output is calculated by
y
out
=w
out
· y
h
+ b
out
=w
1
w
out
x + w
2
w
out
x
2
+ w
3
w
out
x
3
+ (b
h
w
out
+ b
out
)
(1)
where the layer weights {w
1
w
out
,w
2
w
out
,w
3
w
out
} are
the coefficients for the approximating polynomial of
order-3 and the constant term is b
h
w
out
+ b
out
.
chiku: Efficient Probabilistic Polynomial Approximations Library
635

Table 1: Polynomial approximations provided by various Python packages.
Python Library Deterministic Probabilistic
Taylor Fourier Pade Chebyshev Remez ANN
numpy (Harris et al., 2020) ✓
scipy (Virtanen et al., 2020) ✓ ✓
mpmath (mpmath development team, 2023) ✓ ✓ ✓ ✓
chiku (Trivedi, 2023b) (ours) ✓ ✓ ✓ ✓ ✓ ✓
Table 2: ANN coefficients for third-order sin(x) in [−π,π].
ANN Polynomial Coefficients {x
3
,x
2
,x, 1}
{−0.093311,−0.001371,0.858306,−0.001598}
{−0.095412,−0.000617,0.865269,0.005028}
{−0.093075,−0.000522,0.855427,0.000681}
{−0.094316,−3.7255e − 05,0.865397, 0.00162}
{−0.0932,0.00082,0.852329,0.004375}
Table 3: ANN losses for third-order sin(x) in [−π,π].
MAE MSLE Huber Hinge LCH
0.05810 0.00089 0.00223 0.50278 0.00222
0.05634 0.00102 0.00227 0.50395 0.00226
0.05792 0.00091 0.00220 0.50475 0.00219
0.05753 0.00094 0.00222 0.49961 0.00222
0.05776 0.00099 0.00224 0.50833 0.00224
Data: f unction, degrees,range, points,
batch,epochs
Result: coe f f s[]
A ← SampleGen(range, points);
// e.g., points = 2
16
X,Y ← φ;
for every a ∈ A do
Q ← φ;
for every d ∈ degrees do
// e.g., degrees = {1,2,5}
Q ← append a
d
;
end
X ← append Q;
// training samples
Y ← append f unction(a);
// e.g., f unction = cosh
end
Train ANN model M
with X,Y,batch,epochs;
w1,b1,w2,b2 ← ExtractWeights(M);
W = w1 ∗ w2;
// coefficients of variables
bias = (b1 ∗ w2)+ b2;
// constant term of polynomial
coe f f s[] ← bias;
for every w ∈ W do
coe f f s[] ← append w;
end
Algorithm 1: ANN. f it.
Data: x, coe f f s[]
Result: result
result = 0;
for i = 1 to N (number of coefficients) do
result = result +coe f f s[i]∗ (x
i−1
);
end
Algorithm 2: ANN.predict.
Table 4: Taylor (T ), Chebyshev (C) and ANN (A) polyno-
mial approximations for sin(x) in the interval [−π,π].
Appr Coefficients {x
3
,x
2
,x,1}
T
{1,2,3}
{-0.166667, 0.0, 1.0, 0.0}
C
{1,2,3}
{-0.099489, 0.0, 0.919725, 0.0}
A
{1,2,3}
{-0.09312, -0.001206, 0.856151, 0.000987}
A
{1,3}
{-0.093406, 0.0, 0.859662, 0.000514}
A
{2,3}
{0.030449, 0.001666, 0.0, 0.01045}
Our polynomial approximation approach using
ANN can generate polynomials with specified de-
grees. E.g., a user can generate a complete third-order
polynomial for sin(x), which yields a polynomial
−0.0931199x
3
− 0.001205849x
2
+
0.85615075x + 0.0009873845
in the interval [−π,π]. Meanwhile, a user may want
to optimize the above polynomial by eliminating the
coefficients for x
2
to reduce costly multiplications in
FHE, which yields the following:
−0.09340597x
3
+ 0.8596622x + 0.0005142888.
For completeness, we present the coefficients for
various configurations in Table 4 and compare loss
functions of optimized ANN approximation of de-
gree {1,3} relative to third-order Taylor approxima-
tion (centered around 0) in Table 5 and Chebyshev
polynomials in Table 6. Due to the probabilistic na-
ture of the ANN approximation, we may obtain dif-
ferent polynomials each time the algorithm is run,
and the optimal polynomial must be found empiri-
cally. For example, we show different polynomial
Table 5: sin(x) approximation loss of ANN
{1,3}
relative to
Taylor
{1,2,3}
in the interval [−π,π].
MAE MSLE Huber Hinge LCH
0.1621 0.0138 0.0124 0.7781 0.0141
SECRYPT 2024 - 21st International Conference on Security and Cryptography
636

Table 6: sin(x) approximation loss of ANN
{1,3}
relative to
Chebyshev
{1,2,3}
in the interval [−π,π].
MAE MSLE Huber Hinge LCH
0.8562 0.6984 0.5855 1.0617 0.5864
coefficients for different runs for sin(x) approxima-
tion in Table 2 and their respective approximation
losses in Table 3. For example, an ANN polynomial
−0.09331141∗x
3
−0.0013710269∗x
2
+0.8583066∗
x − 0.0015985817 had MAE of 0.05810 and Log-
cosh of 0.00222 while another ANN polynomial
−0.09320046∗x
3
+0.0008205741∗x
2
+0.8523298∗
x + 0.0043750536 recorded MAE of 0.05776 and
Logcosh error of 0.00224 in the interval [−π,π].
3 RELATED WORK
Much research has considered comparison-related op-
erations in FHE schemes, most based on the bit-wise
encryption approach.
3.1 Bit-Wise FHE
(Chillotti et al., 2017) calculate the maximum of two
numbers, of which each bit is encrypted into a par-
ticular ciphertext by a bit-wise HE scheme (Chillotti
et al., 2017; Chillotti et al., 2016). Other works
(Cheon et al., 2015; Crawford et al., 2018; Kocabas
and Soyata, 2015; Togan and Ples¸ca, 2014) imple-
mented a Boolean function corresponding to the com-
parison operation, where input numbers are still en-
crypted bit-wise. (Cheon et al., 2015) calculate a
comparison operation over two 10-bit integers using
the plaintext space Z
2
14
.
Recent work of (Crawford et al., 2018) computes
a comparison result of 8-bit integers. The amortized
running time becomes just a few milliseconds since
the comparison operation can be simultaneously done
in plaintext slots. These bit-wise encryption methods
show good amortized performance on comparison op-
erations. However, polynomial operations could be
more efficient than word-wise encryption methods,
including adding and multiplying large numbers.
3.2 Word-wise FHE
(Boura et al., 2018) compute min /max (absolute)
and compare (sign) over word-wise encrypted num-
bers by approximating the functions via Fourier se-
ries over a target interval. Since the Fourier series is a
periodic function, the approximate function does not
diverge to ∞ outside the interval, while approximate
polynomials obtained by polynomial approximation
methods diverge.
The homomorphic evaluation of the sign function
over word-wise encrypted inputs is also described
in (Bourse et al., 2018); they utilize the bootstrap-
ping technique of (Chillotti et al., 2016) to homo-
morphically extract the sign value of the input num-
ber and bootstrap the corresponding ciphertext at the
same time. Similar to our method, (Chialva and
Dooms, 2018) approximate the sign function over
x ∈ [−0.25, 0.25] by a hyperbolic tangent function
tanh(kx) =
e
kx
−e
−kx
e
kx
+e
−kx
for sufficiently large k > 0.
To efficiently compute tanh(kx), they first approx-
imate tanh(x) to x and then repeatedly apply the
double-angle formula tanh(2x) =
2tanh(x)
1+tanh
2
(x)
where the
inverse operation was substituted by a low-degree
(e.g., 1
st
or 3
rd
-order) minimax approximation poly-
nomial. (Xiao et al., 2019) substitute sign (Equation
2) with parameterized sigmoid.
Sign(s − x) =
(
1 i f s >= x
0 otherwise
(2)
They approximate σ(x; k) with k = 128 by
Chebyshev polynomials of degree = 24.
(Cheon et al., 2019a) approximated
Compare(a,b) =
a
k
a
k
+b
k
and set k = 64. In their
following work, (Cheon et al., 2020) approximated
Sign(x) = {−1,0,1} with two families f
d
n
(Equation
3) and g
d
n
(Algorithm 3) of composite polynomials.
f
n
(x) =
n
∑
i=0
1
4
i
·

2i
i

· x(1 − x
2
)
i
(3)
Data: n ≥ 1, 0 < τ < 1
Result: A polynomial g
n,τ
of order (2n + 1)
g
n,τ
← x;
repeat
δ
0
← minimal δ s.t. g
n,τ
([δ,1]) ⊆
[1 − τ,1];
g
min
← minimax polynomial of (2n +
1) order (1 −
τ
2
) ·
sgn(x) over [−1,−δ
0
] ∪ [δ
0
,1];
g
n,τ
← g
min
;
S ← ||g
n,τ
− (1 −
τ
2
)||
∞,[δ
0
,1]
;
until S ==
τ
2
;
return g
n,τ
Algorithm 3: FindG(n,τ).
(Lee et al., 2021) proposed a novel multi-interval
Remez composite polynomial algorithm with a hy-
perparameter α to control the interval to get close
chiku: Efficient Probabilistic Polynomial Approximations Library
637

Figure 3: Compare(x) approximation in the intervals
[−1,1] (left) and [−5,5] (right).
to 0. They propose to use composite polynomi-
als of varying degrees based on the required multi-
plicative depth of the FHE arithmetic circuit. Their
paper proposes using polynomials of degrees 9, 9,
and 9. In their other work (Lee et al., 2022), they
use iterative polynomials of degrees 7, 15, and 27.
(Kim and Guyot, 2023) approximated Sign(x) with
f 3( f 2( f 1(x))) multi-interval Remez composite poly-
nomial from (Lee et al., 2021) as
f 1(x) = 10.8541842577442x −
62.2833925211098x
3
+ 114.369227820443x
5
−
62.8023496973074x
7
f 2(x) = 4.13976170985111x −
5.84997640211679x
3
+ 2.94376255659280x
5
−
0.454530437460152x
7
f 3(x) = 3.29956739043733x −
7.84227260291355x
3
+ 12.8907764115564x
5
−
12.4917112584486x
7
+ 6.94167991428074x
9
−
2.04298067399942x
11
+ 0.246407138926031x
13
This work does not compare polynomial approxi-
mation to iterative approaches like a composite poly-
nomial since they require more calculations. In FHE,
computing multiplications takes more time and adds
more noise than additions. Thus, we wish to minimize
the multiplicative operations.
Instead, we compare the efficiency of our ANN-
based approach to Chebyshev polynomials of the
same order, which require the same number of mul-
tiplications. For, the polynomials in Equation 4 and
Equation 8 both require four multiplications each, two
multiplications to calculate x
3
and another two for co-
efficient multiplications for x and x
3
each.
4 EXPERIMENTAL RESULTS
We present Chebyshev polynomials of degree ∈ {3,7}
for the Sign(x) function in [−1, 1] and [−5,5].
c
3
1
(x) = −2.16478x
3
+ 2.93015x (4)
c
3
5
(x) = −0.0173183x
3
+ 0.58603x (5)
c
7
1
(x) = −16.3135x
7
+ 33.3593x
5
− 22.0877x
3
+ 5.91907x
(6)
c
7
5
(x) = −0.000208812x
7
+ 0.010675x
5
−0.176701x
3
+ 1.18381x (7)
We further approximate third and seventh-order
polynomials for the Sign(x) function with the pro-
posed ANN method in [−1,1] and [−5,5].
a
3
1
(x) = −2.183534x
3
+ 2.816129x − 0.017685238
(8)
a
3
5
(x) = −0.017504148x
3
+ 0.5667412x + 0.000051538
(9)
a
7
1
(x) = −15.559336x
7
+ 30.594683x
5
−19.622007x
3
+ 5.366039x − 0.004171798 (10)
a
7
5
(x) = −0.00018785524x
7
+ 0.009339935x
5
−0.15198348x
3
+ 1.0683376x − 0.0025376866
(11)
We calculate Chebyshev polynomials for the
Compare(x) function of degree = {3,7} for the in-
tervals [−1,1] and [−5, 5].
c
3
1
(x) = −1.08239x
3
+ 1.46508x + 0.5 (12)
c
3
5
(x) = −0.00865914x
3
+ 0.293015x + 0.5 (13)
c
7
1
(x) = −8.15673x
7
+ 16.6797x
5
−11.0438x
3
+ 2.95953x + 0.5 (14)
c
7
5
(x) = −0.000104406x
7
+ 0.00533749x
5
−0.0883507x
3
+ 0.591907x + 0.5 (15)
We also generate ANN polynomials for the
Compare(x) function using our approach for
degree = {3,7} and the intervals [−1,1] and [−5,5].
a
3
1
(x) = −1.0963224x
3
+ 1.4150281x + 0.50884116
(16)
a
3
5
(x) = −0.008709235x
3
+ 0.28203508x + 0.50143045
(17)
a
7
1
(x) = −7.795442x
7
+ 15.27373x
5
−9.812823x
3
+ 2.6885476x + 0.5056917 (18)
a
7
5
(x) = −9.614773e − 05x
7
+ 0.0047283764x
5
−0.07679807x
3
+ 0.5358904x + 0.4984604 (19)
First, we compare Chebyshev and ANN approxi-
mations for the Sign function (Figure 4). As shown in
Table 11 and 12, we calculate MAE, MSLE, Huber,
Hinge, and Logcosh losses for Chebyshev polynomi-
als described in Equations 4, 5, 6, 7 and ANN polyno-
mials from 8, 9, 10, 11. To show the improvements of
our ANN approach over Chebyshev, we calculate the
loss ratios as shown in Figure 6.
The first two intervals of [−1,1] and [−5,5] cor-
respond to degree = 3 and the last two relates to
SECRYPT 2024 - 21st International Conference on Security and Cryptography
638

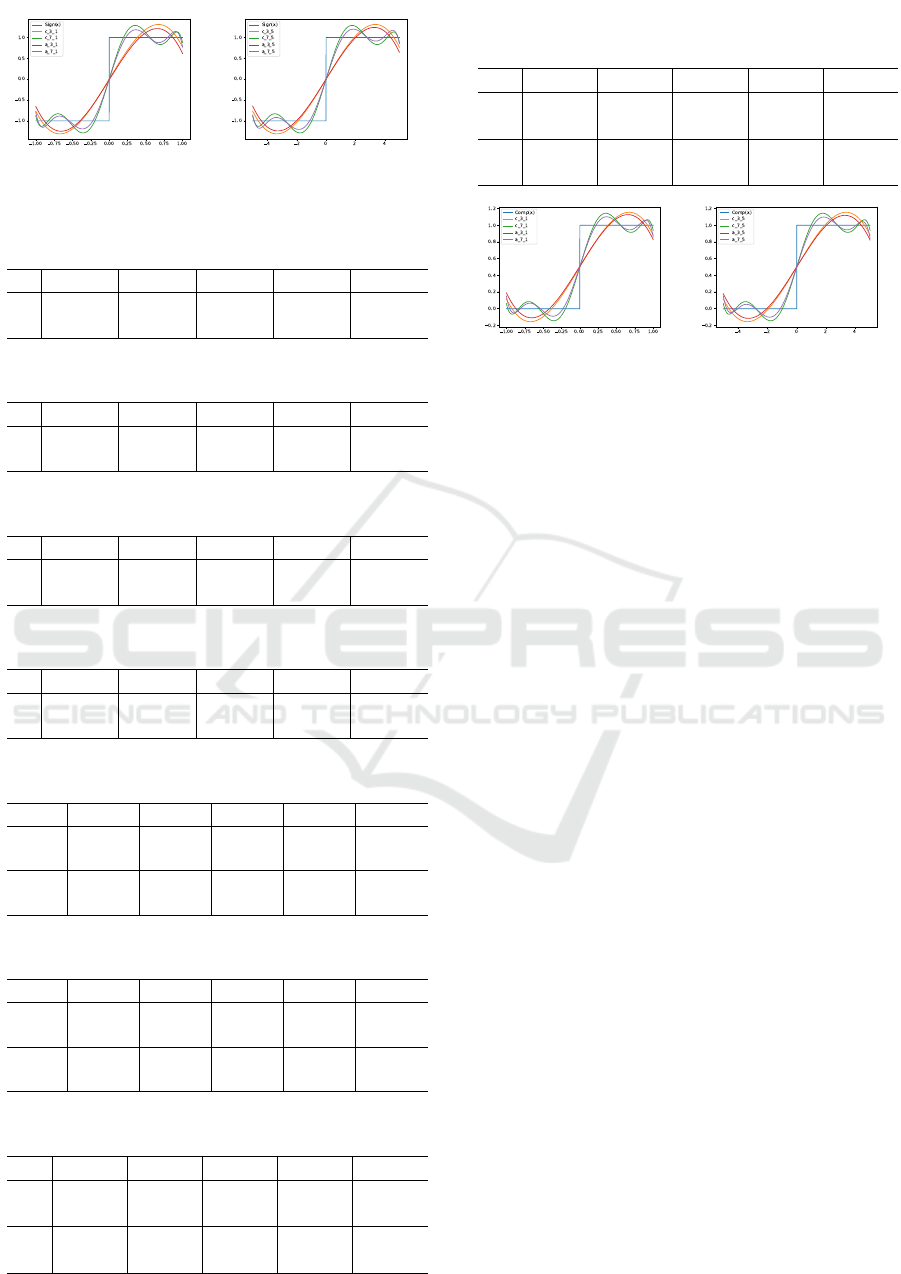
Figure 4: c
3
1
(x),c
7
1
(x),a
3
1
(x),a
7
1
(x) approximations for Sign
with degree ∈ {3,7} in [−1,1] (left) and [−5,5] (right).
Table 7: ANN losses relative to Chebyshev for Sign(x) func-
tion in the interval [−1,1].
d MAE MSLE Huber Hinge LCH
3 0.9382 1.0540 0.9629 1.1147 0.9583
7 0.8893 1.0172 0.9472 1.0178 0.9385
Table 8: ANN losses relative to Chebyshev for Sign(x) func-
tion in the interval [−5,5].
d MAE MSLE Huber Hinge LCH
3 0.9429 0.9968 0.9617 1.0980 0.9576
7 0.8969 1.0204 0.9618 0.9432 0.9536
Table 9: ANN losses relative to Chebyshev for Compare(x)
function in the interval [−1,1].
d MAE MSLE Huber Hinge LCH
3 0.9421 1.0698 0.9633 1.0376 0.9621
7 0.8834 1.0657 0.9466 1.0205 0.9442
Table 10: ANN losses relative to Chebyshev for Compare(x)
function in the interval [−5,5].
d MAE MSLE Huber Hinge LCH
3 0.9393 1.0487 0.9612 1.0350 0.9600
7 0.8757 1.0376 0.9490 1.0152 0.9466
Table 11: Chebyshev and ANN approximation losses for
Sign(x) function in the interval [−1,1].
F
d
i
MAE MSLE Huber Hinge LCH
c
3
1
(x) 0.3003 0.0266 0.0732 0.1882 0.0681
c
7
1
(x) 0.2011 0.0140 0.0396 0.1214 0.0371
a
3
1
(x) 0.2817 0.0280 0.0705 0.2098 0.0653
a
7
1
(x) 0.1788 0.0143 0.0375 0.1236 0.0348
Table 12: Chebyshev and ANN approximation losses for
Sign(x) function in the interval [−5,5].
F
d
i
MAE MSLE Huber Hinge LCH
c
3
5
(x) 0.3003 0.0266 0.0732 0.1882 0.0681
c
7
5
(x) 0.2011 0.0140 0.0396 0.1214 0.0371
a
3
5
(x) 0.2831 0.0265 0.0704 0.2067 0.0653
a
7
5
(x) 0.1804 0.0143 0.0381 0.1145 0.0353
Table 13: Chebyshev and ANN approximation losses for
Compare(x) function in the interval [−1,1].
F
d
i
MAE MSLE Huber Hinge LCH
c
3
1
0.1501 0.0162 0.0183 0.5661 0.0179
c
7
1
0.1006 0.0087 0.0099 0.5408 0.0097
a
3
1
0.1414 0.0173 0.0176 0.5874 0.0173
a
7
1
0.0888 0.0092 0.0094 0.5519 0.0092
Table 14: Chebyshev and ANN approximation losses for
Compare(x) function in the interval [−5,5].
F
d
i
MAE MSLE Huber Hinge LCH
c
3
5
0.1501 0.0162 0.0183 0.5661 0.0179
c
7
5
0.1006 0.0087 0.0099 0.5408 0.0097
a
3
5
0.1410 0.0169 0.0176 0.5859 0.0172
a
7
5
0.0881 0.0090 0.0094 0.5490 0.0092
Figure 5: c
3
1
(x),c
7
1
(x),a
3
1
(x),a
7
1
(x) approximations for
Compare with degree ∈ {3, 7} in the intervals [−1,1] (left)
and [−5,5] (right).
degree = 7. We perform better in most cases, exclud-
ing the Hinge losses. E.g., for degree = 3 and inter-
val [−1,1] we achieve a ratio of 0.9382 for MAE and
1.1147 for Hinge loss.
Similarly, we compare Chebyshev and ANN ap-
proximations for the Compare function (Figure 5).
As shown in Table 13 and 14, we calculate losses for
Chebyshev polynomials described in Equations 12,
13, 14, 15 and ANN polynomials from 16, 17, 18, 19.
We further calculate the loss ratios as shown in Figure
6. E.g., for degree = 7 and interval [−5, 5] we achieve
a ratio of MAE = 0.8757 and Hinge = 1.0152.
As shown in Tables 7,8,9,10, we perform better
for MAE, Huber, and Logcosh losses where our loss
ratio is < 1 compared to Chebyshev and is > 1 for
MSLE and Hinge losses. We justify this by follow-
ing observations. For regression tasks such as this, it
is better to use a convex loss function such as MAE,
as they are more robust to outliers and will be able to
predict the target values more accurately. Hinge loss
is a non-convex function often used for classification
tasks. It is not a good choice for regression tasks be-
cause it is not robust to outliers.
The MAE is less sensitive to errors in the low
range than the MSLE. The absolute difference be-
tween the predicted and target values is near zero
when the predicted values are near zero. This means
that even a tiny error in the predicted value will not
lead to a significant error in the MAE. The σ(x) func-
tion and the tanhx function are convex functions. The
convexity of these functions is essential for the train-
ing of ANN because gradient descent is guaranteed
to converge to the global minimum of a convex func-
tion. If the loss function is convex, gradient descent
will always find the best parameters.
chiku: Efficient Probabilistic Polynomial Approximations Library
639

3 3 7 7
0.0000
0.2500
0.5000
0.7500
1.0000
1.2500
[-1, 1] [-5, 5] [-1, 1] [-5, 5]
MAE MSLE Huber Hinge Logcosh
3 3 7 7
0.0000
0.2500
0.5000
0.7500
1.0000
1.2500
[-1, 1] [-5, 5] [-1, 1] [-5, 5]
MAE MSLE Huber Hinge Logcosh
Figure 6: ANN loss relative to Chebyshev for Sign(x) (left)
and Compare(x) (right) with degree ∈ {3,7} in the intervals
[−1,1] and [−5,5].
5 CONCLUSION
We present a probabilistic polynomial approximation
approach based on Artificial Neural Networks (ANN)
and make it publicly available for the community as
a Python package. Writing C extensions can improve
the current library’s performance. We also wish to in-
corporate other interpolation techniques, such as La-
grange and Power series, in the future.
We empirically showed that ANN polynomials
outperformed Chebyshev polynomials of the same or-
der regarding estimation errors. However, comparing
our polynomials with composite (iterative) and multi-
variate polynomials would make an interesting study.
REFERENCES
Angel, S., Chen, H., Laine, K., and Setty, S. (2018). Pir
with compressed queries and amortized query pro-
cessing. In 2018 IEEE symposium on security and
privacy (SP), pages 962–979. IEEE.
Baker, G. A., Baker Jr, G. A., Graves-Morris, P., and Baker,
S. S. (1996). Pade Approximants: Encyclopedia of
Mathematics and It’s Applications, Vol. 59 George A.
Baker, Jr., Peter Graves-Morris, volume 59. Cam-
bridge University Press, Cambridge.
Bos, J. W., Castryck, W., Iliashenko, I., and Vercauteren,
F. (2017). Privacy-friendly forecasting for the smart
grid using homomorphic encryption and the group
method of data handling. In Progress in Cryptology-
AFRICACRYPT 2017: 9th International Conference
on Cryptology in Africa, Dakar, Senegal, May 24-26,
2017, Proceedings, pages 184–201. Springer.
Boura, C., Gama, N., and Georgieva, M. (2018). Chimera: a
unified framework for b/fv, tfhe and heaan fully homo-
morphic encryption and predictions for deep learning.
IACR Cryptol. ePrint Arch., 2018:758.
Bourse, F., Minelli, M., Minihold, M., and Paillier, P.
(2018). Fast homomorphic evaluation of deep dis-
cretized neural networks. In Advances in Cryptology–
CRYPTO 2018: 38th Annual International Cryptol-
ogy Conference, Santa Barbara, CA, USA, August 19–
23, 2018, Proceedings, Part III 38, pages 483–512.
Springer.
Brakerski, Z., Gentry, C., and Vaikuntanathan, V. (2014).
(leveled) fully homomorphic encryption without boot-
strapping. ACM Transactions on Computation Theory
(TOCT), 6(3):1–36.
Cheon, J. H., Kim, A., Kim, M., and Song, Y. (2017). Ho-
momorphic encryption for arithmetic of approximate
numbers. In Advances in Cryptology–ASIACRYPT
2017: 23rd International Conference on the Theory
and Applications of Cryptology and Information Se-
curity, Hong Kong, China, December 3-7, 2017, Pro-
ceedings, Part I 23, pages 409–437. Springer.
Cheon, J. H., Kim, D., and Kim, D. (2020). Efficient homo-
morphic comparison methods with optimal complex-
ity. In Advances in Cryptology–ASIACRYPT 2020:
26th International Conference on the Theory and
Application of Cryptology and Information Security,
Daejeon, South Korea, December 7–11, 2020, Pro-
ceedings, Part II 26, pages 221–256. Springer.
Cheon, J. H., Kim, D., Kim, D., Lee, H. H., and Lee,
K. (2019a). Numerical method for comparison on
homomorphically encrypted numbers. In Advances
in Cryptology–ASIACRYPT 2019: 25th International
Conference on the Theory and Application of Cryptol-
ogy and Information Security, Kobe, Japan, Decem-
ber 8–12, 2019, Proceedings, Part II, pages 415–445.
Springer.
Cheon, J. H., Kim, D., and Park, J. H. (2019b). Towards
a practical clustering analysis over encrypted data.
IACR Cryptol. ePrint Arch., 2019:465.
Cheon, J. H., Kim, M., and Kim, M. (2015). Search-and-
compute on encrypted data. In Financial Cryptogra-
phy and Data Security: FC 2015 International Work-
shops, BITCOIN, WAHC, and Wearable, San Juan,
Puerto Rico, January 30, 2015, Revised Selected Pa-
pers, pages 142–159. Springer.
Chialva, D. and Dooms, A. (2018). Conditionals in ho-
momorphic encryption and machine learning applica-
tions. arXiv preprint arXiv:1810.12380.
Chillotti, I., Gama, N., Georgieva, M., and Izabachene,
M. (2016). Faster fully homomorphic encryption:
Bootstrapping in less than 0.1 seconds. In Advances
in Cryptology–ASIACRYPT 2016: 22nd International
Conference on the Theory and Application of Cryp-
tology and Information Security, Hanoi, Vietnam, De-
cember 4-8, 2016, Proceedings, Part I 22, pages 3–33.
Springer.
Chillotti, I., Gama, N., Georgieva, M., and Izabach
`
ene, M.
(2017). Faster packed homomorphic operations and
efficient circuit bootstrapping for tfhe. In Advances
in Cryptology–ASIACRYPT 2017: 23rd International
Conference on the Theory and Applications of Cryp-
tology and Information Security, Hong Kong, China,
December 3-7, 2017, Proceedings, Part I, pages 377–
408. Springer.
Chillotti, I., Gama, N., Georgieva, M., and Izabach
`
ene, M.
(2020). Tfhe: fast fully homomorphic encryption over
the torus. Journal of Cryptology, 33(1):34–91.
Crawford, J. L., Gentry, C., Halevi, S., Platt, D., and Shoup,
V. (2018). Doing real work with fhe: the case of
logistic regression. In Proceedings of the 6th Work-
shop on Encrypted Computing & Applied Homomor-
phic Cryptography, pages 1–12.
SECRYPT 2024 - 21st International Conference on Security and Cryptography
640

Dathathri, R., Saarikivi, O., Chen, H., Laine, K., Lauter, K.,
Maleki, S., Musuvathi, M., and Mytkowicz, T. (2019).
Chet: an optimizing compiler for fully-homomorphic
neural-network inferencing. In Proceedings of the
40th ACM SIGPLAN Conference on Programming
Language Design and Implementation, pages 142–
156.
Ducas, L. and Micciancio, D. (2015). Fhew: bootstrap-
ping homomorphic encryption in less than a second.
In Advances in Cryptology–EUROCRYPT 2015: 34th
Annual International Conference on the Theory and
Applications of Cryptographic Techniques, Sofia, Bul-
garia, April 26-30, 2015, Proceedings, Part I 34,
pages 617–640. Springer.
Fan, J. and Vercauteren, F. (2012). Somewhat practical fully
homomorphic encryption. Cryptology ePrint Archive.
Gentry, C. (2009). Fully homomorphic encryption using
ideal lattices. In Proceedings of the forty-first annual
ACM symposium on Theory of computing, pages 169–
178.
Gentry, C., Sahai, A., and Waters, B. (2013). Homomorphic
encryption from learning with errors: Conceptually-
simpler, asymptotically-faster, attribute-based. In Ad-
vances in Cryptology–CRYPTO 2013: 33rd Annual
Cryptology Conference, Santa Barbara, CA, USA, Au-
gust 18-22, 2013. Proceedings, Part I, pages 75–92.
Springer.
George, A. (1985). Mathematical methods for physicists.
Academic press, Cambridge.
Gilad-Bachrach, R., Dowlin, N., Laine, K., Lauter, K.,
Naehrig, M., and Wernsing, J. (2016). Cryptonets:
Applying neural networks to encrypted data with high
throughput and accuracy. In International conference
on machine learning, pages 201–210. PMLR.
Harris, C. R., Millman, K. J., van der Walt, S. J., Gom-
mers, R., Virtanen, P., Cournapeau, D., Wieser, E.,
Taylor, J., Berg, S., Smith, N. J., Kern, R., Picus,
M., Hoyer, S., van Kerkwijk, M. H., Brett, M., Hal-
dane, A., Fern
´
andez del R
´
ıo, J., Wiebe, M., Peter-
son, P., G
´
erard-Marchant, P., Sheppard, K., Reddy, T.,
Weckesser, W., Abbasi, H., Gohlke, C., and Oliphant,
T. E. (2020). Array programming with NumPy. Na-
ture, 585:357–362.
Kim, D. and Guyot, C. (2023). Optimized privacy-
preserving cnn inference with fully homomorphic en-
cryption. IEEE Transactions on Information Forensics
and Security, 18:2175–2187.
Kim, M. and Lauter, K. (2015). Private genome analysis
through homomorphic encryption. In BMC medical
informatics and decision making, volume 15, pages
1–12. BioMed Central.
Kim, M., Song, Y., Wang, S., Xia, Y., Jiang, X., et al.
(2018). Secure logistic regression based on homomor-
phic encryption: Design and evaluation. JMIR medi-
cal informatics, 6(2):e8805.
Kocabas, O. and Soyata, T. (2015). Utilizing homomor-
phic encryption to implement secure and private med-
ical cloud computing. In 2015 IEEE 8th Interna-
tional Conference on Cloud Computing, pages 540–
547. IEEE.
Lee, E., Lee, J.-W., No, J.-S., and Kim, Y.-S. (2021).
Minimax approximation of sign function by compos-
ite polynomial for homomorphic comparison. IEEE
Transactions on Dependable and Secure Computing,
19(6):3711–3727.
Lee, J.-W., Kang, H., Lee, Y., Choi, W., Eom, J., Deryabin,
M., Lee, E., Lee, J., Yoo, D., Kim, Y.-S., et al. (2022).
Privacy-preserving machine learning with fully homo-
morphic encryption for deep neural network. IEEE
Access, 10:30039–30054.
mpmath development team, T. (2023). mpmath: a Python li-
brary for arbitrary-precision floating-point arithmetic
(version 1.3.0).
Press, W. H., Vetterling, W. T., Teukolsky, S. A., and
Flannery, B. P. (1992). Numerical Recipes Example
Book (FORTRAN). Cambridge University Press Cam-
bridge, Cambridge.
Remez, E. Y. (1934). Sur le calcul effectif des polynomes
d’approximation de tschebyscheff. CR Acad. Sci.
Paris, 199(2):337–340.
Smart, N. P. and Vercauteren, F. (2014). Fully homomor-
phic simd operations. Designs, codes and cryptogra-
phy, 71:57–81.
Togan, M. and Ples¸ca, C. (2014). Comparison-based com-
putations over fully homomorphic encrypted data. In
2014 10th international conference on communica-
tions (COMM), pages 1–6. IEEE.
Trivedi, D. (2023a). Brief announcement: Efficient proba-
bilistic approximations for sign and compare. In Inter-
national Symposium on Stabilizing, Safety, and Secu-
rity of Distributed Systems, pages 289–296. Springer.
Trivedi, D. (2023b). GitHub - devharsh/chiku: Polynomial
function approximation library in Python.
Trivedi, D., Boudguiga, A., Kaaniche, N., and Triandopou-
los, N. (2023). Sigml++: Supervised log anomaly
with probabilistic polynomial approximation. Cryp-
tography, 7(4):52.
Virtanen, P., Gommers, R., Oliphant, T. E., Haberland, M.,
Reddy, T., Cournapeau, D., Burovski, E., Peterson, P.,
Weckesser, W., Bright, J., van der Walt, S. J., Brett,
M., Wilson, J., Millman, K. J., Mayorov, N., Nel-
son, A. R. J., Jones, E., Kern, R., Larson, E., Carey,
C. J., Polat,
˙
I., Feng, Y., Moore, E. W., VanderPlas,
J., Laxalde, D., Perktold, J., Cimrman, R., Henriksen,
I., Quintero, E. A., Harris, C. R., Archibald, A. M.,
Ribeiro, A. H., Pedregosa, F., van Mulbregt, P., and
SciPy 1.0 Contributors (2020). SciPy 1.0: Fundamen-
tal Algorithms for Scientific Computing in Python.
Nature Methods, 17:261–272.
Xiao, X., Wu, T., Chen, Y., and Fan, X. (2019). Privacy-
preserved approximate classification based on homo-
morphic encryption. Mathematical and Computa-
tional Applications, 24(4):92.
chiku: Efficient Probabilistic Polynomial Approximations Library
641