Security Analysis for BB84 Key Distillation

Sara Nikula

1 a

, Anssi Lintulampi

1 b

and Kimmo Halunen

2 c

VTT Technical Research Center of Finland, Oulu, Finland

University of Oulu, Oulu, Finland

ﬁ ﬁ ﬁ

Keywords:

Quantum Key Distribution, BB84, Classical Post-processing, Key Distillation, Security Analysis.

Abstract:

Key distillation, also referred to as classical post-processing, plays a pivotal role in Quantum Key Distribution

(QKD) protocols. Key distillation encompasses numerous subroutines, making the analysis of its overall

security implications potentially challenging for those outside the research community. In this paper, we

elucidate the role of the key distillation phase in QKD from a security standpoint. We begin by analyzing the

different components of the key distillation phase individually, followed by an examination of the process as

a whole. We then calculate the bit strength of the produced key, assuming that an attacker is executing an

intercept and resend attack. For our analysis, we employ a practical key distillation implementation linked to

a decoy state BB84 protocol as a case study. Our ﬁndings suggest that the security of the ﬁnal key, post the

key distillation phase, hinges on several factors. These include the theoretical security of the implemented

subroutines, the total information leakage throughout the process, and the choices of subroutine parameters.

Given these assumptions, we can distill 287 secure bits for every 1000 bits that undergo the key distillation

procedure.

1 INTRODUCTION

To facilitate conﬁdential communication between two

parties, an encryption key is required. Traditionally,

this encryption key is agreed upon using asymmet-

ric public-key cryptographic protocols, such as RSA

(Moriarty et al., 2016) or elliptic curves (Nir et al.,

2018). However, these algorithms are vulnerable to

the algorithm presented by Shor (1994), which can

be executed on a cryptographically relevant quantum

computer. This implies that future key agreement pro-

tocols will need to be updated to be resistant to quan-

tum computing.

One solution to this issue is quantum-safe pub-

lic key cryptography (also known as post-quantum

cryptography, PQC), which is based on mathemati-

cal problems that are not easily solvable even with

quantum computing. Another quantum-safe method

for establishing secret encryption keys between two

parties is Quantum Key Distribution (QKD). The pri-

mary advantage of QKD over classical post-quantum

key agreement schemes is that the security of QKD is

grounded in the laws of quantum physics, rather than

https://orcid.org/0000-0002-2299-8030

https://orcid.org/0009-0002-7361-054X

https://orcid.org/0000-0003-1169-5920

on the assumption that certain mathematical problems

are computationally difﬁcult to solve. The ﬁrst QKD

protocol, BB84, was introduced in 1984 by Bennett

and Brassard (2014). The security of the BB84 proto-

col is based on encoding bit information in the polar-

ization of a single photon, with a randomly selected

basis. Measuring the photon will destroy its original

state, ensuring that any potential eavesdropping will

be detected as an increased error rate.

Therefore, in theory, QKD should provide uncon-

ditionally secure encryption keys, as it cannot be com-

promised by any computational algorithms, whether

classical or quantum. However, in practice, the situ-

ation is more complex due to imperfect implementa-

tions and the necessity for the classical key distillation

phase.

The BB84 protocol is composed of two distinct

phases: the quantum phase and the classical phase.

The quantum phase alone is insufﬁcient for the deriva-

tion of an encryption key. To ensure the encryption

key is both secure and error-free, a key distillation

procedure must be executed over the classical chan-

nel. The classical key distillation process encom-

passes the following sub-procedures: authentication,

bit error estimation, error correction, and privacy am-

pliﬁcation. These procedures collectively ensure the

Nikula, S., Lintulampi, A. and Halunen, K.

Security Analysis for BB84 Key Distillation.

DOI: 10.5220/0012717500003767

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 21st International Conference on Security and Cryptography (SECRYPT 2024), pages 407-415

ISBN: 978-989-758-709-2; ISSN: 2184-7711

407

integrity and security of the encryption key.

In this paper, we present a comprehensive anal-

ysis of the key distillation implementation of the

BB84 protocol from an information security perspec-

tive. Several publications already exist that focus on

speciﬁc aspects of the key distillation process. For

instance, the works of Dupuis (2023), Shen et al.

(2023), and Li et al. (2023) emphasize privacy am-

pliﬁcation, while Lizama-Perez (2023) concentrates

on error correction. The general vulnerabilities of

practical quantum channel implementations have also

been explored, as evidenced by the studies of Sun and

Huang (2022) and Reutov et al. (2023). However,

there is a noticeable lack of comprehensive security

analyses of QKD key distillation implementations in

the existing literature.

This paper addresses the considerations that must

be taken into account when integrating theoretically

secure subroutines of the classical key distillation

phase into a QKD system. We propose a model for

estimating the robustness of the key distillation phase,

factoring in the imperfect realization of a quantum

channel. We believe this contribution provides valu-

able insights that bridge the knowledge gap between

the scientiﬁc community and technology providers,

thereby enhancing the practical implementation of

QKD systems.

The primary contributions of our paper are

twofold. First, we provide a straightforward exam-

ple model for estimating the security of a complete

BB84 key distillation procedure. Second, we present

an analysis of how the various components of this pro-

cess inﬂuence the security of the ﬁnal distilled key.

These insights offer a comprehensive understanding

of the key distillation process and its impact on the

overall security of QKD systems.

The organization of the paper is as follows. In

Section 2, we distinguish among the various security

aspects of classical post-processing and make refer-

ences to established QKD standards and tools. Sec-

tion 3 is dedicated to presenting our ﬁndings. Here,

we allocate speciﬁc subsections to detail each key dis-

tillation subroutine, culminating in a comprehensive

security analysis. The implications of our analysis

and the practicality of our proposed methodology are

deliberated in Section 4. Finally, Section 5 encapsu-

lates our conclusions drawn from the research.

2 METHODOLOGY

In this section, we introduce the prevailing standards

and tools associated with QKD protocols and provide

a synopsis of the BB84 key distillation process. Sub-

sequently, we highlight crucial security perspectives

pertinent to key distillation.

The recently introduced ISO/IEC (2023) standard

on QKD delineates security requirements for both the

quantum and classical phases of QKD, taking into

consideration various types of threats. The Interna-

tional Telecommunication Union (ITU) has also is-

sued recommendations concerning various aspects of

QKD, such as the resilience of QKD networks (ITU,

2023) and key management (ITU, 2020). Further-

more, the European Telecommunications Standards

Institute (ETSI) hosts a working group dedicated to

QKD (ETSI, 2024b), which is actively preparing doc-

uments on various aspects of QKD, including the se-

curity of implementation (ETSI, 2024a).

2.1 General Overview of BB84 Key

Distillation

In the process of key distillation, the classical channel

is not intended to be encrypted. However, it requires

authentication to conﬁrm that the key is being shared

with the correct party. The initial step, known as sift-

ing, involves selecting only those photons that were

prepared and measured in the same basis. As a result,

the outcome of the measurement should be determin-

istic (Bennett and Brassard, 2014). Nonetheless, the

sifted bit string is typically not perfect due to channel

imperfections causing some bits to ﬂip. To estimate

the error rate, a subset of the sifted key bits is revealed

and compared with the corresponding bit sequence of

the other party.

Error correction is a process that eliminates bit er-

rors induced by channel noise. During the error cor-

rection phase, parity checks are transmitted over a

public channel. However, these checks inadvertently

disclose some information about the secret key. The

privacy ampliﬁcation step is designed to counteract

this leakage. It reduces the length of the key bit string

to its ﬁnal size.

2.2 Security Implications of Key

Distillation

The security of the key distillation phase is consid-

ered to stem from the protocol’s capacity to miti-

gate information leakage during the quantum phase,

as well as its ability to limit its own information leak-

age, thereby ensuring the output of secure key mate-

rial. Consequently, the combined imperfections of the

quantum protocol and classical post-processing algo-

rithms determine the theoretical security level of the

ﬁnal key.

SECRYPT 2024 - 21st International Conference on Security and Cryptography

408

The objective of the key distillation phase is to

generate a secret key from the information exchanged

during the quantum phase. Therefore, it is neces-

sary to establish certain security assumptions for the

quantum phase. This ensures that the key distilla-

tion process is sufﬁciently efﬁcient to counter poten-

tial threats, such as eavesdropping.

On the one hand, if our focus is solely on the prac-

tical software security of the key distillation phase,

we can be assured that the key distillation process it-

self will not introduce any new security threats. On

the other hand, we will lack information about the se-

curity level of the keys produced by the protocol, as

the security of the keys is dependent on the quantum

phase.

The overall security of the ﬁnal output from the

key distillation process hinges on the assumption that

the information leakage during both quantum and

classical protocols can be accurately quantiﬁed. The

key distillation protocol itself does not interact with

any quantum phenomena. However, if we aim for it

to produce practically secure keys, we must be cog-

nizant of potential limitations in the quantum phase.

For instance, key information can be obtained by tam-

pering with the phase or wavelength of the signal (Sun

et al., 2015; Li et al., 2011), through Trojan horse at-

tacks (Jain et al., 2014), blinding attacks (Weier et al.,

2011), photon number splitting attacks (Hong et al.,

2016), or by exploiting information about the timing

or duration of the signals (Huang et al., 2018; Sun

and Huang, 2022). Countermeasures that mitigate or

expose some of the attacks directed at the quantum

phase have been proposed, for example, by Huang

et al. (2018) and Yoshino et al. (2018).

In this paper, we focus solely on the intercept and

resend attack model as a potential threat emanating

from the quantum channel. This approach is justiﬁed,

as the intercept and resend attack model can be de-

tected or mitigated using key distillation subroutines.

Moreover, a comprehensive discussion of all possible

threat types falls outside the scope of this paper.

An intercept and resend attack involves an eaves-

dropper capturing each individual photon, measuring

it, and then retransmitting it to the intended receiver.

This type of attack can provide the eavesdropper with

substantial information about the secret key, but it also

introduces errors into the resulting key bit string. By

calculating the probability of this attack, we derive

a parameter that represents the likely number of bits

eavesdropped during the quantum phase.

In more complex cases, this parameter could be a

combination of effects of several attack types, cover-

ing all possible leaked bits during the quantum phase.

Each subprocess involved in the key distillation

phase inﬂuences the security level of the protocol’s

ﬁnal output. Therefore, it is crucial to ensure that the

ﬁnal output meets our criteria for a secure encryption

key. This implies that merely proving the security of

the individual subprocesses is insufﬁcient. Instead,

we need to have a comprehensive understanding of

the entire process.

3 RESULTS

In this section, we scrutinize our key distillation im-

plementation using the security aspects outlined in the

previous section. Each step of the key distillation

phase is examined individually: we ﬁrst present the

implementation of the speciﬁc subprocess, followed

by an analysis of its security.

The key distillation software we implemented re-

ceives a bit-sifted noisy key from the quantum layer

and executes steps that result in a distilled secure en-

cryption key. Figure 1 provides an overview of the

classical key distillation steps. It is important to note

that while the messages on the classical channel are

authenticated, they are not encrypted.

The key distillation software that has been imple-

mented is connected to the control interface, the key

management interface, and the quantum channel in-

terface. The control interface signals when a new key

exchange process is about to be initiated. The quan-

tum channel transmits the bit-sifted raw key to the key

distillation software, and the ﬁnal product, a distilled

secure encryption key, is then forwarded to the key

management interface.

3.1 The Quantum Channel

Our QKD system implements the discrete-variable

BB84 protocol (Bennett and Brassard, 2014) with

phase modulation and decoy states. The photons are

transmitted from the preparation device to the mea-

surement device via an optical ﬁber.

The error rate of the implemented quantum chan-

nel is approximately 10% caused by the optical trans-

mitters and receivers. This value is obtained via em-

pirical tests on our quantum channel.

At both ends of the quantum channel, a laptop is

connected to either the preparation device or the mea-

surement device. The Alice side manages the prepa-

ration, while the Bob side handles the measurements.

Once the quantum phase is complete, the laptops re-

ceive the raw bit strings from their respective quantum

interfaces.

In our setup, the bit-sifting process is executed di-

rectly on the laptops that control the quantum proto-

Security Analysis for BB84 Key Distillation

409

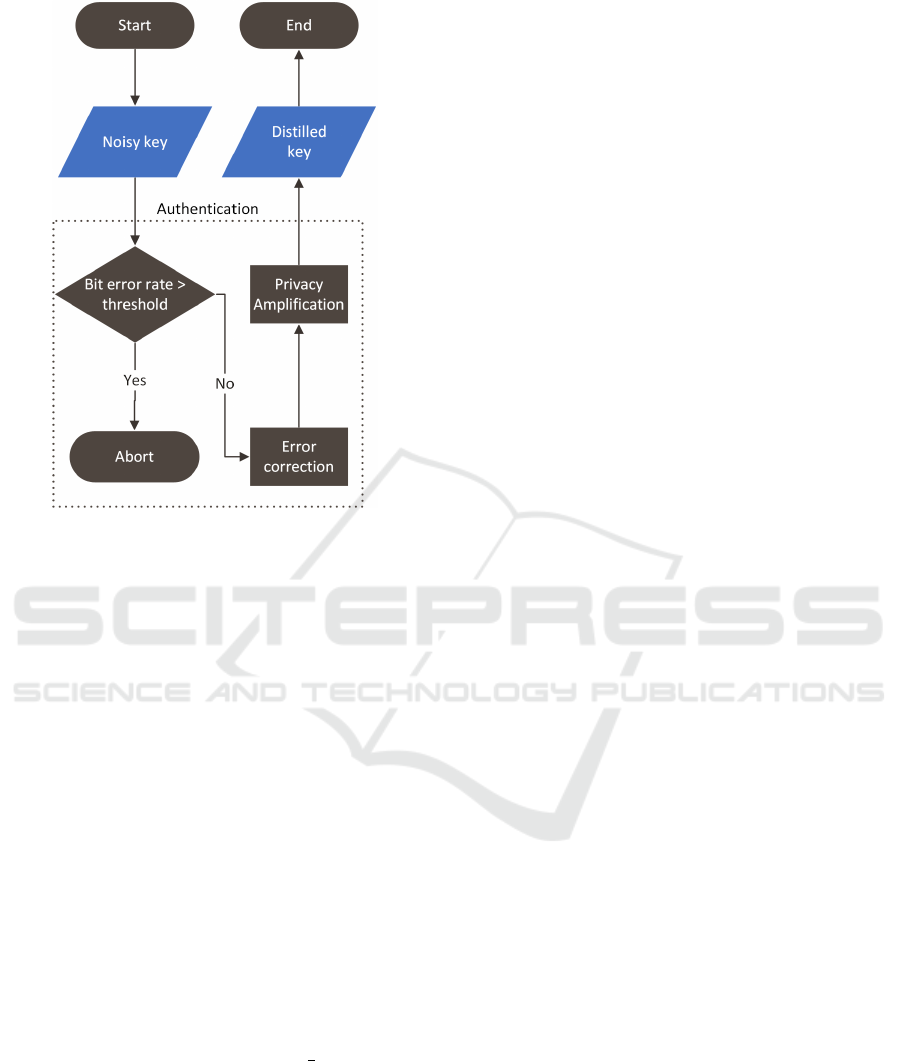
Figure 1: The diagram illustrates the steps involved in the

key distillation software. The process commences when the

noisy key is received from the quantum channel.

col. Consequently, the input received by our key dis-

tillation software is the bit-sifted raw key. Given that

the basis choices of Alice and Bob are public, we ex-

clude the bit-sifting phase from our security analysis.

Each execution of the quantum phase results in 1000

raw bits that are prepared and measured in the same

basis.

3.1.1 Security Analysis: Quantum Channel

The security of the BB84 protocol is predicated on

the assumption that each pulse contains a single pho-

ton (Bennett and Brassard, 2014). Our quantum layer

employs a decoy-state protocol to identify potential

photon-number splitting attacks (Mi et al., 2022).

Consequently, there are two potential sources of er-

ror: natural errors resulting from imperfections in the

quantum channel, and errors induced by intercept-

and-resend attacks. If an attacker intercepts a photon

and subsequently retransmits it, the probability of in-

ducing an error in that speciﬁc bit is

(Bennett and

Brassard, 2014). Given that each intercepted photon

is independent of the others, the number of erroneous

bits in this scenario follows a binomial distribution

with p = 0.25.

In this regard, we have three possible alternatives:

1. assuming that every error is caused by eavesdrop-

ping,

2. assuming that every error is caused by errors in

the quantum channel, or

3. trying to calculate the distribution between these

two, relying on our knowledge about the quantum

channel.

3.2 Authentication

Authenticated steps are delineated in Figure 1. We

have implemented authentication using symmetric

message authentication codes (MACs) and a post-

quantum key encapsulation method to disseminate the

symmetric authentication session key. Speciﬁcally,

our method employs the CRYSTALS–Kyber key en-

capsulation algorithm (Bos et al., 2018) to generate a

conﬁdential authentication session key for Alice and

Bob. We utilized the CRYSTALS–Kyber implemen-

tation and certiﬁcate management functions of the

OpenSSL provider, developed by the Open Quantum

Safe Project (Stebila and Mosca, 2016). Following

the exchange of authentication keys, Alice and Bob

can utilize this session key to generate message au-

thentication codes using a speciﬁed MAC algorithm.

Our implementation employs the HMAC algorithm

(NIST, 2008) to generate secure message authentica-

tion codes using the symmetric key.

3.2.1 Security Analysis: Authentication

The security prerequisites for authentication meth-

ods are as follows: The ﬁnal distilled encryption key

remains uncompromised even if the authentication

method fails after the completion of the QKD. There-

fore, it is sufﬁcient to employ a transiently secure

authentication method. However, the authentication

method in use should maintain its security through-

out the key distillation process. In practice this means

that to obtain more security the parties that are ex-

changing secret keys using QKD should renew their

authentication session key from time to time.

The implemented authentication method seems

like a viable option from the security perspective.

The threat posed by Shor’s algorithm (1994) excludes

classical public key authentication methods and key

encapsulation methods from being used in the authen-

tication. The resilience against quantum computing

is justiﬁed as QKD protocols are considered to be a

secure key exchange method in the era of quantum

computing.

The key encapsulation algorithm CRYSTALS-

Kyber was chosen from the list of algorithms that Na-

tional Institute of Standards and Technology (NIST)

has chosen to be included in the post-quantum pub-

lic key cryptography standard (Alagic et al., 2022).

SECRYPT 2024 - 21st International Conference on Security and Cryptography

410

HMAC is a secure and efﬁcient keyed hashing algo-

rithm and thus was selected.

CRYSTALS–Kyber is still going through stan-

dardization process. First version of the NIST’s

post-quantum public key cryptograhpy standard is ex-

pected in 2024 (NIST, 2017b). Future security of the

authentication method is directly affected if vulner-

abilities are found during the standardization. This

affects also the security promise of QKD key distilla-

tion if vulnerable method is used for authentication.

Security level of the authentication method is

given by security strength categories that NIST has

deﬁned for PQC algorithms in their call for propos-

als (NIST, 2017a). Standardized algorithms should

fulﬁll the security deﬁnitions of these categories. De-

pending on the chosen parameter size, CRYSTALS–

Kyber should correspond to at least the same cryp-

tographic strength as AES128 against both classical

and quantum attacks (CRYSTALS Team, 2023). We

consider this to be sufﬁcient minimum strength for

QKD authentication method. Most security would be

achieved using parameters for security level 5, which

corresponds to security of AES256 (NIST, 2017a).

Security of any authentication method that uses

public key cryptography depends on securely dis-

tributing the public keys of participants. In order to

trust the security of the key encapsulation method we

have to assume that a secure public key infrastructure

exists.

3.3 Error Rate Estimation

In the error estimation phase, Alice randomly selects a

10% portion of the raw bit string. Bob compares these

bits to his respective bits and calculates how many bits

are changed. The error rate estimate is the ratio be-

tween ﬂipped bits and all bits. This step is referred to

as bit error rate estimation or sometimes as parameter

estimation (Wolf, 2021). The sample used for error

rate estimation is removed from the raw bit string to

ensure it does not become part of the ﬁnal secure key.

If the error rate is in acceptable limits, which in

our case is ≤ 12%, Bob will send his error rate es-

timate to Alice. Otherwise, he only sends a signal to

interrupt the distillation process and start the quantum

phase again.

3.3.1 Security Analysis: Error Rate Estimation

Error rate estimate of the raw bit string is needed for

two purposes:

1. High error rate refers to interference on the chan-

nel, which can be caused by intercept and resend

attack. In this case, the parties abort the process

and try again later. Errors can also occur due

to natural factors like photon loss, detection and

misalignment errors, background noise, and dark

counts (Bennett et al., 1992).

2. Error rate estimate is needed when conducting

CASCADE error correction protocol in the error

correction phase.

Estimating the error rate consists of several steps:

(1) one must choose acceptable threshold λ

max

for the

error rate of the bit string, (2) one must choose the

proper size k for the subset of the noisy key that is

revealed, (3) one must calculate the error rate Λ

this subset and (4) in order to continue the execution

of the protocol, the subset must pass a check Λ

≤

max

(Wolf, 2021).

The size k of the subset has to be decided. The

reliability of the estimate depends on the relative size

of the subset: the smaller the subset, the more unre-

liable is the estimate (Lu et al., 2017). Let

denote

the fraction of errors in the k-sized subset, with mean

µ = 0.1. Each X

is a Bernoulli trial with p = 0.1 and

concentrates around µ = E(X

) = p = 0.1 as k in-

creases. The size of k can be estimated, e.g., by max-

imizing the probability P(0.1 − ε ≤ X

≤ 0.1 +ε).

Generally, the proportion of errors Λ

in the sam-

ple S is Λ

, where E is the hamming weight of the

string S

Alice

⊕ S

Bob

(i.e., the number of erroneous bits)

and k is the size of the sample (Wolf, 2021). For ex-

ample, if E = 36 and k = 360 it means that Λ

= 0.1.

High estimate of Λ

requires action: if Λ

> λ

max

the key should be discarded. We deﬁne λ

max

= 0.1 +

ε, where ε is the maximum allowed deviation from the

error rate of the implemented quantum channel.

When the condition Λ

≤ λ

max

is satisﬁed, we in-

put Λ

as the estimated quantum bit error rate to the

CASCADE error correction protocol.

All error rate estimation methods based on the

sample error rate include some amount of uncertainty.

However, during the error correction process, Bob

will get the error rate Λ

of the whole bit string as

he will have a copy of the noisy key and the error

corrected key. At this point, the protocol can still be

aborted if Λ

> Λ

. Thus, the accuracy of Λ

will be

more of a efﬁciency than a security aspect: the eaves-

dropping attempt will be noticed after the error cor-

rection, but this approach will lower the secure key

generation rate.

Deﬁning an exact upper bound for the tolerable

error rate after BB84 protocol is a challenging

question. We must rely on the assumption that with a

high enough probability, if an eavesdropper has been

listening the quantum channel, either the protocol

will abort or the eavesdropper will end up with a small

Security Analysis for BB84 Key Distillation

411

enough amount of information (Gottesman and

Lo, 2001).

We treat the quantum channel here as a binary

symmetric channel, which means that each bit is

ﬂipped with probability p, and the total amount of

ﬂipped bits follows a binomial distribution. We strive

to set the highest tolerable error rate and raw key size

so that it seems highly unlikely to get a key with this

error rate in case that the eavesdropper would actually

have eavesdropped each bit in our quantum phase.

As stated earlier the natural error rate in our quan-

tum channel is 0.1 and the maximum accepted error

rate is 0.12. In our setup, the amount of raw bits com-

ing to the distillation process is 1000. The probabil-

ity for getting a sample of 1000 bits with error rate

of 0.12 or less from a binomial distribution with ac-

tual p = 0.25 is ≈ 9.445 · 10

−25

, which we consider

small enough to rely that the eavesdropper has not

measured all bits in the quantum phase. On the other

hand, probability for getting this error rate or less, i.e.,

probability of the raw bit string passing the error rate

test when there is no eavesdropping activity, is 0.983.

Above we calculated the probability for each pho-

ton in the quantum phase being measured by an eaves-

dropper, so that p = 0.25. The other scenario is that

only some portion of the quantum phase has been

eavesdropped. If we know the error probability of the

channel and we can compute the error in the received

binary string, it is possible to estimate the number of

bits that have been eavesdropped. Let p denote the

probability of an error if a bit is eavesdropped and q

the probability of an error for a bit that is not eaves-

dropped. We will assume q < p and that the prob-

ability of error due to the channel and the probabil-

ity induced by eavesdropping are independent of each

other. We will also assume that the errors for each bit

are independent events.

We denote by n the number of bits received and by

k the number of eavesdropped bits. Now the observed

error R is

R =

× p +

n − k

× q.

Solving for k gives

k =

n(R − q)

p − q

Now if we have the error probability after eaves-

dropping at E

= 0.25 and the error for the channel

at E

= 0.1, we can compute p and q. Obviously,

q = E

= 0.1, but for p we have to note, that both

eavesdropping AND channel error can happen inde-

pendently and thus both possibilities need to be calcu-

lated. Thus p = (1 − E

) × E

+ E

× (1 − E

), which

gives p = 0.3 with the values of E

and E

given

above.

Now we can compute (under the assumptions

given above) the value for k once R has been com-

puted from the received binary string. If we take

R = 0.12 as suggested by the earlier analysis and

n = 1000 we get k = 100, which would mean that 100

bits were eavesdropped. Of course, this being a prob-

abilistic system, this level of accuracy and certainty is

not necessarily warranted. However, this gives some

indication on the likeliest number of eavesdropped

bits, which can then be adjusted with some error mar-

gin to make a good guess on the amount of eaves-

dropped bits.

3.4 Error Correction

For error correction, we utilized the Cascade-Python

library (Rijsman Revision, 2020), a Python-based im-

plementation of the CASCADE protocol (Brassard

and Salvail, 1994). The CASCADE protocol is based

on iterative parity checks: the party with the noisy

version of the key shufﬂes the key bits and requests

parity information for these blocks, while the party

with the original version of the key provides the par-

ity information. This process is repeated until all bit

errors are corrected with a high probability. CAS-

CADE is a probabilistic procedure, meaning it does

guarantee the removal of 100% of the bit errors each

time. However, based on our software tests, CAS-

CADE performed very well when removing bit errors

with an error rate of 0.1.

3.4.1 Security Analysis: Error Correction

The primary security aspect related to the error cor-

rection phase is our ability to quantify the amount of

information leakage during this phase.

Due to the probabilistic nature of CASCADE, the

actual amount of information leakage is only known

after the protocol has concluded. In practice, a re-

sponse to a single parity query leaks one bit of in-

formation (Martinez-Mateo et al., 2015; Mehic et al.,

2020). Our error correction software tracks the num-

ber of leaked bits by counting the responses to parity

queries.

After removing the 10% error rate estimation sub-

set from the 1000 raw key bits, we are left with 900

bits in the error correction phase. Correcting errors

from a 900-bit raw key with CASCADE leaks approx-

imately 513 bits (averaged over 100 test runs using

our software). This leaves us with 387 secret bits af-

ter error correction, assuming that the quantum phase

has not been eavesdropped on.

SECRYPT 2024 - 21st International Conference on Security and Cryptography

412

3.5 Privacy Ampliﬁcation

In our implementation, we conduct privacy ampliﬁ-

cation by multiplication with a Toeplitz matrix. We

construct an n × m sized Toeplitz matrix (where n is

the number of ﬁnal key bits and m is the number of

bits in the error corrected bit string) from a random

seed and multiply the raw bit string with this matrix.

The resulting bit string then becomes the ﬁnal secure

key. Due to the cyclic nature of the Toeplitz matrix,

the length of the seed must be n + m − 1.

3.5.1 Security Analysis: Privacy Ampliﬁcation

The purpose of privacy ampliﬁcation is to mitigate

the information leaked during quantum or classical

protocols. The main security aspects of the privacy

ampliﬁcation steps are: the seed of the hash function

is selected randomly (Bennett et al., 1995; ISO/IEC,

2023); the length of the secure key after privacy am-

pliﬁcation is at most n − t (where n = amount of all

bits and t = amount of bits known to an eavesdrop-

per) (Bennett et al., 1995); and following from the

previous point, we must have a good enough approx-

imation about the maximum number of bits leaked to

a potential eavesdropper. In practice, we will need

to have some extra raw bits to cover situations where

more than the average number of bits are leaked.

For choosing the seed of the Toeplitz matrix, we

have used the function os.urandom in the Python

standard library (Python Software Foundation, 2023).

According to the documentation, this function should

provide enough entropy for cryptographic purposes,

so the randomness aspect should be satisﬁed. Bit

leaks in the quantum phase and the error correction

phase are addressed in the previous sections. The ﬁ-

nal point, the length of the resulting bit string, is ad-

dressed in the next section.

3.6 The Security Level of the Final Key

Let us denote the number of raw bits that enter the

key distillation phase as X. Furthermore, let us de-

note the size of the error rate estimation subset as a,

the amount of leaked information in the error correc-

tion phase as b, and the maximum number of poten-

tially eavesdropped bits as c. After the privacy ampli-

ﬁcation step, as claimed by Bennett et al. (1995), the

length of the distilled key should be at most:

δ = X − a − b − c. (1)

Earlier, we calculated that correcting errors from

a bit string consisting of 900 bits leaks approximately

513 bits, which leaves us with 387 secret bits, assum-

ing that the quantum phase has not been eavesdropped

on. We also calculated that when using the maxi-

mum tolerable error rate of 0.12, the estimated num-

ber of eavesdropped bits in the quantum phase would

be 100.

In our implementation, the ﬁnal secure key was

used as a 256-bit AES key (Dworkin, 2023). A length

of 256 bits was chosen because it is expected to of-

fer a security level of 128 bits in the era of computa-

tionally relevant quantum computers, taking into ac-

count the algorithm by Grover (1996), which achieves

a quadratic speedup in unstructured search.

In our experiments, we obtained the following val-

ues for the maximum tolerable error rate: X = 1000,

a = 100, b = 513 and c = 100. Now, following Equa-

tion 1:

δ = 1000 − 100 − 513 − 100 = 287.

Thus, our key distillation process can distill 287

secure bits for every 1000 raw bits from the quantum

layer. Because 287 > 256, we have obtained enough

secure bits to generate a 256-bit secret key. The ex-

cess bits serve as a security parameter which should

cover unexpected bit leaks in the quantum or classical

phase.

4 DISCUSSION

The conventional method of measuring the security of

encryption algorithms is based on key length; differ-

ent key lengths offer varying levels of security, typi-

cally such that more key bits equate to increased se-

curity against attacks. Consequently, the length of the

distilled encryption key impacts the level of security

it can provide during encryption.

Another factor to consider is the potential for

eavesdropping during the key-establishment process,

which could result in a potential attacker gaining

some knowledge about the key. In our paper, we focus

on the intercept and resend attack, estimate its proba-

bility using statistical means, and collect its probable

effects into a single parameter when deﬁning the se-

curity level of the key.

However, numerous other attacks may threaten

the security of the quantum phase. Thus, in practi-

cal implementations, this parameter must be deﬁned

more comprehensively, taking into account all pos-

sible threats that have not been mitigated with ef-

fective countermeasures. Deﬁning such a parameter,

which collects information about the quantum phase

as a whole, is a topic for further research. Our paper

provides an example of deﬁning and using such a pa-

rameter in conjunction with other parameters derived

from the classical phase.

Security Analysis for BB84 Key Distillation

413

Measuring the exact security level of the produced

key might be impossible because quantum protocols,

such as BB84 used here, are not deterministic in na-

ture but include some random aspects. For instance,

we can calculate the average number of pulses that

may be eavesdropped given the error rate of the bit

string, but this is only an estimate and the actual num-

ber may differ. Thus, the only viable option, in the

case of imperfect devices, appears to be to decide

on a maximum number of eavesdropped bits that can

be tolerated. Evidently, the more secure we want to

be, the more raw bits are needed and the more time-

consuming the key establishment phase will be.

Another important factor is the extent to which

the security countermeasures during key distillation

affect the key generation rate of the protocol. The se-

curity of the distilled keys can always be enhanced

by demanding lower error rates and using more raw

bits, but when implemented in real-life use cases,

a key distillation process must meet certain perfor-

mance requirements, and thus excessive security mea-

sures could render it practically useless.

5 CONCLUSIONS

We have conducted a comprehensive security analysis

of a key distillation phase of a practical QKD based

on the BB84 protocol. We have assumed that cer-

tain security limitations, such as the probability of a

speciﬁc number of photons being eavesdropped, re-

sult from the protocol’s quantum phase, and we have

acknowledged these limitations in our analysis. To

simplify the analysis, we have considered only the in-

tercept and resend attack as a possible source of in-

formation leakage, although we note that many other

attacks threaten practical QKD implementations.

With the help of existing standards and literature,

we have examined every subroutine in the key dis-

tillation phase – authentication, error rate estimation,

error correction, privacy ampliﬁcation – and analyzed

their effects on the security level of the ﬁnal key.

Our analysis contributes to the collection of gen-

eral frameworks that can be used to evaluate QKD key

distillation implementations.

The security level of the ﬁnal key is inﬂuenced by

several parts of the system, and a single unambiguous

measure for this security level should not be consid-

ered sufﬁcient. Instead, due to the non-deterministic

nature of the quantum phase, we propose that the se-

curity level should be considered as a combination of

the bit length of the key and the probability that a cer-

tain portion of these bits is eavesdropped. The secu-

rity level can be enhanced either by increasing the bit

length or by adding safety procedures to the key dis-

tillation phase, such as using more raw bits to produce

the ﬁnal key. As the ﬁnal use case of the secret key is

left open, the ﬁnal computational strength of the key

must be determined separately for each case.

ACKNOWLEDGEMENTS

This work has been supported by the National

Quantum Communication Infrastructure in Finland

(NaQCI.ﬁ) project (Grant Agreement 101091479),

which is part of the European Union’s The European

Quantum Communication Infrastructure (EuroQCI)

initiative.

REFERENCES

Alagic, G., Apon, D., Cooper, D., Dang, Q., Dang, T.,

Kelsey, J., Lichtinger, J., Miller, C., Moody, D., Per-

alta, R., et al. (2022). Status report on the third round

of the NIST post-quantum cryptography standardiza-

tion process. US Department of Commerce, NIST.

Bennett, C. and Brassard, G. (2014). Quantum cryptogra-

phy: Public key distribution and coin tossing. The-

oretical Computer Science, 560:7–11. Theoretical

Aspects of Quantum Cryptography – celebrating 30

years of BB84.

Bennett, C. H., Bessette, F., Brassard, G., Salvail, L., and

Smolin, J. (1992). Experimental quantum cryptogra-

phy. Journal of cryptology, 5:3–28.

Bennett, C. H., Brassard, G., Cr

epeau, C., and Mau-

rer, U. M. (1995). Generalized privacy ampliﬁ-

cation. IEEE Transactions on Information theory,

41(6):1915–1923.

Bos, J., Ducas, L., Kiltz, E., Lepoint, T., Lyubashevsky, V.,

Schanck, J. M., Schwabe, P., Seiler, G., and Stehl

e, D.

(2018). CRYSTALS-Kyber: a CCA-secure module-

lattice-based KEM. In 2018 IEEE European Sympo-

sium on Security and Privacy (EuroS&P), pages 353–

367. IEEE.

Brassard, G. and Salvail, L. (1994). Secret-key reconcil-

iation by public discussion. In Helleseth, T., editor,

Advances in Cryptology — EUROCRYPT ’93, pages

410–423, Berlin, Heidelberg. Springer Berlin Heidel-

berg.

CRYSTALS Team (2023). CRYSTALS–Kyber web-

site. https://pq-crystals.org/kyber/. Last accessed

14.2.2024.

Dupuis, F. (2023). Privacy Ampliﬁcation and Decoupling

Without Smoothing. IEEE Transactions on Informa-

tion Theory, 69(12):7784–7792.

Dworkin, M. J. (2023). Advanced Encryption Standard

(AES). https://doi.org/10.6028/NIST.FIPS.197-upd1.

ETSI (2024a). ETSI GS QKD 016 V2.1.1 (2024-01).

ETSI (2024b). Industry Speciﬁcation Group (ISG) on

Quantum Key Distribution (QKD). https://www.etsi.

org/committee/qkd. Last Accessed 25.1.2024.

SECRYPT 2024 - 21st International Conference on Security and Cryptography

414

Gottesman, D. and Lo, H.-K. (2001). Proof of security of

quantum key distribution with two-way classical com-

munications. IEEE Trans. Inf. Theory, 49:457–475.

Grover, L. K. (1996). A fast quantum mechanical algorithm

for database search. In Proceedings of the twenty-

eighth annual ACM symposium on Theory of comput-

ing, pages 212–219.

Hong, K., Foong, O.-M., and Low, T. (2016). Challenges in

quantum key distribution: A review. In ICINS ’16:

Proceedings of the 4th International Conference on

Information and Network Security, pages 29–33.

Huang, A., Sun, S.-H., Liu, Z., and Makarov, V. (2018).

Quantum key distribution with distinguishable decoy

states. Phys. Rev. A, 98:012330.

ISO/IEC (2023). ISO/IEC 23837-1:2023 - Information se-

curity — Security requirements, test and evaluation

methods for quantum key distribution — Part 1: Re-

quirements.

ITU (2020). ITU-T Recommendations/ ITU-T Y.3803

(12/2020). Last Accessed 25.1.2024.

ITU (2023). ITU-T Recommendations/ ITU-T Y.3815

(09/2023). Last Accessed 25.1.2024.

Jain, N., Anisimova, E., Khan, I., Makarov, V., Marquardt,

C., and Leuchs, G. (2014). Trojan-horse attacks

threaten the security of practical quantum cryptogra-

phy. New Journal of Physics, 16(12):123030.

Li, H.-W., Wang, S., Huang, J.-Z., Chen, W., Yin, Z.-

Q., Li, F.-Y., Zhou, Z., Liu, D., Zhang, Y., Guo,

G.-C., Bao, W.-S., and Han, Z.-F. (2011). Attack-

ing a practical quantum-key-distribution system with

wavelength-dependent beam-splitter and multiwave-

length sources. Phys. Rev. A, 84:062308.

Li, K., Yao, Y., and Hayashi, M. (2023). Tight exponential

analysis for smoothing the max-relative entropy and

for quantum privacy ampliﬁcation. IEEE Transactions

on Information Theory, 69(3):1680–1694.

Lizama-Perez, L. (2023). Reverse reconciliation for optimal

error correction in quantum key distribution. Symme-

try, 15(3).

Lu, Z., Shi, J.-H., and Li, F.-G. (2017). Error rate estima-

tion in quantum key distribution with ﬁnite resources.

Communications in Theoretical Physics, 67(4):360.

Martinez-Mateo, J., Pacher, C., Peev, M., Ciurana, A., and

Martin, V. (2015). Demystifying the information rec-

onciliation protocol cascade. Quantum Info. Comput.,

15:453–477.

Mehic, M., Niemiec, M., Siljak, H., and Voznak, M. (2020).

Error reconciliation in quantum key distribution pro-

tocols. In Ulidowski, I., Lanese, I., Schultz, U. P.,

and Ferreira, C., editors, Reversible Computation:

Extending Horizons of Computing: Selected Results

of the COST Action IC1405, pages 222–236, Cham.

Springer International Publishing.

Mi, S., Dong, S., Hou, Q., Wang, J., Yu, Y., Wei, Z., and

Zhang, Z. (2022). Joint photon-number splitting at-

tack on semi-quantum key distribution. Frontiers in

Physics, 10.

Moriarty, K., Kaliski, B., Jonsson, J., and Rusch, A. (2016).

PKCS #1: RSA Cryptography Speciﬁcations Version

2.2. RFC 8017.

Nir, Y., Josefsson, S., and P

egouri

e-Gonnard, M. (2018).

Elliptic Curve Cryptography (ECC) Cipher Suites for

Transport Layer Security (TLS) Versions 1.2 and Ear-

lier. RFC 8422.

NIST (2008). The Keyed-Hash Message Authentication

code (HMAC). Federal Information Processing Stan-

dards Publication 198-1.

NIST (2017a). Post-quantum cryptography: Call for

proposals. https://csrc.nist.gov/CSRC/media/

Projects/Post-Quantum-Cryptography/documents/

call-for-proposals-ﬁnal-dec-2016.pdf. Last accessed

14.2.2024.

NIST (2017b). Post-quantum cryptography:

Workshops and timeline. https://csrc.nist.

gov/Projects/post-quantum-cryptography/

workshops-and-timeline. Last accessed 14.2.2024.

Python Software Foundation (2023). os, Miscellaneous op-

erating system interfaces. https://docs.python.org/3/

library/os.html. Last accessed 14.2.2024.

Reutov, A., Tayduganov, A., Mayboroda, V., and Fat’yanov,

O. (2023). Security of the decoy-state BB84 pro-

tocol with imperfect state preparation. Entropy,

25(11):1556.

Rijsman Revision, B. (2020). The Cascade informa-

tion reconciliation protocol. https://cascade-python.

readthedocs.io/en/latest/protocol.html. Last accessed

14.2.2024.

Shen, Y.-C., Gao, L., and Cheng, H.-C. (2023). Privacy am-

pliﬁcation against quantum side information via reg-

ular random binning. In 2023 59th Annual Allerton

Conference on Communication, Control, and Com-

puting (Allerton), pages 1–8.

Shor, P. W. (1994). Algorithms for quantum computation:

discrete logarithms and factoring. In Proceedings 35th

annual symposium on foundations of computer sci-

ence, pages 124–134.

Stebila, D. and Mosca, M. (2016). Post-quantum key ex-

change for the internet and the open quantum safe

project. In International Conference on Selected Ar-

eas in Cryptography, pages 14–37. Springer. https:

//openquantumsafe.org/.

Sun, S. and Huang, A. (2022). A review of security eval-

uation of practical quantum key distribution system.

Entropy, 24(2).

Sun, S.-H., Xu, F., Jiang, M.-S., Ma, X.-C., Lo, H.-K., and

Liang, L.-M. (2015). Effect of source tampering in

the security of quantum cryptography. Phys. Rev. A,

92:022304.

Weier, H., Krauss, H., Rau, M., F

urst, M., Nauerth, S., and

Weinfurter, H. (2011). Quantum eavesdropping with-

out interception: an attack exploiting the dead time

of single-photon detectors. New Journal of Physics,

13(7):073024.

Wolf, R. (2021). Quantum Key Distribution - An Introduc-

tion with Exercises, volume 988 of Lecture Notes in

Physics. Springer.

Yoshino, K.-i., Fujiwara, M., Nakata, K., Sumiya, T.,

Sasaki, T., Takeoka, M., Sasaki, M., Tajima, A.,

Koashi, M., and Tomita, A. (2018). Quantum key

distribution with an efﬁcient countermeasure against

correlated intensity ﬂuctuations in optical pulses. npj

Quantum Information, 4(1).

Security Analysis for BB84 Key Distillation

415