Improving Robustness of Satellite Image Processing Using Principal

Component Analysis for Explainability

Ulrike Witteck

, Jan Stambke

, Denis Grießbach

and Paula Herber

Institute of Optical Sensor Systems, German Aerospace Center (DLR), Berlin-Adlershof, Germany

Embedded Systems Group, University of M

unster, Germany

Keywords:

Satellite Image Processing, Robustness Testing, Genetic Algorithms, Principal Component Analysis.

Abstract:

Finding test-cases that cause mission-critical behavior is crucial to increase the robustness of satellite on-board

image processing. Using genetic algorithms, we are able to automatically search for test cases that provoke

such mission-critical behavior in a large input domain. However, since genetic algorithms generate new test

cases using random mutations and crossovers in each generation, they do not provide an explanation why

certain test cases are chosen. In this paper, we present an approach to increase the explainability of genetic

test generation algorithms using principal component analysis together with visualizations of its results. The

analysis gives deep insights into both the system under test and the test generation. With that, the robustness

can be signiﬁcantly increased because we 1) better understand the system under test as well as the selection

of certain test cases and 2) can compare the generated explanations with the expectations of domain experts

to identify cases with unexpected behavior to identify errors in the implementation. We demonstrate the

applicability of our approach with a satellite on-board image processing application.

1 INTRODUCTION

Satellite on-board image processing algorithms have to

meet extremely strict requirements in terms of reliabil-

ity and accuracy in hard real time to guarantee several

years of continuous operation and maintainability in

the orbit. For that, it is important to detect errors and

performance issues early in the development process.

Robustness testing is a powerful method to increase

conﬁdence in the correct behavior of such systems by

executing test cases that cause mission-critical behav-

ior. However, due to the extreme large input domain of

such complex applications, it is infeasible to exhaus-

tively run all possible test cases. Moreover, manual

testing is error-prone as well as time-consuming. A

solution to the problem are genetic algorithms (GAs),

since they are able to perform a guided search in a

large input domain. GAs evaluate test cases (individ-

uals) based on criteria that are speciﬁed by the tester

in terms of a ﬁtness function. The algorithm evolves

test cases with high ﬁtness values over a number of

generations until it reaches a predeﬁned goal applying

evolutionary mechanisms like selection, crossover, and

mutation. A major problem is that the evolutionary

mechanisms are subject to chance, which makes the

evolutionary process hard to understand for the tester.

For example, mutation and crossover are usually ap-

plied randomly to generate new individuals in each

generation. As a consequence, GAs do not provide ex-

planations why certain test cases are chosen. However,

robustness and explainability are fundamental to gain

reliability and conﬁdence in the system and thus the

trust of the user (Holzinger, 2021).

Recent works of (Fyvie et al., 2021), (Wallace

et al., 2021), and (Mouret and Clune, 2015) show

promising concepts in the ﬁeld of explainable artiﬁcial

intelligence (AI) for GAs. In particular, in (Fyvie

et al., 2021) the authors present a principal component

analysis (PCA) on GAs for trajectory mining. A PCA

identiﬁes variables that explain variance in a given

data set, which are called principal components (PCs).

PCs can be used as explanations for variations over

time. Moreover, the authors show that a PCA can be

used to gain better understanding of an evolutionary

process. However, to the best of our knowledge, it has

not been investigated how the results from explainable

AI research can be adopted for genetic test generation

or satellite on-board image processing.

In this paper, we present an approach to increase

the explainability of genetic test generation using PCA

together with visualizations of its results. Our ap-

proach is based on three key ideas.

Witteck, U., Stambke, J., Grießbach, D. and Herber, P.

Improving Robustness of Satellite Image Processing Using Principal Component Analysis for Explainability.

DOI: 10.5220/0012719500003753

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 19th International Conference on Software Technologies (ICSOFT 2024), pages 207-218

ISBN: 978-989-758-706-1; ISSN: 2184-2833

207

First, we adopt the PCA approach presented in

(Fyvie et al., 2021) to genetic test generation by deﬁn-

ing two PCA input data formats that capture domain

speciﬁc aspects of the individuals in a given GA popu-

lation. Second, to explain the GA search process, we

visualize the ratio of explained variance per PC in a

scree plot, the evolutionary process as a trajectory over

PCs, and loading values of PCs in a bar chart. Third,

we introduce a joint analysis of loading values and the

GA’s trajectory in a PC sub-space to reﬂect changes

between speciﬁc GA populations. This enables do-

main experts to identify important test cases as well as

to gain insights why the GA has chosen certain inputs

as suitable test cases. This paper is based on the master

thesis of one of the co-authors (Stambke, 2023).

Our analysis gives deep insights into both the ge-

netic test generation process as well as the system un-

der test. With that, the robustness can be signiﬁcantly

increased because we 1) better understand the perfor-

mance of the algorithm under test for speciﬁc/selected

input parameters, 2) can compare gained explanations

with expectations of domain experts to identify cases

with unexpected behavior, which might be caused by

errors in the implementation. We demonstrate the ef-

fectiveness of our approach on a real-world problem

with experimental results for the ﬁne guidance system

(FGS) of the ESA mission PLAnetary Transits and

Oscillations of Stars (PLATO).

The rest of this paper is structured as follows: We

introduce preliminaries in Section 2 and discuss re-

lated work in Section 3. We present our explainability

approach for genetic test generation using PCA in Sec-

tion 4. We evaluate our approach in Section 5 and

conclude in Section 6.

2 PRELIMINARIES

In this section, we ﬁrst introduce the general ideas of

explainable AI and PCA. Then, we give an overview

of the PLATO mission and its mission-critical FGS

algorithm. Finally, we summarize the genetic test gen-

eration approach presented in (Witteck et al., 2020).

2.1 Explainable Artiﬁcial Intelligence

The goal of explainable AI is to increase conﬁdence in

AI-based algorithms by making the learning process

understandable. There are two ways to achieve this:

First, transparency design offers insights in form of

knowledge about the internal structure of an AI sys-

tem (e.g. decision trees). Transparency design may

reveal explainable aspects like variance in a linear re-

gression to understand single components or provide

algorithmic transparency by understanding the learn-

ing algorithm itself. Second, post-hoc explainable AI

offers knowledge about the algorithm by explaining

its results via e.g. analytic statements, visualization

techniques, or input manipulation to understand the

inﬂuence of single parameters or back propagation to

identify important combinations of nodes and edges in

neural networks. In post-hoc approaches like PCA, the

extraction of information from results has no impact

on the performance of the algorithm itself (Xu et al.,

2019; Do

silovi

c et al., 2018; Lipton, 2018).

2.2 Principal Component Analysis

PCA is a method to reduce the dimensionality of large

data sets. The analysis identiﬁes highly correlated

variables, which can be transformed to PCs to gain

a smaller set of variables with the same amount of

information. PCs contain the variance of the data set in

descending order. This means that the ﬁrst PC contains

most of the information, the second the second most,

etc. Depending on the data analysis objective and the

data set, a small amount of PCs might be sufﬁcient in

their information value.

There are several options to calculate PCs, e.g.

eigendecomposition of the covariance matrix, singular

value decomposition (SVD), eigenvalue approxima-

tion via power iterative computation, or non-linear

iterative partial least squares computation (Wu et al.,

1997). For reasons of numerical stability and imple-

mentation, we apply SVD. By means of SVD, we

calculate eigenvectors and eigenvalues of the variables

in our data set. Eigenvectors are linear combinations of

the original variables and its coefﬁcients describe the

contribution of each variable to the PC. Eigenvalues

provide the amount of variance in the data.

X = USV

(1)

XV = USV

V = US (2)

= s

for i-th data point (3)

As Equation (1) shows, SVD is a factorization of

m × n

matrix

(

samples,

variables) into an

m × m

matrix

, an

m × n

diagonal matrix

, and an

n × n

matrix

is a diagonal matrix with square

roots of the eigenvalues of

(singular values).

Columns of

are orthonormal eigenvectors of the

row-spaced matrix

. Columns of

are orthonor-

mal eigenvectors of the column-spaced matrix

The PCA transforms the data set

according to Equa-

tion (2) into a new representation

by multiplying

the matrix

with eigenvectors

. The column vectors

are PCs. From Equation (3), we obtain eigenval-

ues, that show the variance of the PCs (Shlens, 2014).

ICSOFT 2024 - 19th International Conference on Software Technologies

208

By multiplying eigenvectors with the square root of

eigenvalues, we calculate PCA loading values. Load-

ing values reﬂect the correlation between original vari-

ables and PCs. We analyze the weight of loading

values to ﬁgure out to which extend original variables

contributed to the PCs. The sign of the loading value

indicates whether the correlation is positive or negative.

If two variables have opposite signs in their loading

value, the PC expresses a trade-off between the vari-

ables. Otherwise, the PC reﬂects that the variables

vary in the same way (Reris and Brooks, 2015).

2.3 PLATO Mission

The PLATO mission is the third medium-class mission

in ESA’s long-term space scientiﬁc program Cosmic

Vision (European Space Agency, 2022). The main

goal of the mission is the detection and characteriza-

tion of Earth-like exoplanets orbiting in the habitable

zone of solar-type stars. The scientiﬁc objective is

achieved by large samples of stars with ultra-high pre-

cision for a long period of time without being inter-

rupted. This process requires a very large ﬁeld of view

(FoV) and a low noise level. The required FoV and a

high pupil size are obtained by a novel multicamera ap-

proach: the instrument consists of

normal cameras

and two fast cameras. Each camera is equipped with

four charge coupled devices in the focal plane with

4510 pixel × 4510 pixel

. The normal cameras observe

stars fainter than magnitude 8 with a cadence of

25 s

Fast cameras monitor stars brighter than magnitude 8.

To avoid saturation of the detector, the exposure time

2.5 s

. Additionally, the fast cameras serve as two

independent and redundant FGS to provide precise

attitude measurements to the spacecraft (Grießbach

et al., 2021). The FGS algorithm calculates attitude

data for the telescope by comparing measured star vec-

tors with reference directions in a star catalog. The

attitude calculation is performed with an accuracy of

milliarcseconds since the FGS is set to fulﬁll the mis-

sions scientiﬁc goal of ultra-high precision star data.

Hence, the FGS algorithm is a mission-critical compo-

nent (Martin Pertenais, 2022). It is crucial for mission

success, that the algorithm meets these requirements,

and therefore needs to be tested extensively.

2.4 Genetic Test Generation

To make testing more efﬁcient and less time consum-

ing, it is preferable to examine few test cases that cover

a large part of the system under test. Equivalence class

partition testing is a commonly used solution to this

problem in practice. Equivalence classes (ECs) are

disjoint sub-domains of an input domain or output do-

main. All elements in an EC are expected to provoke

the same system behavior according to a speciﬁcation.

For systematic testing, representative values of each

EC are then chosen. In (Witteck et al., 2019), equiva-

lence class partitioning has been applied to the input

domain of satellite on-board image processing in the

context of PLATO’s FGS algorithm. Satellite on-board

image processing algorithms such as the FGS heavily

depend on the positions of the input stars on the focal

plane assembly (FPA). To include test cases for var-

ious positions, the authors partition the FPA into the

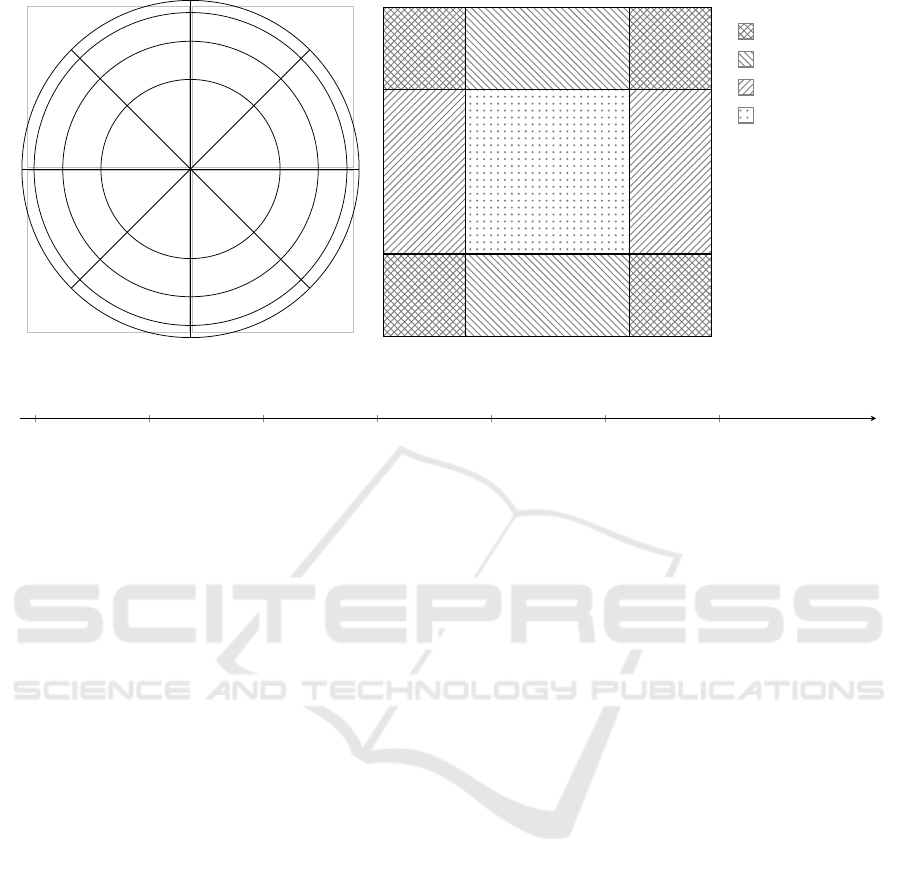
sectors shown in Figure 1a, where the numbers shown

in the picture are used as IDs for the ECs. Further star

parameters are the sub-pixel position and magnitude.

Figure 1b shows an example for partitioning a pixel

and Figure 1c for the magnitude range. An input star is

then described by the combination of its FPA position,

pixel position and magnitude using the IDs of the ECs.

By deﬁning ECs for the parameters of a star repre-

sentation, the number of test inputs is heavily reduced.

However, to test the FGS, combinations of stars are

needed. Previous experiments have shown that 30 in-

put stars provide sufﬁciently good results of the FGS

algorithm (Grießbach et al., 2021). Therefore, we de-

ﬁne a combination of 30 stars as a test case. However,

even with a reduced test suite of stars, the number of

possible combinations is still infeasible high. E.g. with

a testsuite of 768 EC input combinations, there exist



768



= 7.7 · 10

possible FGS test cases.

GAs are capable to automatically search for spe-

ciﬁc test cases in such a large test suite. These search

algorithms are inspired by the concept of biological

evolution to solve complex optimization problems.

Evolutionary mechanisms like selection, mutation, and

crossover are applied to possible solutions until a spe-

ciﬁc termination criterion is met. In the context of GAs,

possible solutions are individuals that consist of genes.

The GA aims to optimize combinations of genes to

maximize a predeﬁned ﬁtness function. To achieve

this, the algorithm randomly selects a number of indi-

viduals from a given search space and evaluates each

individual by means of the ﬁtness function. Individuals

with a high ﬁtness value are more likely to be selected

to the next generation. In the context of genetic test

generation, an individual represents a test case. In

(Witteck et al., 2020), the authors present a GA that

searches for test cases that provoke mission-critical

behavior with respect to reliability and mathematical

accuracy of satellite on-board image processing appli-

cations. To achieve this, they deﬁne a ﬁtness function

that captures the accuracy and execution time of the

system under test. They partition the input domain

in ECs and deﬁne genes as EC combinations, which

signiﬁcantly reduces the search space.

Improving Robustness of Satellite Image Processing Using Principal Component Analysis for Explainability

209

5 6

910

13 14

1718

21 22

2526

29 30

(a) FPA Position ECs.

Pix-EC-0

Pix-EC-1

Pix-EC-2

Pix-EC-3

(b) Pixel ECs.

7 6.6 6.3 6 5.8 5.6 5.5

Mag-EC-0 Mag-EC-1 Mag-EC-2 Mag-EC-3 Mag-EC-4 Mag-EC-5

magnitude

0.4 0.6 0.9 1.1 1.3 1.5 1.7

·10

photons

Figure 1: Partitioning examples for FPA, pixel and star magnitude parameters.

3 RELATED WORK

While there are various approaches of explainability

for deep learning algorithms, the ﬁeld of explainable

metaheuristics is widely unexplored. In (Xu et al.,

2019) and (Islam et al., 2022), the authors offer re-

views in terms of history, research, and application

of explainable AI. Besides post-hoc explainability via

PCA as proposed in (Fyvie et al., 2021), recent re-

search shows further explainability techniques with

innovization (Deb et al., 2014), MAP-Elites (Mouret

and Clune, 2015), and surrogate ﬁtness functions (Wal-

lace et al., 2021; Brownlee et al., 2021). Further, there

exist concepts to increase trust in GA solutions, such

as the conﬁdence measure from (Mirjalili et al., 2015).

In (Mirjalili et al., 2015), the authors propose ro-

bust optimization of evolutionary algorithms by deﬁn-

ing a neighborhood with radius r around every solution.

If there are multiple diverse solutions available in that

neighborhood, conﬁdence for a valid GA solution is

increased. Mirjalili et al. integrate this metric in meta-

heuristic operations for robust optimization of single-

and multi-objective ﬁtness functions. This conﬁdence

measure successfully reduces faulty optima in a GA

run, which are caused by uncertainties in operating

conditions, manufacturing tolerance or due to mea-

surement errors. However, we aim to achieve a form

of trust by giving explanations about the GA’s evolu-

tion steps, by highlighting the relevance of individual

genes for the ﬁtness score.

In (Deb et al., 2014), the authors introduce in-

novization as an explainability technique that describes

the process of analyzing and discovering knowledge in

properties of near-Pareto-optimal solutions. Innoviza-

tion focuses on multi-objective optimization tasks with

conﬂicting objectives. In contrast to their problem, we

focus on single-objective optimization.

MAP-Elites (multi-dimensional archive of phe-

notypic elites) (Mouret and Clune, 2015) is an illu-

minating algorithm, designed to return the highest-

performing solution at each point in the feature space.

The algorithm uses evolutionary algorithm concepts

by evolving generations of solutions through crossover

and mutation operations. Contrary to a classic GA,

MAP-Elites illuminates the ﬁtness potential of the en-

tire feature space by creating an archive of distributed

high-performing solutions. This is achieved by storing

differing individuals in predeﬁned bins. If a bin is al-

ready occupied, a higher performing individual is able

to replace the former contender. In (Urquhart et al.,

2019), the authors provided end-users with the abil-

ity to review a bins history of solutions and highlight

the highest performing solutions based on speciﬁed

criteria. Further research shows explainability oppor-

tunities in automated rule extraction from MAP-Elite

archives (Urquhart et al., 2021). While MAP-Elites

focuses on providing multiple solutions for an opti-

mization problem, the authors in (Wallace et al., 2021)

offer an approach to explain a single solution via sur-

rogate ﬁtness functions. The concept of surrogates

ICSOFT 2024 - 19th International Conference on Software Technologies

210

originates in the motivation to increase the speed of a

GA’s search process. Parallel to the optimization run,

the authors train a surrogate model to approximate the

true ﬁtness function. Since true ﬁtness functions are

typically costly in computing an individuals ﬁtness,

the surrogate can be used to evaluate the majority of

solutions at a faster rate. Wallace et al. argue, that

”the surrogate is an explicit model of what the algo-

rithm has learned about high-ﬁtness solutions”. Hence,

the surrogate model can be mined to gain information

about the algorithms decision process. For example, a

high performing solution can be evaluated with the sur-

rogate by modifying single variables and recording the

variation in ﬁtness. Since the surrogate represents the

learning process, the user is able to create a ranking of

variable importance within a solution. Thus, the user

can identify decisive components in individuals, which

can help in adjusting GA’s operation parameters.

MAP-Elites and surrogate functions represent valid

approaches to be exploited besides the PCA presented

in (Fyvie et al., 2021). However, both approaches

require the deﬁnition of a feature space or surrogate

functions to generate explanations in parallel with the

optimization process. In contrast, with a post-hoc

explainability approach like PCA we are able to get

explanations for results generated by an existing GA

by reducing the data dimensionality. This allows us

to analyze the performance of the algorithm under

test as well as reveal unexpected behavior caused by

implementation errors by investigating PCA loading

values. In this paper, we increase the explainability

of genetic test generation using PCA. We leave the

investigation of MAP-Elites and surrogate functions

to gain further explanations as subject to future work.

EXPLAINABILITY OF GENETIC

TEST GENERATION USING PCA

The input domain of satellite on-board image process-

ing algorithms is extremely large. This makes robust-

ness testing challenging since it is infeasible to exhaus-

tively execute all possible test cases. As a solution

to this problem, the authors in (Witteck et al., 2020)

propose a GA that automatically searches in a large in-

put domain for test cases that provoke mission-critical

behavior and therefore support robustness testing. In

our case study, mission-critical are scenarios where

the pointing of the satellite cannot be stabilized as re-

quired due to a low precision of the calculated attitude.

However, the solutions generated by the GA do not

provide an explanation for changes in the populations

and thus makes it hard for a user to understand the

optimization process.

To overcome this problem, we propose an approach

to increase the explainability of genetic test generation

algorithms using PCA together with visualizations of

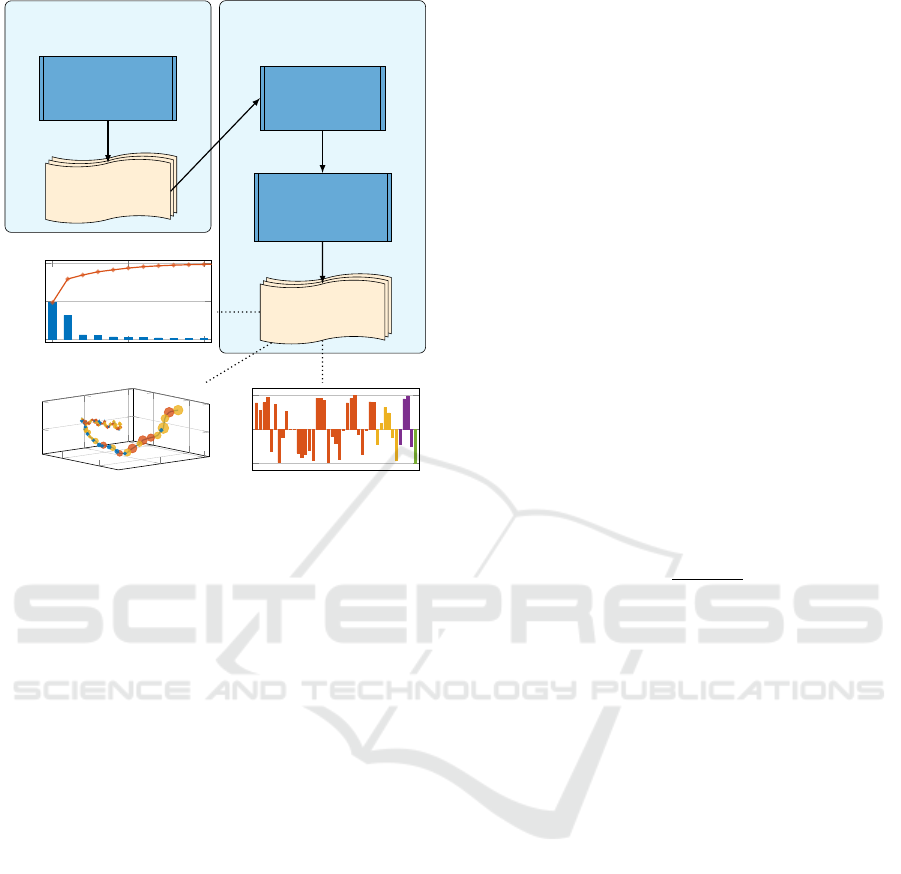
its results. The overall approach is shown in Figure 2.

At its core, we extend the genetic test generation of

(Witteck et al., 2020) with an explainability approach

as proposed by (Fyvie et al., 2021). Each test case is

an individual of the GA that contains a combination

30 stars

. Thus, a gene is a star that can be described

by an EC combination. To explain the results of the

genetic test generation algorithm (i.e., the test cases),

we deﬁne two dedicated data formats that record the

change in GA solutions throughout the generations.

The goal is to explain which gene modiﬁcations have

the highest effect on the ﬁtness value. After preprocess-

ing the GA results in our data formats, we apply PCA

on the data to remove redundant information and thus

reduce the dimensionality of the formats. We deﬁne re-

dundant information as gene modiﬁcations that appear

over all generations and correlate with the ﬁtness value.

Finally, we analyze these correlations within the newly

constructed dimensions, the PCs, by combining three

visualization approaches: a) we visualize the ratio of

explained variance between the calculated PCs as scree

plot as shown in the diagram in the middle of the left

side in Figure 2. The scree plot enables us to select the

most important PCs, e.g. PCs that contain the highest

ratio of explained variance, for further analysis and di-

mensionality reduction. Then, b) we apply the existing

explainable AI approach of GA trajectory mining in

(Fyvie et al., 2021). We use the PCA results to visu-

alize a trajectory of GA population changes and thus

highlight actual differences between generations as

shown in the lower left diagram of Figure 2. Finally, c)

we visualize PC loading values to analyze covariances

(correlations on standardized data) between genes and

ﬁtness value. The lower right diagram in Figure 2

shows an example for PC loading values. We consider

loading values as coefﬁcients scaled by eigenvalues to

include the PC’s variance. High correlations allow us

to generate a ranking of variable importance, which

gives us a better understanding of the search process.

The resulting visualizations enable domain experts to

quickly identify decisive genes, as well as important

generation steps in the trajectory. The increased con-

ﬁdence in the GA results increases the conﬁdence in

speciﬁcally generated test cases for mission-critical

scenarios for robustness testing, and helps to identify

cases where explanations do not match expectations,

e.g., due to implementation errors.

In the following, we describe the PCA preprocess-

ing with our novel data formats and how PCA results

can be used as explanations to gain a deeper under-

standing of genetic test generation.

Improving Robustness of Satellite Image Processing Using Principal Component Analysis for Explainability

211

Genetic

Algorithm

Test Cases

Data

Preprocessing

Principal

Component

Analysis

Explainable

Results

Test Generation

Explainability

approach

PC1

PC2

PC3

Pos-01

Pos-02

Pos-03

Pos-04

Pos-05

Pos-06

Pos-07

Pos-08

Pos-09

Pos-10

Pos-11

−1

PC1

0 5 10

0.5

Principal Comp onents

Variance Ratio

Figure 2: Overview of the PCA explainability approach.

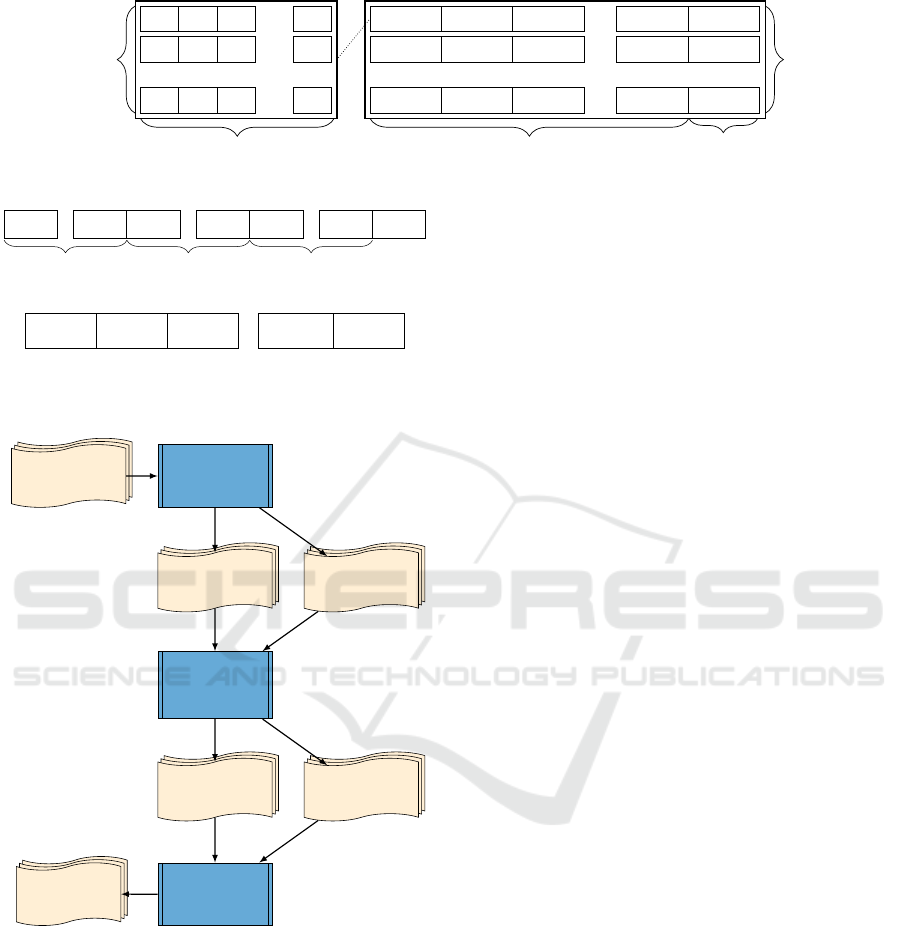
4.1 Data Preprocessing

The preprocessing of the generated test cases by the

GA is an important step to ensure meaningful results

of the PCA. We propose a data format that records

changes in the GA generations throughout the evolu-

tionary process. To achieve this, we count all gene

occurrences within all individuals in each generation

and additionally provide the average ﬁtness value. Fig-

ure 3 illustrates our data format concept. The left side

of the ﬁgure presents an example of individuals with

their genes in the ﬁrst generation. Value ”1” means

the respective gene is included in the individual and

value ”0” means it is not included. The right side of

the ﬁgure shows the gene count for each generation.

n(g

i, j

)

denotes the number of occurrences of the j-th

gene within all individuals in the i-th generation, and

the average. On the right side in the example, one

individual in the ﬁrst generation (ﬁrst line) contains

the ﬁrst gene, two individuals contain the second gene

and three individuals contain the n-th gene. Through

this aggregated representation, we obtain information

about which gene modiﬁcation has the biggest effect

on the ﬁtness value.

In the context of the PLATO FGS, we aim to get

information on the inﬂuence of speciﬁc ECs on the

FGS performance as well as information on the perfor-

mance of EC combinations (that represent single stars).

To achieve this, we deﬁne two data formats: First, the

EC data format records the occurrences of single ECs

per parameter in the populations’ individuals. For ex-

ample, the EC ID

Pos

occurs in no gene of the ﬁrst

individual in the ﬁrst generation,

Pos

occurs in two

genes, etc. The PCs calculated from this format are

linear combinations of all ECs of the input parameters.

Second, the starID data format records occurrences of

star IDs per generation. For example,

Star

occurs in

ﬁve individuals in the ﬁrst generation, ﬁve individuals

contain

Star

, etc. The PCs calculated from this for-

mat are linear combinations of all available star IDs

in the input test suite. Figure 4a and Figure 4b illus-

trate the idea of our data formats, where

denotes the

number of occurrences and µ the average.

Figure 5 shows that after constructing the data for-

mats on the GA results, we accumulate the data of both

formats for all GA runs in terms of mean, minimum,

and maximum ﬁtness value per generation. As shown

in Figure 5, the last step of the preprocessing is the

standardization of the data. Since the ﬁtness value and

data variables have different ranges of variation, we

apply a standardization method to center and scale the

data. For a data matrix

with

individuals, repre-

sented by

features, the standardized scores for value

i j

are deﬁned as:

i j

− µ

(4)

where

is the mean of the

-th feature and

is the

respective standard deviation. As a result, standardized

scores have zero mean and unit standard deviation.

We extract correlations between the data variables by

applying PCA on the standardized data.

4.2 Principal Component Analysis and

Explainable Results

We apply PCA to reduce the dimensionality of stan-

dardized data. Through the use of SVD, we decompose

our standardized data matrix

into eigenvectors and

eigenvalues as described in Section 2.2. The resulting

PCs explain the variation in our data set. We discard

PCs with lower variances since we assume that PCs

with higher variance provide reasonable explanations

of the original data set (Shlens, 2014). To simplify the

evaluation of PCA results, we use three visualizations

to plot the distribution of data variance in the PCs:

scree plot, loading bar chart, and trajectory plot.

Scree Plot. The scree plot visualizes data variance

for each PC as a bar chart (an example is shown with

our experimental results in Figure 7). The plot indi-

cates whether variables in the data set are correlated

or not. In measurements of uncorrelated variables the

redundancy is low. Hence, the variance in all PCs is

ICSOFT 2024 - 19th International Conference on Software Technologies

212

1 1

. . .

0 0

. . .

Generation 0

Gene 0..N

Individuals

n(g

m,0

) n(g

m,1

) n(g

m,2

)

. . .

n(g

m,n

)

µ( f it

)

n(g

1,0

) n(g

1,1

) n(g

1,2

)

. . .

n(g

1,n

)

µ( f it

)

1 2 1

. . .

µ( f it

)

Data Format

Generation 0..M

Count of Gene 0..N

Average ﬁtness

Figure 3: Concept of PCA data format.

n(P os

)

. . .

n(P os

) n(M ag

)

. . .

n(Mag

) n(Pix

)

. . .

n(P ix

)

µ(fit)

position

magnitude sub-pixel

(a) EC data format per individual.

n(Star

) n(Star

)

. . .

n(Star

768

) µ(fit)

(b) StarID data format per generation.

Figure 4: Data formats.

Test Cases

Construct

Data Format

StarID

Data Format

Aggregate

(mean,

max, min)

MeanMaxMin

StarID

MeanMaxMin

Standardize

Data Format

PCA Inputs

Figure 5: Data preprocessing.

low as well and we have to select a lot of PCs to gain

sufﬁcient information about the data set. In this case,

PCA is not able to reduce the dimensionality of the

original data set. However, if variables are highly cor-

related, measurements are highly redundant and PCA

signiﬁcantly reduces the data dimensionality. In this

case, the scree plot shows that higher ranked PCs are

associated with most of the data variance.

In addition to the data variance, our scree plot

shows the accumulated variance ratio to provide better

visibility of the required number of PCs to reach a

speciﬁc threshold. For example, Figure 7 in Section 5

shows that the ﬁrst three PCs are associated with more

than

80 %

of the data variance. Thus, the scree plot al-

lows us to quickly decide these three PCs are sufﬁcient

to provide explanations for our GA results.

Loading Bar Chart. PCA loading values represent

the correlation between original variables and calcu-

lated PCs. We generate for each PC of interest a load-

ing bar chart that plots the loading values of the vari-

ables within our data formats. For the EC data format,

we are particularly interested in the correlation be-

tween the ﬁtness variable and the EC variables, and

for the starID data format in the correlation between

the ﬁtness variable and the star ID variables. For ex-

ample, Figures 9 to 11 present the loading values of

the EC data format of our experimental results. The

ﬁgure shows that we group the EC variables according

to the corresponding input parameter and highlight

the ﬁtness variable. For the starID data format, we

group stars based on their EC ID for a preselected in-

put parameter and again highlight the ﬁtness variable.

Moreover, we are able to visualize the loading values

for a speciﬁc EC as shown in Figure 12 in Section 5.

As a result, the loading bar chart allows us to analyze

which EC or star ID variables vary in the same way as

the average ﬁtness value.

Trajectory Plot. Fyvie et al. propose in (Fyvie et al.,

2021) the concept of PCA to visualize trajectories for

GA results. They transform GA results into PCs and

use the ﬁrst three PCs to generate a trajectory. The

authors point out that the resulting trajectory does not

reveal the ﬁtness landscape but shows the direction

and magnitude of population variations in the new

subspace. We use the approach to generate a trajectory

of our GA results in the subspace of the ﬁrst three

PCs. With that, we capture and visualize changes in

the evolution of GA solutions. Using the trajectory,

we can quickly analyze whether the solutions follow

a speciﬁc path or whether the solutions are subject

to chance. We extend the approach by highlighting

PCs with the most inﬂuence on a speciﬁc generation.

Improving Robustness of Satellite Image Processing Using Principal Component Analysis for Explainability

213

To do so, we compare the distances of each PC value

in each generation with the PC value of the former

generation. This allows us to apply a joint analysis of

trajectory plot and loading bar chart. Hence, we know

from the trajectory plot which PC has the most impact

in a generation and are able to understand from the

respective loading bar chart of the PC which variables

correlate with the ﬁtness value.

5 EVALUATION

We evaluate our proposed explainability approach with

the FGS of the PLATO mission. The main goal is

to gain insights into the evolutionary process of the

genetic test generation, and in turn to gain a deeper

understanding of the most critical inputs and the FGS

algorithm itself. A known behavior of the FGS algo-

rithm is that in some cases, jitter in the input data has

a strong inﬂuence on the accuracy of the results. To

validate our PCA approach, we have deﬁned a novel ﬁt-

ness function, which explicitly searches for test cases

where the jitter does have strong inﬂuence on the cal-

culated FGS attitude. With the new ﬁtness function,

the test generation algorithm searches for critical test

inputs with respect to the jitter inﬂuence. To show

the applicability of our explainability approach, we

aim at a better understanding for which input stars the

accuracy of the FGS drops for some jittered inputs and

are thus suited for robustness testing.

In the following, we ﬁrst present our novel ﬁtness

function that encodes the inﬂuence of the jitter on the

mathematical accuracy of the FGS. Then, we brieﬂy

summarize the main characteristics of the implemen-

tation of our PCA approach and the conﬁguration of

the genetic test generation algorithm we have used in

the experiments. Finally, we present our experimental

results from running the PCA on the test generation

algorithm results and show the visualizations.

5.1 Adaptation of the Test Generation

Approach

In (Witteck et al., 2020), the authors deﬁne a ﬁtness

function that searches for test cases that provoke long

execution times or a low accuracy, represented by a

high quality index. This is a well-suited approach for

robustness testing, as mission-critical behavior is de-

tected. However, the newest version of the PLATO

FGS has deterministic execution times. Furthermore,

while it is useful to search for test cases that provoke a

high quality index to speciﬁcally target the mathemat-

ical accuracy of the algorithm, it is highly desirable

Dash app

Python

Plot PCA

dataframes

pandas; plotly

Preprocessing

Python

Process HDF5-Files

H5py; pandas;

scikit-learn

PCA

Python

Process

dataframes

pandas; numpy.svd

GA-PCA

GA HDF5-Files

Preprocessed

dataframes

PCA dataframes

Figure 6: Overview of the implementation.

to identify star combinations where input jitter has a

strong inﬂuence on the calculated FGS attitude.

In this paper, we present a novel ﬁtness function

for the genetic test approach based on the FGS atti-

tude error. We ﬁrst calculate for each FGS exposure

the deviation between the jitter inserted in the image

data and the jitter of the calculated attitude data. We

express the deviation as euler angles

(x,y,z)

in milliarc-

seconds. Then, we calculate the standard deviation of

each angle over all exposures. The ﬁtness value

f it

an individual is determined with

f it =

+ σ





, (5)

where

is the standard deviation for all angles. Each

angle represents the jitter deviation per exposure. In

the context of PLATO, the rotations around the

and

-axis are the raw, pitch and roll angles of the

satellite. According to internal PLATO speciﬁcations,

roll angle errors affect point shifts on the cameras ﬁeld

of view by factor of four.

5.2 PCA Implementation

We have designed our implementation in such a way

that we are able to process GA results of the developed

test framework presented in (Witteck et al., 2020). We

have implemented our PCA in Python 3. For scalabil-

ity we offer the usage of our tool rendered in a web

browser or by using the command line interface. The

tool is deployed on an x86-64 Ubuntu 18.04 machine.

Figure 6 shows the structure of our implementation.

We use Dash, a framework developed by Plotly (Plotly

Technologies Inc., 2015) to build data applications,

for our web application. Since the test framework

stores the GA results in an HDF5 data format (The

HDF Group, 2006), we use the python library H5py to

read the data. Our application generates preprocessed

data formats by means of pandas (The pandas devel-

opment team, 2022) and uses scikit-learn (Pedregosa

et al., 2011) to standardize the data. Further, we use

the SVD implementation in the numpy (Harris et al.,

2020) package to perform the PCA.

ICSOFT 2024 - 19th International Conference on Software Technologies

214

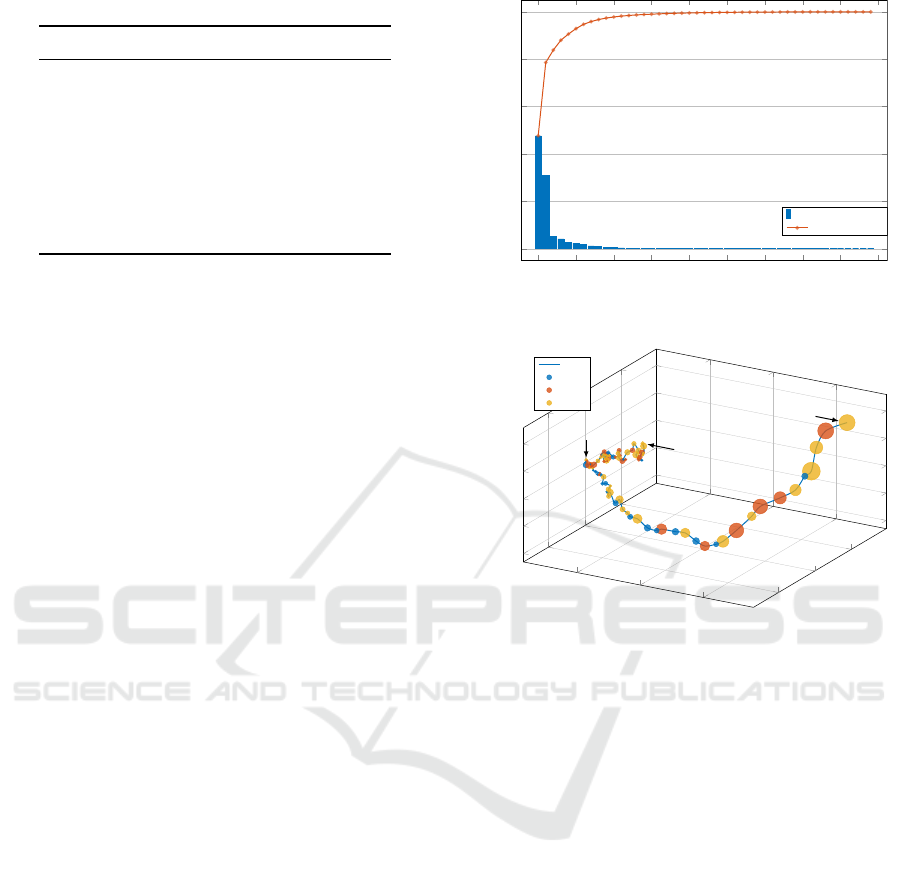
Table 1: Default GA conﬁguration.

Parameter Value

FGS exposures 1000

Population size 100

Number of genes 30

Crossover probability 0.5

Mutation probability 0.06

Tournament size 7

Maximum generation number 100

Repetition number 10

5.3 GA Conﬁguration

The search space of our GA is based on a test suite of

768 stars. Each star is described by three input parame-

ters: position on the FPA in pixel, e.g. (1969.4, 322.5),

magnitude, e.g. 6.5, and sub-pixel position in pixel,

e.g. (0.9, 0.4). Since the test suite covers all EC combi-

nations, the number of star results from the number of

input parameter EC (see Figure 1): 32 classes for the

position on the FPA, 6 classes for the magnitude, and

4 classes for the sub-pixel position. For each star, we

simulate 1000 images of

6 pixel × 6 pixel

as input of

the FGS algorithm. During our experiments, we used

the parameters in Table 1 as default GA conﬁguration.

5.4 Experimental Results

In our experiments, we ran the GA 10 times with the

conﬁguration shown in Table 1. Our goal was to ﬁnd

test cases that increase the jitter deviation of the FGS

attitude. The resulting average ﬁtness value in the last

generation over all runs was

∼19.14 milliarcseconds

This is a signiﬁcant increase over the average ﬁtness

value of

∼5.56 milliarcseconds

in the ﬁrst generation.

Thus, the GA has successfully generated test cases that

provoke high jitter deviation.

To gain a better understanding which input star

parameters or EC combinations are responsible for

increased jitter deviation, we have transformed the GA

results into our starID data format as well as EC data

format and have performed the PCA on our GA results.

The resulting scree plot, trajectory, and PC loading

values are shown in Figures 7 to 11.

The scree plot in Figure 7 shows that most data

variation is explained in PC1 and PC2. Together with

PC3 the PCs captures

83.86 %

of the explained vari-

ance. This means that the PCA successfully reduces

the dimensionality of the input space and is suitable to

generate explanations for the evolutionary test process.

The trajectory of our experimental data in Figure 8

illustrates the average direction of the GA populations

over all runs. The trajectory depicts a steady devel-

0 5 10 15 20 25 30 35 40 45

0.2

0.4

0.6

0.8

Principal Components

Variance Ratio

PC Variance

Accu. Variance

Figure 7: Jitter deviation ﬁtness - scree plot.

−5

−4

−2

ﬁrst generation

last generation

generation 45

PC1

PC2

PC3

Path

PC1

PC2

PC3

Figure 8: Jitter deviation ﬁtness - trajectory.

opment along the PC1 axis, but also temporary direc-

tional changes along axes PC2 and PC3. Figure 8

shows that the evolution along the PC1 axis decreases

after generation 45. The ﬁtness value of generation

45 is

∼17.86 milliarcseconds

, which is

90.75 %

of the

GA’s explored ﬁtness. As the trajectory shows, the GA

performed most of the individual evolution until this

point and is only able to optimize the next generations

to a lesser extent.

The loading value of the ﬁtness value in PC1 shown

in Figure 9 suggests that negative values along the PC1

axis correspond to strong improvements of the ﬁtness

value. We can therefore infer from the ﬁgure that

stars positioned on the lower left part of the FPA (ref.

Figure 1a), with high and low magnitude (Mag-00 and

Mag-05) as well as sub-pixel positions in the center

and on the corner (Pix-00 and Pix-03) correlate with

a high ﬁtness value. After analyzing the Point Spread

Function (PSF) shapes of the test stars, we have seen

that stars located on the lower left part of the FPA have

a wide shape due to optical aberrations. Since wide

PSF shapes lead to inaccurate centroid estimations,

the jitter of the calculated attitude is high as well. A

further reason for selecting these EC is the distribution

of stars on the FPA. Close star positions lead to a high

Improving Robustness of Satellite Image Processing Using Principal Component Analysis for Explainability

215

Pos-00

Pos-01

Pos-02

Pos-03

Pos-04

Pos-05

Pos-06

Pos-07

Pos-08

Pos-09

Pos-10

Pos-11

Pos-12

Pos-13

Pos-14

Pos-15

Pos-16

Pos-17

Pos-18

Pos-19

Pos-20

Pos-21

Pos-22

Pos-23

Pos-24

Pos-25

Pos-26

Pos-27

Pos-28

Pos-29

Pos-30

Pos-31

Mag-00

Mag-01

Mag-02

Mag-03

Mag-04

Mag-05

Pix-00

Pix-01

Pix-02

Pix-03

Fitness

−1

−0.5

0.5

Equivalence Classes

PC1

Pos-EC Mag-EC Pix-EC Fitness

Figure 9: Loading values for PC1.

roll angle error (Grießbach et al., 2021) and thus lead

to high residual noise of the estimated star centroids.

We generally expect more faint stars (high magni-

tude) in the resulting star combination, since they have

less information for centroid estimation than bright

stars (Grießbach et al., 2021). However, the loading

values show that besides faint stars in Mag-00, also

brighter stars in Mag-04 and Mag-05 correlate with

the ﬁtness value. If we consider the magnitude and the

position of a star together, we ﬁnd that the signal of

bright stars with a wide PSF shape is evenly distributed

over many pixels but the signal-to-noise ratio is low.

This provides a good explanation why the centroid

estimation is less accurate.

Figure 9 shows that stars in Pix-00 (pixel center)

and Pix-03 (pixel corner) lead to a high ﬁtness value.

We expect a high ﬁtness value if a star is located on the

pixel corner, since the centroid may move to neighbor-

ing pixels due to jitter movement and therefore cause

deviations in the pixel illumination. However, a star

position in the pixel center leads to a low amount of

signal in neighboring pixel since the star’s ﬂux is only

distributed in a few pixel. A low number of pixel con-

taining star information leads to a decreased precision

of the star position estimation (Grießbach et al., 2021).

This applies especially to faint stars and gives an ex-

planation for the GA results. However, we did not

expect stars located in the pixel center to have same

correlations to the ﬁtness value as stars on the pixel

corner. The results give reason to review the effect and

the deﬁnition of the pixel ECs in future work.

The loading values of PC1 in Figure 9 indicates

that the star position on the FPA was the driver of the

GA evolution in the ﬁrst 45 generations. Because the

loading values show that the GA selects no speciﬁc

magnitude or pixel value but rather faint and bright

stars as well as stars located in the pixel center and

pixel corner. The trajectory in Figure 8 shows that

Pos-00

Pos-01

Pos-02

Pos-03

Pos-04

Pos-05

Pos-06

Pos-07

Pos-08

Pos-09

Pos-10

Pos-11

Pos-12

Pos-13

Pos-14

Pos-15

Pos-16

Pos-17

Pos-18

Pos-19

Pos-20

Pos-21

Pos-22

Pos-23

Pos-24

Pos-25

Pos-26

Pos-27

Pos-28

Pos-29

Pos-30

Pos-31

Mag-00

Mag-01

Mag-02

Mag-03

Mag-04

Mag-05

Pix-00

Pix-01

Pix-02

Pix-03

Fitness

−1

−0.5

0.5

Equivalence Classes

PC2

Pos-EC Mag-EC Pix-EC Fitness

Figure 10: Loading values for PC2.

Pos-00

Pos-01

Pos-02

Pos-03

Pos-04

Pos-05

Pos-06

Pos-07

Pos-08

Pos-09

Pos-10

Pos-11

Pos-12

Pos-13

Pos-14

Pos-15

Pos-16

Pos-17

Pos-18

Pos-19

Pos-20

Pos-21

Pos-22

Pos-23

Pos-24

Pos-25

Pos-26

Pos-27

Pos-28

Pos-29

Pos-30

Pos-31

Mag-00

Mag-01

Mag-02

Mag-03

Mag-04

Mag-05

Pix-00

Pix-01

Pix-02

Pix-03

Fitness

−0.4

−0.2

0.2

0.4

0.6

Equivalence Classes

PC3

Pos-EC Mag-EC Pix-EC Fitness

Figure 11: Loading values for PC3.

after generation 45, PC2 becomes more important.

The loading values of PC2 in Figure 10 indicate that

stars located on the pixel corner (Pix-03) lead to a

high ﬁtness value. In contrast to PC1, the stars are

more distributed on the FPA. It is obvious that the GA

improves the ﬁtness by selecting stars based on their

pixel position. We observe from the trajectory that

in the last generations, PC3 dominates. The loading

values of PC3 in Figure 11 indicate that the GA mainly

selects faint stars located on the outer FPA to increase

the ﬁtness value.

In summary, the PCA extracts relevant information

from our GA results such that we are able to ﬁnd useful

explanations for the evolutionary test process. We can

conclude that stars positioned on the lower left part

of the FPA, with high or low magnitude as well as

sub-pixel positions in the center and on the corner are

critical for the precision of the FGS and are therefore

suitable as test cases for FGS robustness tests.

ICSOFT 2024 - 19th International Conference on Software Technologies

216

Detection of Errors. So far, we have only evaluated

the PCA results on the EC data format. Since both

data formats preprocess the same GA results and an

EC combination is related to a star ID, the results from

the starID data format highlight the same ECs as the

results from the EC data format. Therefore, we use the

EC data format to show a more detailed view on the

effect of speciﬁc input parameters.

However, the PCA results on the starID data format

provides a view on the evolutionary process that is

tailored to understand the role of particular stars. We

have grouped the loading values for the starID data

format based on star parameters to record trends in

the parameter ECs. By comparing the loading values

of both data formats, we have detected some cases,

where the PCA results for the starID data format do

not match with the understanding gained from the EC

data format. Interestingly, this means that we have

identiﬁed cases where star loading values should not

correlate with the ﬁtness loading value according to

the analysis performed on the EC data format, but still

lead to a high jitter deviation, as shown by their high

correlation with the ﬁtness loading value on the starID

data format and the other way around.

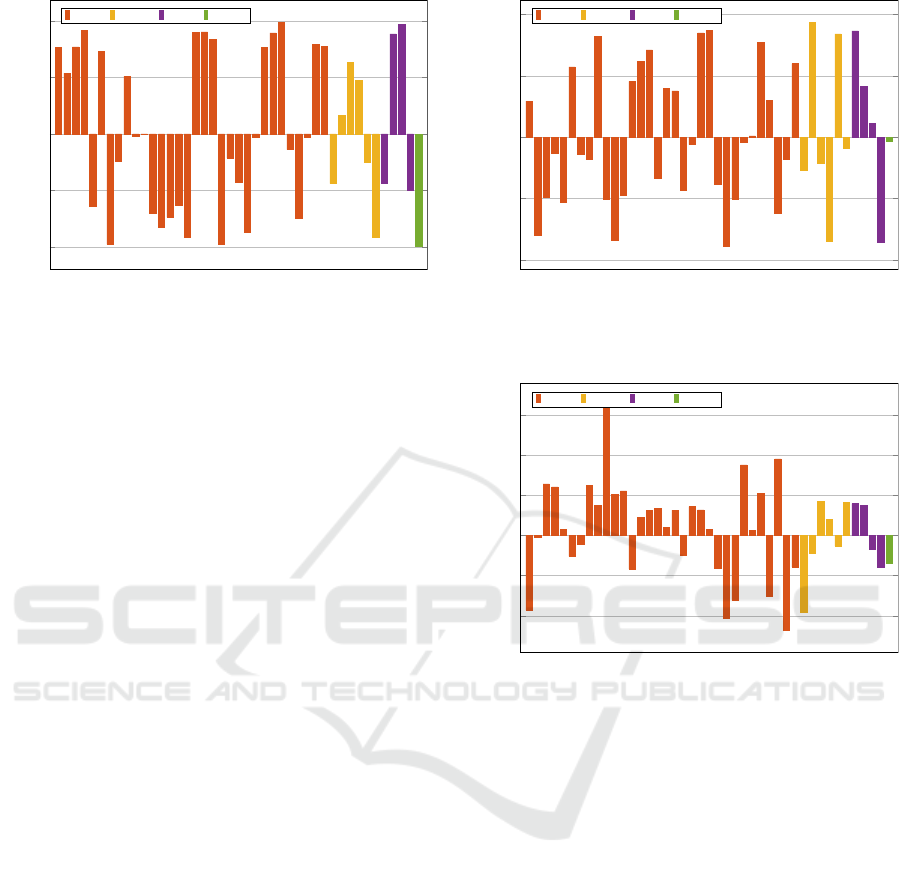
From Figure 9, we see that the FPA position class

Pos-16 does not correlate with the ﬁtness value, but

Pos-20 does. Considering the loading values of the

starID data format grouped for ECs Pos-16 in Fig-

ure 12a and Pos-20 in Figure 12b we notice that the

majority of the loading values show the same behavior

to the ﬁtness value as Figure 9. However, Figure 12a

depicts a high correlation between star ID 387 that

belongs to Pos-16 and the ﬁtness value. Moreover,

we see in Figure 12b that star ID 499 in Pos-20 does

not correlate with the ﬁtness value. After a closer

analysis of the calculated star centroid position, we

have detected an error in a coordinate transformation

that affected a few stars. The error leads to an incor-

rect attitude and thus to an exceptional ﬁtness value.

The visualizations and explanations generated from

the PCA on the starID data format proved to be very

helpful to detect and ﬁx the error in the FGS algorithm.

6 CONCLUSION

In this paper, we have presented an approach for post-

hoc explainability of genetic test generation algorithms.

Our key contributions are two novel data formats to

prepare the data generated by the genetic test genera-

tion algorithm for a PCA, a technique to apply a PCA

to these data formats, as well as a method to visualize

and evaluate the resulting data. Our approach simpli-

ﬁes the analysis of test cases generated by the GA and

401

398

399

400

402

397

404

405

406

407

403

396

384

394

385

386

387

388

395

390

391

392

393

389

−1

−0.8

−0.6

−0.4

−0.2

0.2

0.4

0.6

0.8

Star ID’s

PC1

Pos-16

Fitness

(a) StarID loading values, Pos-16.

494

503

502

501

500

499

498

497

496

495

493

492

491

481

482

483

484

485

480

487

488

489

490

486

−0.6

−0.4

−0.2

0.2

0.4

0.6

0.8

Star ID’s

PC1

Pos-20

Fitness

(b) StarID loading values, Pos-20.

Figure 12: Loading values per starID.

enables us to identify parameters that inﬂuence the GA

solution. This makes it possible to reveal explanations

why the test generation algorithm has chosen certain

inputs and input combinations. These explanations

increase the conﬁdence in the generated test cases and

can be used to gain a deeper understanding of the test

generation process and the system under test.

We have applied our proposed approach to the FGS

of the PLATO mission. The FGS computes the atti-

tude of the satellite from given images of input stars.

We have used an existing GA together with a novel

ﬁtness function to search for input star combinations

where jitter has a high inﬂuence on the precision of the

results. Then, we have used our novel explainability

approach to identify which input stars mostly inﬂu-

ence the precision of the FGS algorithm. Moreover,

the results helped to ﬁnd an error in the FGS algorithm

that affected only a few stars.

In future work, we plan to use our explainability

approach also to identify stars that are particularly well

suited as guide stars for the FGS of the PLATO mission.

Further, we plan to investigate other approaches such

as MAP-Elites and surrogate ﬁtness functions.

Improving Robustness of Satellite Image Processing Using Principal Component Analysis for Explainability

217

REFERENCES

Brownlee, A., Wallace, A., and Cairns, D. (2021). Min-

ing markov network surrogates to explain the results of

metaheuristic optimisation. In SICSA eXplainable Artif-

ical Intelligence Workshop 2021, pages 64–70. CEUR

Workshop Proceedings.

Deb, K., Bandaru, S., Greiner, D., Gaspar-Cunha, A., and

Tutum, C. C. (2014). An integrated approach to auto-

mated innovization for discovering useful design prin-

ciples: Case studies from engineering. Applied Soft

Computing, 15:42–56.

silovi

c, F. K., Br

c, M., and Hlupi

c, N. (2018). Ex-

plainable artiﬁcial intelligence: A survey. In 2018 41st

International convention on information and commu-

nication technology, electronics and microelectronics

(MIPRO), pages 0210–0215. IEEE.

European Space Agency (2022). ESA - cosmic vi-

sion. https://www.esa.int/Science Exploration/Space

Science/ESA s Cosmic Vision.

Fyvie, M., McCall, J. A., and Christie, L. A. (2021). To-

wards explainable metaheuristics: Pca for trajectory

mining in evolutionary algorithms. In International

Conference on Innovative Techniques and Applications

of Artiﬁcial Intelligence, pages 89–102. Springer.

Grießbach, D., Witteck, U., and Paproth, C. (2021). The ﬁne

guidance system of the PLATO mission. In Cugny, B.,

Sodnik, Z., and Karafolas, N., editors, International

Conference on Space Optics — ICSO 2020, volume

11852, page 118523H. International Society for Optics

and Photonics, SPIE.

Harris, C. R., Millman, K. J., van der Walt, S. J., Gommers,

R., Virtanen, P., Cournapeau, D., Wieser, E., Taylor,

J., Berg, S., Smith, N. J., Kern, R., Picus, M., Hoyer,

S., van Kerkwijk, M. H., Brett, M., Haldane, A., del

ıo, J. F., Wiebe, M., Peterson, P., G

erard-Marchant,

P., Sheppard, K., Reddy, T., Weckesser, W., Abbasi,

H., Gohlke, C., and Oliphant, T. E. (2020). Array

programming with NumPy. Nature, 585(7825):357–

362.

Holzinger, A. (2021). The next frontier: Ai we can re-

ally trust. In Joint European conference on machine

learning and knowledge discovery in databases, pages

427–440. Springer.

Islam, M. R., Ahmed, M. U., Barua, S., and Begum, S.

(2022). A systematic review of explainable artiﬁcial

intelligence in terms of different application domains

and tasks. Applied Sciences, 12(3):1353.

Lipton, Z. C. (2018). The mythos of model interpretability:

In machine learning, the concept of interpretability is

both important and slippery. Queue, 16(3):31–57.

Martin Pertenais, P. P. T. (2022). Instrument technical re-

quirement document. PLATO-DLR-PL-RS-0001.

Mirjalili, S., Lewis, A., and Mostaghim, S. (2015). Con-

ﬁdence measure: a novel metric for robust meta-

heuristic optimisation algorithms. Information Sci-

ences, 317:114–142.

Mouret, J.-B. and Clune, J. (2015). Illuminating search

spaces by mapping elites. arXiv e-prints, pages arXiv–

1504.

Pedregosa, F., Varoquaux, G., Gramfort, A., Michel, V.,

Thirion, B., Grisel, O., Blondel, M., Prettenhofer, P.,

Weiss, R., Dubourg, V., Vanderplas, J., Passos, A.,

Cournapeau, D., Brucher, M., Perrot, M., and Duch-

esnay, E. (2011). Scikit-learn: Machine learning

in Python. Journal of Machine Learning Research,

12:2825–2830.

Plotly Technologies Inc. (2015). Collaborative data science.

https://plot.ly.

Reris, R. and Brooks, J. P. (2015). Principal component

analysis and optimization: A tutorial. 14th INFORMS

Computing Society Conference, pages 212–225.

Shlens, J. (2014). A tutorial on principal component analysis.

arXiv preprint arXiv:1404.1100.

Stambke, J. (2023). Principal component analysis for ex-

plainability of genetic test generation in satellite image

processing.

The HDF Group (2006). Hierarchical Data Format, version

5. https://github.com/HDFGroup/hdf5.

The pandas development team (2022). pandas-dev/pandas:

Pandas. https://doi.org/10.5281/zenodo.4309786.

Urquhart, N., Guckert, M., and Powers, S. (2019). Increasing

trust in meta-heuristics by using map-elites. In Pro-

ceedings of the Genetic and Evolutionary Computation

Conference Companion, pages 1345–1348.

Urquhart, N., H

ohl, S., and Hart, E. (2021). Automated,

explainable rule extraction from map-elites archives.

In International Conference on the Applications of

Evolutionary Computation (Part of EvoStar), pages

258–272. Springer.

Wallace, A., Brownlee, A. E., and Cairns, D. (2021). To-

wards explaining metaheuristic solution quality by data

mining surrogate ﬁtness models for importance of vari-

ables. In International Conference on Innovative Tech-

niques and Applications of Artiﬁcial Intelligence, pages

58–72. Springer.

Witteck, U., Grießbach, D., and Herber, P. (2019). Equiva-

lence class deﬁnition for automated testing of satellite

on-board image processing. In International Confer-

ence on Software Technologies, pages 3–25. Springer.

Witteck, U., Grießbach, D., and Herber, P. (2020). A genetic

algorithm with tournament selection for automated

testing of satellite on-board image processing. In Inter-

national Conference on Software Technologies, pages

134–157. Springer.

Wu, W., Massart, D., and de Jong, S. (1997). The kernel

pca algorithms for wide data. part i: Theory and al-

gorithms. Chemometrics and Intelligent Laboratory

Systems, 36(2):165–172.

Xu, F., Uszkoreit, H., Du, Y., Fan, W., Zhao, D., and Zhu,

J. (2019). Explainable ai: A brief survey on history,

research areas, approaches and challenges. In CCF in-

ternational conference on natural language processing

and Chinese computing, pages 563–574. Springer.

ICSOFT 2024 - 19th International Conference on Software Technologies

218