Evaluating the Multifactorial Effects on SARS-CoV-2 Spread in

Tokyo Metropolitan Area with an Agent-Based Model

Jianing Chu

and Yu Chen

SCS Laboratory, The University of Tokyo, Kashiwanoha 5-1-5, Chiba, Japan

Keywords: Agent-Based Modelling, COVID-19, IgG, PCR Testing, Vaccination.

Abstract: The eighth wave of Coronavirus infection in Tokyo hit high records in December 2022. This paper aims to

build a Tokyo-based down-scaled simulation environment to explain the eight epidemic trends using agent-

based modelling and extended SEIR denotation. Four key factors are examined in this research, that are: 1.

Vaccination, 2. Virus mutation, 3. Government policy and 4. PCR test. Our investigation uncovers that the

reported cases during the eight epidemic waves represent merely a fraction of the true extent of infections.

Additionally, our study innovates by simulating the decline of antibodies at the individual level. Our study

also innovates in combining agent-based modelling and extended SEIR modelling to simulate eight

continuous epidemic waves in Tokyo, considering circumstances like Olympics, state of emergency

declaration, traveling policies etc. Upon analyzing the simulated outcomes, we observe a correlation between

the onset of new epidemic waves and the decrease in the population possessing antibodies. Our simulation

further indicates the necessity for aligning the level of PCR testing with the available medical resources.

Finally, by comparing the simulation results with actual data for the eighth wave, we forewarned of a potential

resurgence in the epidemic during May and June 2023.

1 INTRODUCTION

On May 8, 2023, a significant measure was taken in

Japan as the government downgraded COVID-19

from a class 2 infectious disease to a class 5 disease,

marking a pivotal moment in the country's fight

against the virus. This reclassification signifies a shift

in the severity and risk assessment of COVID-19 in

Japan, prompting a re-evaluation of public health

policies and strategies. This paper specifically

focuses on the critical contribution of epidemiology

in the context of SARS-CoV-2 in Japan, aiming to

shed light on its vital role in advancing global health

objectives during the ongoing COVID-19 pandemic.

At the initiation of our study, we posit that the

epidemic trend is chiefly shaped by four aspects:

vaccination; virus mutation; government policy, and

PCR testing. This assumption is grounded in the

following considerations: 1) vaccination plays a

crucial role in generating antibodies, thereby curbing

the spread of the Coronavirus; 2) mutations in the

https://orcid.org/0009-0009-0495-1376

https://orcid.org/0000-0002-7075-2457

Table 1: Summary of agents’ health status.

virus can potentially enhance its transmissibility by

evading immunity; 3) government policies, such as

travel restrictions, aim to mitigate the spread of the

virus; and 4) the adequacy of PCR testing capacity

significantly influences the tally of confirmed cases.

This study utilizes an extended SEIR framework

(refer to Table 1) along with the construction of an

States Meanings

S1 Susceptible, healthy, no antibody or vaccination

E Exposed, within the infection range to I1

I1 Infected, unconfirmed and not tested

I2 Infected, confirmed via PCR test

V Healthy, vaccinated, possess antibody

R Healthy, cured, possess antibody

S2 Healthy, susceptible, vaccinated, lose antibody

D Dead

Chu, J. and Chen, Y.

Evaluating the Multifactorial Effects on SARS-CoV-2 Spread in Tokyo Metropolitan Area with an Agent-Based Model.

DOI: 10.5220/0012726400003708

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 9th International Conference on Complexity, Future Information Systems and Risk (COMPLEXIS 2024), pages 30-42

ISBN: 978-989-758-698-9; ISSN: 2184-5034

agent-based model. Further elaboration on these

methods will be presented in Sec. 3. The actual data

pertaining to the four factors mentioned are sourced

from the Tokyo Metropolitan Government and will be

utilized for model validation. Our primary objective

is to replicate the onset, peak, decline, and maximum

daily infection rates of each wave. In continuation of

our previous study (Chu et al., 2023), our goal is to

not only explain the occurrence of the eight waves but

to simulate possible infectious diseases in the future.

The paper is structured as follows: Firstly, we

review existing literature on Coronavirus modelling

research, covering both international and Japanese

studies (Sec. 2). Next, in the data and methodology

section (Sec. 3), we explore the four key

considerations and elaborate on our research

methodology. Following that, in the model

construction section (Sec. 4), we explain how the

model was developed. Then, in the verification and

calibration phase (Sec. 5), we offer substantial

evidence of the model's effectiveness, a long with

a cautious calibration process. Subsequently, we

conduct analysis and depict findings from simulations

(Sec. 6). Finally, we summarize recommendations

and draw conclusions (Sec. 7).

2 LITERATURE REVIEW

2.1 A Review of International Research

To provide a comprehensive overview, this literature

review begins by examining the current state of

international research in the field.

Purkayastha and colleagues compare the

simulation results among five epidemiological

models for transmission of SARS-CoV-2 in India

(Purkayastha et al., 2021). According to their

research, SEIR-FANSY model outperforms others by

having the highest certainty in terms of width of 95%

credible interval. Still their research fails to capture

the government interventions or citizen’s behavioural

changes. While policies like lockdown across India

did play an unignorable role in epidemic spreads.

Chadi and others pointed out the problems of

vaccine distribution, whether to prioritize vaccinating

those who had received the first dose or those who

had never vaccinated (Saad-Roy et al., 2021). Despite

the controversy surrounding this approach, many

jurisdictions have decided to proceed with the

delayed second dose strategy. This has resulted in a

significant increase in the number of people who have

been vaccinated. Researchers, however, argue that

one-dose strategies may be effective in the short term,

but may not be the best approach in the long term if

they do not account for immune robustness. Their

study serves as inspiration to properly ensure the

vaccination rate of the second dose when conducting

vaccination simulations.

Hoertel and others build a stochastic ABM model

based on real-world data, including information on

the demographics of the French population, the

transmission dynamics of the virus, and the

effectiveness of various NPIs (Hoertel et al., 2020).

The model was applied to simulate the spread of the

disease under different scenarios, including the

implementation of different NPIs such as social

distancing, mask wearing, and contact tracing. Their

model is well calibrated and validated with a

Pearson’s R value of 0.99 for ICU-bed occupancy as

well as cumulative mortality. One of the limitations

of their research is not considering the decline of

antibodies which an individual acquires through

either recovery or vaccination.

Cai and his team developed an age-structured

stochastic compartmental susceptible-latent-

infectious-removed-susceptible model to simulate

transmission of SARS-CoV-2 Omicron in China (Cai

et al., 2022). Furthermore, their model takes into

account specific data on vaccine coverage among

different age groups, the effectiveness of vaccines

against various clinical outcomes, the gradual decline

of immune protection over time, the utilization of

diverse antiviral therapies, and the implementation of

nonpharmaceutical interventions. Nonetheless, the

mortality rate was assumed to remain constant over

the projection period, while it actually depends on

multiple factors such as virulence and medical

resources.

2.2 A Review of Japanese Research

To delve deeper into the subject matter, the literature

review then shifts focus to research conducted by

Japanese scholars.

Chiba outlines strategies for controlling the

spread of epidemics in Japan, focusing on mobility

restrictions, reduced restaurant operating hours, and

remote work (Chiba, 2021).

Yamauchi et al. investigate the relationship

between epidemic trends, governmental

interventions, and daytime population density in

Tokyo. Their findings indicate a positive correlation

between increased contact opportunities and higher

infection rates (Yamauchi et al., 2022).

Murakami et al. employ agent-based modelling

and GPS analysis to simulate the spread and

containment of infections in Tokyo. Their research

Evaluating the Multifactorial Effects on SARS-CoV-2 Spread in Tokyo Metropolitan Area with an Agent-Based Model

underscores the significance of city-wide lockdowns

and preventive measures in service establishments

(Murakami et al., 2022).

While several studies have contributed valuable

insights into the transmission dynamics and control

strategies of COVID-19, there are still important

research gaps that need to be addressed, such as the

absence of simulation models that incorporate

antibody decline on an individual level, the lack of

consideration for the impact of declining immunity

due to recovery or vaccination, and the need to

explore optimal vaccination strategies. Furthermore,

existing research often fails to capture the oscillatory

growth and decay behavior of the virus incidence

curve, particularly in terms of the subsequent waves

after the initial outbreak. This limitation in

predictability is particularly relevant given the

observation that the number of confirmed patients in

the eight epidemic waves in the Tokyo were only the

tip of the iceberg. Difference in prediction and

observation suggests a need for more comprehensive

modelling approaches. Moreover, the literature

review reveals that previous studies have not fully

accounted for the interplay between government

interventions, citizen behavioral changes, and the

dynamics of virus transmission. Understanding the

role of government policies and individual behaviors

in the spread of the virus is crucial for designing

effective control measures.

To address all these research gaps, this study aims

to explain the eight epidemic waves in the Tokyo

using agent-based modelling and an extended SEIR

denotation. By incorporating the dynamics of

antibody decline on an individual level and

considering factors such as vaccination, virus

mutation, government policy, and PCR test, this

research seeks to provide a more comprehensive

understanding of the transmission dynamics and

control strategies for COVID-19 in the Tokyo area.

3 DATA AND METHODOLOGY

3.1 Data Collection

We conducted a preliminary examination of the four

proposed factors using publicly available data and

information from the Tokyo Metropolitan website.

All the gathered data and information are utilized in

the model development outlined in Sec. 4.

Severe rate = The number of severe patients receiving

medical treatment/ The number of confirmed patients.

3.1.1 Vaccination

It is clear that mass vaccination plays a crucial role in

decreasing the severity and mortality rates (Larrauri

et al., 2022). Table 2 provides an overview of the five

vaccination rounds

conducted in Tokyo.

Table 2: Timeline of vaccination rounds in Tokyo and

vaccination rates as of Nov. 30, 2022.

Table 3: Timeline of mutated variants first detected in

Tokyo and the relative severe rates.

Date Events Severe

rate

2020.01.24 1

COVID-19 case detected 23.81%

2021.01.12 1

Gamma case detected 0.76%

2021.04.20 1

Delta case detected 1.00%

2021.08.31 1

Delta N501S case detected 0.84%

2021.11.30 1

Omicron case detected 3.57%

2021.12.25

(Approx.)

Omicron BA.2 case detected 0.56%

2022.04.12 1

Omicron XE case detected 0.02%

2022.04.22 1

Omicron BA.4 case detected 0.02%

2022.04.29 1

Omicron BA.5 case detected 0.02%

2022.07.13 1

Omicron BA.2.75 case detected 0.05%

2022.07-

2022.10

(Approx.)

Omicron BA.4.6 case detected

Omicron BF.7 case detected

Omicron BN.1 case detected

Omicron BQ.1 case detected

Omicron BQ1.1 case detecte

0.02%

~0.06%

2022.10.28 1

Omicron XBB case detected 0.01%

Vaccination

round

Starting

Date

Interval

between doses

Vaccination

rate

2021.04.12 Not applicable 78.1%

2021.05.03 3~8 weeks 77.5%

2021.12.01 6~7 months 65.7%

2022.05.25 5~6 months 80.4% for

the elderly

Bivalent 2022.09.20 3 months -

COMPLEXIS 2024 - 9th International Conference on Complexity, Future Information Systems and Risk

3.1.2 Virus Mutation

Table 3 provides an overview of the initial detection

dates of notable mutated viruses in Japan, alongside

their corresponding severity rates. As depicted in

Table 3, there is an observable trend indicating a

decrease in virus lethality.

3.1.3 Government Policy

When examining governmental measures, this paper

highlights municipal governance, healthcare

interventions, border controls, and preventative

measures related to the Olympics. The Tokyo

Metropolitan Government implemented seven states

of emergency, as detailed in Table 4. While standard

regulations were enforced during four of these

emergencies, the remaining three saw relaxed

regulations. Additionally, Tokyo adopted Highly

Active Antiretroviral Therapy (HAART Therapy) for

COVID-19 treatment starting July 19, 2021 (Table 5).

Table 4: Timeline of state of emergency/ quasi-state of

emergency in Tokyo.

Events Duration

wave state of emergency 2020.04.07~2020.05.25

wave state of emergency 2021.01.08~2021.03.21

wave quasi-state of emergency 2021.04.12~2021.04.24

wave state of emergency 2021.04.25~2021.06.20

wave quasi-state of emergency 2021.06.21~2021.07.11

wave state of emergency 2021.07.12~2021.09.30

wave quasi-state of emergency 2022.01.21~2022.03.21

Table 5: Government approved COVID-19 therapies and

relevant death rates of the confirmed cases.

Therapies Duration Death%

Before HAART Therapy 2020.01.26 ~ 2021.07.18 1.2%

HAART Therapy applied 2021.07.19 ~ 2021.12.23 0.45%

Lagevrio and Paxlovid 2021.12.24 ~ 2022.11.27 0.10%

Distribution of ‘Xocova’ 2022.11.28 ~ 2023.01.02 0.001%

The Ministry of Health, Labour and Welfare of

Japan authorized the emergency use of Shionogi's

oral medication, 'Xocova,' for COVID-19 treatment

on November 22, 2022 (Matsuyama, 2022).

Distribution of 'Xocova' commenced on November

28, 2022, benefiting approximately 1 million citizens.

This development contributed to a further decrease in

the severity and mortality rates (refer to Table. 5).

Regarding border measures, Japan briefly opened

its borders to foreign residents twice in 2020. Since

Oct 11, 2022, Japan has ceased border operations,

fully reopening its border to independent travellers

with no daily cap.

Japan held the Tokyo Olympics from July 23 to

August 8, 2021. The first Olympic team arrived in

Japan on June 1, 2021 (Zhang, 2021). Athletes were

required to depart within 48 hours of completing their

events (International_Olympic_Committee, 2021),

implying a departure period from July 25 to August

10, 2021. Approximately 79,000 individuals travelled

to Japan for the Tokyo Olympics (McCurry, 2021).

3.1.4 PCR Test

The PCR (Polymerase Chain Reaction) test detects

genetic material from specific pathogens and is

widely used for diagnosing COVID-19. In Tokyo,

PCR testing is conducted either by medical

institutions or health centers, with the latter primarily

responsible for conducting major inspections.

Typically, Tokyo residents undergo PCR testing on a

voluntary basis, following the advice of their

physicians and assessing their own health conditions.

Criticism regarding the shortage of PCR testing

capacity has been persistent.

As of March 6, 2022, PCR testing has been

covered by medical insurance. This allows medical

facilities to directly solicit tests from private testing

institutes and other entities. Additionally, with

insurance coverage approval for the antigen detection

kit "Lumipulse SARS-CoV-2 Ag", saliva-based tests

were accessible to asymptomatic patients from July

17, 2022 (MHLW, 2023b). Moreover, residents can

opt to register on the Tokyo Metropolitan

Government website to receive a complimentary

antigen test kit delivered to their home if they believe

they have symptoms or have been in close contact

with an infected individual. This measure helps

alleviate the burden on medical facilities for testing

and consultations. In the event of a positive antigen

test result, the individual can promptly begin a 14-day

self-quarantine to mitigate further transmission of the

infection.

3.1.5 Other Considerations

Another aspect taken into account in this study is

school breaks. During winter, spring, and summer

vacations, students tend to travel longer distances

compared to regular term periods.

Evaluating the Multifactorial Effects on SARS-CoV-2 Spread in Tokyo Metropolitan Area with an Agent-Based Model

3.2 Methodology Discussion

3.2.1 Agent-Based Modelling

In this research, we utilize NetLogo (Wilensky,

1999), a beautiful agent-based modelling (ABM)

software, to simulate the dynamics of the epidemic.

The rationale behind this choice is rooted in ABM's

ability to capture the nuanced individual

heterogeneity within complex environments. When

studying large-scale epidemic phenomena, it's crucial

to account for variations in individual attributes due

to the significant social and physical interactions

among them. ABM can be fine-tuned by adjusting

model parameters to ensure that the calculated R0

aligns with real-world measurements.

3.2.2 Extended SEIR Denotation

Our model incorporates individual health statuses,

drawing inspiration from the SEIR model (Hethcote,

2000), while also introducing additional statuses such

as 'Vaccinated' and 'Dead', enhancing the precision of

health status description (Refer to Table 1).

4 MODEL CONSTRUCTION

4.1 Space and Population

A total of 13,920,000 individuals reside in Tokyo,

resulting in a population density of 6,264 individuals

per square kilometre (Statistics Bureau of Japan,

2021). The city has approximately 7,291 hospital

beds in total. Assuming uniform distribution of static

properties (such as infrastructure) and identical

distribution of dynamic properties (such as

population movement) throughout Tokyo city, our

approach involves constructing a rectangular block

measuring 2 kilometres in length, designed to mimic

the geometry of the Tokyo area. Epidemic dynamics

are simulated within this block using downscaled

population and infrastructure figures. Refer to Fig 1

for further details.

By applying the aforementioned uniformity

assumptions, the entire Tokyo region, comprising 23

municipalities, is linearly downscaled into a

rectangular block measuring 2 kilometres in length and

1 kilometre in width. It should be emphasized that the

population density and hospital’s capacity depicted in

Fig. 1 correspond to actual data. The adjusted count of

entries and exits to and from a block fluctuates with

each time interval in response to governmental

directives and incoming and outgoing data.

Figure 1: Illustration of post-scaled simulation

environment.

4.2 Social Contact

In the model, agents are initially distributed

randomly, with their location recorded as their place

of residence. We presume that at the start of each day,

all agents, excluding the quarantined ones, have the

freedom to roam outdoors randomly for up to 8 hours

in any direction within a radius denoted as 𝑟



. This

range matches their typical daily activities and varies

based on their identity (whether they are employed,

students, or unemployed). During these random

walks, agents have opportunities to encounter other

pedestrians, potentially leading to infection

transmission. At the end of the day, agents return to

their designated residences.

Although the social contact model described in

this paper may not fully account for individual

interactions at a precise level, we expect that its

collective results will closely mirror those observed

in broader epidemic contexts. A similar principle is

evident in the microscopic modelling of fluid

dynamics: despite variations in the molecules and

interaction potentials of distinctive fluids, large-scale

flow dynamics adhere to the same governing

equation. This concept is echoed by Wolfram in his

book on complex systems (Wolfram & Gad-el-Hak,

2003), where he highlights that although the

underlying rules may differ across systems, the

overall outcomes remain consistent.

4.3 Detailed Model Construction

The comprehensive system flowchart is depicted in

Fig 2. Initially, we establish the patches area,

synthetic population, and central hospital.

Subsequently, the model processes input data from a

file, which includes various parameters such as the

COMPLEXIS 2024 - 9th International Conference on Complexity, Future Information Systems and Risk

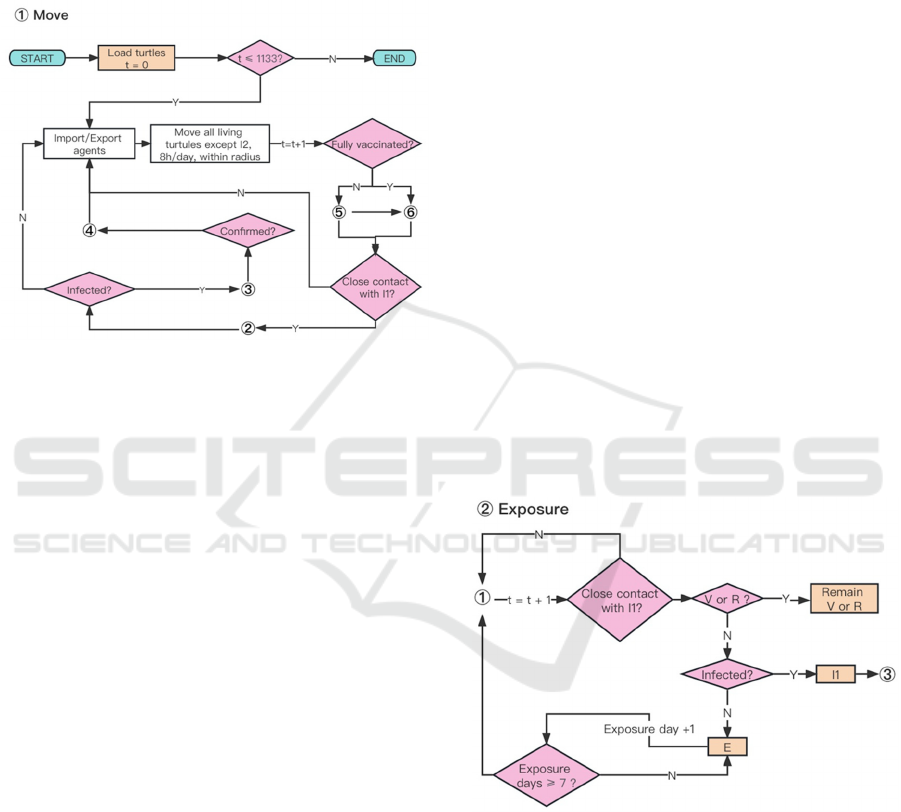
daily vaccine capacity, number of daily entries and

exits, daily quota for PCR tests, infection probability

for three levels of social distancing, maximum daily

travel distance for three occupational categories, and

mortality rates associated with different virus

variants.

Figure 2: System flow chart of the simulation process.

Using published inbound and outbound traveler

statistics, we introduce unconfirmed patients

(represented as agents in category I1) and randomly

export agents on a daily basis. Imported agents are

also categorized based on their occupation. All

surviving agents, with the exception of those in

category I2, are permitted to move within specified

distance boundaries corresponding to their respective

occupations.

4.3.1 Health States and Population

We extend the SEIR categorization to encompass a

total of eight health statuses for agents. (refer to Table

1). Furthermore, we segment the infected state into

two subcategories, namely I1 and I2. Upon

identification, confirmed cases (I2) are required to

self-quarantine at home, thereby reducing their

potential for public transmission compared to

unconfirmed infected agents (I1). There are 𝑁



agents in this synthetic population. Among these

agents, populations in different states are represented

as 𝑁



, 𝑁



, 𝑁



, 𝑁



, 𝑁



, 𝑁



, 𝑁



, 𝑁



respectively.

4.3.2 Susceptible

At the onset of the simulation (t=0), all agents are

initially set to be susceptible (S1), with no individuals

infected with the Coronavirus. Agents' home

positions are noted, and they are permitted to travel

from their homes to locations within a designated

radius denoted as 𝑟



. Agents are allowed to venture

out for a duration of eight hours daily, with movement

unrestricted in direction. Upon reaching the boundary

of the designated space, agents will rebound.

4.3.3 Exposure

Since the onset of imported cases spreading across the

Tokyo on January 24, 2020, we designate this date as

t=1. Over time, individuals who come into contact

with asymptomatic cases (agents in state I1) have a

chance of infection if they lack antibodies (see Fig.

3). The probability of transitioning from the

Susceptible state to the Exposed state (S1→E) is

calculated as follows:

𝑃

→

𝐻𝑑

,

𝑑



 (1)

Here, 𝐻𝑥represents the Heaviside step function,

and 𝑑

,

denotes the shortest distance between agents

in state X and agents in state Y. The threshold

distance, denoted as 𝑑



, is set to 2 units of patch size,

based on facts provided by the Ministry of Health,

Labour, and Welfare, which states that physical

proximity within 2 meters is considered close contact

with a possibility of Coronavirus transmission

(MHLW, 2023a).

Figure 3: ‘Exposure’ in ABM.

4.3.4 Infection

Agents in state I1 have the potential to transmit

Coronavirus to nearby agents (all surviving agents

except for I1 and I2), exposing them to the virus

within a specified distance. However, agents with

antibodies above a certain threshold (in states V or R)

cannot transition to the Exposed state (E). Exposed

agents have a probability of developing symptoms

and becoming infected within the subsequent 14 days.

Evaluating the Multifactorial Effects on SARS-CoV-2 Spread in Tokyo Metropolitan Area with an Agent-Based Model

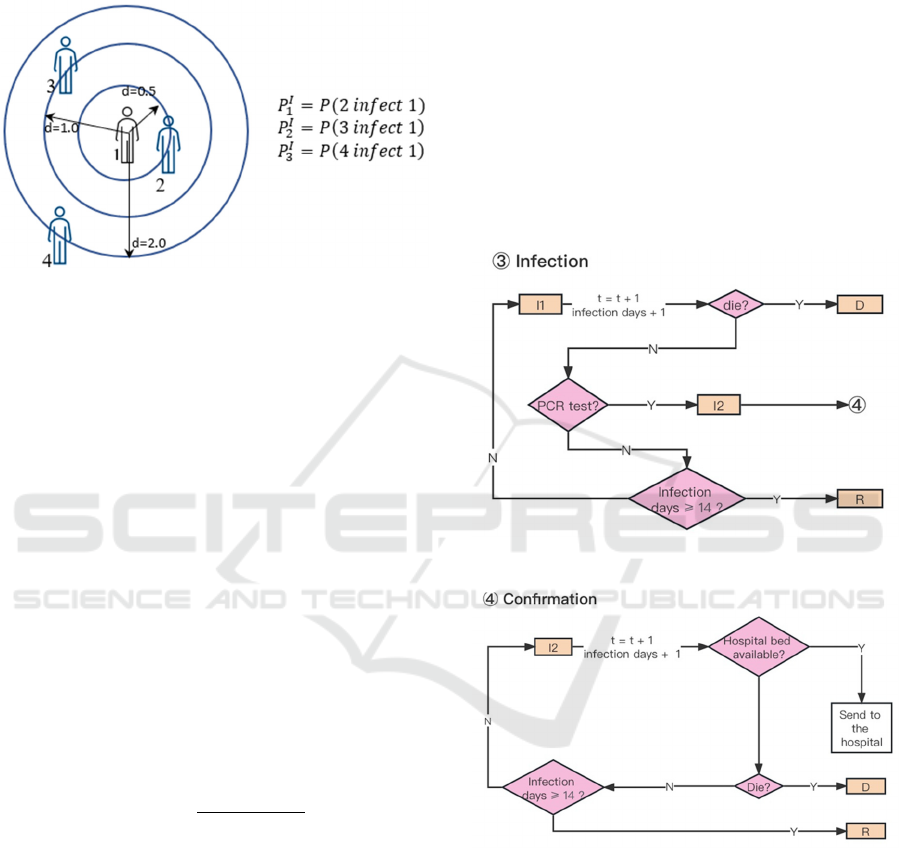
The likelihood of an exposed agent (in state E)

contracting Coronavirus relys on the distance at

which the agent encountered another agent in state I1,

as illustrated in Fig. 4.

Figure 4: Illustration of agents’ infection pattern.

The probability of infection (𝑃

→

) is defined as,

𝑃

→



𝑃





0𝑑

,

0.5

𝑃





0.5𝑑

,

1.0

𝑃





1.0𝑑

,

2.0

(2)

Whenever the virus undergoes mutation, the

probabilities of infection are adjusted based on the

characteristics of the viruses. If exposed agents are

fortunate enough to avoid infection, their states will

revert back to S1 (E→S1). All agents, except the ones

confirmed with infection (in state I2), will undergo

PCR tests with a probability denoted as 𝑃





𝑛



/𝑁



 𝑁



 𝑁



 per day, where 𝑛



represents the data of downscaled PCR tests released

by the Tokyo Metropolitan Government. Upon

confirmation of infectivity through PCR tests, the I1

state agents will be reclassified as I2 state (see Fig. 5).

This implies that the transition probability for an

individual can be computed as follows:

𝑃

→























. (3)

If an agent is currently in I2 state, movement shall

be restricted until the subsequent state transition

occurs, either to R (recovery) or D (death).

4.3.5 Recovery or Death

Agents testing positive for Coronavirus (in state I2)

immediately begin a 14-day self-quarantine. Some

may be hospitalized if beds are available, reducing

mortality rates compared to home isolation. If not

confirmed within 14 days, infected agents (in state I1)

may move freely until recovery (I1→R) or death (I1

→ D). Deceased agents are removed from the

simulation, while recovered agents gain antibodies

and resume movement (see Fig. 6).

4.3.6 Vaccination

The daily vaccine supply quota prioritizes individuals

for their second dose within three to seven weeks,

with subsequent doses spaced accordingly (Fig. 7).

All surviving individuals except confirmed, are

eligible for vaccination while quotas last. Pfizer

vaccine efficacy, estimated at 52% for the first dose

and 91% for the second (Polack et al., 2020), is

modelled despite vaccine brand options. Our model

accounts for antibody titer decay, a factor often

overlooked in existing literature.

Figure 5: ‘Infection’ in ABM.

Figure 6: ‘Confirmation’ in ABM.

4.3.7 Antibody Decline

Antibodies are gained via vaccination or recovery,

with natural recovery showing slower decline rates

(Israel et al., 2022). The IgG test measures COVID-

19 antibodies, with Narasimhan et al. setting a

positive threshold at 50 AU/mL (Narasimhan et al.,

2021), while Ebinger et al. suggest 4160 AU/mL for

serum neutralizing activity (Ebinger et al., 2021).

COMPLEXIS 2024 - 9th International Conference on Complexity, Future Information Systems and Risk

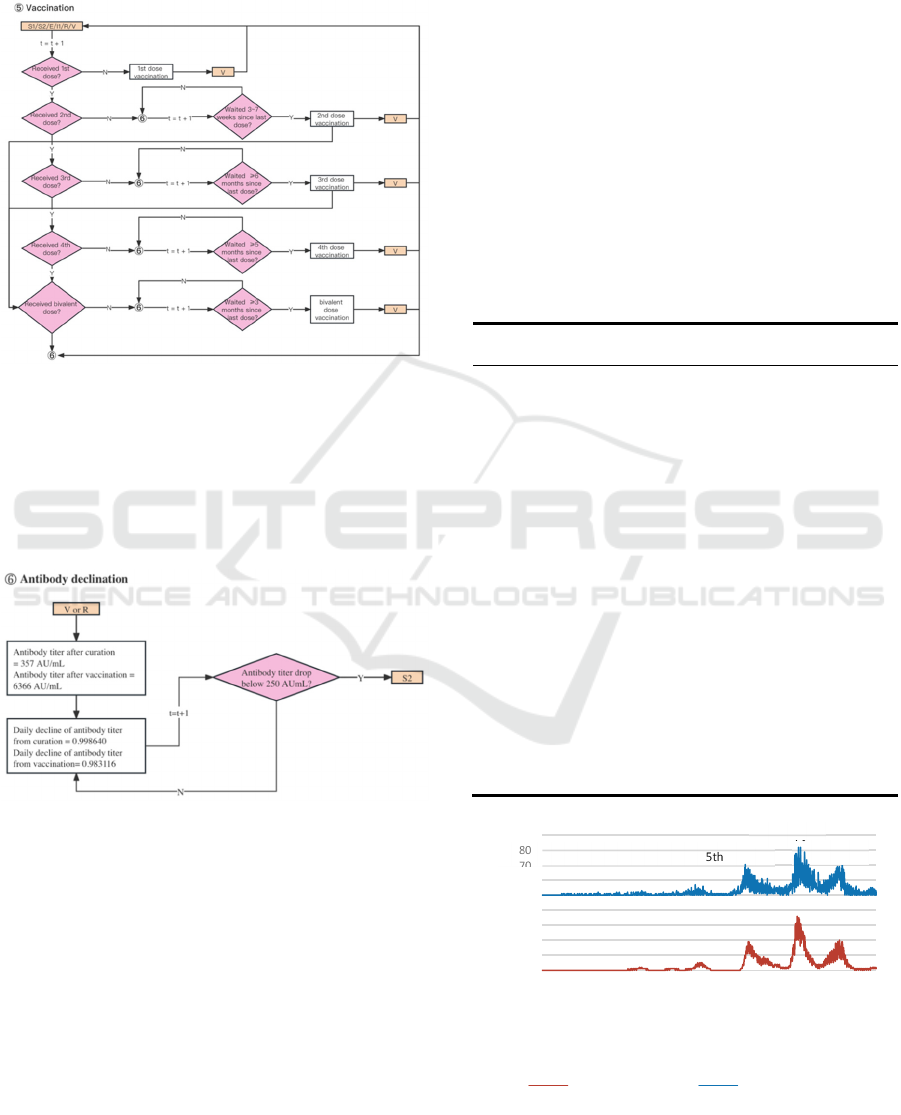
In our model, individual antibody levels decrease

over time based on previous studies. Once levels drop

below a calibrated threshold, individuals transition to

S2 status (V/R→S2).

Figure 7: ‘Vaccination’ in ABM.

As per Ariel Israel et al., recipients of the Pfizer-

BioNTech mRNA vaccine exhibit varying antibody

levels compared to those who contracted the SARS-

CoV-2 virus (see Fig. 8). Antibody concentrations

gained via vaccination are initially higher but decline

at a quicker pace (Israel et al., 2022).

Figure 8: ‘Antibody decline’ in ABM.

5 VERIFICATION AND

CALIBRATION

5.1 Verification of Linear Scaling

In Sec 4.1, Tokyo is downscaled into a 2km by 1km

block, accommodating 12,528 susceptible agents and

a hospital for 6 infected agents. We use a factor 𝜆

1 to demonstrated that simulation results can be

scaled back to the real Tokyo scale post-simulation.

Specifically, we designed four sizes of simulation

environments along with adjusted parameters

𝑆



:𝑆



:𝑆



:𝑆



4:1:1/4:1/16. Test results

from simulation show that the following relation

holds true 𝑁





/4𝑁





4𝑁





16𝑁





, therefore

𝑁



𝜆𝑆,𝜆𝑁



; 𝑡 𝜆𝑁



𝑆,𝑁



; 𝑡.

Moreover, the shape of the simulation area has

trivial impact to results. Hence, we are confident to

proceed the current model to perform simulations.

5.2 Calibration of the Model

To fine-tune this model, we utilize data on confirmed

infection cases spanning from January 24, 2020, to

May 8, 2023. Initial parameters like hospital capacity

and population size are established within the code’s

initialization module (See Table 6).

Table 6: Parameters and parameter values.

Parameters Value Parameters Value

Initial population 12,528 Antibody titer after

cured

357 AU/mL

Hospital capacity 6 Decline rate for

vaccinated

0.980916

Labor force

participation rate

62% Decline rate for

cured

0.998640

Student rate 17% Vaccine efficacy

threshold

250 AU/mL

dose efficacy 52% Vaccination

fatality rate

8.1  10



dose efficacy 91% Self-isolation days 14 days

Antibody titer 2

dose 1,629 1

/ 2

dose

Interval

21~49 days

Antibody titer 3

dose 3,419 2

/ 3

dose

Interval

≧180 days

Antibody titer 4

dose 3,655 3

dose

Interval

≧150 days

Figure 9: Actual results (scaled) vs. Simulation results.

01/jan/00

25/fev/00

20/abr/00

14/jun/00

08/ago/00

02/out/00

26/nov/00

20/jan/01

16/mar/01

10/mai/01

04/jul/01

28/ago/01

22/out/01

16/dez/01

09/fev/02

05/abr/02

30/mai/02

24/jul/02

17/set/02

11/nov/02

05/jan/03

01/mar/03

Number of Agents

Date

Actual results (scaled) Simulation results + 50

1st 2nd 3rd 4th 5th 6t

Evaluating the Multifactorial Effects on SARS-CoV-2 Spread in Tokyo Metropolitan Area with an Agent-Based Model

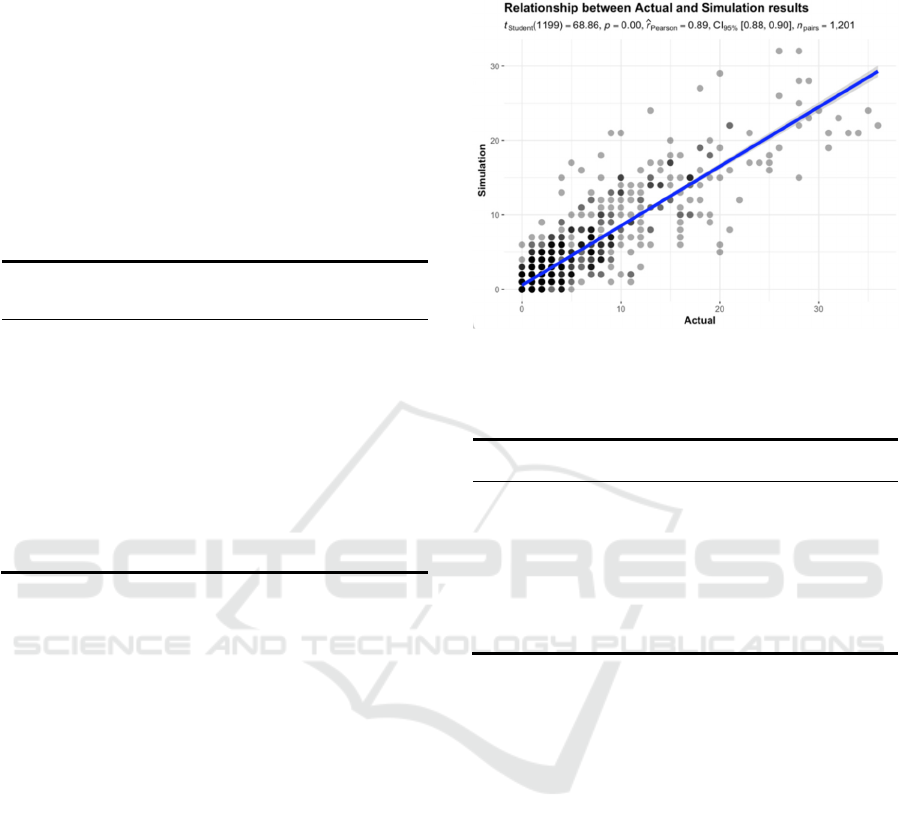
6 ANALYSIS AND FINDINGS

6.1 Reproducing the Eight Waves

Fig. 9 compares scaled actual data with simulated daily

COVID-19 infections in Tokyo from January 24, 2020,

to May 8, 2023. The simulation, averaged over 60

iterations, successfully replicates the seven infection

waves in Tokyo and predicts the highest daily

confirmed cases in each wave, detailed in Table 7.

Table 7: Comparison of the maximum value between post-

scaled actual results and simulation results.

Epidemic

waves

in Tokyo

Maximum daily

confirmed cases

(post-scaling)

Maximum daily

confirmed cases

(simulation results)

wave 0 (April 27, 2020) 0 (April 14, 2020)

wave 0 (August 1, 2020) 1 (August 1, 2020)

wave 2 (January 7, 2021) 1 (January 7, 2021)

wave 1 (May 8, 2021) 2 (May 17, 2021)

wave 5 (August 13, 2021) 4 (August 11, 2021)

wave 19 (February 2, 2022) 19 (January 24, 2022)

wave 36 (July 28, 2022) 33 (August 1, 2022)

wave 20 (December 27, 2022) 19 (December 27, 2022)

6.2 Analysis of Metrics

Fig. 10 depicts the scatter plot alongside marginal

density and histogram, generated using

‘ggscatterstats’ function in the package ‘ggstatsplot’

(Patil, 2021). The number of observations 𝑛





1201 corresponds to 2020.01.24 ~ 2023.05.08.

The graph demonstrates a significant rejection of

the null hypothesis with 𝑝0.000.05. The

rejection is support by 𝑟̂



0.89, which lies in

𝐶𝐼

%

0.88,0.90. Overall, the statistical analysis

indicates a strong agreement between the simulation

results and actual data.

Furthermore, Granger causality tests were

conducted on the two datasets. The F test statistic

yielded a value of 64.008, with a corresponding

p-value of 𝑃𝑟



2.210



0.05.

Consequently, we reject the null hypothesis,

suggesting that the simulation results effectively

predict the actual outcomes.

Examining the accuracy of the forecasts, the

RMSE of 2.57 signifies the average absolute

magnitude of forecast errors. Additionally, the DA of

0.76 indicates that the forecasts correctly predicted

the direction of the actual values approximately 76%

of the time.

Figure 10: ‘ggstatsplot’ of results comparison.

Table 8: Evaluation metrics obtained from the calculation

of actual and simulated results.

Evaluation

metrics

Reference

range

Desired value Value

R-Pearson [0,1] Closer to 1 (strong positive

linear relationship)

0.89

R-squared [0,1] Closer to 1 (more

variance explained)

0.79

Root Mean

Squared Error

(RMSE)

[0,+∞) Closer to 0 (minimized

as much as possible)

2.57

Directional

Accuracy (DA)

[0,1] Closer to 1 (high proportion

of correct predictions)

0.76

6.3 Findings

6.3.1 The ‘Hidden’ Infections

Fig 11 illustrates the counts of agents in E, I1, and I2

states from January 24, 2020, to May 8, 2023. Fig 12

shows vaccination doses administered during the

same period.

Observations reveal:

1. The rise in I1 population correlates with an

increase in E population, indicating a positive

infection loop. Waves 1 to 4 depend on individual

recovery and antibody production, with

underreported cases due to insufficient testing.

2. Coronavirus mutations lead to a convergence of E

and I1 populations until the late 6th wave. The 4

dose vaccination campaign, starting on May 25,

2022, mitigates the rise in E cases.

3. Despite a decrease in I1 population post-7

wave,

expanded PCR testing capacity results in reported

cases exceeding previous waves.

COMPLEXIS 2024 - 9th International Conference on Complexity, Future Information Systems and Risk

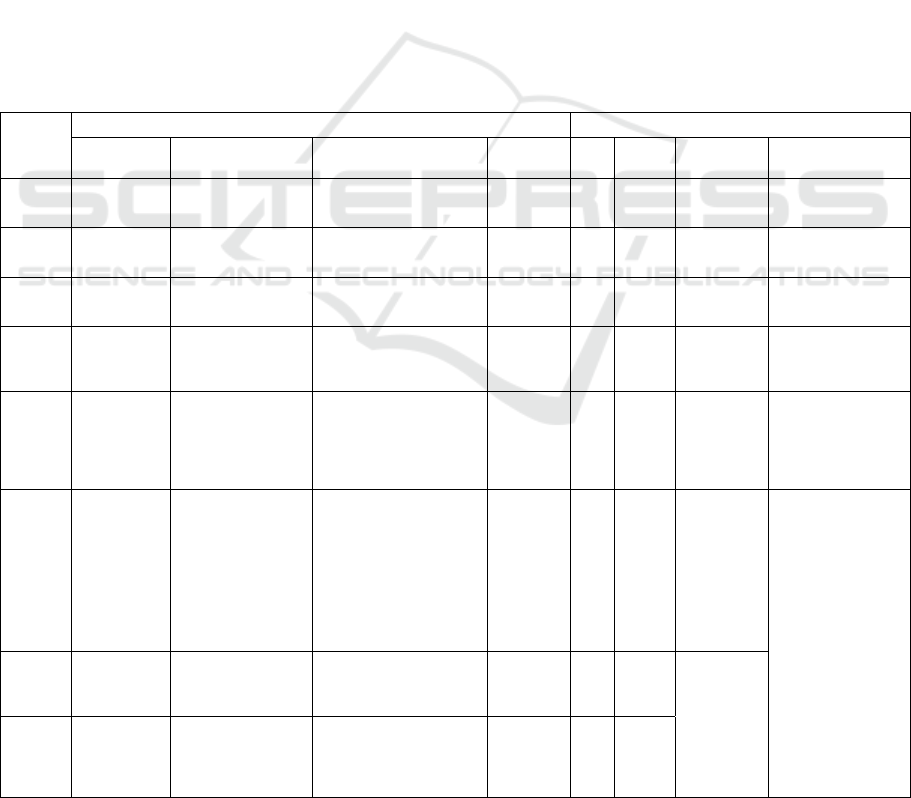
The robust correlation observed between PCR tests

and confirmed cases indicates that the reported cases

represent only a fraction of actual infections.

6.3.2 Antibody from Vaccination and Cure

Following vaccination rollout, antibody levels surged

rapidly across the community. By October 2021,

effectiveness waned, but rebounded in January 2022

with the Omicron variant and third vaccine dose

introduction.

Amid escalating transmission and virus

mutations, antibody levels increased gradually. The

timely fourth /bivalent dose introduction further

elevated population antibody levels to record highs.

6.3.3 Reasons Behind the Eight Waves

We outline features of the infection trends in Tokyo

in Table 9. Here are the factors contributing to these

characteristics:

1. Tokyo commenced its first vaccine dose during

the 4

wave, later than New York and London,

rendering it susceptible to future mutations

(Tokyo: April 12, 2021; New York: December 14,

2020; London: December 8, 2020).

2. Insufficient PCR testing capacity in waves 1-5

failed to accurately reflect infection trends.

3. Improved PCR testing during the Omicron-

dominated 6

wave revealed historically high

confirmed cases, despite reduced severity and

mortality rates due to previous vaccination and

self-recovery (Larrauri et al., 2022).

4. BA.2.75 variant, identified in the 7

& 8

wave, evades most antibodies, hindering control

efforts even with high vaccination rates (Fig 11 &

Fig 12). Increased PCR testing primarily led to

higher daily confirmed cases without effectively

curbing overall infection trends.

Table 9: Summary of the eight epidemic waves in Tokyo with key assumptions and result.

Epidemic

waves

Key assumptions Key results

Vaccination Virus mutation Government policies

Daily PCR

tests

I1 I2

Vaccination

antibody

Infection antibody

1st wave

(2020.01~

2020.05

)

/ 1st COVID-19 case

(2020.01.24)

1st state of emergency

(2020.04.07~ 2020.05.25)

Low

(ave. 500)

High Low / Start to increase due to

self-healing

2nd wave

(2020.05~

2020.10

)

/ / Bans entry from 159

countries and regions

(

2020.08.28

)

Low

(ave. 3600)

Low Low / Start to decrease due

to antibody decline

3rd wave

(2020.10~

2021.03)

/ 1st Gamma case

(2021.01.12)

2nd state of emergency

(2021.01.07~2021.03.21)

Low

(ave. 7900)

Low Low / Stable due to limited

infection

.4th wave

(2021.03~

2021.06)

1st dose start

(2021.04.12)

2nd dose start

(2021.05.13)

1st Delta case

(2021.04.20)

1st quasi state of emergency

(2021.04.12~ 2021.04.24)

3rd state of emergency

(2021.04.25~ 2021.06.20)

Low

(ave. 8600)

Low Low Start to

increase

Increase due to mass

infection

5th wave

(2021.06~

2021.10)

/ 1st Delta N501S

(2021.08.31)

2nd quasi state of emergency

(2021.06.21~ 2021.07.11)

4th state of emergency

(2021.07.12~ 2021.09.30)

Medium

(ave.

11,100)

High Low Dose 1 and 2

effectiveness

start to

decrease due

to antibody

decline

Continue to increase

6th wave

(2021.12~

2022.06)

3th dose start

(2021.12.01)

4th dose start

(2022.05.25)

1st Omicron case

(2021.11.30)

1st Omicron BA.2

(Approx.2021.12.25)

1st Omicron XE

(2022.04.12)

1st Omicron BA.4

(2022.04.22)

1st Omicron BA.5

(

2022.04.29

)

3rd quasi state of emergency

(2022.01.09~ 2022.03.21)

Limited foreign travel

groups,

up to 20,000 daily

(2022.06.01)

High

(ave.

17,100)

High Medium

high

Dose 3 and 4

effectiveness

start to

increase due

to booster

doses

vaccination

Previous antibodies

become less protective

faced with Omicron

strains;

Infection antibodies

targeting Omicron

strains start to

increase.

7th wave

(2022.06~

2022.09)

Bivalent dose

start

(2022.09.20)

1st Omicron BA.2.75

(2022.07.13)

Omicron XBB

(

2022.10.28

)

Allow short-term trips

organized by travel agencies,

up to 50,000 daily

(

2022.09.07

)

High

(ave.

23,500)

High High Dose 3 and

dose 4

become less

protective;

Bivalent dose

effectiveness

start to

increase

8th wave

(2022.10~

2023.01)

Fully reopen (2022.10.11) High

(ave.

16,400)

High Medium

high

Evaluating the Multifactorial Effects on SARS-CoV-2 Spread in Tokyo Metropolitan Area with an Agent-Based Model

Figure 11: Number of agents in E, I1 and I2 states.

Figure 12: 1

, 2

, 3

, 4

doses of vaccination.

7 RECOMMENDATION AND

CONCLUSION

7.1 Recommendation

The decline in confirmed cases in late January led to

a decrease in testing, indicating a reduced perception

of infection risk among the public. This trend, known

as the "testing dilemma," illustrates that fewer

confirmed cases may result in decreased testing rates,

potentially leading to fewer reported cases.

Report from The Japan News reveals a consistent

rise in cases since April to May 2023. This surge may

be attributed to the "testing dilemma." Moreover,

cases continued to rise in June (Otake, 2023), with a

significant increase in new patients reported.

To combat recurring outbreaks, it's crucial to

maintain vigilance and promptly mobilize healthcare

resources, including testing capabilities and hospital

beds. Japan's opening-up policy must be monitored

closely alongside daily confirmed cases, mutation

detection, and fatality rates. Although fatality rates

have decreased, the risk of new troublesome variants

remains.

7.2 Conclusion

The resurgence of COVID-19 cases in late May and

June highlights the importance of maintaining

vigilance and mobilizing resources. Despite the low

rates of severe cases and deaths, PCR tests may not

significantly reduce infections but should be

maintained to detect potential severe variants.

Tokyo's existing healthcare infrastructure is

deemed satisfactory, taking into account the available

hospital beds and anticipated low severe cases.

However, the mobility to swiftly expand hospital bed

capacity is imperative to manage potential outbreaks

and imported mutated virus. High vaccination rates

for third and fourth doses enhance immunity against

Omicron variants, aligning closely with forecasted

scenarios. A correlation exists between confirmed

cases and testing levels, with fewer cases reported

during reduced testing due to the "testing dilemma."

Novelty of this study lies in its demonstration of

the importance of COVID-19 infection forecasting

concerning vaccination, virus mutation, government

policy, and PCR testing. It pioneers in continuously

simulating and reproducing eight epidemic waves in

Tokyo, considering factors like Olympics, state of

emergency declarations, and immigration policies.

The extension of the traditional SEIR model to adapt

to Tokyo's context, along with an agent-based

approach, ensures high accuracy and practicality.

This model may serve as a general framework for

analysing epidemics in other regions, emphasizing

the importance of local considerations for better

simulation results.

There are several flaws in this work. Firstly, this

study focuses on four significant factors influencing

epidemic trends but acknowledges that there are

numerous other variables that may also impact these

trends. While the theory of large-scale flow dynamics

1000

2000

3000

4000

5000

6000

24/jan/20

22/mar/20

19/mai/20

16/jul/20

12/set/20

09/nov/20

06/jan/21

05/mar/21

02/mai/21

29/jun/21

26/ago/21

23/out/21

20/dez/21

16/fev/22

15/abr/22

12/jun/22

09/ago/22

06/out/22

03/dez/22

30/jan/23

29/mar/23

Number of Agents

Date

E I1 I2

2000

4000

6000

8000

10000

12000

14000

24/jan/20

22/mar/20

19/mai/20

16/jul/20

12/set/20

09/nov/20

06/jan/21

05/mar/21

02/mai/21

29/jun/21

26/ago/21

23/out/21

20/dez/21

16/fev/22

15/abr/22

12/jun/22

09/ago/22

06/out/22

03/dez/22

30/jan/23

29/mar/23

Number of Agents

Date

1st dose 2nd dose

3rd dose 4th dose

V+R

COMPLEXIS 2024 - 9th International Conference on Complexity, Future Information Systems and Risk

is proposed to address agent movement, further

refinement is needed to better represent real-world

complexities. Additionally, demographic factors such

as natural birth and death rates, as well as family

dynamics, are not considered in this research,

highlighting the need for future models to incorporate

these elements. The simulation's strategy of randomly

selecting agents for PCR tests diverges from real-

world testing practices, which could affect the

accuracy of results and should be addressed in future

iterations. Lastly, the complexity of immune response,

as highlighted by Dr. Israel, poses challenges in

accurately incorporating antibody titer data into

simulations due to individual variations and decay

rates, emphasizing the importance of cautious

interpretation in future studies.

ACKNOWLEDGEMENTS

First and foremost, I am grateful to Dr. Zhiyi Zhang

who inspired me to develop this research. I also thank

M.D. Ariel Israel for his inspiring paper and

feedback. I would like to express my gratitude to the

WINGS-CFS Program and the Japan Society for the

Promotion of Science for providing research funding.

Moreover, the authors acknowledge the

development of the TokyoCovSim-VVGP model

which was designed and implemented by Jianing Chu.

The model plays a pivotal role in simulating the eight

waves of COVID-19 in Tokyo combining four key

factors (Vaccination, Virus mutation, Government

policy and PCR test). For further details about

TokyoCovSim-VVGP, interested readers can access

it via the following link: https://github.com/J-

Chu52/TokyoCovSim-VVGP.git

REFERENCES

Cai, J., Deng, X., Yang, J., Sun, K., Liu, H., Chen, Z., . . .

Zou, J. (2022). Modeling transmission of SARS-CoV-

2 omicron in China. Nature medicine, 28(7), 1468-

1475.

Chiba, A. (2021). The effectiveness of mobility control,

shortening of restaurants' opening hours, and working

from home on control of COVID-19 spread in Japan.

Health Place, 70, 102622. https://doi.org/10.1016/

j.healthplace.2021.102622

Chu, J., Morikawa, H., & Chen, Y. (2023). Simulation of

SARS-CoV-2 epidemic trends in Tokyo considering

vaccinations, virus mutations, government policies and

PCR tests. Biosci Trends, 17(1), 38-53.

https://doi.org/10.5582/bst.2023.01012

Ebinger, J. E., Fert-Bober, J., Printsev, I., Wu, M., Sun, N.,

Prostko, J. C., . . . Braun, J. G. (2021). Antibody

responses to the BNT162b2 mRNA vaccine in

individuals previously infected with SARS-CoV-2.

Nature medicine, 27(6), 981-984.

Hethcote, H. W. (2000). The mathematics of infectious

diseases. SIAM review, 42(4), 599-653.

Hoertel, N., Blachier, M., Blanco, C., Olfson, M., Massetti,

M., Rico, M. S., . . . Leleu, H. (2020). A stochastic

agent-based model of the SARS-CoV-2 epidemic in

France. Nature medicine, 26(9), 1417-1421.

International_Olympic_Committee. (2021). Tokyo 2020

Olympic Village(s) Period of stay Guidelines for the

NOCs.

https://stillmedab.olympic.org/media/Document%20Li

brary/OlympicOrg/News/2020/12/Tokyo-2020-

Olympic-Village-Guidelines-for-NOCs-in-relation-to-

period-of-stay-eng.pdf

Israel, A., Shenhar, Y., Green, I., Merzon, E., Golan-Cohen,

A., Schäffer, A. A., . . . Magen, E. (2022). Large-scale

study of antibody titer decay following BNT162b2

mRNA vaccine or SARS-CoV-2 infection. Vaccines,

10(1), 64.

Larrauri, B., Malbran, A., & Larrauri, J. A. (2022).

Omicron and vaccines: An analysis on the decline in

COVID-19 mortality. medRxiv.

Matsuyama, K. (2022, 2022-11-22T21:22:33+09:00).

Shionogi COVID-19 pill Xocova wins emergency

approval in Japan | The Japan Times. @japantimes.

Retrieved January 19, from https://www.japan

times.co.jp/news/2022/11/22/national/science-health/

shionogi-covid-xocova-approval/

McCurry, J. (2021, 2021-05-20). 79,000 people flying in for

Tokyo Olympics, Japanese media reports. @guardian.

Retrieved January 19, from http://www.theguardian.

com/sport/2021/may/20/organisers-of-tokyo-olympics

-press-ahead-despite-covid-fears

MHLW. (2023a). COVID-19 Q&A. Retrieved January 19,

from https://www.mhlw.go.jp/stf/covid-19/qa.html

MHLW. (2023b). COVID-19 tests. Ministry of Health,

Labour and Welfare. Retrieved January 19, from

https://www.mhlw.go.jp/stf/seisakunitsuite/bunya/000

0121431_00182.html

Murakami, T., Sakuragi, S., Deguchi, H., & Nakata, M.

(2022). Agent-based model using GPS analysis for

infection spread and inhibition mechanism of SARS-

CoV-2 in Tokyo. Sci Rep, 12(1), 20896.

https://doi.org/10.1038/s41598-022-25480-z

Narasimhan, M., Mahimainathan, L., Araj, E., Clark, A. E.,

Markantonis, J., Green, A., . . . Fankhauser, K. (2021).

Clinical evaluation of the Abbott Alinity SARS-CoV-2

spike-specific quantitative IgG and IgM assays among

infected, recovered, and vaccinated groups. Journal of

clinical microbiology, 59(7), e00388-00321.

Otake, T. (2023). COVID wave looms in Japan after case

numbers nearly double in a month. @japantimes.

Polack, F. P., Thomas, S. J., Kitchin, N., Absalon, J.,

Gurtman, A., Lockhart, S., . . . Group, C. C. T. (2020).

Safety and Efficacy of the BNT162b2 mRNA Covid-19

Evaluating the Multifactorial Effects on SARS-CoV-2 Spread in Tokyo Metropolitan Area with an Agent-Based Model

Vaccine. N Engl J Med, 383(27), 2603-2615.

https://doi.org/10.1056/NEJMoa2034577

Purkayastha, S., Bhattacharyya, R., Bhaduri, R., Kundu, R.,

Gu, X., Salvatore, M., . . . Mukherjee, B. (2021). A

comparison of five epidemiological models for

transmission of SARS-CoV-2 in India. BMC infectious

diseases, 21(1), 1-23.

Saad-Roy, C. M., Morris, S. E., Metcalf, C. J. E., Mina, M.

J., Baker, R. E., Farrar, J., . . . Levin, S. A. (2021).

Epidemiological and evolutionary considerations of

SARS-CoV-2 vaccine dosing regimes. Science,

372(6540), 363-370.

Wilensky, U. (1999). NetLogo. Evanston, IL: Center for

connected learning and computer-based modeling,

Northwestern University. In.

Wolfram, S., & Gad-el-Hak, M. (2003). A new kind of

science. Appl. Mech. Rev., 56(2), B18-B19.

Yamauchi, T., Takeuchi, S., Uchida, M., Saito, M., &

Kokaze, A. (2022). The association between the

dynamics of COVID-19, related measures, and daytime

population in Tokyo. Scientific Reports, 12(1), 1-12.

Zhang, Y. (2021, 2021-06-01). Australia’s softball players

are among the first Olympic athletes to arrive in Japan.

(Published 2021). @nytimes. Retrieved January 19,

from https://www.nytimes.com/2021/06/01/world/asia/

australia-olympics-tokyo-japan-softball.html

COMPLEXIS 2024 - 9th International Conference on Complexity, Future Information Systems and Risk