Study of Track Segmentation for Lap Time Optimization

Jaroslav Klap

alek

1,2 a

, Ond

rej Benedikt

1 b

, Michal Sojka

2 c

and Zden

ek Hanz

alek

2 d

Faculty of Electrical Engineering, Czech Technical University in Prague, Technick

a 2, 166 27 Prague, Czech Republic

Czech Institute of Informatics, Robotics and Cybernetics, Czech Technical University in Prague,

Jugosl

avsk

ych partyz

u 3, 160 00 Prague, Czech Republic

Keywords:

Lap Time Optimization, Scaled-Down Autonomous Racing, F1Tenth, F1/10.

Abstract:

Lap time minimization is of interest in every automotive racing competition. However, ﬁnding an optimal

racing line is not a trivial task. In this work, we study one particular part of the racing line optimization

problem, namely the track segmentation problem. We analyze how different track segmentation methods

inﬂuence the racing line quality. Further, we present Automated Segmentation based on Curvature (ASC)

method, which creates segments adaptively according to the track layout. Using lap time estimation based on

a vehicle model, we compare ASC with two other methods from the literature. The preliminary results show

that optimization based on ASC is able to outperform the other tested approaches by up to 15 % for the given

number of iterations while converging to a good solution 3.88 times faster than the second-best method.

1 INTRODUCTION

The optimal racing line problem is of a common in-

terest in an automotive racing environment (Calefﬁ

et al., 2023). Its goal is to ﬁnd a trajectory between

two points, ensuring a minimum driving time when

followed. On a closed circuit, this time is referred to

as lap time.

Lap time minimization is one of the main goals

of the International F1/10 Autonomous Racing Com-

petition (https://f1tenth.org/), a racing event for stu-

dent teams gathered from all around the world, uti-

lizing 1:10 scaled-down car models, so-called F1/10

cars (Agnihotri et al., 2020).

Many techniques exist to ﬁnd an optimal racing

line, e.g., Evolution Strategies (O’Kelly et al., 2020),

Genetic Algorithms (Klap

alek et al., 2021), Model

Predictive Control (Heilmeier et al., 2020; Cataffo

et al., 2022), or one of the various machine learn-

ing methods (Evans et al., 2024). In (Braghin et al.,

2008), authors use a genetic algorithm to minimize

the following two criterions: (i) the path length so the

distance the car has to drive is the shortest (i.e., short-

est path), or (ii) the path curvature so that the max-

imum speed allowed by the surface friction is maxi-

https://orcid.org/0000-0001-8816-2773

https://orcid.org/0000-0002-7365-844X

https://orcid.org/0000-0002-8738-075X

https://orcid.org/0000-0002-8135-1296

mized (i.e., minimum curvature path).

Some of the above techniques rely on represent-

ing the racing track as a small number of disjoint

track segments, where each of them represents a unit

of optimization, thereby reducing the computational

complexity. The track segmentation can be applied

as follows. Each segment is associated with a single

waypoint. The racing line is represented efﬁciently

as an interpolation of a sequence of waypoints. Posi-

tion of the waypoints within the segments is typically

found by various optimization techniques (such as lo-

cal search or genetic algorithms). Note that there ex-

ists a trade-off between the number of segments and

the quality of the racing line. A large number of seg-

ments increase the solution space but slow the opti-

mization convergence, whereas a low number of seg-

ments reduce the quality of the racing line or even

make the problem unsolvable.

Speciﬁcally, the track segmentation approach

is used in the following works. Garlick and

Bradley (Garlick and Bradley, 2022) use it for train-

ing a neural network to ﬁnd a racing line. In (Braghin

et al., 2008), the authors have segmented the track

equidistantly (meaning that the length of a segment

along the centerline is constant), whereas, in the work

of (Botta et al., 2012), the size of the segments was

inversely proportional to the curvature of the track.

In both works, the racing line waypoints were placed

on a line perpendicular to the centerline. We call this

452

Klapálek, J., Benedikt, O., Sojka, M. and Hanzálek, Z.

Study of Track Segmentation for Lap Time Optimization.

DOI: 10.5220/0012728600003702

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 10th International Conference on Vehicle Technology and Intelligent Transport Systems (VEHITS 2024), pages 452-455

ISBN: 978-989-758-703-0; ISSN: 2184-495X

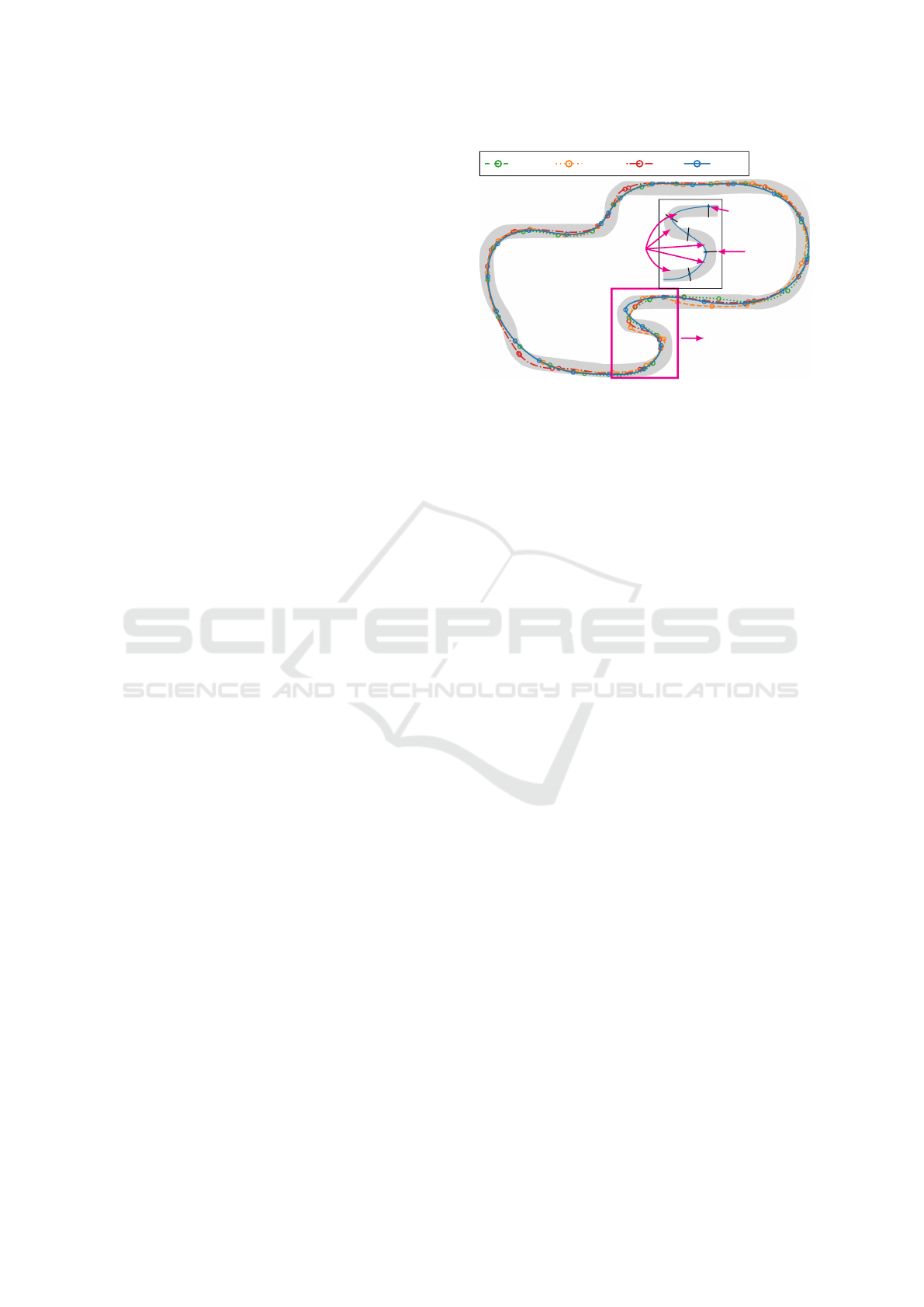
line a cut and two consecutive cuts deﬁne a segment

in between. This way, each waypoint is deﬁned by

its position in the sequence of segments and a single

scalar variable describing its position on the cut, as

can be seen in Fig. 1.

The exact way of segmenting the track likely in-

ﬂuences the quality of the resulting racing line. How-

ever, the previous works did not study their relation

in great detail and instead used simple and straight-

forward approaches. In this work, we study the effect

of the track segmentation on the resulting racing line,

considering both the solution quality (lap time) and

computational effort (convergence of the algorithm).

Speciﬁcally, the contribution of this paper is as fol-

lows: (i) we propose a method called Automated Seg-

mentation based on the Curvature (ASC in short), and

(ii) we compare ASC to two other approaches pro-

posed in (Braghin et al., 2008) and (Botta et al., 2012),

respectively. We show that given the same number of

segments, our method is able to converge faster and

yields lower lap times.

2 METHODOLOGY

We compare three different methods for the track seg-

mentation: (i) uniform equidistant segmentation (UE)

based on (Braghin et al., 2008), (ii) uniform seg-

mentation with respect to the curvature (UC) based

on (Botta et al., 2012), and (iii) the Automated Seg-

mentation based on the Curvature (ASC) method pro-

posed in this work.

Considering the UE method, the quality of the rac-

ing line depends on the position of the initial segment.

Thus, we evaluate multiple variants by moving the

segments on the track along the centerline by α · ∆,

where α ∈ {0 %,10%, .. . , 90 %} represents the shift

and ∆ is the length of the segment. We denote the

method as UEα.

The UC method samples the cuts on the track uni-

formly with respect to the curvature, i.e. it places

more cuts at the corners and less in the straight sec-

tions. However, to obtain a sufﬁcient number of cuts

in the straight sections, this method results in an un-

necessarily high number of segments in the turns. We

argue that the worse performance of the UC (in com-

parison to the UE-like approach as presented in (Botta

et al., 2012)) was caused by a large number of seg-

ments in turns.

Similarly to UC, our ASC method places cuts

based on track curvature. Contrary to the prior work,

we generally divide the track into less segments. The

ASC method works as follows: (i) positive and nega-

tive peaks on the curvature are found and populated

Problematic

“S-turn”

segments

cut

waypoint

UE20 UE40 UC ASC

Figure 1: Ruudskogen map from TORCS (Wymann et al.,

2014) with racing lines of selected methods and their way-

points, along with an illustration of segments, cuts, and

waypoints.

by cuts, (ii) close cuts are merged to avoid redun-

dancy, (iii) long cut-less sections of the track are arti-

ﬁcially ﬁlled with equidistant cuts, (iv) sections of the

track between two consecutive cuts where the sign of

the curvature changes are populated with additional

cuts, and (v) close cuts are ﬁltered out once again.

Therefore, the method segments the track automat-

ically given the following parameters: threshold of

curvature peaks, minimum distance between two cuts,

and distance between cuts in the straight sections.

All the tested methods segment the track differ-

ently. To ﬁnd the waypoints given the segmenta-

tion, we use a genetic algorithm powered by Never-

grad (Rapin and Teytaud, 2018). Note that the partic-

ular choice of the optimization technique is not that

important, as any other optimization technique can

be used instead. To get the racing line, we interpo-

late found waypoints by a cubic spline as presented

in (Braghin et al., 2008). Finally, to evaluate the lap

time t

lap

given the racing line, we use a sequential

two-step algorithm (Kapania et al., 2016). This al-

gorithm computes a velocity proﬁle using a dynamic

bicycle model (with parameters suitable for an F1/10

car) to maximize the vehicle speed at any given point

while not exceeding the maximum permissible vehi-

cle speed (which depends on friction and the racing

line curvature with a corresponding centripetal force)

and acceleration limits.

We perform the experimental evaluation on the

Ruudskogen map from TORCS (Wymann et al.,

2014) shown in Fig. 1. The track is scaled by a factor

of 1/10 to match the environment of the F1/10 com-

petition. To ensure a fair comparison, the number of

segments is ﬁxed to 26. All of the tested methods

(UE0, UE10, . . . , UE90, UC, ASC) are executed three

times, each time with a limit of 10,000 iterations (bud-

Study of Track Segmentation for Lap Time Optimization

453

get parameter of Nevergrad). The repeated evaluation

is performed in order to mitigate the non-determinism

of the optimizer.

3 RESULTS

The results of the experiments are shown in Fig. 2,

illustrating the relation between the iteration num-

ber and best-so-far solutions found by the respective

methods. Each data line represents the average of

the three runs, with the ﬁlled area showing the stan-

dard deviation. Lap times achieved after 10,000 iter-

ations are shown in the legend. Results for methods

UE50, . . . , UE90 are not presented since no feasible

racing line was found in any of the runs. A racing line

is infeasible if any part of it lies outside of the track.

Note that the large standard deviation of the UC is

caused by a large number of segments in the turns,

which has a diverse impact on the optimizer conver-

gence.

From Fig. 2 we conclude that ASC surpasses the

best-performing variant of UE method (UE20) by

0.24 s (0.88 %) and UC by 3.49 s (11.47 %). Even

though the difference between ASC and UE20 is not

particularly high, note that UE20 is one of the possi-

ble rotations of UE method, while the success of indi-

vidual rotations is a priori unknown.

The highest differences are most apparent in the

early iterations. For example, after the ﬁrst 500 it-

erations, using the ASC yields lap time that is 0.84 s

(2.92 %) better than UE20, and 5.18 s (15.64 %) bet-

ter than UC.

Figure 1 shows the racing lines for ASC, UE20,

UE40, and UC methods. The most challenging part is

the “S-turn” in the bottom part of the track, where cuts

at inconvenient places negatively affects the lap time.

Detailed view of the “S-turn” and how the selection

of cuts inﬂuences a set of possible trajectories consid-

ered by the optimization algorithm is shown in Fig. 3.

For example, we can see that the solution space of

UE60 has only a small overlap with the track in the

0 1,000 2,000 3,000 4,000 5,000 6,000 7,000 8,000 9,000 10,000

number of iterations [–]

lap

[s]

UE0 (27.53 ± 0.14 s) UE40 (28.12 ± 0.15 s)

UE10 (27.56 ± 0.16 s) UC (30.45 ± 1.02 s)

UE20 (27.20 ± 0.12 s) ASC (26.96 ± 0.19 s)

UE30 (27.57 ± 0.10 s)

Figure 2: Comparison of tested methods, an average lap

time is shown, along with the standard deviation repre-

sented as a ﬁlled area.

Table 1: Average number of iterations for given lap time.

lap

[s] ASC UE0 UE10 UE20 UE30 UE40 UC

32.00 1 1 1 1 1 442 1,014

31.00 28 227 27 42 106 659 2,607

30.00 64 378 142 161 212 1,041 –

29.00 144 518 295 361 387 1,721 –

28.00 457 1,776 787 1,094 1,210 – –

27.70

798 3,418 2,470 2,099 2,361 – –

27.40 1,434 – – 3,700 – – –

27.20 2,542 – – 9,872 – – –

27.00 9,160 – – – – – –

(a) UE20. (b) UE60. (c) UC. (d) ASC.

Figure 3: Cuts and solution spaces (dotted areas) of selected

methods. The resulting racing line of each method has to lie

in its solution space.

top part, which results in all potential solutions being

infeasible. A racing line, which is feasible in the top

left segment will be infeasible in the segment below it

and vice versa.

Finally, Table 1 shows the average number of it-

erations needed to achieve certain lap times for the

tested methods. Note that only ASC is able ﬁnd to the

best lap time under 27 s. In addition, ASC reaches the

lap time of 27.2 s almost 4 times faster than UE20.

4 CONCLUSION AND FUTURE

WORK

Lap time minimization is a common problem in rac-

ing competitions, and it strongly correlates with the

quality of the racing line. In this paper, we studied the

effects of track segmentation on racing line optimiza-

tion. This preliminary study revealed the ﬂaws of the

previously used methods. Speciﬁcally, the uniform

equidistant segmentation (UE) method may not adapt

to the properties of the track, while the uniform seg-

mentation with respect to the curvature (UC) method

suffers from its dependency on the curvature smooth-

ness.

We proposed the Automated Segmentation based

on the Curvature (ASC) method overcoming these

ﬂaws and improving both the optimization conver-

gence and the solution quality.

In the future, we plan to test ASC also on other

tracks. Moreover, we plan to make the selection of

various ASC parameters fully automatic and to vali-

date it experimentally on a real F1/10 car. Besides, we

VEHITS 2024 - 10th International Conference on Vehicle Technology and Intelligent Transport Systems

454

want to test the effect of different interpolation func-

tions (such as the B

ezier curve). We believe that this

study shows the high potential of adaptive track seg-

mentation.

ACKNOWLEDGEMENTS

This work was supported by the Grant Agency of

the Czech Technical University in Prague, grant No.

SGS22/167/OHK3/3T/13 and co-funded by the Euro-

pean Union under the project ROBOPROX (reg. no.

CZ.02.01.01/00/22 008/0004590).

REFERENCES

Agnihotri, A., O’Kelly, M., Mangharam, R., and Abbas,

H. (2020). Teaching Autonomous Systems at 1/10th-

scale: Design of the F1/10 Racecar, Simulators and

Curriculum. In Proceedings of the 51st ACM Tech-

nical Symposium on Computer Science Education,

SIGCSE ’20, pages 657–663, New York, NY, USA.

Association for Computing Machinery.

Botta, M., Gautieri, V., Loiacono, D., and Lanzi, P. L.

(2012). Evolving the optimal racing line in a high-end

racing game. In 2012 IEEE Conference on Computa-

tional Intelligence and Games (CIG), pages 108–115.

ISSN: 2325-4289.

Braghin, F., Cheli, F., Melzi, S., and Sabbioni, E.

(2008). Race driver model. Computers & Structures,

86(13):1503–1516.

Calefﬁ, F., Rodrigues, L. d. S., Stamboroski, J. d. S., Rorig,

B. V., Santos, M. M. C. d., Zuchetto, V., and Raguz-

zoni,

I. B. (2023). A systematic review of hardware

technologies for small-scale self-driving cars. Ci

encia

e Natura, 45(esp. 1):84071.

Cataffo, V., Silano, G., Iannelli, L., Puig, V., and Glielmo,

L. (2022). A Nonlinear Model Predictive Control

Strategy for Autonomous Racing of Scale Vehicles.

In 2022 IEEE International Conference on Systems,

Man, and Cybernetics (SMC), pages 100–105.

Evans, B. D., Trumpp, R., Caccamo, M., Jordaan, H. W.,

and Engelbrecht, H. A. (2024). Unifying f1tenth au-

tonomous racing: Survey, methods and benchmarks.

arXiv:2402.18558.

Garlick, S. and Bradley, A. (2022). Real-time optimal tra-

jectory planning for autonomous vehicles and lap time

simulation using machine learning. Vehicle System

Dynamics, 60(12):4269–4289.

Heilmeier, A., Wischnewski, A., Hermansdorfer, L., Betz,

J., Lienkamp, M., and Lohmann, B. (2020). Min-

imum curvature trajectory planning and control for

an autonomous race car. Vehicle System Dynamics,

58(10):1497–1527.

Kapania, N. R., Subosits, J., and Christian Gerdes, J.

(2016). A Sequential Two-Step Algorithm for Fast

Generation of Vehicle Racing Trajectories. Jour-

nal of Dynamic Systems, Measurement, and Control,

138(9):091005.

Klap

alek, J., Nov

ak, A., Sojka, M., and Hanz

alek, Z.

(2021). Car racing line optimization with genetic

algorithm using approximate homeomorphism. In

2021 IEEE/RSJ International Conference on Intelli-

gent Robots and Systems (IROS), pages 601–607.

O’Kelly, M., Zheng, H., Jain, A., Auckley, J., Luong, K.,

and Mangharam, R. (2020). Tunercar: A superopti-

mization toolchain for autonomous racing. In 2020

IEEE International Conference on Robotics and Au-

tomation (ICRA), pages 5356–5362.

Rapin, J. and Teytaud, O. (2018). Nevergrad

- A gradient-free optimization platform.

https://GitHub.com/FacebookResearch/Nevergrad.

Wymann, B., Espi

e, E., Guionneau, C., Dimitrakakis, C.,

Coulom, R., and Sumner, A. (2014). TORCS, The

Open Racing Car Simulator. http://www.torcs.org.

Study of Track Segmentation for Lap Time Optimization

455