Estimation of Height of Building Using High Resolution Satellite
Image
Nitin Laxmanrao Gavankar
1a
, Ravindra Ramkishan Rathod
2b
and Vivek N. Waghmare
3c
1
Department of Computer Science and Engineering, Walchand College of Engineering, Vishrambag, Sangli, India
2
Department of Information Technology, Walchand College of Engineering, Vishrambag, Sangli, India
3
Department of Computer Engineering, PVG’s College of Engineering & S.S. Dhamankar Institute of Management,
Nashik, India
Keywords: K-Means Algorithm, Building Shadow Width, Sun-Satellite Geometry Method, Bounding Rectangle.
Abstract: Buildings along with their properties such as, shape, rooftop reflectance, structure, etc. are one of the most
commonly observed structures in urban areas. Two-dimensional (2D) building footprint along with building
height information play an important role in the field of urban development, urban planning, population
estimation, map making, disaster management, and various other socioeconomic applications. Shadow cast
by buildings plays a vital role in estimation of height of building. In this study, sun-satellite geometry method
using shadow cast by building has been used to estimate height of building. However, accurate shadow
detection, extraction, and measuring width of the shadow zone are some of the important aspects in estimation
of height of building. In order to detect and extract width of the shadow zone accurately, OBIA has been used.
Further, accuracy in measuring width of the shadow zone has been improved by introducing a new algorithm
and considering sun illumination direction and orientation of building. OBIA along with new algorithm to
measure width of the shadow zone provides a sound methodology for estimation of height of all types and
shape of buildings.
1 INTRODUCTION
Earth observation satellite images provides very
important information about earth surface and play a
vital role in various remote sensing applications like
change detection, disaster management, urban
planning, Land Use Land Cover (LULC) mapping
and many other socio-economic happenings. In
addition, multispectral characteristics of satellite
images further helps to improve feature recognition
and LULC mapping. Applications such as, feature
recognition has considerably increased since High
Resolution Satellite (HRS) images from
QUICKBIRD, IKONOS, RapidEye, WorldView, etc.
have been made available for research and
development. Especially, HRS images found its
applications in various urban applications wherein
they play an important role to identify and extract
a
https://orcid.org/0000-0002-8511-5143
b
https://orcid.org/0000-0003-2311-2358
c
https://orcid.org/0000-0002-7776-6683
various urban related features such as, buildings,
trees, roads, and other natural or manmade features.
Buildings having different structure, shape, and
rooftop reflectance are one of the most commonly
observed structures in urban regions. In various
applications such as, urban planning, urban
development, land use analysis, map making, climate
studies, change detection, and disaster management
two-dimensional building footprints (2D) and three-
dimensional building models (3D) provide an
important information (Sırmaçek and Ünsalan, 2008;
Sırmaçek and Ünsalan, 2011; Gavankar & Ghosh,
2018).
Estimation of height of a building is an important
application of urban remote sensing using HRS data.
Height of a building may be estimated from remotely
sensed data by using different types of data sources,
such as, HRS image, Synthetic Aperture Radar
(SAR), Light Detection and Ranging (LIDAR) point
Gavankar, N., Rathod, R. and Waghmare, V.
Estimation of Height of Building Using High Resolution Satellite Image.
DOI: 10.5220/0012731600003696
Paper published under CC license (CC BY-NC-ND 4.0)
In Proceedings of the 10th International Conference on Geographical Information Systems Theory, Applications and Management (GISTAM 2024), pages 83-93
ISBN: 978-989-758-694-1; ISSN: 2184-500X
Proceedings Copyright © 2024 by SCITEPRESS – Science and Technology Publications, Lda.
83

cloud, Digital Elevation Model (DEM), and Digital
Surface Model (DSM).
Building height information using remote sensing
data may be extracted by investigating the effect of
building on surroundings, such as, by measuring
width of shadow cast by a building (Massalabi et al.,
2004). In order to estimate height of building from
shadow, accurate detection, extraction, and
measuring shadow length are some of the important
yet challenging steps. However, extent of shadow
visible in satellite image is entirely depends on the
position of sun and satellite at the time of acquisition
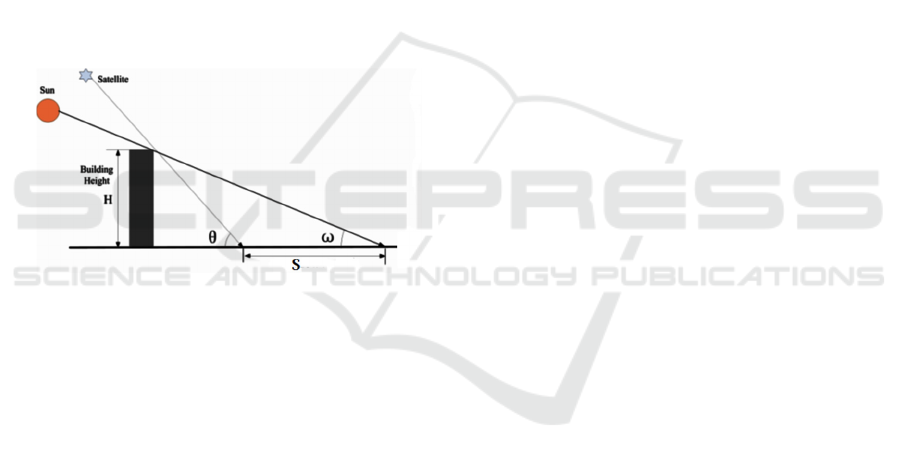
of image. A typical view of sun-satellite geometry
formed with respect to building and shadow cast by a
building is shown in Fig. 1. Further, height of a
building may be calculated by deriving a suitable
trigonometric relation, considering sun-satellite-
building geometry formed.
In Fig. 1, S is the width of shadow cast by the
building, ω is altitude of sun and θ is altitude of
satellite.
Figure 1: The relationship of the sun, satellite and building
at the time of image acquisition (Wang et al., 2014).
In order to estimate height of building from single
HRS image, sun-satellite geometry method has been
widely used in various studies. However,
methodology for measuring width of shadow cast by
building, a crucial step during estimation of height of
building, has been largely neglected. In some studies,
Bounding Rectangle (box) method has been used to
measure the width of shadow zone to estimate height
of the building (Shettigara & Sumerling, 1998; Raju
et al., 2014) yet it is suitable for regular shape
buildings. Further, it has been observed that
Bounding Box method used to measure shadow
length, gives large error during estimation of height
in case of irregular shape buildings. Also sun
illumination, its direction and orientation of building
plays a key role in shadow cast by irregular shape
building, has not been considered. Some of the
challenges in estimation of height of building from
HRS image are as given below:
i) Require suitable technique to extract shadow
precisely from HRS image.
ii) Slight error in measuring width of shadow cast by
building may cause large error in estimation of
height of building.
iii) Development of suitable relationship to
determine height of building considering sun-
satellite geometry at the time of image acquisition.
In order to provide common solution to estimate
height of all types of buildings, there is need for an
improved or a new technique. A new technique
should ideally be able to extract shadow precisely
from HRS image, provide reliable shadow width
measuring technique, and provide suitable relation
(equation) to represent sun-satellite geometry formed
at the time of image acquisition, in order to estimate
height of a building.
The main objective of this study is to estimate
height of different types/shapes of buildings from
shadow cast by a building using HRS multispectral
image.
2 LITERATURE REVIEW
Extraction of building footprints from satellite images
has been a difficult task due to their different
structural and spectral properties. In different studies,
various automatic and semi-automatic techniques for
extraction of building footprints from remotely
sensed image have been discussed. Similarly, large
number of studies has been carried out for estimation
of height of building by different researchers. The
objective of this section is to present a detailed review
of different techniques for extraction of shadow of
buildings and methods for estimating the height of
building using High Resolution satellite (HRS)
image/images.
Satellite images provide valuable information
about the ground. One such application is extraction
of building and estimation of building height from
satellite image. This information may be important
aspect for urban remote sensing, such as, urban
change detection, natural disaster monitoring,
preparing and updating building inventory database,
taxation, etc. In literature, many studies have been
carried out using Synthetic Aperture Radar (SAR)
images (Guillaso et al., 2005; Guida et al., 2010;
Brunner et al., 2010) or from fused of SAR and high
resolution optical images (Sportouche et al., 2011).
Since, building height information using optical
remote sensing data may be extracted by investigating
the effect of building on the surroundings, such as, by
GISTAM 2024 - 10th International Conference on Geographical Information Systems Theory, Applications and Management
84

measuring shadow cast by the building (Massalabi et
al., 2004). Although, shadows have been considered
as noise in many remote sensing applications, shadow
cast by a building plays a vital role in estimation of
building height. In order to estimate building height
from shadow, accurate detection, extraction, and
measurement of shadow width are some of the
important and challenging steps. During estimating of
height of building using shadow width, a key
assumption has been made that the surface on which
shadow fall is flat surface and that the shadow cast by
building does not fall on another building.
In general, shadow extraction from satellite
imagery has been a fundamental step in estimation of
building height. Various studies have been carried out
in order extract shadow from satellite imagery
(Sarabandi et al., 2004; Arévalo et al., 2008; Liu and
Yamazaki, 2012; Song et al., 2014). Subsequently,
this information have been used in various
applications, such as, detection of buildings (Chen et
al., 2014), estimation of height of building (Raju et al,
2014; Shao et al., 2011), removal of shadow (Dare,
2005; Guo et al., 2010), etc.
Cheng and Thiel (1995) estimated height of a
building from shadow width using SPOT
panchromatic image. Experimentation has been
carried out on a 42 high-rise building and result shows
a Root-Mean-Square (RMSE) error of 3.69 m in
height estimation. In another study carried out by
Hartl and Cheng, (1995) reported 6.13m RMSE error
in height estimation for 77 buildings in the study area.
Shettigara and Sumerling (1998) introduced a
sun-sensor-shadow geometry method, later referred
as sun-satellite geometry method, to estimate height
of building using shadow width. In order to calculate
height of building (h
t
), Eq. 1 has been derived by
using sun-satellite geometry at the time of imaging.
The early attainment of the proposed methodology
has been the accuracy obtained, which is nearly one
third of the size of panchromatic pixel. However, the
limitation of the proposed technique is applicable for
estimating height of only extended objects situated on
flat terrain.
ℎ

=
𝑆


𝑐𝑜𝑠
(
ϕ

)
𝑡𝑎𝑛
(
θ

)
−

𝑐𝑜𝑠
(
ϕ

)
tan (
θ

)



(1)
where, S is the shadow width (area of the shadow
zone divided by the width of the zone), ϕ
sun
, ϕ
sa
are
the azimuth angle of sun and satellite, and θ
su
, θ
sa
are
the elevation of sun and satellite respectively.
The concept of sun-satellite geometry method has
been further explained in detail by Massalabi et al.,
(2004), with the help of perspective view and plane
view, (Fig. 2). Estimation of building height from
shadow width depends on several parameters, such
as, sun elevation angle, sun azimuth angle, relative
position of the sun, shadow of the object, and sensor.
Here, sun azimuth and elevation angle determines the
orientation of shadow, while their relative position
determines the proportion and component of shadow
viewed by the sensor.
(a) Perspective view (b) Plane view
Figure 2: Position of sun, building, and satellite with
respective to North at the time of image acquisition
(Massalabi et al., 2004).
Wang and Wang (2009) proposed a methodology
to extract information of buildings along with density
of buildings in Kunming, China using QuickBird
imagery. During experimentation, calculation of
height of building has been carried out on the basis of
hypothesis made and sun-satellite geometry formed at
the time of imaging. In order to estimate height of
building, sun and satellite elevation and azimuth
angle is required and these are available in the
metadata file available with satellite data. The results
obtained suggest that with increase in height of
building, error in height estimation reduces. Further,
results obtained show that height of building
calculated from shadow and height investigated on
sites, forms a linear relationship, represented by the
following equation.
𝐻

=𝛼𝐻

+ 𝛽
(2)
where, H
t
and H
x
are the height calculated from
shadow and investigated height respectively, α and β
are the coefficient of formula.
Shao et al. (2011) presented a simple sun-building
shadow relationship model for estimating height of
high-rise buildings from IKONOS image for a part of
Bangkok city. In order to delineate shadows of high
rise buildings from low and connected building
shadows, proposed methodology uses object shape
index. The object shape index has been obtained by
calculating a ratio of perimeter of shadow to the area
of shadow. Further, width of the shadow object has
been measured in the direction of sun azimuth angle
Estimation of Height of Building Using High Resolution Satellite Image
85

and height of building has been calculated using
following sun-building shadow relationship.
𝐻=𝐿 ×tan
(
Ѳ
)
(3)
where, H is the height of the building, L is the
width of shadow, and Ѳ is the sun elevation angle.
Results show that less than 8m error has been reported
for nearly 62% of buildings.
Liasis and Stavrou (2016) used a similar sun-
building shadow relationship and estimated height of
building using Eq. 3. Further, the aggregate variance
(error) reported in estimating height of building have
been 4.13%, which includes buildings of all
categories, such as, office, residential, and their
combination.
A rule-based approach has been presented by
Comber et al., (2012) in order to estimate height of
building from ALOS data, using shadow width.
Initially, segmentation have been carried out using
parameters, such as, scale, shape, and compactness.
Thereafter, classification has been performed using
rule-based approach. Further, rules have been defined
to allocate shadow objects to different building
classes, which have been used in conjunction with
geo-located photographs. The defined rules have been
derived on the basis of spatial properties, width and
shape of the shadow objects, along with their
adjacency to building. Thereafter, height of building
(H) has been calculated using following equation:
𝐻=
𝑊
cos(𝜑

+90+ 𝜑
 )
tan
(
𝜑sun
)
(4)
where, W is the shadow width, φ
sun
and φ
az
are the
sun angle and sun azimuth angle respectively.
However, during estimation of building height,
satellite azimuth and elevation angles have been
ignored.
Lee and Kim (2013) proposed Volumetric
Shadow Analysis (VSA) based automatic building
height extraction method by using mono-scopic
imagery. The proposed algorithm offers several
advantages, such as, less impact of shadow detection
error on estimation of height of building, need not to
consider all building boundaries and whole shadow
region during estimation of height, etc. Further,
performance of the proposed method has been tested
on HRS image and compared to manually extracted
building height. The experimental result shows that,
RMSE in estimation of building height using
proposed method has been less than 3m.
Raju et al. (2014) estimated height of the
buildings using two different methods, sun-satellite
geometry method as proposed by Shettigara and
Sumerling (1998) and ratio method, which is a
manual method, in which shadow width has been
measured manually. Further, different parameters
with respective to position of sun and satellite at the
time of imaging, have been used in order to estimate
height of building (Eq. 1). Initially, building and
shadow extraction has been carried out by both
manual and automatic method using ENVI’s object-
based classification. However, methodology for
measuring shadow width, which has been a critical
step in estimation of height of building, has not been
clearly explained. Since, shadows casted by buildings
having different size and shapes and do not have
uniform shape which further adds difficulty in
measuring shadow width. Further, results show that,
mean error in estimation of height using ratio
method/manual method (0.67m) have been better
than rule based/automatic method (0.96m), yet rule
based method have been best suited for estimation of
height. Since, manual method is time consuming and
requires more knowledge and selection of training
sample, it slows down processing speed of the
proposed methodology.
Wang et al. (2014) also used sun satellite
geometry method, in order to estimate height of
building using Chinese No.3 resource satellite (ZY3)
image, for Shanghai, China. In the proposed
methodology, initially, building and shadow region
have been classified using MBI, MSI and eCognition
based object-oriented approach. Further, height of
building has been estimated using following
equation:
𝐻=𝑆
𝑡𝑎𝑛ω 𝑡𝑎𝑛Ѳ
𝑡𝑎𝑛
Ѳ
−
𝑡𝑎𝑛
ω
(5)
where, S is the shadow width, ω and Ѳ are the
altitude of the sun and satellite respectively. Further,
obtained result shows that absolute and relative error
during estimation of height of building have been
below 3m and below 5% respectively.
The detailed literature survey suggests that
accuracy in estimation of building height from
satellite image is highly dependent on accuracy of
shadow extraction and shadow width measurement
procedures. Above studies largely avoided the
consideration of various shapes of the building, their
orientation, and shadow cast by these buildings due
to their different/unlike shape.
3 METHODOLOGY
Methodology adopted for estimation of height of
building using sun-satellite geometry method is
GISTAM 2024 - 10th International Conference on Geographical Information Systems Theory, Applications and Management
86

shown in Fig. 3. The proposed methodology estimates
height of the building using relationship between
shadow cast by building and sun-satellite azimuth and
sun elevation angle.
The input to the proposed methodology is a
shadow image (Fig 4b), which has been obtained
from the object-based building extraction technique
(Gavankar & Ghosh, 2019), shown in Fig 4a. The
input image (Fig 4b) includes shadow objects cast by
various buildings in the region.
Figure 3: Methodology adopted for estimation of building
height.
Sun and satellite geometry (angle) at the time of
image acquisition reveals important information,
which may be used to estimate height of building. The
intrinsic relationship of angle produced by sun-
satellite with respective to building normal, length,
and width of the shadow cast by building together has
been used to estimate height of building
Figure 4: (a) Scene selected from IKONOS MS data set (b)
Shadow class.
In general, there are three important steps while
estimating height of building, based on the analysis of
shadow.
i) Extraction of shadow from satellite image
ii) Measurement of shadow width
iii) Estimation of height of building using sun-
satellite geometry
3.1 Extraction of Shadow from Satellite
Image
In general, extraction of shadow from optical imagery
has been a fundamental step in estimation of height of
building using shadow. Various studies have been
carried out in order extract shadow from satellite
imagery (Sarabandi et al., 2004; Arévalo et al., 2008;
Liu and Yamazaki, 2012; Song et al., 2014), which
have been further found effective during estimation
of height of building.
Considering various advantages of OBIA, here,
an object-based technique has been used to extract
shadow from HRS image. The proposed shadow
extraction methodology consists of three steps;
i) Improving spatial resolution of MS image: In
this step, HCS pan sharpening algorithm has been
used to enhance spatial resolution of multispectral
image
ii) Segmentation: Segmentation has been carried
out by using ENVI’s edge-based segmentation
method.
iii) Classification: Unsupervised K-means clustering
algorithm has been used to classify segmented
image into five predefined classes, such as,
vegetation, roads, barren land, building, and
shadow. Further, the extracted shadow class has
been used for estimation of height of building.
3.2 Measurement of Shadow Width
Measurement of shadow width has been a major issue
during estimation of height of building. In general,
shadow width may be calculated by measuring the
distance from detected corner of that building to the
respective corners of shadow. However, relating or
finding corresponding corners of building and
shadow is a challenging task. In order to overcome
this problem the relation (Eq.6) used by (Shettigara
and Sumerling, 1998; Raju et al., 2014) has been
used.
𝑆=
𝐴
𝑟𝑒𝑎 𝑜𝑓 𝑠ℎ𝑎𝑑𝑜𝑤 𝑧𝑜𝑛𝑒
𝑊𝑖𝑑𝑡ℎ 𝑜
𝑓
𝑡ℎ𝑒 𝑧𝑜𝑛𝑒
(6)
where,
Extraction of shadow
object boundary
Examining shadow line
azimuth angle
Shadow length
measurement
Apply sun satellite geometry
method for estimation of
height of building
Shadow
length
Shadow class from
object-based building
ihi
Estimation of Height of Building Using High Resolution Satellite Image
87

S is the width of shadow.
Further, the obtained shadow width along with
sun-satellite elevation and azimuth angles at the time
of image acquisition has been used to estimate height
of building.
The proposed methodology considers, azimuth of
shadow line and sun illumination direction while
measuring width of shadow cast by building.
However, in the proposed methodology (Shettigara
and Sumerling, 1998; Raju et al., 2014) has not
considered following issues related to the shadow cast
by special or irregular shaped buildings:
i) Shadow cast by special or irregular shaped
buildings are also irregular in nature.
ii) These shadows may be extended in one direction
due to building line azimuth, shape of building,
and sun azimuth at the time of image acquisition.
iii) A part of the building, which is opposite to sun
illumination direction, also casts shadow of roof
of building, instead of the shadow of vertical
edges of the building.
In addition, during field/ground observation, it has
been observed that, shadow cast by building edges
which is exposed to direct sunlight gives true shadow
with respect to vertical edges (height) of building and
that shadow line observes uniform angle theta (θ)
with respect to North. However, edges of building
opposite to sun illumination direction cast shadow of
roof of building instead of vertical building edges and
do not follow any specific angle with respect to
North. Similar observations may be seen for a typical
shape building and extracted shadow, cast by such
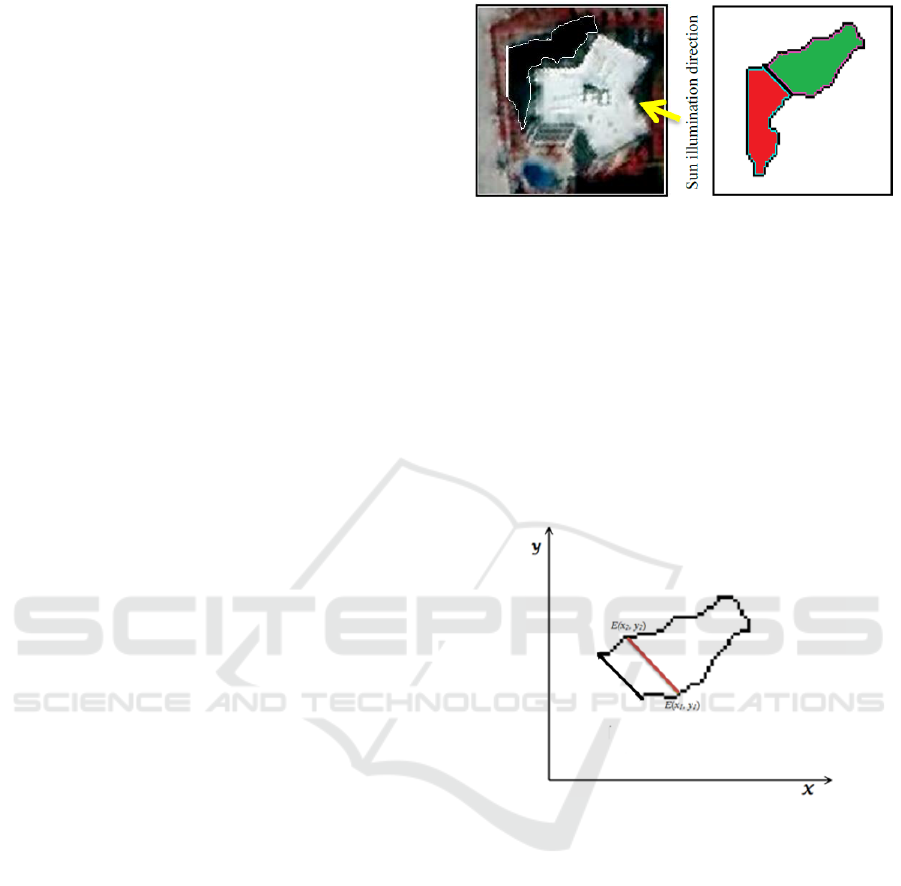
building, in the study area (Fig. 5).
Here, shadow cast by a typical shape building
(Fig. 5), clearly shows the relationship between sun
illumination direction and the shadow cast by
building. Green portion represents shadow cast by
vertical edges of the building, which have been
directly exposed to the sun illumination direction and
clearly observes a uniform angle theta (θ) with
respect to North. However, the red portion represents
shadow cast by part of building, which is opposite to
sun illumination direction and does not follow any
regular relationship with North direction and building
line. In addition to that, shadow cast by roof of
building may be seen in the red portion of the shadow
zone. Unlike other shadow edges, a straight vertical
line may be seen, which represents projection of roof
edge of building.
In order to measure the actual width of the shadow
cast by a building, parallel lines to shadow line
connecting every two opposite edge pixels of shadow
edges (E(x1,y1) to E(x2,y2)), considering sun
illumination direction have been drawn. However,
(a) Typical shape building (b) Extracted shadow
Figure 5: Shadow cast by a typical shape building.
during measuring shadow length, shadow cast by part
of building exposed to sun illumination direction has
been considered (green portion in Fig 5 (b)). Since, a
part of building, which has been exposed to sun
illumination direction, projects shadow with respect
to vertical edges (height) of building. Further, the line
having maximum length amongst all parallel lines has
been considered as width of shadow cast by building
and used further for estimation of height of building
(Fig. 6).
Figure 6: Measurement of shadow width.
3.3 Measurement of Shadow Width
Sun-satellite geometry at the time of image
acquisition plays a key role during estimation of
height of building. A part of the shadow seen on
satellite image depends on its location with respect to
Sun and building (Raju et al. 2014). A typical end
view of sun-satellite-building geometry at the time of
imaging is shown in Fig. 7 and 8 respectively.
In this method, while estimating height of object
(building), following assumptions have been made.
i) Object (building) has been assumed to be vertical,
i.e. object is perpendicular to surface of Earth
which is also flat.
ii) Shadow has been projected directly onto flat
ground.
GISTAM 2024 - 10th International Conference on Geographical Information Systems Theory, Applications and Management
88

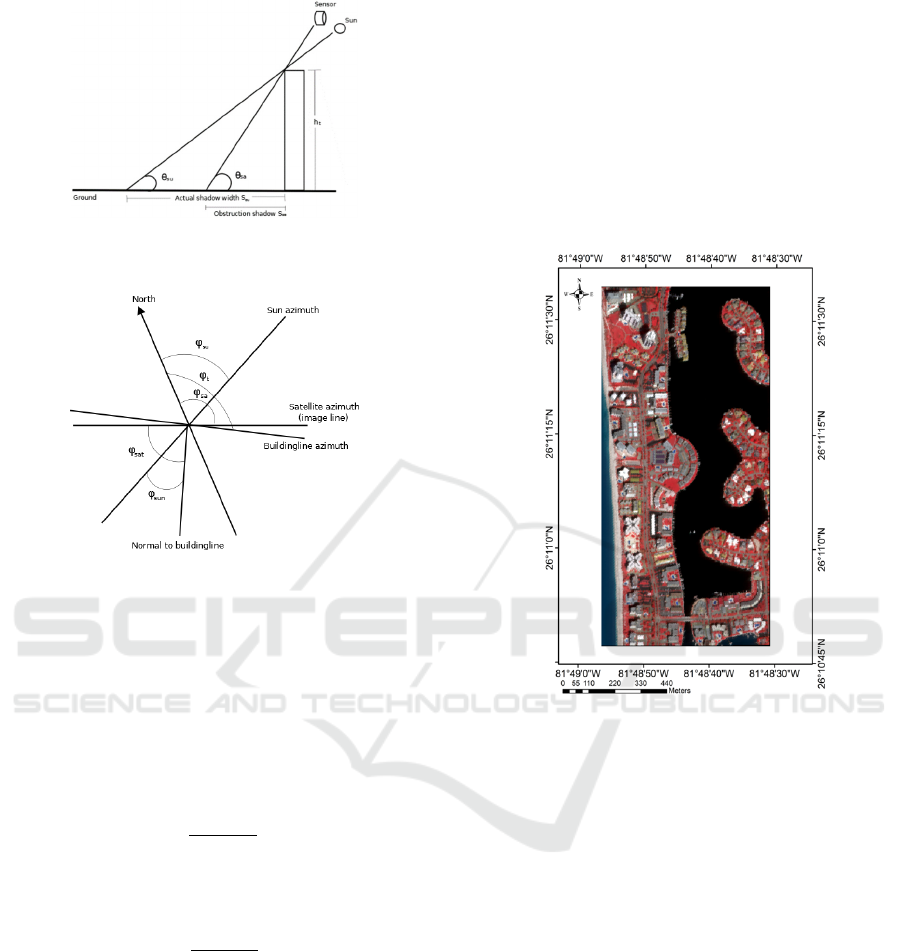
Figure 7: End view of the sun-satellite-building
configuration as seen during imaging (Raju et al., 2014).
Figure 8: Sun-satellite-building geometry (Raju et al.,
2014).
i) Shadow line starts immediately from the bottom
of the building line.
Following equations have been derived by using the
sun-satellite geometry (Fig. 7, Fig. 8), shadow cast by
building, and assumptions made. The width of
shadow along the sun azimuth (S
su
) may be expressed
as
𝑆

=
ℎ

𝑡𝑎𝑛
(
𝜃

)
(7)
The width of shadow obstructed along azimuth of
sensor by the object in the sensor's field of view (S
sa
)
𝑆

=
ℎ

𝑡𝑎𝑛
(
𝜃

)
(8)
And
𝜙

= 𝜙

+90− 𝜙

(9)
ϕ

= ϕ

+90− ϕ

(10)
where, ϕ
su
, ϕ
sa
, ϕ
t
are the azimuth of sun, image scan
line (satellite azimuth), and building line respectively.
Further, height of building (h
t
) may be represented as
ℎ

=
𝑆


𝑐𝑜𝑠
(
ϕ

)
𝑡𝑎𝑛
(
θ

)

−

𝑐𝑜𝑠
(
ϕ

)
tan (θ

)



(11)
where, S is the shadow width (area of the shadow
zone divided by the length of the zone).
4 STUDY AREA
Extraction of building from remotely sensed data has
been a difficult task due to their diverse structural and
spectral
IKONOS data of Dec 21, 2006, has been taken for
study, is located close to Naples, USA, lying between
the latitude and longitudes ranges of (26°11´45´´N to
26°10´45´´ N) and (81°48´56´´W to 81°48´ 30´´ W)
respectively (Fig. 9).
Figure 9: Study area/Location map: Naples, USA.
Naples is located near the Gulf of Mexico in
southwest Florida, known for its high-end shopping
and golf courses. Naples is one of the wealthiest cities
in the United States, with the sixth highest per capita
income in America. According to the United States
Census Bureau, the city has a total area of 42.59Km2.
The uniqueness of this image selected is that the
buildings have different shapes interspersed with
good coverage of vegetation, having different layout.
Some of the buildings are condominium type having
a good length of the shadow, while others low height
isolated buildings, very typical of resort areas.
5 RESULT AND DISCUSSION
Estimation of building height from HRS data is one
area to tropical interest to researchers. Here, shadow
of building has been defined separately as a class, and
obtained from object-based building extraction
technique (Gavankar & Ghosh, 2019). The same has
Estimation of Height of Building Using High Resolution Satellite Image
89

been used as an input to estimate height of the
building. The input shadow class, obtained from
object-based technique is shown in Fig. 4(b).
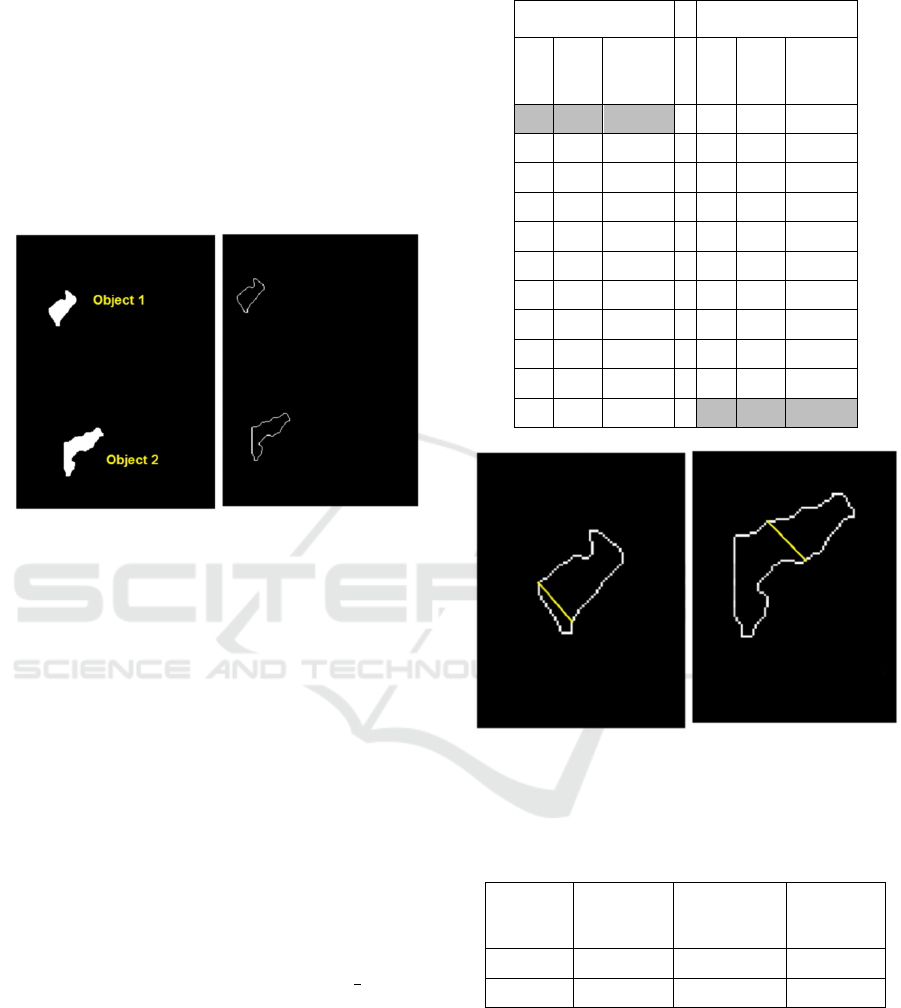
Further, building shadow objects highlighted in
Fig 4(b) have been selected for estimation of height
of building (Fig. 10(a)). The shadow objects selected
includes, the shadow cast by a regular shape building
(Object 1) and a typical or special shape building
(Object 2). Thereafter, boundaries of selected objects
have been extracted 10(b)), and used further for
estimation of height of building.
(a) Shadow objects (b) Boundaries of shadow
objects
Figure 10: Selected building shadow objects; object 1:
shadow cast by regular shape building, object 2: shadow
cast by typical or special shape building.
In the next step, considering azimuth of sun
illumination and shadow line azimuth, parallel lines
connecting every two opposite edge pixels of shadow
edges have been drawn. Thereafter, the line having
maximum length amongst all the parallel lines has
been selected as the width of shadow zone. Table 1
shows the length of sample/few parallel lines in terms
of number of pixels for both shadow objects. Fig. 11
(a) and (b) shows selected maximum length shadow
line for both shadow objects.
After selecting maximum length of the line, width
of the shadow zone is calculated by considering
number of pixels comprises line and resolution of
image (i.e number of pixels comprises line × image
resolution) (Table 2).
Table 1: Length of parallel lines.
Shadow object 1 Shadow object 2
X Y
Length
of the
line
X Y
Length
of the
line
43 364 22 63 537 21
44 363 21 64 536 21
45 362 21 66 536 20
47 361 20 67 536 18
48 360 20 69 536 17
49 359 20 71 535 17
50 358 20 73 534 17
51 357 20 74 533 18
52 356 20 75 532 20
55 355 18 76 531 22
56 354 18 78 530 23
(a) Shadow object 1 (
b
) Shadow object 2
Figure 11: Maximum length line for measuring shadow
width.
Table 2: Width of shadow zone.
Shadow
object
Length of
the line
(pixels)
Resolution
of image
(m)
Width of
shadow
zone (m)
Object 1 22 1 13.20
Object 2 23 1 13.80
(Shettigara and Sumerling 1998; Raju et al., 2014)
used Bounding/Enclosing rectangle method to
measure the width of shadow zone. In Bounding
Rectangle method, a rectangle with minimum area of
arbitrary orientation enclosing every pixel of the
polygon under consideration has been drawn (Fig.
12). Further, width of rectangle which has been
considered as width of shadow zone and area of
GISTAM 2024 - 10th International Conference on Geographical Information Systems Theory, Applications and Management
90

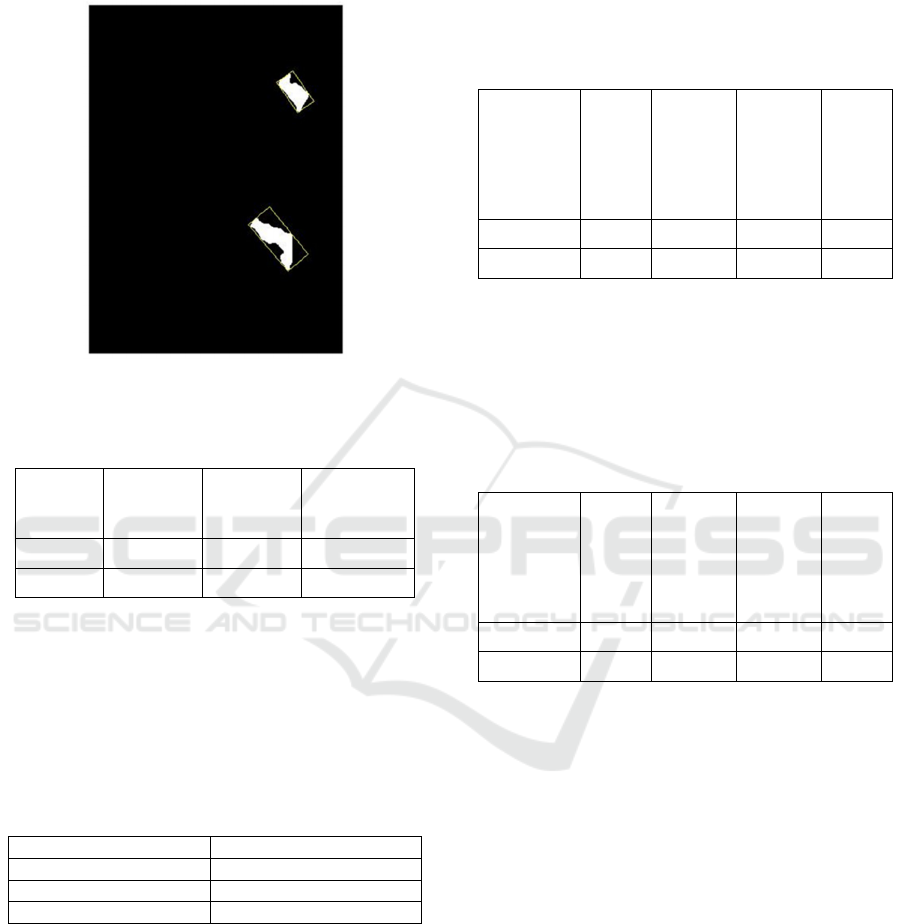
rectangle has been used to estimate height of building.
Table 3 shows area and width of rectangle obtained
by using Bounding Rectangle method.
Figure 12: Minimum bounding rectangle for measuring
shadow width.
Table 3: Area and width of minimum bounding rectangle.
Shadow
object
Area of
rectangle
(sqm)
Width of
rectangle
(m)
Width of
shadow
zone (m)
Object 1 397.49 14.48 14.48
Object 2 897.52 19.91 19.91
Thereafter, height of building has been estimated
using sun-satellite geometry method (Shettigara &
Sumerling, 1998; Raju et al., 2014), as explained in
Section 3.3. In sun-satellite geometry method, the
required sun and satellite elevation and azimuth angle
have been acquired from image metadata file (Table
4).
Table 4: Sun and satellite elevation and azimuth angle.
Sun elevation 49.3
Sun azimuth 163.7
Satellite elevation 63.8
Satellite azimuth 208.2
Thereafter, width of shadow (S) and height of the
building (h
t
) have been calculated using Eq. 6 and 11
respectively and obtained results are given in Table 5.
Table 5 shows that for regular shape building
(building 1) error in estimation of height of building
is less (2.55 m), however for typical or special shape
building (building 2) error is high (22.65 m). The
error observed in estimation of building height for
typical or special shape building is mainly due to the
3 reasons as explained in Section 3.2. Hence,
methodology proposed by Raju et al., (2014) for
estimation of height of building gives acceptable
result for regular shape building, however, may not
be suitable for special or typical shape buildings.
Table 5: Estimation of height of building using Raju et al.,
(2014) method.
Building
Width
of
shadow
(S)
(m)
Estimate
d height
of
building
(h
t
) (m)
Actual
height of
building
(Emporis
Dictionar
y)
(m)
Error
in
height
estimat
ion
(m)
Building 1 27.45 31.55 29 2.55
Building 2 45.08 51.22 28.57 22.65
In order to resolve the problem in estimation of height
of building having special or typical shape, sun-
satellite-shadow relationship proposed by Comber et
al., (2012) has been used (Eq. 4) and the results
obtained are given in Table 6.
Table 6: Estimation of height of building using Comber et
al., (2012) method.
Building
Width
of
shadow
(W)
(m)
Estimate
d height
of
building
(H) (m)
Actual
height of
building
(Emporis
Dictionar
y)
(m)
Error
in
height
estimat
ion
(m)
Building 1
13.20 28.09 29 0.91
Building 2
13.80 29.36 28.57 0.79
Table 6 shows that error in estimation of height of
building is acceptable for both regular and typical or
special shape buildings. However, Comber et al.,
(2012) have not considered methodology to measure
the width of the shadow cast by the building, which is
an important criterion during estimation of height of
building, especially for typical or special shape
building.
In this study, methodology for measuring width of
shadow cast by the building has been proposed.
Further, proposed methodology addresses the
fundamental issues related to the measurement of
width of shadow cast by the typical or special shape
building. Here, sun illumination direction has also
been considered during shadow width measurement.
Proposed methodology has been found suitable to
measure the width of shadow cast by building, during
estimation of height of building using Comber et al.,
(2012) method.
Estimation of Height of Building Using High Resolution Satellite Image
91

6 CONCLUSION AND FUTURE
SCOPE
High spatial resolution satellite image and OBIA
approach provides a comprehensive methodology to
detect and extract shadows cast by buildings.
Proposed object-based framework successfully
extracts shadow precisely from HRS multi-spectral
image, which is a preliminary requirement for
estimation of height of building.
Methodology proposed for measuring width of
the shadow zone considering sun illumination
direction and orientation of building has been found
efficient during estimation of height for all types of
different shape buildings. The error observed in
estimation of height of building for both regular shape
and special shape buildings are 0.91 m. and 0.71 m.
respectively, which is acceptable when compared to
earlier studies. Proposed shadow measuring
technique for estimation of height of building may be
tested for other typical or special shape buildings.
7 MAJOR ACHIVEMENT
Methodology for measuring width of the shadow
zone has been proposed to estimate height of all types
of buildings considering effect of sun illumination
direction and orientation of building. Proposed
methodology resolves an important issue of
measuring width of the shadow zone, especially for
shadow cast by special or typical shape building,
which is novel in the sense that no such study has
been reported earlier.
REFERENCES
Arévalo, V., González, J. and Ambrosio, G., 2008. Shadow
detection in colour high‐resolution satellite images.
International Journal of Remote Sensing, 29(7), 1945–
1963.
Brunner, D., Lemoine, G., Bruzzone, L. and Greidanus, H.,
2010. Building height retrieval from VHR SAR
imagery based on an iterative simulation and matching
technique. IEEE Transactions on Geoscience and
Remote Sensing, 48(3), 1487–1504.
Chen, D., Shang, S. and Wu, C., 2014. Shadow-based
building detection and Segmentation in High-resolution
Remote Sensing Image. journal of multimedia, 9(1),
181–188.
Cheng, F. and Thiel, K.H., 1995. Delimiting the building
heights in a city from the shadow in a panchromatic
SPOT-image—Part 1 test of forty-two buildings.
Remote Sensing, 16(3), 409–415.
Comber, A., Umezaki, M., Zhou, R., Ding, Y., Li, Y., Fu,
H., Jiang, H. and Tewkesbury, A., 2012. Using shadows
in high-resolution imagery to determine building
height. Remote sensing letters, 3(7), 551–556.
Dare, P.M., 2005. Shadow analysis in high-resolution
satellite imagery of urban areas. Photogrammetric
Engineering & Remote Sensing, 71(2), 169–177.
Gavankar, N.L. and Ghosh, S.K., 2018. Automatic building
footprint extraction from high-resolution satellite image
using mathematical morphology. European Journal of
Remote Sensing, 51(1), pp.182-193
Gavankar, N.L. and Ghosh, S.K., 2019. Object based
building footprint detection from high resolution
multispectral satellite image using K-means clustering
algorithm and shape parameters. Geocarto
international, 34(6), pp.626-643
Guida, R., Iodice, A. and Riccio, D., 2010. Height retrieval
of isolated buildings from single high-resolution SAR
images. IEEE Transactions on Geoscience and Remote
Sensing, 48(7), 2967–2979.
Guillaso, S., Ferro-Famil, L., Reigber, A. and Pottier, E.,
2005. Building characterization using L-band
polarimetric interferometric SAR data. IEEE
Geoscience and Remote Sensing Letters, 2(3), 347–
351.
Guo, J., Liang, L. and Gong, P., 2010. Removing shadows
from Google Earth images. International Journal of
Remote Sensing, 31(6), 1379–1389.
Hartl, P. and Cheng, F., 1995. Delimiting the building
heights in a city from the shadow on a panchromatic
SPOT-image: Part 2: Test of a complete city. Remote
Sensing, 16(15), 2829–2842.
Lee, T. and Kim, T., 2013. Automatic building height
extraction by volumetric shadow analysis of
monoscopic imagery. International journal of remote
sensing, 34(16), 5834–5850.
Liasis, G. and Stavrou, S., 2016. Satellite images analysis
for shadow detection and building height estimation.
ISPRS Journal of Photogrammetry and Remote
Sensing, (119), 437–450.
Liu, W. and Yamazaki, F., 2012. Object-based shadow
extraction and correction of high-resolution optical
satellite images. IEEE Journal of Selected Topics in
Applied Earth Observations and Remote Sensing, 5(4),
1296–1302.
Massalabi, A., He, D.C., Benie, G.B. and Beaudry, E.,
2004. Detecting information under and from shadow in
panchromatic IKONOS images of the city of
Sherbrooke. In Proceedings of IEEE on Geoscience and
Remote Sensing Symposium (IGARSS04), (3), 2000–
2003.
Raju, P.L.N., Chaudhary, H. and Jha, A.K., 2014. Shadow
analysis technique for extraction of building height
using high resolution satellite single image and
accuracy assessment. The International Archives of
Photogrammetry, Remote Sensing and Spatial
Information Sciences, 40(8), 1185.
GISTAM 2024 - 10th International Conference on Geographical Information Systems Theory, Applications and Management
92

Sarabandi, P., Yamazaki, F., Matsuoka, M. and
Kiremidjian, A., 2004. Shadow detection and
radiometric restoration in satellite high resolution
images. In Proceedings of IEEE 4th Symposium on
Geoscience and Remote Sensing (IGARSS), (6), 3744–
3747.
Shao, Y., Taff, G.N. and Walsh, S.J., 2011. Shadow
detection and building-height estimation using
IKONOS data. International journal of remote sensing,
32(22), 6929–6944.
Shettigara, V.K. and Sumerling, G.M., 1998. Height
determination of extended objects using shadows in
SPOT images. Photogrammetric Engineering and
Remote Sensing, 64(1), 35–43.
Sırmaçek, B. and Ünsalan, C., 2008. Building detection
from aerial images using invariant color features and
shadow information. In 23rd IEEE International
Symposium on Computer and Information Sciences
(ISCIS), 1–5.
Sırmaçek, B. and Ünsalan, C., 2011. A probabilistic
framework to detect buildings in aerial and satellite
images. IEEE Transactions on Geoscience and Remote
Sensing, 49(1), 211–221.
Song, H., Huang, B. and Zhang, K., 2014. Shadow
detection and reconstruction in high-resolution satellite
images via morphological filtering and example-based
learning. IEEE Transactions on Geoscience and
Remote Sensing, 52(5), 2545–2554.
Sportouche, H., Tupin, F. and Denise, L., 2011. Extraction
and three-dimensional reconstruction of isolated
buildings in urban scenes from high-resolution optical
and SAR spaceborne images. IEEE Transactions on
Geoscience and Remote Sensing, 49(10), 3932–3946.
Wang, J. and Wang, X., 2009, May. Information extraction
of building height and density based on quick bird
image in Kunming, China. In IEEE Joint Event on
Urban Remote Sensing, 1–8.
Wang, X., Yu, X. and Ling, F., 2014. Building heights
estimation using ZY3 data-A case study of Shanghai,
China. In IEEE international Symposium on
Geoscience and Remote Sensing (IGARSS), 749–1752.
Estimation of Height of Building Using High Resolution Satellite Image
93