A Novel Approach in Testing Life-Monitoring Technologies for Ageing in

Place: A Focus on Fall Detection and Behavioural Alerts

Nicolas Bioul

1, 2, 3, 5

, Arthur Pisvin

1, 2, 3, 5

, Maxim Lamirande

, J

ome Lecl

ere

1, 2, 3, 5

Lucas El Raghibi

1, 2, 3

, Adrien Denis

1, 2, 3

and Beno

ıt Macq

1, 2, 3, 5 a

OpenHub Place du Levant 3, Louvain-la-Neuve, Belgium

Pixels and Interactions Lab, UCLouvain, Place du Levant 3, Louvain-la-Neuve, Belgium

ICTEAM, UCLouvain, Place du Levant 3, Louvain-la-Neuve, Belgium

Inter’Act, ULi

ege, All

ee de la d

ecouverte 9, BuildingB52/3, Li

ege, Belgium

TRAIL Institute, Belgium

Keywords:

AI, Digital Twin, Silver Economy, Innovative Testing Methods, Fall Detection, Assistive Technology,

Geriatrics.

Abstract:

Addressing the issues of age and disability, our study presents a systematic technique for evaluating smart

home technology designed to improve independent living. While acknowledging companies’ efforts in this

ﬁeld, we created a framework to assess potential solutions using a rigorous demographic study that deﬁned

various user proﬁles - or personae - as the foundation for our comparison research. Our methodology is based

on a dual-focused analytical approach: analysing installation processes and operating performance, with a

particular emphasis on fall detection and behaviour analysis. To evaluate fall detection, we developed a test

protocol, which resulted in the compilation of a large database. We pioneered the use of virtual personae

in a game engine for behavioural analysis, which are simulated in living contexts via probabilistic activity

generation. This novel approach allowed the creation of virtual sensor data, which was then analysed by AI

algorithms thus generating alerts. This study emphasises the possibility for combining IoT and AI to reduce

the need for institutional care by offering real-time help and monitoring. Our methodology takes a thorough

approach to assessing the efﬁcacy of smart home devices, ensuring that they are adaptable to the real-world

demands of the ageing population and people with disabilities.

1 INTRODUCTION

Currently, many ageing people or people with disabil-

ities are unable to live independently due to issues

within their daily lives such as cognitive problems,

general health issues or a simple fall down a ﬂight of

stairs . . . the responsibility often falls on family mem-

bers, commonly resulting in their placement in spe-

cialised institutions or retirement homes. This prac-

tice not only impacts the emotional and physical well

being of the older population but also represents a sig-

niﬁcant ﬁcial burden for governments, which invest

heavily in subsidising these facilities.

Recent studies have shown that the life expectancy

of individuals in long-term care facilities, including

nursing homes, can be notably lower compared to

https://orcid.org/0000-0002-7243-4778

those living independently. For instance, an older

people moving to a long-term care facility might see

a drastic reduction in life expectancy, with mortality

rates as high as 50%−60% within the ﬁrst year of res-

idence. In contrast, seniors living in retirement com-

munities, which offer a more supportive and engaging

environment, might enjoy a longer and stronger life

(Boucaud-Maitre et al., 2023), (Lubitz et al., 2003),

(Nugraha and Aprilia, 2019).

This contrast raises an important question: Could

smart home IoT technologies, combined with Artiﬁ-

cial Intelligence (IA), offer a sustainable alternative

for elder and disabled care? Integrating these tech-

nologies into daily routines may delay institutional-

isation by assisting, monitoring, and alerting care-

givers in real-time.

Several companies have asked themselves this

Bioul, N., Pisvin, A., Lamirande, M., Leclère, J., El Raghibi, L., Denis, A. and Macq, B.

A Novel Approach in Testing Life-Monitoring Technologies for Ageing in Place: A Focus on Fall Detection and Behavioural Alerts.

DOI: 10.5220/0012733200003699

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 10th International Conference on Information and Communication Technologies for Ageing Well and e-Health (ICT4AWE 2024), pages 98-107

ISBN: 978-989-758-700-9; ISSN: 2184-4984

question and propose different kinds of solutions to

support beneﬁciaries in their lives such as falls de-

tector, behavioural monitoring, sensors and emotion

detectors . . .

Through this paper, we aim to propose a new

framework that allows for an easy yet thorough test-

ing of these technologies, assessing their practical

capabilities in real-world scenarios. This endeavor

is not just a technological assessment but a step to-

wards re-imagining care for this speciﬁc population,

offering a vision where the older and disabled can

lead happier, longer lives within the comfort of their

homes, supported by ethical applications of AI and

IoT sensors.

2 DEFINING THE PROBLEM

The increasing prevalence of older institutionaliza-

tion poses signiﬁcant challenges for healthcare sys-

tems worldwide. Understanding the determits that

lead to institutionalization is crucial for developing

strategies to extend the period that older individuals

can safely live at home. This section explores ﬁve de-

termits identiﬁed during a specialized conference held

in March 2023.

2.1 Sleep and Aging

Sleep quality signiﬁcantly affects cognitive function-

ing and aging. Age-related changes in sleep needs and

patterns can lead to insomnia and other sleep disor-

ders, which are prevalent in the older resulting from

commorbities induced by age (Ancoli-Israel, 2009).

Poor sleep quality, including issues like sleep frag-

mentation and sleep apnea, is linked to reduced cog-

nitive abilities and daily functioning, potentially ac-

celerating the institutionalization process (Foley et al.,

2004).

2.2 Malnourishment in Ageing

Malnutrition in ageing individuals, often resulting

from an imbalance in energy and protein intake, is

a critical factor contributing to frailty and depen-

dency (Kaiser et al., 2010). Factors like involuntary

weight loss, appetite control disorders, dental prob-

lems, medication side effects, and changes in body

composition exacerbate this issue, leading to mus-

cle loss, physical weakness, and cognitive impair-

ments, which can hasten the loss of autonomy (Volk-

ert, 2013).

2.3 Social Isolation

Social isolation has profound impacts on both men-

tal and physical health. Prolonged loneliness can de-

crease life quality, even in institutional settings (Corn-

well and Waite, 2009). A lack of social interaction

can increase mortality risk and negatively affect brain

function, highlighting the necessity of meaningful so-

cial engagement to prevent institutionalization (Holt-

Lunstad et al., 2015).

2.4 Physical Activity and Aging

Physical inactivity in the older leads to muscle mass

loss, reduced endurance, and weakness. Regular

physical activity is crucial for preventing falls, a ma-

jor reason for institutionalization (Rubenstein, 2006).

It also slows cognitive decline, enhances oxygen con-

sumption, and prevents sarcopenia, underscoring the

importance of an active lifestyle for maintaining inde-

pendence (Ferrucci et al., 2016).

2.5 Cognitive Disorders

Cognitive impairments affect daily routines and

decision-making, leading to disorientation and confu-

sion. Introducing technology to maintain routines can

be beneﬁcial, but simplicity is key, as learning new

technologies can be stressful for those with cognitive

disorders (Mowszowski et al., 2012). Personalized

activities and routines are vital for maintaining self-

esteem and autonomy in these individuals (Klompstra

et al., 2013).

Understanding the determits of institutionaliza-

tion is essential for developing effective interventions

to extend the independent living of ageing adults.

This section highlighted the importance of addressing

sleep quality, nutrition, social engagement, physical

activity, and cognitive health. The judicious use of

technology can support these efforts, though it should

be implemented with consideration of the individual’s

capabilities and preferences.

A number of companies offer solutions to enable

the ageing people or people with disabilities to re-

main in their own homes. The solutions offered by

these companies are diverse. This paper considers so-

lutions that detect punctual problems such as falls and

analyse the person’s behaviour in order to detect any

problems in their lifestyle. The objective is to present

a framework to study and compare these technologies

in order to select one or more technologies that meets

the needs of these people and provides them with the

best possible support.

A Novel Approach in Testing Life-Monitoring Technologies for Ageing in Place: A Focus on Fall Detection and Behavioural Alerts

3 PERSONA ANALYSIS

Personae are designed to create representations of hu-

man behaviour as a way to support project develop-

ment. According to (Nielsen, 2018), “To get prod-

uct design closer to the everyday lives of the users,

design personae are a means to capture the everyday

experiences and needs of users and customers”. In

this research project, personae were devised to frame

the representations of a speciﬁc target audience. In

total seven personae were created who each capture

different key characteristics of both mainstream and

outlying user groups. This diversity provides fertile

grounds to explore and understand our target audience

as well as open the project to explore new or under re-

searched areas.

Personae were constructed by crossing raw data

provided by our research partners, testimonials from

32 semi-structured interviews conducted in Spring

2023 with older adults, adults with disabilities, and

professional care provides, as well as census data

published by the Belgian governments, and World

Health Organisation. Key research partners include

four non-proﬁt organizations who either provide hu-

man support to older adults or adults with disabilities,

or technological support in the form of medical alert

bracelets and necklaces that connect the caller to a

dedicated helpline. Data was extracted and analyzed

from 11158 beneﬁciaries across Belgium, as well as

the medical alert calls made to the provider between

2020 and 2022 (292 251 calls).

The personae were constructed using four layers

that incrementally crossed and compiled new char-

acteristics. The ﬁrst layer identiﬁed user pathologies

crossed with the types of support provided. This in-

cluded disabilities linked to motor, cognitive, or vi-

tal functions and whether the person was totally iso-

lated, lived with others, or received formal and infor-

mal support.

This ﬁrst layer was then crossed with data about

different types of domiciles. Characteristics included

whether the person lived in a single-story apartment,

and multi-story home, or other alternative living situ-

ations (such as living in a camper / Recreational ve-

hicle (RV) during the summer). Pairings were vali-

dated with some regression analyses but were found

to overweight mainstream lifestyles and overshadow

any diversity. Driven by the project framing and to

create a variety of personae on which the technolo-

gies could be tested, reasonable pairings were made.

For instance, it seemed more reasonable for an older

couple living with their daughter and grandchildren

and who have minor health issues to be paired with

a multi-story home whereas a widowed woman with

mobility concerns was paired with a small furnished

studio in the city center to help combat social isola-

tion.

The third layer added factors related to the instal-

lation and use of new in-home monitoring technolo-

gies. Here, a balanced distribution of reasonable char-

acteristics supported by census data were paired with

the developing personae. This includes whether the

persona rents or owns the apartment (and can make

permanent changes to the space), if they have Wi-Fi

access, or if they have stable and continuous access to

electricity.

Finally, to breathe life into the personae, testi-

monials and user characteristics from semi-structured

interviews were combined with compatible personae

to provide human qualities, such as a reluctance to

try new technologies, a newfound sense of freedom,

a stubbornness to refuse help, a fear of bothering

friends, family, and service providers, or a desire to

stay connected with younger family members though

new technologies.

Overall, from these personae, many features were

taken into consideration when constructing their dig-

ital twin, as detailed in section 5.2. Key categories

include types of assistance (formal and informal),

health conditions (physical, sensory, vital, cogni-

tive, and other health issues), autonomy levels, and

living situations (house types and technological ac-

cess). Common features across personae involve a

detailed consideration of their living environments,

health challenges, and the support network, ensuring

a nuanced simulation base for technology testing.

4 METHODICAL APPROACH

The objective of this section is to elucidate the pro-

cess of comparing and classifying the different ser-

vices to be installed inside homes to launch alerts.

Speciﬁcally, the study aims to bring together a range

personal assistance solutions that enable alerts to be

issued in the event of problems.

The comparison process comprises several dis-

tinct steps. Firstly, the installation process is com-

pared, considering that time is a precious resource for

large-scale installations and must be taken into ac-

count. Secondly, two categories of alert triggers are

considered: alerts resulting from a fall and alerts re-

sulting from a change in daily routines.

4.1 Installation

The transition through aging should be navigated

smoothly. This is why the installation of technolo-

ICT4AWE 2024 - 10th International Conference on Information and Communication Technologies for Ageing Well and e-Health

100

gies is a critical point that must meet a number of cri-

teria. To be installed in a home, they need to be as

discreet as possible and put into operation as quickly

as possible, without causing any damage. In addition,

it shouldn’t be noticeable on the electricity bill, ei-

ther for the wallet or for the planet. These criteria are

summarized on table 1 and are the reference for the

installation testing.

Table 1: installation criteria.

Criteria Description

Kit supplied All components for the

installation are provided and

safe.

Installation time Total time to install the

solution.

Discretion All components are

seemlessly integrated in a

home.

Damage Installation caused

permanent damage on the

wall, ground, etc.

Consumption Electrical power

consumption of all devices.

4.2 Alerting

Tasks such as fall detection and triggering alerts for

behavioural changes belong to the broader classiﬁca-

tion tasks family, as they involve distinguishing be-

tween positive and negative outcomes. In this paper,

we counted the number of True Positive (TP), False

Positive (FP), True Negative (TN) and False Negative

(FN) to ﬁnd the F1-score.

• True Positives (TP) are instances where the sys-

tem correctly predicts the positive alert.

• False Positives (FP) are instances where the sys-

tem incorrectly predicts the positive alert when it

is actually negative.

• True Negatives (TN) are instances where the sys-

tem correctly predicts the negative alert.

• False Negatives (FN) are instances where the sys-

tem incorrectly predicts the negative alert when it

is actually positive.

This F1-score considers the balance between pre-

cision and recall. Precision measures the accuracy

of positive predictions, calculated as the ratio of true

positives to the sum of true positives and false posi-

tives.

Precision =

T P

T P + FP

(1)

Recall, on the other hand, measures the proportion

of actual positives that were correctly identiﬁed, cal-

culated as the ratio of true positives to the sum of true

positives and false negatives.

Recall =

T P

T P + FN

(2)

The F1-score combines these metrics into a single

value, providing a harmonic mean of precision and

recall. It is calculated using the formula:

F1-score =

2 ·(Precision ·Recall)

Precision + Recall

(3)

This score ranges from 0 to 1, where a higher

value indicates better performance in terms of both

precision and recall.

5 METHOD IMPLEMENTATION

This section explain how experiments are conducted

in order to compare solutions from different compa-

nies.

5.1 Falls

Fall detectors utilize various sensor types, including

wearables and wall-mounted devices. To conduct a

comprehensive comparative study, the authors estab-

lished a simulated living room environment. Modu-

lar rooms representing bedrooms, kitchens, or living

rooms were created by arranging furniture and deco-

rations. A set of predeﬁned environments facilitated

a reproducible set of experiments. Wall-mounted sen-

sors were strategically placed according to the manu-

facturer’s guidelines as shown in Figure 1.

Figure 1: Example of set-up falls.

The authors conducted a series of falling scenar-

ios, totaling over 300 falls in the experimental room.

For each fall, experimenters recorded which sensors

detected the event and applied the scoring method

outlined in the previous section.

A Novel Approach in Testing Life-Monitoring Technologies for Ageing in Place: A Focus on Fall Detection and Behavioural Alerts

101

One signiﬁcant contribution of this study is the

creation of a comprehensive database. Bascom cam-

eras recorded every fall during testing, providing

high-quality footage (1920 x 1080 resolution, 25 fps)

with wide-angle lenses (112

◦

) and infrared night vi-

sion (up to 20 meters) in complete darkness. This

database comprises over 300 recorded falls, along

with various other situations (such as interactions

with animals or sitting on a sofa), resulting in many

hours of footage from the experimental room. Addi-

tionally, recordings were made in a real home to en-

hance contextual variability. These recordings, cat-

egorized into falls and non-falls, are available upon

request to the authors.

5.2 Behaviour Analysis

Among the solutions commercialized by companies,

some use learning aptitudes to capture the behaviour

of beneﬁciaries by recording and analysing their

movements within their homes. This is accomplished

through various means such as movement sensors,

door-opening sensors, or wearable sensors. Behind

these solutions, machine learning algorithms were

employed. These algorithms require data to learn ben-

eﬁciaries’ habits and detect outliers that may corre-

spond to alerts.

A straightforward approach to test these algo-

rithms involved installing each solution in multiple

homes and then requesting feedback from the bene-

ﬁciaries to conﬁrm or deny the triggering of alerts.

However, evidently, this approach was ultimately dis-

carded to prevent any potential inconvenience and

ethical issues due to monitoring.

The primary novelty of this paper lies in its unique

approach. Rather than using real homes, the authors

opted for virtual homes along with virtual beneﬁcia-

ries, effectively forming a digital twin. To model

habits within this virtual environment, the authors em-

ployed a sophisticated system of layers, combining

various statistical tools explained in Appendix A.

A set of characters are accommodated for each

simulation, residing in various homes according to the

personae identiﬁed in the section 3. Indeed, in a real

individual’s life, it’s crucial to incorporate their entire

environment (family, friends and pets). We decided to

represent the entire environment by forming a family

consisting of several personae whose lives intertwine.

Each persona is characterized by a set of attributes, as

outlined in Table 2. Ultimately, once the simulation

has run, our aim is to generate a comprehensive list of

visited rooms within the home for each time step (1

minute).

The lives of personae are structured around vari-

Table 2: Attributes of persona.

Attribute Description

Name This unique name identifying the

persona

Family This binds the persona to a group

of persona represented by family

friends and pets.

Owner This value represents if the persona

is a home owner.

Stack Data structure gathering current

running activities.

ous activities, such as breakfast, reading or family vis-

its. Activities were divided in two sections; planned

activities (daily, weekly and monthly activities) and

unplanned activities (such as episodical events, see

Figure 2). In the simulation, each activity is com-

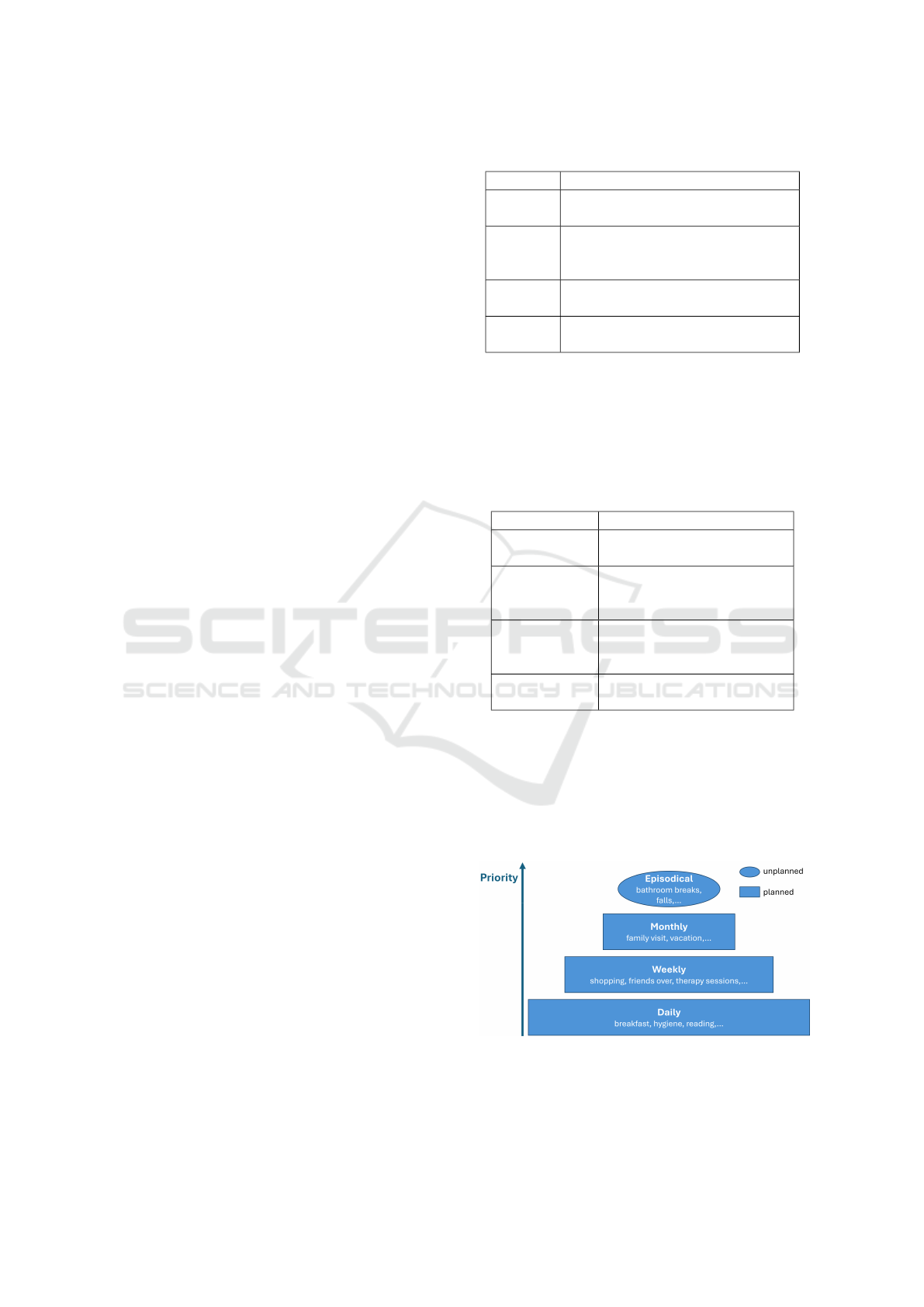
prised of different attributes, as detailed in Table 3.

Table 3: Attributes of activity.

Attribute Description

Name This unique name

identifying the activity

Priority Integer representing the

relative importance of an

activity

Activation

distribution

Statistical distribution

representing the probability

that this activity is activated.

List of rooms Rooms visited in this

activity.

The priority assigned to an activity reﬂects its rel-

ative importance compared to other activities, as illus-

trated in Figure 2. What is referred to as daily activ-

ities are what were classiﬁed as activities of ”unim-

portance” or leisure activities. The priority of each

activity can be adjusted in regards to the situation and

the persona.

Figure 2: Activities priority level.

As an example if a person reads in their living

room around 10 a.m, then one would usually ﬁnd

them reading there. Say now that a bathroom break

ICT4AWE 2024 - 10th International Conference on Information and Communication Technologies for Ageing Well and e-Health

102

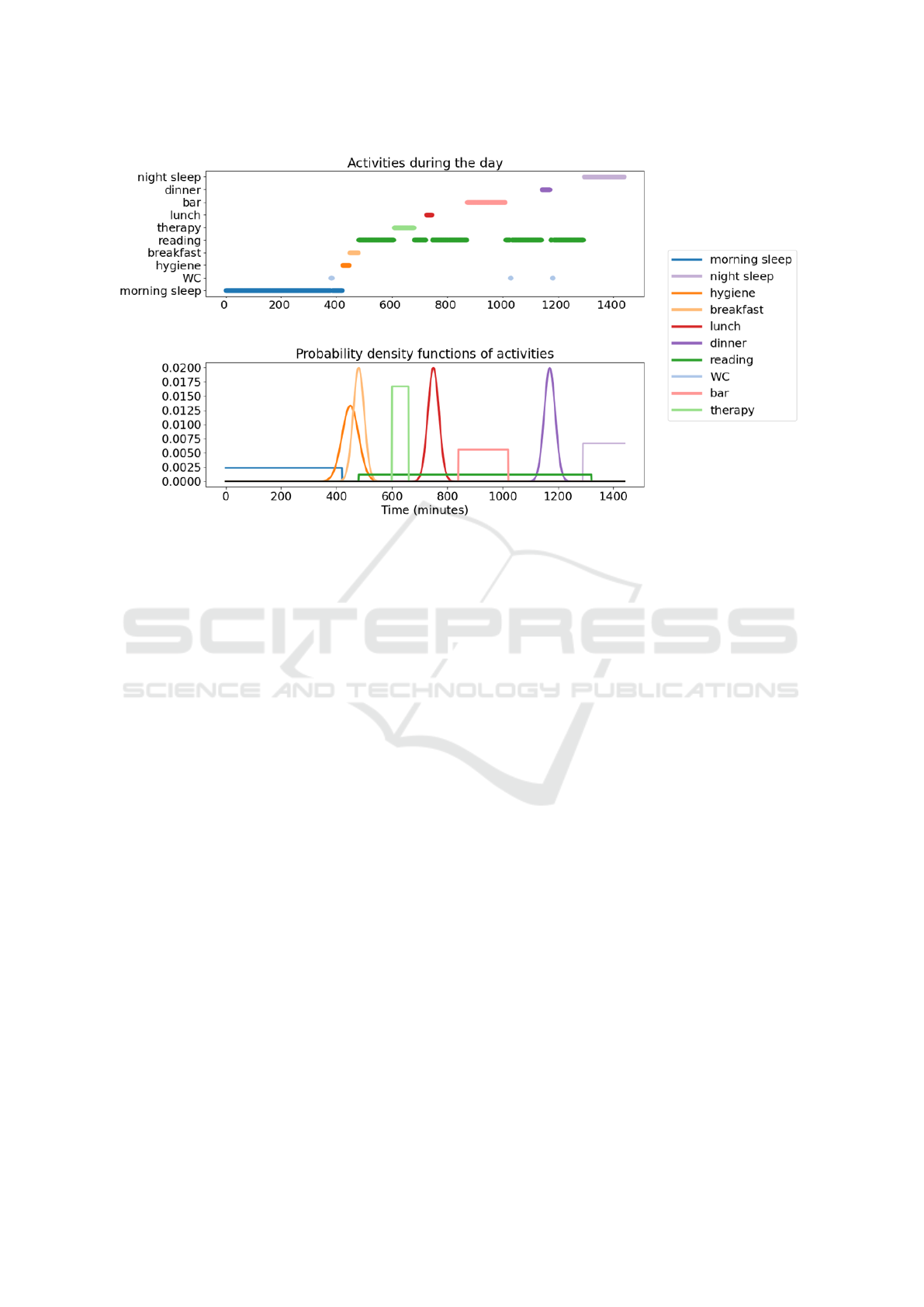
Figure 3: Activation function based on probability density functions (on the bottom) for each activity (on top) a persona may

undertake during a standard day.

is selected, the priority will ensure that the persona

will not ﬁnish its reading activity before going to the

bathroom. The bathroom break activity will directly

kick-in and reading will resume after the bathroom

break ﬁnishes. Note that once resuming, the remain-

ing amount of time for reading will have been reduced

by the time spent in the bathroom.

In that same regard, if a shopping session (consid-

ered a weekly event) overlaps with a reading activity,

the shopping session takes precedence. This layered

system enables the simulation of different days while

maintaining the same daily routine meaning each day

is based on the same pattern but is never quite the

same. At the highest level of the priority hierarchy

are episodic activities, which are unpredictable com-

pared to planned activities. Episodic activities re-

group things like urinary urgencies, trips to the hos-

pital, falling and other unforseen events.

For every persona, a stack is maintained to moni-

tor their current activity. A stack is a linear data struc-

ture ordered by priority rules, where activities are ar-

ranged based on their urgency or importance, with

the highest priority at the top. The activity with the

highest priority is treated as the current activity and is

pushed onto the stack.

Two scenarios can introduce a new activity to the

stack. First, if a higher priority activity than the cur-

rent one is activated, it’s added on top of the stack and

reconsidered as the current one. During each time

step, the duration of all activities in the stack is re-

duced by one minute. When an activity’s remaining

duration reaches zero minutes, it’s removed from the

stack. This process ensures that the most urgent or

important activities are promptly addressed for each

persona. Secondly, if the current activity terminates

without another activity in the stack, all activation

functions of activities are triggered, and the activity

with the highest value of the activation function is

chosen as the new current activity. An example of

generated activities and probability density functions

are illustrated in Figure 3.

To introduce sociological interaction into the sim-

ulation, the authors introduced a special type of ac-

tivity known as ”common activities”. These activi-

ties, initiated by one persona, are added to the stack

of other personas who are involved. This method fos-

ters interaction between personas, a crucial element

for creating a realistic simulation that mirrors real-life

scenarios.

The global randomness of each day resides in the

selection of each activities and the randomness of

their duration in a set of predeﬁned possible activi-

ties and duration. Based on personas description, a

set of possible activities are established. An example

of activities for one personna is given in Appendix C.

When an activity begins, a set of rooms are visited to

complete this activity. Each room is visited during a

certain amount of time. This time is also given by a

random distribution. As an example, when one wakes

up in the morning, usually a hygiene activity is initi-

A Novel Approach in Testing Life-Monitoring Technologies for Ageing in Place: A Focus on Fall Detection and Behavioural Alerts

103

ated. This entails 3 rooms: the toilet, the bathroom

and the bedroom, where waking up, taking a shower

or washing up, urinating and getting dressed success-

fully take place. The order in which these take place

leaves more room for randomness.

After generating all activities and visited rooms

for each persona, the next step is to create a virtual en-

vironment to model displacement inside homes. Un-

real Engine

was selected as the platform to construct

the digital twin. Each persona is represented by a

meta-human

. These meta-humans move within the

home based on generated data.

The solutions proposed by the companies we

aimed to test rely on motion detectors to provide

alerts. To simulate these sensors within Unreal En-

gine, virtual sensors are created. These sensors acti-

vate when a meta-human is in motion inside the vir-

tual environment as shown in Figure 4. All data col-

lected by the virtual sensors is stored in memory for

analysis.

Figure 4: Example of simulation where a meta-human is in

motion in one room (green box). The other empty room has

a white box.

At the conclusion of this process, we gather all

the data extracted from the virtual sensors. This data

encompasses the movements and interactions of the

meta-humans within the simulated environment, pro-

viding a comprehensive record of their presence in

different rooms. With the generated data in the form

of a CSV ﬁle, the companies could successfully test

their algorithms. The authors manually changed ac-

tivities to correspond to outliers to simulate abnormal

activities. As an example, a fall could be translated

by an abnormal 3 hours stay in the toilet or bathroom.

Dementia or a loss of memory could be translated by

an extended amount of time shopping; instead of a

typical 2 hours shopping session, we’d have a 5 hours

shopping session. By recovering the output of these

algorithms, we are therefore capable of assessing their

Unreal Engine (UE) is a series of 3D computer graph-

ics game engines developed by Epic Games

A Meta-human is a hyper-realistic digital representa-

tion of a human. These digital entities are designed to

mimic human emotions, actions, and intricacies perfectly.

precision by comparing and matching inputs and out-

puts.

6 CONCLUSION

This paper has outlined a thorough framework for as-

sessing life-monitoring technologies intended to sup-

port aging individuals in maintaining independence at

home, with speciﬁc emphasis on fall detection and be-

havioral alerts. Through our analysis and experimen-

tation, we have developed a structured approach that

facilitates comparison and evaluation of solutions of-

fered by various companies in this domain. Grounded

in persona analysis, our methodology provides a sys-

tematic framework for assessing the practical capabil-

ities of smart home devices in real-world settings. By

simulating living environments and conducting exten-

sive experiments using digital representations of de-

ﬁned personas, we have gained insights into alert trig-

gers and behavior analysis within smart homes.

However, it is important to recognize the limita-

tions of our study. While our framework introduces

a novel methodology for evaluating life-monitoring

technologies, there are inherent challenges and com-

plexities that must be addressed. For instance, the

simulated environment may not fully replicate the in-

tricacies of real-life situations, particularly regarding

the subtle nuances of human behavior. Additionally,

this environment aimed to capture data from motion

sensors only. More sophisticated sensors like cameras

cannot be replicated in this software.

Moving forward, future research should prioritize

addressing these limitations and reﬁning our method-

ology to improve its effectiveness and relevance. This

includes conducting more extensive user studies to

gather feedback and insights from aging individuals

and individuals with disabilities. Furthermore, ongo-

ing collaboration between researchers, industry stake-

holders, and end-users is essential to drive innovation

and advancement in the realm of smart home tech-

nologies tailored for aging in place.

REFERENCES

Ancoli-Israel, S. (2009). Sleep and its disorders in aging

populations. Sleep Medicine, 10:S7–S11. The Art

of Good Sleep Proceedings from the 6th International

Sleep Disorders Forum: Sleep and Society.

Boucaud-Maitre, D., Letenneur, L., Dram

e, M., Taub

Teguo, N., Dartigues, J.-F., Amieva, H., and Tabu

Teguo, M. (2023). Comparison of mortality and hos-

pitalizations of older adults living in residential care

ICT4AWE 2024 - 10th International Conference on Information and Communication Technologies for Ageing Well and e-Health

104

facilities versus nursing homes or the community. a

systematic review. PLOS ONE, 18(5):1–14.

Cornwell, E. Y. and Waite, L. J. (2009). Social discon-

nectedness, perceived isolation, and health among

older adults. Journal of Health and Social Behavior,

50(1):31–48. PMID: 19413133.

Ferrucci, L., Cooper, R., Shardell, M., Simonsick, E. M.,

Schrack, J. A., and Kuh, D. (2016). Age-related

change in mobility: perspectives from life course epi-

demiology and geroscience. Journals of gerontology

series a: biomedical sciences and medical sciences,

71(9):1184–1194.

Foley, D., Ancoli-Israel, S., Britz, P., and Walsh, J. (2004).

Sleep disturbances and chronic disease in older adults:

Results of the 2003 national sleep foundation sleep in

america survey. Journal of Psychosomatic Research,

56(5):497–502.

Holt-Lunstad, J., Smith, T. B., Baker, M., Harris, T.,

and Stephenson, D. (2015). Loneliness and so-

cial isolation as risk factors for mortality: A meta-

analytic review. Perspectives on Psychological Sci-

ence, 10(2):227–237. PMID: 25910392.

Kaiser, M. J., Bauer, J. M., R

amsch, C., Uter, W., Guigoz,

Y., Cederholm, T., Thomas, D. R., Anthony, P. S.,

Charlton, K. E., Maggio, M., Tsai, A. C., Vellas, B.,

Sieber, C. C., and for the Mini Nutritional Assessment

International Group (2010). Frequency of malnutri-

tion in older adults: A multinational perspective using

the mini nutritional assessment. Journal of the Amer-

ican Geriatrics Society, 58(9):1734–1738.

Klompstra, L., Jaarsma, T., and Str

omberg, A. (2013). An

in-depth, longitudinal examination of the daily physi-

cal activity of a patient with heart failure using a nin-

tendo wii at home: a case report. Journal of Rehabili-

tation Medicine, 45(6):599–602.

Lubitz, J., Cai, L., Kramarow, E., and Lentzner, H. (2003).

Health, life expectancy, and health care spending

among the elderly. New England Journal of Medicine,

349(11):1048–1055. PMID: 12968089.

Mowszowski, L., Hermens, D. F., Diamond, K., Norrie, L.,

Hickie, I. B., Lewis, S. J., and Naismith, S. L. (2012).

Reduced mismatch negativity in mild cognitive im-

pairment: associations with neuropsychological per-

formance. Journal of Alzheimer’s Disease, 30(1):209–

219.

Nielsen, L. (2018). Design personas – new ways, new con-

texts. Persona Studies, 4(2):1–4.

Nugraha, S. and Aprilia, T. (2019). Quality of life of the

elderly living in community and nursing home (study

on 5-dimension quality of life).

Rubenstein, L. Z. (2006). Falls in older people: epidemi-

ology, risk factors and strategies for prevention. Age

and Ageing, 35(suppl 2):ii37–ii41.

Volkert, D. (2013). Malnutrition in Older Adults - Urgent

Need for Action: A Plea for Improving the Nutritional

Situation of Older Adults. Gerontology, 59(4):328–

333.

APPENDIX

A Statistic Tools

The uniform distribution is characterized by a con-

stant probability density function over a speciﬁed in-

terval. In the context of behaviour modeling, it’s often

used to represent situations where all outcomes within

a range are equally likely. For example, it can be used

to model the probability to sit in the living room over

the afternoon. The distribution is deﬁned by two pa-

rameters: the minimum and maximum values of the

interval.

f (x) =

−t

for t

≤ x ≤t

(4)

The Gaussian distribution, also known as the nor-

mal distribution, is one of the most widely used distri-

butions in statistics. It’s characterized by a symmetric

bell-shaped curve, with the mean (average) at the cen-

ter and the majority of the data clustered around the

mean. Many natural phenomena follow a normal dis-

tribution, making it particularly useful for modeling

behaviour when the underlying process is inﬂuenced

by multiple independent factors. An example is the

morning wake-up time, which revolves around a cer-

tain mean (µ) with a certain standard deviation (σ).

f (x) =

√

2π

−

(x−µ)

2σ

(5)

behaviour modeling often involves analyzing the

time intervals between successive events. The expo-

nential distribution provides a mathematical frame-

work for modeling these inter-event times.

f (x;λ) = λe

−λx

(6)

Where λ represents the mean.

A Poisson process is a stochastic process that

models a sequence of events occurring randomly in

time or space. It is widely used in various ﬁelds such

as queueing theory, telecommunications, and relia-

bility engineering. The deﬁning characteristics of a

Poisson process are:

1 Independence: Events occur independently of

each other.

2 Stationarity: The probability of an event occur-

ring in a given interval of time or space is the same

for all equivalent intervals.

3 Ordinariness: The process has no simultaneous

events; events occur singularly.

The key formulae associated with a Poisson pro-

cess include:

A Novel Approach in Testing Life-Monitoring Technologies for Ageing in Place: A Focus on Fall Detection and Behavioural Alerts

105

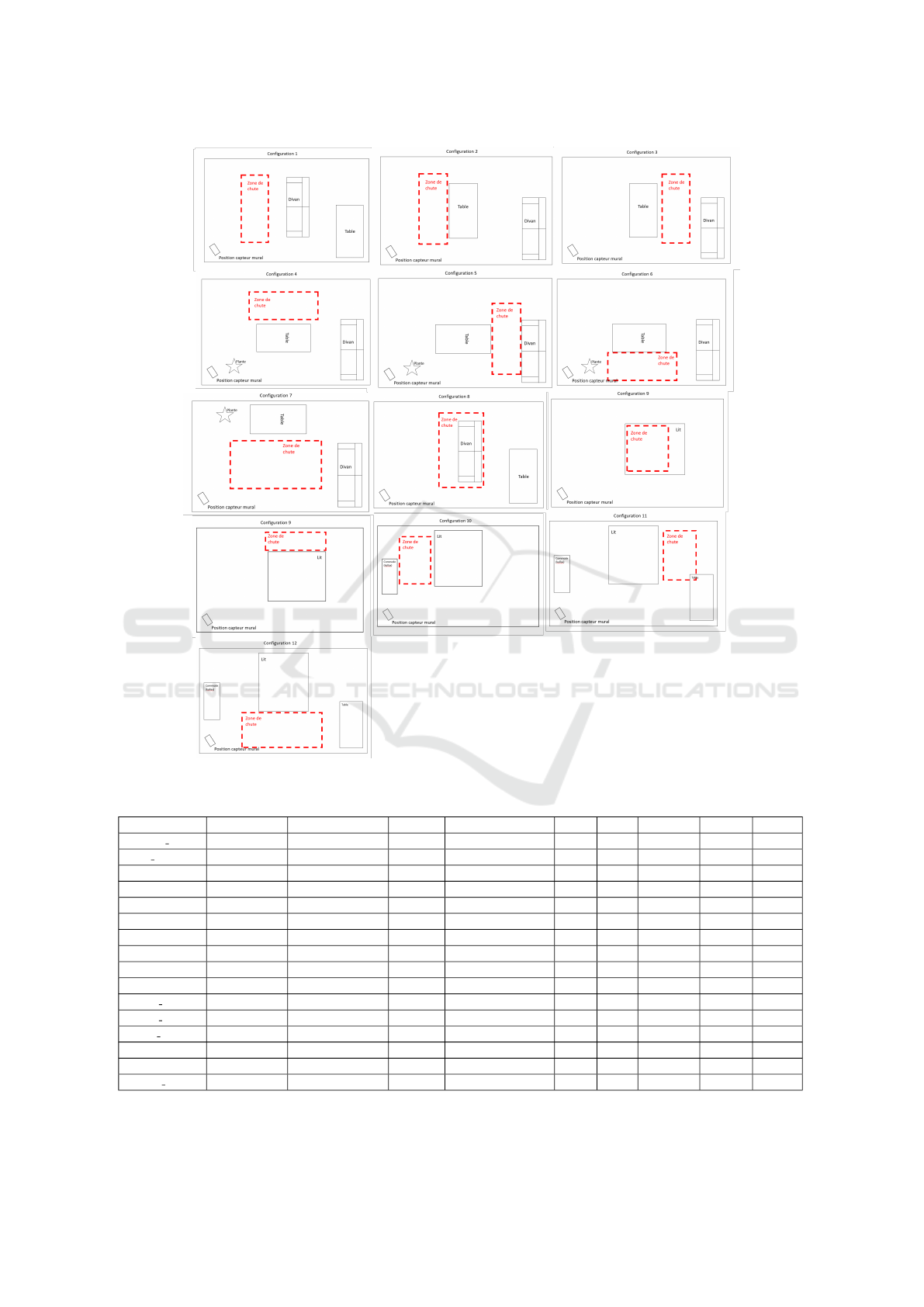
Figure 5: Different room conﬁgurations for fall detection.

Table 4: Example of possible activity for one personna.

Activity Name Activity Type Distribution Type Average Standard Deviation Start End Common Unique Day

morning sleep Routine uniforme 0 420

night sleep Routine uniforme 1290 1440

hygiene Routine normale 450 30 TRUE

breakfast Routine normale 480 20 TRUE

lunch Routine normale 750 20 TRUE

diner Routine normale 1170 20 TRUE

reading Routine uniforme 480 1320 FALSE

WC Episodical poisson 300 FALSE

coffee Weekly uniforme 840 1020 TRUE 0;1;3;5

therapist Weekly uniforme 600 660 0;

friends over Monthly normale TRUE TRUE 2;27

friends support Weekly normale 900 1140 2;4;5

family diner Monthly normale TRUE TRUE 12;30

escapade Monthly uniforme 660 780 16;

shopping Weekly uniforme 600 660 TRUE 4;

random kitchen Episodical poisson 960 540 1020 FALSE

ICT4AWE 2024 - 10th International Conference on Information and Communication Technologies for Ageing Well and e-Health

106

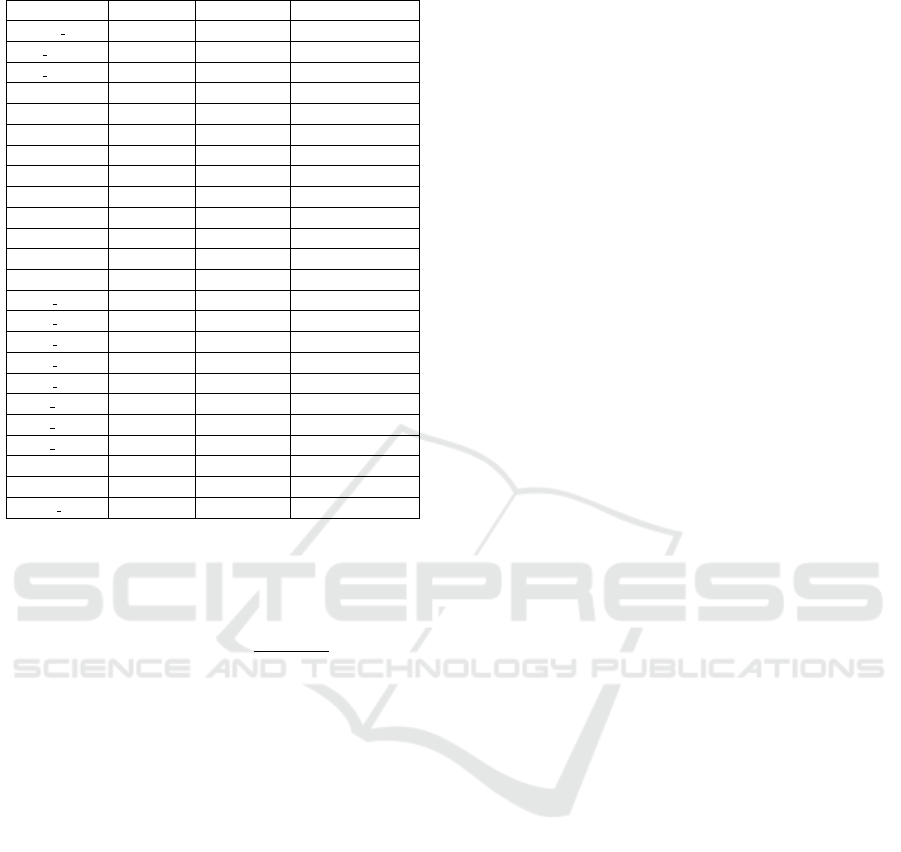
Table 5: Example of rooms to visit for one personna.

Activity Name State Name Average Time Standard Deviation

morning sleep Bedroom 40 20

night sleep Bathroom 10 2

night sleep Bedroom 240 30

hygiene Bathroom 20 5

hygiene Bedroom 15 3

hygiene WC 5 1

breakfast Kitchen 30 5

lunch Kitchen 30 5

diner Kitchen 40 10

reading Living Room 30 10

wc WC 5 1

coffee Outdoor 180 40

therapist Outdoor 70 10

friends over Living Room 30 5

friends over Kitchen 40 5

friends over Living Room 30 10

friends support Living Room 30 5

friends support Kitchen 40 5

family diner Kitchen 15 5

family diner Living Room 40 10

family diner Living Room 20 5

escapade Outdoor 2880 50

shopping Outdoor 180 20

random kitchen Kitchen 15 5

• Probability of n events in time t: The probability

that exactly n events occur in a ﬁxed interval of

time t is given by the Poisson distribution formula:

P(N(t) = n) =

−λt

(λt)

(7)

where N(t) is the number of events occurring by

time t, λ is the rate parameter of the process (aver-

age rate at which events occur per time unit), e is

the base of the natural logarithm (approximately

equal to 2.71828), and n! denotes n factorial.

• Inter-arrival Times: The time between consecu-

tive events in a Poisson process follows an expo-

nential distribution with probability density func-

tion deﬁned in equation 6.

These formulae encapsulate the mathematical

structure of a Poisson process, describing both the dis-

tribution of the number of events within a given time

frame and the statistical properties of the intervals be-

tween these events. For example, the Poisson process

can be used to model the time between going to the

toilet.

B More on Sensor Testing

During sensor testing, various conﬁgurations of room

setups were systematically analysed to evaluate the

efﬁcacy of sensor-based monitoring systems designed

to detect falls and behavioural anomalies among the

elderly living independently. The testing environ-

ments mimicked typical residential settings, incor-

porating common furniture arrangements and living

spaces. Twelve distinct conﬁgurations were assessed

(see Figure 5), each varying in the spatial layout and

positioning of key furniture pieces such as sofas, ta-

bles, and beds, as well as the strategic placement of

wall-mounted sensors to maximise coverage and min-

imise blind spots. These conﬁgurations also included

open spaces to simulate potential fall zones, delimited

by red dashed lines, indicating the areas where fall in-

cidents were emulated during the trials. The diversity

in room setups provided a comprehensive range of

scenarios to test the sensors’ responsiveness to actual

falls versus routine activities, ensuring robustness in

varied domestic landscapes. The sensor systems were

challenged with different angles and distances from

the fall zones, furniture obstructions, and varying lev-

els of ambient lighting, all of which are critical factors

in the real-world application of such technologies.

C Possible Activities for a Personna

As described in section 5.2, days are statistically gen-

erated using a speciﬁcally written algorithm. How-

ever this algorithm has a base. This base is comprised

of activity names, states and important parameters for

each distribution. That is, each activity will be a series

of states and each state will yield a speciﬁc distribu-

tion based on the average time and standard deviation

in the following tables. The distribution type is dic-

tated by the activity (see table 4) and appears chron-

ically depending on the frequence (column Activity

Type in table 4.) As can be noticed, some distributions

don’t require average time and standard deviation.

For the more complexe activities, some have start-

ing and ending points (in order to avoid morning sleep

at 10pm at night) and others are unique in order to

avoid, for example, having lunch twice. Finally for

the non-daily activities, days of the week and month

are given in order to make this activities happen only

on these given dyas. Keep in mind that for weekly

activities, the given days range from 0 to 6 while for

monthly activities, these days are given from 0 to 30.

Within the month, weekly activities loop using a 7 day

congruence in order to loop. That is of every Mon-

day, the persona goes swimming, then the date of the

month will be converted into the day of the week us-

ing the residue of the euclidienne division by seven.

A Novel Approach in Testing Life-Monitoring Technologies for Ageing in Place: A Focus on Fall Detection and Behavioural Alerts

107