Low-Performance Embedded Internet of Things Devices and the Need

for Hardware-Accelerated Post-Quantum Cryptography

Philipp Grassl

, Matthias Hudler

and Manuel Koschuch

Competence Center for IT-Security, University of Applied Sciences FH Campus Wien,

Favoritenstraße 226, 1100 Vienna, Austria

Keywords:

Post-Quantum Cryptography, Internet of Things, Embedded Security.

Abstract:

Quantum computers pose a serious threat to currently widely deployed cryptographic protocols and to data

security. New cryptographic algorithms have been developed with the aim to be resistant to attacks by both

conventional and quantum computers. While these have been designed to perform well on modern computer

hardware, the performance on embedded devices like e.g. used in the Internet Of Things may limit their

practical usability. In this position paper, we provide a thorough performance review of the post-quantum

algorithms currently evaluated by the National Institute of Standards and Technology on different Raspberry

Pi generations, advocating the need for development of post-quantum cryptography application-speciﬁc inte-

grated circuits to off-load calculations and improve performance.

1 INTRODUCTION AND

RELATED WORK

The rise of quantum computing poses serious threats

to current cryptosystems, especially of the asymmet-

ric variety. Whether they are used for key-agreement

like (Elliptic-Curve)-Difﬁe-Hellman, Signatures (like

(Elliptic-Curve)-Digital Signature Algorithms) or for

en- and decryption (like RSA), the respective underly-

ing hard mathematical problems could - at least from

a currently theoretical point of view - be easily solved

by quantum computers of a certain size.

In order to address this challenge, the NIST held a

competition to ﬁnd new post-quantum usable crypto-

graphic algorithms (PQC), in order to still be able to

securely exchange symmetric keys and reliably sign

data in the presence of actual quantum computers.

These algorithms, however, seem mostly ill suited

for embedded systems, with low performance and/or

memory characteristics. With this position paper

we want to add another data point to this discus-

sion by providing measurements of the current NIST

PQC candidates on a range of different Raspberry Pi

boards, showing quite clearly that for practical appli-

cations, even these comparatively powerful systems

struggle under the load of these new algorithms.

https://orcid.org/0009-0009-4048-164X

https://orcid.org/0000-0003-4879-018X

https://orcid.org/0000-0001-8090-3784

1.1 Related Work

(Marzougui and Kr

amer, 2019) conducted measure-

ments of multiple post-quantum signature schemes

on ARM Cortex-R5 processors and concluded that

the lattice based qTESLA scheme and the hash based

XMSS scheme are the most promising signature

scheme candidates for use in embedded devices.

urstinghaus-Steinbach et al., 2020) integrated

Kyber and SPHINCS+ into the embedded TLS library

mbed TLS and tested this combination on a Raspberry

Pi 3 B+ (ARM Cortex-A53), on an ESP32-PICO-

KIT V4 (Xtensa LX6), on a Fieldbus Option Card

(ARM966E-S) and on an LPC11U68 LPCXpresso

board (ARM Cortex-M0+). The tests were conducted

as a comparison of SPHINCS+ to ECDSA opera-

tions and of Kyber to ECDH operations. They con-

cluded that SPHINCS+ takes ”signiﬁcantly longer”

than ECDSA for signing operations, but that imple-

menting hardware support for hash functions would

signiﬁcantly speed up these operations and that there-

fore appropriate hardware acceleration should be in-

tegrated for server components.

(Chung et al., 2022) measured the runtimes and

transmitted data sizes of multiple schemes for key ex-

change and digital signatures (including Kyber and

SPHINCS+) on Raspberry Pi 3 and Raspberry Pi 4

devices. They also compared the measurements to

the same measurements with ECDH and ECDSA. It

shows that while Kyber is comparable in response

Grassl, P., Hudler, M. and Koschuch, M.

Low-Performance Embedded Internet of Things Devices and the Need for Hardware-Accelerated Post-Quantum Cryptography.

DOI: 10.5220/0012736800003705

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 9th International Conference on Internet of Things, Big Data and Security (IoTBDS 2024), pages 329-338

ISBN: 978-989-758-699-6; ISSN: 2184-4976

329

times and data sizes to ECDH, SPHINCS+ shows sig-

niﬁcantly higher response times and data sizes than

ECDSA when performing signing and veriﬁcation op-

erations.

During measurements of power consumptions

of post-quantum signature and key establishment

schemes, (Tasopoulos et al., 2023) found that there

are scheme combinations available that show power

consumption comparable to RSA and ECDH. How-

ever, only one key length combination of Dilithium

and Kyber was able to use less energy than

ECDSA+ECDH.

In this work we provide additional data points by

performing measurements of the current NIST PQC

candidates on a variety of Raspberry Pi boards with

a multitude of different parameters, to provide an

overview and guide on which candidates in which

conﬁguration might be suitable for practical applica-

tions on low-end hardware.

The remainder of this work is now structured as

follows: Section 2 brieﬂy provides some background

information on cryptographic primitives and associ-

ated systems, while Section 3 describes the speciﬁc

quantum and post-quantum challenges. Finally, Sec-

tions 4 and 5 describes our measurement setup and

our preliminary conclusions, respectively.

2 BACKGROUND

This section describes the underlying concepts for

context as used in this work.

2.1 Symmetric Cryptography

Symmetric cryptography is the concept of encrypting

and decrypting data using the same key for both op-

erations. This means that all data that has ever been

encrypted with a key K can always be decrypted once

the key K is known to the party wanting to decrypt

the data. To establish secure communication between

two parties it is therefore imperative that:

1. Both parties have prior knowledge of the shared

key and

2. No other party has any knowledge about the

shared key.

To meet these prerequisites, this common key for

encryption and decryption must be agreed upon by

the communicating parties without other parties be-

ing able to ascertain the key by monitoring the com-

munication. This process is called key establishment.

While the shared key can be communicated through

out-of-band means like a person traveling between the

parties with a physical, printed copy of the key, this

method is not feasible for the scale of today’s internet

communication. Therefore, asymmetric cryptography

is usually being used for key agreement (Boyd et al.,

2020a).

2.2 Asymmetric Cryptography

In contrast to symmetric cryptography, for asymmet-

ric (public-key) cryptography, two different keys, a

so-called key-pair, are used - one for encryption and

one for decryption. As such, one key can be made

public and the other can be kept secret (private). This

offers multiple use cases, the most important ones de-

scribed in the following.

2.2.1 Asymmetric Encryption

Upon generation of a key-pair, the encryption key

can be made public and the key for decryption kept

private. In this scenario, every other party that has

received the public encryption key in some way is

able to encrypt data with this key. Decryption how-

ever is only possible using the private decryption key

which has been kept secret. This way, private keys

never have to be transmitted to another party and can

therefore more easily be kept secret from attackers.

One typical, wide-spread algorithm for asymmetric

encryption is Rivest-Shamir-Adleman (RSA). Due to

its low performance, asymmetric encryption is almost

never used for bulk data encryption, but mainly as

a key encapsulation mechanism (KEM), whereby a

symmetric key is asymmetrically encrypted and trans-

ferred (Shoup, 2001).

2.2.2 Digital Signatures

Digital signature algorithms can be seen as a re-

verse of the aforementioned asymmetric encryption,

whereby the private key is used for signature gener-

ation (signing), and the public one for signature ver-

iﬁcation. As long as the private key is kept secret,

it proves to other parties that the party that signed a

message with this key is indeed the intended party

and not an attacker. RSA can also be used for digital

signatures, another example is the Elliptic Curve Dig-

ital Signature Algorithm (ECDSA) (Johnson et al.,

2001).

2.2.3 Key Exchange

When asymmetric cryptography is used by two par-

ties to establish a common symmetric key, using al-

gorithms that do not allow an attacker to effectively

ascertain the symmetric key just by capturing the ex-

IoTBDS 2024 - 9th International Conference on Internet of Things, Big Data and Security

330

changed messages, the process is called a key ex-

change or key agreement. Typical examples of key

exchange methods include the Difﬁe-Hellman (DH)

and Elliptic Curve Difﬁe-Hellman (ECDH) key ex-

changes (Boyd et al., 2020b).

2.3 IoT Devices

With the rise of progressively smaller and more pow-

erful devices as well as better wireless networking in-

frastructure, many household and smart home devices

are now connected to local networks and to the in-

ternet. As such, huge amounts of private and busi-

ness data are communicated by IoT devices to servers

or other IoT devices and commands are sent back to

those devices. One simple example for this would be

an environmental sensor in an apartment, measuring

the current temperature, communicating it to a server

which in turn communicates on- and off-commands to

a heating switch. To prevent attackers from being able

to alter, inject or intercept sensor data or commands,

encryption is a key technology in IoT devices.

While these IoT devices become more and more

powerful, usually they are limited in their ability to

perform computationally expensive cryptography due

to their size and power consumption constraints.

2.4 Quantum Computers

While conventional computers use bits, usually an

electrical signal that describes a discrete value of ei-

ther zero or one, quantum computers use so-called

qubits. A qubit describes the concept of using a

quantum-mechanical property of a system to repre-

sent information. This represented information can be

described as probabilities of being one of two states,

called zero or one (a superposition). During calcula-

tions using qubits, these probabilities are altered and

the superposition ﬁnally collapses into, again, a dis-

crete value of either zero or one.

Many mathematical problems that have been

shown to have no or no known efﬁcient solution in

conventional computing can be solved efﬁciently us-

ing quantum computers, as will be described in the

following sections.

3 POST QUANTUM

CRYPTOGRAPHY

3.1 Problem Statement

Many mathematical problems that were not efﬁciently

solvable using conventional computers are coming

into reach of becoming solvable using quantum com-

puting. Some of these problems form the basis of

asymmetric cryptography, like the integer factoriza-

tion problem for RSA and the discrete logarithm

problem for DH.

In 1994, Peter Shor was able to show in (Shor,

1994) that using quantum computers an algorithm

can be constructed which can efﬁciently (meaning in

polynomial runtime) solve many mathematical prob-

lems that have been thought to have no efﬁcient so-

lution before. This includes the Integer Factoriza-

tion Problem (IFP), the Discrete Logarithm Prob-

lem (DLP) and the Elliptic Curve Discrete Logarithm

Problem (ECDLP) which are used throughout asym-

metric cryptography, as in RSA, DH, ECDSA, ECDH

and more. Using such an algorithm on a quantum

computer effectively breaks the security of conven-

tional asymmetric algorithms completely.

Grover’s algorithm as described in (Grover, 1996)

is an algorithm that is able to reduce the time com-

plexity of searches in unordered data from O(n) to

O(n

1/2

). Using this algorithm, the time complexity

of breaking symmetric keys can be reduced signiﬁ-

cantly. However, the reduction of time complexity

can be mitigated by doubling the key length of the

symmetric algorithm.

3.1.1 Security with Quantum Computing

Table 1 shows a list of currently widely used algo-

rithms and key sizes and compares the security of the

algorithm and key size between conventional comput-

ers and quantum computers.

Table 1: Security level comparison (Mavroeidis et al.,

2018).

Algorithm Key Size

Security Level [Bits]

Classical Quantum

RSA 1024 80 0

RSA 2048 112 0

ECC 256 128 0

ECC 384 256 0

AES 128 128 64

AES 256 256 128

This result means that once sufﬁciently power-

ful quantum computers have been developed, current

asymmetric algorithms like RSA and ECC will have

to be considered insecure. At the time of writing this

paper, Fujitsu Limited has estimated, that approxi-

mately 10,000 qubits and 2.23 trillion quantum gates

would be needed to effectively break RSA (Fujitsu

Limited, 2023). At the same time, IBM plans to build

a quantum computer system called Blue Jay in 2033,

able to contain 2,000 qubits with one billion quantum

Low-Performance Embedded Internet of Things Devices and the Need for Hardware-Accelerated Post-Quantum Cryptography

331

gates. While these facts sound promising in the sense

that current communication is secure, using ”harvest

now, decrypt later”, data can now be collected and

stored, and be later decrypted, once sufﬁciently pow-

erful quantum computers exist. As such, it is impor-

tant to implement and deploy so-called post-quantum

cryptography, which is resistant to quantum computer

algorithms, as quickly as possible.

3.2 Post-Quantum Cryptography

Standardization

Algorithms developed for so-called post-quantum

cryptography (PQC) feature mathematical problems

that cannot effectively be broken using either con-

ventional or quantum computers. Many such algo-

rithms have been developed and the National Insti-

tute of Standards and Technology (NIST) has started a

standardization process to select algorithms that have

been found to be secure, unburdened by patents or re-

strictive licenses and future-proof (NIST, 2017a).

During the initial submission to the standardiza-

tion process in 2017, 69 algorithms were submit-

ted (NIST, 2017b) and most were withdrawn or elim-

inated in the process. At the end of the rigorous se-

lection process, four ﬁnalists remained (NIST, 2022):

one key-establishment algorithm (CRYSTALS Kyber)

and three digital signature algorithms (CRYSTALS

Dilithium, FALCON and SPHINCS+).

CRYSTALS Kyber, CRYSTALS Dilithium and

FALCON are all implemented uses the hardness

of mathematical problems in the ﬁeld of multidi-

mensional lattice based mathematics. Each one

leverages a different problem over lattices, how-

ever. CRYSTALS Kyber (Cryptographic Suite for

Algebraic Lattices, 2020) uses Learning With Errors

(LWE) based problems (Regev, 2009), CRYSTALS

Dilithium (Cryptographic Suite for Algebraic Lat-

tices, 2021) uses the Fiat-Shamir with Aborts tech-

nique (Lyubashevsky, 2009), and FALCON (Fouque

et al., 2021) uses the Short Integer Solution (SIS)

problem (Ajtai, 1996).

SPHINCS+ (SPHINCS+, 2023) on the other hand

is implemented using so-called hyper-trees, a con-

struction of multiple trees constructed using the Ex-

tended Merkle Signature Scheme (Huelsing et al.,

2018).

All these algorithms and their key length varia-

tions were classiﬁed into ﬁve categories as lined out

by (NIST, 2016). Of these categories, submitters

were advised to focus their efforts on categories one

through three, as these are considered by NIST in the

same document to be sufﬁciently secure ”for the fore-

seeable future”.

3.3 Implementation and Adoption

All submissions to the NIST standardization process

were required to include a reference implementation,

compilable using the GCC compiler suite and run-

ning on a 64-Bit Intel processor under Windows or

Linux. While the requirements document invited tests

on other platforms, they were not required for submis-

sion. (NIST, 2016)

While other organizations, like (eBACS, 2019),

have measured the performance of PQC algorithms

on 64-Bit platforms and powerful ARM Cortex-A

processors, there is little data on complex PQC al-

gorithm implementations on smaller devices. How-

ever, since also low performance IoT devices have

the need for secure communication, the usability of

PQC algorithms on such devices and operating sys-

tems should be tested and plans on how to create de-

vices that are secure in the foreseeable future must

be made. We therefore conducted preliminary mea-

surements of NIST standardization process ﬁnalists

on different single board computers to explore the us-

ability of PQC on embedded devices.

4 MEASUREMENTS

The Open Quantum Safe (OQS) project develops

and maintains a library, liboqs, implementing many

post-quantum cryptography algorithms, including the

NIST process ﬁnalists. The library can be run on mul-

tiple different platforms and on Linux (Open Quan-

tum Safe, 2024).

We therefore decided to use Linux and liboqs for a

ﬁrst benchmarking on embedded devices. To measure

the complexity of calculations of the NIST process ﬁ-

nalists, each submitted variant of each algorithm that

is supported by liboqs was measured on multiple de-

vices. The devices that were used are listed in Table 2

in the appendix.

While all used devices come from the popular

Raspberry Pi (Raspberry Pi Ltd, 2024b) series and

feature relatively powerful ARM Cortex-A proces-

sors, it was found to be enough information for a ﬁrst

overview of the general performance of post-quantum

algorithms and to ascertain the usability of these algo-

rithms on even smaller and less powerful devices. The

selection of Raspberry Pi devices has the added ben-

eﬁt of being built for and supporting Linux. As op-

erating system, the Raspberry Pi OS Lite (Raspberry

Pi Ltd, 2024a), released February 21

2023, kernel

version 5.15, Debian Linux version 11 has been used.

For each device, the image has been conﬁgured for

headless mode, to minimize disturbances by back-

IoTBDS 2024 - 9th International Conference on Internet of Things, Big Data and Security

332

ground services as much as possible. Control access

was gained through an SSH server on the devices. De-

vices without ethernet connector were connected us-

ing Wi-Fi.

To perform calculations and measure the perfor-

mance, both liboqs (Code: (Open Quantum Safe,

2023)) and a library for accessing the ARM Perfor-

mance Monitoring Unit (PMU), pqax (Code: (pqax,

2021)) were compiled and installed on the target.

Since liboqs at the time of writing does not support

ARMv6 processors, the code for accessing the PMU

had to be adapted for these processors.

The builtin benchmarking tests of liboqs were

used to perform performance tests of the algorithms.

The benchmarks were set to last at least 10 seconds

and the used processor cycles and time were recorded.

This process was repeated twice and the results were

averaged over both repetitions. This does not neces-

sarily result in the lowest possible run-times, but at

least tries to paint a realistic picture of the average

expectable real-world performance

The results of the measurements can be seen in

Tables 3 through 9 in the Appendix.

The measurements of the key establishment algo-

rithm Kyber show that it displays good performance

on all platforms (maximum time for any operation on

any device and security level: 17ms). Kyber might

therefore also be suitable for more constrained de-

vices to establish keys between communicating par-

ties.

Meanwhile, runtime measurements for digital sig-

nature algorithms display much higher runtimes. For

this paper, key generation will be thought of as be-

ing off-loadable, so it compares the times needed for

signature generation and veriﬁcation. While the Fal-

con and Dilithium algorithms have been shown to

perform relatively well (maximum time was the sig-

nature generation using Falcon-1024 on a Raspberry

Pi 1 B with 212ms), the SPHINCS+-algorithm has

proven to generally take long times on these devices

(SPHINCS+-SHAKE256-192s-robust signature gen-

eration on a Raspberry Pi 1 B took more than 22 min-

utes).

Since we assume calculation times of up to 500

milliseconds as being acceptable in practice, Tables 3

through 9 in the Appendix have been colored with a

grey gradient, starting at 500 milliseconds to better

visualize the performance of algorithms.

5 CONCLUSIONS

While there may be a combination of algorithms

that works acceptably well on performance-strong

embedded devices, it can be argued that current

post-quantum cryptography algorithms are simply too

complex for smaller and more constrained embedded

processors.

Some steps have been taken towards implemen-

tations of post-quantum cryptography algorithms in

programmable logic devices like FPGAs. Even

though issues have arisen in this undertaking (Li et al.,

2022), it is the position of the authors of this paper

that the implementation of post-quantum cryptogra-

phy on FPGAs and later ASICs is the only way to

provide small, constrained devices with the ability to

stay secure in a world with ever evolving better quan-

tum computers.

ACKNOWLEDGEMENTS

The authors want to thank their former colleague Pol

olzmer, without whom the measurements in this

work would not have been possible.

REFERENCES

Ajtai, M. (1996). Generating hard instances of lattice

problems (extended abstract). In Proceedings of the

Twenty-Eighth Annual ACM Symposium on Theory of

Computing, STOC ’96, page 99–108, New York, NY,

USA. Association for Computing Machinery. https:

//doi.org/10.1145/237814.237838 [Online; accessed

2024-02-05].

Boyd, C., Mathuria, A., and Stebila, D. (2020a). Authenti-

cation and Key Transport Using Public Key Cryptog-

raphy, pages 135–164. Springer Berlin Heidelberg,

Berlin, Heidelberg.

Boyd, C., Mathuria, A., and Stebila, D. (2020b). Key Agree-

ment Protocols, pages 165–240. Springer Berlin Hei-

delberg, Berlin, Heidelberg.

urstinghaus-Steinbach, K., Krauß, C., Niederhagen, R.,

and Schneider, M. (2020). Post-quantum tls on em-

bedded systems: Integrating and evaluating kyber and

sphincs+ with mbed tls. In Proceedings of the 15th

ACM Asia Conference on Computer and Communica-

tions Security, ASIA CCS ’20, page 841–852, New

York, NY, USA. Association for Computing Machin-

ery. https://doi.org/10.1145/3320269.3384725 [On-

line; accessed 2024-02-05].

Chung, C.-C., Pai, C.-C., Ching, F.-S., Wang, C., and Chen,

L.-J. (2022). When post-quantum cryptography meets

the internet of things: an empirical study. In Proceed-

ings of the 20th Annual International Conference on

Mobile Systems, Applications and Services, MobiSys

’22, page 525–526, New York, NY, USA. Association

for Computing Machinery.

Cryptographic Suite for Algebraic Lattices (2020). Kyber.

https://pq-crystals.org/kyber/. [Online; accessed

2024-02-05].

Low-Performance Embedded Internet of Things Devices and the Need for Hardware-Accelerated Post-Quantum Cryptography

333

Cryptographic Suite for Algebraic Lattices (2021).

Dilithium. https://pq-crystals.org/dilithium/. [Online;

accessed 2024-02-05].

eBACS (2019). eBACS: ECRYPT Benchmarking of Cryp-

tographic Systems. https://bench.cr.yp.to/. [Online;

accessed 2024-02-05].

Fouque, P.-A., Hoffstein, J., Kirchner, P., Lyubashevsky, V.,

Pornin, T., Prest, T., Ricosset, T., Seiler, G., Whyte,

W., and Zhang, Z. (2021). Falcon. https://falcon-sig

n.info/. [Online; accessed 2024-02-05].

Fujitsu Limited (2023). Fujitsu quantum simulator assesses

vulnerability of RSA cryptosystem to potential quan-

tum computer cryptography threat. https://www.fujits

u.com/global/about/resources/news/press-releases/20

23/0123-01.html. [Online; accessed 2024-02-05].

Grover, L. K. (1996). A fast quantum mechanical algorithm

for database search. https://arxiv.org/abs/quant-ph/96

05043 [Online; accessed 2024-02-05].

Huelsing, A., Butin, D., Gazdag, S.-L., Rijneveld, J., and

Mohaisen, A. (2018). XMSS: eXtended Merkle Sig-

nature Scheme. RFC 8391. https://www.rfc-editor.or

g/info/rfc8391 [Online; accessed 2024-02-05].

Johnson, D., Menezes, A., and Vanstone, S. (2001). The el-

liptic curve digital signature algorithm (ecdsa). Inter-

national Journal of Information Security, 1(1):36–63.

Li, H., Tang, Y., Que, Z., and Zhang, J. (2022). FPGA Ac-

celerated Post-Quantum Cryptography. IEEE Trans-

actions on Nanotechnology, 21:685–691. https://ieee

xplore.ieee.org/abstract/document/9931964 [Online;

accessed 2024-02-05].

Lyubashevsky, V. (2009). Fiat-shamir with aborts: Appli-

cations to lattice and factoring-based signatures. In

Matsui, M., editor, Advances in Cryptology – ASI-

ACRYPT 2009, pages 598–616, Berlin, Heidelberg.

Springer Berlin Heidelberg. https://www.iacr.org/a

rchive/asiacrypt2009/59120596/59120596.pdf [On-

line; accessed 2024-02-05].

Marzougui, S. and Kr

amer, J. (2019). Post-quantum cryp-

tography in embedded systems. In Proceedings of

the 14th International Conference on Availability, Re-

liability and Security, ARES ’19, New York, NY,

USA. Association for Computing Machinery. https:

//doi.org/10.1145/3339252.3341475 [Online; ac-

cessed 2024-02-05].

Mavroeidis, V., Vishi, K., Zych, M. D., and Jøsang, A.

(2018). The Impact of Quantum Computing on

Present Cryptography. International Journal of Ad-

vanced Computer Science and Applications, 9(3). ht

tp://dx.doi.org/10.14569/IJACSA.2018.090354 [On-

line; accessed 2024-02-05].

NIST (2016). Submission Requirements and Evaluation

Criteria for the Post-Quantum Cryptography Stan-

dardization Process. https://csrc.nist.gov/CSRC/m

edia/Projects/Post-Quantum-Cryptography/docume

nts/call-for-proposals-final-dec-2016.pdf. [Online;

accessed 2024-02-05].

NIST (2017a). Post-Quantum Cryptography Standardiza-

tion. https://csrc.nist.gov/projects/post-quantum-cry

ptography/post-quantum-cryptography-standardizati

on. [Online; accessed 2024-02-05].

NIST (2017b). Round 1 Submissions. https://csrc.nist.go

v/Projects/post-quantum-cryptography/post-quantum

-cryptography-standardization/round-1-submissions.

[Online; accessed 2024-02-05].

NIST (2022). Selected Algorithms 2022. https://csrc.nist.

gov/Projects/post-quantum-cryptography/selected-a

lgorithms-2022. [Online; accessed 2024-02-05].

Open Quantum Safe (2023). Git code repository. https:

//github.com/open-quantum-safe/liboqs/tree/d61d81

c526da8bb62e363f5a75191689572151cb. [Online;

accessed 2024-02-05].

Open Quantum Safe (2024). Software for the transition to

quantum-resistant cryptography. https://openquantu

msafe.org/. [Online; accessed 2024-02-05].

pqax (2021). Git code repository. https://github.com/mup

q/pqax/tree/331415e1c309175674c8c700b96b0164

2b3241db. [Online; accessed 2024-02-05].

Raspberry Pi Ltd (2024a). Operating system images. https:

//www.raspberrypi.com/software/operating-systems/.

[Online; accessed 2024-02-05].

Raspberry Pi Ltd (2024b). Raspberry pi homepage. https:

//www.raspberrypi.com/. [Online; accessed 2024-02-

05].

Regev, O. (2009). On lattices, learning with errors, random

linear codes, and cryptography. J. ACM, 56(6). https://

doi.org/10.1145/1568318.1568324 [Online; accessed

2024-02-05].

Shor, P. (1994). Algorithms for quantum computation: dis-

crete logarithms and factoring. In Proceedings 35th

Annual Symposium on Foundations of Computer Sci-

ence, pages 124–134. https://ieeexplore.ieee.org/do

cument/365700 [Online; accessed 2024-02-05].

Shoup, V. (2001). A proposal for an ISO standard for public

key encryption. IACR Cryptol. ePrint Arch., page 112.

SPHINCS+ (2023). Sphincs+. https://sphincs.org/. [Online;

accessed 2024-02-05].

Tasopoulos, G., Dimopoulos, C., Fournaris, A. P., Zhao,

R. K., Sakzad, A., and Steinfeld, R. (2023). En-

ergy consumption evaluation of post-quantum tls 1.3

for resource-constrained embedded devices. In Pro-

ceedings of the 20th ACM International Conference

on Computing Frontiers, CF ’23, page 366–374, New

York, NY, USA. Association for Computing Machin-

ery. https://doi.org/10.1145/3587135.3592821 [On-

line; accessed 2024-02-05].

IoTBDS 2024 - 9th International Conference on Internet of Things, Big Data and Security

334

APPENDIX

Table 2: Platforms used for benchmarking.

ID Device Name Architecture

Kernel

Cores

Frequency RAM

Arch [GHz] [GB]

r1b Raspberry Pi 1 B ARM1176JZF-S armv6l 1 0.7 0.25

r1b+ Raspberry Pi 1 B+ ARM1176JZF-S armv6l 1 0.7 0.5

rzw Raspberry Pi Zero W Rev 1.1 ARM1176JZF-S armv6l 1 0.7 0.5

r2b Raspberry Pi 2 B Rev 1.1 ARM Cortex-A7 armv7l 4 0.9 1

r3b Raspberry Pi 3 B Rev 1.2 ARM Cortex-A53 armv8 4 1.2 1

r3b+ Raspberry Pi 3 B+ Rev 1.3 ARM Cortex-A53 armv8 4 1.4 1

r4b Raspberry Pi 4 B Rev 1.4 ARM Cortex-A72 armv8 4 1.5 8

Table 3: Runtime measurement results: Key Encapsulation Mechanism: Key Generation.

Level Algorithm

Platforms

r1b r1b+ rzw r2b r3b r3b+ r4b

1 Kyber512 5.3ms 4.9ms 3.2ms 1.4ms 0.1ms 0.1ms 0.1ms

1 Kyber512-90s 1.1ms 1.2ms 0.8ms 0.6ms 0.3ms 0.3ms 0.1ms

3 Kyber768 8.3ms 7.7ms 5.0ms 2.2ms 0.2ms 0.2ms 0.1ms

3 Kyber768-90s 1.8ms 1.9ms 1.2ms 1.0ms 0.5ms 0.4ms 0.2ms

5 Kyber1024 13.0ms 12.1ms 7.9ms 3.4ms 0.3ms 0.2ms 0.1ms

5 Kyber1024-90s 2.7ms 2.8ms 1.8ms 1.5ms 0.8ms 0.7ms 0.3ms

Table 4: Runtime measurement results: Key Encapsulation Mechanism: Encapsulation.

Level Algorithm

Platforms

r1b r1b+ rzw r2b r3b r3b+ r4b

1 Kyber512 6.8ms 6.2ms 4.0ms 1.7ms 0.1ms 0.1ms 0.1ms

1 Kyber512-90s 1.4ms 1.5ms 1.0ms 0.8ms 0.4ms 0.3ms 0.1ms

3 Kyber768 10.6ms 9.8ms 6.4ms 2.7ms 0.2ms 0.2ms 0.1ms

3 Kyber768-90s 2.2ms 2.2ms 1.5ms 1.2ms 0.6ms 0.5ms 0.2ms

5 Kyber1024 15.9ms 14.7ms 9.6ms 4.1ms 0.3ms 0.2ms 0.1ms

5 Kyber1024-90s 3.2ms 3.2ms 2.1ms 1.7ms 0.9ms 0.8ms 0.3ms

Table 5: Runtime measurement results: Key Encapsulation Mechanism: Decapsulation.

Level Algorithm

Platforms

r1b r1b+ rzw r2b r3b r3b+ r4b

1 Kyber512 5.7ms 5.3ms 3.4ms 1.6ms 0.1ms 0.1ms <0.1ms

1 Kyber512-90s 1.6ms 1.6ms 1.1ms 0.9ms 0.5ms 0.4ms 0.1ms

3 Kyber768 9.2ms 8.6ms 5.6ms 2.6ms 0.2ms 0.1ms 0.1ms

3 Kyber768-90s 2.4ms 2.5ms 1.6ms 1.4ms 0.7ms 0.6ms 0.2ms

5 Kyber1024 14.2ms 13.1ms 8.6ms 3.9ms 0.2ms 0.2ms 0.1ms

5 Kyber1024-90s 3.5ms 3.6ms 2.4ms 2.0ms 1.0ms 0.9ms 0.3ms

Table 6: Runtime measurement results: Digital Signature: Key Generation.

Level Algorithm

Platforms

r1b r1b+ rzw r2b r3b r3b+ r4b

1 Falcon-512 656ms 652ms 486ms 281ms 79ms 71ms 41ms

1 SPHINCS+-Haraka-128f-simple 110ms 111ms 76ms 72ms 13ms 11ms 7ms

1 SPHINCS+-Haraka-128s-simple 7s 7s 5s 5s 808ms 705ms 430ms

1 SPHINCS+-SHA256-128f-simple 76ms 77ms 46ms 28ms 13ms 11ms 5ms

1 SPHINCS+-SHA256-128s-simple 5s 5s 3s 2s 777ms 691ms 289ms

1 SPHINCS+-SHAKE256-128f-simple 896ms 784ms 632ms 179ms 13ms 12ms 6ms

1 SPHINCS+-SHAKE256-128s-simple 57s 51s 46s 12s 826ms 742ms 360ms

1 SPHINCS+-Haraka-128f-robust 158ms 159ms 108ms 102ms 22ms 19ms 12ms

1 SPHINCS+-Haraka-128s-robust 10s 10s 7s 6s 1s 1s 760ms

Low-Performance Embedded Internet of Things Devices and the Need for Hardware-Accelerated Post-Quantum Cryptography

335

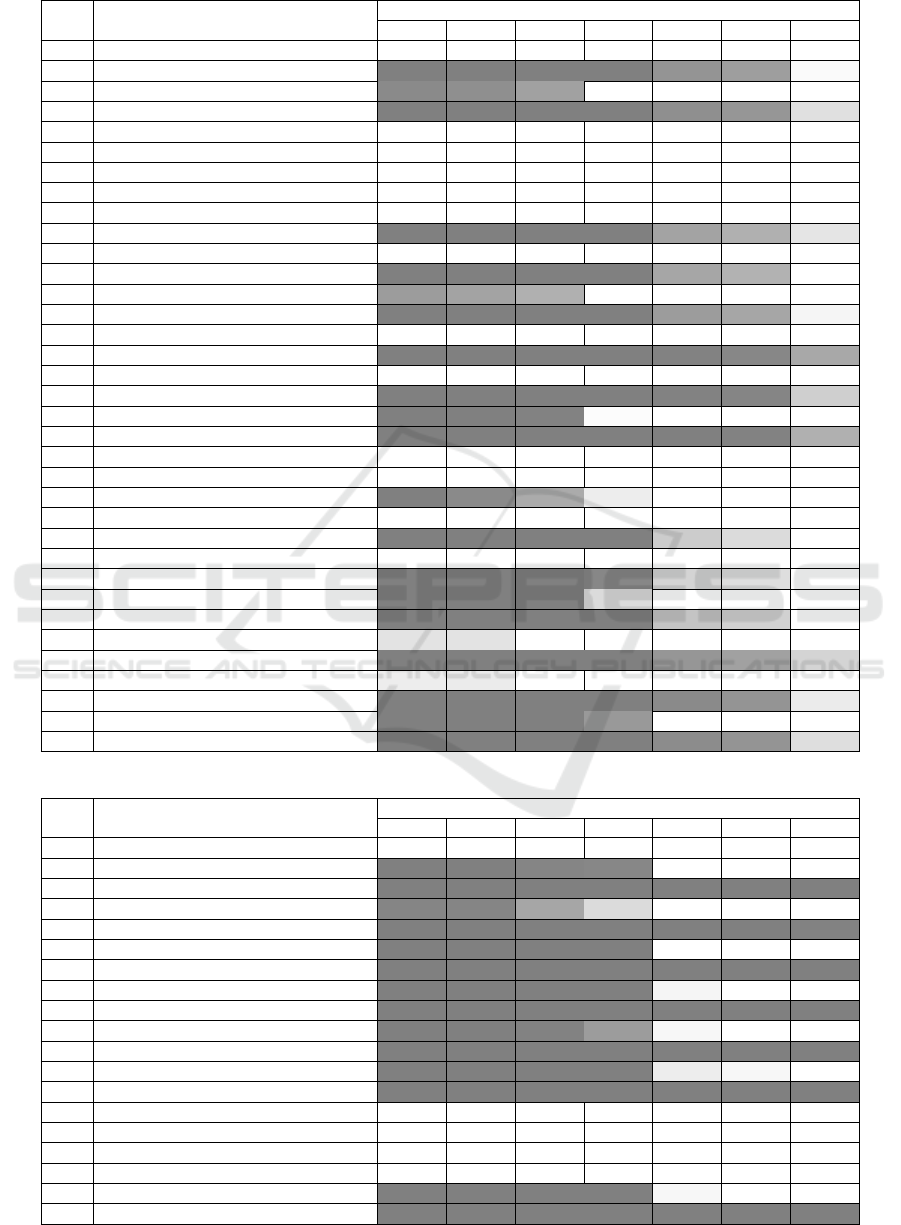
Table 7: Runtime measurement results: Digital Signature: Key Generation.

Level Algorithm

Platforms

r1b r1b+ rzw r2b r3b r3b+ r4b

SPHINCS+-SHA256-128f-robust 144ms 143ms 85ms 53ms 22ms 19ms 8ms

1 SPHINCS+-SHA256-128s-robust 9s 9s 5s 3s 1s 1s 524ms

1 SPHINCS+-SHAKE256-128f-robust 2s 2s 1s 345ms 24ms 22ms 10ms

1 SPHINCS+-SHAKE256-128s-robust 2min 2min 1min 22s 2s 1s 672ms

2 Dilithium2 19ms 18ms 14ms 4ms <1ms <1ms <1ms

2 Dilithium2-AES 5ms 5ms 4ms 2ms 1ms 1ms <1ms

3 Dilithium3 34ms 31ms 25ms 8ms 1ms 1ms <1ms

3 Dilithium3-AES 8ms 8ms 6ms 3ms 1ms 1ms 1ms

3 SPHINCS+-Haraka-192f-simple 163ms 164ms 111ms 106ms 19ms 16ms 10ms

3 SPHINCS+-Haraka-192s-simple 10s 10s 7s 7s 1s 1s 635ms

3 SPHINCS+-SHA256-192f-simple 112ms 113ms 68ms 40ms 18ms 16ms 7ms

3 SPHINCS+-SHA256-192s-simple 7s 7s 4s 3s 1s 1s 432ms

3 SPHINCS+-SHAKE256-192f-simple 1s 1s 1s 264ms 19ms 17ms 8ms

3 SPHINCS+-SHAKE256-192s-simple 1min 1min 1min 17s 1s 1s 555ms

3 SPHINCS+-Haraka-192f-robust 234ms 239ms 159ms 152ms 32ms 28ms 18ms

3 SPHINCS+-Haraka-192s-robust 15s 15s 10s 10s 2s 2s 1s

3 SPHINCS+-SHA256-192f-robust 202ms 207ms 122ms 77ms 33ms 29ms 12ms

3 SPHINCS+-SHA256-192s-robust 13s 13s 8s 5s 2s 2s 786ms

3 SPHINCS+-SHAKE256-192f-robust 3s 2s 2s 510ms 35ms 32ms 15ms

3 SPHINCS+-SHAKE256-192s-robust 3min 2min 2min 32s 2s 2s 1s

5 Dilithium5 59ms 53ms 43ms 13ms 1ms 1ms <1ms

5 Dilithium5-AES 12ms 12ms 9ms 5ms 2ms 2ms 1ms

5 Falcon-1024 3s 2s 1s 597ms 217ms 195ms 114ms

5 SPHINCS+-Haraka-256f-simple 431ms 435ms 294ms 282ms 50ms 44ms 27ms

5 SPHINCS+-Haraka-256s-simple 7s 8s 5s 5s 794ms 696ms 423ms

5 SPHINCS+-SHA256-256f-simple 301ms 295ms 177ms 110ms 47ms 42ms 18ms

5 SPHINCS+-SHA256-256s-simple 5s 5s 3s 2s 752ms 675ms 281ms

5 SPHINCS+-SHAKE256-256f-simple 3s 3s 3s 695ms 51ms 46ms 22ms

5 SPHINCS+-SHAKE256-256s-simple 54s 49s 44s 11s 861ms 769ms 369ms

5 SPHINCS+-Haraka-256f-robust 644ms 650ms 437ms 405ms 86ms 76ms 47ms

5 SPHINCS+-Haraka-256s-robust 10s 10s 7s 6s 1s 1s 748ms

5 SPHINCS+-SHA256-256f-robust 593ms 605ms 363ms 239ms 100ms 90ms 38ms

5 SPHINCS+-SHA256-256s-robust 9s 10s 6s 4s 2s 1s 610ms

5 SPHINCS+-SHAKE256-256f-robust 7s 6s 5s 1s 95ms 86ms 41ms

5 SPHINCS+-SHAKE256-256s-robust 2min 2min 1min 21s 2s 1s 684ms

Table 8: Runtime measurement results: Digital Signature: Signature Generation.

Level Algorithm

Platforms

r1b r1b+ rzw r2b r3b r3b+ r4b

1 Falcon-512 96ms 96ms 65ms 57ms 19ms 17ms 11ms

1 SPHINCS+-Haraka-128f-simple 3s 3s 2s 2s 322ms 281ms 172ms

1 SPHINCS+-Haraka-128s-simple 55s 56s 38s 36s 6s 6s 3s

1 SPHINCS+-SHA256-128f-simple 2s 2s 1s 691ms 311ms 274ms 115ms

1 SPHINCS+-SHA256-128s-simple 37s 38s 23s 14s 6s 5s 2s

1 SPHINCS+-SHAKE256-128f-simple 22s 19s 16s 4s 319ms 288ms 140ms

1 SPHINCS+-SHAKE256-128s-simple 7min 6min 6min 1min 6s 6s 3s

1 SPHINCS+-Haraka-128f-robust 4s 4s 3s 3s 552ms 476ms 299ms

1 SPHINCS+-Haraka-128s-robust 1min 1min 55s 52s 11s 10s 6s

1 SPHINCS+-SHA256-128f-robust 3s 3s 2s 1s 541ms 477ms 202ms

1 SPHINCS+-SHA256-128s-robust 1min 1min 40s 25s 11s 9s 4s

1 SPHINCS+-SHAKE256-128f-robust 41s 37s 30s 8s 589ms 533ms 257ms

1 SPHINCS+-SHAKE256-128s-robust 14min 12min 10min 3min 11s 10s 5s

2 Dilithium2 45ms 40ms 32ms 12ms 1ms 1ms <1ms

2 Dilithium2-AES 19ms 18ms 13ms 7ms 4ms 3ms 1ms

3 Dilithium3 74ms 65ms 51ms 19ms 2ms 2ms 1ms

3 Dilithium3-AES 28ms 27ms 19ms 11ms 6ms 5ms 2ms

3 SPHINCS+-Haraka-192f-simple 5s 5s 3s 3s 544ms 478ms 291ms

3 SPHINCS+-Haraka-192s-simple 2min 2min 1min 1min 12s 10s 6s

IoTBDS 2024 - 9th International Conference on Internet of Things, Big Data and Security

336

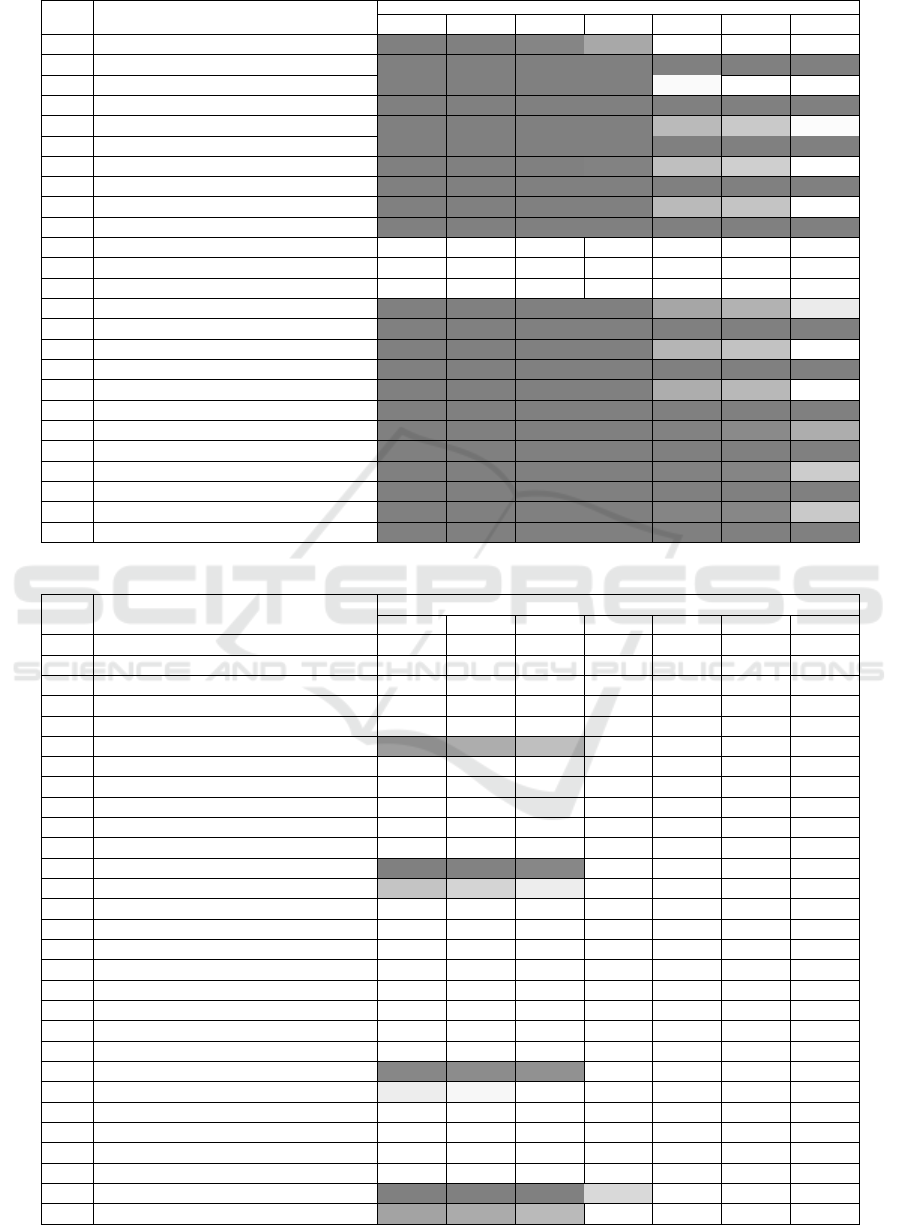
Table 8: Runtime measurement results: Digital Signature: Signature Generation. (continued)

Level Algorithm

Platforms

r1b r1b+ rzw r2b r3b r3b+ r4b

3 SPHINCS+-SHA256-192f-simple 3s 3s 2s 1s 498ms 446ms 183ms

3 SPHINCS+-SHA256-192s-simple 1min 1min 39s 24s 11s 9s 4s

3 SPHINCS+-SHAKE256-192f-simple 35s 32s 29s 7s 526ms 476ms 227ms

3 SPHINCS+-SHAKE256-192s-simple 12min 11min 10min 3min 12s 10s 5s

3 SPHINCS+-Haraka-192f-robust 7s 7s 5s 5s 944ms 821ms 512ms

3 SPHINCS+-Haraka-192s-robust 3min 3min 2min 2min 21s 18s 11s

3 SPHINCS+-SHA256-192f-robust 6s 6s 3s 2s 898ms 788ms 329ms

3 SPHINCS+-SHA256-192s-robust 2min 2min 1min 45s 19s 17s 7s

3 SPHINCS+-SHAKE256-192f-robust 1min 1min 54s 14s 940ms 848ms 412ms

3 SPHINCS+-SHAKE256-192s-robust 23min 21min 19min 5min 21s 19s 9s

5 Dilithium5 94ms 89ms 67ms 24ms 2ms 2ms 1ms

5 Dilithium5-AES 32ms 32ms 23ms 13ms 7ms 6ms 2ms

5 Falcon-1024 212ms 208ms 143ms 126ms 43ms 36ms 25ms

5 SPHINCS+-Haraka-256f-simple 10s 10s 7s 6s 1s 1s 613ms

5 SPHINCS+-Haraka-256s-simple 2min 2min 1min 1min 12s 10s 6s

5 SPHINCS+-SHA256-256f-simple 6s 6s 4s 2s 985ms 873ms 368ms

5 SPHINCS+-SHA256-256s-simple 57s 58s 35s 21s 9s 8s 3s

5 SPHINCS+-SHAKE256-256f-simple 1min 1min 57s 14s 1s 957ms 457ms

5 SPHINCS+-SHAKE256-256s-simple 11min 10min 9min 2min 10s 9s 4s

5 SPHINCS+-Haraka-256f-robust 15s 15s 10s 10s 2s 2s 1s

5 SPHINCS+-Haraka-256s-robust 3min 3min 2min 2min 20s 18s 11s

5 SPHINCS+-SHA256-256f-robust 12s 13s 8s 5s 2s 2s 795ms

5 SPHINCS+-SHA256-256s-robust 2min 2min 1min 46s 20s 17s 7s

5 SPHINCS+-SHAKE256-256f-robust 2min 2min 2min 27s 2s 2s 827ms

5 SPHINCS+-SHAKE256-256s-robust 20min 18min 16min 4min 18s 16s 8s

Table 9: Runtime measurement results: Digital Signature: Signature Veriﬁcation.

Level Algorithm

Platforms

r1b r1b+ rzw r2b r3b r3b+ r4b

1 Falcon-512 3ms 3ms 2ms 1ms <1ms <1ms <1ms

1 SPHINCS+-Haraka-128f-simple 175ms 177ms 121ms 110ms 19ms 17ms 10ms

1 SPHINCS+-Haraka-128s-simple 65ms 66ms 45ms 44ms 7ms 6ms 4ms

1 SPHINCS+-SHA256-128f-simple 105ms 110ms 63ms 40ms 17ms 15ms 7ms

1 SPHINCS+-SHA256-128s-simple 38ms 39ms 24ms 14ms 6ms 5ms 2ms

1 SPHINCS+-SHAKE256-128f-simple 1s 1s 894ms 248ms 18ms 16ms 8ms

1 SPHINCS+-SHAKE256-128s-simple 409ms 371ms 340ms 86ms 6ms 5ms 3ms

1 SPHINCS+-Haraka-128f-robust 258ms 258ms 176ms 167ms 34ms 29ms 19ms

1 SPHINCS+-Haraka-128s-robust 103ms 100ms 70ms 66ms 13ms 11ms 7ms

1 SPHINCS+-SHA256-128f-robust 208ms 207ms 121ms 78ms 32ms 28ms 12ms

1 SPHINCS+-SHA256-128s-robust 69ms 72ms 43ms 26ms 11ms 10ms 4ms

1 SPHINCS+-SHAKE256-128f-robust 2s 2s 2s 499ms 34ms 30ms 15ms

1 SPHINCS+-SHAKE256-128s-robust 851ms 755ms 595ms 170ms 12ms 11ms 5ms

2 Dilithium2 18ms 17ms 13ms 4ms <1ms <1ms <1ms

2 Dilithium2-AES 6ms 6ms 4ms 2ms 1ms 1ms <1ms

3 Dilithium3 32ms 29ms 23ms 7ms 1ms 1ms <1ms

3 Dilithium3-AES 9ms 9ms 7ms 3ms 1ms 1ms <1ms

3 SPHINCS+-Haraka-192f-simple 253ms 254ms 176ms 167ms 29ms 25ms 15ms

3 SPHINCS+-Haraka-192s-simple 96ms 96ms 65ms 63ms 10ms 9ms 6ms

3 SPHINCS+-SHA256-192f-simple 160ms 162ms 96ms 57ms 25ms 23ms 9ms

3 SPHINCS+-SHA256-192s-simple 55ms 57ms 32ms 20ms 9ms 8ms 3ms

3 SPHINCS+-SHAKE256-192f-simple 2s 2s 1s 366ms 27ms 24ms 11ms

3 SPHINCS+-SHAKE256-192s-simple 596ms 537ms 493ms 124ms 9ms 9ms 4ms

3 SPHINCS+-Haraka-192f-robust 391ms 394ms 268ms 254ms 51ms 44ms 28ms

3 SPHINCS+-Haraka-192s-robust 153ms 155ms 105ms 99ms 19ms 17ms 11ms

3 SPHINCS+-SHA256-192f-robust 298ms 307ms 182ms 114ms 49ms 43ms 18ms

3 SPHINCS+-SHA256-192s-robust 102ms 110ms 64ms 41ms 18ms 16ms 6ms

3 SPHINCS+-SHAKE256-192f-robust 4s 3s 3s 717ms 50ms 45ms 22ms

3 SPHINCS+-SHAKE256-192s-robust 1s 1s 947ms 239ms 18ms 16ms 8ms

Low-Performance Embedded Internet of Things Devices and the Need for Hardware-Accelerated Post-Quantum Cryptography

337

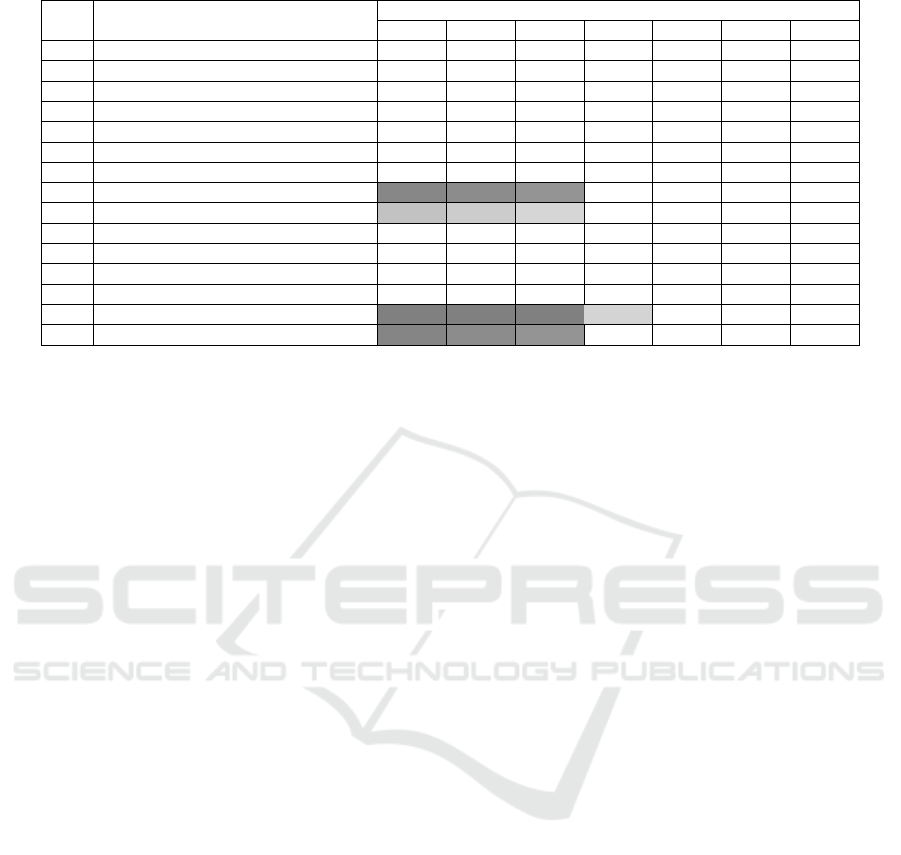
Table 9: Runtime measurement results: Digital Signature: Signature Veriﬁcation. (continued)

Level Algorithm

Platforms

r1b r1b+ rzw r2b r3b r3b+ r4b

5 Dilithium5 57ms 51ms 41ms 13ms 1ms 1ms <1ms

5 Dilithium5-AES 14ms 14ms 10ms 5ms 2ms 2ms 1ms

5 Falcon-1024 5ms 5ms 4ms 2ms 1ms 1ms <1ms

5 SPHINCS+-Haraka-256f-simple 273ms 274ms 188ms 181ms 31ms 27ms 16ms

5 SPHINCS+-Haraka-256s-simple 149ms 151ms 102ms 98ms 16ms 14ms 9ms

5 SPHINCS+-SHA256-256f-simple 162ms 159ms 96ms 60ms 25ms 23ms 9ms

5 SPHINCS+-SHA256-256s-simple 80ms 83ms 49ms 30ms 12ms 11ms 5ms

5 SPHINCS+-SHAKE256-256f-simple 2s 2s 1s 372ms 28ms 25ms 12ms

5 SPHINCS+-SHAKE256-256s-simple 870ms 801ms 733ms 183ms 15ms 13ms 6ms

5 SPHINCS+-Haraka-256f-robust 425ms 430ms 293ms 269ms 55ms 48ms 29ms

5 SPHINCS+-Haraka-256s-robust 233ms 237ms 159ms 150ms 29ms 26ms 16ms

5 SPHINCS+-SHA256-256f-robust 340ms 345ms 204ms 141ms 58ms 52ms 22ms

5 SPHINCS+-SHA256-256s-robust 175ms 177ms 110ms 69ms 30ms 26ms 11ms

5 SPHINCS+-SHAKE256-256f-robust 4s 3s 3s 742ms 53ms 47ms 22ms

5 SPHINCS+-SHAKE256-256s-robust 2s 2s 1s 365ms 26ms 24ms 11ms

IoTBDS 2024 - 9th International Conference on Internet of Things, Big Data and Security

338