Races in Extended Input/Ouput Automata, Their Compositions and
Related Reactive Systems
Evgenii Vinarskii
1
, Natalia Kushik
1
, Nina Yevtushenko
2
, Jorge L
´
opez
3
and Djamal Zeghlache
1
1
SAMOVAR, T
´
el
´
ecom SudParis, Institut Polytechnique de Paris, Palaiseau, France
2
Ivanikov Institute for System Programming, Russian Academy of Sciences, Moscow, Russia
3
Airbus, Issy-Les-Moulineaux, France
Keywords:
Distributed Reactive Systems, Races, Extended Input/Output Automata, Software Defined Networking.
Abstract:
Reactive systems can be highly distributed and races in channels can have a direct impact on their functioning.
In order to detect such races, model-based testing is used and in this paper, we define races in the Extended
Input Output Automata (EIOA) which are related to races in a corresponding distributed system. We de-
fine various race conditions in an EIOA modeling them by Linear Temporal Logic (LTL) formulas. As race
conditions can be resolved in the corresponding EIOA implementations, we also discuss how a generated
counterexample (if any) can be used for provoking a race in a distributed system implementation with the
given level of confidence. Software Defined Networking (SDN) framework serves as a relevant case study
along the paper.
1 INTRODUCTION
Distributed reactive systems are actively developing
nowadays and are becoming more and more adopted
in industrial environments and various application ar-
eas, such as for example, mobile networking (Silva
et al., 2021). These systems are composed of vari-
ous interacting components and thus, a particular at-
tention should be paid to the interoperability of these
components. Even if two components have been care-
fully verified up to some extent, it is still possible
that their composition can contain inconsistencies. It
is also possible that two or more wrongly config-
ured/developed components implement the entire sys-
tem in a reliable way (bugs can mask one another,
for example). In this work, we focus on the interac-
tions between two (or more) components of a reactive
system. In particular, considering a reactive system
shown in Fig. 1, we are interested in the interactions
between components C and S of the reactive system
and between C and its external applications where S
is an embedded component.
The main goal of the paper is the analysis and de-
tection of races in distributed reactive systems. Such
races can take place in the channels between the
interacting system components, or even in a given
component between some of its inputs and outputs,
Figure 1: Reactive system with embedded EIOAs.
at a designated state. Finally, several actions pro-
duced/accepted by the environment, can also com-
pete when sending/getting requests to/from the reac-
tive system.
One of the widely spread approaches for detect-
ing concurrency issues in distributed systems is to
establish the causality relationship between requests
as seen in PCatch (Li et al., 2023), or to construct
a happens-before (HB) graph, as proposed by (Liu
et al., 2017) in DCatch. A request e2 causally de-
pends on another request e1, denoted as e1 → e2, if
the execution of e2 is directly influenced by the ap-
pearance of e1. Li et al. (Li et al., 2022) have ex-
tended the application of the HB model to SDNs, im-
plementing the detection of race conditions in SPI-
DER. (Vinarskii et al., 2019) and (Vinarskii et al.,
2023) have explored a complementary domain, fo-
cusing on model checking and model-based testing
techniques for proactive SDN race detection, and pro-
vided a study on concurrency issues within an SDN
Vinarskii, E., Kushik, N., Yevtushenko, N., López, J. and Zeghlache, D.
Races in Extended Input/Ouput Automata, Their Compositions and Related Reactive Systems.
DOI: 10.5220/0012737900003687
Paper published under CC license (CC BY-NC-ND 4.0)
In Proceedings of the 19th International Conference on Evaluation of Novel Approaches to Software Engineering (ENASE 2024), pages 727-734
ISBN: 978-989-758-696-5; ISSN: 2184-4895
Proceedings Copyright © 2024 by SCITEPRESS – Science and Technology Publications, Lda.
727

implementation. Scheduling approach for races de-
tection has been studied in (Veeraraghavan et al.,
2011). However, these approaches do not guarantee
that races identified in the specification will also ap-
pear in the implementation at hand. Moreover, to the
best of our knowledge, there remains a lack of studies
on developing a probabilistic model to predict race
occurrences in distributed reactive systems with the
given confidence level. Such a model would bridge
the gap between concurrency issues in specifications
and those that actually occur in implementations.
To address these challenges, we employ EIOAs to
model the behavior of the system components and af-
terwards, their composition. We introduce the defini-
tions of various types of races and use specific LTL
formulas (Baier and Katoen, 2008) to describe the
race-free system behavior. Various model checkers
such as Spin (Holzmann, 2003), Uppaal (Behrmann
et al., 2004), etc. can be utilized for verifying the
formulas against the EIOA composition, for which
counterexamples that violate LTL formulas present
potential races. However, identifying potential races
through model checking is only the first step. We em-
phasize the importance of the second step of studying
the conditions for provoking races in an implementa-
tion at hand. The third step is to check whether the
above first steps are helpful when testing races in real
reactive systems. Our work aims to reduce the gap be-
tween such specification analysis and observable sys-
tem behavior, providing a more accurate study of race
conditions in reactive systems.
The main contributions of this work are: i) defi-
nitions of input/output, input/input and output/output
races for EIOAs and their composition, ii) study of
the correlation between races in an EIOA and in a
corresponding distributed reactive system when the
probability message delay distribution in channels is
known, and iii) experimental evaluation of the corre-
lation between races in an SDN framework.
The structure of the paper is as follows. Section
2 presents the necessary background. Section 3 is
devoted to the description of our SDN case study.
Section 4 introduces the notions of input/output,
input/input and output/output races in EIOAs and
presents their modeling via LTL formulas. Section 5
contains a study of the probability to detect races for
an SDN framework, together with some experimental
results, while Section 6 concludes the paper.
2 BACKGROUND
In this paper, we consider races in Extended Finite
Input/Output Automata, EIOAs, for short. The def-
inition given below, is taken from (Vinarskii et al.,
2019). An EIOA A is a tuple (S,I,O,V,T, s
0
), where
S is a finite nonempty set of states with the desig-
nated initial state s
0
; I and O are finite input and
output alphabets, I ∩ O =
/
0; V is a finite, possibly
empty set of context variables with set D
V
of vec-
tors of context variables’ values if V ̸=
/
0; T is a set
of transitions. Inputs and outputs can be parameter-
ized, i.e., inputs and outputs of the EIOA are pairs
(input, vector of input parameters’ values) or (output,
vector of output parameters’ values) and D
I
(D
O
) is
the set of vectors of input (output) parameters’ val-
ues if the set of parameters is not empty. A transi-
tion is a 6-tuple (s, a, P,v
p
,v
o
,s
′
) where s,s
′
∈ S are
initial and final states of the transition; a ∈ I ∪ O;
P : D
V
× D
I
→ {True,False} is the transition pred-
icate; v
p
: D
V
× D
I
→ D
V
is the context update tran-
sition function; v
o
: D
V
× D
I
→ D
O
is the output up-
date function. Transition (s,a,P,v
p
,v
o
,s
′
) is executed
only when transition predicate P evaluates to true
and the vectors of context variables’ values and out-
put parameters’ values are updated according to func-
tions v
p
and v
o
after the transition execution. A trace
tr = a
1
.a
2
.... .a
n
of EIOA A is a sequence of actions
generated by the sequence of transitions of A. The
set of traces generated by A is denoted as Traces(A).
Given a trace tr over an alphabet I ∪ O, subtrace tr|
I
(tr|
O
) of trace tr where only letters from I (O) are
retained is referred to as I-projection (O-projection)
of tr. We note that, the EIOA model can be more
complicated, for example, the set of states can have a
defined subset of the final states or non-observable ac-
tions can be considered, etc. Nevertheless, these cases
are not taken into account in this paper and we further
demonstrate that such simplification is useful when
checking with respect to the race related properties.
As usual, we assume that when dealing with an
EIOA, no input is accepted and no output is produced
when a transition is executed. However, when both
an input and an output are defined at a state, they
can ‘compete’ between themselves, i.e., what the ma-
chine does first - accepts the input or produces the
output is nondeterministically decided. We hereafter
refer to such ‘competition’ as an input/output (or out-
put/input) race (a race between input and output ac-
tions). Likewise, at a given state of an EIOA two
(or more) inputs can be defined, these inputs can also
compete to be accepted. In this case, we talk about
an input/input race. Similarly, if two (or more) out-
puts can be produced at the same state, then an out-
put/output race can take place.
As we mention in Section 1, usually, a reactive
system is organized as a collection of interacting com-
ponents. The composition operator is well defined for
ENASE 2024 - 19th International Conference on Evaluation of Novel Approaches to Software Engineering
728

Figure 2: Topology of the SDN framework.
classical FSMs and automata, while there is no gen-
eral definition of the parallel dialogue-based compo-
sition operator for EIOAs. In this paper, we study a
special case of the binary composition operator when
one of the components is an embedded component
and has no context variables; moreover, there are no
infinite external output sequences (oscillations) in the
composition. We also assume some limitations on
the context variables in another component: the set
of context vectors is finite. In this case, the compo-
sition can be derived based on a truncated successor
tree. The nodes of the tree are pairs of states of the
components, along with context vectors, while edges
are labeled with external and internal input and out-
put actions. The root of the tree is labeled by the
pair of initial states of the components and the initial
context vector. We then ‘hide’ internal actions cal-
culating parameters’ values by composing functions
via a corresponding path that is finite, as there are
no oscillations. In the same way, we collect func-
tions for context variables. Note that despite such
limitations for embedded components, this operator
allows to model the composition of controller-based
distributed systems, for example, the SDN controller
and switch composition.
For the race detection in EIOAs and their compo-
sitions, formal verification can be used based on LTL
formulas. An LTL formula is a formula ϕ ::= a|ϕ
1
∧
ϕ
2
|¬ϕ|Xϕ|ϕ
1
Uϕ
2
|Fϕ|Gϕ, where: a is an atomic
proposition, X denotes the ‘next’ operator, U denotes
the ‘until’ operator, F denotes the ‘eventually’ opera-
tor and G denotes the ‘globally’ operator. The condi-
tions when a path satisfies the LTL formula ϕ can be
found in (Baier and Katoen, 2008).
3 CASE STUDY
In this paper, we use an SDN framework as a relevant
case study (Fig. 2). Such framework allows to exper-
imentally evaluate the proposed methodology which
aims at detecting race conditions within the compo-
sition of EIOAs and provoking related concurrency
issues in reactive systems. Namely, as our case study,
we use the SDN framework that allows to dynami-
cally reconfigure the network by decoupling the con-
trol plane from the data plane and pushing flow rules
by the controller to the switches’ flow tables (forward-
ing devices) (McKeown et al., 2008). These flow
rules are responsible for redirecting traffic incoming
to switches on the data plane.
Since we are interested in detecting race condi-
tions affecting the data plane paths, we derive the
EIOAs to model the behavior of the SDN controller
(see Fig. 3), Open vSwitch (see Fig. 4), and their
composition (see Fig. 6). To construct these EIOAs,
we rely on the approach considered in (Vinarskii
et al., 2019) and refer to the ONOS project docu-
mentation (Berde et al., 2014), the OpenFlow spec-
ification (McKeown et al., 2008), and the REST API
guidelines (Koshibe et al., 2014). The inputs and out-
puts within these EIOAs are defined with specific se-
mantics to accurately represent the interactions within
the SDN infrastructure.
• (?PF, id, τ): the controller receives from the en-
vironment a request for adding a flow rule with the
identification number id having the timeout equal
to τ seconds.
• (?GF, id): the controller receives from the envi-
ronment a request for retrieving information about
the flow rule with the identification number id.
• (?DF, id): the controller receives from the envi-
ronment a request for deleting the flow rule with
the identification number id.
• (!RF, id): the controller sends a message to the
environment with information about the flow rule
with the identification number id, i.e., (!RF, id) is
the response to (?GF, id).
• (!FD, id): the controller sends a message to the
environment of deleting a flow rule with the iden-
tification number id, i.e., (!FD, id) is the response
to (?DF, id).
• (!FE, id): the controller sends a message to the
environment of expiring a flow rule with the iden-
tification number id, i.e., (!FE, id) is the response
to (?PF, id, τ).
To distinguish the internal communication be-
tween the controller and the switch from the external
communication, we annotate these interactions with
the index
CS
. The fragment of the EIOA C shown
in Fig. 3 models the behavior of the SDN controller.
Since we focus on the race detection related to the
configurations of a flow table, EIOA C has the states
with the following semantics: c
0
is the initial state,
Races in Extended Input/Ouput Automata, Their Compositions and Related Reactive Systems
729

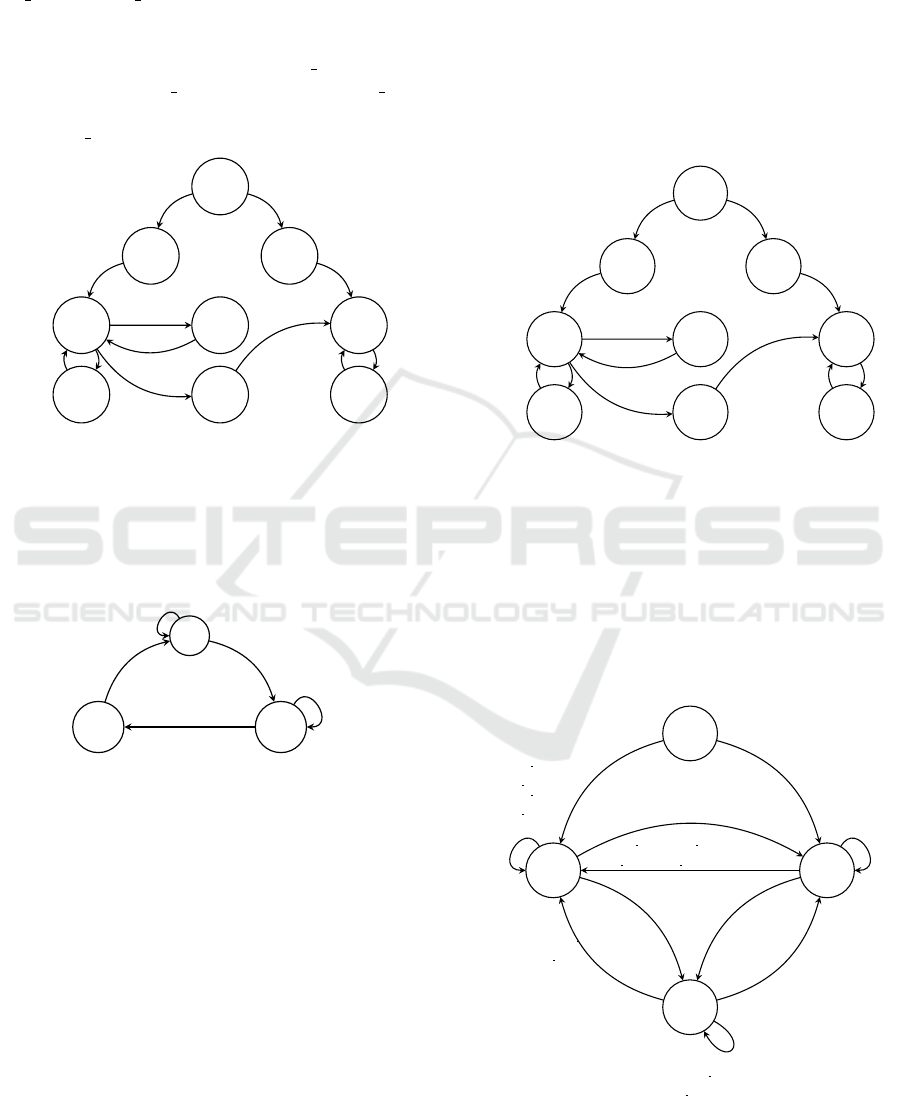
c
1
corresponds to the behavior of the controller after
receiving input (?PF, id, τ) (transition T1). At the
same time, EIOA C has the context variables ct, tt,
g f f lag and d f f lag with the following semantics:
ct is a Boolean array, which indicates the installed
flow rules, tt is an integer array with the timeout val-
ues for the flow rules. For every f low id the follow-
ing holds: if ct[ f low id] = T RUE and tt[ f low id] >
0, then after the execution of each transition the value
of tt[ f low id] is reduced by one unit.
c
0
c
1
c
7
c
4
c
2
c
3
c
6
c
8
c
5
T1: (?PF,id, τ)
ct[id] = 1
tt[id] = τ T2: (?GF,id)
T3: (!PF
CS
,id, τ)
T4: (?F E
CS
,id)
T5: (?PF,id, τ)
ct[id] = 1
tt[id] = τ
T6: (?GF,id)
T7:
i f ((ct[id] == 1)
&& (tt[id] == 0))
(!FE,id)
ct[id] = 0
T8: (!PF
CS
,id, τ)
T9: (!GF
CS
,id)
T10: (?PF,id, τ)
ct[id] = 1
tt[id] = τ
T11: (!GF
CS
,id)
T12: (!PF
CS
,id, τ)
Figure 3: EIOA C.
The fragment of EIOA S shown in Fig. 4 models
the behavior of the OpenVSwitch. Since the composi-
tion described in Section 2 requires that an embedded
EIOA does not have context variables, this EIOA has
only input/output parameters.
q
0
q
1
q
2
TS1: (!FE
CS
,id)
TS2: (?PF
CS
,id,τ)
TS3: (?GF,id)TS4: (?DF,id)
TS5: (!FE
CS
,id)
TS6: (?PF
CS
,id,τ)
TS7: (!RF
CS
,id)
Figure 4: EIOA S.
The fragment of the composition is shown in
Fig. 5 where the controller communicates with the
environment that is represented by one or more ap-
plications via external actions (actions at the North-
bound interface) and with the switch via internal ac-
tions (actions at the Southbound interface); at the
same time, the switch communicates only with the
controller. These components communicate in the
following way:
• When the controller executes an external action,
the switch does not execute any actions. For ex-
ample, in Fig. 5, the controller moves from state
c
0
to state c
1
after receiving (?GF,id), while the
switch remains at state q
0
.
• When the controller and switch are ready to ex-
ecute the same internal action (possibly, with the
same parameter value), they both execute this ac-
tion and move to the next states. Here we notice
that if this internal action is an input (resp. output)
action in the controller, then this action is an out-
put (resp. input) action in the switch. For exam-
ple, in Fig. 5 when the controller sends (!GF
CS
,id)
at state c
1
, it moves to state c
2
, while the switch
moves from state q
0
to state q
1
after receiving
(?GF
CS
,id).
(c
0
,q
0
)
(c
1
,q
0
) (c
7
,q
0
)
(c
4
,q
0
)
(c
2
,q
0
)
(c
3
,q
0
)
(c
6
,q
1
)
(c
8
,q
1
)
(c
5
,q
0
)
T1: (?PF,id, τ)
ct[id] = 1
tt[id] = τ T2: (?GF,id)
T3: (!PF
CS
,id,τ)
T4: (?F E
CS
,id)
T5: (?PF,id, τ)
ct[id] = 1
tt[id] = τ
T6: (?GF,id)
T7:
i f ((ct[id] == 1)&&
(tt[id] == 0))
(!FE,id)
ct[id] = 0
T8: (!PF
CS
,id,τ)
T9: (!GF
CS
,id)
T10:
(?PF,id,τ)
ct[id] = 1
tt[id] = τ
T11: (!GF
CS
,id)
T12: (!PF
CS
,id,τ)
Figure 5: EIOA C&S
ext
with internal actions.
After hiding internal actions (Barrett and Lafor-
tune, 1998), we obtain the composition of the con-
troller and the switch shown in Fig. 6. The pair of
states (c
0
,q
0
) in Fig. 5 corresponds to the state s
0
in
Fig. 6, whereas the pair (c
4
,q
2
) in Fig. 5 corresponds
to the state s
1
in Fig. 6.
Coming back to the topology shown in Fig. 2,
there are four hosts and four switches on the data
plane. The flow table for switch s
1
has two dis-
s
0
s
1
s
2
s
3
T1: (?GF,id)
T2: (?PF,id, τ)
ct[id] = 1
tt[id] = τ
T3: (?GF,id)
T4: (?DF,id)
ct[id] == 0
T5: i f((ct[id] == 1) &&
(tt[id] == 0))
(!FE,id)
ct[id] = 0
T6: i f(gf f lag)
(!RF,id)
g f f l ag = 0
T7: i f(d f f lag)
(!FD,id)
d f f lag = 0
T8: (?PF,id, τ)
ct[id] = 1
tt[id] = τ
T9: i f(g f f lag) T10: i f(d f f lag) T11: (?PF, id, τ)
(!RF,id) (!FD,id) ct[id] = 1
g f f l ag = 0 d f f lag = 0 tt[id] = τ
T12: (?DF,id)
ct[id] == 0
T13: (?GF,id)
T14: i f((ct[id ] == 1)
&& (tt[id] == 0))
(!FE,id)
ct[id] = 0
T15: i f(g f f lag)
(!RF,id)
g f f l ag = 0
T16: (?PF,id, τ)
ct[id] = 1
tt[id] = τ
T17: (?GF,id)
T18: (?DF,id)
ct[id] == 0
T19: i f(d f f lag)
(!FD,id)
d f f lag = 0
T20: i f((ct[id ] == 1)&&(tt [id] == 0))
(!FE,id)
ct[id] = 0
Figure 6: EIOA C&S without internal actions.
ENASE 2024 - 19th International Conference on Evaluation of Novel Approaches to Software Engineering
730

tinct flow rules: the first rule redirects all the in-
coming traffic from switch s
1
to s
2
with the time-
out of one second. The SDN controller pushes this
flow rule to s
1
after getting an input (?PF
CS
,1,1).
After one second the first flow rule expires and the
SDN controller will produce (!FE, 1). The second
rule has the timeout of two seconds redirecting all
the incoming traffic from switch s
1
to s
4
. The SDN
controller pushes this flow rule to s
1
after getting an
input (?PF
CS
,2,2). The second flow rule expires,
and (!FE,2) is produced. Due to unknown delays
in the internal input channel it can happen that even
if (?PF, 1, 1) arrives before (?PF,2,2) to the con-
troller, (?PF
CS
,2,2) arrives before (?PF
CS
,1,1) to the
switch. As a result, the second flow rule can ex-
pire earlier than the first one, i.e., output sequence
(!FE,2).(!FE,1) will be observed, instead of the ex-
pected (!FE, 1).(!FE,2). It is the output/output race
and some packets can be redirected to a longer path
h
1
→ s
1
→ s
2
→ s
4
→ h
4
instead of a shorter one
h
1
→ s
1
→ s
4
→ h
4
. Therefore, the concurrency be-
tween some inputs and outputs can influence the data
plane configuration. The possibility of the above sit-
uation can be presented as a violation of the fol-
lowing LTL-formula: (?PF,1,1)&&X(?PF, 2,2) →
XX¬(¬(!FE,1)U(!FE,2))
1
, that means that if
(?PF, 1,1) precedes (?PF,2,2) then (!FE, 1) has to
be produced before (!FE,2).
4 RACES IN AN EIOA
In Section 2, we discussed the composition operator
for EIOAs, ensuring that the resulting compositions
remain within the class of EIOAs discussed in this
paper. The latter allows to define races for a single
EIOA and extend such races’ definitions for the com-
position of EIOAs.
Input/Output Races. These races can occur when
there exists a state of a corresponding EIOA where
both an input and an output are specified, i.e., at a
given state the decision of accepting an input or pro-
ducing an output is made nondeterministically by the
EIOA.
Definition 1. Given an EIOA A = (S, I,O,V, T,s
0
)
and a pair (i,o) ∈ I × O, A is i/o-race-sensitive if
there exists a trace β leading to a state s where input
i and output o are defined, i.e., tr = β.o, tr
′
= β.i ∈
Traces(A). Otherwise, A is i/o-race-free.
As an example, we consider EIOA C&S shown
in Fig. 6 and input/output pair (?PF,0, 1)/(!FE, 0).
1
There can be more complex formulas which take into
account timeouts of the flow rules.
EIOA C&S is (?PF, 0, 1)/(!FE,0)-race-sensitive
since (?PF,0,1) and (!FE,0) are defined at state
s
2
, (?PF,0, 1).(?GF,0) brings C&S to state s
2
,
and traces tr
1
= (?PF,0, 1).(?GF,0).(?PF, 0,1)
and tr
2
= (?PF,0,1).(?GF,0).(!FE, 0) are both
in Traces(C&S). This race can occur if two si-
multaneous requests for adding rules are pushed
by both applications and a sudden expiration of
the flow rule with id = 0 occurs before accept-
ing request (?PF,0, 1) for adding a flow rule
from another application, i.e., (!FE,0) precedes
(?PF, 0,1). This situation can be presented as a
violation of LTL-formula Φ
in out
= G((?PF,0,1) →
X(¬(¬(?PF, 0, 1)U(!FE,0)))) (see Section 5).
Input/Input Races. We hereafter keep working with
the topology shown in Fig. 1, where two applications
submit their requests to the reactive system. These
requests can compete and thus, provoke input/input
races for the corresponding EIOA.
Definition 2. Given an EIOA A = (S, I,O,V, T,s
0
)
and two applications APP
1
, APP
2
, A is input/input
race-sensitive if there exist state s where inputs i
1
and
i
2
are defined, β ∈ (I ∪ O)
∗
leading to state s, α, α
′
∈
(I ∪O)
∗
and traces tr = β.i
1
.i
2
.α, tr
′
= β.i
2
.i
1
.α
′
such
that tr,tr
′
∈ Traces(A) and tr|
O
̸= tr
′
|
O
.
Consider again EIOA C&S shown in Fig. 6,
inputs (?PF,0, 1) and (?DF,0) that are defined at
state s
2
and sequence β = (?GF, 0) bringing C&S
to state s
2
. Suppose that (?PF, 0, 1) is pushed by
APP
1
, while (?DF,0) is pushed by APP
2
. Traces
tr = (?GF,0).(?PF,0,1).(?DF,0).(!FD, 0) and
tr
′
= (?GF, 0).(?DF,0).(?PF, 0,1).(!FE, 0) are in
Traces(C&S). Since tr|
O
̸= tr
′
|
O
, C&S is input/input
race-sensitive. The following LTL-formula Φ
in in
=
((?DF, 0)&&X(?PF,0,1) || (?PF, 0, 1)&&X(?DF,0))
→ XX(¬(¬(!FD,0)U(!FE,0))) can be considered
for that matter, which means that if a trace starts
from (?PF,0,1).(?DF,0) or (?DF,0).(?PF,0, 1) then
(!FE,0) cannot appear before (!FD, 0).
Output/Output Races. Similarly to the input/input
races, output/output races for reactive systems can oc-
cur at a state of EIOA where both outputs are defined
and can compete to be produced.
Definition 3. Given an EIOA A = (S,I, O,V,T, s
0
),
state s and outputs o
1
and o
2
defined at state s, A
is output/output race-sensitive if there exist β ∈ (I ∪
O)
∗
leading to state s and traces tr = β.o
1
.o
2
, tr
′
=
β.o
2
.o
1
such that tr,tr
′
∈ Traces(A).
Consider again EIOA C&S shown in Fig. 6 and
outputs (!FE,0) and (!FE, 1) defined at state s
1
.
Trace (?PF,0,1).(?PF,1, 1) brings C&S to state s
1
,
and tr = (?PF,0,1).(?PF,1, 1).(!FE,0).(!FE,1) and
tr
′
= (?PF,0, 1).(?PF,1,1).(!FE, 1).(!FE, 0) are in
Races in Extended Input/Ouput Automata, Their Compositions and Related Reactive Systems
731

Traces(C&S). The latter makes C&S output/output
race-sensitive (see (Vinarskii et al., 2019) for details).
This situation can be presented as a violation of LTL-
formula Φ
out out
= G(((?PF, 0, 1)&&X(?PF,1,1)) →
XX(¬(¬(!FE, 0)U(!FE,1)))).
In order to check that the EIOA (the composition
of EIOAs) satisfies LTL-formulas, various model-
checkers can be used. However, identifying a race
condition within an EIOA does not necessarily imply
its appearance in the related reactive system when a
counterexample is applied. This discrepancy can of-
ten be caused by the reactive system’s nondeterminis-
tic behavior, which may be influenced by the channel
timeouts. Consequently, we need to study the condi-
tions when a corresponding race can be provoked in
an implementation at hand, and we further show that
this can happen if we apply the corresponding coun-
terexample several times. In Section 5, we present an
estimation of the probability that a race condition oc-
curs in the reactive system when the counterexample
is applied an appropriate number of times.
5 FROM EIOA RACES TO RACES
IN REACTIVE SYSTEMS
In Section 4, we introduced the race definition for
an EIOA that in this paper, is considered as the for-
mal model (the specification) of a reactive system (an
implementation at hand). As usual, the specification
cannot describe all the aspects of the implementation
behavior, and thus, not all races in a reactive system
can be detected when using the composition of EIOAs
as its specification. Moreover, the specification de-
scribing the behavior of a reactive system does not
have timed variables, while for some implementation
an input/output race significantly depends on message
delays in external and internal channels and the EIOA
model does not capture this issue. However, usually
the message delays in the channels are normally dis-
tributed (Sukhov et al., 2016) and therefore, for ini-
tiating a trace under interest it is needed to apply a
corresponding counterexample several times to the re-
active system at hand (if we want to observe the race
in the implementation). We calculate the number of
times to apply a counterexample by counting an in-
stant when the probability for observing every pos-
sible specification trace for a given sequence of ap-
plied requests exceeds the given threshold. We further
show how this can be done for the SDN framework
from Section 3 in Fig. 7 and Fig. 8 when the message
delays in all channels have the normal distribution.
5.1 Estimating the Race Probability in
Distributed Reactive Systems
We consider the reactive system shown in Fig. 1,
there are four channels via which messages are
transmitted. Those are two external channels and
two internal channels. Let t
A
1
C
,t
A
2
C
,t
CA
1
,t
CA
2
,t
CS
,t
SC
be random variables that specify the time that re-
quests from/to applications APP
1
and APP
2
spend
in the corresponding channel. We assume that
t
A
1
C
,t
A
2
C
,t
CA
1
,t
CA
2
,t
CS
,t
SC
∈ N (µ, σ
2
), i.e., have the
normal distribution with the same parameters: the
mean µ and the variance σ.
Consider input/output pairs (i
1
,o
1
) and (i
2
,o
2
)
that can be executed at the same state s of the com-
position of EIOAs where input i
1
is pushed by APP
1
and i
2
is pushed by APP
2
. If i
1
and i
2
are pushed at the
same timestamp T then o
1
and i
2
(i
1
and o
2
) start to
compete in the internal channel to/from the embedded
EIOA. Let inputs i
1
and i
2
be accepted by EIOA C at
time instances T
i
1
= T +t
A
1
C
and T
i
2
= T +t
A
2
C
corre-
spondingly while o
1
and o
2
are produced by C at time
instances T
o
1
= T
i
1
+t
CS
+t
SC
and T
o
2
= T
i
2
+t
′
CS
+t
′
SC
.
In the above formula, t
CS
+ t
SC
and t
′
CS
+ t
′
SC
are time
delays for messages to spend in internal channels. We
assume that the system behavior allows to accept in-
puts i
1
and i
2
in any order but the next input should be
applied later than the output to the previous input is
produced. The reason is as follows. Assume that be-
ing at state s EIOA C accepts i
1
earlier than i
2
, then C
moves to state s
′
. The expected behavior for C being
at state s
′
is to accept i
2
. However, due to (i
2
,o
1
)-race
it can happen that output o
1
is produced earlier than
input i
2
arrives, denoted as o
1
≺ i
2
. In this case, after
producing o
1
the EIOA moves to state s
′′
that can dif-
fer from s
′
. Thus, (i
2
,o
1
)-race affects the behavior of
the EIOA. Since o
1
≺ i
2
happens when T
o
1
< T
i
2
, the
probability Pr(o
1
≺ i
2
) = Pr(T
o
1
< T
i
2
). By defini-
tion, T
o
1
= T
i
1
+t
CS
+t
SC
and T
i
2
= T +t
A
2
C
, and thus,
Pr(T
o
1
< T
i
2
) implies that Pr((T +t
A
2
C
+t
CS
+t
SC
) <
(T +t
A
1
C
)) = Pr((t
A
1
C
−t
A
2
C
−t
CS
−t
SC
) > 0). Since
random variables t
A
1
C
, t
A
2
C
, t
CS
and t
SC
have the nor-
mal distribution with the same mean µ and variance
σ
2
, (t
A
1
C
− t
A
2
C
− t
CS
− t
SC
) ∈ N (−2µ,4σ
2
). There-
fore, Pr((t
A
1
C
−t
A
2
C
−t
CS
−t
SC
) > 0) =
∞
R
0
e
−
(t+2µ)
2
2σ
2
dt
and Pr(o
1
≺ i
2
) =
∞
R
0
e
−
(t+2µ)
2
2σ
2
dt.
ENASE 2024 - 19th International Conference on Evaluation of Novel Approaches to Software Engineering
732

5.2 Studying the Race Probability in the
SDN Framework
In order to confirm that our approach can be applied
for studying real reactive systems, we performed ex-
perimental evaluation with the SDN framework. Sim-
ilar to (Vinarskii et al., 2019), experiments were per-
formed with the ONOS Controller and the Mininet
(de Oliveira et al., 2014) simulator, executed under a
virtual machine running on VirtualBox Version 5.1.34
for Ubuntu 16.04 LTS with 4GB of RAM, and a quad
AMD A6-7310 APU with AMD Radeon R4 Graph-
ics processor. Our experimental setup corresponds to
the topology in Fig. 2, i.e., the simulated network con-
tains the ONOS Controller and a single Open vSwitch
version v2.11.0 and two applications implemented as
Perl scripts. The goal of the experiments is (i) to de-
rive a distribution for the message delay in channels
and show that it can be approximated with the normal
distribution, and (ii) estimate the efficiency of the pro-
posed strategy for race detection in the composition of
the ONOS Controller and the Open vSwitch. All the
Perl and Python scripts utilized in the experimental
setup are accessible via (Vinarskii, 2024).
We first evaluate the distribution of random vari-
able t = t
A
1
C
+ t
CS
+ t
SC
+ t
CA
1
, assuming that t is
the continuous random variable defined over inter-
val [0,∞). For this purpose, we consider the topol-
ogy with a single switch and two applications. At
the first step we get the probability density func-
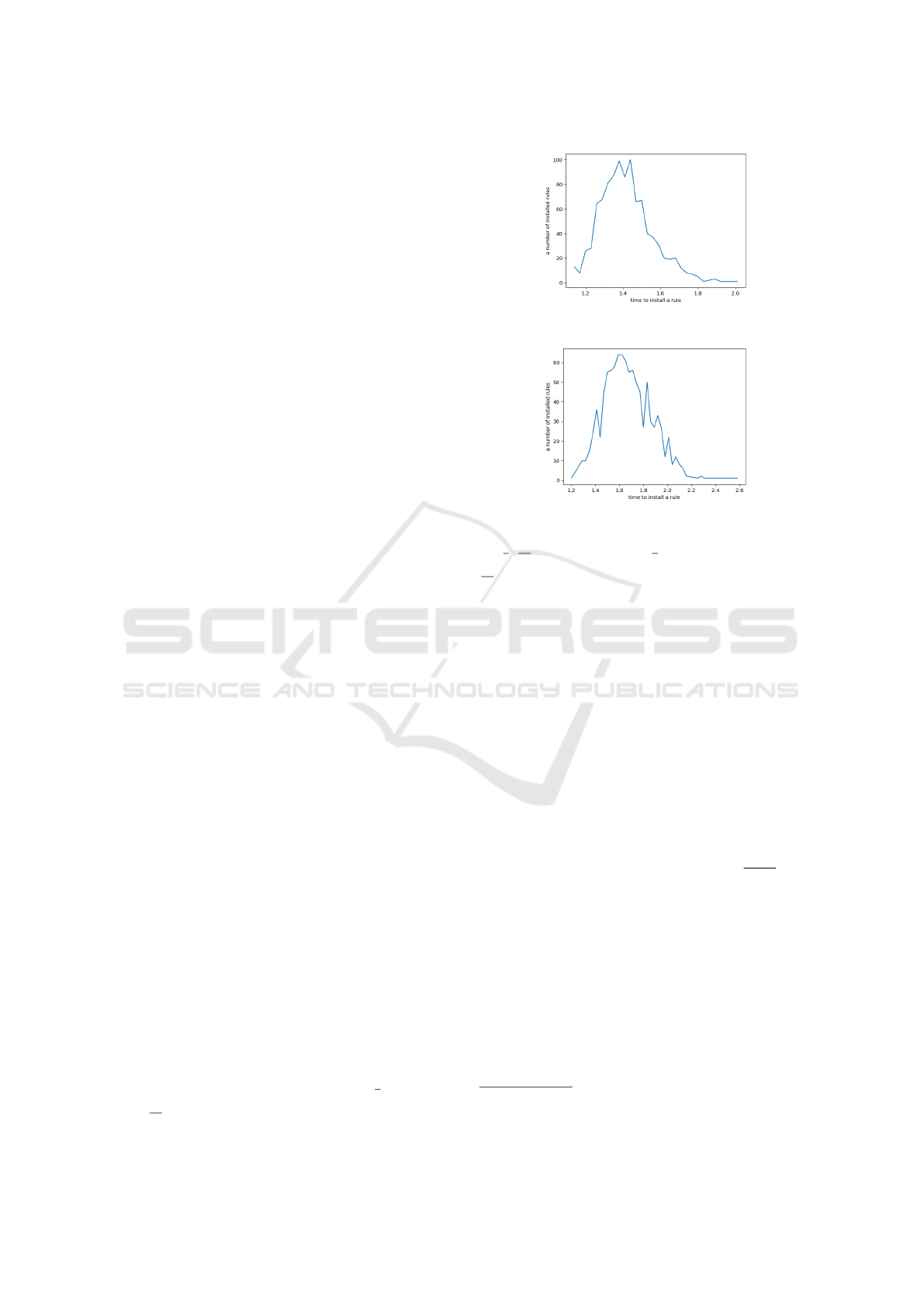
tion for installing a single message. For this rea-
son, one rule is pushed 1000 times in order to collect
the necessary statistical data; the results are shown in
Fig. 7. According to the distribution density function
shown in Fig. 7, the distribution can be approximated
with the normal distribution with mean µ
1
= 1.42
and variance σ
2
1
= 0.02, i.e., N (1.42,0.02). In or-
der to exclude the influence of the whole system in-
stallation on this distribution, we have got the evalu-
ation of the probability density function for installing
two messages. Similarly, according to the distribu-
tion density function shown in Fig. 8, this distribu-
tion can be also approximated with the normal distri-
bution N (1.67,0.04) with mean µ
2
= 1.67 and vari-
ance σ
2
2
= 0.04. The difference of these two dis-
tributions can be considered as the rough estimate
for the message delay in external and internal chan-
nels. This difference also is normal with parameters
µ = µ
2
− µ
1
= 0.25 and σ
2
= σ
2
2
+ σ
2
1
= 0.06, i.e.,
t ∈ N (µ,σ
2
) = N (0.25,0.06). Therefore, since t =
t
A
1
C
+ t
CS
+ t
SC
+ t
CA
1
and t
A
1
C
,t
A
2
C
,t
CA
1
,t
CA
2
,t
CS
,t
SC
are normally distributed, t
A
1
C
,t
A
2
C
,t
CA
1
,t
CA
2
,t
CS
,t
SC
are also normally distributed with mean
µ
4
and vari-
ance
σ
2
4
, i.e., their distribution is approximated with
Figure 7: Time distribution for pushing one flow rule.
Figure 8: Time distribution for pushing two flow rules.
N (
µ
4
,
σ
2
4
), i.e., with mean
µ
4
= 0.0625 and variance
σ
2
4
= 0.0015.
Coming back to the SDN topology shown in
Fig. 2, consider the EIOA (see Fig. 6) which models
the SDN controller and switch s
1
composition. As-
sume that APP
1
deletes rules from the flow table, i.e.,
it sends input ?DF to the composition. At the same
time, APP
2
inserts rules to the flow table, i.e., it sends
input ?PF to the composition. Thus, the input/output
race occurs when output !FD is produced earlier than
input ?PF is obtained by the composition.
Consider sequences seq
1
=?DF
j
.!FD
j
(from
APP
1
) and seq
2
=?PF
j
.!FE
j
(from APP
2
) where j is
the index
2
of the flow rule. The race condition in-
volves a conflict between output action !FD
j
of APP
1
,
and input action ?PF
j
of APP
2
. The race occurs if
input action ?PF
j
happens after output action !FD
j
.
The probability Pr(FD
1
j
≺ PF
2
j
) =
∞
R
0
e
−
(t+2µ)
2
2σ
2
dt =
{µ = 0.25,σ
2
= 0.06} ≈ 0.187. Thus, with the proba-
bility 1 −0.187 = 0.813 the race will not occur in the
experiment. Now we check how many times inputs
?DF
j
and ?PF
j
have to be applied in order to guaran-
tee that the race will be observed with the probability
of at least 0.99. Since 0.187
23
< 0.01, the race will
be detected with the probability of at least 0.99, if the
experiment is performed at least 23 times.
In order to provoke this race in the experimental
setup, we have run two applications simultaneously
2
In the experiments, as an index we use the priority of
the flow rule.
Races in Extended Input/Ouput Automata, Their Compositions and Related Reactive Systems
733

23 times: seq
1
of APP
1
and seq
2
of APP
2
. In order to
distinguish between different runs, we have run flow
rules with priority 40000 + i. If there are no races,
then as a result, we should get the empty flow table of
the rules of switch s
1
. However, according to the per-
formed experiments, after observing sequences seq
1
and seq
2
23 times, the rule with the priority 40022 is
still in the table after the script execution. The results
clearly show that in this case, the probability thresh-
old 0.99 is sufficient to observe the (?PF,!FD)-race.
6 CONCLUSIONS
In this paper, we considered concurrency issues in the
composition of EIOAs and reactive systems which
can be modeled by EIOAs. In particular, we in-
troduced the formal definitions of input/output, in-
put/input and output/output races that can occur in
the composition of EIOAs. We used a probabilistic
approach to establish the correlation between races in
the composition of EIOAs and their appearance in a
reactive system implementation. In order to check,
how practical is our approach, we performed an ex-
perimental evaluation with the SDN framework.
This paper opens a number of directions for future
work. Despite the fact that the proposed approach is
generic, experiments were only carried for the SDN
framework. The proposed approach relies on the LTL
based model checking solutions for describing and
detecting races in SDN; in the future, other formal
verification techniques and their applicability to the
problem of interest can be investigated.
REFERENCES
Baier, C. and Katoen, J.-P. (2008). Principles of Model
Checking. The MIT Press.
Barrett, G. and Lafortune, S. (1998). Bisimulation, the su-
pervisory control problem and strong model matching
for finite state machines. Discrete Event Dynamic Sys-
tems: Theory & Applications, 8:377–429.
Behrmann, G., David, A., and Larsen, K. G. (2004). A
tutorial on uppaal. In International School on Formal
Methods for the Design of Computer, Communication,
and Software Systems, Bertinora, Italy, September 13-
18, 2004, pages 200–236.
Berde, P., Gerola, M., Hart, J., Higuchi, Y., Kobayashi, M.,
Koide, T., Lantz, B., O’Connor, B., Radoslavov, P.,
Snow, W., et al. (2014). Onos: towards an open, dis-
tributed sdn os. In Proceedings of the third workshop
on Hot topics in software defined networking, pages
1–6.
de Oliveira, R. L. S., Schweitzer, C. M., Shinoda, A. A.,
and Prete, L. R. (2014). Using mininet for emulation
and prototyping software-defined networks. In 2014
IEEE Colombian Conference on Communications and
Computing (COLCOM), pages 1–6.
Holzmann, G. (2003). The Spin model checker: primer and
reference manual. Addison-Wesley Professional.
Koshibe, A., O’Connor, B., Milkey, R., Vachuska, T.,
Hall, J., Gebert, S., Higuchi, Y., Li, J., Hart, J.,
Lantz, B., and Koti, S. P. (2014). ONOS - Appendix
B: REST API. https://wiki.onosproject.org/display/
ONOS/Appendix+B%3A+REST+API.
Li, A., Padhye, R., and Sekar, V. (2022). Spider: A prac-
tical fuzzing framework to uncover stateful perfor-
mance issues in sdn controllers. https://doi.org/10.
48550/arXiv.2209.04026.
Li, J., Zhang, Y., Lu, S., Gunawi, H. S., Gu, X., Huang, F.,
and Li, D. (2023). Performance bug analysis and de-
tection for distributed storage and computing systems.
ACM Trans. Storage, 19:1–33.
Liu, H., Li, G., Lukman, J. F., Li, J., Lu, S., Gunawi, H. S.,
and Tian, C. (2017). Dcatch: Automatically detecting
distributed concurrency bugs in cloud systems. In Pro-
ceedings of the Twenty-Second International Confer-
ence on Architectural Support for Programming Lan-
guages and Operating Systems, pages 677–691.
McKeown, N., Anderson, T., Balakrishnan, H., Parulkar,
G., Peterson, L., Rexford, J., Shenker, S., and Turner,
J. (2008). Openflow: enabling innovation in campus
networks. ACM SIGCOMM Computer Communica-
tion Review, 38:69–74.
Silva, R., Santos, D., Meneses, F., Corujo, D., and Aguiar,
R. L. (2021). A hybrid sdn solution for mobile net-
works. Computer Networks, 190:107958.
Sukhov, A. M., Astrakhantseva, M. A., Pervitsky, A. K.,
Boldyrev, S. S., and Bukatov, A. A. (2016). Generat-
ing a function for network delay. J. High Speed Net-
works, 22:321–333.
Veeraraghavan, K., Chen, P. M., Flinn, J., and
Narayanasamy, S. (2011). Detecting and surviving
data races using complementary schedules. In Pro-
ceedings of the 23rd ACM Symposium on Operating
Systems Principles 2011, pages 369–384.
Vinarskii, E. (2024). https://github.com/vinevg1996/races-
in-eioa-and-reactive-systems. https://github.com/
vinevg1996/Races-in-EIOA-and-reactive-systems.
Vinarskii, E. M., Kushik, N., Yevtushenko, N., L
´
opez, J.,
and Zeghlache, D. (2023). Timed transition tour for
race detection in distributed systems. In Proceedings
of the 18th International Conference on Evaluation of
Novel Approaches to Software Engineering, ENASE
2023, pages 613–620.
Vinarskii, E. M., L
´
opez, J., Kushik, N., Yevtushenko, N.,
and Zeghlache, D. (2019). A model checking based
approach for detecting SDN races. In Testing Soft-
ware and Systems - 31st IFIP WG 6.1 International
Conference, pages 194–211.
ENASE 2024 - 19th International Conference on Evaluation of Novel Approaches to Software Engineering
734