Generalized Automatic Item Generation for Graphical Conceptual

Modeling Tasks

Paul Christ

1 a

, Torsten Munkelt

and Jörg M. Haake

1 b

Department of Cooperative Systems, Distance University Hagen, Universitätsstraße 11, Hagen, Germany

Faculty of Informatics and Mathematics, HTWD, Dresden, Germany

Keywords:

AIG, Automatic Item Generation, Conceptual Modeling, Competency-Based Learning, E-Assessment,

E-Learning, Bloom’s Taxonomy, Business Process Modeling, Graph-Rewriting, Generative AI,

Large Language Models.

Abstract:

Graphical conceptual modeling is an important competency in various disciplines. Its mastery requires self-

practice with tasks that address different cognitive processing dimensions. A large number of such tasks is

needed to accommodate a large number of students with varying needs, and cannot be produced manually.

Current automatic production methods such as Automatic Item Generation (AIG) either lack scalability or fail

to address higher cognitive processing dimensions. To solve these problems, a generalized AIG process is

proposed. Step 1 requires the creation of an item speciﬁcation, which consists of a task instruction, a learner

input, an expected learner output and a response format. Step 2 requires the deﬁnition of a generator for the

controlled generation of items via a conﬁgurable generator composition. A case study shows that the approach

can be used to generate graphical conceptual modeling tasks addressing the cognitive process dimensions

Analyze and Create.

1 INTRODUCTION

Conceptual modeling is the process of abstracting a

model from a real or proposed system (Robinson,

2008). The outcome of conceptual modeling is an ab-

straction or graphical representation of the modelled

system in the chosen modeling language (He et al.,

2007; Delcambre et al., 2018; Guarino et al., 2019).

The modality of the conceptual model depends on the

type of modeling language, e.g. textual or graphical.

As laid out by Striewe et al., conceptual modeling

is a core component of the curriculum of Business In-

formatics and neighbouring disciplines (Striewe et al.,

2021) (Soyka et al., 2022). Multiple organizations,

such as the Association for Computing Machinery

(ACM) and the Gesellschaft für Informatik (GI) rec-

ommend including conceptual modeling into the cur-

ricula of various IT-disciplines (ACM, 2021; GI,

2017).

In IT-related disciplines, graphical conceptual

modeling may be applied to construct diagrams for

designing databases and software or business pro-

https://orcid.org/0000-0002-6096-7403

https://orcid.org/0000-0001-9720-3100

cess models to abstract a planned or existing area

of an organization. Beyond that, conceptual model-

ing is broadly applicable in different disciplines, e.g.

mathematical modeling (Dunn and Marshman, 2019),

molecular modeling (Taly et al., 2019) or modeling

schemata in music theory (Neuwirth et al., 2023).

To teach, learn and assess graphical conceptual

modeling, summative and formative assessments are

required (Meike and Constantin, 2023). An assess-

ment is a set of one or many assessment-items (items).

An item refers to a statement, question, exercise,

or task for which the test taker is to select or con-

struct a response, or perform a task (American Ed-

ucational Research Association and American Psy-

chological Association, 2014). Assessments may ad-

dress different cognitive processing dimensions. To

model these cognitive processing dimensions, we uti-

lize the revised Bloom’s taxonomy (Anderson et al.,

2001), due to its popularity for structuring modeling

tasks (Soyka et al., 2022; Bork, 2019; Bogdanova and

Snoeck, 2017).

Striewe et al. further argue, that there is

a large unmet demand for a shift from lecturer-

centered to student-centered teaching. This shift

requires strengthening problem-solving and self-

Christ, P., Munkelt, T. and Haake, J.

Generalized Automatic Item Generation for Graphical Conceptual Modeling Tasks.

DOI: 10.5220/0012753200003693

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 16th International Conference on Computer Supported Education (CSEDU 2024) - Volume 1, pages 807-818

ISBN: 978-989-758-697-2; ISSN: 2184-5026

807

learning skills of students. This, in turn, requires the

creation of competence-oriented assessments, partic-

ularly assessments that address higher cognitive di-

mensions. Using traditional multiple choice (MC)

questions or other closed task formats make it chal-

lenging to address these higher cognitive dimensions.

Conceptual modeling is especially affected by this

limitation, as it is the practical application of model-

ing methods and tools that is of importance (Striewe

et al., 2021).

The construction of conceptual modeling tasks is

demanding. This is especially true for conceptual

modeling tasks that address higher cognitive process-

ing dimensions, as they require a meaningful problem

description, instructions and at least a sample solution

model. Thus, only a small amount of tasks is available

to students, which limits their opportunity to exercise

their abilities and therefore hinders their learning pro-

cess.

To solve the problem of insufﬁcient amounts of

conceptual modeling tasks, addressing higher cog-

nitive processing dimensions, we identiﬁed 3 ap-

proaches:

1. Traditional item development (Rudolph et al.,

2019), which represents the manual effort of cre-

ating graphical conceptual modeling tasks. This

approach does not scale to a large amount of tasks

to be created, since lecturing staff is a limited re-

source.

2. Automatic item generation (AIG) (Gierl et al.,

2021), which utilizes human-made task-templates

and computer technology, to create many tasks ac-

cording to that template. This approach generally

only applies to closed task formats, that make it

challenging to address higher cognitive process-

ing dimensions.

3. Domain-speciﬁc methods (Schüler and Alpers,

2024; Yirik et al., 2021; Ghosh and Bashar, 2018),

which commonly utilize transformation rules, to

transform a (often textual) representation into a

valid model of a formal modeling language. This

approach requires lecturing staff to provide sepa-

rate input for each task to be generated, and thus

does not scale.

Because all three approaches have serious disad-

vantages, it is an open research question how to pro-

vide a sufﬁcient amount of graphical conceptual mod-

eling tasks for each cognitive processing dimension of

the revised Bloom’s taxonomy.

Chapter 2 provides a deeper analysis of the re-

search question and deﬁnes requirements for potential

solutions. Chapter 3 gives an overview of the current

state of the art and its shortcomings with respect to

the deﬁned requirements. Chapter 4 presents the pro-

posed solution to the deﬁned question. Chapter 5 val-

idates the proposed solution by utilizing a case study

to show that the requirements are met. Chapter 6 pro-

vides a summary of the paper and an overview of open

questions and future research.

2 ANALYSIS

To answer how to provide a sufﬁcient amount of

graphical conceptual modeling tasks for each cogni-

tive processing dimension, one must ﬁrst deﬁne 1.)

what graphical conceptual modeling tasks are, 2.)

how a speciﬁc graphical conceptual modeling task ad-

dresses a speciﬁc cognitive dimension and 3.) what a

sufﬁcient amount of each graphical conceptual mod-

eling task is.

1.) and 2.) are best answered in conjunction, by

deﬁning a mapping of cognitive process dimensions

to potential types of graphical conceptual modeling

tasks. We utilize the work of (Bork, 2019), which

maps the cognitive processing dimensions to poten-

tial conceptual modeling tasks, and specify a concrete

conceptual modeling task with an item speciﬁcation

for each dimension. An item speciﬁcation, akin to

Gierl’s deﬁnition of a cognitive model, refers to the

concepts, assumptions and logic to create and the as-

sumptions about how examinees are expected to solve

a content-speciﬁc task (Gierl et al., 2021).

Table 1 shows the mapping of cognitive process

dimension to each item speciﬁcation. The cognitive

process dimensions refer to the 6 dimensions of the

revised Bloom’s taxonomy. A placeholder is signi-

ﬁed by angle brackets. An item speciﬁcation holds

the information required to perform the task, that is

described by it. An item speciﬁcation consists of an

instruction template, an input placeholder, an output

placeholder and a response format. The instruction

template speciﬁes what task the learner is expected

to perform, the input placeholder contains the con-

tent that is required to perform the task, the output

placeholder contains an expected solution, and the re-

sponse format governs how the learner’s response is

retrieved.

The placeholders must be ﬁlled with a concrete in-

stance of the placeholder type. This can be done man-

ually or via an automated production process. Once

the placeholders are ﬁlled, an item-instance is created.

The ﬁrst row in Table 1 shows an example item

speciﬁcation of a task that is speciﬁed for the dimen-

sion Remember. In this case, it is a selected-response

task, e.g. MC. The instruction guides the learner to

select the correct name of an element of a modeling

AIG 2024 - Special Session on Automatic Item Generation

808

Table 1: Cognitive Process Dimension Mapped to Item Speciﬁcation of Conceptual Modeling Tasks.

Dimension Item Speciﬁcation

Instruction

Template

Input

Placeholder

Output

Placeholder

Response

Format

Remember Select the correct name

of the shown syntactical

element in the notation

of 〈MODELING LAN-

GUAGE〉.

〈SYNTACTICAL

ELEMENT〉

〈SOLUTION〉

〈DISTRACTOR

〉

Selected-

Response

Understand Select the correct semantic

concept of the shown con-

struct.

〈MODEL CON-

STRUCT〉

〈SOLUTION〉

〈DISTRACTOR

〉

Selected-

Response

Apply Use 〈SET OF OPER-

ATIONS〉 to transform

〈PROCESS PART〉 into

〈TRANSFORMED PRO-

CESS PART〉.

〈MODEL〉 〈TRANSFORMED

MODEL〉

Constructed-

Response

Analyze Find and mark syntactical

errors in the shown model.

〈ERRONEOUS

MODEL〉

〈MARKED

MODEL〉

Constructed-

Response

Evaluate Find and mark the inconsis-

tencies between the textual

and graphical model repre-

sentation.

〈MODEL WITH

LABELS〉 〈TEX-

TUAL MODEL

DESCRIPTION〉

〈MARKED

MODEL〉

〈MARKED MODEL

DESCRIPTION〉

Constructed-

Response

Create Create a model from the

given textual description in

the notation of 〈MODEL-

ING LANGUAGE〉.

〈TEXTUAL

MODEL DE-

SCRIPTION〉

〈MODEL WITH

LABELS〉

Constructed-

Response

language, that has yet to be speciﬁed. The learner is

presented an input, more precisely a graphical syntac-

tical element of a modeling language. The learner is

then expected to select one of the presented options,

of which one is the solution and the remainder being

distractors.

Other tasks include the application of model trans-

formations on a presented model, ﬁnding and marking

errors in a erroneous model, ﬁnding inconsistencies

between a textual and a graphical representation of a

model and the manual creation of a model, given a

textual description of the model.

The generation of the aforementioned conceptual

modeling tasks require the generation of viable in-

stances of the speciﬁed input and output placeholder,

that ﬁt the instruction (Requirement R1).

To answer 3.), what determines the sufﬁcient total

number of items A, we propose the following simpli-

ﬁed model:

Let I

be the number of items for a cognitive pro-

cessing dimension c, and let I

∑

|C|

c=1

be the num-

ber of items for all cognitive processing dimensions

C, that we assume necessary for students exercising

and the assessment of students. Let o

be the number

of learning objectives of a module m. The total num-

ber O

of learning objectives for all modules M is

then calculated as O

∑

|M|

m=1

. Let T be the num-

ber of teachers. As teachers may prefer the formu-

lation and style of the items to be conforming to the

rest of their learning material, they each might need

separate items. Thus, we arrive at

A = T ∗ O

∗ I

(1)

for computing the number of items needed. I

may be broken down further as the sum of the num-

ber of items required in a set S of different scenarios

∑

|C|

c=1

∑

|S|

s=1

. Different scenarios may include

(I) the number of items required in the coursework

, (II) the number of items a learner requires for

individual practice I

or (III) the number of items

for exams I

. In the case of individual practice, it

may be required to provide a number of personal-

ized items for a number of learners L, resulting in

∑

l=1

In the case of exams, it may be required

to provide a.) new items for every exam in order to

avoid memorization and b.) different items per exam-

inee in order to minimize cheating, which introduces

the factor of the number of examinees X and breaks

down further into the sum of required items per

exam I

∑

e=1

∗ X.

Generalized Automatic Item Generation for Graphical Conceptual Modeling Tasks

809

In the example of a university course teaching

business process modeling, which deals with 2 dis-

tinct conceptual modeling languages, no item person-

alization, a cohort of 50 students, 2 potential exam

offerings with an initial failure quote of 20% and a

respective participation quote of 100%, we arrive at

T = 1, M = 1, O = 2, I

= 3, I

= 10 and I

∑

|C|=3

c=1

2 ∗ 50 + 2 ∗ 10 = 460, yielding a required num-

ber of items A = 1 ∗ 2 ∗ 460 = 920.

The ATOMIC-formula gives the reader a way to

determine an appropriate number for their use case.

To potentially cover all scenarios described above,

a production method for items must address each fac-

tor of the ATOMIC-formula individually and in a

scalable manner (Requirement R2).

3 STATE OF THE ART

3.1 Traditional Item Development

Traditional item development relies on a method in

which a subject matter expert (SME) creates items in-

dividually (Gierl et al., 2021). Under the best condi-

tion, traditional item development is an iterative pro-

cess where highly trained groups of SMEs use their

experience and expertise to produce new items. Then,

after these new items are created, they are edited,

reviewed, and revised by another group of highly

trained SMEs until they meet the appropriate standard

of quality (Haladyna, 2015).

This approach has two major limitations: 1.) Item

development is time-consuming and expensive be-

cause it relies on the item as the unit of analysis (Stark

et al., 2006). Each item in the process is unique and

therefore, each item must be individually written, and

ideally, edited, reviewed, and revised (Gierl et al.,

2021). 2.) The traditional approach to item develop-

ment is challenging to scale efﬁciently and econom-

ically. When one item is required, one item is writ-

ten by the SME because each item is unique. Hence,

large numbers of SMEs who can write unique items

are needed to scale the process. (Gierl et al., 2021).

As a result, traditional item development does not

meet requirement R2 and can not be considered a fea-

sible method to generate a sufﬁcient amount of con-

ceptual modeling tasks.

3.2 Automatic Item Generation

AIG is the process of using models to generate items

using computer technology (Gierl et al., 2021). Gierl

et al. describe AIG as the three-step process for gener-

ating items depicted in ﬁgure 1 (Gierl and Lai, 2016).

Figure 1: Three-step process of AIG (Gierl et al., 2021).

In step 1, the content for item generation is created

in the form of a cognitive model which highlights the

knowledge, skills and problem-solving processes re-

quired to solve the generated task (Gierl et al., 2012).

In step 2, an item model is created, that speciﬁes

which parts and which content in the task can be ma-

nipulated to create new items (Laduca et al., 1986).

The parts include the stem, the options and the aux-

iliary information to generate selected-response items

(e.g. MC) (Gierl et al., 2021). In step 3, all possible

combinations of the created content are placed into

the item model, for which different computer-based

assembly systems are used (Kucharski et al., 2023;

Gierl et al., 2008).

One of the main limitations of existing AIG-

methods is the simplicity of generated questions, as

most generated questions use closed response-formats

(Kurdi et al., 2020; Falcão et al., 2023), which make it

challenging to target higher cognitive dimensions (be-

yond remember and understand) (Kurdi et al., 2020).

While closed target formats may address the higher

processing dimensions, apply and analyze, even pro-

ponents of these formats agree, that they can’t address

the highest processing dimensions evaluate and cre-

ate (Haataja et al., 2023).

Thus, current AIG-methods fail to meet require-

ment R1 and therefore are not a feasible method to

produce conceptual modeling tasks that address the

highest cognitive processing dimensions.

3.3 Subject Speciﬁc Methods

To overcome the limitations of traditional item de-

velopment and AIG-methods, we consider the utiliza-

tion of subject-speciﬁc construction methods for pro-

ducing the required inputs and outputs for conceptual

modeling tasks described in section 2. Different sub-

ject matter domains provide methods for transform-

ing a potentially fuzzy model representation, such

as textual descriptions in natural language into po-

tentially many valid representations in the respective

formal modeling language. Examples include the

transformation of business process descriptions into

a graphical modeling language (Schüler and Alpers,

2024), the generation of constitutional isomer chem-

ical spaces from molecular structural formula (Yirik

et al., 2021) or the generation of entity-relationship

diagrams from a set of textual requirements in natural

language. (Ghosh and Bashar, 2018).

Two major limitation of utilizing subject-speciﬁc

AIG 2024 - Special Session on Automatic Item Generation

810

production methods are 1.) their lack of generaliza-

tion across subject matter domains and 2.) the need

for lecturing staff to provide separate input, in order

to create item variants.

Thus, subject-speciﬁc methods fail to meet re-

quirement R2 and are therefore not a feasible method

to produce sufﬁcient amounts of conceptual modeling

tasks across different subject matter domains.

3.4 Delta to Existing Methods for

Generating Graphical Conceptual

Modeling Tasks

Traditional item development and subject-speciﬁc

methods fulﬁll requirement R1 but fail to address re-

quirement R2. Conversely, current AIG-methods ful-

ﬁll requirement R2 but fail to address requirement R1

fully.

Thus, a solution to the posed research question of

how to generate a sufﬁcient amount of graphical con-

ceptual modeling tasks, for each cognitive dimension

of the revised Bloom’s taxonomy, must fulﬁll the re-

quirements R1 and R2 simultaneously.

4 APPROACH

Our proposed solution for the AIG for graphical con-

ceptual modeling tasks consists of a two-step process.

The ﬁrst requires the item-developer to create an item

speciﬁcation. As shown in table 1, an item speciﬁ-

cation consists of an instruction template, an input

placeholder, an output placeholder and a response for-

mat. The item speciﬁcation speciﬁes what task the

learner is expected to perform via the instruction tem-

plate, what content is required to perform the task via

the input placeholder, what the expected solution is

via the output placeholder, and how the learner’s re-

sponse is selected via the response format.

The second step requires the item-developer to

specify a generator, that generates instances for the

input and output placeholder of the item speciﬁcation

speciﬁed in the ﬁrst step. A generator is a function

G(I) = O, that takes an input I and produces an output

O. A generator may consist of multiple other genera-

tors.

The proposed two-step process is a generalization

of AIG as described in subsection 3.2, which will

from here on be called generalized AIG (gAIG). This

generalization uses AIG for generating items address-

ing the ﬁrst two cognitive dimensions (see item spec-

iﬁcation shown in table 2).

To generate a generic single choice question, a

Table 2: Item speciﬁcation for a generic single choice ques-

tion.

Instruction

Template

Select the correct answer for

the given statement.

Input

Placeholder

〈STEM〉〈OPTIONS〉

Output

Placeholder

〈CORRECT OPTION〉

Response

Format

Selected Response

generator must generate a 〈STEM〉 that formulates

a question, corresponding 〈OPTIONS〉 which consist

of multiple distractors and a 〈CORRECT OPTION〉.

As described by Gierl et al., AIG generates such

〈STEM〉, which contains the content or question the

examinee is required to answer and the 〈OPTIONS〉,

a set of alternative answers with one correct option

and one or more incorrect options (Gierl et al., 2021).

Thus, AIG can be applied as a generator in the second

step of the gAIG-process, that produces the necessary

input and output placeholders of the item speciﬁcation

described in table 2.

But, as already discussed in section 2, AIG is

not able to produce the speciﬁed graphical conceptual

modeling tasks, that address cognitive levels above

the cognitive processing dimension of Apply, as they

require different input and output placeholders. As a

consequence, different generators are needed.

4.1 Generators for Graphical

Conceptual Modeling Tasks

Addressing Higher Cognitive

Dimensions

In the following we introduce 3 generators, that are

able to produce instances of the required input and

output placeholders, using the following 3 technolo-

gies: 1.) a graph-rewriting system (GRS), 2.) a large

language model (LLM) and 3.) a text-template engine

(TTE).

These technologies were chosen because: 1.) they

can produce the required output modalities, 2.) they

are subject matter domain independent, and 3.) their

generation behavior is conﬁgurable.

Figure 2 depicts a simpliﬁed model of the

generator-elements. The abstract class GENERA-

TORELEMENT has a generate-method which takes a

generic input I and produces a generic output O. The

generate-method of the GRS receives a GRSINPUT

and produces a GRAPH as output, which consists of

an array of nodes, an array of edges and an array of

subgraphs. The GRSINPUT consists of:

Generalized Automatic Item Generation for Graphical Conceptual Modeling Tasks

811

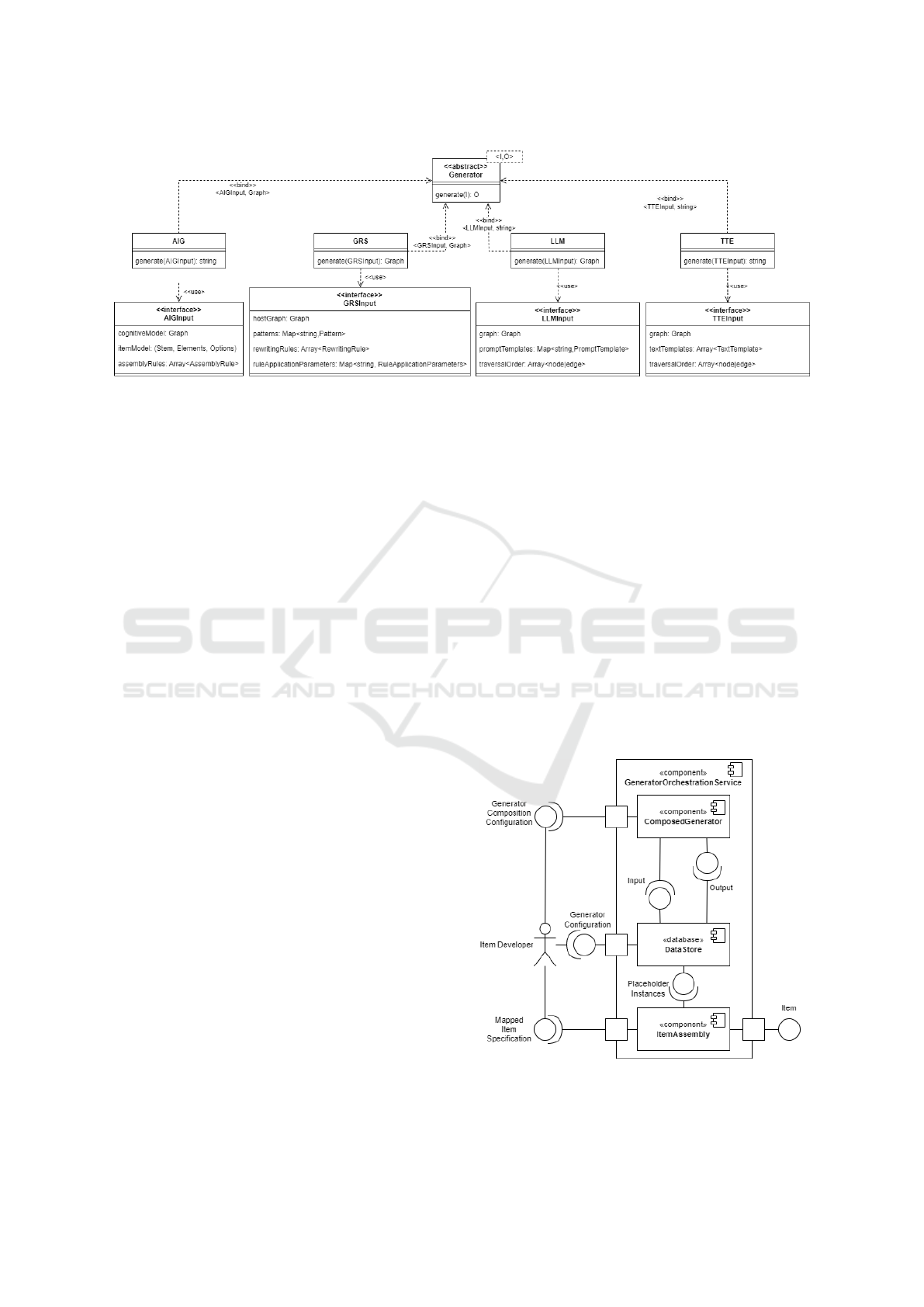
Figure 2: Simpliﬁed class diagram of generators.

• A host graph g, on which all rewriting operations

are performed,

• a set of patterns, where each element consists of

a name and a pattern. Upon calling, a pattern cre-

ates a randomized pattern-instance that conforms

to the pattern-structure, a set of input parameters

and potential constraints.

• An array of rewriting rules, and each rewriting

rule r(g, L, R) contains a pattern graph L and a re-

placement graph R, and an instance of L is to be

replaced with an instance of R in g. A rule is only

applied if an instance of L can be found in g.

• A set of parameters, that guide the application of

the rewriting rules:

– how often each rule must be applied,

– an execution order of the rules, and

– ﬁlter options for the selection of potential in-

stances of L found in g, from which a random

instance is then selected for rewriting.

The generate-method of the LLM receives a

LLMINPUT and produces a GRAPH, where each

node, edge and subgraph has been labeled. The

LLMINPUT consists of:

• an input graph, that is to be labelled,

• a set of prompt-templates, that are associated to

patterns and are used to elicit the generation of

labels, and

• an order in which to traverse the elements of the

input graph.

The generate-method of the TTE receives a

TTEINPUT and produces a string. The TTEINPUT

consists of:

• an input graph, that may contain labels and is to

be transformed into text,

• a set of text-templates, that the TTE uses to trans-

form the associated pattern instances and the con-

tained subgraph-, node-, and edge-labels into text,

and

• an order in which to traverse the elements of the

input graph.

In order to generate instances of some of the re-

quired input and output placeholder types, generators

need to be composed into larger generators. E.g. gen-

erating labels for a graph, requires the graph to be

generated ﬁrst. To assemble the full item according to

the item speciﬁcation, the generated outputs must be

mapped to the placeholders of the item speciﬁcation.

These additional requirements are fulﬁlled by another

component called generator-orchestration service.

4.2 Generator-Orchestration Service

Figure 3: Component diagram of the generator-

orchestration service.

AIG 2024 - Special Session on Automatic Item Generation

812

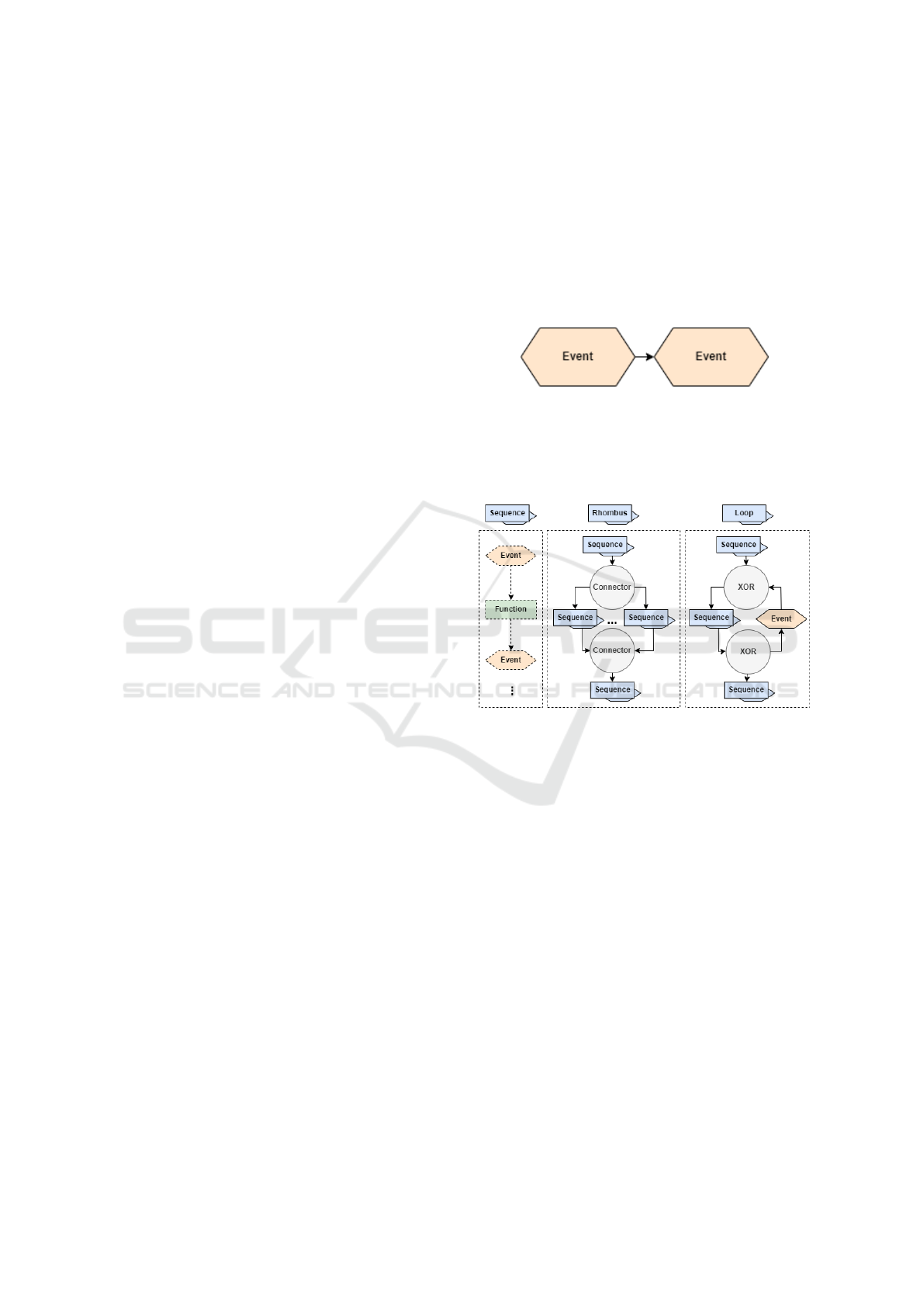
Figure 3 gives an overview of the generator-

orchestration service. In order to compose genera-

tors, the nested generators must follow an execution

order, the associated inputs have to be speciﬁed, and

the intermediate outputs need to be persisted. The ex-

ecution order and the associated inputs of generators

are referred to as generator composition conﬁguration

and must be provided by the item developer. Interme-

diate outputs of nested generators and composed gen-

erators are persisted in a store for future reference.

The input for a nested or composed generator can be

provided by the item developer or previously gener-

ated outputs of other generators. To assemble the

item, the item developer must provide an item speciﬁ-

cation and map the therein contained placeholders to

the data in the data store.

The modularity of the approach allows for reusing

nested and composed generators. Furthermore, it

enables the extensibility of the approach by adding

more types of generators. This increases the poten-

tial for generalization across different subject matters

and multiple task-types beyond graphical conceptual

modeling tasks. Manual efforts for analyzing the item

quality can be drastically reduced since the quality

of the process of the item generation must only be

checked once, as was already pointed out by Stark et

al. (Stark et al., 2006), instead of checking the quality

of each generated item.

5 CASE STUDY

To verify that the solution proposed in section 4 meets

both requirements deﬁned in section 2, we present

a case study that shows the production of multiple

tasks for the subject matter domain of Business Pro-

cess Modeling. Due to its simple and concise syntax,

we utilize Event-Driven Process Chains (EPC) (Keller

et al., 1992) as a process modeling language.

It is crucial to understand the notation of EPCs to

create generators that yield syntactically valid EPCs.

The following provides a short overview of the basic

notation of EPCs that is required to follow along.

The EPC notation consists of the following sym-

bols: events, functions, process route signs, logical

connectors (AND, OR, XOR) and connection arrows.

Roles, responsibilities and data are omitted for the

sake of simplicity.

Each process starts and ends with an event. Events

and functions must alternate. Symbols must be con-

nected by directed lines. Splitting connectors must

have one incoming and at least two outgoing arrows.

Conversely, merging connectors must have at least

two incoming and one outgoing arrow. Splitting OR-

and XOR-operators must not follow an event.

5.1 Speciﬁcation of a GRS to Generate

EPCs

To generate graphical conceptual modeling tasks, we

utilize an instance of the GRS-generator as a founda-

tional step for all tasks. In the following, we specify

the required inputs for the GRS-generator-instance.

Figure 4: Host graph for the production of EPCs.

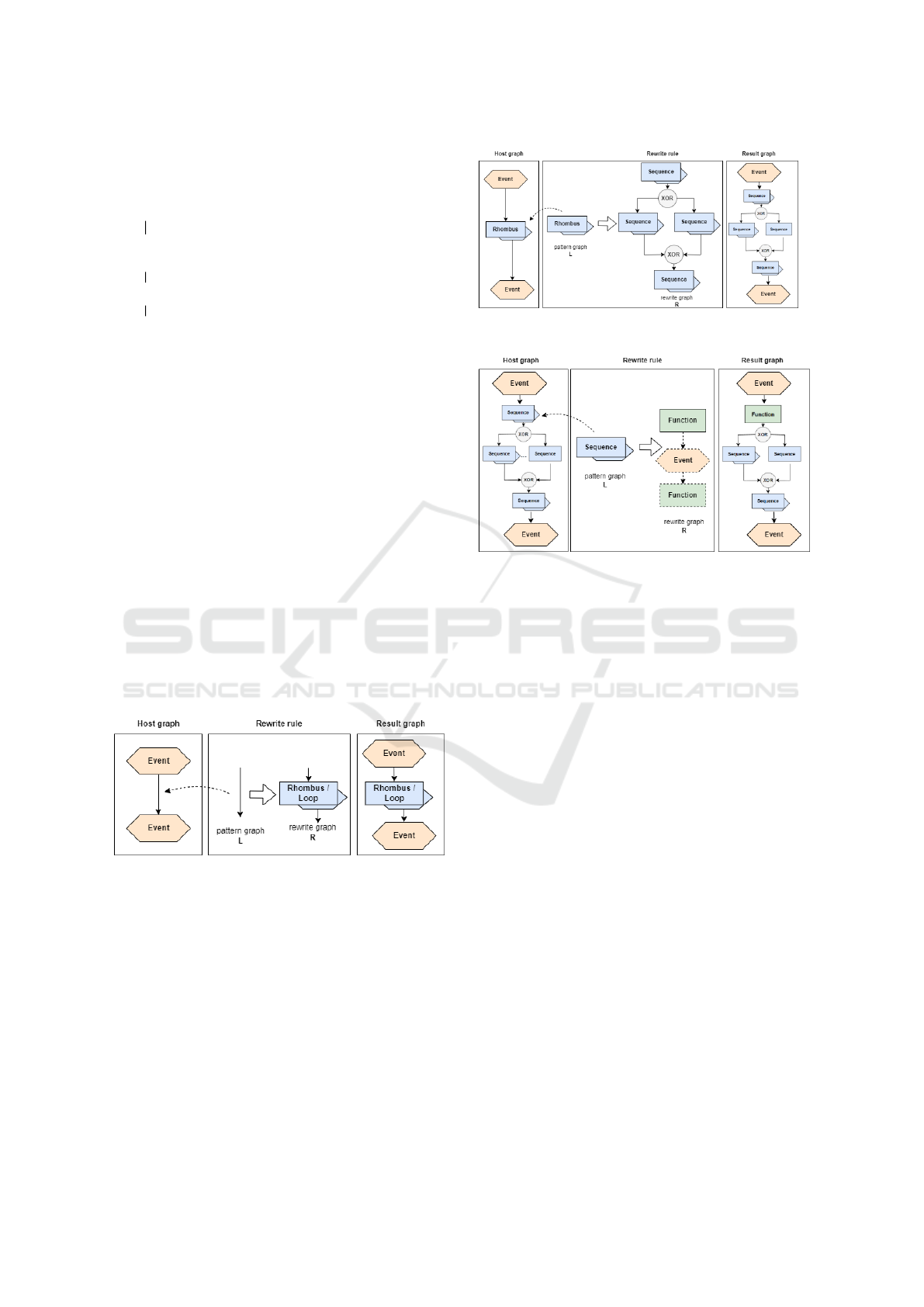
Given the above notation, we chose the host graph

depicted in ﬁgure 4, which consists of two joined

events. Note, that the host graph is not yet compli-

ant with the notation of EPCs.

Figure 5: Three possible patterns to create EPCs.

Then, we formulate the patterns depicted in ﬁgure

5. Each pattern is depicted as a process route sign.

The sequence-pattern includes a variable amount of

events and functions, that are alternating and con-

nected by arrows. Its construction function can be

described as P

, E

, N), where E

is a function to

determine the required element-type to start the se-

quence with, E

is a function to determine the re-

quired element-type to end the sequence with and N

is the number of nodes to generate between the start-

ing and ending element of the sequence. E

is de-

scribed in algorithm 1 and receives the parent node of

where the pattern-instance is to be inserted and tra-

verses the chain of parent nodes, until it discovers an

element of either type "Event" or "Function" and then

returns "Function" or "Event". E

functions similarly,

but additionally receives the result of E

and traverses

the chain of child elements instead. The parameter N

speciﬁes the overall length of the EPC to be gener-

ated.

Generalized Automatic Item Generation for Graphical Conceptual Modeling Tasks

813

Data: E: Node

Result: T: string

while E.type ̸= "Event" or E.type ̸=

"Function" do

E = E.parent;

end

if E.type = "Event" then

return "Function"

else

return "Event"

end

Algorithm 1: Function E

, that ﬁnds the element-type of

the parent-element.

The rhombus-pattern includes a variable num-

ber of branches between the connectors and a vari-

able connector-type. Its construction function can

be described as P

(N, T ), where N is the number of

branches to be created and T is the connector-type.

The loop-pattern consists of one forward-branch

and one backward-branch with exactly one event be-

tween the connectors, and the connector-type is ﬁxed

to a "XOR"-type.

With those patterns, we formulate a set of

rewriting-rules to be performed on the host graph. A

rule consists of the pattern graph L and the replace-

ment graph R. An instance of L in the host graph is

randomly chosen from a list of found matches. An in-

stance of L is replaced with an instance of L in the host

graph g. The rewrite graph is the resulting graph, af-

ter the rewrite rule has been applied to the host graph,

and the rewrite graph becomes the new host graph.

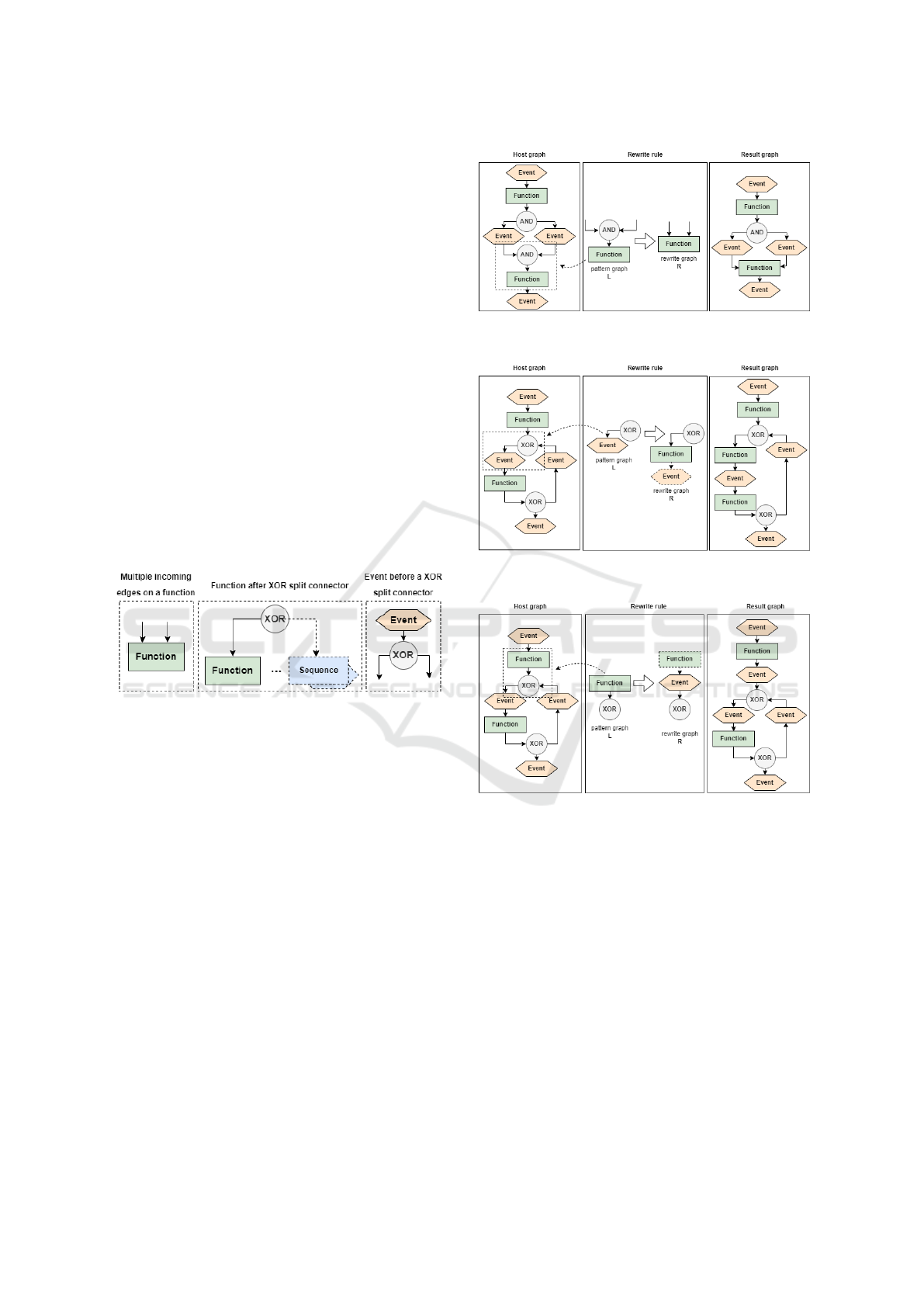
Figure 6: Rewrite rule 1.

Rule 1, depicted in ﬁgure 6, shows how complex

patterns are introduced into the host graph. The rule

selects a pattern graph in the shape of single connec-

tion arrow and replaces it with either a rhombus- or

loop-pattern and an incoming and an outgoing edge.

This rule assumes a random selection of the rhombus-

xor the loop-pattern for simpliﬁcation purposes.

Rule 2, depicted in ﬁgure 7, shows how complex

patterns are instantiated. In the given example, a ran-

domly selected rhombus-pattern is replaced by an in-

stance of a rhombus-pattern. For simpliﬁcation pur-

poses it is assumed, that a random pattern-instance is

Figure 7: Rewrite rule 2.

Figure 8: Rewrite rule 3.

instantiated.

Rule 3, depicted in ﬁgure 8, shows how sequences

are instantiated. In the given example, a randomly se-

lected sequence-pattern is replaced by an instance of a

sequence-pattern. The sequence with the least amount

of nodes is determined by the function E

and E

de-

scribed in algorithm 1 when calling the construction

function P. For simpliﬁcation purposes, it is assumed

that the number of additional nodes N is 0.

Applying the patterns and rules in a GRS ran-

domly would yield a large amount of vastly dis-

tinct EPCs. To achieve a more controlled generation,

guidance-parameters may be utilized, such as the ex-

act number a rule must be applied, an execution order

of the rules and more restrictive ﬁlter operations for

the pattern graph selection, such as the selection of

nested pattern graphs.

It is important to note, that this is merely one pos-

sible formulation of a GRSInput to yield syntactically

valid EPCs and that there exist many more. Moreover,

the presented patterns and rules do not cover the entire

space of possible and syntactically correct EPC.

In the following, we demonstrate the proposed

gAIG process. As discussed in section 2, AIG is able

to generate tasks for the cognitive processing dimen-

sions Remember and Understand. As described in

section 4, AIG is a generator that can be directly ap-

plied in our proposed two-step process. As the ap-

proach for AIG has been described many times by

AIG 2024 - Special Session on Automatic Item Generation

814

prior works, we only showcase the solution approach

for newly introduced generators. We do so with the

example of the task types associated with the cogni-

tive process dimensions Analyze and Create.

5.2 Generation of Graphical

Conceptual Modeling Tasks for

EPCs that Address the Cognitive

Process Dimension Analyze

Mapping the task for the cognitive process dimension

of Analyze described in table 1 to the concrete model-

ing language of EPC requires an unlabeled EPC that

includes identiﬁable error patterns.

Thus, the required generator is a GRS, as de-

scribed in section 5.1 above, with the addition of rules

that introduce error patterns. The addition of error

patterns may be performed in a new GRS or after the

rewriting rules to construct a valid EPC have been ap-

plied. For the sake of simplicity, the following ex-

ample assumes the host graph to be an already valid

EPC.

Figure 9: Common error patterns in modeled EPCs amongst

learners.

We chose three commonly occurring syntactical

errors made by students (Szcz˛e

sniak, 2011), depicted

in ﬁgure 9, but arbitrarily many error patterns can

be introduced. The error-patterns shown include 1.)

multiple incoming edges to a function, 2.) the use of

a function or a process route sign (as the hidden sub-

process has to start with a function) after a XOR split

connector and 3.) the use of an event before a XOR

split connector.

To introduce these patterns into the graph, another

set of rewriting rules is required.

Error rule 1, depicted in ﬁgure 10, shows how er-

ror 1.) is introduced into a valid EPC. As this error

pattern has no variability and thus can not add unex-

pected errors elsewhere, no additional conditions are

needed. The construction function of this pattern is

thus simply its identity function.

Error rule 2, depicted in ﬁgure 11, shows how er-

ror 2.) is introduced into a valid EPC. To avoid fur-

ther unintended errors, the construction function of

this error pattern needs to ensure that the following se-

Figure 10: Error rule 1.

Figure 11: Error rule 2.

Figure 12: Error rule 3.

quences remain syntactically correct. This is achieved

by utilizing the same function E

, which is used to

ensure the syntactical validity of the EPC when in-

stantiating a sequence-pattern. Thus, the construction

function of this pattern is P

Error rule 3, depicted in ﬁgure 11, shows how er-

ror 3.) is introduced into a valid EPC. Similarly to

error rule 2, the construction function of this error

pattern needs to ensure the syntactical validity out-

side the error pattern. This is achieved by utilizing

the function E

to ensure the validity for the previ-

ous sequences. Thus, the construction function of this

pattern is P

Note, that applying multiple error patterns simul-

taneously requires additional constraints to avoid un-

expected errors. A simple way to avoid unexpected

Generalized Automatic Item Generation for Graphical Conceptual Modeling Tasks

815

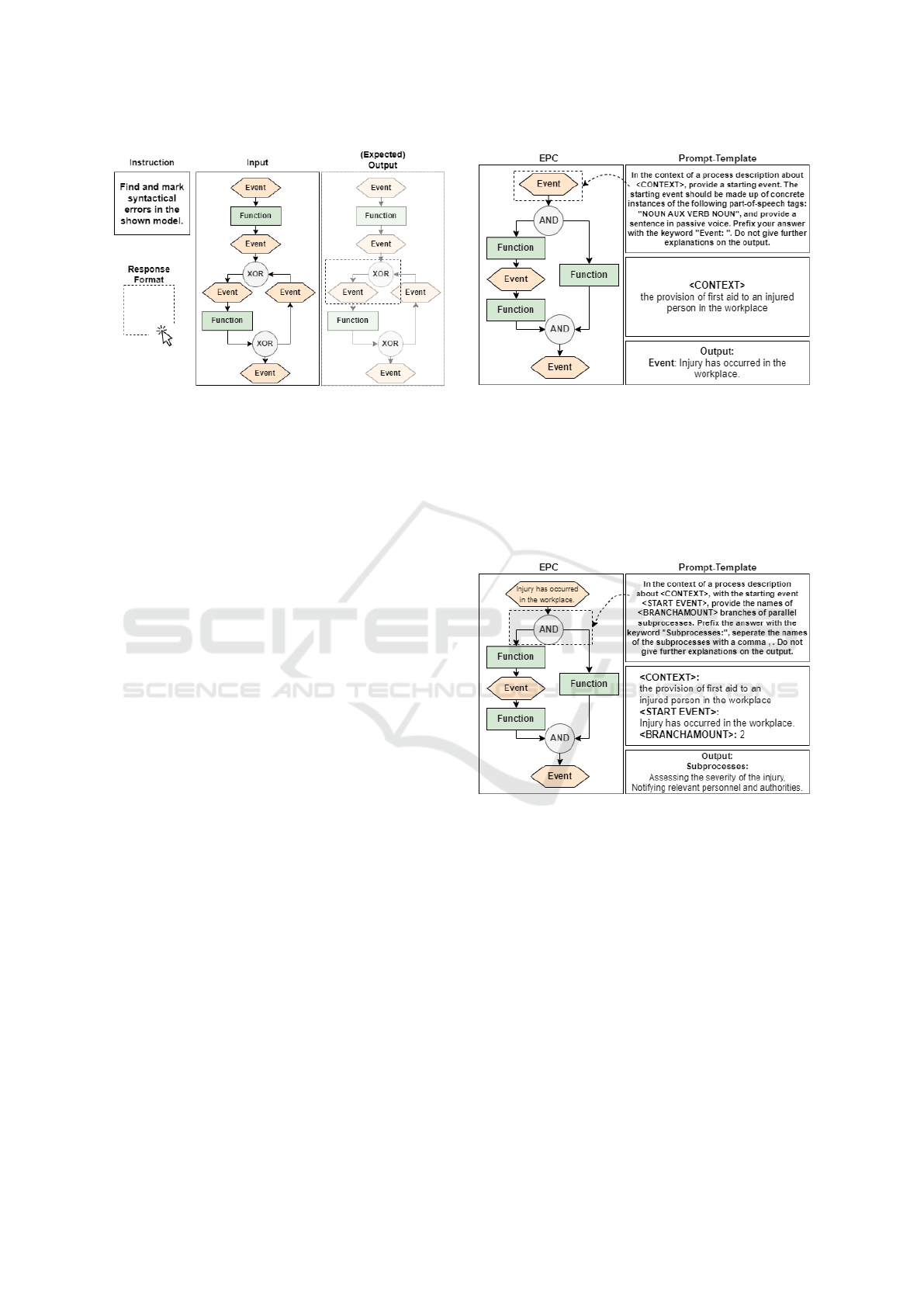
Figure 13: Analyze-task for graphical conceptual modeling.

errors would be to exclude instances of error-patterns

created by previous rewrite rules in the host graph.

To ﬁnally assemble the complete item, the gener-

ated outputs must be associated with the item speciﬁ-

cation. The generated erroneous model is assigned

to the input placeholder 〈ERRONEOUS MODEL〉

and the same generated erroneous model with visu-

alised subgraphs for the error-pattern (i.e. the solu-

tion) is assigned to the output placeholder 〈MARKED

MODEL〉.

5.3 Generation of Graphical

Conceptual Modeling Tasks for

EPCs that Address the Cognitive

Process Dimension Create

Mapping the task for the cognitive process dimension

of Create described in table 1 to the concrete model-

ing language of EPC requires a textual description of

a labeled EPC.

To produce these outputs, a composed generator

is required, which utilizes the GRS, as described in

section 5.1, a LLM and a TTE. For the sake of sim-

plicity and to avoid redundancy, the following exam-

ple assumes an already generated EPC by the GRS as

a starting point.

The LLM then traverses the GRS and applies

prompt-templates to recognized pattern-instances in

the EPC. The starting point is always the ﬁrst event-

node. For the sake of simplicity, a predetermined path

is assumed.

Figure 14 shows the ﬁrst step of the traversal of

an unlabeled EPC and the application of a prompt-

template that was matched to the traversed pattern.

The start-event is mapped to a corresponding prompt-

template. The prompt-template is structured into four

sentences. The ﬁrst sentence contains a placeholder

and sets the context for the LLM. As it is the ﬁrst

Figure 14: Step 1 of labeling an EPC with prompt-templates

and a LLM.

node to be labeled, the context is provided as a start

parameter. The second sentence speciﬁes the shape

of the desired textual output. The third sentence spec-

iﬁes to generate a preﬁx before the output, to make

it machine-readable. The fourth sentence speciﬁes to

limit the generated output, to reduce potential noise.

Figure 15: Step 2 of labeling an EPC with prompt-templates

and a LLM.

Figure 15 shows the second step of the traver-

sal and labeling. In this step, the branching AND-

operator is mapped to a corresponding prompt-

template, which describes the start of parallel subpro-

cesses. The placeholders of the prompt-template are

ﬁlled with the existing context, the generated start-

event and the extracted branch-amount of the cur-

rently viewed subgraph. The generated output names

the two subprocesses for later reference.

Figure 16 shows the third step of the traversal and

labeling. In this step, the prompt-template is mapped

to a sequence that is nested inside a parallel process.

The placeholders are then ﬁlled with the generated

name of the subprocess, the type of subprocess, and

the amount and type of elements in the sequence.

AIG 2024 - Special Session on Automatic Item Generation

816

Figure 16: Step 3 of labeling an EPC with prompt-templates

and a LLM.

To avoid repetition, the remainder of the labeling

process is not explicitly demonstrated. This approach

can be extended to match any graph pattern to a de-

ﬁned prompt-template. The context information is

built-up incrementally by the generator and reused to

generate output that maintains the semantic congruity

of the entire process model.

In a similar fashion to the LLM, the TTE also tra-

verses the graph and applies predeﬁned text-templates

to the mapped patterns. The TTE extracts the la-

bels and additional structural information from the la-

beled graph and ﬁlls the current text-template. Once

the graph is traversed, the individually ﬁlled text-

templates are joined together to form a textual rep-

resentation of the graph.

Figure 17 shows one instance of a fully labeled

model and a textual representation as an output of

the presented composed generator. The output can

be used to ﬁll the placeholders 〈TEXTUAL MODEL

DESCRIPTION〉 and 〈MODEL WITH LABELS〉 for

the task that addresses the dimension Create.

Figure 17: Instances for the input and output placeholders

of the Create-task.

6 CONCLUSION

Graphical conceptual modeling is an important com-

petency in various disciplines, and its mastery re-

quires self-practice and the exposure to tasks that ad-

dress different cognitive processing dimensions. The

production of such tasks in large numbers is challeng-

ing, and current automatic production methods either

lack scalability or fail to address higher cognitive pro-

cessing dimensions.

This paper proposes a generalized AIG approach

and introduces new generation methods for the pro-

duction of items. The proposed solution is able to

produce graphical conceptual modeling tasks in large

numbers that address all cognitive processing dimen-

sions according to the revised Bloom’s taxonomy, and

thus meets requirement R1. The approach is capable

of controlled generation of items with different de-

grees of complexity and difﬁculty on the ﬂy, and thus

meets requirement R2. This may facilitate advance-

ments in computerized adaptive testing. Conversely,

the approach also allows for freezing parameters that

govern the complexity and merely alters surface level

features. This allows for the scalable generation of

fair exams, that provide different items for each ex-

aminee and thus reduces the risk of cheating, without

compromising on consistent difﬁculty levels between

exam instances.

The approach presented makes no assumption re-

garding the presentation and interaction layer for

the task types presented. As the approach targets

mostly task types with open response-formats, such

as constructed-response, future work should consider

unifying technology-enhanced items and AIG. Utiliz-

ing computerized assessment environments allow for

data mining and learning analytics. This may open

the path for future work on how to provide individual

feedback for a solution attempt on an automatically

generated item.

REFERENCES

ACM, A. f. C. M. (2021). Curricula recommendations.

American Educational Research Association and American

Psychological Association (2014). Standards for Edu-

cational and Psychological Testing, National Council

on Measurement in Education (2014). American Ed-

ucational Research Association, Washington, DC.

Anderson, L. W., Krathwohl, D. R., Airasian, P. W., Cruik-

shank, K. A., Richard, M., Pintrich, Raths, J., and Wit-

trock, M. C. (2001). A Taxonomy for Learning, Teach-

ing, and Assessing: A Revision of Bloom’s Taxonomy

of Educational Objectives.

Bogdanova, D. and Snoeck, M. (2017). Domain modelling

Generalized Automatic Item Generation for Graphical Conceptual Modeling Tasks

817

in bloom: Deciphering how we teach it. In The Prac-

tice of Enterprise Modeling.

Bork, D. (2019). A framework for teaching conceptual

modeling and metamodeling based on bloom’s revised

taxonomy of educational objectives. In Hawaii Inter-

national Conference on System Sciences.

Delcambre, L. M. L., Liddle, S. W., Pastor, O., and Storey,

V. C. (2018). A reference framework for concep-

tual modeling. In Conceptual Modeling, pages 27–42,

Cham. Springer International Publishing.

Dunn, P. K. and Marshman, M. F. (2019). Teaching math-

ematical modelling: a framework to support teachers’

choice of resources. Teaching Mathematics and its

Applications: An International Journal of the IMA,

39(2):127–144.

Falcão, F., Pereira, D. M., Gonçalves, N., De Champlain,

A., Costa, P., and Pêgo, J. M. (2023). A suggestive ap-

proach for assessing item quality, usability and valid-

ity of automatic item generation. Advances in Health

Sciences Education, 28(5):1441–1465.

Ghosh, S. and Bashar, R. (2018). Automated generation

of e-r diagram from a given text in natural language.

2018 International Conference on Machine Learning

and Data Engineering (iCMLDE), pages 91–96.

GI, G. f. I. e. (2017). Rahmenempfehlung für die ausbildung

in wirtschaftsinformatik an hochschulen.

Gierl, M., Lai, H., and Turner, S. (2012). Using automatic

item generation to create multiple-choice test items.

Medical education, 46:757–65.

Gierl, M. J. and Lai, H. (2016). A process for reviewing and

evaluating generated test items. Educational Measure-

ment: Issues and Practice, 35(4):6–20.

Gierl, M. J., Lai, H., and Tanygin, V. (2021). Advanced

Methods in Automatic Item Generation.

Gierl, M. J., Zhou, J., and Alves, C. (2008). Developing a

taxonomy of item model types to promote assessment

engineering. The Journal of Technology, Learning and

Assessment, 7(2).

Guarino, N., Guizzardi, G., and Mylopoulos, J. (2019).

On the philosophical foundations of conceptual mod-

els. In European-Japanese Conference on Information

Modelling and Knowledge Bases.

Haataja, E. S., Tolvanen, A., Vilppu, H., Kallio, M., Pel-

tonen, J., and Metsäpelto, R.-L. (2023). Measur-

ing higher-order cognitive skills with multiple choice

questions –potentials and pitfalls of ﬁnnish teacher ed-

ucation entrance. Teaching and Teacher Education,

122:103943.

Haladyna, Mark R. Raymond, T. M. S. L., editor (2015).

Handbook of Test Development. Routledge, New

York, 2 edition.

He, X., Ma, Z., Shao, W., and Li, G. (2007). Metamodel

for the notation of graphical modeling languages. vol-

ume 19, pages 219–224.

Keller, G., Scheer, A.-W., and Nüttgens, M. (1992). Se-

mantische Prozeßmodellierung auf der Grundlage"

Ereignisgesteuerter Prozeßketten (EPK)". Inst. für

Wirtschaftsinformatik.

Kucharski, S., Damnik, G., Stahr, F., and Braun, I. (2023).

Revision of the aig software toolkit: A contribute

to more user friendliness and algorithmic efﬁciency.

pages 410–417.

Kurdi, G., Leo, J., Parsia, B., Sattler, U., and Al-Emari,

S. (2020). A systematic review of automatic ques-

tion generation for educational purposes. Interna-

tional Journal of Artiﬁcial Intelligence in Education,

30(1):121–204.

Laduca, A., Staples, W. I., Templeton, B., and Holz-

man, G. B. (1986). Item modelling procedure for

constructing content-equivalent multiple choice ques-

tions. Medical Education, 20(1):53–56.

Meike, U. and Constantin, H. (2023). Automated as-

sessment of conceptual models in education. Enter-

prise Modelling and Information Systems Architec-

tures (EMISAJ) - International Journal of Conceptual

Modeling, 15, Nr. 2:1–15.

Neuwirth, M., Finkensiep, C., and Rohrmeier, M. (2023).

Musical Schemata: Modelling Challenges and Pattern

Finding (BachBeatles). In Mixing Methods. Practical

Insights from the Humanities in the Digital Age, pages

147–164. De Gruyter.

Robinson, S. (2008). Conceptual modelling for simulation

part i: Deﬁnition and requirements. Journal of the

Operational Research Society, 59:278–290.

Rudolph, M. J., Daugherty, K. K., Ray, M. E., Shuford,

V. P., Lebovitz, L., and DiVall, M. V. (2019). Best

Practices Related to Examination Item Construction

and Post-hoc Review. American Journal of Pharma-

ceutical Education, 83(7):7204.

Schüler, S. and Alpers, S. (2024). State of the Art: Auto-

matic Generation of Business Process Models, pages

161–173.

Soyka, C., Schaper, N., Bender, E., Striewe, M., and Ull-

rich, M. (2022). Toward a competence model for

graphical modeling. ACM Trans. Comput. Educ.,

23(1).

Stark, S., Chernyshenko, O. S., and Drasgow, F. (2006).

Detecting differential item functioning with conﬁrma-

tory factor analysis and item response theory: Toward

a uniﬁed strategy. Journal of Applied Psychology,

91(6):1292–1306. Place: US Publisher: American

Psychological Association.

Striewe, M., Forell, M., Houy, C., Pfeiffer, P., Schiefer,

G., Schüler, S., Soyka, C., Stottrop, T., Ullrich, M.,

Fettke, P., Loos, P., Oberweis, A., and Schaper, N.

(2021). Kompetenzorientiertes e-assessment für die

graﬁsche, konzeptuelle modellierung. HMD Praxis

der Wirtschaftsinformatik, 58(6):1350–1363.

Szcz˛e

sniak, B. (2011). Syntax errors in ﬂat EPC diagrams

made by persons learning the methodology. Zeszyty

Naukowe / Akademia Morska w Szczecinie, nr 27 (99)

z. 2:75–79.

Taly, A., Nitti, F., Baaden, M., and Pasquali, S. (2019).

Molecular modelling as the spark for active learning

approaches for interdisciplinary biology teaching. In-

terface Focus, 9(3):20180065.

Yirik, M. A., Sorokina, M., and Steinbeck, C. (2021). MAY-

GEN: an open-source chemical structure generator for

constitutional isomers based on the orderly generation

principle. Journal of Cheminformatics, 13(1):48.

AIG 2024 - Special Session on Automatic Item Generation

818