Characterization of Consensus Correctness in Ripple (XRP) Networks

Rudrapana K. Shyamasundar

Department of Computer Science and Engineering, Indian Institute of Technology Bombay,

Powai, Mumbai 400076, India

Keywords:

Blockchain, POW, POS, Consensus, Correctness, Forking.

Abstract:

Ripple network or the XRP network is one of the most versatile blockchain platforms used worldwide for

payment systems, healthcare applications etc. The abstract protocol called XRP ledger consensus protocol

(XRPL for short) is a reﬁned version of the initial design referred to as Ripple Protocol consensus algorithm

(RPCA). It is based on the Byzantine fault-tolerant (BFT) agreement protocol but does not use the standard

models or implementation but utilizes collectively-trusted sub-networks within a large network. Consensus

is achieved by maintaining a certain level of “trust” for the sub-networks and a certain minimal connectivity

throughout the network so that the network can be robust in the face of Byzantine failures. For each server

in the XRP network called there is sub-network of validators, referrred to as the Unique Node List (UNL)

consisting of a subset of the servers of the whole network. To be robust against Byzantine failures, XRPL

enforces 80% quorum and a certain overlap of nodes across the UNLs. The overlap was initially speciﬁed to

be 20% and was later enhanced to be greater than 90% to satisfy conditions of safety and liveness. However,

even with such an enhancement, safety and liveness are not satisﬁed. In this paper, we characterize, the XRP

Ledger Consensus protocol (abbreviated XRPL) for consensus correctness using a notion of similarity metric

called rand-index (RI) used for cluster analysis of networks. We establish that XRPL with 80% quorum and

UNLs satisfying 50% RI similarity, is robust against 20% failures, that is, no fraudulent transactions will be

accepted by the network. Further, the network satisﬁes consensus correctness if the UNLs of the network are

more than 50% RI similar that would imply at least 80% quorum across all the UNLs.

1 INTRODUCTION

The XRP network is a blockchain-based distributed

payment system that enables users to transfer funds

seamlessly around the world. One of the main chal-

lenges for any of the electronic cash system has been

the avoidance of double spending. Transactions in an

XRP rely on a consensus protocol to validate account

balances and prevent double spending. The initial

protocol designed (Schwartz et al., 2014) was referred

to as RPCA (Ripple Protocol Consensus Algorithm)

and subsequent reﬁned consensus protocols go under

the general name of XRP Ledger Consensus Proto-

col (XRPL for short). These consensus protocols ba-

sically use Byzantine fault tolerant agreement proto-

col over collectively trusted sub-networks. Note that

the Ripple network does not run with a proof-of-work

(POW) system like Bitcoin or a proof-of-stake (POS)

system like Ethereum but achieves a good scalabil-

ity and performance; this is one of the main reasons

https://orcid.org/0000-0001-6966-0507

for Ripple to have been widely adopted for payment

systems worldwide. The crux of correctness of pay-

ment systems depends on consensus correctness and

is briefed below:

1. Consensus:

(C1): Every non-faulty node makes a decision in

ﬁnite time.

(C2): All non-faulty nodes reach the same deci-

sion value

(C3): 0 and 1 are both possible values for all

non-faulty nodes; this removes the trivial solu-

tion in which all nodes decide 0 or 1 regardless

of the information they have been presented.

2. No-Forking: There is no possibility of two blocks

being attached to the ledger at the same time (i.e.,

the ledger extension is deterministic) and thus,

avoiding double spending.

3. Finality or Liveness: Eventual happening of the

transaction requested.

Other properties like fairness, maximal extractable

value (MEV) etc., will not be discussed in the paper.

Shyamasundar, R.

Characterization of Consensus Correctness in Ripple (XRP) Networks.

DOI: 10.5220/0012759300003767

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 21st International Conference on Security and Cryptography (SECRYPT 2024), pages 103-113

ISBN: 978-989-758-709-2; ISSN: 2184-7711

103

There have been a number of explorations in the

literature (Schwartz et al., 2014; Armknecht et al.,

2015; Chase and MacBrough, 2018; Amores-Sesar

et al., 2021; Tumas et al., 2023; Mauri et al., 2020) on

various aspects of Ripple protocol like safety, forking,

liveness etc.

A brief state-of-the-art on XRPL consensus cor-

rectness is briefed in the following. The original

white paper by Schwartz et al. (Schwartz et al., 2014),

describe the UNL model, and claim that with 80%

quorum requirement for consensus, it is necessary to

have 20% common nodes across UNLs to avoid fork-

ing. Armknecht et al. (Armknecht et al., 2015), show

that the overlap of 20% is not sufﬁcient for reaching

consensus and every pair of nodes needs an overlap

of at least 40%. Chase and MacBrough (Chase and

MacBrough, 2018) show that the minimum overlap

of 90% of the UNLs is needed for realizing consen-

sus and further show that even with 99% overlap of

UNLs and without faulty nodes, liveness is violated

. Security analysis has been made in (Amores-Sesar

et al., 2021) starting from abstraction of the consen-

sus protocol from the actual code and has elucidated

the issues of safety and liveness of XRPL. In (Mauri

et al., 2020) and (Tumas et al., 2023), some of the

issues mentioned above have been explored using a

formal approach and a graph theoretic exploration of

the network respectively.

Study of several works briefed above indicates

that just a structural overlap of node may not be

enough and the pattern of shared communications in

the underlying sub-networks of the UNLs play a vital

role.

In this paper, we characterize consensus correct-

ness in terms of a “similarity measure” of UNLs that

captures the structure of overlap and the communica-

tions that should be shared across UNLs. Our simi-

larity is based upon the metric rand-index (RI)

that

has been used for cluster-analysis (Wikipedia, 2023;

Wikipedia, 2022); recently such a similarity has been

used for analysing byzantine failures in (Roy and

Shyamasundar, 2023) but not for consensus correct-

ness. We establish that XRPL with 80% quorum

maintains consensus correctness if the similarity of

the UNLs is at least 50% that implies an overlap of

at least 80% across UNLs. Such a characterization

is shown to preserve safety and transaction liveness.

While several authors had analysed the XRPL proto-

col for security and correctness and providing counter

examples for various ad hoc characterizations, this is

the ﬁrst time, a characterization of consensus correct-

RI has been been used widely for gene similarities;

for applications of RI similarities,the reader is referred to

(Chac

on and Rastrojo, 2023).

ness has been established using a easy-to-understand

through RI.

Rest of the paper is organized as follows: after in-

troduction in section 2, XRP protocols are reviewed

in section 2. Section 3 is entirely devoted to discus-

sion of consensus correctness of XRPL; it further de-

scribes a similarity measure for UNLs and establishes

the robustness of XRPL under 80% consensus starting

from 80% similarity. Relationship between overlap of

nodes and the rand-index similarity measure of UNLs

is described. Section 4 explores the quantiﬁcation of

similarity requirements. In section 4.1, we describe

how from a 80% similarity of UNLs, one can opti-

mize the requirement of similarity in relation to the

overlap across UNLs keeping the requirement of 80%

quorum in tact. The paper concludes with section 5.

2 XRPL: AN OVERVIEW

The XRP network has one of the highest cryptocur-

rency market capitalization and is aimed at fast global

cross-border payments, asset exchange and settle-

ment. The main challenges of XRP ledger is to pre-

vent double spending and assure network-wide con-

sensus on the state of user accounts and balances. The

consensus protocol referred to as, XRP Ledger Con-

sensus Protocol (abbreviated XRPL), was called Rip-

ple Consensus Protocol Algorithm (RPCA) in the ini-

tial design phase (Schwartz et al., 2014). It is gen-

erally considered to be based on a Byzantine fault-

tolerant agreement protocol that uses a Byzantine

fault tolerant agreement protocol over collectively

trusted sub-networks. Note that the XRP network

does not run with a proof-of-work (POW) system

like Bitcoin or a proof-of-stake (POS) system like

Ethereum but guarantees consistency with only a par-

tial agreement on who participates, allowing a decen-

tralized open network. Thus, XRPL does not depend

on mining but uses a voting process based on valida-

tor nodes of each of the servers. It is through such

a voting process, it but achieves a good scalability

and performance. This is one of the main reasons for

XRP to have been widely adopted for payment sys-

tems worldwide.

The main function of XRPL is only to make the

network reach agreement on sets of transactions and

not on the content or outcome of those transactions.

That is, it provides a common global order for the

transactions submitted by clients to all participat-

ing nodes in spite of faulty or malicious (Byzantine)

nodes. Note that, in RPCA, there is no global knowl-

edge of all participating nodes.

For a good understanding of evolution of the cor-

SECRYPT 2024 - 21st International Conference on Security and Cryptography

104

rectness of consensus algorithms, we present:

1. ﬁrstly, the initial designed protocol called

Ripple Protocol Consensus Algorithm (RPCA)

(Schwartz et al., 2014), followed by

2. the XRPL protocol that handles merging of forks

arising out of asynchrony of the XRP network

keeping the algorithm deterministic.

The protocol components used and terminology is

described below.

Protocol Components and Terminology: It consists

of (Schwartz et al., 2014):

1. Server: A server is any entity running the XRP

Server software (as opposed to the XRP Client

software which only lets a user send and receive

funds), which participates in the consensus pro-

cess.

2. Ledger: It is a record of the amount of currency

in each user’s account and represents the “ground

truth” of the network. The ledger is repeatedly

updated with transactions that successfully pass

through the consensus process.

3. Last-Closed Ledger: IT is the most recent ledger

that has been ratiﬁed by the consensus process and

thus represents the current state of the network.

4. Open Ledger: It is the current operating status

of a node (each node maintains its own open

ledger). Transactions initiated by end users of a

given server are applied to the open ledger of that

server, but transactions are not considered ﬁnal

until they have passed through the consensus pro-

cess, at which point the open ledger becomes the

last-closed ledger.

5. Unique Node List (UNL): Each server, s, main-

tains a unique node list, which is a set of other

servers that s queries when determining consen-

sus. Only the votes of the other members of

the UNL of s are considered when determining

consensus. Thus, the UNL represents a subset

of the network which when taken collectively, is

“trusted” by s to not collude in an attempt to de-

fraud the network. Note that this deﬁnition of

“trust” does not require that each individual mem-

ber of the UNL be trusted. For any server node P

UNL

denotes its’ UNL list, n

= |U NL

|, a pa-

rameter called quorum, q

denotes the number of

nodes in UNL

from whom P

should get a con-

currence before committing to a decision.

6. Proposer: Any server can broadcast transactions

to be included in the consensus process, and every

server attempts to include every valid transaction

when a new consensus round starts. During the

consensus process; however, only proposals from

servers on the UNL of a server s are considered

by s for taking a decision.

2.1 RPCA Steps

The main steps of RPCA (Schwartz et al., 2014) are:

1. Initially, each server takes all valid transactions

seen prior to the consensus round that have not al-

ready been applied and makes them public in the

form of “candidate set”. It includes new transac-

tions initiated by end-users of the server and the

transactions held over from the previous consen-

sus process.

2. Each server then amalgamates the candidate sets

of all servers on its UNL, and votes on the veracity

of all transactions.

3. Transactions that receive more than a minimum

percentage of “yes” votes are passed on to the next

round, transactions that do not receive enough

votes will either be discarded or included in the

candidate set for the beginning of the consensus

process on the next ledger.

4. Final round of consensus requires a minimum per-

centage of 80% of a server’s UNL agreeing on a

transaction (this is treated as quorum). All trans-

actions that meet this requirement are applied to

the ledger, closing it - new last-closed ledger.

2.2 Characteristic Properties of RPCA

Consensus Correctness

Some of the salient properties that have been argued

in (Schwartz et al., 2014) are given below:

1. Assuming RPCA is correct, it must be the case

that if 80% of the UNL of a server agree with

the transaction, the transaction will be approved.

Thus, for an UNL of n nodes in the network, the

consensus protocol will maintain correctness so

long as f ≤ n − 1/5 where f is the number of

Byzantine failures.

2. Since the UNL for each server can be differ-

ent, agreement across servers is not inherently

guaranteed by the correctness proof. For in-

stance(Schwartz et al., 2014), if there are no re-

strictions on the membership of the UNL, and the

size of the UNL is not larger than 0.2∗n

total

where

total

is the number of nodes in the entire network,

then a fork is possible. An simple example of

two cliques connected without any common mem-

bers can achieve independent decisions leading to

forks. If the connectivity of the two cliques sur-

passes 0.2 ∗ n

total

, then a fork is no longer pos-

sible, as disagreement between the cliques would

Characterization of Consensus Correctness in Ripple (XRP) Networks

105

prevent consensus from being reached at the 80%

agreement threshold that is required. It is fur-

ther argued that a fork becomes much more dif-

ﬁcult to achieve, due to the greater entanglement

of the UNLs of all nodes. Note that there are

no assumptions about the nature of intersecting

nodes like Byzantine or honest. I.e, according to

(Schwartz et al., 2014), RPCA achieves correct-

ness and agreement as long as 80% quorum and

the intersection of UNLs surpasses 0.2 ∗ n

total

Implicit Assumptions in RPCA (Schwartz et al.,

2014) Are Given Below:

1. The network is peer-to-peer.

2. For every node P

and P

∈ UNL

, there is a reli-

able authenticated channel for P

to receive mes-

sages from P

3. Byzantine accountability: all nodes including

Byzantine ones cannot send different messages to

different nodes. This was assumed such behav-

ior in a peer-to-peer network as it could be identi-

ﬁed and corrected by honest nodes. However, due

to asynchrony and the possibility of honest nodes

being temporarily partitioned. This assumption

has been dropped in later versions. Note that

the counterexample to safety shown in (Amores-

Sesar et al., 2021) cannot arise if that assumption

is kept. this will become clear in the sequel.

2.3 A Brief on XRPL

XRPL is a reﬁned version of RPCA

, taking into ac-

count the task of dealing with short-term forks that

arise due to network asynchrony and merging them

with progress of time. The broad steps of XRPL

(Chase and MacBrough, 2018; Amores-Sesar et al.,

2021) consists of the following three phases:

1. Deliberation: Deliberation is the component of

Ripple consensus in which nodes attempt to agree

on the set of transactions to apply towards ledgers

they validate. Clients submit transactions to one

or more nodes in the network, who in turn broad-

cast the transaction to the rest of the network.

Each node maintains a set of these pending trans-

actions that have not been included in a ledger.

Starting from this set, a node iteratively proposes

new transaction sets based on the support of in-

dividual transactions among the sets proposed by

Ripple has started using terms like XRP ledger rather

than RPCA as used in the ﬁrst white paper (Schwartz et al.,

2014) to avoid a plausible misconception that Ripple owns

the XRP ledger. However, in order to be in line with the

terms used in the literature referred, we make it explicit to

avoid confusion.

nodes in its UNL as highlighted in the RPCA

steps.

2. Validation: Once a quorum of validations from

the UNL to its server for the same ledger is

reached, that ledger and its ancestors are deemed

fully validated and its state is authoritative and ir-

revocable.

3. Preferred Ledger: In times of asynchrony, net-

work difﬁculty, or Byzantine failure, nodes may

not initially validate the same ledger for a given

sequence number. In order to make forward

progress and fully validate later ledgers, nodes

use the ledger ancestry of trusted validations to

resume deliberating on the network’s preferred

ledger

It is easy to see that the ﬁrst two steps capture the

major steps of RPCA. A similarity can also be seen

to the proof of stake ﬁnality gadget steps introduced

introduced in (Buterin and Grifﬁth, ). The third one

is the one which is the additional phase, that is intro-

duced to merge the short-term forks that arise due to

asynchrony; the rule is similar to that of the GHOST

rule (Sompolinsky and Zohar, 2015); we will not go

into further details, as the details are not very essential

for the discussions; interested readers are referred to

(Chase and MacBrough, 2018; Amores-Sesar et al.,

2021).

3 CORRECTNESS OF XRPL

While we have discussed some of the claims of RPCA

in section 2.2, in the following, we discuss the issues

of XRPL highlighted by several authors in (Schwartz

et al., 2014; Armknecht et al., 2015; Chase and

MacBrough, 2018; Amores-Sesar et al., 2021).

As discussed in section 2.2, the authors of

(Schwartz et al., 2014) discuss conditions to avoid

forking through possible overlap of nodes in the

UNLs; in a sense, the overlap of UNLs brings out the

qualitative requirements of connectivity in the XRP

network. The authors of (Amores-Sesar et al., 2021)

have provided counter examples to show how the re-

quirement of overlap does not preserve safety and

liveness .

As mere overlap of UNLs is not able to character-

ize correctness, we explore abstraction of connections

(communications) among the overalpping nodes of

UNLs. In this paper, we shall explore the use of sim-

ilarity measure used for cluster analysis (Wikipedia,

2023) like rand-index (Wikipedia, 2022) and adapt it

for consensus correctness.

SECRYPT 2024 - 21st International Conference on Security and Cryptography

106

As highlighted in (Wikipedia, 2023), Cluster anal-

ysis or clustering is the task of grouping a set of ob-

jects in such a way that objects in the same group,

called a cluster, are more similar, in a way, to each

other than to those in other groups (clusters). The no-

tion of a ”cluster” cannot be precisely deﬁned, which

is one of the reasons why there are so many clustering

algorithms like connectivity models, centroid models,

graph-based models etc. For instance, in graph-based

models, a clique, that is, a subset of nodes in a graph

such that every two nodes in the subset are connected

by an edge can be considered as a prototypical form of

cluster. Relaxations of the complete connectivity re-

quirement (a fraction of the edges can be missing) are

known as quasi-cliques. We use cluster and cliques

interchangeably often.

The authors of (Schwartz et al., 2014) argue the

overlap requirements for avoiding forking through the

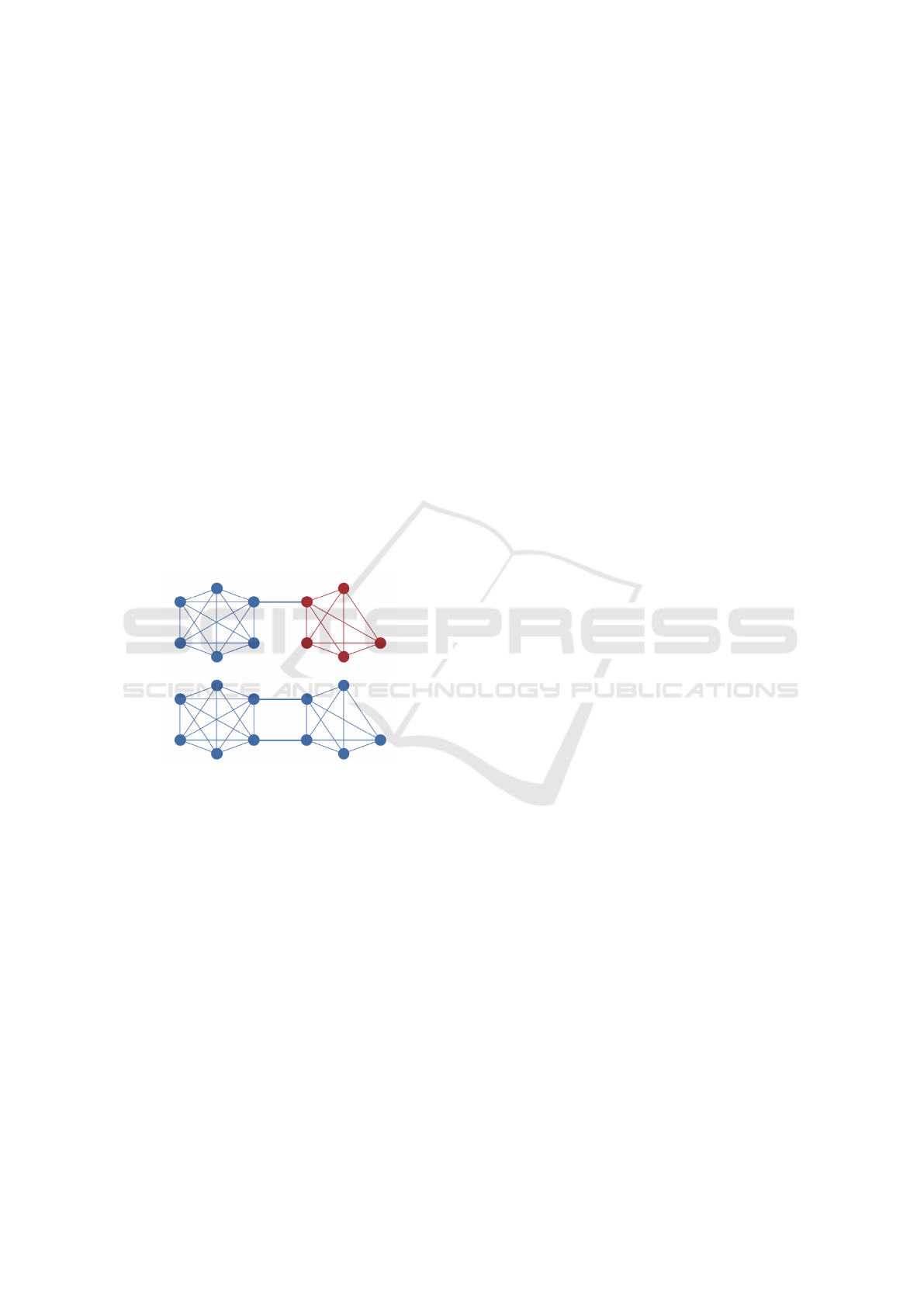
networks depicted in Figure 1, where the top ﬁgure

shows two cliques connected by a bridge and bottom

one connected by two bridges. As already highlighted

the overlap requirements are not sufﬁcient as eluci-

dated in (Amores-Sesar et al., 2021).

Figure 1: Connectivity Requirements of two UNL Cliques

(Schwartz et al., 2014).

Let us consider two UNLs, U NL

and U NL

. If

they are completely disjoint, then each of the UNLs

can take an independent decision (thus, easily could

lead to forks in an obvious way).

In the following, we shall adapt the notion of clus-

ter highlighted above (Wikipedia, 2023) that has both

overlap and connections and arrive at the notion of

similarity measure with respect to UNLs. Note that

as in (Schwartz et al., 2014), no assumptions are

made on the nature of intersecting nodes like hon-

est or Byzantine. The similarity measure we pro-

pose, combines the number of nodes and communi-

cations among them and generalizes the concept of

rand-index analysis recently envisaged for exploring

the BFT properties (Roy and Shyamasundar, 2023).

Before discussing similarity, ﬁrst let us look at the

representation of UNLs as sets of clusters.

3.1 Representation of UNLs as Voting

Clusters

A cluster is essentially a sub-network where each

node Byzantine or honest cannot send contradictory

messages to members in the same cluster. However,

if it is connected through a common node to another

cluster, a Byzantine common node can send incon-

sistent or contradictory messages to its directly con-

nected clusters.

A cluster of n nodes could be represented either

as a clique of n nodes if every node is connected to

every other node, or as a connected graph G = (V,E)

where E denotes the set of edges or communications

possible in the network. A graph with n nodes can

have a range of edges varying from 0 to n(n − 1)/2)

edges. A graph with n nodes can be represented as a

union of clusters where any two clusters share some

of the vertices or some of the edges. A single edge

can be treated a clique of 2 nodes. Thus, we can rep-

resent any network as a union of clusters. For illus-

trative purposes, the network shown later in Figure

5 could be represented as {{(a,b),(b,c),(a,c)}, {(c,d),

(c,e), (d,e)}} where c is common node between the

two clusters. If c is a Byzantine node, it can send dif-

ferent messages to {a,b} and {d,e}. The classic no-

tion of condensed graph shows connections between

strongly connected components in a graph. For illus-

trative purposes,

• the top sub-graph shown in Figure 1 which is an

UNL can be represented by a set of clusters con-

sisting of the leftmost cluster, the single bridge

(one edge), and the rightmost cluster,

• the bottom UNL can be represented through a set

of clusters consisting of the leftmost cluster, the

two bridges and rightmost cluster.

A Voting cluster is a peer-to-peer network that

converges on the transactions of its members by vot-

ing. For simplicity, we can consider transactions to

be just values on which the members are voting. Let

us explore the representation of UNLs as clusters. A

sub-graph with (i) a single node is a cluster or a clique

(one node and no edge), (ii) a single edge is a cluster

with two nodes and one connection, (iii) a triangle is

a cluster with three nodes and three connections, (iv)

a polygon with n nodes with n nodes and n(n − 1)/2

edges is a cluster (clique), and (v) if the graph is con-

nected and the number edges is less than n(n − 1)/2,

it is referred to as a quasi-cluster.

In a cluster or a quasi cluster, a node even if it

is Byzantine cannot send conﬂicting or contradictory

messages to any other member in the same cluster

as members can observe the communications in the

Characterization of Consensus Correctness in Ripple (XRP) Networks

107

same cluster. This is illustrated through a 3-node clus-

ter shown in Figure 2.

Figure 2: A Three Node Cluster

Suppose, B and C are in a cluster and a node A,

sends a message m, to B and a message m’ (m ̸= m

′

to C at the same time, then B and C immediately rec-

ognize the Byzantine nature of A. Assuming cryp-

tography is unbreakable, in the case of a two-node

cluster, say {A,B}, neither of them can repudiate

the messages exchanged between them. However,

a Byzantine node in one cluster can send one mes-

sage to member(s) in one cluster and another one to

member(s) in another cluster. For example, the UNL

shown in Figure 9 (shown later) can be represented

as { {(1,n+1), ... , (n,n+1)},{(n+1)}, {(n+1, n+2), ...,

(n+1,2n+1)}. The node labelled n + 1 could send one

message to its left cluster and another one to its right

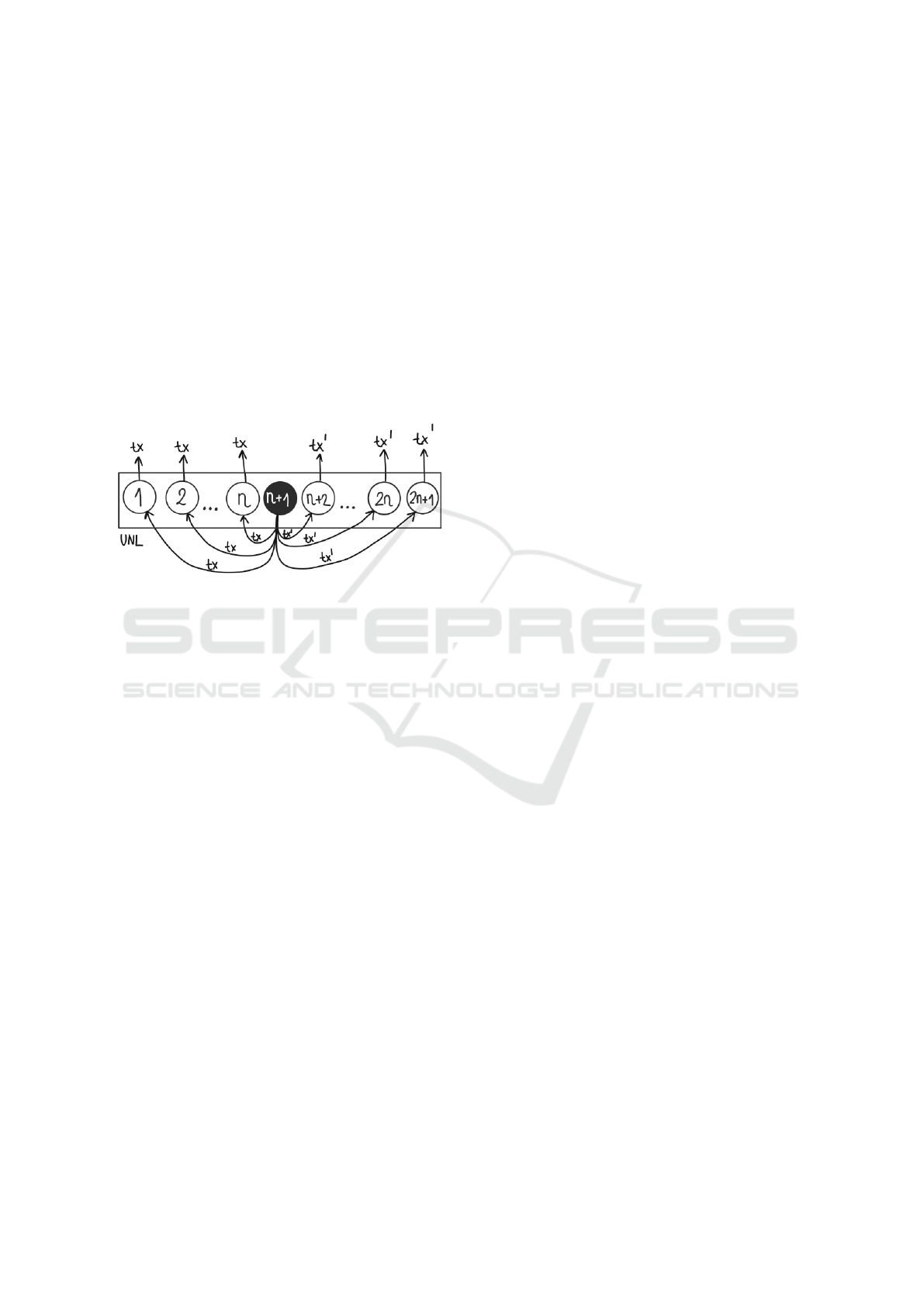
cluster.

3.2 Rand-Index: A Brief Background

Deﬁnition 1: Rand-Index (RI) is a similarity measure-

ment of two data clusters (Wikipedia, 2022). Through

rand-index, we can calculate the number of agree-

ments and disagreements in terms of node pairs from

the same or different clusters.

Consider a network with N nodes, with two clus-

ters of the network, say C

′

= (C

′

,. .. ,C

′

) and

′′

= (C

′′

,. .. ,C

′′

) such that the union of the two

is equal to N. Note that the set of all unordered pairs

of the network having





pairs is the disjoint union

of the following sets:

1. A = {pairs that are in the same clusters under C

′

and C

′′

2. B = {pairs that are in different clusters under C

′

and C

′′

3. C = {pairs that are in the same cluster under C

′

but different in cluster C

′′

4. D = {pairs that are in different cluster under C

′

but in the same cluster under C

′′

The Rand Index measure of similarity of clusters C

′

and C

′′

is given by

RI =

|A| + |B|

|A| + |B| + |C| + |D|

|A| + |B|





2(|A| + |B|)

N(N − 1)

(1)

Here, |A| + |B| can be considered as the number of

agreements between C

′

and C

′′

, and |C| + |D| as the

number of disagreements between C

′

and C

′′

. Notice

that as the denominator |A| + |B| + |C| + |D| is the to-

tal number of unordered pairs of nodes, so it can be

written as





The Rand index has a value between 0 and 1, with

0 indicating that the two data clusters do not agree

on any pair of points and 1 indicating that the data

clusters are exactly the same.

3.3 Rand-Index Similarity Adaptation

for Ripple Analysis

UNLs themselves can be treated as a cluster of clus-

ters of the XRP network. UNLs in Ripple consensus

can be treated as two different sets of clusters; the

members are essentially cliques or quasi-cliques sim-

ilar to that described in Figure 1; the top UNL can

be described by {left blue-cluster, center-blue-edge,

right-red cluster}; similarly the bottom UNL is given

by {left-blue-cluster, top blue edge, bottom blue edge,

rightmost blue cluster}.

Sets A and B deﬁned above can be interpreted as

follows:

1. Set A corresponds to saying as they are in the

same cluster – communications can be trusted.

2. Set B corresponds to saying that as they are to-

gether either in the same cluster or different clus-

ters together –communications can be trusted.

Thus, using A and B, the agreement analysis of any

two UNLs highlight agreement of the behaviour of the

nodes (honest/Byzantine) while C and D highlight the

Byzantine behaviour of the nodes.

3.4 Similarity Analysis of UNLs

As highlighted already, it is the categories A and B

given in the deﬁnition of Rand Index that matters for

similarity. As UNL is selected from among the total

number of nodes in the network, there will be pos-

sibly some overlap. Thus, in any UNL, we can iden-

tify two components: common members across UNLs

and some that are not-common Let us analyse the sim-

ilarity of UNL clusters based on the common mem-

bers. For simplicity, to begin with, consider two sim-

ple UNLs with two not-common members that share

a single common member, two common members and

three common members shown in Fig 3, Fig 4 and Fig

5, four common members etc. The similarity or RI of

these UNLs are given below:

1. Fig. 3, depicts two clusters corresponding to two

UNLs, each having two disjoint members, and c

SECRYPT 2024 - 21st International Conference on Security and Cryptography

108

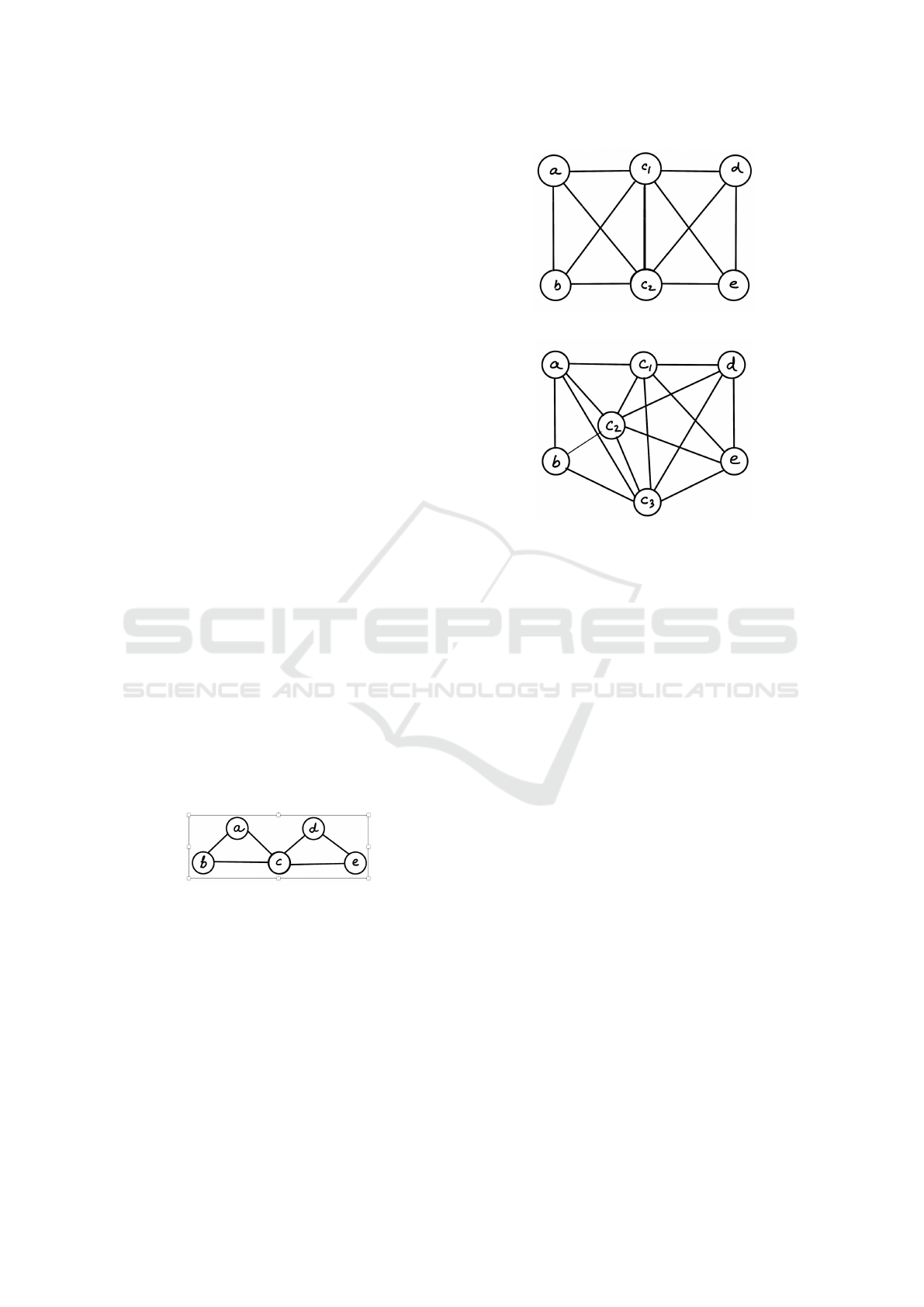
is the common member; cluster is abstracted as-

suming the common member can communicate

with all other members in the respective UNLs.

The two clusters corresponding to the two UNLs

are C’= {(a,b),(b,c),(a,c)} and C” = {(c,d), (c,e),

(d,e)}.

• It is easy to observe that RI is 0.

• If c becomes byzantine naturally, it easily fol-

lows that there will be no consensus.

2. Figure 4, depicts two clusters corresponding to

two UNLs, each having two disjoint members,

and c, d are the two common members; cluster

is abstracted assuming the common members can

communicate with all other members in the re-

spective UNLs. The two clusters corresponding to

the two UNLs are C’={(a,b), (a,c1), (a,c2), (b,c1),

(b,c2), (c1,c2)} and C”= {(c1,d), (c1,e), (c2,d),

(c2,e), (d,e), (c1,c2)}.

• (c1,c2) is the only member corresponding to

clause A and B in Deﬁnition 1, between C’ and

C”. Thus, RI is 1 ÷





. With N being 6, RI

will be 1/15. Again here, consensus need not

be there due to some of the common members

becoming Byzantine.

3. In Fig 5, on the same lines, we get C’={(a,b),

(a,c1), (a,c2), (a,c3), (b,c1), (b,c2), (b,c3), (c1,c2),

(c1,c3), (c2,c3)} and C”= {(c1,d), (c1,e), (c2,d),

(c2,e), (c3,d), (c3,e), (d,e), (c1,c2), (c1,c3),

(c2,c3)}.

• Members of sets A and B as per Deﬁnition 1,

are (c1,c2), (c1,c3), (c2,c3).

• RI = 3 ÷





; N being 7, RI will 3/21 =1/7.

4. Continuing in this manner for say till m common

members, RI for that network will be









Figure 3: Two UNLs sharing One Common Member.

Note: If the non-common members are increased ar-

bitrarily, naturally the quorum of 80% stipulated ear-

lier gets effected; however, this also decreases the

similarity of the UNLs. Thus, there is no need to treat

the impact of non-common members explicitly.

3.5 Failures Tolerated with 80%

Similarity

As XRPL requires 80% quorum, let us start arbitrar-

ily with 80% similarity requirement of UNLs and see

Figure 4: Two UNLs sharing Two Common Members.

Figure 5: Two UNLs sharing Three Common Members.

whether it preserves consensus correctness. Later, we

shall explore optimal requirements of similarity.

Lemma 1: With 80% quorum, RPCA maintains cor-

rectness for each transaction with its UNL in an iso-

lated way, as long as f ≤ (n − 1)/5 where f is the

number of Byzantine failures and n is the number of

nodes in the XRP network.

Proof: Follows from (Schwartz et al., 2014).

Lemma 2: With 80% quorum, RPCA will not be able

to guarantee that there will be no contradictory trans-

actions across distinct UNLs and its servers, even if

the overlap of the UNLs is 80%.

Proof: Consider the structure shown in Figure 6 taken

from (Amores-Sesar et al., 2021). Consider the two

UNLs L={1,2,3,4,5} and L’ = {3,4,5,6,7}. It is easy

to see that the UNLs have 60% overlap. As assumed

in (Amores-Sesar et al., 2021), node 4 is Byzantine

while the others are trusted ones. As node 4 can give

contradictory votes to L and L’, it can be seen that

both of them can get 80% quorum leading to contra-

dictory transactions in L and L’. Hence, the lemma.

Lemma 3: If two UNLs are at least 80% similar then

it implies the overlap is at least 89.44%.

Proof: From the RI expression (4) in 3.4, we have,

similarity measure of the two UNLs, s of the form

RI =









= m(m − 1)/n(n − 1) ≈ m

=(m/n)

Thus, 80% similarity of UNLs corresponds to saying

(m/n)

≥ 80%. Hence, m/n is > 89.44% which can

be interpreted as: overlap of the two UNLs is more

than 89.44%.

Characterization of Consensus Correctness in Ripple (XRP) Networks

109

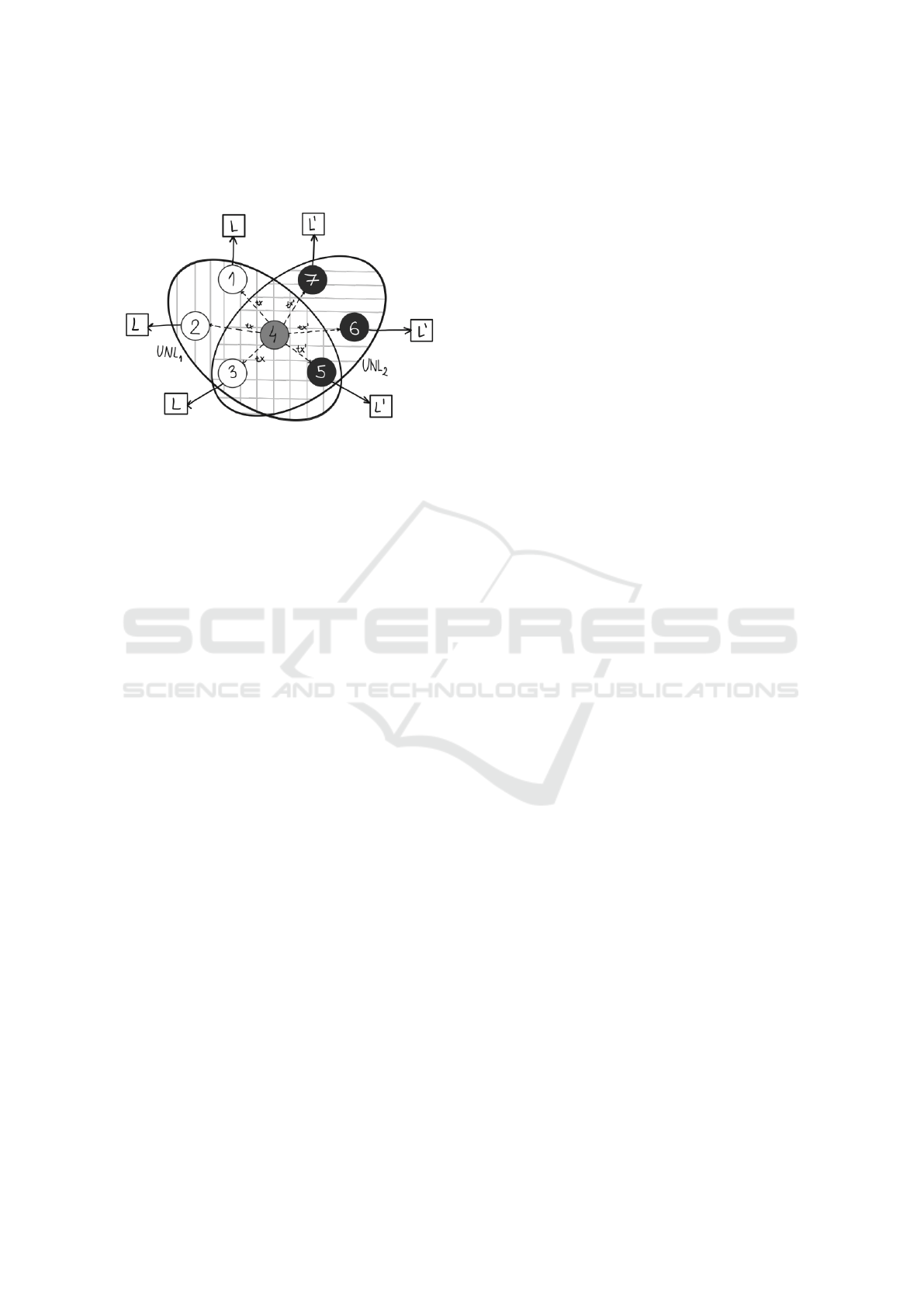
Note: If L and L’ are more than 80% similar, intro-

ducing non-common-members to L or L’ will lead to

reducing 80% similarity

Figure 6: Safety Violation Example from (Amores-Sesar

et al., 2021).

Lemma 4: If two UNLs are at least 80% similar, then

the UNLs cannot have two contradictory concurrent

transactions assuming at most 20% failures (Byzan-

tine)

Proof: Let L and L’ be the two UNLs. Assume

the contradictory: L concurs Tx and L’ concurs TX’

where Tx and Tx’ are conﬂicting transactions. As-

suming 20% failure, Tx or TX’ would have to be se-

lected by the remaining 69.44% (89.44-20–ignoring

for simplicity ceiling functions required to realize in-

tegers) of the UNL members that are behaving cor-

rectly. As majority forms the basis of selection, it

follows that some of the 19.44% processors have to

show Byzantine behaviour if both Tx and Tx’ have

to be selected - contradicting the hypothesis that only

20% can fail.

In the next section, we explore optimization of

similarity requirements.

4 HOW MUCH SIMILARITY IS

ESSENTIAL?

First, let us look at existing hints for the formation of

UNLs as highlighted by the designers in practice. In

(Schwartz et al., 2014), it is argued that UNLs are not

created randomly but done using the notion of fault

tolerance to avoid the formation of a nefarious cartels.

Formally stating, if p

is the probability the node will

decide to collude and join a nefarious cartel, then the

probability of correctness, p

∗

is given by

∗

= Σ

⌈(n−1)/5⌉

i=0





(1 − p

)

n−i

∗

represents the likelihood that the size of the nefari-

ous cartel will remain below the maximal threshold of

Table 1: Similarity vs Overlap in Networks.

RI Similarity (O(n

)) =⇒ Overlap (O(N))

50% 70.7

60% 77.46

70% 83.66

75% 86.6

80% 89.44

Byzantine failures, for a given p

. As binomial distri-

bution is followed, p

greater than 20% will result in

expected cartels of size greater than 20% of the net-

work - thus short circuiting the consensus process.

Authors in (Christodoulou et al., 2020) explore the

use of tools available in Ripple to arrive at network

health monitoring measures. They suggest that a large

UNL overlap is needed only with more than 20% of

malicious nodes in the network.

Below, we discuss the use of similarity measure

RI for characterizing consensus correctness.

4.1 Consensus Correctness via RI

Given that 80% quorum is a requirement of RPCA

and XRPL, let us see how much similarity must be en-

forced on UNLs to preserve safety. Purpose of UNLs

is to enhance the performance and thus, reduction of

similarity yield higher performance.

We have already shown that 80% similarity over-

comes conﬂicting transactions. The question remain-

ing is: How much is necessary?

First, let us analyze RI similarity and overlap func-

tions in terms of the total number of nodes in the net-

work. Similarity function is quadratic in term of the

nodes of the network (i.e., O(n

)) as we consider pairs

of nodes (could be interpreted as communication be-

tween the two) while overlap is linear in terms of the

nodes of the network (i.e., O(N)). Note that quo-

rum again is based on the total number of nodes in

the network. Below, we give a simple enumeration of

the similarity and the corresponding overlap require-

ments for satisfaction of the similarity, in terms of the

number of nodes in the network denoted N.

It must be kept in mind the overlap value is an in-

teger; by using the ”ceiling” function we can obtain

the same from Table 1. For instance 80% similarity

leads to nearly 90% overlap as highlighted by a magic

ﬁgure in other papers discussed earlier in (Armknecht

et al., 2015; Amores-Sesar et al., 2021). Our analysis

provides a clear understanding as to why 90% overlap

is not sufﬁcient as consensus demands a dense con-

nections among the nodes.

Lemma 5: If two UNLs are at least 50% similar,

then the UNLs cannot have two contradictory concur-

rence of transactions assuming at most 20% failures

(Byzantine).

SECRYPT 2024 - 21st International Conference on Security and Cryptography

110

Proof: From Table 1, it can be seen that anything

larger than 50% similarity corresponds to greater than

71% overlap. Now from the proof of Lemma 4, the

result follows.

Reducing similarity below 50% will lead to sce-

narios wherein majority voting (greater than 50%)

cannot be guaranteed ( note that actual number is the

ceiling of the overlap percentage). Hence, 50% sim-

ilarity is a requirement for overcoming acceptance of

fraudulent transactions.

Theorem 1: No fraudulent transactions will be pos-

sible with 80% quorum and 50% RI similar UNLs.

Proof: Follows from Lemma 5.

Now let us see the requirement for accepting

transactions.

Theorem 2: RPCA or XRPL will be safe with 80%

quorum and a RI similarity of UNLs that would imply

80% overlap requirement.

Proof: The overlap implication of similarity is shown

in Table 1. Now, the proof follows from Lemma 5.

Corollary 1: The RI similarity of the network shown

in Figure 6 is less than 50% with respect to the XRP

network and thus, does not guarantee non-conﬂicting

transaction.

Proof: Communications in L are given by { (1,4),

(2,4),(3,4), (4,5)} and those of L’ are given by {

(3,4),(4,5),(4,6),(4,7)} and hence RI = 2 ÷





=2 ÷

21 < 50%. From Lemma 4, it follows that it does not

guarantee non-conﬂicting transaction.

Lemma 6: The network can get stuck in XRPL even

with more than 90% Overlap of UNLs and without a

node being Byzantine.

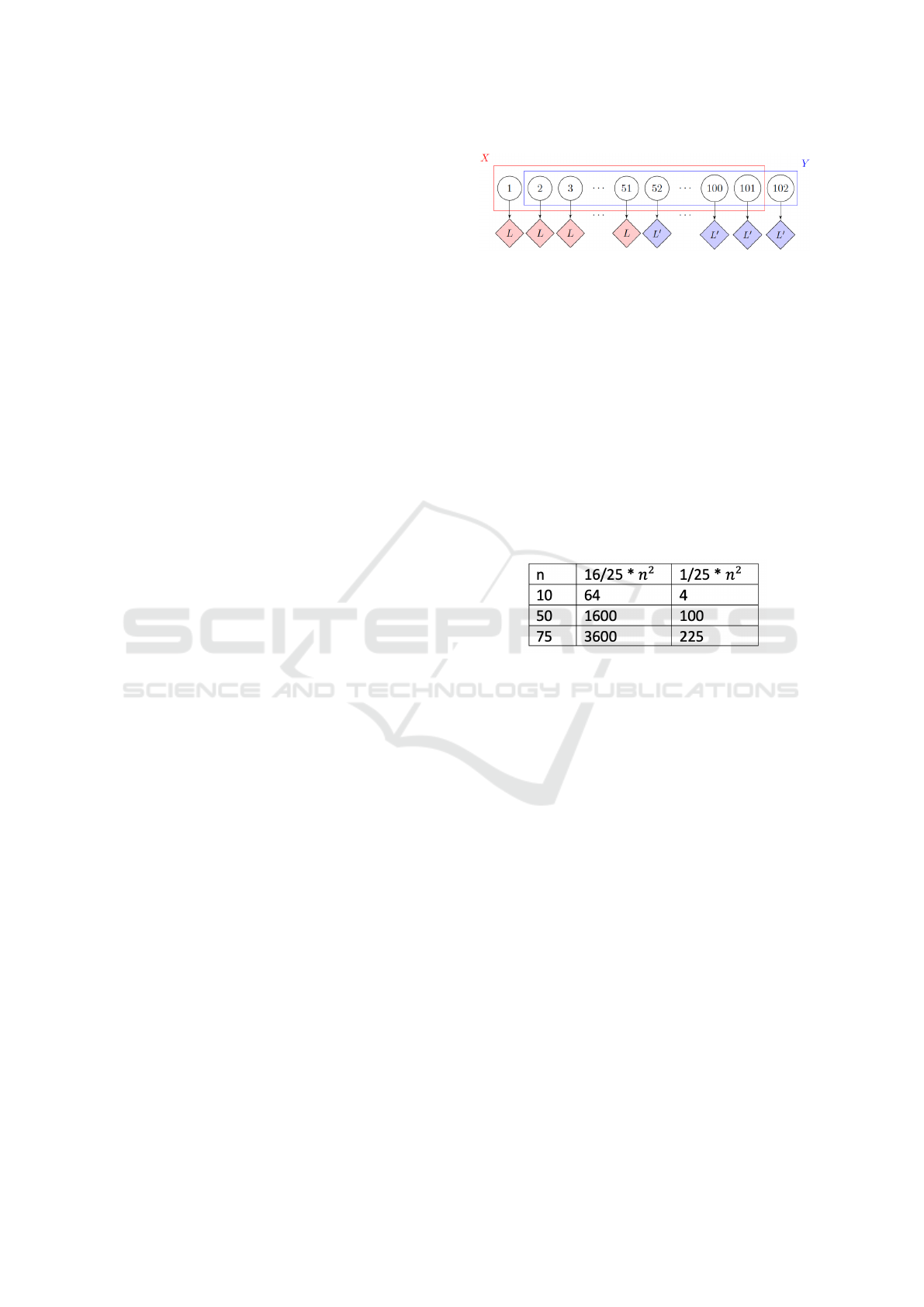
Proof: Figure 7 from (Chase and MacBrough, 2018)),

illustrates an example of two UNLs even 90% over-

lap do not converge on consensus. There are two

UNLs, X (in red) = {P1,P2, . . . ,P101} and Y (in

blue) = P2,P3,...,P102. Peers 1··· 51 use X and peers

52· ·· 102 use Y . There are two ledgers, L and L’.

Nodes listening to X validate a descendant of L, while

the nodes listening to Y validate a descendant of L’.

Since 51 > 0.5|X| nodes in X validate a descendant

of L. Thus, according to the preferred branch proto-

col, the nodes listening to X cannot switch branch to

L’. Similarly, since 51 > 0.5|Y | nodes in Y all vali-

date a descendant of L, the nodes listening to Y can-

not switch branch to L’. Thus, network cannot ever

rejoin without manual intervention.

Note: Note that 90% overlapping UNLs could even

have zero similarity. However, satisfaction of Theo-

rem 2 will overcome issues of getting stuck as one

group or other will be able to validate as the similar-

ity is larger than 50%.

Figure 7: Stuck-in-Net, 99% Overlap & No Byzantine

Node.

4.2 Assessing Loss of Communications

In the XRP network, due to failures, communica-

tion links between peer-to-peer nodes also fail. Let

us try to have at least a qualitative understanding of

the quantum of connections that can get lost due to

Byzantine failures. Recalling that the similarity of

a UNL of n nodes is of the order of (n)(n − 1)/2

or is proportional to n

. If we assume 20% failures

and assuming that the corresponding connections also

fail, the remaining working connections will be pro-

portional to (16/25) ∗ n

and connections lost will be

proportional to (1/25) ∗ n

. A simple estimate is tab-

ulated below assuming clique connection:

Figure 8: Density of Loss of Connections Due to Failures.

From Table 1, it is easy to see that if N is reason-

ably large, the cluster will have a dense set of com-

munications in a network that is at least 50% similar;

i.e., Byzantine node failure will only remove a small

number of connections (communications) and thus,

clusters will not become disjoint or remain connected.

From Figure table, it can be easily seen that the order

of the number of communications lost is quite small

small.

4.3 Stuck-Free Net & Liveness: RI

Lemma 8: If the UNLs are at least 50% similar then

a partition as shown in shown in Figure 7 cannot take

place.

Proof: Let UNL1 = {C11, ... C1m} and UNL2

= {C21, ... C2m}. Assuming 20% byzantine at the

worst, there will be overlap of more than 50% honest

nodes. As the density of edges will have to main-

tained to keep up the assumed 50% similarity, ignor-

ing 20% of the byzantine nodes, there will be enough

connections (cf.Figure 8) in the network that allows

exchange of values without leading to disjoint parti-

tions that arises if one had considered only overlap of

Characterization of Consensus Correctness in Ripple (XRP) Networks

111

nodes.

Lemma 9: There are UNLs with just one Byzantine

node leading to liveness violation in spite of 80% quo-

rum.

Proof: The authors of (Amores-Sesar et al., 2021) il-

lustrate through an example shown in Figure 9 that

depicts a system with 2n correct nodes and one single

Byzantine node. All nodes are assumed to trust each

other, i.e., there is one common UNL containing all

2n + 1 nodes. Based on Figure, the byzantine node

suggests Tx to 1-n and TX’ to n+2 to 2n+1. This ob-

viously leads to situation where neither nodes from

{1,...,n} nor {n+1, ... 2n+1} switch from Tx to Tx’

or Tx’ to Tx respectively as per the preferred ledger

rule.

Figure 9: Single Node Byzantine Creating Liveness Viola-

tion (Amores-Sesar et al., 2021).

Lemma 10: The UNL shown in Figure 9 has RI = 0

with respect to the XRP peer-to-peer network, assum-

ing the arrows shown are the only possible communi-

cations.

Proof: The UNL shown in can be represented as {

{(1,n+1), ... , (n,n+1)},{(n+1)}, {(n+1, n+2), ...,

(n+1,2n+1)}. It easily follows from the deﬁnition of

RI, that RI of the network is 0.

Lemma 11: Let α be the similarity greater than 50%

across UNLs. If α satisﬁes 80% overlap then there

cannot be any liveness violation with at most 20%

failures (or byzantine).

Proof: Let the UNL be represented by {C1, C2,

...cm}. A similarity of 50% implies more than

⌈71.41%⌉ overlap pairwise. Hence, even if 20% fail-

ures occur there will be other nodes that will vote on

seeing the other value (cf. Figure 8). As the algo-

rithm is deterministic, one of the Tx will go through

and there will be no liveness violation.

5 CONCLUSIONS

In this paper, we have described a similarity measure

based on rand-index for UNLs, and shown that XRPL

maintains consensus correctness with 80% consensus

and a similarity that is more than 50% that implies

at least 80% overlap. The similarity measure binds

the UNLs tightly that enables it to maintain consen-

sus correctness. We have also related the similarity

measure with the overlap of UNLS and shown that

the XRPL preserves safety and maintains transaction

liveness under 20% Byzantine failures if the similar-

ity of UNLs is more than 50% and implies an overlap

at least 80%. If the system must be further failure tol-

erant of say up to the limit of 1/3 failure of the total

number of nodes (as per the original byzantine tol-

erant algorithm) in the XRP network, the similarity

must be enhanced. While several authors had anal-

ysed the XRPL protocol for security and correctness

and provided counter examples for various overlap

condistions, this is the ﬁrst time, a characterization

of consensus correctness has been established using a

easy-to-understand metric rand-index. The notion of

similarity and correctness established here, in a sense

indicates as to how the XRP network has been work-

ing robustly in practice.

Whenever, one looks at UNL based consensus,

one wonders as to how the UNLs can be formed to

enhance performance keeping the correctness invari-

ant. While in section 4, we discussed informal hints,

we opine that the notion of similarity shall provide a

basis on which UNLs can be effectively designed. So

far, even with overlap notions, there has been no clear

indication of how much performance gain is obtained

either in theory or practice through the use of UNL

based consensus. It would be interesting to evaluate

how much performance can be gained through a rigor-

ous design of UNLs both theoretically and practically.

REFERENCES

Amores-Sesar, I., Cachin, C., and Mi

c, J. (2021). Se-

curity Analysis of Ripple Consensus. In 24th Inter-

national Conference on Principles of Distributed Sys-

tems (OPODIS 2020), volume 184, pages 10:1–10:16.

Armknecht, F., Karame, G. O., Mandal, A., Youssef, F.,

and Zenner, E. (2015). Ripple: Overview and out-

look. In Conti, M., Schunter, M., and Askoxylakis,

I., editors, Trust and Trustworthy Computing, pages

163–180, Cham. Springer International Publishing.

Buterin, V. and Grifﬁth, V. Casper the friendly ﬁnality gad-

get. https://arxiv.org/abs/1710.09437,October2017.

Chac

on, J. and Rastrojo, A. (2023). Minimum adjusted rand

index for two clusterings of a given size. Advances in

Data Analysis and Classiﬁcation, 17:125–133.

Chase, B. and MacBrough, E. (2018). Analysis of the

xrp ledger consensus protocol. CoRR, http://arxiv.org/

abs/1802.07242, Mon, 13 Aug 2018 16:47:54 +0200.

Christodoulou, K., Iosif, E., Inglezakis, A., and Themisto-

cleous, M. (2020). Consensus crash testing: Exploring

SECRYPT 2024 - 21st International Conference on Security and Cryptography

112

ripple’s decentralization degree in adversarial environ-

ments. Future Internet, 12(3).

Mauri, L., Cimato, S., and Damiani, E. (2020). A formal

approach for the analysis of the xrp ledger consensus

protocol. In Proc. 6th, ICISSP 2020, Valletta, Malta,

pages 52–53. SCITEPRESS.

Roy, S. and Shyamasundar, R. K. (2023). An analysis of

hybrid consensus in blockchain protocols for correct-

ness and progress. In 37th Annual IFIP WG 11.3 Con-

ference, DBSec 2023, Sophia-Antipolis, France, July

19–21, 2023, page 404–412. Springer-Verlag.

Schwartz, D., Youngs, N., and Britto, A. (2014). The ripple

protocol consensus algorithm. In Ripple Inc., White

Paper.

Sompolinsky, Y. and Zohar, A. (2015). Secure high-rate

transaction processing in bitcoin. In B

ohme, R. and

Okamoto, T., editors, Financial Cryptography, vol-

ume 8975 of Lecture Notes in Computer Science,

pages 507–527. Springer.

Tumas, V., Rivera, S., Magoni, D., and State, R. (2023).

Topology analysis of the xrp ledger. In Proceedings of

the 38th ACM/SIGAPP Symposium on Applied Com-

puting, page 1277–1284, New York, NY, USA. Asso-

ciation for Computing Machinery.

Wikipedia (2022). Rand index. https://en.wikipedia.org/

wiki/Rand index, [Online; accessed 30-Dec-2022].

Wikipedia (2023). Cluster analysis. https://en.wikipedia.

org/wiki/Cluster analysis, [Online; accessed 10-Dec-

2023].

Characterization of Consensus Correctness in Ripple (XRP) Networks

113