Encrypted KNN Implementation on Distributed Edge Device Network

B. Pradeep Kumar Reddy

, Ruchika Meel

and Ayantika Chatterjee

Indian Institute of Technology, Kharagpur, India

Keywords:

Machine Learning, IoT, Security, Fully Homomorphic Encryption, Distributed Computing, Privacy.

Abstract:

Machine learning (ML) as a service has emerged as a rapidly expanding ﬁeld across various industries like

healthcare, ﬁnance, marketing, retail and e-commerce, Industry 4.0, etc where a huge amount of data is gen-

erated. To handle this amount of data, huge computational power is required for which cloud computing used

to be the ﬁrst choice. However, there are several challenges in cloud computing like limitations of bandwidth,

network connectivity, higher latency, etc. To address these issues, edge computing is prominent nowadays,

where the data from sensor nodes is collected and processed on low-cost edge devices. As simple sensor

nodes are not capable of handling complex computations of ML models, data from sensor nodes need to be

transferred to some nearest edge devices for further processing. If this sensor data is related to some security-

critical application, the privacy of such sensitive data needs to be preserved both during communication from

sensor node to edge device and computation in edge nodes. This increased need to perform edge-based ML

on privacy-preserved data has led to a surge in interest in homomorphic encryption (HE) due to its ability to

perform computations on encrypted form of data. The highest form of HE, Fully Homomorphic Encryption

(FHE), is capable of theoretically handling arbitrary encrypted algorithms but comes with huge computational

overhead. Hence, the implementation of such a complex encrypted ML model on a single edge node is not

very practical in terms of latency requirements. Our paper introduces a low-cost encrypted ML framework on

a distributed edge cluster, where multiple low-cost edge devices (Raspberry Pi boards) are clustered to perform

encrypted distributed K-Nearest Neighbours (KNN) algorithm computations. Our experimental result shows,

KNN prediction on standard Wisconsin breast cancer dataset takes approximately 1.2 hours, implemented on

a cluster of six pi boards, maintaining end-to-end data conﬁdentiality of critical medical data without any re-

quirement of costly cloud-based computation resource support.

1 INTRODUCTION

The integration of edge computing and machine

learning (ML) has signiﬁcantly impacted smart net-

working and the Internet of Things (IoT) in recent

years. However, this convergence brings forth press-

ing concerns regarding data privacy and security, par-

ticularly due to data collection by low-cost sensor

nodes lacking the computational power for complex

ML algorithms (Singh et al., 2021), (Xiao et al.,

2019), (Rizvi et al., 2020).

Encrypted machine learning (ML) at the edge is

vital for safeguarding sensitive information during

processing (Chien et al., 2023). However, leveraging

homomorphic encryption (HE) for privacy-preserving

ML at the edge presents challenges. The signiﬁcant

https://orcid.org/0000-0002-6377-4535

https://orcid.org/0009-0005-1043-9134

https://orcid.org/0000-0001-6368-0718

computational overhead associated with HE, particu-

larly for complex ML models and large datasets, can

slow down inference, which is critical in resource-

constrained edge computing environments. Addition-

ally, ensuring compatibility between HE schemes and

ML algorithms is challenging, as many popular algo-

rithms rely on encrypted operations not directly sup-

ported by existing HE libraries (Gouert et al., 2023).

Balancing security and efﬁciency is delicate, with

stronger encryption often leading to increased com-

putational complexity. Lastly, managing key distribu-

tion becomes complex in distributed edge computing

scenarios, where multiple devices may need to col-

laborate for encrypted ML tasks. Overcoming these

challenges is crucial for realizing the full potential of

HE in enabling secure and privacy-preserving ML at

the edge (Shrestha and Kim, 2019).

The ultimate form of HE, FHE promises imple-

mentation of arbitrary algorithms in encrypted do-

main theoretically. In practice, that adds several

680

Reddy, B., Meel, R. and Chatterjee, A.

Encrypted KNN Implementation on Distributed Edge Device Network.

DOI: 10.5220/0012761100003767

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 21st International Conference on Security and Cryptography (SECRYPT 2024), pages 680-685

ISBN: 978-989-758-709-2; ISSN: 2184-7711

challenges, particularly in terms of memory and la-

tency(Sinha et al., 2022) in resource-constrained en-

vironments. Additionally, it introduces considerable

latency due to the computational complexity of homo-

morphic operations, which involve numerous mod-

ular arithmetic operations on encrypted data. As a

result, performing even simple computations can be

time-consuming. Hence, secure ML processing in

edge should be inherently distributed and decentral-

ized to mitigate huge latency and memory require-

ments by exploring techniques for parallelization and

optimization (Natarajan and Dai, 2021). However, in

recent reported ML works, most of the works are done

for cloud-based infrastructure.

With this motivation, the main goal of this work

is to implement K-Nearest Neighbour (KNN) algo-

rithm prediction steps on encrypted data using a dis-

tributed edge (Raspberry Pi) cluster. It is to be noted

that we are exploring only a single ML algorithm in

this work. However, to realize encrypted ML as a ser-

vice, all other ML algorithms will be incorporated

into this distributed framework with suitable modi-

ﬁcations. The speciﬁc contributions here are as fol-

lows:

1. Evaluation and minimization of computational

overhead introduced by encrypted data operations

with distributed and concurrent computing on the

edge devices network.

2. Further, we explore the realization of the KNN al-

gorithm on encrypted data, where the algorithm

needs to be realized in the circuit-based represen-

tation and computations should be performed us-

ing FHE gates.

3. Finally, we analyze how the proper choice of FHE

library differs according to the choice of plat-

forms, and that affects heavily the overall perfor-

mance. Implementation of the ML model is eval-

uated using two different HE libraries: NuFHE

library (NuF, ) and OpenFHE library (Ope, ),

where NuFHE can exploit GPU advantages and

OpenFHE claims to support faster bootstrapping.

The paper structure is as follows: Section 2 ex-

plores challenges and limitations of adapting single-

edge implementation of encrypted KNN on a dis-

tributed platform. Section 3 details the implementa-

tion of encrypted KNN for the distributed platform.

Finally, Section 4 demonstrates the timing require-

ment of the proposed framework and Section 5 men-

tions the conclusion and some future directions of this

work.

Overall, most of the existing works related to ML

algorithms on encrypted data are either limited to

cloud computation or applicable to speciﬁc schemes,

where partial HE is sufﬁcient. In this paper, we

will highlight the implementation of encrypted KNN,

which can not be translated to encrypted domain only

with the support of partial homomorphic schemes.

This is because KNN requires handling of complex

encrypted sorting. Hence, we explore this standard

ML model on encrypted data with FHE representa-

tion on distributed edge network (Raspberry Pi). To

the best of our knowledge, this is the ﬁrst effort in

literature to realize end-to-end encrypted KNN pro-

cessing on distributed edge nodes.

In this work, we mostly use NuFHE library (NuF, )

which is the extension of TFHE(TFH, ) and OpenFHE

(Ope, ). Due to the limitation of space, we are omit-

ting the details.(follow the link for more details: https:

//eprint.iacr.org/2024/648 ).

In TFHE or its variant, bootstrapping is the most

costly operation and reduction of bootstrapping in

overall computation remains an important area of

research. There have been many improvements to

the efﬁciency of bootstrapping in TFHE, but it re-

mains a challenging problem. OpenFHE imple-

ments improved bootstrapping proposed in (Miccian-

cio and Polyakov, 2021), which is fastest (75ms) com-

pared to earlier bootstrapping (126ms). This im-

proved bootstrapping makes OpenFHE faster com-

pared to NuFHE library. Hence, in this work we con-

sider NuFHE as well as OpenFHE implementation re-

sults where NuFHE may exploit GPU advantages and

OpenFHE can support faster bootstrapping.

2 LIMITATIONS OF ADAPTING

SINGLE EDGE ENCRYPTED

KNN IMPLEMENTATION FOR

DISTRIBUTED PLATFORM

The KNN is a supervised learning classiﬁer that op-

erates in a non-parametric manner. It leverages the

proximity of data points to classify or predict the

grouping of a given individual data point. The query

data point is assigned a class label based on plurality

voting among K (an integer) nearest neighbors, with

each representing a speciﬁc label. The major steps in

implementing the KNN algorithm are: (a.) Distance

computation between test data points (T

) and training

data points (Tr

), (b.) Sorting of the computed dis-

tances to ﬁnd out the K nearest neighbors and (c.) K

nearest neighbors voting based on the class label of

neighbors.

Implementing the KNN algorithm in an encrypted

domain presents a signiﬁcant challenge, as it requires

the execution of all these steps on encrypted data

Encrypted KNN Implementation on Distributed Edge Device Network

681

throughout. This entails encrypting the dataset, per-

forming distance calculations, and making predic-

tions, all in an encrypted manner. Encrypted KNN

implementation was explored in (Reddy and Chatter-

jee, 2019). However, direct adaptation of that existing

implementation is not feasible in distributed scenario.

To highlight this point, we revisit the encrypted sort-

ing step explained in (Reddy and Chatterjee, 2019).

The proposed encrypted sorting in (Reddy and Chat-

terjee, 2019) is feasible for single nodes only, where

all computed distances are present in a single dis-

tance matrix. However, it cannot be adapted for dis-

tributed platform as individual distance submatrices

are present in each node, and it will not be useful

to sort the encrypted distance matrices of individual

nodes as that will not improve the complexity of sort-

ing over a single node technique. Here, we select K

nearest neighbours from each of the distance subma-

trices, so that K ∗ n values need to be sorted ﬁnally

in the single node. Since the number of nodes in the

cluster n is much smaller than the total number of data

points, the complexity of sorting K ∗ n data is very

small. With this observation, in distributed frame-

work, we implement parallel sorting in edge cluster

to minimize the computational overhead of encrypted

sorting. Partition-based sorting algorithms like merge

sort are indeed popular for their efﬁciency in parallel

sorting. However, when applied to FHE data, these

kinds of partition-based sorts are not applicable. The

reason is that FHE allows computations on encrypted

data without decryption, but it introduces complexi-

ties like the inability to detect exact partition indices

and handling encrypted condition-based loops, as ex-

plained in (Chatterjee and Sengupta, 2015).

In this context, we propose distributed encrypted

sorting and the modiﬁed framework for encrypted

KNN computation on distributed Raspberry Pi clus-

ter.

3 PROPOSED ENCRYPTED KNN

ALGORITHM FOR

DISTRIBUTED PLATFORM

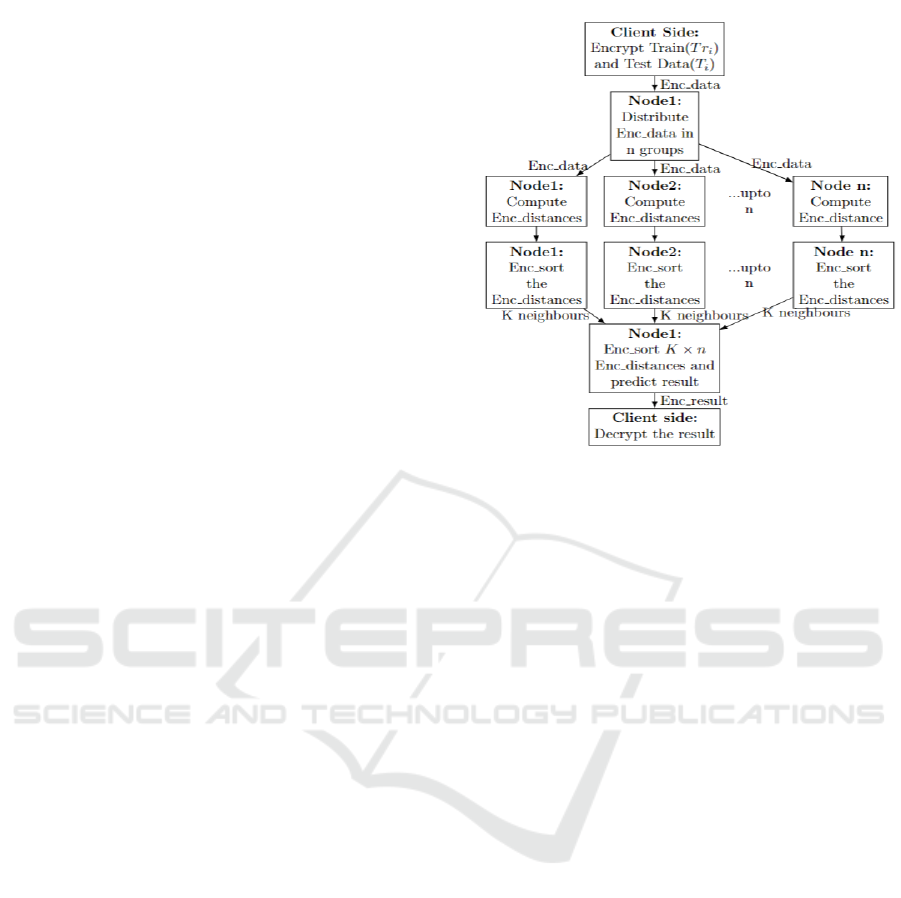
This section introduces our framework tailored to

expedite secure ML utilizing distributed HE, illus-

trated in Figure 1, which performs encrypted pre-

diction within distributed Raspberry Pi nodes. The

framework comprises two primary phases: initial-

ization and prediction, as depicted in Figure 1. In

the initialization phase, the client generates a public-

secret key pair, encrypts the data using these keys and

transfers the encrypted data to edge Node1. Node1

Figure 1: Proposed Distributed Edge Network.

distributes encrypted datasets to all nodes (Node1,

Node2, Node3, . . . Node n) to perform encrypted par-

tial prediction steps concurrently on distributed data

independently. For our work, star topology is the per-

fect ﬁt where Node1 works as the central master node

and due to its scalability we can add or remove nodes

which does not affect the rest of the network. We have

ensured that communication and computation time

overlap to prevent wasting signiﬁcant time only for

communication between master and secondary nodes.

In the next few subsections, we discuss encrypted

KNN implementation following the steps mentioned

in Section 2. For that, we revisit the design of a

few FHE operations (distance computation, encrypted

sorting, etc.) to make them suitable for distributed

platforms.

3.1 Distance Computation

To ﬁnd the nearest data points to the test instance,

the ﬁrst step is to compute the distance from each

train data point. Let us consider the train point vector

as Tr = {C

,.. .,C

} and the test point vector

as T = {C

,.. .,C

}, where m and n are the

number of features for train and test instances respec-

tively, and C

, C

t j

indicate the feature instance of train

data and test data respectively, where i ∈ [1,m] and

j ∈ [1,n].

There are various types of distance available, such

as Minkowski distance, Euclidean distance, Manhat-

tan distance, Hamming distance, and Cosine distance.

The Euclidean distance function is the most popular

one among all of them, but since the multiplication

SECRYPT 2024 - 21st International Conference on Security and Cryptography

682

operation is costly in the encrypted domain compared

to other addition and subtraction operations, we con-

sider the Manhattan distance here for the computa-

tion of the distance matrix. Manhattan distance is

computed as follows: Manhattandistance(Tr,T) =

∑

i=1

−C

In this work, we have distributed encrypted dis-

tance (Enc distance) matrix computation operations

across n number of Raspberry Pi edge devices. The

encrypted train data points are split into n groups

and sent over n edge nodes (Node

, Node

,...Node

)

along with the encrypted test data. For each group

of test data, the Enc distance submatrices dist

[i][ j],

dist

[i][ j],...dist

[i][ j] are calculated. Here, dist

[i][ j]

is the distance submatrix for node k, where i is the in-

dex of the Enc train data and j = 0 shows the value of

Enc distance, and j = 1 shows the label of the Enc -

train data.

For the computation of the Manhattan distance,

two sub-operations are performed in the encrypted

domain (Reddy and Chatterjee, 2019): FHE subtrac-

tion (FHE Subtraction) and encrypted absolute value

computation of the FHE Subtraction result. In case

the FHE Subtraction result is negative, to get the ab-

solute value, we need to take the two’s complement

of the result.

To compute the two’s complement in the en-

crypted domain, ﬁrst, all bits are inverted for the en-

crypted data, and then Enc(1) is added to get the abso-

lute value of the encrypted data (Chatterjee and Sen-

gupta, 2018).

Since it is important to check if the FHE -

Subtraction result is positive or negative, this en-

crypted decision-making is done using FHE mul-

tiplexer (FHE Mux) (Reddy and Chatterjee, 2019),

where the most signiﬁcant bit (MSB or sign bit (sbit))

of the subtraction result is given as the selection line.

If the FHE Subtraction result is positive, then the sbit

is Enc(0), selecting the FHE Mux result as (C

−C

Otherwise, if the FHE Subtraction result is negative,

then the sbit is Enc(1), selecting the FHE Mux re-

sult as −(C

− C

) . After computation of absolute

values of encrypted distance for individual features,

these distances are added together with FHE Adder

(Reddy and Chatterjee, 2019) circuit to compute the

ﬁnal Enc distance between two encrypted data points.

Final computed Enc distance values are stored in dis-

tance submatrices (dist

[i][ j]) of each node. Further,

encrypted sorting is performed on these distance sub-

matrices to ﬁnd out K nearest neighbours from each

distributed dataset.

3.2 Proposed Distributed Sorting

Algorithm

Algorithm 1: Encrypted Sorting on Distributed Platform.

# Compute Enc distances submatrices in

Node1,Node2,...Node n

# Enc sort on Node1,Node2,...,Node n:

1: for k ← 0 to n do

2: for i ← 0 to len(dist

) do

3: for j ← 0 to len(dist

) − i − 1 do

# create temporary variable v1,v2

4: v1[0] ← dist

[ j][0]

5: v1[1] ← dist

[ j][1]

6: v2[0] ← dist

[ j + 1][0]

7: v2[1] ← dist

[ j + 1][1]

8: temp ← FHE

Subtraction(v1[0],v2[0],size)

9: sbit ← temp[size − 1]

10: snbit ← sbit

11: dist

[ j][0] ← FHE Mux(sbit,v1[0],v2[0])

12: dist

[ j + 1][0] ← FHE Mux(snbit,v1[0], v2[0])

13: dist

[ j][1] ← FHE Mux(sbit,v1[1],v2[1])

14: dist

[ j + 1][1] ← FHE Mux(snbit,v1[1], v2[1])

15: end for

16: end for

17: end for

#get smallest k (number of neighbours) elements from all n nodes and

store in Dist[i][ j] matrix

18: for i ← 0 to n do

19: for i

′

← 0 to K − 1 do

20: Dist[i × K +i

′

][0] ← dist

′

][0]

21: Dist[i × K +i

′

][1] ← dist

′

][1]

22: end for

23: end for

#Enc sort k × n neighbours in Dist matrix with the same algorithm

24: for i ← 0 to len(Dist) do

25: for j ← 0 to len(Dist) − i − 1 do

# create temporary variable v1,v2

26: v1[0] ← Dist[ j][0]

27: v1[1] ← Dist[ j][1]

28: v2[0] ← Dist[ j + 1][0]

29: v2[1] ← Dist[ j + 1][1]

30: temp ← FHE Subtraction(v1[0],v2[0],size)

31: sbit ← temp[size − 1]

32: snbit ← sbit

33: Dist[ j][0] ← FHE Mux(sbit,v1[0],v2[0])

34: Dist[ j + 1][0] ← FHE Mux(snbit,v1[0],v2[0])

35: Dist[ j][1] ← FHE Mux(sbit,v1[1],v2[1])

36: Dist[ j + 1][1] ← FHE Mux(snbit,v1[1],v2[1])

37: end for

38: end for

In this work, we have proposed a distributed en-

crypted sorting (Enc sort) algorithm on n number of

edge nodes. After Enc distance computation, the

Enc

distance submatrices dist

[i][ j] are obtained for

each edge node. Bubble sort is applied to each en-

crypted distance submatrix, where two consecutive

Encrypted KNN Implementation on Distributed Edge Device Network

683

elements are compared and swapped if the ﬁrst ele-

ment is greater. To compare encrypted data, we use

FHE Subtraction and the sign bit (sbit) (Enc(0) or

Enc(1)) of the result is used to check which data is

greater, then FHE Mux circuit is used to store data in

a sorted manner, using the sbit as a selection line, as

shown in sorting Algorithm 1 in lines[2 − 16]. This

process runs concurrently in n edge devices, reducing

signiﬁcant timing overhead.

To decide K nearest neighbors in the entire en-

crypted train dataset, K nearest data from all n nodes

Enc distance submatrices are collected in Dist[i][ j]

matrix at Node1 and sorted again with bubble sort to

obtain the ﬁnal K nearest neighbors as shown from

line 24, in sorting Algorithm 1. These ﬁnal K neigh-

bours will be used for voting.

3.3 K Nearest Neighbours Voting and

Class Label Assignment

After getting K nearest neighbours, the next step is

plurality voting based on class labels of the neigh-

bours and the majority voted label is assigned to test

data input. Here train data labels (L

) are taken as +1

(positive class) and -1 (negative class) in plaintext. To

assign plurality-voted label to test data input, we need

to check which label count is greater than the thresh-

old value (half of the number of neighbours(K/2)). To

perform this, we add MSBs (most signiﬁcant bits) of

the labels for K neighbours using FHE Adder circuit

(Reddy and Chatterjee, 2019), which will be Enc(0)

for +1 label and Enc(1) for −1 label. If positive class

labels (+1) are more than negative class labels (-1),

then the FHE Adder result will be less than K/2 and

vice versa. This FHE Adder result is compared with

the threshold value (K/2) with the help of the FHE -

Subtraction circuit and the MSB of FHE Subtraction

is used as the selection line of FHE Mux to predict

the label of test data.

This predicted encrypted label result is sent to the

client side, where it is decrypted using the secret key

to ﬁnd out the ﬁnal class label of the test instance.

4 RESULTS

In this section, we showcase the experimental out-

comes validating the effectiveness of our framework.

To demonstrate its efﬁcacy, we conduct comparisons

with a centralized HE learning framework, where

overall processing is done on a single Raspberry Pi

node. Additionally, we perform ablation studies to an-

alyze the pivotal factors inﬂuencing the performance

of our framework. These comparative analyses allow

Table 1: Six NAND Gate Operations Distribution on Edge

Nodes.

Node1 Node2 Node3

NuFHE

(Time)

OpenFHE

(Time)

6 0 0 65.7sec 44.68sec

4 2 0 42.84sec 29.82sec

3 3 0 34.59sec 22.38sec

2 2 2 22.14sec 14.91sec

us to assess the impact and advantages of our pro-

posed framework clearly and concisely.

Table 2: Arithmetic Operations on Edge Device.

Operation

NuFHE (Time) OpenFHE (Time)

Addition 56.79sec 32.31sec

Subtraction 43.40sec 39.31sec

Multiplication 32.46min 23.89min

We have employed an encrypted ML algorithm on

a distributed edge cluster. The client side, responsible

for encrypting data and decrypting results, utilizes an

Intel CoreTM i7-8700 CPU @ 3.20GHz × 12 running

Ubuntu 22.04.3 LTS. For performing encrypted oper-

ations on the encrypted data, the edge device Rasp-

berry Pi 4 model B (Broadcom BCM2711, quad-core

Cortex-A72 (ARM v8) 64-bit SoC @ 1.5GHz, 8GB

RAM) is employed. Encrypted data ﬁle sharing and

parallel task execution are facilitated using the Fabric

API. All processes operate in the multicore environ-

ment of Raspberry Pi boards and to alleviate computa-

tion overhead, operations are distributed across mul-

tiple Raspberry Pi devices, forming a distributed edge

device network.

Before implementing encrypted KNN, ﬁrst, we

distributed basic gate logic operations among edge

nodes to observe the timing gain using FHE primi-

tive gates provided by NuFHE and OpenFHE library.

However, in the OpenFHE library, serialization and

ﬁle writing for binary context (BinFHEContext) are

not supported in Python currently. Consequently, our

OpenFHE implementations have been restricted to

single-node setups. Nevertheless, we have included

estimated execution times for distributed edge clus-

ters to facilitate comparison. This is in anticipation

of the possibility of enabling ﬁle writing in the fu-

ture. We have distributed 6 NAND gate operations,

and the timing overhead is reduced signiﬁcantly af-

ter distributing among edge nodes as shown in Table

1. Certain mathematical operations, including addi-

tion, subtraction, and multiplication, were also ana-

lyzed after being translated in their encrypted form

on a single pi board(Table2).

Following the successful evaluation of the ba-

sic gate-level performance, the subsequent step in-

volved implementing the encrypted KNN algorithm

SECRYPT 2024 - 21st International Conference on Security and Cryptography

684

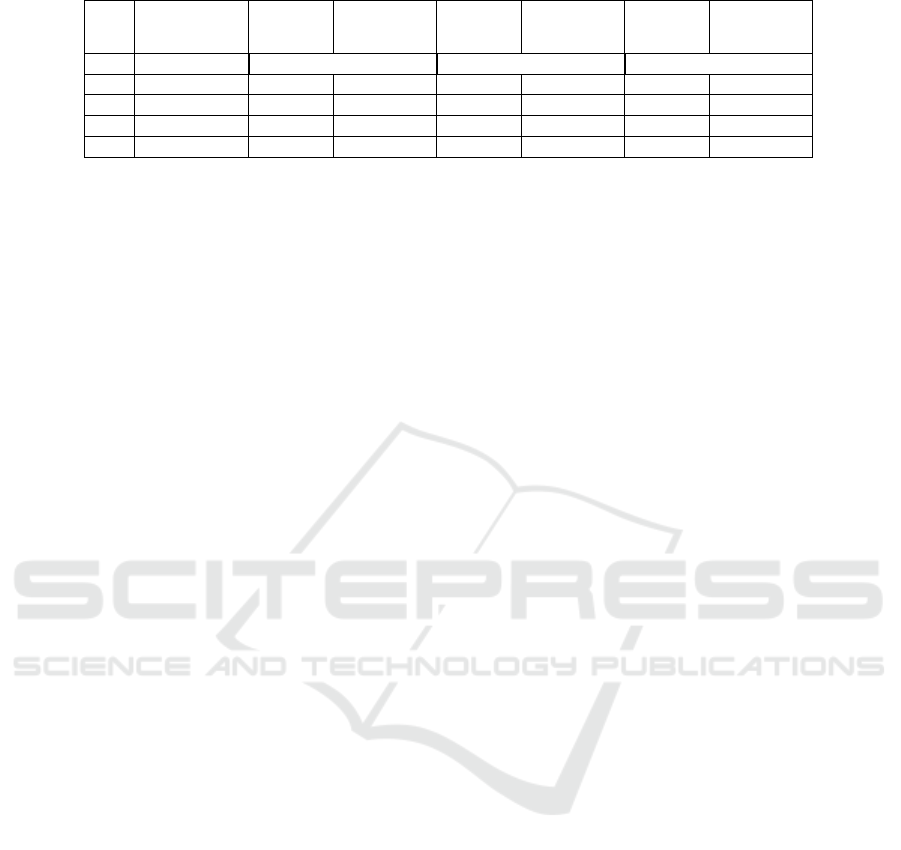
Table 3: Distributed KNN prediction time for K = 3, 5, 7.

S.N.

No. of Edge

Nodes (n)

NuFHE

(Time)

OpenFHE

(Time)

NuFHE

(Time)

OpenFHE

(Time)

NuFHE

(Time)

OpenFHE

(Time)

K=3 K=5 K=7

1 1 11.06hr 7.31hr 11.12hr 7.38hr 11.16hr 7.54hr

2 2 5.54hr 3.66hr 5.55hr 3.71hr 5.57hr 3.77hr

3 3 3.67hr 2.43hr 3.70hr 2.48hr 3.72hr 2.50hr

4 6 1.84hr 1.20hr 1.85hr 1.23hr 1.87hr 1.25hr

on a distributed edge network. The experimentation

was conducted using varying numbers of edge nodes

and different standard neighbor values (K), speciﬁ-

cally 3, 5, and 7. The comparison results for NuFHE

and OpenFHE framework for distributed encrypted

KNN computation are presented in Table3. It is ob-

served that NuFHE with its supported parallel pro-

cessing power works better when more than 20 cores

are present in the selected platform. However, in

our Raspberry Pi board only 4 cores are present and

OpenFHE with the improved bootstrapping works

better in this scenario.

5 CONCLUSION AND FUTURE

WORK

In this work, we have distributed the encrypted com-

putations for KNN among up to six edge devices.

The prediction process takes around 1.2 hours. Al-

though some may argue that the encrypted ML pro-

cessing time is slower than plaintext prediction time

and therefore not practical for real-world applications,

it is important to note that our end-to-end encrypted

framework is suitable for applications where real-time

ML prediction may not be a requirement and out-

comes are acceptable within a few hours. In our future

work, we plan to incorporate other standard ML algo-

rithms in this encrypted ML processing framework on

the edge cluster.

REFERENCES

NuFHE. [Online] https://github.com/nucypher/nufhe.

OpenFHE. [Online] https://www.openfhe.org/.

TFHE. [Online] https://tfhe.github.io/tfhe/.

Chatterjee, A. and Sengupta, I. (2015). Searching and sort-

ing of fully homomorphic encrypted data on cloud.

IACR Cryptol. ePrint Arch., 2015:981.

Chatterjee, A. and Sengupta, I. (2018). Translating algo-

rithms to handle fully homomorphic encrypted data

on the cloud. IEEE Transactions on Cloud Comput-

ing, 6(1):287–300.

Chien, H.-J., Khalili, H., Hass, A., and Sehatbakhsh, N.

(2023). Enc2: Privacy-preserving inference for tiny

iots via encoding and encryption. In Proceedings of

the 29th Annual International Conference on Mobile

Computing and Networking, pages 1–16.

Gouert, C., Mouris, D., and Tsoutsos, N. (2023). Sok: New

insights into fully homomorphic encryption libraries

via standardized benchmarks. Proceedings on privacy

enhancing technologies.

Micciancio, D. and Polyakov, Y. (2021). Bootstrapping in

fhew-like cryptosystems. In Proceedings of the 9th on

Workshop on Encrypted Computing & Applied Homo-

morphic Cryptography, WAHC ’21, page 17–28, New

York, NY, USA. Association for Computing Machin-

ery.

Natarajan, D. and Dai, W. (2021). Seal-embedded: A

homomorphic encryption library for the internet of

things. IACR Transactions on Cryptographic Hard-

ware and Embedded Systems, pages 756–779.

Reddy, B. and Chatterjee, A. (2019). Encrypted Classiﬁca-

tion Using Secure K-Nearest Neighbour Computation,

pages 176–194.

Rizvi, S., Orr, R., Cox, A., Ashokkumar, P., and Rizvi,

M. R. (2020). Identifying the attack surface for iot

network. Internet of Things, 9:100162.

Shrestha, R. and Kim, S. (2019). Integration of iot with

blockchain and homomorphic encryption: Challeng-

ing issues and opportunities. In Advances in comput-

ers, volume 115, pages 293–331. Elsevier.

Singh, S., Sulthana, R., Shewale, T., Chamola, V., Bensli-

mane, A., and Sikdar, B. (2021). Machine-learning-

assisted security and privacy provisioning for edge

computing: A survey. IEEE Internet of Things Jour-

nal, 9(1):236–260.

Sinha, S., Saha, S., Alam, M., Agarwal, V., Chatterjee,

A., Mishra, A., Khazanchi, D., and Mukhopadhyay,

D. (2022). Exploring bitslicing architectures for en-

abling fhe-assisted machine learning. IEEE Trans-

actions on Computer-Aided Design of Integrated Cir-

cuits and Systems, 41(11):4004–4015.

Xiao, Y., Jia, Y., Liu, C., Cheng, X., Yu, J., and Lv, W.

(2019). Edge computing security: State of the art and

challenges. Proceedings of the IEEE, 107(8):1608–

1631.

Encrypted KNN Implementation on Distributed Edge Device Network

685