A White-Box Watermarking Modulation for Encrypted DNN in

Homomorphic Federated Learning

Mohammed Lansari

1,2 a

, Reda Bellafqira

, Katarzyna Kapusta

, Vincent Thouvenot

Olivier Bettan

and Gouenou Coatrieux

IMT Atlantique, Inserm UMR 1101 , 29200 Brest, France

ThereSIS, Thales SIX, 91120 Palaiseau, France

Keywords:

DNN Watermarking, Federated Learning, Homomorphic Encryption, Intellectual Property Protection.

Abstract:

Federated Learning (FL) is a distributed paradigm that enables multiple clients to collaboratively train a model

without sharing their sensitive local data. In such a privacy-sensitive setting, Homomorphic Encryption (HE)

plays an important role by enabling computations on encrypted data. This prevents the server from reverse-

engineering the model updates, during the aggregation, to infer private client data, a signiﬁcant concern in

scenarios like the healthcare industry where patient conﬁdentiality is paramount. Despite these advancements,

FL remains susceptible to intellectual property theft and model leakage due to malicious participants during the

training phase. To counteract this, watermarking emerges as a solution for protecting the intellectual property

rights of Deep Neural Networks (DNNs). However, traditional watermarking methods are not compatible with

HE, primarily because they require the use of non-polynomial functions, which are not natively supported by

HE. In this paper, we address these challenges by proposing the ﬁrst white-box DNN watermarking modulation

on a single homomorphically encrypted model. We then extend this modulation to a server-side FL context

that complies with HE’s processing constraints. Our experimental results demonstrate that the performance of

the proposed watermarking modulation is equivalent to the one on unencrypted domain.

1 INTRODUCTION

Federated Learning (FL) enables multiple data own-

ers to collaboratively train machine learning or deep

learning models without sharing their private data

(McMahan et al., 2017). In a FL round, each client

trains the shared model with its own data. Subse-

quently, the server selects a subset of clients, gathers

and aggregates their model updates, and forms what

is known as the global model for the current round.

This aggregated model is then distributed back to the

clients for further rounds of training, a process re-

peated until the global model converges. Despite the

advantages of data privacy, the integrity of the server

and clients cannot always be ensured, leading to sev-

eral security challenges.

The server may exhibit an honest-but-curious be-

havior, meaning that while it follows to the federated

learning (FL) protocol, it might attempt to infer in-

formation about client data based on the updates re-

ceived in each round. Common inference attacks in-

clude inversion attacks (He et al., 2019) and member-

https://orcid.org/0009-0004-8025-5587

ship inference attacks (Hu et al., 2022; Shokri et al.,

2017), aiming to reconstruct training data from model

parameters. A solution to this issue is the use of Ho-

momorphic Encryption (HE) (Benaissa et al., 2021),

which encrypts client updates before they are sent

to the server for aggregation. HE allows the server

to perform aggregation on encrypted updates without

decryption, thus preventing the server or external ad-

versaries from conducting inference attacks (Zhang

et al., 2020; Xiong et al., 2024).

The second concern involves the potential for

model redistribution by malicious participants, either

during or after the training process, which could lead

to unauthorized proﬁts. Protecting the intellectual

property (IP) of the model is important in this con-

text. Watermarking (Uchida et al., 2017; Fan et al.,

2019; Darvish Rouhani et al., 2019; Bellafqira and

Coatrieux, 2022; Kallas and Furon, 2023; Pierre et al.,

2023), which embeds a secret watermark into the

model’s parameters or behavior for later extraction by

the owner, has emerged as a promising solution. This

technique can be applied either client-side or server-

side in FL context.

186

Lansari, M., Bellafqira, R., Kapusta, K., Thouvenot, V., Bettan, O. and Coatrieux, G.

A White-Box Watermarking Modulation for Encrypted DNN in Homomorphic Federated Learning.

DOI: 10.5220/0012764300003767

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 21st International Conference on Security and Cryptography (SECRYPT 2024), pages 186-197

ISBN: 978-989-758-709-2; ISSN: 2184-7711

Although several solutions propose watermark-

ing the model from the client-side (Liu et al., 2021;

Liang and Wang, 2023; Yang et al., 2023; Li et al.,

2022; Yang et al., 2022), which are compatible with

clients’ update encryption, no existing solution com-

bines server-side watermarking with homomorphic

encryption in a Federated Learning (FL) context.

This is primarily because embedding the watermark

server-side, when updates are encrypted, poses chal-

lenges due to the complexity of the watermarking pro-

cess under HE constraints. Furthermore, server-side

watermarking has been shown to be more robust and

efﬁcient than client-side watermarking (Shao et al.,

2024). More clearly, if each client watermarks its lo-

cal model, the aggregation stage may lead to water-

mark collusion, and consequently, some clients’ wa-

termarks may not be effectively inserted.

For these reasons, in this paper, we explore the

possibility of server-side watermarking in FL using

HE as a privacy-preserving mechanism. Our contri-

butions are as follows:

• We leverage existing FL White-Box watermark-

ing algorithms (Shao et al., 2024; Li et al., 2022)

along with homomorphic encryption in order to

watermark a model with minimal modiﬁcations

of the FL procedure. Speciﬁcally, we address the

challenge posed by non-polynomial functions in

the embedding process, which can be approxi-

mated by low-degree polynomial functions.

• We then implement this scheme within a client-

server FL framework, demonstrating that it is

possible to protect both the conﬁdentiality of

model parameters and intellectual property from

an honest-but-curious server tasked with water-

marking the model.

• Our experimental results indicate that embedding

the watermark using approximated functions does

not detrimentally impact the primary learning task

or the effectiveness of the watermark, even when

subjected to removal attacks such as ﬁne-tuning

and pruning.

2 BACKGROUND & RELATED

WORKS

In this section, we give a brief overview of HE. Then

we deﬁne FL and how HE can be used as a security

mechanism against an honest-but-curious server. Fi-

nally, we introduce FL watermarking to position our

work among existing solutions.

2.1 Homomorphic Encryption

Homomorphic Encryption (HE) is a form of encryp-

tion that allows computations to be carried out on ci-

phertexts, generating an encrypted result that, when

decrypted, matches the outcome of operations per-

formed on the plaintext. This capability enables

secure processing of encrypted data without giving

access to the underlying data, thus preserving the

privacy and conﬁdentiality of data during process-

ing (Bouslimi et al., 2016; Baumstark et al., 2023;

Wang et al., 2024). HE can be categorized into three

types: Partially Homomorphic Encryption (PHE),

which supports a single type of operation (either ad-

dition or multiplication) unlimited times (e.g., Pail-

lier cryptosystem (Paillier, 1999)); Somewhat Ho-

momorphic Encryption (SHE), allowing both addi-

tion and multiplication but with a limited computation

depth, including early versions of FHE schemes (e.g.,

BFV scheme (Fan and Vercauteren, 2012)); and Fully

Homomorphic Encryption (FHE), enabling unlimited

operations of both addition and multiplication on ci-

phertexts. FHE includes schemes like Gentry’s orig-

inal construction, BGV (Brakerski et al., 2014), and

TFHE (Chillotti et al., 2021). BGV and TFHE expand

the capabilities of FHE, with BGV allowing compu-

tations only over integer arithmetic and TFHE en-

abling a broader range of operations, including non-

polynomial functions, but they are unpractical for var-

ious cases regarding the time consumption (Clet et al.,

2021)

The CKKS scheme (Cheon et al., 2017) is par-

ticularly used for enabling operations on encrypted

ﬂoating-point numbers, indispensable for applica-

tions requiring high precision such as machine learn-

ing and statistical analysis. Its scalability and efﬁ-

ciency are advantageous for computational tasks in-

volving vectors, making CKKS suitable for large-

scale applications. Despite its advantages, CKKS is

primarily designed to support the computation over

polynomial functions.

2.2 Secure Federated Learning

Federated Learning (FL) is a machine learning frame-

work that enables K ∈ N

∗

participants to collabora-

tively train a model M

across R rounds of exchange

while maintaining the privacy of their data D

. In the

client-server model of FL (McMahan et al., 2017),

the server initializes the global model M

. At each

round t, the global model M

is distributed to a subset

⊆ {1, . .. , K} consisting of C ×K randomly selected

clients, where C ∈ (0, 1]. Each client k ∈ S

trains

the model locally using their private dataset D

and

A White-Box Watermarking Modulation for Encrypted DNN in Homomorphic Federated Learning

187

sends their updated model M

t+1

back to the server.

The server then aggregates these updates to construct

the new global model M

t+1

. This process repeats until

R rounds are completed (t = R).

The primary vulnerability of FL lies in potential

privacy attacks, such as membership inference (Hu

et al., 2022; Shokri et al., 2017) and model inversion

attacks (He et al., 2019). Speciﬁcally, in client-server

FL, the server aggregates the parameters of received

models at each round. However, the server may be

honest but curious, attempting to infer information

about the client’s data from their parameters without

violating the FL protocol. This concern highlights the

necessity for Secure FL. HE is a prevalent method

employed to mitigate this privacy issue (Zhang et al.,

2020).

Several FL frameworks already support fully ho-

momorphic encryption. For instance, the NVFLARE

FL framework (NVIDIA, 2023) developed by

NVIDIA implements the CKKS cryptosystem using

the TenSEAL library (Benaissa et al., 2021).

For the remainder of this paper, following the ap-

proach proposed in (Zhang et al., 2020), we consider

a Fully Homomorphic Encryption (FHE) cryptosys-

tem characterized by an encryption function Encrypt,

a corresponding decryption function Decrypt, and

a pair of public and private keys (Pub

key

, Priv

key

Clients encrypt their models M

using E and the

public key Pub

key

before transmission to the server.

An encrypted model is denoted as E (M

), meaning

all parameters {w

, . . . , w

} of M are encrypted as

{E (w

), . . . , E (w

)}. Leveraging HE, the server can

aggregate these encrypted models, for instance, us-

ing FedAvg (McMahan et al., 2017). When clients

receive the encrypted model E (M

t+1

), they decrypt

it using Decrypt and the private key Priv

key

to con-

tinue training on M

t+1

. The CKKS cryptosystem is

particularly suitable for FL due to its computational

and communication efﬁciency, making it an optimal

choice for addressing the challenges of FL (Miao

et al., 2022).

2.3 FL Watermarking

Inspired by multimedia watermarking (Bas et al.,

2016), DNN watermarking is a promised solution to

prove ownership of ML models (Sun et al., 2023;

Boenisch, 2021; Bellafqira and Coatrieux, 2022; Li

et al., 2021b; Lukas et al., 2022; Xue et al., 2021).

This technique involves introducing a secret modiﬁ-

cation into the model’s parameters or behavior to em-

bed a watermark (a secret message), which the owner

can later use to verify the presence of the embedded

watermark. We distinguish two types of watermark-

ing according to the setting: Black-Box and White-

Box. Black-Box watermarking consists of embedding

the secret into the behavior of the model. The veriﬁ-

cation process can then be performed without having

full access to the model. In this article, we focus on

the White-Box setting. This latter aims to hide the

secret in the model by assuming that we have access

to its parameters during the veriﬁcation stage. Usu-

ally, the goal is to insert a robust watermark (a binary

string b) into the model’s parameters while preserving

the DNN model performance in the main task.

Despite great results in centralized training, DNN

watermarking solutions are hardly utilizable in FL.

Tekgul et al. (Tekgul et al., 2021) illustrates well

the fact that using existing centralized watermarking

techniques in FL is possible in two ways: embedding

the watermark before the FL or at the end. However,

both approaches risk the model being redistributed by

a malicious client with the watermark either absent

or barely present. Addressing DNN watermarking

within the FL context introduces new constraints and

security considerations (Lansari et al., 2023). Based

on these considerations, two main strategies for em-

bedding have been explored. The ﬁrst allows each

client k to watermark their local model M

, treating

the server as honest but curious. Various techniques

supporting client-side embedding have been proposed

(Li et al., 2022; Yang et al., 2023; Yang et al., 2022;

Liu et al., 2021; Liang and Wang, 2023), which are

compatible with encrypting updates before transmis-

sion to the server, as indicated in Table 1. Never-

theless, client-side watermarking faces several draw-

backs:

1. Client Selection: This approach involves selecting

a subset of clients in each round for communica-

tion efﬁciency, yet the effectiveness of the embed-

ding process in this context remains unproven.

2. Cross-Device Setting: Implementing client-side

watermarking can be challenging when K ≥ 10

and devices have limited computational power.

3. Multiple Watermarks: With multiple clients at-

tempting to embed their binary strings, the tech-

nique must prevent conﬂicts and interference be-

tween the various watermarks.

Given these challenges, server-side watermark-

ing presents a more viable solution. In this context,

the server embeds the watermark post-aggregation.

Several server-side techniques have been developed

(Tekgul et al., 2021; Shao et al., 2024; Chen et al.,

2023a; Li et al., 2021a; Yu et al., 2023); however, as

shown in Table 1, none of the current state-of-the-art

watermarking solutions incorporate HE (Homomor-

phic Encryption) as a privacy measure to prevent the

SECRYPT 2024 - 21st International Conference on Security and Cryptography

188

Table 1: Our method among existing FL White-Box watermarking techniques.

Existing Works White-Box Embedding HE Compatibility

FedIPR (Li et al., 2022) ✓ Client(s) ✓

FedCIP (Liang and Wang, 2023) ✓ Client(s) ✓

FedTracker (Shao et al., 2024) ✓ Server ✗

Yu et al. (Yu et al., 2023) ✓ Server ✗

Proposed method ✓ Server ✓

server from inferring information about the clients’

datasets during the watermark embedding process.

3 PROPOSED METHOD

In this section, we present an overview of our new

white-box watermarking modulation in the context of

Homomorphic Encrypted Federated Learning. We

then detail how the embedding and extraction pro-

cesses are conducted on the context of a single en-

crypted model before generalizing to the context of

homomorphic encrypted federated learning.

3.1 Overview of the Proposed Method

In this subsection, we introduce the ﬁrst watermark-

ing modulation compatible with homomorphically

encrypted DNN models in the context of Federated

Learning (FL). Our approach relies on existing FL

White-Box watermarking algorithms, adapting them

to function with encrypted parameters using Fully

Homomorphic Encryption (FHE). Our contributions

include the redesign of the embedding processes by

approximating non-polynomial functions with low-

degree polynomials.

Figure 1 provides an overview of our proposed

method when deployed in a client-server FL frame-

work. At the initialization phase (Step 1), the server

has unencrypted access to the initial global model M

and watermarks it using our watermarking modula-

tion until the watermark b is successfully embedded.

This initial step does not compromise the privacy of

client data since the global model is not yet trained on

clients’ data.

Once the model is watermarked, it is scattered

to clients for training on their private data (Step 2

in Figure 1). After the clients’ models are updated,

each client encrypts its model and sends it back to

the server, which gathers/aggregates them to form the

new global model (Step 3 in Figure 1). The server

then watermarks the aggregated encrypted model us-

ing our proposed modulation (Step 4 in Figure 1) and

scatters it back to the clients for a new round of train-

ing (Step 5 in Figure 1). This cycle of scattering, local

training by clients, gathering, and watermarking by

the server is repeated until the global model achieves

convergence.

For the sake of simplicity, we ﬁrst explain how

to embed our White-Box watermark in an encrypted

model that is supposed to be in a centralized setting.

Then we generalize the algorithm to K clients in a

client-server FL framework. The following embed-

ding technique is inspired by the White-Box insertion

proposed by (Li et al., 2022; Shao et al., 2024) and

can be viewed as an extension of this type of tech-

nique in the encrypted domain.

3.2 Watermark an Encrypted Model

The White-Box watermarking process aims to embed

a watermark b ∈ {−1, 1}

, coded into N bits, into

the model’s parameters. To do so, we deﬁne an ex-

traction function Ext(.) that will extract a subset of

the model parameters, based on a secret key K

ext

, in

which we embed the watermark. Then we deﬁne a

projection function Pro j(.) that will project the se-

lected parameters into the watermark space using a

secret key K

pro j

. During the watermark veriﬁcation

stage, these two functions will be used to recover the

embedded watermark b.

In the sequel, we note by E (M) (E(b)), the ho-

momorphic encrypted version of the model M (the

watermark b) where all its parameters (components)

are encrypted element-wise by an FHE, respectively.

To embed the watermark b in the model M from its

encrypted version E (M) without decrypting it. And

as stated previously, the ﬁrst step consists of deﬁning

where we want to insert b in M. To do so, we deﬁne

Ext(E (M), K

ext

) as the function that secretly returns,

based on the secret key K

ext

, the encrypted parameters

E (w) in which the watermark will be embedded, the

ext

could be the positions of the parameters selected

to carry the watermark:

Ext(E (M), K

ext

) = E (w) (1)

The second step consists on deﬁning

Pro j(E (w), K

pro j

), a projection function that

maps the extracted parameters into the watermark

space ”{−1, 1}

”. This function is parameterized by

a secret key K

pro j

. Most of White-Box watermarking

A White-Box Watermarking Modulation for Encrypted DNN in Homomorphic Federated Learning

189

Client 1 Client 2 Client 3

Encrypt Encrypt Encrypt

Server

Watermark

Re-Embedding

Server

Client 1 Client 2 Client 3

Decrypt Decrypt Decrypt

Client 1 Client 2 Client 3

Local Training

Step 1 & 2 Step 3 & 4 Step 5

: Encrypted DNN

: Freshly Watermarked DNN

Local Training

Server

Watermark

Pre-Embedding

Local Training

: Freshly Trained DNN

Figure 1: High-level view of the proposed method. (Step 1) The server initializes the global model, performs a pre-embedding

to watermark it, and distributes it to the clients; (Step 2) Each client trains the model on its private dataset; (Step 3 & 4) Each

client encrypts and sends its updated model to the server which aggregates them to get the new global model. The server then

embeds the watermark using the method described in Section 3.2; (Step 5) The server distributes the global model to each

client, which decrypts it; Steps 2 to 5 are repeated until the global model converges.

schemes (Uchida et al., 2017; Li et al., 2022; Shao

et al., 2024) consider K

pro j

as random matrix of size

m × N where m = |E (w)| is the size of the extracted

parameters and N = |b| is the size of the watermark.

The projection function is deﬁned as follows:

Pro j (E (w), K

pro j

) = E (w)K

pro j

= E (b

pro j

) (2)

Note that the multiplication in Equation 2 is pos-

sible because the model parameters E (w) are homo-

morphically encrypted. Once the extraction and pro-

jection functions are deﬁned, along with their cor-

responding secret keys, the embedding process in-

volves minimizing the distance between b

pro j

and b

in their homomorphically encrypted forms, E (b

pro j

)

and E(b), using a distance metric d, given as follows:

E = min

d(E (b), E (b

pro j

)) (3)

In our work, we utilize the Hinge-loss (Fan et al.,

2019) as a distance function. This is used to measure

the distance between b and b

pro j

as follow:

d(E (b), E (b

pro j

)) =

∑

i=1

ReLU(µ − E (b

)E (b

pro j

))

(4)

Where µ is set to 1. The ReLU (Li and Yuan,

2017) function is not polynomial and therefore can-

not be efﬁciently computed using state-of-the-art FHE

(some of the recent works on FHE focuses on solving

this problem, ex. using programmable bootstrapping

(Chillotti et al., 2020; Chillotti et al., 2021)). This

issue is well-known in the ﬁeld of secure encrypted

neural networks (Chen et al., 2018) (Bellafqira et al.,

2019). The problem leveraged by ReLU (or any non-

polynomial function) can be solved by approximating

this latter by its a-degree polynomial approximation.

In this context, we take the second-degree polyno-

mial approximation from Gottemukkula et al. (Gotte-

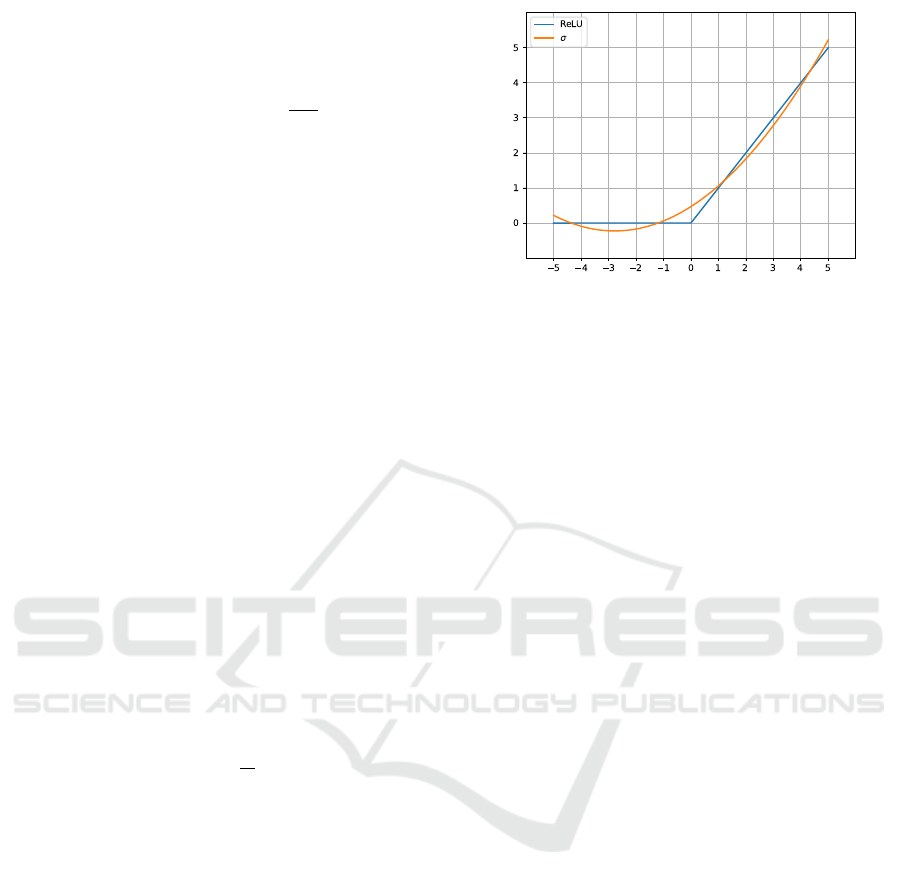
mukkula, 2019) which is represented in Figure 2 and

is deﬁned as:

σ(x) = 0.09x

+ 0.5x + 0.47 (5)

Replacing ReLU by σ results in the following dis-

tance for our loss term :

d(E (b), E (b

pro j

)) =

∑

i=1

σ(µ − E (b

)E (b

pro j

)) (6)

σ is a good approximation for x ∈ [−5; 5]. To have x as

close as possible to this interval, we add an L

-norm

regularisation term on the parameters E(w)

(w) =

∑

h=0

E (w

)

= E (

∑

h=0

) (7)

Finally, we have the following loss function to em-

bed the watermark:

L = d(E (b), E (b

pro j

)) +

(w)

∑

i=1

σ(µ − E (b)

E (b

pro j

)

) +

(w) (8)

where λ is a hyper-parameter to control the impact of

the L

-norm on the model parameters (aka the weight

decay parameter (Loshchilov and Hutter, 2017)).

SECRYPT 2024 - 21st International Conference on Security and Cryptography

190

To optimize the equation 8, and update the ex-

tracted parameters, we use the gradient descent (Du

et al., 2019) which is given as:

E (w

t+1

) = E (w

) − α

∂L

∂w

(9)

where α is the learning rate and w

t+1

represents the

updated parameters from w

. The partial derivative in

equation 9 is feasible because the loss function L is

homomorphically encrypted.

The watermark retrieval process is straightforward

and it requires the knowledge of the secret keys (K

ext

pro j

). Let us consider a plain-text suspicious model

∗

, to extract the watermark, the ﬁrst step consists of

computing:

pro j

= Pro j (Ext (M

∗

, K

ext

), K

pro j

) (10)

where b

pro j

is the reconstructed watermark from M

∗

where its components are not necessarily belongs to

{−1, 1}. To get a watermark with the same range as

the embedded watermark, we threshold b

pro j

based

on the sign of its components using the function

sgn(b

pro j

) = b

ext

where

sgn(x) =

(

1 if x > 0

−1 otherwise

(11)

Then we can compare b and b

ext

to evaluate the

embedding. To quantify this we use a common met-

ric for static White-Box watermarking which is the

Watermark Detection Rate (WDR). This metric is ex-

pressed using the following formula

WDR(b, b

ext

) = 1 −

× H(b, b

ext

) (12)

where b is the message that we want to insert, b

ext

the reconstructed binary string (see Equation 10) and

H is the distance deﬁned, in the case of two binary

sequences a and c of N bits, as

H(a, c) = |{i ∈ [1; N]|a

= c

}| (13)

Where |.| is the cardinal of the set. If

WDR(b, b

ext

) is near to 1 or 0, b and b

ext

are highly

correlated which correspond to a good embedding of

b in M while WDR(b, b

ext

) close to 0.5 correspond to

a wrong embedding.

3.3 FL Encrypted Watermarking

Performing DNN watermarking from the server side

consists of embedding the watermark b just after the

aggregation of the clients’ updates following the ex-

traction and projection steps described in 3.2. In the

literature, we generally distinguish two steps: a pre-

embedding and a re-embedding phases (Tekgul et al.,

Figure 2: ReLU and its second degree approximation σ in

the [−5;5] interval.

2021; Li et al., 2022; Shao et al., 2024). The ﬁrst

one performs embedding before the training and the

other one at each round. Both are based on the same

function but with different hyperparameters. In our

paper, they are different with regard to the use of ho-

momorphic encryption. Following the encryption and

decryption functions deﬁned in Section 2.2, we sup-

pose that the server owns Pub

key

, the public encryp-

tion key, and since it is in charge of the watermark

embedding it also owns the watermarking parameter

set θ = {b, K

ext

, K

pro j

} with b the watermark, K

ext

the

secret extraction feature key and K

pro j

the secret pro-

jection matrix. On their side, each client only owns

(Pub

key

, Priv

key

), i.e., the public and private encryp-

tion keys, respectively.

In the sequel, we depict the initialization of FL

watermarking in the plain-text domain, i.e., our pre-

embedding phase, and by next our re-embedding

phase, in the context of K clients in the encrypted do-

main.

3.3.1 FL Watermarking Initialization

The ﬁrst step of this procedure consists of randomly

initializing the model M to get M

. Once the model

is initialized one can perform the second step which

aims to embed the desired binary string b directly

in the un-encrypted version of M

to have parame-

ters already optimized for the watermarking embed-

ding later. Doing so reduces the number of epochs

needed for re-embedding the watermark during the

FL. It is this embedding we deﬁne as the Watermark

Pre-Embedding function (WPE(M

, θ)). It simply

embeds the watermark into the initialized model M

following the method described in Section 3.2 using

the secret parameters θ until the watermark is embed-

ded resulting in a watermarked model

, where ”ˆ.”

denotes the result of a watermark embedding proce-

dure.

A White-Box Watermarking Modulation for Encrypted DNN in Homomorphic Federated Learning

191

Note that since the server works with the plaintext

version of M

, as exchanges with clients have not yet

started, it has no limitation in the number of compu-

tations nor epochs performed for the embedding con-

trarily to the re-embedding phase, where the server

will manipulate homomorphically encrypted model

parameters. Thus one can perform this embedding

until the watermark is perfectly embedded. The em-

bedding is done when the watermark is perfectly em-

bedded i.e., WDR(b, b

ext

) = 1. The model is then en-

crypted, using Encrypt and Pub

key

, and the resulting

encrypted model E (

) is sent to the clients.

3.3.2 FL Watermarking Round

In a FL round t, the server randomly selects C × K

clients from the K clients available. This set of clients

is designated by S

. Then the encrypted global model

E (

t−1

) is sent to each client k ∈ S

to perform local

training as follow:

• LocalTrain(

t−1

, D

): Local training of the

client k on his dataset D

using the received

global model

t−1

, decrypted using Decrypt and

Priv

key

. Client k send back the encrypted updated

model E (M

Once all clients send their encrypted model to the

server. This latter performs aggregation. The aggre-

gation algorithm needs to be compatible with FHE.

In this case, we use FedAvg (McMahan et al., 2017).

This produces the encrypted global model E (M

) to

which the server applies the re-embedding function.

This step has the aim of keeping the watermark on the

model since the local training can degrade the pres-

ence of the watermark. Contrary to the embedding

during initialization, this embedding is performed in

the encrypted domain. This increases the computation

time and leads to restrictions on the number of pos-

sible updates performed as a hyper-parameter. This

re-embedding function (W RE) is deﬁned as follow:

• W RE(E (M

), θ): embedded the watermark into

the encrypted global model E (M

) following the

method described in Section 3.2 using the secret

parameters θ for a ﬁxed number of epoch. This

function returns an encrypted watermarked model

model E (

This procedure is repeated until t = R which cor-

responds to the end of the FL training. We deﬁne

the ﬁnal global model with the watermark.

Algorithm 1 shows the associated pseudo code.

3.3.3 IP Veriﬁcation

The IP veriﬁcation aims to determine if a plagiarized

model comes from FL. Regarding the security hy-

Input : M the global FL model to train; K

the number of clients; θ are the set

of parameters used for the

watermarking; D

local dataset with

samples of the client k;

(Pub

key

, Priv

key

) the public and

private encryption keys,

respectively.

Output: Final watermarked model

1 M

← Initialize(M);

← W PE(M

, θ);

3 for each round t=1,. . . ,R do

4 S

← Randomly select C × K clients;

5 for each client k ∈ S

t−1

← Decrypt(E (

t−1

), Priv

key

);

7 M

← LocalTrain(

t−1

, D

);

8 E (M

) ← Encrypt(M

, Pub

key

);

9 end

10 E (M

) ←

∑

k∈S

∑

k∈S

E (M

);

11 E (

) ← W RE(E (M

), θ);

12 end

Algorithm 1: Proposed FL Watermarking technique with

FHE.

pothesis, this leak can come from the clients during

the FL or after when the model is deployed. To re-

solve this issue, a third honest party is called to get θ

from the server. This one computes sgn(b

pro j

) from

the decrypted suspect model M

∗

; b

pro j

is deﬁned as:

pro j

= Pro j (Ext (M

∗

, K

ext

), K

pro j

) (14)

Then, if WDR(b, sgn(b

pro j

)) ≥ T , where T is the

threshold from which the IP is veriﬁed, then M

∗

comes from the federation. This decision is simpli-

ﬁed by the following function

Verify(M

∗

, θ) =

(

1 if WDR(b, sgn(b

pro j

)) ≥ T

0 otherwise

(15)

4 EXPERIMENTAL RESULTS

The experimental section is divided into two conﬁgu-

rations:

Real FHE: The ﬁrst one is conducted using a real

Fully Homomorphic Encryption (FHE) library. For

computational efﬁciency, we employ a one-layer neu-

ral network with a small message size b (N = 16).

This conﬁguration evaluates the impact of the water-

marking on the model performance (ﬁdelity) using a

subset of the public dataset MNIST. The primary aim

SECRYPT 2024 - 21st International Conference on Security and Cryptography

192

of this part is to demonstrate a proof of concept for

our watermark modulation on homomorphically en-

crypted parameters.

Simulated FHE: The second conﬁguration is con-

ducted in plaintext, allowing greater ﬂexibility regard-

ing the number of tests and the size of b (N = 256).

We evaluate, using ResNet18 and the public dataset

CIFAR10, the performance differences for both the

main task and the watermark embedding, depending

on the use of polynomial approximation. Addition-

ally, we evaluate the watermark’s robustness against

attacks such as ﬁne-tuning and pruning.

FL Setting: In both experimental setups, we set the

number of clients to K = 10. At each round, half

of the clients are randomly selected by the server to

contribute to the aggregation process (C = 0.5). Ad-

ditionally, each client performs ﬁve local epochs of

training on their IID dataset.

Metrics: Model performance is evaluated using Acc,

which denotes accuracy over the testing set, while

WDR is used to measure the effectiveness of the wa-

termark embedding. The accepted threshold for the

watermark, T , is set at 0.98, and the allowable differ-

ence between the un-watermarked and watermarked

model is set at ε = 0.05.

For readability purposes, the details of both set-

tings are summarized in Table 2.

4.1 Real FHE Training

In this subsection, we evaluate the performance of

our watermarking modulation in terms of effective-

ness, ﬁdelity, and efﬁciency, while also providing de-

tails on the computational overhead complexity. We

use a simple one-layer neural network and the CKKS

scheme as an FHE cryptosystem from TenSEAL.

4.1.1 Fidelity & Effectiveness

Fidelity requires that the performance of the model

with a watermark (

) should be as close as possible

to that of the model without a watermark (M

). We

assess this by comparing the accuracy of

with M

using the test set D

test

. If the difference in accuracy is

less than the tolerated error ε, then the watermarking

technique satisﬁes the ﬁdelity requirement.

Effectiveness involves ensuring that the water-

mark modulation properly embeds the watermark into

the model. This is veriﬁed by comparing the original

watermark b with the watermark extracted (b

ext

) from

the ﬁnal model M

. The effectiveness is quantiﬁed

by the Watermark Detection Rate (WDR, see Equa-

tion 12) and compared against a predeﬁned threshold

T (as deﬁned in Table 2). The WDR must exceed

the threshold to certify the intellectual property pro-

tection of the model.

These requirements can be summarized as fol-

lows:

1. Verify(

, θ) = 1

2. |Acc(

, D

test

) − Acc(M

, D

test

)| < ε

Table 3 presents the test accuracy and the WDR

between M

and

. The ﬁrst requirement is consis-

tently met by

, as for all test runs, WDR(

, θ) =

1.00, which is above the threshold T = 0.98. From

this data, we observe that the watermark has a

negligible impact on performance, as evidenced by

|Acc(

, D

test

) − Acc(M

, D

test

)| = 0, which is less

than ε.

4.1.2 Efﬁciency: Computational Overhead

As clearly deﬁned by Tekgul et al. (Tekgul et al.,

2021) the watermark embedding should not in-

crease the communication and computation complex-

ity overhead. Our method does not increase the com-

munication overhead compared to a FL with HE as a

privacy mechanism. However, we increase the com-

putation in the WRE (i.e., Watermark Re-Embedding

function) step. To perform one epoch for the em-

bedding, W RE computes exactly one forward pass to

compute b

pro j

and one backward pass over the loss

(Equation 8).

L =

∑

n=1

σ(µ − b

E (b

pro j

)) + λ

∑

h=0

E (w

)

(16)

Regarding the matrix multiplications performed dur-

ing the backward pass, the computation complexity is

O(2N)+O(2MN) homomorphic multiplication in the

worst case where N is the size of the watermark b and

M the number of rows in K

pro j

4.2 Simulated FHE Training

In this subsection, we evaluate the robustness of the

proposed watermarking modulation against the ﬁne-

tuning and pruning attacks. We evaluate as well the

impact of the approximation of the ReLU function

and verify the robustness of our watermark. Due to

the use of HE, which seriously increases computation

time, these experiments were conducted using a sim-

ulated framework, that is to say, a framework where

computations are conducted on clear values but with

exactly the same calculations in clear as if HE was

used.

A White-Box Watermarking Modulation for Encrypted DNN in Homomorphic Federated Learning

193

Table 2: Experimental settings used for each conﬁguration.

Simulated FHE Real FHE

Dataset CIFAR10 (Krizhevsky et al., 2009) Binary classiﬁcation of ”3” and ”8”

with MNIST (LeCun and Cortes, 2010)

Watermark Size N = 256 N = 16

Model ResNet18 One-layer neural network

FL Setting C = 0.5 clients are selected among 10 clients at each round. 5 epochs are

performed by the selected clients. The distribution is I.I.D.

Metrics Acc is used for the main task accuracy while WDR is used for the watermark.

The accepted threshold for the watermark recovery is deﬁned by T = 0.98. The

accepted difference between the un-watermarked model and the watermarked

one is ﬁxed to ε = 5e − 2.

Table 3: Comparison of the test accuracy and WDR for M

and

. Values shown are mean and their corresponding

standard deviation computed over 5 runs.

Accuracy WDR

Test b

With Watermark 0.97 ± 9e − 4 1.00 ± 0.00

Without Watermark 0.97 ± 2e − 3 0.46 ± 0.10

Table 4: Comparison of the test accuracy and WDR accord-

ing to the use of an approximation for the embedding. Show

values are mean and their corresponding standard deviation

computed over 5 runs.

Accuracy WDR

Test b

ReLU 0.81 ± 1e − 3 1.00 ± 0.00

σ & R 0.81 ± 2e − 3 1.00 ± 0.00

4.2.1 Impact of the Approximation

The error generated by the ReLU approximation in

the distance function d (see Equation 4) needs to be

quantiﬁed experimentally. Table 4 shows the differ-

ence between both approaches. The ﬁrst line shows

the loss function that uses ReLU (corresponding to

Equation 4 and denominated as ”ReLU” in the Table

4). The other one corresponds to the loss function

that uses the approximation deﬁned in Equation 8 and

is denominated by ”σ + R” in the Table 4. From this

result, we can see that using the approximation does

not affect both the main task and the watermark.

4.2.2 Robustness

The watermark should be robust against various types

of attacks. The attacker can try to remove the water-

mark using techniques such as ﬁne-tuning and prun-

ing. The primary goal of the attacker is to derive a sur-

rogate model that does not contain the watermark. At

the same time, he seeks to maintain the performance

of the attacked model on the main task. These two

goals need to be reached with a signiﬁcantly lower

Table 5: Fine-tuning of a watermarked model during 100

epochs with the whole dataset.

Accuracy WDR

Epoch Test b

0 0.81 1.00

25 0.82 1.00

50 0.83 1.00

75 0.84 1.00

100 0.84 1.00

complexity than training the model from scratch or

having access to all the training data, which is difﬁ-

cult to achieve, especially in a federated context. In

other words, the attacker aims to build a model M

from

following the two conditions

• Verify(M

, θ) = 0

• |Acc(M

, D

test

) − Acc(

, D

test

)| < ε

Fine-Tuning. The ﬁne-tuning attack consists of con-

tinuing to perform the training algorithm with a train

set to erase the watermark. In this tests, we ﬁne-tuned

in centralized training during 100 epochs assum-

ing that the attacker has access to the whole training

dataset; a very strong hypothesis. The learning rate

was ﬁxed to 1e − 2. As we can see from Table 5, per-

forming ﬁne-tuning cannot degrade the detection of

the watermark.

Pruning Pruning (Blalock et al., 2020) is a common

method used to erase the watermark since the parame-

ters used during the embedding are often not the same

for the main task. In this experiment, we used the

pruning method that consists of zeroing out the pa-

rameters with the lowest L

-norm. As we can see

from Figure 3 the WDR is equal to 1.00 until 90%

of parameters are pruned. These results demonstrate

that our watermark is resistant to pruning since the

IP of the model can be veriﬁed for any percentage of

parameters pruned.

SECRYPT 2024 - 21st International Conference on Security and Cryptography

194

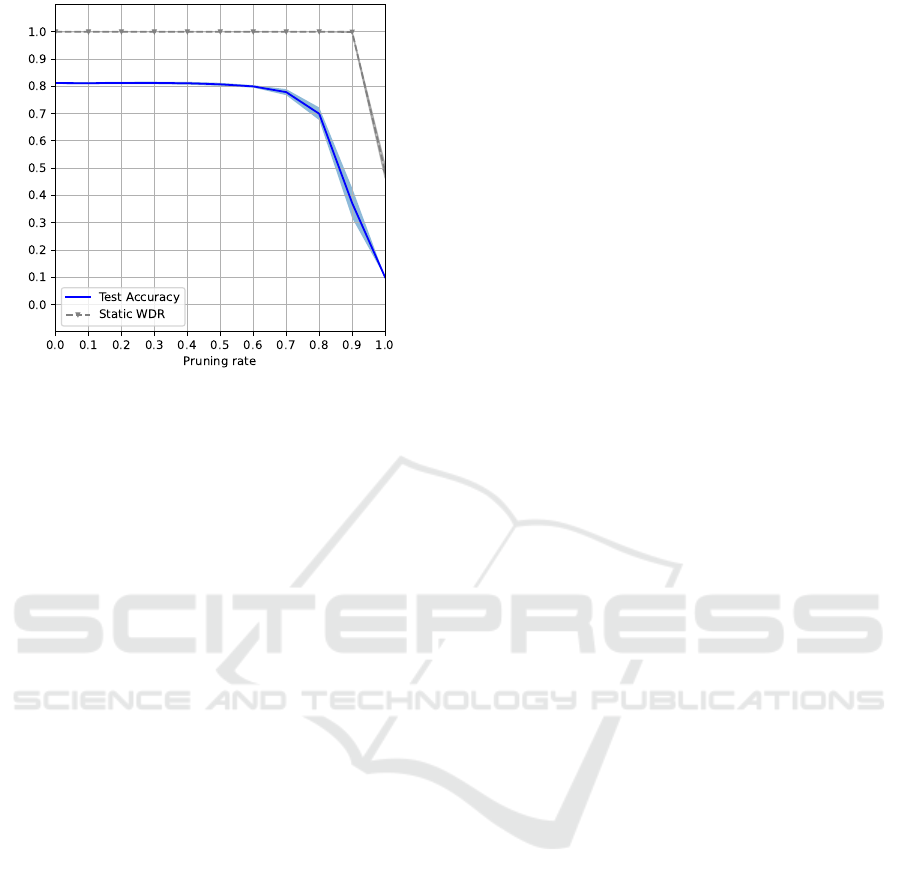
Figure 3: Test accuracy and WDR according to the pruning

rate. Values shown are mean and their corresponding stan-

dard deviation computed over 5 runs.

5 DISCUSSION & LIMITATION

OF THE STUDY

Our watermarking modulation has the same perfor-

mance in terms of robustness compared to the one

performed without HE in FedTracker (Shao et al.,

2024) and FedIPR (Li et al., 2022). However, it is

well known in the literature that this type of tech-

nique is not resistant to some attacks such as overwrit-

ing (Darvish Rouhani et al., 2019), Privacy Inference

Attack (PIA) (Wang and Kerschbaum, 2019), and

ambiguity attack (Kapusta et al., 2024; Chen et al.,

2023b). Our method proves the feasibility of White-

Box watermarking in this speciﬁc context but other

White-Box watermarking techniques (e.g. (Nie and

Lu, 2024; Lv et al., 2023)) can be adopted follow-

ing the same proposed methodology. As mentioned

before, the main issue remains in the non-polynomial

operations. They can be approximated by an a-degree

polynomial but the overhead can grow exponentially

with a, so it is a compromise to be found according to

the application’s needs.

As discussed before, the main issue with FHE

cryptosystems is their computation overhead. Each

computation, such as vector-matrix multiplication

performed in Equation 2, can grow exponentially the

embedding time. For the watermarking embedding,

this overhead mainly comes from the sizes of b and

w. Inserting a larger binary string increases the num-

ber of columns for K

pro j

while choosing a larger w in-

creases the rows of K

pro j

. On the other hand, the main

advantage of this modulation is the fact that we em-

bed the watermark in one targeted layer (using K

ext

)

which allows us to perform the embedding without

considering the depth of the model.

In Section 4, we ﬁxed the number of epochs per-

formed in W RE to two because the White-Box wa-

termarking is sufﬁciently robust to resist against the

learning process (as shown in Section 4.2.2) and a

few steps of the re-embedding process are enough to

preserve the watermark during the FL. However, it is

clear that even if the server is in charge of embed-

ding the watermark, it cannot use Verify (Equation

15) since the reconstructed watermark E (b

pro j

) is en-

crypted. Moreover, he cannot perform early-stopping

or increase the number of epochs if the watermark is

not fully embedded since the embedding is blind.

6 CONCLUSION

In this work, we demonstrate the feasibility of wa-

termarking an encrypted neural network in Homo-

morphic FL. We ﬁrst demonstrate how we can ap-

ply White-Box watermarking to encrypted parameters

and shift this method to Homomorphic FL. Our ex-

periments demonstrate the capability of our method

using a TenSeal, a concrete FHE library. However,

current FL White-Box watermarking approaches have

known limitations, such as their vulnerability to over-

writing, and extensive research needs to be done to

design a new HE-compatible White-Box watermark-

ing technique that is more robust to such attacks. Our

next work will investigate how to apply the most re-

cent White-Box watermarking scheme with HE while

minimizing the computation overhead of the homo-

morphic encryption.

ACKNOWLEDGMENTS

This work is funded by the European Union under

Grant Agreement 101070222. Views and opinions ex-

pressed are however those of the author(s) only and do

not necessarily reﬂect those of the European Union or

the European Commission (granting authority). Nei-

ther the European Union nor the granting authority

can be held responsible for them. Additionally, this

work is supported by the CYBAILE industrial chair,

which is leads by Inserm with the support of the Brit-

tany Region Council, as well as by French govern-

ment grants managed by the Agence Nationale de la

Recherche under the France 2030 program, bearing

the references ANR-22- PESN-0006 (PEPR digital

health TracIA project).

A White-Box Watermarking Modulation for Encrypted DNN in Homomorphic Federated Learning

195

REFERENCES

Bas, P., Furon, T., Cayre, F., Do

err, G., Mathon, B., Bas, P.,

Furon, T., Cayre, F., Do

err, G., and Mathon, B. (2016).

A quick tour of watermarking techniques. Watermark-

ing Security, pages 13–31.

Baumstark, P., Monschein, D., and Waldhorst, O. P. (2023).

Secure plaintext acquisition of homomorphically en-

crypted results for remote processing. In 2023 IEEE

48th Conference on Local Computer Networks (LCN),

pages 1–4. IEEE.

Bellafqira, R. and Coatrieux, G. (2022). Diction: Dy-

namic robust white box watermarking scheme. arXiv

preprint arXiv:2210.15745.

Bellafqira, R., Coatrieux, G., Genin, E., and Cozic, M.

(2019). Secure multilayer perceptron based on homo-

morphic encryption. In Digital Forensics and Water-

marking: 17th International Workshop, IWDW 2018,

Jeju Island, Korea, October 22-24, 2018, Proceedings

17, pages 322–336. Springer.

Benaissa, A., Retiat, B., Cebere, B., and Belfedhal, A. E.

(2021). Tenseal: A library for encrypted tensor oper-

ations using homomorphic encryption. arXiv preprint

arXiv:2104.03152.

Blalock, D., Gonzalez Ortiz, J. J., Frankle, J., and Guttag, J.

(2020). What is the state of neural network pruning?

Proceedings of machine learning and systems, 2:129–

146.

Boenisch, F. (2021). A systematic review on model water-

marking for neural networks. Frontiers in big Data,

4:729663.

Bouslimi, D., Bellafqira, R., and Coatrieux, G. (2016). Data

hiding in homomorphically encrypted medical images

for verifying their reliability in both encrypted and

spatial domains. In 2016 38th Annual International

Conference of the IEEE Engineering in Medicine and

Biology Society (EMBC), pages 2496–2499. IEEE.

Brakerski, Z., Gentry, C., and Vaikuntanathan, V. (2014).

(leveled) fully homomorphic encryption without boot-

strapping. ACM Transactions on Computation Theory

(TOCT), 6(3):1–36.

Chen, H., Gilad-Bachrach, R., Han, K., Huang, Z., Jalali,

A., Laine, K., and Lauter, K. (2018). Logistic regres-

sion over encrypted data from fully homomorphic en-

cryption. BMC medical genomics, 11:3–12.

Chen, J., Li, M., and Zheng, H. (2023a). Fedright: An effec-

tive model copyright protection for federated learning.

arXiv preprint arXiv:2303.10399.

Chen, Y., Tian, J., Chen, X., and Zhou, J. (2023b). Effec-

tive ambiguity attack against passport-based dnn in-

tellectual property protection schemes through fully

connected layer substitution. In Proceedings of the

IEEE/CVF Conference on Computer Vision and Pat-

tern Recognition, pages 8123–8132.

Cheon, J. H., Kim, A., Kim, M., and Song, Y. (2017). Ho-

momorphic encryption for arithmetic of approximate

numbers. In Advances in Cryptology–ASIACRYPT

2017: 23rd International Conference on the Theory

and Applications of Cryptology and Information Se-

curity, Hong Kong, China, December 3-7, 2017, Pro-

ceedings, Part I 23, pages 409–437. Springer.

Chillotti, I., Gama, N., Georgieva, M., and Izabach

ene, M.

(2020). Tfhe: fast fully homomorphic encryption over

the torus. Journal of Cryptology, 33(1):34–91.

Chillotti, I., Joye, M., and Paillier, P. (2021). Programmable

bootstrapping enables efﬁcient homomorphic infer-

ence of deep neural networks. In Cyber Security Cryp-

tography and Machine Learning: 5th International

Symposium, CSCML 2021, Be’er Sheva, Israel, July

8–9, 2021, Proceedings 5, pages 1–19. Springer.

Clet, P.-E., Stan, O., and Zuber, M. (2021). Bfv, ckks,

tfhe: Which one is the best for a secure neural net-

work evaluation in the cloud? In Applied Cryp-

tography and Network Security Workshops: ACNS

2021 Satellite Workshops, AIBlock, AIHWS, AIoTS,

CIMSS, Cloud S&P, SCI, SecMT, and SiMLA, Ka-

makura, Japan, June 21–24, 2021, Proceedings, pages

279–300. Springer.

Darvish Rouhani, B., Chen, H., and Koushanfar, F. (2019).

Deepsigns: An end-to-end watermarking framework

for ownership protection of deep neural networks. In

Proceedings of the Twenty-Fourth International Con-

ference on Architectural Support for Programming

Languages and Operating Systems, pages 485–497.

Du, S., Lee, J., Li, H., Wang, L., and Zhai, X. (2019). Gra-

dient descent ﬁnds global minima of deep neural net-

works. In International conference on machine learn-

ing, pages 1675–1685. PMLR.

Fan, J. and Vercauteren, F. (2012). Somewhat practical fully

homomorphic encryption. Cryptology ePrint Archive.

Fan, L., Ng, K. W., and Chan, C. S. (2019). Rethinking

deep neural network ownership veriﬁcation: Embed-

ding passports to defeat ambiguity attacks. Advances

in neural information processing systems, 32.

Gottemukkula, V. (2019). Polynomial activation functions.

He, Z., Zhang, T., and Lee, R. B. (2019). Model inversion

attacks against collaborative inference. In Proceed-

ings of the 35th Annual Computer Security Applica-

tions Conference, pages 148–162.

Hu, H., Salcic, Z., Sun, L., Dobbie, G., Yu, P. S., and Zhang,

X. (2022). Membership inference attacks on machine

learning: A survey. ACM Computing Surveys (CSUR),

54(11s):1–37.

Kallas, K. and Furon, T. (2023). Mixer: Dnn watermarking

using image mixup. In ICASSP 2023 - 2023 IEEE In-

ternational Conference on Acoustics, Speech and Sig-

nal Processing (ICASSP), pages 1–5.

Kapusta, K., Mattioli, L., Addad, B., and Lansari, M.

(2024). Protecting ownership rights of ml models us-

ing watermarking in the light of adversarial attacks.

AI and Ethics, pages 1–9.

Krizhevsky, A., Hinton, G., et al. (2009). Learning multiple

layers of features from tiny images.

Lansari, M., Bellafqira, R., Kapusta, K., Thouvenot, V.,

Bettan, O., and Coatrieux, G. (2023). When feder-

ated learning meets watermarking: A comprehensive

overview of techniques for intellectual property pro-

tection. Machine Learning and Knowledge Extrac-

tion, 5(4):1382–1406.

SECRYPT 2024 - 21st International Conference on Security and Cryptography

196

LeCun, Y. and Cortes, C. (2010). MNIST handwritten digit

database.

Li, B., Fan, L., Gu, H., Li, J., and Yang, Q. (2022). Fedipr:

Ownership veriﬁcation for federated deep neural net-

work models. IEEE Transactions on Pattern Analysis

and Machine Intelligence.

Li, F.-Q., Wang, S.-L., and Liew, A. W.-C. (2021a). To-

wards practical watermark for deep neural networks in

federated learning. arXiv preprint arXiv:2105.03167.

Li, Y., Wang, H., and Barni, M. (2021b). A survey of deep

neural network watermarking techniques. Neurocom-

puting, 461:171–193.

Li, Y. and Yuan, Y. (2017). Convergence analysis of two-

layer neural networks with relu activation. Advances

in neural information processing systems, 30.

Liang, J. and Wang, R. (2023). Fedcip: Federated client

intellectual property protection with traitor tracking.

arXiv preprint arXiv:2306.01356.

Liu, X., Shao, S., Yang, Y., Wu, K., Yang, W., and Fang,

H. (2021). Secure federated learning model veriﬁca-

tion: A client-side backdoor triggered watermarking

scheme. In 2021 IEEE International Conference on

Systems, Man, and Cybernetics (SMC), pages 2414–

2419. IEEE.

Loshchilov, I. and Hutter, F. (2017). Decoupled weight de-

cay regularization. arXiv preprint arXiv:1711.05101.

Lukas, N., Jiang, E., Li, X., and Kerschbaum, F. (2022).

Sok: How robust is image classiﬁcation deep neural

network watermarking? In 2022 IEEE Symposium on

Security and Privacy (SP), pages 787–804. IEEE.

Lv, P., Li, P., Zhang, S., Chen, K., Liang, R., Ma, H., Zhao,

Y., and Li, Y. (2023). A robustness-assured white-box

watermark in neural networks. IEEE Transactions on

Dependable and Secure Computing.

McMahan, B., Moore, E., Ramage, D., Hampson, S., and

y Arcas, B. A. (2017). Communication-efﬁcient learn-

ing of deep networks from decentralized data. In Ar-

tiﬁcial intelligence and statistics, pages 1273–1282.

PMLR.

Miao, Y., Liu, Z., Li, H., Choo, K.-K. R., and Deng, R. H.

(2022). Privacy-preserving byzantine-robust feder-

ated learning via blockchain systems. IEEE Transac-

tions on Information Forensics and Security, 17:2848–

2861.

Nie, H. and Lu, S. (2024). Fedcrmw: Federated model own-

ership veriﬁcation with compression-resistant model

watermarking. Expert Systems with Applications,

249:123776.

NVIDIA (2023). NVFLARE: NVIDIA Federated Learning

Application Runtime Environment. Accessed: 2023-

04-21.

Paillier, P. (1999). Public-key cryptosystems based on com-

posite degree residuosity classes. In International

conference on the theory and applications of crypto-

graphic techniques, pages 223–238. Springer.

Pierre, F., Guillaume, C., Teddy, F., and Matthijs, D. (2023).

Functional invariants to watermark large transformers.

arXiv preprint arXiv:2310.11446.

Shao, S., Yang, W., Gu, H., Qin, Z., Fan, L., and Yang, Q.

(2024). Fedtracker: Furnishing ownership veriﬁcation

and traceability for federated learning model. IEEE

Transactions on Dependable and Secure Computing.

Shokri, R., Stronati, M., Song, C., and Shmatikov, V.

(2017). Membership inference attacks against ma-

chine learning models. In 2017 IEEE symposium on

security and privacy (SP), pages 3–18. IEEE.

Sun, Y., Liu, T., Hu, P., Liao, Q., Ji, S., Yu, N., Guo, D., and

Liu, L. (2023). Deep intellectual property: A survey.

arXiv preprint arXiv:2304.14613.

Tekgul, B. A., Xia, Y., Marchal, S., and Asokan, N. (2021).

Wafﬂe: Watermarking in federated learning. In 2021

40th International Symposium on Reliable Distributed

Systems (SRDS), pages 310–320, Los Alamitos, CA,

USA. IEEE Computer Society.

Uchida, Y., Nagai, Y., Sakazawa, S., and Satoh, S. (2017).

Embedding watermarks into deep neural networks. In

Proceedings of the 2017 ACM on international con-

ference on multimedia retrieval, pages 269–277.

Wang, B., Chen, Y., Li, F., Song, J., Lu, R., Duan, P.,

and Tian, Z. (2024). Privacy-preserving convolutional

neural network classiﬁcation scheme with multiple

keys. IEEE Transactions on Services Computing.

Wang, T. and Kerschbaum, F. (2019). Attacks on digi-

tal watermarks for deep neural networks. In ICASSP

2019-2019 IEEE International Conference on Acous-

tics, Speech and Signal Processing (ICASSP), pages

2622–2626. IEEE.

Xiong, R., Ren, W., Zhao, S., He, J., Ren, Y., Choo, K.-

K. R., and Min, G. (2024). Copiﬂ: A collusion-

resistant and privacy-preserving federated learning

crowdsourcing scheme using blockchain and homo-

morphic encryption. Future Generation Computer

Systems, 156:95–104.

Xue, M., Wang, J., and Liu, W. (2021). Dnn intellectual

property protection: Taxonomy, attacks and evalua-

tions. In Proceedings of the 2021 on Great Lakes Sym-

posium on VLSI, pages 455–460.

Yang, W., Shao, S., Yang, Y., Liu, X., Xia, Z., Schae-

fer, G., and Fang, H. (2022). Watermarking in se-

cure federated learning: A veriﬁcation framework

based on client-side backdooring. arXiv preprint

arXiv:2211.07138.

Yang, W., Yin, Y., Zhu, G., Gu, H., Fan, L., Cao, X., and

Yang, Q. (2023). Fedzkp: Federated model owner-

ship veriﬁcation with zero-knowledge proof. arXiv

preprint arXiv:2305.04507.

Yu, S., Hong, J., Zeng, Y., Wang, F., Jia, R., and Zhou, J.

(2023). Who leaked the model? tracking ip infringers

in accountable federated learning. arXiv preprint

arXiv:2312.03205.

Zhang, C., Li, S., Xia, J., Wang, W., Yan, F., and Liu, Y.

(2020). {BatchCrypt}: Efﬁcient homomorphic en-

cryption for {Cross-Silo} federated learning. In 2020

USENIX annual technical conference (USENIX ATC

20), pages 493–506.

A White-Box Watermarking Modulation for Encrypted DNN in Homomorphic Federated Learning

197