Risk-Stratified Multi-Objective Resource Allocation for Optimal

Aviation Security

Eva K. Lee

1,2,3

, Taylor J. Leonard

2,4

and Jerry C. Booker

The Data and Analytics Innovation Institute, Atlanta GA 30309, U.S.A.

Georgia Institute of Technology, Atlanta GA 30322, U.S.A.

Accuhealth Technologies, Atlanta GA 30310, U.S.A.

The United States Department of Air Force, Pentagon,

Washington

D.C. 20330, U.S.A.

The Transportation Security Administration, The United States Department of Homeland Security, U.S.A.

Keywords: Data-Driven Enterprise Risk Assessment, Aviation Security, Transportation Security, Border Security,

Security Measures, Multi-Objective Portfolio Optimization, Resource Allocation, Risk-Informed Decision,

Mixed Integer Program.

Abstract: This study aims to establish a quantitative construct for enterprise risk assessment and optimal portfolio

investment to achieve the best aviation security. We first analyze and model various aviation transportation

risks and establish their interdependencies via a topological overlap network. Next, a multi-objective portfolio

investment model is formulated to optimally allocate security measures. The portfolio risk model determines

the best security capabilities and resource allocation under a given budget. The computational framework

allows for marginal cost analysis which determines how best to invest any additional resources for the best

overall risk protection and return on investment. Our analysis involves cascading and inter-dependency

modeling of the multi-tier risk taxonomy and overlaying security measures. The model incorporates three

objectives: (1) maximize the risk posture (ability to mitigate risks) in aviation security, (2) minimize the

probability of false clears, and (3) maximize the probability of threat detection. This work presents the first

comprehensive model that links all resources across the 440 federally funded airports in the United States.

We experimented with several computational strategies including Dantzig-Wolfe decomposition, column

generation, particle swarm optimization, and a greedy heuristic to solve the resulting intractable instances.

Contrasting the current baseline performance to some of the near-optimal solutions obtained by our system,

our solutions offer improved risk posture, lower false clear, and higher threat detection across all the airports,

indicating a better risk enterprise strategy and decision process under our system. The risk assessment and

optimal portfolio investment construct are generalizable and can be readily applied to other risk and security

problems.

1 INTRODUCTION

In the aftermath of the September 11, 2001, terrorist

attacks, the President of the United States signed the

Aviation and Transportation Security Act into law

requiring screening conducted by federal officials,

100 percent checked baggage screening, and

expansion of the Federal Air Marshal Service and

reinforced cockpit doors. The Transportation Security

Administration (TSA) was subsequently created to

oversee security in all modes of transportation.

Specifically, a computer-assisted passenger pre-

https://orcid.org/0000-0003-0415-4640

https://orcid.org/0000-0002-6753-9743

screening system, Computer-Assisted Passenger Pre-

screening System (CAPPS) was developed to

evaluate all passengers. The current generation,

Secure Flight, is a risk-based passenger pre-screening

program that matches passengers' names against

trusted traveler lists and watchlists and categorizes

them as high or low-risk (Administration, n.d.). Based

on information derived from both government and

commercial databases, Secure Flight conducts risk

assessments to determine which passengers might be

eligible for TSA precheck screening or standard

screening. The results also prevent potential

104

Lee, E., Leonard, T. and Booker, J.

Risk-Stratiﬁed Multi-Objective Resource Allocation for Optimal Aviation Security.

DOI: 10.5220/0012769000003756

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 13th International Conference on Data Science, Technology and Applications (DATA 2024), pages 104-117

ISBN: 978-989-758-707-8; ISSN: 2184-285X

passengers on the No-Fly List and Centers for

Disease Control and Prevention Do Not Board List

from boarding an aircraft (Sadler, 2016).

Security constructs have been designed as multi-

layered systems to incorporate several security

measures for effective screening. Although numerous

optimization models have been proposed for aviation

security prior to 9/11, the first screening models were

developed post 9/11. These models target checked

baggage for high-risk passengers screened for

explosives, selectee, and non-selectee screening,

where the objectives determine how to deploy and use

limited baggage screening devices optimally.

Subsequently, multiple baggage security models were

developed (McLay, 2011). Other models tackle how

to match the limited security measures to the number

of passengers who need to be screened (Poole &

Passantino, 2003), where findings reveal that a risk-

based system might be more effective than the system

where all passengers and bags receive equal scrutiny.

Multilevel allocation criteria where every

would-be passenger is assigned an assessed threat

value, which quantifies the risk associated with the

characteristics of the passenger was also explored

(McLay, 2011). A similar approach considers how to

allocate explosive-screening devices for checked

baggage in multiple airports settings where

passengers are divided into classes according to their

perceived risk levels were also studied (Sewell et al.,

2012). For device allocation, Sewell et al. modelled

the inherent trade-off decision between using faster,

more accurate, and expensive devices versus slower,

less reliable, but less expensive devices, or some

combination of the two. And Nie et al. modelled the

fraction of passengers who are assigned to threat class

and the staffing needs at each check station within

each screening group.

Stewart and Mueller (Stewart & Mueller, 2017)

are the only publication/s that include all security

measures, though no mathematical analyses and

tradeoffs have been performed. There exists no

mathematical models developed that integrate all

screenings (Checked baggage, Carry-on baggage, and

Passenger) into a comprehensive risk-based system.

In this paper, we integrate passenger, baggage,

and cargo screening operations to model complex

airport security paths. The work adds new

contributions towards the Department of Homeland

Security (DHS)’s on-going risk enterprise

management (ERM) efforts and its desire to

implement an all-encompassing model. This new

system allows TSA to perform risk-aware decisions

to better allocate new resources to benefit overall

aviation security. It maximizes the policymakers’

ability to protect against risks and helps organizations

to utilize their resources in a smart way to achieve

their organizational and strategic objectives.

2 METHODS AND DESIGN

Contribution: In this study, we establish a

comprehensive enterprise risk management-based

resource allocation model that expands upon previous

research and combines all models and security

measures into a single multi-objective portfolio

investment optimization model framework. We also

introduce the concept of “Risk Posture” to measure

the TSA’s resilience and capabilities against any

potential risks. By integrating various aviation

transportation risks and modeling their

interdependencies, the ERM-based model provides a

robust framework for allocating security measures

efficiently across the U.S. aviation sector. The biggest

knowledge gap in previous research is that any type

of optimization model concerning enterprise risk

management was performed only at an operational

level. This work represents the first model that

encompasses a full multi-tier enterprise risk

management approach across strategic, tactical, and

operational levels. It is also the first model to

establish and focus in depth on risk posture. The

security measure and device allocation problem,

combined with a passenger risk assessment policy,

can be used to structure a risk-based screening

strategy to use limited screening resources

effectively. The model is generalizable and can

accommodate additional / different measures, new

technology, or new airport setup.

2.1 Risk Quantification

The Department of Homeland Security defines risk as

“the potential for an unwanted outcome resulting

from an incident, event, or occurrence, as determined

by its likelihood and the associated consequences”

(Council, 2010). By incorporating enterprise risk

management into its strategy, TSA can use a

consistent analytic framework to balance risk and cost

on a common basis across the enterprise (Minsky,

2013). Risk assessments must be connected to goals

and activities within a risk taxonomy to give purpose

and measurement of effectiveness. Only by

quantifying risks and tolerances upfront and using a

common framework can the allocation of resources

be applied to the methods that manage them

effectively.

Risk-Stratiﬁed Multi-Objective Resource Allocation for Optimal Aviation Security

105

We will apply network topology to quantify and

correlate risks. The topological overlap matrix

(TOM) is a similarity measure for biological

networks. TOM was first introduced to analyze

metabolic networks with distinct organisms that are

organized into connected topological modules that

combine in a hierarchical manner (Ravasz, 2002).

The generalized topological overlap measure

(GTOM) introduces a general class of node

dissimilarity measures. It can be used to identify

network modules (sets of tightly connected nodes)

(Yip, 2007), or define novel measures of node

connectivity. These GTOM-based connectivity

measures go beyond the usual nodal degree (number

of connections) by considering higher-order

connections. They are useful in the context of gene

co-expression network analysis.

A topological representation of the TSA risk

factors became a natural fit. GTOM provides a means

to detail the interdependencies and hierarchy for a

correlated risk network that operates without

quantitative values. The resulting risk expressions

will then be integrated into an objective function

within the portfolio optimization problem.

2.1.1 Risk Correlation

Risk correlation influences the overall risk of projects

within an organization. Developing the

interdependencies in enterprise risk for TSA is an

intricate process. It requires an understanding of the

TSA enterprise, their risk appetite, and the associated

risks. Although TSA is a governmental organization

that does not ascribe to a capitalist set of objectives,

ERM is still a very critical tool for the organization to

implement. We proceed by reviewing all current TSA

enterprise risks, tracking their associated risk

appetites, and then defining interdependence

relationships between all the risk factors. Due to

sensitivity issues, we use generic names to discuss the

evolution of a risk interdependency mapping for

TSA, without naming the precise risk terminologies.

Let 𝐴= 𝐴



 be a symmetric adjacency matrix

with entries in [0,1]. For an unweighted network, the

entries take on binary values of 0 or 1 depending on

whether the two nodes are adjacent (connected). A

more complex network might depend on the degree

of interaction between nodes. The matrix is then

normalized such that the diagonals are equal to 1. The

off diagonals are scaled values, thereby extending the

adjacency matrix from the binary case to values in the

range of [0,1]. In a hierarchical network, nodes can be

connected by links carrying a weight 𝐽



. The

weighted degree of node i is defined as: 𝑤



∑



:

𝐽



The original TOM does not account for the

presence of weights 𝑂











∩





|







|











|,|







|





The presence of weights can be accounted for by

replacing the unweighted adjacency matrix with the

normalized coupling matrix (𝐽



/𝐽



) 𝑂









∑





















{



,



}







. If 𝑂



=1 then the node with

fewer connections satisfies the conditions that all its

neighbors are also neighbors of the other node, and it

is connected to the other node. Alternatively, 𝑂



if 𝑖 and 𝑗 are unconnected and the two nodes do not

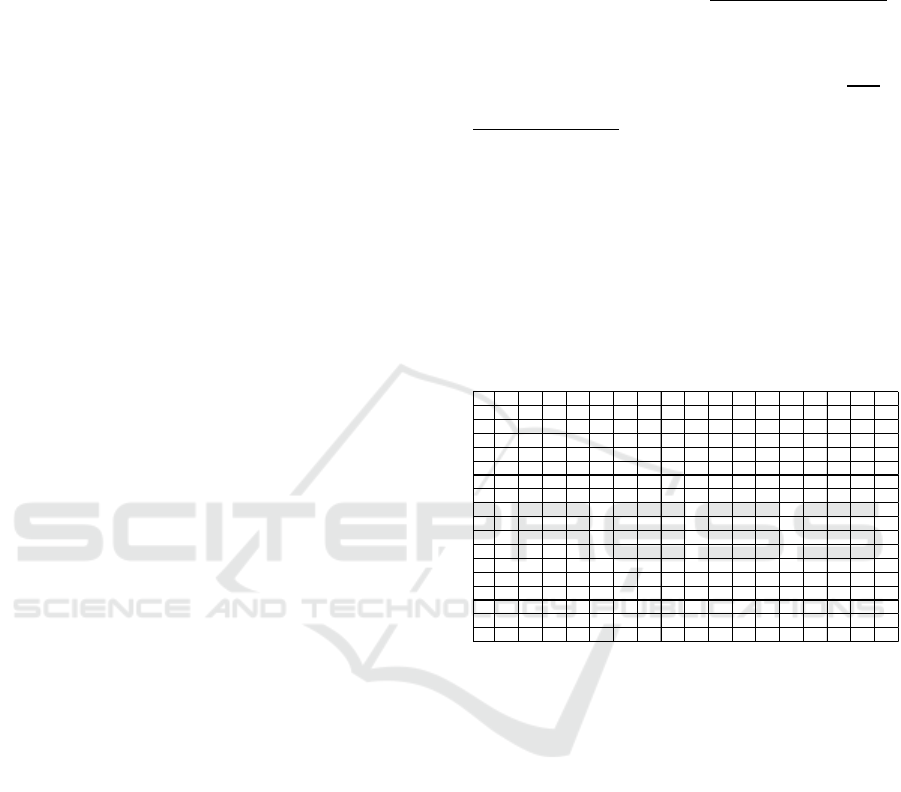
share any neighbors. Table 1 shows the weighted

topological overlap matrix established for 17 TSA-

identified enterprise risk factors.

Table 1: The Weighted Topological Overlap Matrix for 17

TSA-identified enterprise risk factors.

TSA employs a system of interconnected security

layers to deter, detect, and prevent the exploitation of

commercial aviation by terrorists. Figure 1 shows an

example of layers of U.S. aviation security (Kean et

al., 2004). The analysis herein incorporates all current

and newly tested measures but is not a comprehensive

list of security measures employed. Each security

measure has an interdependent relationship with the

enterprise risk factors identified by TSA risk

management leaders. Table 2 shows a security

measure assignment (SMA) matrix that shows the

direct relationships between 26 security measures

against the 17 TSA-identified enterprise risk factors.

The assignment matrix allows us to relate the risk

taxonomy to the security measures put in place.

Depending on the security measure, a failure to detect

a threat could impact multiple risk elements of the

taxonomy.

R1 R2 R3 R4 R5 R6 R7 R8 R9 R10 R11 R12 R13 R14 R15 R16 R17

R1 1.00 0.22 0.13 0.17 0.07 0.07 0.07 0.13 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00

R2 0.17 1.00 0.17 0.07 0.07 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00

R3 0.07 0.17 1.00 0.00 0.17 0.07 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00

R4 0.11 0.14 0.14 1.00 0.14 0.11 0.33 0.21 0.00 0.00 0.00 0.00 0.17 0.00 0.17 0.00 0.00

R5 0.00 0.07 0.17 0.00 1.00 0.17 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00

R6 0.00 0.00 0.08 0.00 0.20 1.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00

R7 0.06 0.06 0.06 0.33 0.06 0.06 1.00 0.33 0.00 0.00 0.00 0.00 0.22 0.00 0.22 0.00 0.00

R8 0.24 0.24 0.24 0.30 0.24 0.24 0.33 1.00 0.19 0.00 0.00 0.00 0.20 0.00 0.20 0.11 0.00

R9 0.33 0.33 0.33 0.00 0.33 0.33 0.00 0.33 1.00 0.14 0.00 0.00 0.20 0.00 0.20 0.11 0.00

R10 0.18 0.26 0.22 0.10 0.22 0.18 0.00 0.00 0.00 1.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00

R11 0.00 0.00 0.00 0.00 0.40 0.40 0.00 0.00 0.00 0.00 1.00 0.00 0.00 0.29 0.00 0.00 0.00

R12 0.27 0.21 0.27 0.19 0.27 0.33 0.22 0.22 0.30 0.33 0.29 1.00 0.41 0.33 0.41 0.24 0.22

R13 0.00 0.00 0.00 0.19 0.00 0.00 0.22 0.22 0.22 0.11 0.00 0.00 1.00 0.00 0.38 0.00 0.00

R14 0.00 0.00 0.11 0.00 0.33 0.33 0.00 0.00 0.00 0.00 0.00 0.00 0.00 1.00 0.00 0.00 0.00

R15 0.26 0.36 0.30 0.33 0.30 0.23 0.22 0.13 0.00 0.00 0.00 0.00 0.17 0.00 1.00 0.14 0.07

R16 0.21 0.18 0.26 0.14 0.26 0.26 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 1.00 0.17

R17 0.25 0.18 0.25 0.14 0.23 0.25 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.14 1.00

DATA 2024 - 13th International Conference on Data Science, Technology and Applications

106

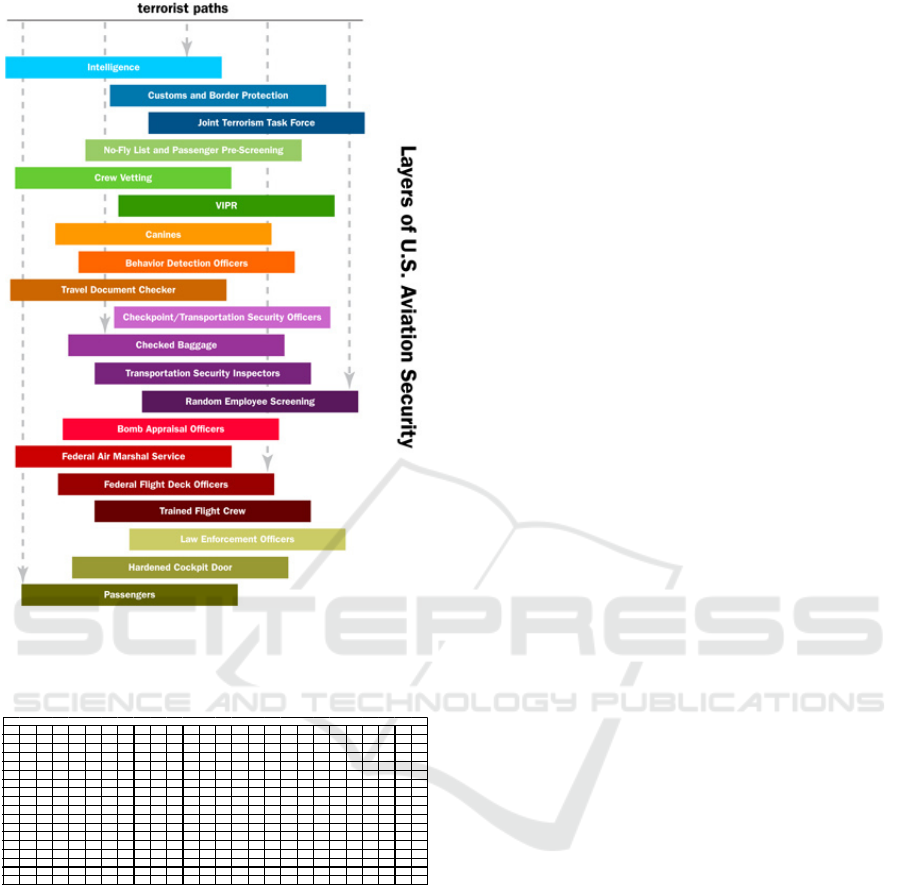
Figure 1: Layers of U.S. Aviation Security (Kean et al.,

2004).

Table 2: Security Measure Assignment (SMA) Matrix.

2.1.2 Risk Posture

We introduce the term “Risk Posture” to describe the

overall readiness to take risks, which is an accurate

description of TSA’s strategy to always be prepared.

We develop a method to calculate the risk posture

evaluation metric as a means to integrate the risk

factors and security measures that are put in place by

TSA. Our goal is to maximize the overall risk posture.

This allows us to utilize the probability of detection

versus the probability of attack. While the exact

values for the probability of detection are unknown,

there are estimated values of the conditional

probability of detection for device type

d given a

particular type of threat, 𝑝



∀ 𝑑∈𝐷, that are derived

from manufacturer capability tests.

The risk posture is calculated by multiplying the

adjusted risk values by the selected security

measures, as summarized below:

 Risk Impact Values (RIV) = TOM*SMA

 Adjusted Risk Values (ARV) = 𝑝



× 𝑅𝐼𝑉



 Risk Posture =

∑





𝑥



× 𝐴𝑅𝑉



(OBJ1)

2.2 Data Collection and Inclusion

In the context of the type of passenger prescreening

system exemplified by Secure Flight, we want to

determine an optimal allocation of threat detection

devices and measures for screening checked baggage,

carry-on baggage, and passengers across a set of

airports so as to maximize the risk posture, maximize

the number of threats to be detected, and minimize the

overall false clear rate while considering passenger

threat classification. We impose constraints on time

available at each check station, flow capacity at

security stations, budget, as well as staffing needs at

each check station.

At airports, all passengers and items pass through

various check stations, with each outfitted with

several security measures for threat detection. It is

standard practice that all passengers and items are

subjected to a series of screenings at mandatory

check-ins. For example, document verification, walk

through metal detectors/body scanners, baggage

scanners, etc. After inspection of a passenger/item,

the screening measure or personnel will give a clear

signal (No Threat) or an alarm signal (Threat). There

are four types of alarms, and while all four are

critically important, the two alarms that we are most

concerned with are true alarms and false clears. True

alarms correctly detect existing threats, and false

alarms give an alarm when no threat exists.

False alarm and false clear probabilities are

performance measures for the screening system.

Higher performance means lower values of these

probabilities. False alarms increase inspection delays

and mean that the system is not as reliable as we hope,

while false clears can be potentially fatal for allowing

threats to go undetected.

Risk-based security paradigms classify

passengers into different security classes based on the

perceived risk of each passenger, where the

passengers and their checked and carry-on baggage

are screened using pre-specified combinations of

detection devices (e.g., magnetometer, x-ray

machine) and procedures (e.g., hand search, pat-

down). Within each security class, a passenger or bag

may undergo screening from multiple devices or

procedures. A passenger or bag clears the security

SM1 SM2 SM3 SM4 SM5 SM6 SM7 SM8 SM9 SM10 SM11 SM12 SM13 SM14 SM15 SM16 SM17 SM18 SM19 SM20 SM21 SM22 SM23 SM24 SM25 SM26

11111111111111111111111111

00000000111111111111111111

11111111111111111111111111

11111111000111101100011111

00011000111111111111111111

11111111111111111111111111

00000000000111101100000000

00111110000000100100001001

00000000111111100000000000

11001111111111011111100000

00000000111111100000000000

11111111111111111111111111

11000011011000011111100000

00111110000000000100001111

10111111000000101111111111

11110000000000000000000000

Security Measure

Risk-Stratiﬁed Multi-Objective Resource Allocation for Optimal Aviation Security

107

checkpoint only if all devices and procedures used in

this class detect no threat. If a threat is detected or if

reasonable suspicion of a threat arises, then the

passenger or bag undergoes additional screening,

usually through a more threat-specific, time-

consuming process. The use of devices as part of the

security operations endures costs associated with

installing, operating, and maintaining the devices.

The preponderance of costs associated with screening

procedures is associated with employing personnel

and implementing these procedures. The fixed costs

are associated with installing devices and maintaining

the devices for screening procedures. The costs

associated with operating the devices are based on the

expected life and time in the operation of each device,

while the implementation costs of screening

procedures are based on the employee compensation

of security personnel. In addition to these cost

restrictions, each device is manufactured to provide a

maximum throughput capacity. Thus, the expected

number of passengers in each security class aids in

determining the capacity requirements for deploying

existing and new detection devices at each airport.

These decisions are highly influenced by resource

constraints, including cost, personnel, and space

availability, hence the decision as to the type and

number of devices and procedures to use for

screening high-risk and low-risk passengers to

maximize the total security (probability of threat

detection) can be very challenging. This is especially

so when considering a limited number of devices

available to deploy across a set of airports, each with

its own individual resource constraints.

2.3 Multi-Objective Mixed Integer

Program Portfolio Investment

Model

Several assumptions are made when formulating our

mathematical model for this problem.

 A passenger pre-screening system (Secure Flight)

is used in a risk-based security screening approach

to quantify the perceived risk of each passenger.

 The resulting threat assessment is viewed as an

accurate representation of the passenger’s true

risk to the air transportation system, based on

intelligence gathered by the TSA pertaining to

prior travel history, origin and destination

itinerary, ticket purchase method, current

behavioral attributes, and other security-sensitive

information.

 The detection devices used to screen passengers

and their baggage operate independently of one

another, such that the use of one type of device

does not affect the cost or threat detection

performance associated with any other device

under consideration.

 There is no cost associated with removing existing

devices from an airport security checkpoint.

In the context of the type of passenger

prescreening system exemplified by Secure Flight,

we want to determine an optimal allocation of threat

detection devices and measures for screening checked

baggage, carry-on baggage, and passengers across a

set of airports so as to (1) maximize risk posture, (2)

minimize the overall false clear rate, and (3)

maximize the number of threats to be detected while

considering passenger threat classification. We

impose constraints on time available at each check

station, flow capacity at security stations, local and

overall budget, as well as staffing needs at each check

station.

The parameters and decision variables used in the

model are summarized as follows.

Parameter Description

T The total number of airports under consideration

k Index for airport k=1, 2,…,T

D The number of screening device types

d Detection device type d=1, 2,…,D

J Number of screening groups (e.g., checked bags,

carry-on bags, passenger ID check, passenger

screening)

j Screening group j = 1,…, J

D(j) Detection devices d within screening group j

Number of passenger classes at airport k

C Index for passenger class c=1, 2,…,M

(e.g., high-

risk, regular, precheck)

Average value of perceived risk for passengers

assigned to class c at airport k

Number of checked bags per hour screened in

class c at airport k

Number of carry-on bags per hour screened in

class c at airport k

H’

Number of passengers (ID) per hour screened in

class c at airport k

Number of passengers (body) per hour screened

in class c at airport k

Cj Maximum throughput (passengers or bags/hour)

within screening group j

Number of existing devices of security measure

type d at airport k

Fixed Cost ($/device) associated with device type d

The capacity of device d at airport k

Installation cost ($/device) associated with device

type d

Operating cost ($/device) associated with device

type d

Conditional probability of detecting a threat given

there is a threat for device type d

Probability of a passenger belonging to passenger

DATA 2024 - 13th International Conference on Data Science, Technology and Applications

108

class c

𝛼



The conditional probability that passenger carries

a threat given they belong to class c carries a

threat

𝛽



The conditional probability that there is a threat

in screening group j given a class c

Conditional probability of clearing a non-threat

item given there is no threat for device type d

Total hourly budget ($) available at airport k

Time taken to check one passenger or bag at

device d

Number of device type d available for installation

Time multiplier to verify any alarm at any device

Decision Variables Description

cdk

Binary variable where x

cdk

= 1(0), if security

measure type d is (not), used to screen class c

passenger at airport k

Number of security measure type d to be used at

airport k (integer)

Number of security measure type d to be installed

at airport k (integer)

The number of devices of type 𝑑 to be installed at

each airport, 𝑠



, Equation (M1), is found by

subtracting the number of devices of type 𝑑 currently

existing from the number of devices of type 𝑑 used in

total at each airport.

𝑠



= 𝑦



−𝐸





Device Installation Constraint



(M1)

provided 𝑦



≥𝐸



(and 0 otherwise), for 𝑑=

1,2, … , 𝐷 and 𝑘=1,2,…,𝑇.

Using the notation provided, the installation,

operating, and total fixed costs at each airport 𝑘 can

be found such that the combined installation,

operating, and fixed costs satisfy the total hourly

budget, 𝑇𝐵



, for airport 𝑘= 1,2,...,𝑇.

For discussion, let {B, G, H’, H} denote the four

screening groups: checked bag, carry-on bag,

passenger ID check, and passenger screening,

respectively. In what follows, we use checked bag,

group B, as an example.

We next consider the number of new devices (for

each screening group) to be installed at each airport,

𝑦

()

, Equation (M2). This relies on the capacity

performance of the screening devices, captured by the

number of checked bags (screening group B) each

device type can handle per hour, 𝐶



, and the number

of bags screened in each class within a particular

airport, 𝐵



. Dividing the hourly rate of bags screened

in class c at airport k by the maximum throughput of

device type 𝑑 yields the number of security devices

of type 𝑑=1,2,…,𝐷 necessary to screen all checked

bags using this particular device,

𝑦



(



)

= 







𝐵



𝑥



/𝐶



 𝑑=1,2,…,𝐷,

𝑘=1,2,…,𝑇

(M2)

(

Resource Capacity Constraint

)

Lastly, Constraint (M3) reflects device resource

availability, namely the number of new devices

installed at all airports must be less than or equal to

the total number of new devices available.







𝑠



≤𝑈



, ∀𝑑=1,2,…,𝐷 (M3)

(

Resource Availability Constraint

)

We next model the expectation of false alarms,

time logistics and staffing needs at each check station

within each screening group.









(

1 −𝛼



)

𝑐𝑝









1 −

∈()

𝑞



𝑥



 ≤𝛿 𝑘

=1,2,…,𝑇

(

)

𝐻′









𝑐𝑝





∈

(



)

𝑥



⎝

⎜

⎛

1+𝑧



⎝

⎜

⎛

𝑝











𝛽



𝛼



𝑐𝑝



(

1 −𝑞



)









(

1 −𝛼



)

𝑐𝑝



⎠

⎟

⎞

⎠

⎟

⎞

𝑡



≤𝐶





∈

(



)

𝐾



𝑘=1,2,…,𝑇

(

)

𝐵









𝑐𝑝





∈

(



)

𝑥



⎝

⎜

⎛

1+𝑧



⎝

⎜

⎛

𝑝











𝛽



𝛼



𝑐𝑝



(

1 −𝑞



)









(

1 −𝛼



)

𝑐𝑝



⎠

⎟

⎞

⎠

⎟

⎞

𝑡



≤𝐶



∈

(



)

𝐾



𝑘=1,2,…,𝑇

(

)

𝐺









𝑐𝑝





∈

(



)

𝑥



⎝

⎜

⎛

1+𝑧



⎝

⎜

⎛

𝑝











𝛽



𝛼



𝑐𝑝



(

1 −𝑞



)









(

1 −𝛼



)

𝑐𝑝



⎠

⎟

⎞

⎠

⎟

⎞

𝑡



≤𝐶



∈

(



)

𝐾



𝑘=1,2,…,𝑇

(

)

𝐻









𝑐𝑝





∈

(



)

𝑥



⎝

⎜

⎛

1+𝑧



⎝

⎜

⎛

𝑝











𝛽



𝛼



𝑐𝑝



(

1 −𝑞



)









(

1 −𝛼



)

𝑐𝑝



⎠

⎟

⎞

⎠

⎟

⎞

𝑡



≤𝐶



∈

(



)

𝐾



𝑘=1,2,…,𝑇

(

)

Risk-Stratiﬁed Multi-Objective Resource Allocation for Optimal Aviation Security

109

Here, Constraint (M4) ensures that the false alarm

probability is within the upper bound, 𝛿, set by the

appropriate security authority. Constraints (M5) –

(M8) guarantee that checking of baggage or

passengers at each screening group is completed

within the allotted time.

Both false alarms and false clears at airport

screening can pose significant challenges and risks,

but they have different implications. While false

alarms take up unnecessary resources, slow down

airport operations, and lead to delays, inconvenience

and stress for travellers, false clears typically are

considered more serious as they can potentially allow

dangerous items or individuals to bypass security

measures, compromising safety. Our model

emphasizes on maximizing safety. The objective

function, Equation (OBJ2), describes the probability

of false clear across each airport.









𝑐𝑝



𝛼









𝛽





∈()

(

1 −𝑝



)

𝑥



∀𝑘∈𝑇 (𝐎𝐁𝐉𝟐)

Equation (M9) formulates the probability of

detecting a threat within security class 𝑐 at airport 𝑘,

𝐿



, and is calculated as the probability that at least

one of the device types used in that class detects the

threat correctly.

𝐿



(



)

=1−

∏

∈

(



)

(

1 −𝑃



)

𝑥



(M9)

∀ 𝑐=1,2,…,𝑀



, 𝑘=1,2,…,𝑇, 𝑗∈

{

𝐵, 𝐺, 𝐻



, 𝐻

}

The risk level of each class, 𝑅



, is defined as the

average perceived risk value of the passengers in

security class 𝑐 at airport 𝑘 times the rate of baggage

/ passenger screened within that class. This value is

normalized between zero and one by dividing over

the total risk associated with all security classes

within airport 𝑘 , as shown in Equation (M10):

𝑅

()

𝐴



𝐵



∑











𝐴







𝐵







(

M10

)

The risk level of each security class relies heavily

on the assumption that the prescreening system

provides an accurate (estimation of) risk perception

of the passenger population.

The threat detection objective function for the

allocation model is obtained by weighting each

airport by the rate at which passengers/checked

bags/carry-on bags must be screened at that airport

and the risk level associated with screening these

groups using either new or existing detection devices.

Using Equations (M9) and (M10), the objective

function value at each airport for checked bag

screening is defined as the expected number of

detected threats in Equation (M11),

𝑆𝐿

()

= 







𝐿

()

𝐵



𝑅

()

(

M11

)

By summing over all the screening groups and

airports under consideration, the total security level

captures the expected total number of detected

threats, as given by Equation (OBJ3):

∑

𝑆𝐿







∑





∑

𝑆𝐿

()



∑∑

𝐿

(



)

𝐻′



𝑅

(



)











+ 𝐿

()

𝐵



𝑅

()

𝐿

()

𝐺



𝑅

()

+𝐿

()

𝐻



𝑅

()

(

𝐎𝐁𝐉𝟑

)

Combining the three objectives Equations

(OBJ1), (OBJ2), and (OBJ3), the security measure

allocation problem for multiple airports can be

formulated as a nonlinear multi-objective integer

program.

Nonlinear Multi-Objective Portfolio Optimization

for Security Measures Allocation

Maximize















𝑥



𝑝



× 𝑅𝐼𝑉



𝑘=1,2,…,𝑇 (𝐎𝐁𝐉𝟏)

−







𝑐𝑝



𝛼









𝛽





∈

(



)

(

1 −𝑝



)

𝑥



𝑘

=1,2,…,𝑇 (𝐎𝐁𝐉𝟐)















𝑆𝐿



𝑥



𝑘=1,2,…,𝑇 (𝐎𝐁𝐉𝟑)

Subject to

𝑠



≥𝑦



−𝐸



, 𝑑=1,2,…,𝐷, 𝑘=1,2,…,𝑇

(M1)

𝑦



= 







𝑗



𝑥



/𝐶



, 𝑑=1,2,…,𝐷

(

𝑗

)

𝑗∈

{

𝐵, 𝐺, 𝐻



, 𝐻

}

, 𝑘=1,2,…,𝑇 (M2)







𝑠



≤𝑈



𝑑=1,2,…,𝐷. (M3)









(

1 −𝛼



)

𝑐𝑝









1 −

∈

(



)

𝑞



𝑥



 ≤𝛿

𝑘=1,2,…,𝑇 (M4)

DATA 2024 - 13th International Conference on Data Science, Technology and Applications

110

𝑗









𝑐𝑝





∈

(



)

𝑥



⎝

⎜

⎛

1+𝑧



⎝

⎜

⎛

𝑝











𝛽



𝛼



𝑐𝑝



(

1 −𝑞



)









(

1 −𝛼



)

𝑐𝑝



⎠

⎟

⎞

⎠

⎟

⎞

𝑡



≤𝐶



∈

(



)

𝐾



, 𝑗∈

{

𝐵, 𝐺, 𝐻



, 𝐻

}

, 𝑘=1,2,…,𝑇

(

)

−(M8)







(

𝑦



𝐹



+ 𝑠



𝐼



)

+ 













𝑥



𝑂



𝐵



≤𝑇𝐵



𝑘=1,2,…,𝑇 (M12)

𝑥



∈{0,1}, 𝑦



∈𝑍



, 𝑠



∈𝑍



Constraint (M1) is the device installation

constraint, and Constraint (M2) reflects the resource

capacity based on the screening rates for each of the

four screening groups. Constraint (M3) models the

overall resource availability. Constraint (M4) ensures

that the false alarm probability is within an upper

bound, 𝛿, set by the appropriate security authority.

Constraints (M5) - (M8) guarantee that screening for

each group at each station is completed within the

allotted time. Constraint (M12) describes the budget

at each airport.

The resulting integer program is nonlinear due to

the product of the 𝑥



decision variables contained

in the false alarm constraint in (M4), and in the threat

detection term, 𝐿



, in (M9). Constraint (M3)

effectively ties together the decision variables across

all airports, potentially impacting the ability to

decouple the problem and solve for each individual

airport.

2.4 Computational Challenges

Computationally, the formulated nonlinear MIP

instance (with 45,760 decision variables and 35,666

constraints) is intractable by existing commercial or

research solvers. To linearize the risk structures, a

decomposition is necessary. Dantzig-Wolfe

decomposition can be applied to reduce the original

decision variables to a single composite binary

decision variable representing whether or not a

specific security measure combination for the threat

classes at airport 𝑘 is applied. This changes the

problem structure and looks at a full enumerated

security measure combination list for all 440 airports.

There are 1,048,576 possible security measure

combinations for two classes of passengers and 26

security measures. The resulting decomposed model

has 461,373,440 binary and integer decision variables

and 466 constraints.

We apply sensible and knowledge-based

preprocessing to reduce the number of decision

variables to 128,480,000. Decomposition increases

the number of decision variables, but drastically

decreases the number of constraints, hence reducing

the size of the Simplex basis. However, the model

remains intractable. We derive fast heuristics to

obtain near-optimal solutions that offer the best set of

security measures (with respect to the objectives) for

each airport.

2.4.1 Optimization Strategies

Numerous studies have been conducted to compare

and contrast various optimization approaches for

solving multi-objective models. Sawik provides a

comprehensive analysis of weighting, lexicographic,

and reference point approaches to multi-objective

portfolio optimization (Sawik, 2011). A hierarchical

or lexicographic approach assigns a priority to each

objective and optimizes the objectives in decreasing

priority order. At each step, the best solution is found

for the current objective, but only from the solutions

that do not degrade the solution quality for higher-

priority objectives. Lexicographic optimization

generates efficient solutions by sequential

optimization of the objectives. For our

implementation, we normalize the three objectives

into comparable values and weigh them equally for

unbiased analyses.

Multi-Swarm Particle Swarm Optimization

Particle swarm optimization (PSO) is a fast heuristics

that works by having a population of candidate

solutions (particles) and moving the particles around

in the search space based on the particles’ position

and velocity.

The PSO is initialized with a group of random

particles (mixed-integer variable solutions). The

algorithm searches for optima by updating the

generations of particles. In each iteration, the particles

are updated by two “best” values. First, the algorithm

records the best solution (fitness, objective function

value) achieved by the particle thus far. The objective

value is stored as p

best

. Second, the algorithm also

records the best value obtained thus far by any

particle in the population, known as the global best

and stored as g

best

. When a particle takes part of the

population as its topological neighbors, the best value

is a local best and is denoted by l

best

. The formulation

of the swarm is determined by the specific problem,

and in this study, each particle represents a complete

Risk-Stratiﬁed Multi-Objective Resource Allocation for Optimal Aviation Security

111

set of portfolio (a set of security measures) selected

for all the airports. Therefore, each particle of a

swarm (denoted by index i) must include the decision

variables r

ikj

=1(0) denoting if security measure

combination portfolio j is (not) selected for airport k,

and z

idk

∈𝑍



denoting the quantity of each security

measure assigned to airport k.

After finding the two best values, the particle

updates its velocity and position according to

Equations (P1) to (P3). Here 𝜔



and 𝜔



denote

uniform random numbers between 0 and 1. t denotes

the iteration number while 𝑣𝑧





denotes the velocity

of variable z within particle i, and 𝑣𝑟





denotes the

velocity of variable r within particle i. 𝑣𝑧





will be

updated if security measure d is selected by the

portfolio of security measures within particle i at

iteration t+1. Thus, particle i moves at iteration t+1

as follows:

𝑣𝑟





= 𝑣𝑟





+ 𝑐



𝜔



𝑟



−𝑟







+ 𝑐



𝜔



𝑟



−𝑟





 (P1)

𝑟





= 𝑟𝑜𝑢𝑛𝑑









−𝛼



, 𝑤ℎ𝑒𝑟𝑒 𝜃= 𝑟





𝑣𝑟





𝑎𝑛𝑑 𝛼 is set to 0.06 (P2)

𝑣𝑧





= 𝑣𝑧





+ 𝑐



𝜔



𝑧



−𝑧







+𝑐



𝜔



𝑧



−𝑧





 𝑖𝑓 𝑟





𝑣𝑧





= 𝑣𝑧





𝑜𝑡ℎ𝑒𝑟𝑤𝑖𝑠𝑒 (P3)

For a given particle, if the velocity on the

dimension r





is zero, this particle will not move in

that dimension at iteration 𝑡+1. Suppose 𝑣𝑟





and r





=0, hence 1/

(

1+𝑒



)

=0.5 and round(0.5)

= 1, which means that particle i will move in

dimension 𝑟



𝑟





=1 at iteration t+1. To avoid

such an unwanted move, we can use 𝛼, as seen in

Equation (P2).

The search terminates when stop criteria are

satisfied: when the maximum number of iterations

has been reached, or the minimum error condition is

satisfied. An advantage of PSO is that not many

parameters require tuning. The number of particles

(solutions to record) is in the range of 20 to 40; while

difficult problems may require 100 – 200. In our

instances, the dimension of the particles (dimension

of solution set) is prohibitively large, requiring us to

keep the number of particles to a minimum size. The

range of particles is determined by the upper and

lower bounds of the decision variables. v

max

determines the maximum change one particle can

take during one iteration. We require two v

max

due to

the presence of both binary and integer variables.

The multi-swarm PSO (MSPSO) modification is

a more recent popular approach (Pluhacek, 2016). In

the multi-swarm approach, the population is divided

into multiple sub-populations (sub-swarms) with

different levels of communication. The benefit of this

approach is that the population can maintain

divergence, search for multiple promising regions,

and partially converge to multiple optima. In (García-

Nieto and Alba, 2012), the optimal swarm (sub-

swarm) size is discussed in great detail. It is proposed

that six particles per swarm might be the optimal

number for PSO-based algorithms. Pluhacek

demonstrates that the multi-swarm performance was

superior to the single swarm PSO in all cases

(Pluhacek, 2016). We decide to utilize a multi-swarm

PSO, with five sub-swarms, and varying particle sizes

from 5 to 10 particles per swarm. The control

parameters are set as follows:

 Population Size: {5,6,7,8,9,10}

 Iterations: 5

 v

initial

: 10% of the position

 w

max

: 0.9

 w

min

: 0.4

 c

, c

= 1.49445 (learning factors)

The multi-swarm PSO is based on the local

version of PSO with a new neighborhood topology.

Many existing evolutionary algorithms require large

populations, while PSO needs a comparatively

smaller population size. A population with three to

five particles can achieve satisfactory results for

simple problems. According to many reported results,

PSO with small neighborhoods performs better on

complex problems. Hence, to slow down

convergence speed and increase diversity to achieve

better results on multimodal problems, in the

MSPSO, small neighborhoods are used. The

population is divided into small-sized swarms. Each

sub-swarm uses its own members to search for better

regions in the search space.

The multi-swarm optimization algorithm works

as follows:

Input: MOP (1)

Swarm_size: number of the swarm particles

No_subswarms: number of subswarms

Step 1: Calculate Subswarm size=

Swarm_size/No_subswarms

Step 2: For subswarm = 1 to No_subswarms do

For t=1 to Max_iterations do

Apply PSO algorithm

Update leaders archive

Update external archive

End For

Return final result in the external archive

Append the result to the results file

End For

DATA 2024 - 13th International Conference on Data Science, Technology and Applications

112

Ad-Hoc Heuristics Approaches

For comparison, we apply column generation and

additional solutions techniques to contrast solution

speed and quality. To expedite the column generation

method, we consider breaking apart the domain to

accommodate a large number of options. This

separation inspires two heuristics briefly described

below.

Heuristic 1: The full set of portfolio options are

randomized, and broken into buckets of 250

combinations each. The associated set is optimized

across all 440 airports. This allows for rapid solution

time as we can massively run all these column

generation subproblems. Not all fidelity is lost since

we maintain all 440 airports in each subproblem and

keep quantity assignment variables intact.

Heuristic 2: Portfolios are again randomized and

separated into buckets, and this time, along with the

airports as well. Each subproblem then represents a

subset of both the airports and the possible portfolio

combinations.

In both randomized heuristics, optimization is

performed at every iteration. The selected

combinations (not the quantities of security

measures) are placed into a pool of optimal

combinations. The pool of portfolios is then used in

a final optimization to construct a complete solution.

3 COMPUTATIONAL ANALYSES

3.1 Data for Modeling

Data were collected from aviation articles that

presented strong models (McLay et al., 2006; Nie et

al., 2009; Poole & Passantino, 2003; Sewell et al.,

2012, 2013; Virta et al., 2003). With the assistance of

our TSA collaborators, the fixed and installation costs

are determined through the expected useful life of the

device and on the amount of time the device would

spend in operation over one year. These values reflect

the yearly cost (in US dollars) divided by the total

number of hours spent in operation over the year,

based on a peak 6 hours of operation per day, per

device.

Passengers are assigned to a two-class system

based on perceived risk information generated

through the Secure Flight a prescreening system. This

classifies passengers as being either high-risk or low-

risk, where the majority of passengers constitute the

latter group. In the computational analysis reported

herein, 85% of passengers are deemed low-risk and

assigned to Class 1, while the remaining 15% of

passengers are assigned to the high risk security Class

The total number of passenger enplanements

reflects the actual enplanement data from 2016-2019

collected from faa.gov (Transportation, n.d.). The

hourly airport budget is based on an estimated annual

budget value to be distributed across all airports.

Individual airport budgets are simply distributed

based on the proportion of passengers with a set

minimum value. The total number of passengers

screened per hour at an airport is based on the average

airport being operational 365 days a year and having

16 regular working hours per day. The operating cost

of each security screening device or method is based

on the annual operating cost of that device/method

divided by the average hourly passenger screening

rate. The maximum and minimum hourly screening

rates per device are pulled from actual manufacturer

device specifications. Lastly, the perceived risk

values are generated from a normal distribution with

mean 0.26 and standard deviation 0.12 for the low-

risk passengers assigned to Class 1, and with mean

0.55 and standard deviation 0.12 for the high-risk

passengers assigned to Class 2.

Combinations of all possible subsets of device

types are generated for evaluation. The combinations

of the security measures are grouped by screening

group and are estimated by assuming which security

measures should always be constant and which are

optional. For example, as seen in Table 3 below, for

the checked baggage screening, it was assumed that

all checked bags are screened by a CT scanner with

additional screening performed by hand search.

Therefore, all combinations must have both methods

employed. Canine units and Explosive Trace

Detection are both treated as secondary screening

measures since they are not typically a primary line

of defense at any airport, and there is no way to

provide support to all airports. Based on this

information, there are then four possible

combinations of checked baggage security measures

that can be employed. This same approach was

conducted for all screening measure groups.

Table 3: Example of Security Measure Combination

Restriction.

A potential combination of device types is chosen

from these 1024 possible configurations for each

passenger class for every airport, where each airport

may have a different combination from any other

Disruption Rate 1-DR Security Measure 1234

SM1 50% 50% Hand Search 1111

SM2 80% 20% Canine Unit (unit consists of two to four teams, 1 handler/2 Dogs per team)0011

SM3 70% 30% Explosive Trace Detection (open bag trace) 0101

SM4 80% 20% Computed Tomography (CT) Scan (Electronic Detection System) 1111

Risk-Stratiﬁed Multi-Objective Resource Allocation for Optimal Aviation Security

113

airport. We obtain the number of device types used at

each airport by dividing the hourly rate of passengers

screened at that airport by the device hourly

throughput rate.

3.2 Results

The nonlinear mixed integer programs were

generated in Python 3.7.3 using the gurobipy module

and solved with Gurobi 9.0. The Gurobi parameters

were kept at their default values, apart from turning

the pre-solve option off so that Gurobi would spend

less time expanding the node structure.

The data for all independent scenario instances

remained consistent and incorporated all 440 airports.

1024



different combinations were produced, based

on the security measures available. Table 4 shows an

example output.

Table 4: A Snapshot of one solution output for each airport.

The model allows scenario-based risk assessment and

evaluation analyses which will be discussed in detail

in a future paper. Herein, we report briefly the

computational results obtained from 11 solution

methods.

 Model 1: Multi-Swarm PSO – 5 particles

 Model 2: Multi-Swarm PSO – 6 particles

 Model 3: Multi-Swarm PSO – 7 particles

 Model 4: Multi-Swarm PSO – 8 particles

 Model 5: Multi-Swarm PSO – 9 particles

 Model 6: Multi-Swarm PSO – 10 particles

 Model 7: Combined Solution MSPSO

 Model 8: Heuristic 1

 Model 9: Heuristic 2

 Model 10: Column Generation Pricing with

Multi-Swarm PSO

 Model 11: Column Generation Branch-and-Price

Exact Algorithm

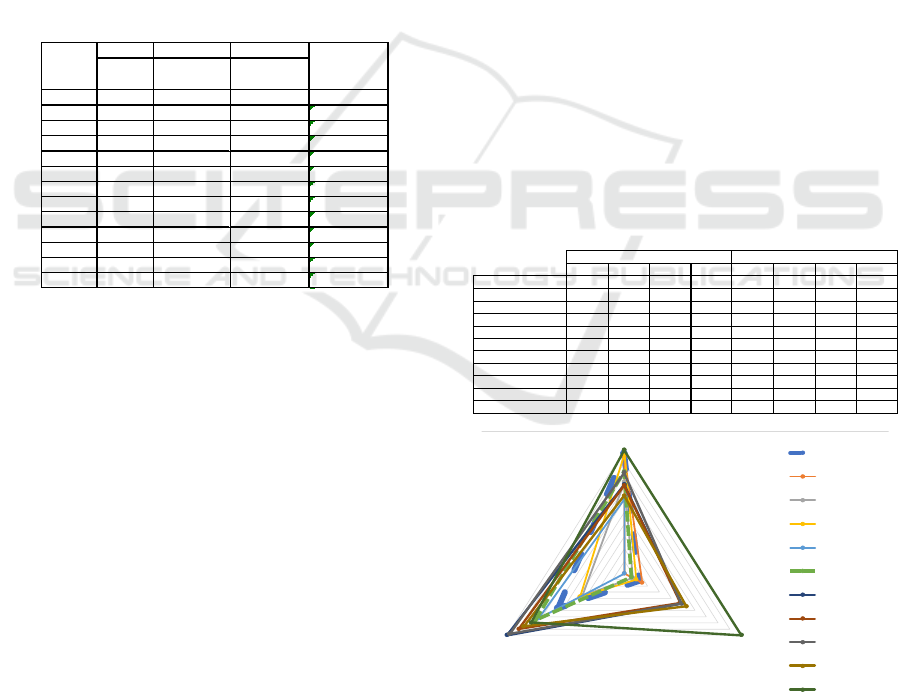
Table 5 presents the computational results for theses

11 different model formulations and solution

strategies. For comparison, we use equally-weighted

outputs after normalizing the objectives into a scalar

to improve the ability to compare values. The first six

are multi-swarm PSO results with varying population

size. The first four columns display the equally-

weighted multi-objective results. Population size

does not appear to be significant for running the

MSPSO algorithm. In fact, more particles do not

guarantee better results. Heuristic 1 and Heuristic 2

are the ad-hoc greedy heuristics. The Combined

MSPSO took all the portfolio results from each of the

MSPSOs and solved the optimization problem based

on all the options. The CG Price MSPSO model took

the column generation construct but solvedd the

pricing problem using the MSPSO instead of having

to solve the individual subproblems for each airport.

CG Final is the full column generation solution using

the standard column generation algorithm and applied

to the Dantzig decomposition to achieve the optimal

solution. Since these are heuristic results, they may

not lie on the Pareto efficient frontiers. CG Final

result (a non-dominated solution) provides the best

overall results, since the instance is solved to

optimality. The MSPSO solutions tend to bias

towards Obj1, while Combined MSPSO improves the

solution with good scores for both Obj1 and Obj3.

The two ad-hoc heuristics offer excellent scores for

Obj3 with reasonable Obj1.

Table 5: Summarized Model Results.

Figure 2: Triangle Radar Plot, Performance Metric

Comparison.

The triangle radar plot in Figure 2 displays the

normalized results. If the model line reaches 1, then

Obj 1 Obj 2 Obj 3

Max Risk

Posture

Min Prob

False Clear

Max Threat

Detection

Overall 87207.61 -436.8090570 236837341.60 236924112.40

1 277.05 -0.9889654 25013040.24 25013316.30

2 277.05 -0.9889654 14250702.99 14250979.05

3 277.05 -0.9889654 15596221.45 15596497.51

4 277.05 -0.9889654 9096180.76 9096456.83

5 277.05 -0.9889654 11182118.68 11182394.74

6 277.05 -0.9889654 9215989.36 9216265.43

7 277.05 -0.9889654 9869503.37 9869779.44

8 277.05 -0.9889654 5863353.98 5863630.05

9 277.05 -0.9889654 6824083.49 6824359.55

10 277.05 -0.9889654 8128292.47 8128568.54

11 277.05 -0.9889654 7196422.29 7196698.35

12 277.05 -0.9889654 7419652.11 7419928.18

Airports Overall

Obj 1 Obj 2 Obj 3 Total Obj 1 Obj 2 Obj 3 Total

MSPSO 5 0.792 0.121 0.533 1.446 0.968 0.123 0.565 1.657

MSPSO 6 0.777 0.150 0.257 1.184 0.949 0.153 0.0 1.102

MSPSO 7 0.620 0.070 0.432 1.122 0.743 0.071 0.358 1.171

MSPSO 8 0.793 0.098 0.441 1.332 0.970 0.100 0.376 1.446

MSPSO 9 0.513 0.001 0.614 1.128 0.602 0.0 0.730 1.333

MSPSO 10 0.684 0.059 0.628 1.370 0.826 0.060 0.758 1.644

Combined MSPSO 0.676 0.475 0.734 1.885 0.816 0.485 0.976 2.278

Heuristic 1 0.603 0.480 0.746 1.828 0.720 0.490 1.0 2.210

Heuristic 2 0.598 0.467 0.696 1.761 0.713 0.477 0.898 2.089

CG Price MSPSO 0.535 0.519 0.675 1.729 0.631 0.531 0.855 2.016

CG Final 0.816 0.978 0.645 2.439 1.0 1.0 0.793 2.793

Normalized Model ResultsModel Results

Obj 1

Obj 2Obj 3

PSO 5

PSO 6

PSO 7

PSO 8

PSO 9

PSO 10

Combine PSO Final

CG Price PSO

CG Final

DATA 2024 - 13th International Conference on Data Science, Technology and Applications

114

the objective has reached the maximum value

amongst the various models. If a line is barely

registering (achieving very low value), then the

objective value result is basically inconsequential in

comparison.These scenarios allow us to observe how

security measure allocations differ when varying the

number of inputs into the overall model. This

technique gives us insight into determining if it is

beneficial to dedicate the time to find an optimal

solution. The PSO methods take the least amount of

time, and if the solutions are potentially just as strong,

then it is possible that they can be utilized regularly.

The decision-makers are also able to witness multiple

options and consider what results remain consistent

throughout the runs or what results change drastically

depending on the model.

3.3 Summary of Findings

The classical portfolio optimization model uses the

variance as the risk measure and relies on the

covariance matrix. Without reliable estimates for the

covariance/correlation, we utilize network topology

analysis techniques to make a pseudo correlation

matrix. We construct and introduce a network of

interdependent risk factors that can be represented by

a weighted adjacency matrix. This matrix is then

combined with the topological overlap matrix, a

similarity measure construct that allows us to define

and quantify the topological and interdependent

relationships between the security measures and the

risk factors.

As a means to integrate the risk factors and

security measures that are put in place by TSA, we

introduce the term “Risk Posture” and a method to

calculate it. Risk Posture is calculated based on the

optimal security measure portfolios selected and their

interdependent relationship with the TSA risk

taxonomy. With Risk Posture, we maximize the

resilience of the system so that no matter the risk,

TSA/the country should be able to face it. There are

no standard Risk Posture calculations, and the term

has been associated with Cyber-security readiness

(since 2018). Our goal is to maximize the overall

improvement in risk posture by minimizing risk.

Nearly all security measures have been addressed

in small groupings in previous research over the past

20 years, but none all together in a single enterprise

risk optimization model. Stewart and Mueller

(Stewart & Mueller, 2017) are the only publication/s

that include all security measures, though no

mathematical analyses and tradeoffs have been

performed. No prior optimization model has

attempted to incorporate multiple screening areas into

a single model. Our work is the first to incorporate

Stewart and Mueller’s (Stewart & Mueller, 2017)

reliability construct to include Checked baggage,

Carry-on baggage, and Passenger screening. ERM

portfolio optimization models are typically tied to the

Insurance and Finance industries and follow a very

traditional modeling approach (Al-Qudah, 2023;

Oliva, 2016; Olson & Wu, 2010; Soliman & Adam,

2017). There is currently no ERM portfolio

optimization model in aviation security measures.

Our model is comprehensive in which previous

Sewell’s SADM and Nie’s operational models are

sub-models within our global ERM-based model.

The output of the model allocates available

security measures/screening devices across airports

nationwide to

 Maximize the risk posture of the TSA (threat

detection capability concerning the

interdependent network of TSA risk elements)

 Minimize the probability of false clears

 Maximize the total security level (probability

of threat detection)

4 CONCLUSIONS

This paper offers a pioneering approach to optimizing

enterprise risk management (ERM) in aviation

security through a comprehensive multi−objective

portfolio investment model. By integrating various

aviation transportation risks and modeling their

interdependencies, the ERM-based model provides a

robust framework for allocating security measures

efficiently across the U.S. aviation sector. The

model’s strength lies in its ability to correlate

resource allocation with risk mitigation, maximizing

risk posture while minimizing false clears and

enhancing threat detection rates.

The comprehensive ERM-based resource

allocation model expands upon previous research and

combines all previous models into a single multi-

objective portfolio investment optimization model

framework. We utilize the concept of topological

overlap network to establish interdependencies

among the various aviation transportation risks. We

also introduce Risk Posture, capturing the cascading

and inter-dependency of the multi-tier risk taxonomy

and overlaying security measures, to quantify the

TSA’s resilience and capabilities against any

potential risks. The biggest knowledge gap in

previous research is that any type of optimization

model concerning enterprise risk management was

performed only at an operational level. This work

represents the first model that encompasses a full

Risk-Stratiﬁed Multi-Objective Resource Allocation for Optimal Aviation Security

115

multi-tier enterprise risk management approach

across strategic, tactical, and operational levels. It is

also the first model to establish and concentrate on

risk posture. The security measure and device

allocation problem, combined with a passenger risk

assessment policy, can be used to structure a risk-

based screening strategy to use limited screening

resources effectively. The model is generalizable and

can accommodate additional / different measures,

new technology, or new airport setups.

This paper presents a practical solution

methodology for solving the security screening

device allocation model across multiple airports.

Given budget constraints, including the installation,

operation, and fixed costs associated with screening

devices and procedures at airport checkpoints, the

ERM-based model facilitates the allocation of new

devices and procedures across airports nationwide to

maximize the total security level over all the airports

under consideration. To accomplish this, we compute

a risk factor for security classes using either the new

or existing detection devices, based on the hourly

throughput rate of each of the device types and the

perceived risk of the passengers. The passenger risk

is obtained using a prescreening system and allows

security operations to partition passengers into high

or low-risk categories for undergoing higher or lower

intensity screening.

We present a Dantzig-Wolfe decomposition

approach to tackle the resulting nonlinear intractable

instances, where optimal solutions are shown to be

obtained in several seconds through multiple

computational examples. The fast solution engines

and interpretable results ensure scalability and

adaptability of the proposed framework to other

contexts beyond aviation security.

The findings have significant implications for

policy and practice, particularly in enhancing aviation

security in a post−9/11 landscape. By demonstrating

a quantifiable improvement in risk management

through strategic resource allocation, this work adds

new and critical knowledge to the field of risk

assessment and optimization in aviation security.

Future research will be conducted to expand on this

foundation to explore adaptive strategies in response

to evolving security threats and the integration of

real−time data analytics for dynamic risk assessment.

In Leonard and Lee (2020), we applied this

quantitative ERM-based framework for optimizing

security measure investments to achieve the most

cost-effective deterrence and detection capabilities

for the U.S. Customs and Border Patrol (CBP).

We modeled the CBP ERM in 3 tiers: satellites

monitoring the geographic area of the border;

High Altitude Long Endurance drones with high-fuel

capacity for extended surveillance; and the ground

layer of a variety of security surveillance systems

and manned outposts. Under physical / cyber /

resource / logistics constraints, the ERM-based

model optimizes the allocation of limited

quantities of deterrence and detection security

measures across the entire southern continental

U.S. border so as to (1) maximize the total utility

of the measures utilized, (2) maximize the

probability of deterrence and/or detection, and (3)

minimize cost.

The CBP work introduces the concept of utility

for each security measure as a means to rate its

impact, and incorporates the probability of success,

along with multiple objectives. To the best of our

knowledge, our work presents the first

mathematical model that optimizes security

strategies for the CBP and is the first to introduce

a utility factor to emphasize deterrence and

detection impact. It also offers insights into the

broader applicability of our ERM-based

computational framework.

ACKNOWLEDGEMENTS

This material is based upon work supported by the

U.S. Department of Homeland Security under Grant

Award Number 17STQAC00001-01. The views and

conclusions contained in this document are those of

the authors and should not be interpreted as

necessarily representing the official policies, either

expressed or implied, of the U.S. Department of

Homeland Security. The authors thank the

anonymous reviewers for their insightful comments.

REFERENCES

Agliari, E., Barra, A., Galluzzi, A., Guerra, F., Tantari, D.,

& Tavani, F. (2015). Retrieval capabilities of

hierarchical networks: from Dyson to Hopfield.

Physical review letters, 114, 028103.

Agliari, E., Barra, A., Galluzzi, A., Guerra, F., Tantari, D.,

& Tavani, F. (2015). Topological properties of

hierarchical networks. Physical Review E, 91, 062807.

Al-Qudah, L. A. (2023). The Mediating Role of Corporate

Governance in the Relationship between the Enterprise

Risk Management (ERM) Model and Reducing

Business Risks in Jordanian Commercial Banks. Jordan

Journal of Business Administration, 19(3).

Babu, V. L., Batta, R., & Lin, L. (2006). Passenger

grouping under constant threat probability in an airport

DATA 2024 - 13th International Conference on Data Science, Technology and Applications

116

security system. European Journal of Operational

Research, 168, 633644.

Cura, T. (2009). Particle swarm optimization approach to

portfolio optimization. Nonlinear analysis: Real world

applications, 10, 2396-2406.

Council, N. R., & others. (2010). Review of the Department

of Homeland Security's approach to risk analysis.

National Academies Press.

Emerging Technology. (n.d.). Retrieved from https://www

.tsa.gov/travel/security-screening/emerging-technology

Fletcher, K. C. (2011). Aviation Security: A Case for Risk

Based Passenger Screening. Master's thesis, Monterey,

California. Naval Postgraduate School.

Fletcher, K. C., & Abbas, A. E. (2018). A Value Measure

for Public Sector Enterprise Risk Management: A TSA

Case Study. Risk Analysis, 38, 9911008.

Garcia Nieto, J., & Alba, E. (2012). Why six informants is

optimal in PSO. Proceedings of the 14th annual conf.

on Genetic and evolutionary computation, (pp. 2532).

Gounaris, C. E., Rajendran, K., Kevrekidis, I. G., &

Floudas, C. A. (2016). Designing networks: A Mixed‐

Integer Linear Optimization Approach. Networks,

68(4), 283-301.

Kean, T. H., Hamilton, L., Ben-Veniste, B., Kerrey, B.,

Fielding, F. F., Lehman, J. F., Gorelock, J.S., Roemer,

T. J., Gorton, S., & Thompson, J.R. (2004). The 9/11

Commission: Final report of the National Commission

on Terrorist Attacks upon the United States.

Harrisonburg, VA: R.R. Donnelley.

Kos, M., Mikac, M., & Mikac, D. (2002). Topological

Planning of Communication Networks. Journal of

Information and Organizational Sciences, 26, 5768.:

Leonard, T., & Lee, E. K. (2020). US-Mexico Border:

Building a Smarter Wall through Strategic Security

Measure Allocation. Journal of Strategic Innovation

and Sustainability, 15(1): 156-182.

McLay, L. A., Jacobson, S. H., & Kobza, J. E. (2006). A

multilevel passenger screening problem for aviation

security. Naval Research Logistics (NRL), 53, 183-197.

McLay, L. A. (2011). Risk Based Resource Allocation

Models for Aviation Security. In

Safety and Risk Modeling and Its Applications (pp. 243-

261). Springer.

Minsky, S. (2013, March 07). TSA adopts Enterprise Risk

Management. Retrieved from https://www.logicmana

ger.com/resources/general/tsa-adopts-erm-residual-risk/

Nie, X., Batta, R., Drury, C. G., & Lin, L. (2009). Passenger

grouping with risk levels in an airport security system.

European Journal of Operational Research, 194, 574-

584.

Oliva, F. L. (2016). A maturity model for enterprise risk

management. International Journal of Production

Economics, 173.

Olson, D. L., & Wu, D. (2010). Enterprise risk management

models. In Enterprise Risk Management Models.

https://doi.org/10.1007/978-3-642-11474-8

Pluhacek, M., Senkerik, R., Viktorin, A., & Zelinka, I.

(2018). Single swarm and simple Multiswarm PSO

comparison. Proceedings of The 9th EUROSIM

Congress on Modelling and Simulation, EUROSIM

2016, The 57th SIMS Conference on Simulation and

Modelling SIMS 2016, (pp. 556-560).

Poole, R. W., & Passantino, G. M. (2003). Risk based

Airport Security Policy. Tech. rep., Reason Public

Policy Institute Los Angeles, CA.

Rai, A., & Modiano, E. (2019, May). Topology Discovery

Using Path Interference. In 2019 IFIP Networking

Conference (IFIP Networking) (pp. 1-2). IEEE.

Ravasz, E., Somera, A. L., Mongru, D. A., Oltvai, Z. N., &

Barabási, A. L. (2002, 8). Hierarchical organization of

modularity in metabolic networks. Science (New York,

N.Y.), 297. doi:10.1126/science.1073374

Sawik, B. (2011). Multiobjective Portfolio Optimization by

Mixed Integer Programming. Ph.D. dissertation, AGH

University of Science and Technology.

Sewell, E. C., Attagara, J., Kobza, J. E., & Jacobson, S. H.

(2012). Allocating Explosive Screening Devices for

Aviation Security. Journal of Transportation Security,

141-155.

Sewell, E. C., Lee, A. J., & Jacobson, S. H. (2013). Optimal

allocation of aviation security screening devices.

Journal of Transportation Security, 6, 103-116.

doi:10.1007/s1219801301062

Staff Contributor. (2022, April 28). What is network

topology? Best Guide to Types & Diagrams. Retrieved

from https://www.dnsstuff.com/what-is-network-

topology

Stewart, M. G., & Mueller, J. (2017). Risk and economic

assessment of expedited passenger screening and TSA

PreCheck. Journal of transportation security, 10, 122.

Sadler, S. Written testimony of TSA Office of Intelligence

assistant administrator Steve Sadler for a House

Committee on Homeland Security, Subcommittee on

Transportation Security Hearing titled "Safeguarding

Privacy and Civil Liberties While Keeping our Skies

Safe". (2014, September 18).

Soliman, A., & Adam, M. (2017). Enterprise risk

management and firm performance: An integrated

model for the banking sector. Banks and Bank Systems,

12(2). https://doi.org/10.21511/bbs.12(2).2017.12

Transportation, U. S. (n.d.). Retrieved from Federal

Aviation Administration: faa.gov

TSA. (2014). Transportation Security Administration

Enterprise Risk Management: Emergency Risk

Management Policy Manual. TSA.

Virta, J. L., Jacobson, S. H., & Kobza, J. E. (2003).

Analyzing the cost of screening selectee and

nonselectee baggage. Risk Analysis: An International

Journal, 23, 897-908.

Yip, A. M., & Horvath, S. (2007). Gene network

interconnectedness and the generalized topological

overlap measure. BMC bioinformatics, 8, 22.

Yuan, X., & Cormack, A. N. (2002). Efficient algorithm for

primitive ring statistics in topological networks.

Computational materials science, 24 (3), 343-360.

Risk-Stratiﬁed Multi-Objective Resource Allocation for Optimal Aviation Security

117