Performance Improvement of a Vertical Turbine Pump Accounting

for the Solid-Water Two-Phase Flow Conditions

Thomas Alphonse Mbock Singock and Guyh Dituba Ngoma

University of Quebec in Abitibi-Témiscamingue, School of Engineering,

445, Boulevard de l’Université, Rouyn-Noranda, Quebec, J9X 5E4, Canada

Keywords: Vertical Turbine Pump, Two-Phase Flow, ANSYS-CFX.

Abstract: A numerical study of the performance of a vertical turbine pump is carried out accounting for the flow of

water with solid particles through the pump. For this purpose, the governing equations of two-phase flow are

applied and solved using the ANSYS-CFX software. The achieved numerical pump model is validated by

comparison with the experimental results when the pump is subjected to clear water to generate the reference

pump model. Under two-phase flow, the performance of the reference pump drops drastically. Thus, the

results obtained reveal that the morphology of the pump studied favors the obstruction of the hydraulic

channels of the diffuser under two-phase flow. Based on this, a geometrical enlargement of hydraulic channels

compared to the reference pump model is adopted. The performance under two-phase flow is

enhanced while

it is observed its slight decrease under single-phase flow.

1 INTRODUCTION

The need to move fluids has led to the development

of mechanisms exploiting energy transfer. These

mechanisms of which pump are exploited in various

field and the environment where pumps are in

operation may change over time. This is the case of

some wells used to ensure the storage tanks for

wastewater from mines: the water contains solid

particles when its level drops in the tanks.

In the dewatering well, the submersible pump is

subjected to a single-phase flow and then gradually to

a two-phase flow. With these unusual pumping

conditions, when a pump is sized for clear water, it is

obvious that a performance problem will quickly arise.

The main challenge in this case is to determine a

suitable shape at the pump, allowing it to present

close performance when the pump is working under

single-phase flow and two-phase flow. To ensure a

good efficiency of a pump working under different

conditions mentioned, it is necessary to understand

the flow inside hydraulic channels and the impact of

solid particles on the pump performance. For this fact,

some techniques developed in other fields are applied

to pumps for two-phase flow applications.

Several numerical and experimental research

works have been accomplished on the vertical turbine

pumps in line with improving performance. The

aspect on the fluid flow through the pumps, the pump

shaft failure and the vibrations acting on the pump

shaft have been investigated inter alia by the authors

(Birajdar R. S. et al., 2021; Gao Y. et al., 2023;

Mohapatra J. N. et al., 2023; Nikumbe A. Y. et al.,

2015; Sunil P., 2022; Trivedi J. B. et al., 2016; Xia Y.

et al., 2015).

Indeed, the one-way fluid structure interaction

(FSI) method has been used for a vertical turbine

pump to find out the interaction between the fluid and

the structure to determine the vibration displacements

(Birajdar R. S. et al., 2021). The authors have

demonstrated that this approach can be applied to

understand and predict the fluid-induced vibrations in

any vertical turbine Pump.

Considering a liquid single-phase flow, a

performance study of a multi-stage vertical turbine

with different outlet setting angles of the space

diffuser has been realized accounting of the high

rotating speed of the shaft (Gao Y. et al., 2023). The

results obtained reveal that the outlet setting angle of

90° corresponds to an optimal solution.

Moreover, a shaft of a vertical turbine pump has

been examined experimentally in terms of failure in

tie with the pump operating conditions and the service

history of the pump (Mohapatra J. N. et al., 2023). In

addition, a modal analysis of a vertical turbine pump

112

Singock, T. and Ngoma, G.

Performance Improvement of a Vertical Turbine Pump Accounting for the Solid-Water Two-Phase Flow Conditions.

DOI: 10.5220/0012769100003758

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 14th International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH 2024), pages 112-119

ISBN: 978-989-758-708-5; ISSN: 2184-2841

has been done by the authors (Nikumbe A. Y. et al.,

2015). The results achieved of the experimental

modal analysis and the finite element modal analysis

are compared.

The authors (Trivedi J. B. et al., 2016) have

analyzed numerically a vertical turbine pump to

predict initial design of the pump geometries. They

have considered a pump including the impeller and

the suction bell. Using a liquid single-phase flow, the

streamline and the contours of the pressure and the

velocity have been achieved and examined. In the

paper (Xia Y. et al., 2015), the authors are described

an approach to design and optimize a vertical turbine

pump. The sources of loss of efficiency have been

identified employing the results of the CFD analysis.

According to this approach, the predicted

performance of the optimized pump is validated by a

physical testing.

In sum, analyzing the previous research works on

the vertical turbine pumps, it is observed that the

presented results cannot be automatically generalized

to all types of vertical turbine pumps. Thus, any new

investigation on a vertical turbine pump presents a

challenge.

Therefore, in this work, a numerical modeling

approach is developed to study in-depth the

performance of a vertical turbine pump considering

the single-phase flow and the two-phase flow basing

on an existing vertical turbine pump. The obtained

model of a vertical turbine pump is numerical

characterized and validated. Furthermore, the effects

of the solid-water two-phase flow, and the diffuser

vane number on the pump performance are analyzed.

2 MODEL DESCRIPTION AND

GOVERNING EQUATIONS

Figure 1 illustrates the main components of the

reference vertical turbine pump studied in this

research: a suction bell, an impeller, and a diffuser.

To describe the equations of the single-phase flow

(liquid flow) and the two-phase flow (solid-liquid

two-phase flow) for the flow through a vertical

turbine pump as depicted in Figure 1, the assumptions

are made. For the liquid single-phase flow, the liquid

flow is assumed to be steady-state and three-

dimensional; the liquid is considered incompressible;

the liquid is a Newtonian liquid; and the liquid

thermophysical properties are constant with the

temperature.

Figure 1: Single-stage pump components (School of

Engineering; Mbock Singock, T. A., 2018).

Moreover, for the solid-liquid two-phase flow,

the solid phase consists of dispersed solid particles;

the heat transfer and the mass transfer between

discrete and continuous phases are negligible; the

mixture of phases is heterogeneous; the solid phase is

assumed to be uniform spherical particles, and its

physical property is unchangeable; the liquid phase is

clear water; and the effects of the mass and energy

exchange between the solid phase and the liquid

phase are negligible.

2.1 Single-Phase Flow: Liquid Flow

Accounting for the assumptions for the liquid single-

phase flow, the theoretical analysis of the liquid flow

in the passages of the impeller, the diffuser vane and

the suction bell is based on the continuity and the

momentum equations (La Roche-Carrier et al., 2013;

ANSYS Inc., 2023). For the three-dimensional liquid

flow through these components as shown in Figure 1,

the continuity equations are given by:

.0∇=



(1)

where

()()()

()

U=U u x,y,z ,v x,y,z ,w x,y,z



is the liquid

flow velocity vector.

The momentum equations are expressed by:

.( ) .( ( ) )

∇⊗=−∇+∇∇+∇ +

  



eff

UU p U U

ρμ

(2)

where p is the pressure; ρ is the density; μ

eff

is the

effective viscosity accounting for turbulence, it is

defined as

eff t

μ = μ + μ

, μ is the dynamic viscosity

and

is the turbulence viscosity. It is linked to

turbulence kinetic energy

κ and dissipation ε; and 𝑆

⃗



represents the vector Coriolis, the centrifugal effect,

Performance Improvement of a Vertical Turbine Pump Accounting for the Solid-Water Two-Phase Flow Conditions

113

and the drag effect. It is equal to zero for the flow in

the stationary components like the diffuser and the

suction bell.

More particularly, for the flow in a rotating

impeller at a constant angular speed

ω, the source

term can be written as follows:

()

SxUxxr

ρω ωω

=− +







(3)

2.2 Two-Phase Flow: Solid-Liquid

Two-Phase Flow

Related to the solid-liquid two-phase flow through a

vertical turbine pump, it is highlighted that the

Sommerfeld collision model is applied to consider the

collision between particles, and the collision between

the solid particles and the wall (

ANSYS Inc., 2023;

Sommerfeld M., 1982). For that, due to the nature of the

mining rocks, the collision is assumed to be fully

elastic. To specify the drag, the Schiller Naumann

drag model is used supposing that the solid particles

are spherical, and the Reynolds number is sufficiently

large for inertial effects to dominate viscous effects.

Moreover, the dispersed phase zero equation model is

applied as the turbulence model. The wear of the

pump parts by erosion is not assessed in this study.

The volume fraction is given by:

(4)

where V

is the volume occupied by the phase i (i = α

for the liquid phase and i =

β for the solid phase); and

V is the volume containing both phases.

According to the particle model, the transfer of the

momentum between the solid particles and the water

is characterized by the interfacial area density. The

interphase contact area can be expressed as follows:

αβ

6ξ

(5)

where d

is the mean diameter of spherical solid

particles and

is the volume fraction of the solid

phase.

To ensure that the area density is not null, the particle

model is modified and the Equation (5) becomes:



αβ

6ξ

(6)

where

β min β max

max min β max

max

max(ξ ,ξ ) if ξ <ξ

1-ξ

max ξ ,ξ if ξ >ξ

1-ξ



















(7)

The values of

min

and ξ

max

in Equation (7) are

respectively 10

-7

and 0.8.

Furthermore, the mass conservation equations of

the liquid and solid phases are formulated by:

()

.0∇=



ii i

ξρ

(8)

where i =

α for the liquid phase and i = β for the solid

phase;

is the volume fraction of the phase i; ρ

is the

density of the phase i; and U

is the flow velocity of

the phase i.

Adding the left member of the Equation (8) for the

solid phase and the water phase, the Equation (9) is

found:

()()

..0∇+∇=



αα α ββ β

ξρ ξρ

(9)

In addition, the volume conservation equation

restraint the sum of the volume fraction of both

phases to unity at any time, as follows:

1+=

αβ

ξξ

(10)

Moreover, the momentum equations for the solid and

the liquid phases can be given by:

()

(

)



∇⊗=−∇+++





∇∇+∇ +













iii i ii i Mi

ii i i

UU p gS

ξρ ξ ρ

ξμ

(11)

where p

is the pressure of the phase i; μ

is the

dynamic viscosity of the phase i;

𝑆

⃗

is the source

term vector in the context of the two-phase flow. It is

formulated as follows:

()

2=− +







Mi i i i

SxUxxr

ρω ωω

(12)

Additionally, the characteristics of the solid

particles in the liquid that the pump can drain in the

mining environment are not always known in

advance.

Therefore, considering that the solid particles are

dispersed, the diameter, the volume fraction and the

specific gravity of a solid particle are varied

according to the Table 1.

SIMULTECH 2024 - 14th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

114

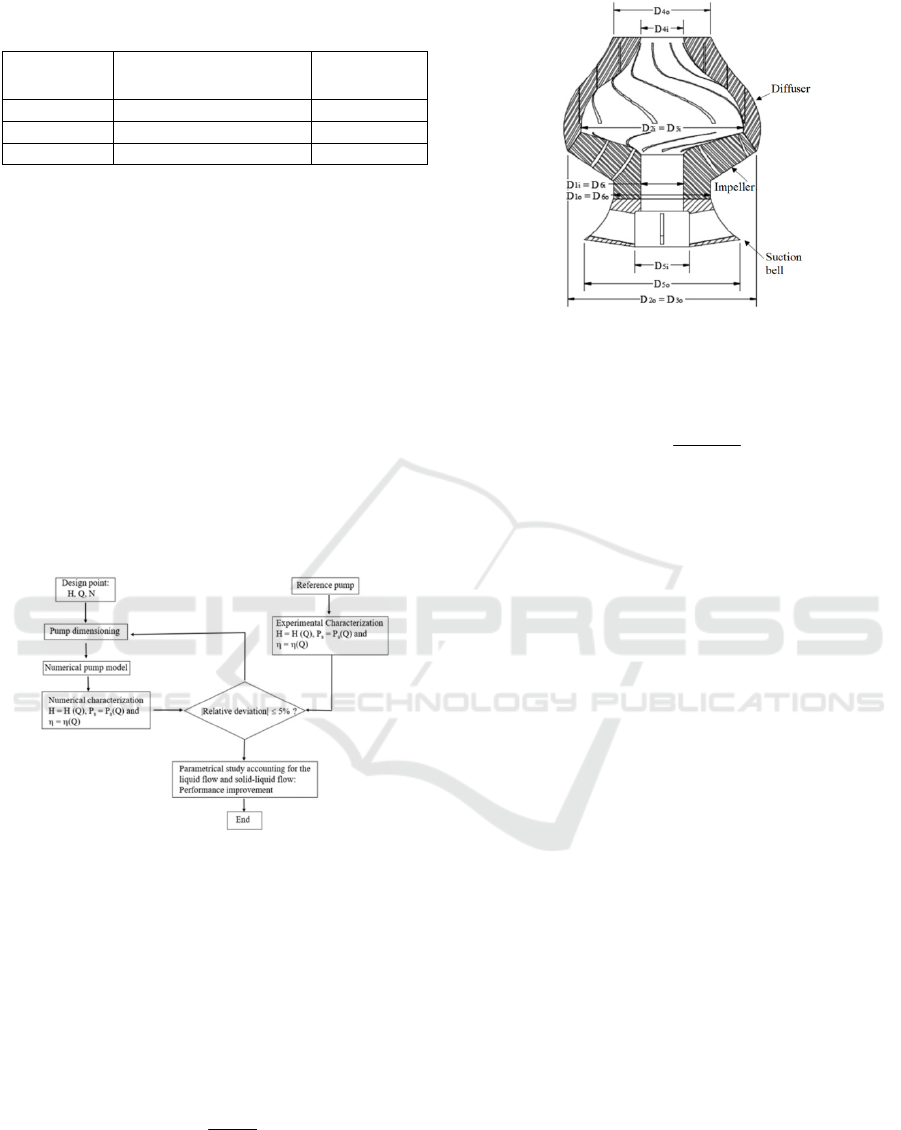
Table 1: Discrete phase parameters for dispersed solid

analysis.

Diameter

[mm]

Volume concentration

[%]

Specific

gravity [-]

1 10 1

2 20 2

3 30 3

3 DESIGN PARAMETERS OF

THE COMPONENTS OF A

VERTICAL TURBINE PUMP

The developed numerical approach to design the

impeller, the diffuser and the suction bell of a vertical

turbine pump is based on an existing physical pump

and a process of trial and error using the references

(Dicmas J. L., 1987; La Roche-Carrier et al., 2013; Peng

W. W., 2008; Stepanoff A. J., 1957)

. This approach

accounts for the operating conditions of the pump

which is the mining environment. Thus, Figure 2

shows the steps from the design point to the numerical

characterization of the vertical turbine pump.

Figure 2: Steps of the numerical characterization of the

vertical turbine pump.

Furthermore, the parameters of the impeller, the

suction bell, and the diffuser are depicted in Figure 3.

To achieve the numerical model of the vertical

turbine pump, the design point used is described by a

flow rate of 0.11 m

/s, a pump head of 35 m and a

rotating speed of 1785 rpm. The pump type is

determined calculating the specific speed which is

given by:

1/ 2

3/4

(13)

where Q is the flow rate, H is the pump head, and N

is the rotating speed.

Figure 3: Suction bell, impeller, and diffuser.

The corresponding dimensionless specific speed can

be expressed as follows:

()

1/2

3/4

(14)

where

ω is the angular speed.

According to the value of N

, the reference

vertical pump under study is Francis’s type (Peng W.

W., 2008). This geometry is classified between radial

and axial pumps. Physically, this reflects the fact that

the flow inside the Francis-type pump is semi-axial.

Moreover, the following assumptions are

formulated for the dimensioning of the impeller, the

diffuser, and the suction bell: the inlet flow in the

impeller is considered without circumferential

component; the outlet blade angle of the pump

impeller is considered as constant; and the ratio of the

inner and the outer radius of the impeller is kept

constant.

4 ELEMENT MESH, VERTICAL

TURBINE PUMP MODELING

AND BOUNDARY

Equations (1), (2), (9) and (11) resulting from the

mathematical modeling are solved numerically while

accounting for the boundary conditions and the

turbulence model by means of the ANSYS-CFX code

to obtain the distributions of the liquid flow velocity

and the pressure for the liquid single-phase flow and

the solid-liquid two-phase flow. In the cases

examined involving the pump stage, the boundary

conditions are formulated as follows: the static

pressure is given at the stage inlet, while the flow rate

is specified at the stage outlet. The frozen rotor

condition is applied for the impeller-diffuser interface

Performance Improvement of a Vertical Turbine Pump Accounting for the Solid-Water Two-Phase Flow Conditions

115

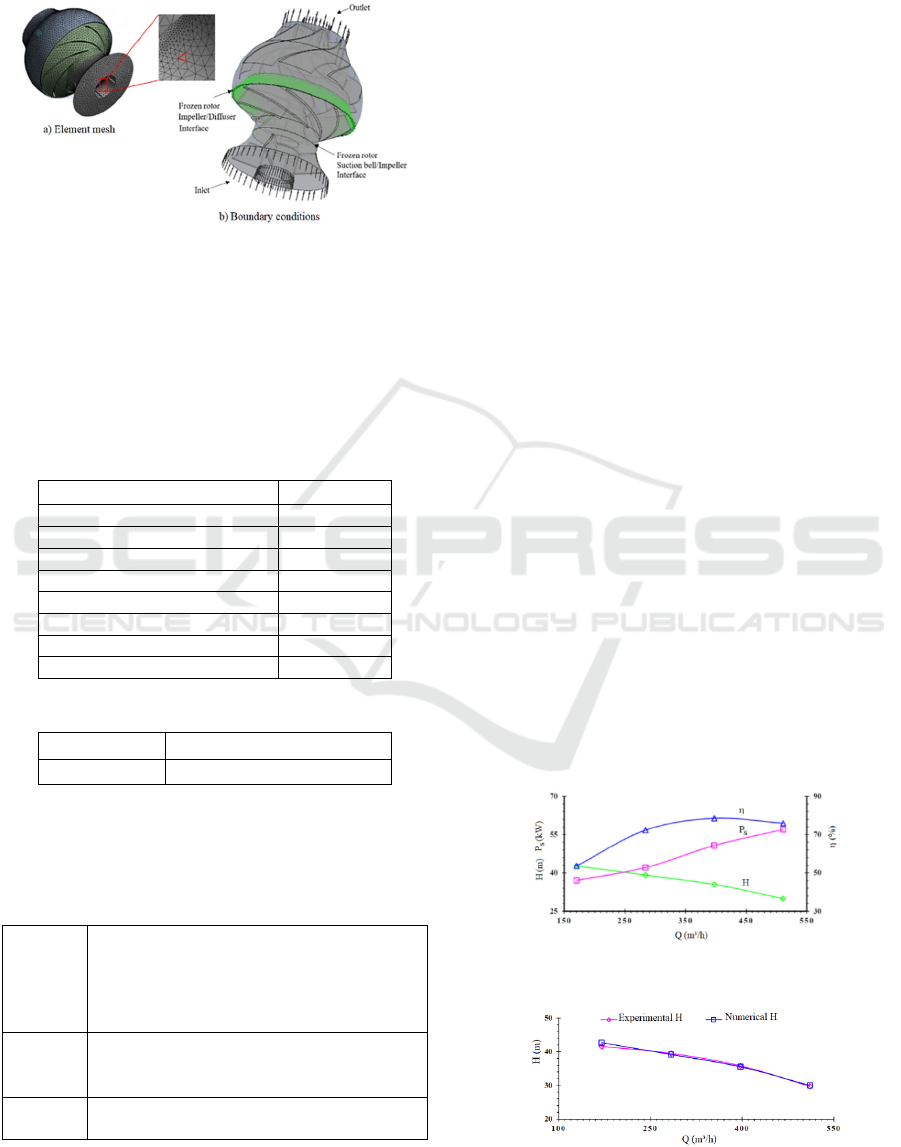
and the suction bell-impeller interface. In sum, Figure

4 shows the element mesh and the boundary

conditions for the pump model.

Figure 4: Element mesh and pump boundary conditions.

5 RESULTS AND DISCUSSION

The used properties of the 17-4PH steel (impeller,

diffuser, and shaft) and the water in this study are

indicated in Tables 2 and 3.

Table 2: Properties of the 17-4PH steel.

Young’s modulus [Pa] 1.96x10

Poisson ratio 0.3

Compressibility module [Pa] 1.63x10

Shear modulus [Pa] 7.53x10

Resistance coefficient [Pa] 9.2x10

Ductility coefficient [Pa] 10

Yield strength [Pa] 7.93x10

Ultimate tensile strength [Pa] 1.103x10

Densit

/m³] 7750.4

Table 3: Properties of water in 25 °C.

Density [kg/m³] Kinematic viscosity [m

/s]

997 0.884x10

-6

Furthermore, the main reference data for the impeller,

diffuser and

suction bell

are indicated in Table 4.

Table 4: Reference data for the impeller, the diffuser and

the suction bell.

Impeller D

= 70 mm; D

= 160 mm;

= 123 mm; D

= 310.6 mm;

= 288.64 mm; D

= 288.64 mm;

= 64 mm; b

= 38 mm; β

= 19°;

= 27.5°; and Z = 7.

Diffuser D

= 310.6 mm; D

= 266.68 mm;

= 160 mm; lc = 190.9 mm;

= 45.12 mm; β

= 30°; β

= 90°; and Z

=8.

Suction

ell

= 256.17 mm; D

= 160 mm;

= 68, 45 mm; R

= 115.36 mm; and Z

=4.

As regards the numerical simulations performed,

three cases are analyzed for the performance

assessment of the considered vertical turbine pump:

a) the characterization and the validation of the

numerical model using water single-phase flow; b)

the effect of the solid-water two-phase flow; and c)

the effect of the diffuser vane number.

5.1 Characterization and Validation of

the Numerical Model

To characterize the developed numerical pump model

in terms of head, brake horsepower and efficiency

using the water single-phase flow, the flow rate range

from 170.25 m³/h to 520.75 m³/h are selected keeping

the other parameters constant. Figure 5 represents the

pump head, the brake horsepower and the efficiency

as a function of the flow rate. From this figure, it can

be seen the trend of the performance curves of the

vertical turbine pump. The head decreases with

increasing flow rate. The brake horsepower raises

with the augmentation of the flow rate, whereas the

efficiency raises till the best efficiency point (BEP),

then it decreases with growing flow rate. At the BEP,

the flow rate is 397.25 m³/h, the head is 35.52 m, the

brake horsepower is 50.73 kW and the efficiency is

78.54 %. Furthermore, the numerical results are

compared with the experimental results to validate the

numerical pump model. A very good agreement is

achieved for the curves of the head and the efficiency

as depicted in Figures 6 and 7 respectively. The

corresponding relative gaps in absolute value of the

comparison results as a function of the flow rate are

shown in Figure 8. Thus, the validated numerical

model is designated as a reference model for the

analysis of performance improvement accounting for

the two-phase flow of water and solid particles.

Figure 5: Head, brake horsepower and efficiency versus

flow rate.

Figure 6: Head comparison.

SIMULTECH 2024 - 14th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

116

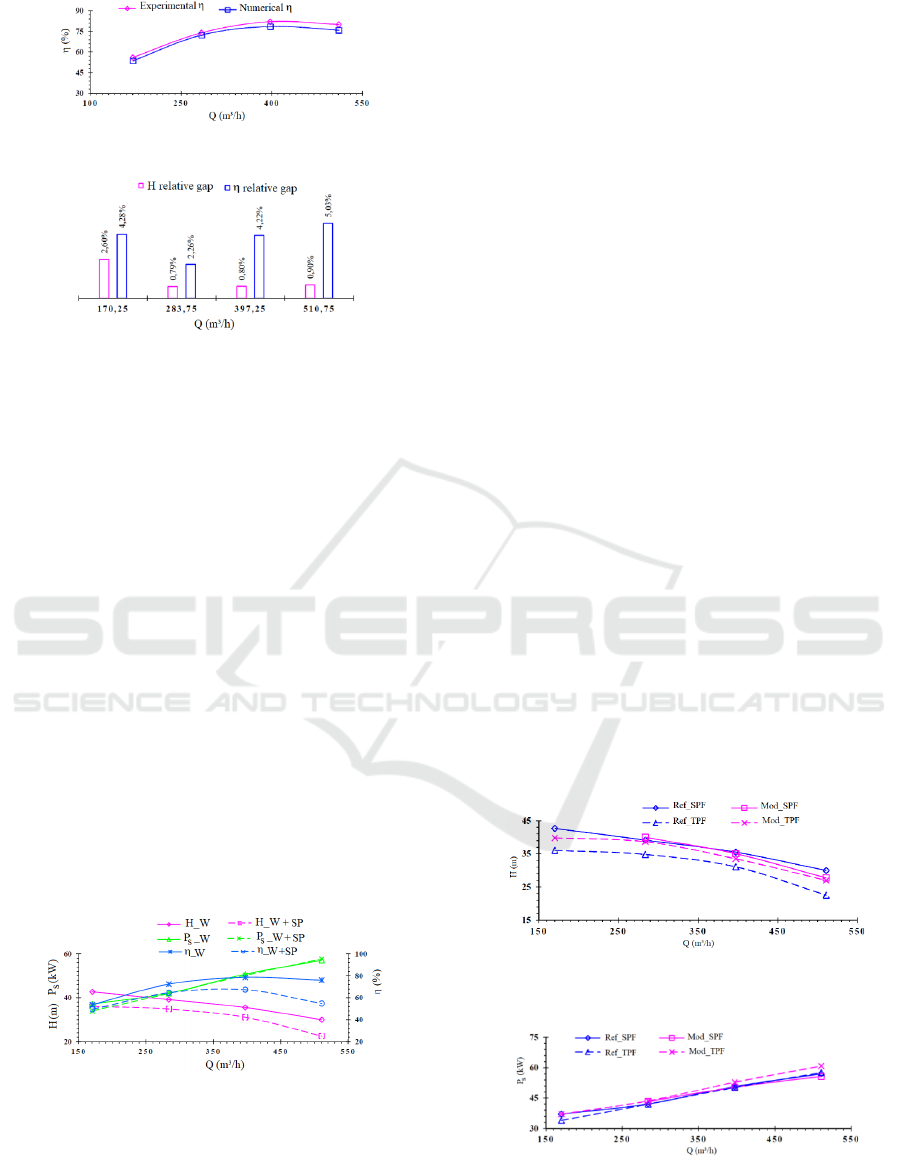
Figure 7: Pump efficiency comparison.

Figure 8: Relative gap between experimental and numerical

results.

5.2 Effect of the Solid-Water

Two-Phase Flow

To analyze the effect of the solid-water two-phase

flow on the pump head, the brake horsepower and the

efficiency, the reference model is used considering

the two-phase flow of water and solid discrete

particles. The applied values for the volume fraction

of solid particles, the solid particles diameter and the

specific gravity of the solid particles are 10 %, 1 mm

and 2, respectively. In addition, the flow rate range

from 170.25 m³/h to 520.75 m³/h are selected. Figure

9 illustrates the pump head, the brake horsepower and

the efficiency as a function of the flow rate for water

flow and the solid-water two-phase flow. From there,

it can be seen that the head and the efficiency for the

water flow are better than these for the solid-water

two-phase flow, whereas the brake horsepower is

almost identical for both flow types. The drops in the

pump head and the efficiency represent the impact of

the solid particles on the flow field in the pump.

Figure 9: Head and efficiency versus flow rate: single-phase

(W) and two-phase (W+SP) flow.

5.3 Effect of the Diffuser Vane Number

To investigate the effect of the diffuser vane number

on the pump performance accounting for the water

single-phase flow (SPF) and the solid-water two-

phase flow (TFP), the vertical turbine pump model

with 7 diffuser vanes is selected while holding the

other parameters constant for the flow rate from 280.5

m³/h to 510 m³/h. This pump model is designated as

modified model to distinguish it from the reference

model that has 8 diffuser vanes. Figs. 10-12 show the

pump head, the brake horsepower and the efficiency

as a function of the flow rate with the diffuser vane

number as a parameter. From Figure 10, it is observed

that the pump head for the solid-water two-phase flow

with the modified model is greater than that with the

reference model. Moreover, the gap between the

pump heads for the water flow with the reference and

the modified models is lower than the gap for the

solid-water two-phase flow with the reference and

modified models. In addition, Figure 11 shows that

the brake horsepower for the solid-water two-phase

flow with the modified model is slightly higher than

the brake horsepower of all other cases. Relating to

the pump efficiency, Figure 12 illustrates that the

efficiency for the solid-water two-phase flow with the

modified model is between the efficiencies for the

water single-phase flow and the solid-water two-

phase flow with the reference model. Thus,

comparing the efficiencies of the reference and the

modified models accounting for the solid-water two-

phase flow, it can be mentioned that the efficiency is

better for the modified model. This can show that the

modified model is at this level of assessment, best

suited to withstand the variations required by the

transition from water flow to solid-water two-phase

flow without any functional or installation

modification.

Figure 10: Head versus flow rate: reference and modified

models.

Figure 11: Brake horsepower versus flow rate: reference

and modified models.

Performance Improvement of a Vertical Turbine Pump Accounting for the Solid-Water Two-Phase Flow Conditions

117

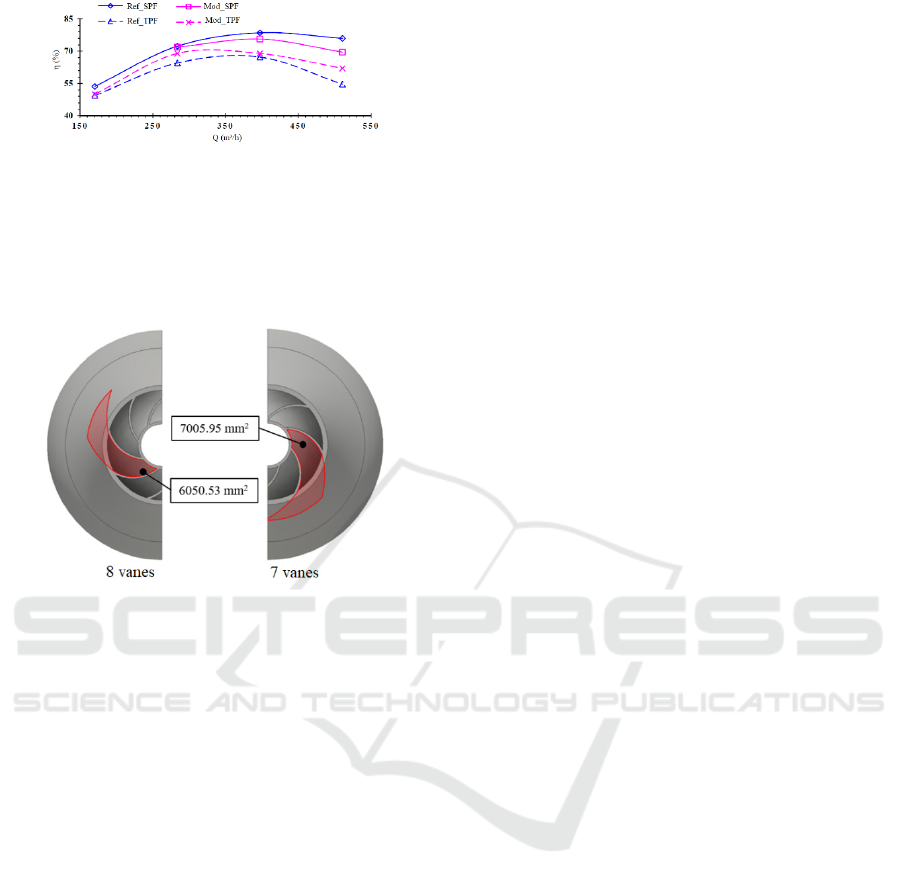
Figure 12: Efficiency versus flow rate: reference and

modified models.

In sum, it is to highlight that the use of 7 diffuser

vanes in the modified pump model leads to a

widening of the diffuser channels of 13.8 % as

indicated in Figure 13.

Figure 13: Modified diffuser channels.

6 CONCLUSIONS

This study deals with the design and the numerical

characterization of a vertical turbine pump in the

context of the performance enhancement. Based on

the design point, the numerical model of a vertical

turbine pump of Francis type is developed. By means

of the ANSYS CFX code, the pump head, the brake

horsepower and the efficiency are determined in

different operating conditions using the water single-

phase flow to obtain the reference model after

validation. A very good agreement is achieved

comparing the numerical results from the reference

model and the experimental results. Then,

simulations are accomplished with the reference

model considering the sold-water two-phase flow. It

is observed that the pump head and the efficiency for

the water two-phase flow are lower than those for the

water single-phase flow, whereas the brake

horsepower is remained almost unchanged. Thus, to

improve the performance of the reference model in

the case of the solid-water two-phase flow, the

diffuser with 7 vanes is used keeping the impeller

blade number of 7 to obtain the modified model. The

comparison of the numerical results between the

reference model and the modified model revealed an

improvement of the head and the efficiency for the

modified model. Further research work is planned to

analyze the effects of the induced forces and stresses

on the vertical turbine pump performance in the

mining environment.

ACKNOWLEDGEMENTS

The authors are grateful to the Technosub Inc.,

Industrial pumps manufacturing and distribution in

Quebec (Canada) and the Turbomachinery

laboratory

of the Engineering School of the University of

Quebec in Abitibi-Témiscamingue.

REFERENCES

ANSYS Inc., ANSYS CFX-Solver Theory Guide Release

2023 R1. Canonsburg, PA, USA, 2023.

Birajdar R. S., Keste A. A., and Gawande S. H. (2021).

Critical Hydraulic Eccentricity Estimation in Vertical

Turbine Pump Impeller to Control Vibration,

International Journal of Rotating Machinery.

Dicmas J. L. (1987). Vertical turbine, mixed flow, and

propeller pumps, McGraw-Hill Book Company New

York.

Gao Y., Cao W., Zhang Y., Cao G. and Zhao X. (2023).

Investigation of high-speed deep well pump

performance with different outlet setting angle of space

diffuser, Frontiers in Energy Research.

La Roche-Carrier N., Dituba Ngoma G., and Ghie W.

(2013). Numerical investigation of a first stage of a

multistage centrifugal pump: impeller, diffuser with

return vanes, and casing. ISRN Mechanical

Engineering, Vol. 2013, Article ID 578072, 15 pages.

Lazarkiewicz, S., TROSLANSKI, A. T. (1965). Impeller

pumps. Pergamon Press Ltd., Headington Hill Hall,

Oxford.

Mbock Singock, T. A. (2018). Conception et caractérisation

numérique d'une pompe à turbine verticale de grande

capacité. Université du Québec en Abitibi-

Témiscamingue.

Mohapatra J. N., Gujare R. R., Dabbiru S. K., Sah R.

(2023). Failure Analysis of Vertical Turbine Pump

Shaft, Journal of Failure Analysis and Prevention

(JFAP).

Nikumbe A. Y., Tamboli V. G., Wagh H. S. (2015). Modal

Analysis of Vertical Turbine Pump, International

Advanced Research Journal in Science, Engineering

and Technology.

Peng W. W. (2008). Fundamentals of turbomachinery,

John Wiley & Sons, California.

School of Engineering, Turbomachinery laboratory (E-

216), University of Quebec in Abitibi-Témiscamingue

(UQAT), www.uqat.ca.

SIMULTECH 2024 - 14th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

118

Sommerfeld M. (1982). Modelling of Particle-Wall

Collisions in Confined Gas-Particle Flows,

International Journal of Multiphase Flow, 18(6), pp.

905-926.

Stepanoff A. J. (1957), Centrifugal and Axial Flow Pumps,

Theory, Design, and Application, Jonh Wiley & Sons,

New York.

Sunil P. (2022). Testing of Mixed Flow Vertical Turbine

Pump, International research journal of engineering and

technology (IRJET).

Trivedi J. B., Trivedi J., Chauhan V. (2016). Hydraulic

Analysis of Vertical Turbine Pump, INROADS- An

International Journal of Jaipur National University.

Xia Y., Maddox G., S. Lowry and Ding H. (2015), Design

and Optimization of a Vertical Turbine

Pump, Proceedings of the ASME/JSME/KSME. Joint

Fluids Engineering Conference. Volume 1: Symposia.

Seoul, South Korea. V001T33A008. ASME. DOI:

10.1115/AJKFluids2015-33233.

Performance Improvement of a Vertical Turbine Pump Accounting for the Solid-Water Two-Phase Flow Conditions

119