FPGA Implementation of AES-Based on Optimized Dynamic s-Box

Calvo Mayaud

on Haroldo

, Nakojah Chris David

, Mahdi Madani

2 a

and El-Bay Bourennane

Faculty of Science and Technology, University of Burgundy, Dijon, France

ImViA Laboratory (EA 7535), University of Burgundy, 21000 Dijon, France

Keywords:

Dynamic S-Box, FPGA Implementation, AES Algorithm, Hardware Metrics, Timing Performance,

Cryptographic Analysis.

Abstract:

In this paper, we present a hardware implementation of an enhanced version of the AES (Advanced Encryp-

tion Standard) algorithm, and evaluate its performance. In the proposed design, we replaced the original static

S-boxes with a robust dynamic S-box generator mechanism. The principle consists of using the secret key

to generate new dynamic S-boxes by applying a bitwise XOR operation with all 256 bytes of the AES stan-

dardized S-box. Then, the architecture is implemented on a Xilinx XC7Z020 PYNQ-Z2 FPGA platform to

accelerate the calculations, and its robustness is evaluated using many security tests. The experimental results

prove the satisfaction of our design for several cryptographic properties, such as nonlinearity, bijectivity, and

strict avalanche criterion that conﬁrm its resistance against the main cryptanalysis attacks.

1 INTRODUCTION

Communication or information sharing is a key as-

pect of life that comes in various forms, such as text

format, images, and videos. Images are the most com-

monly used visual form of communication in today’s

digital age. Digital or wireless communication comes

with its own security challenges, with the transmit-

ted information being vulnerable to attacks; hence,

its conﬁdentiality and integrity are of great concern.

Data encryption, or simply cryptography, is a method

of transforming data (plaintext, either texts or images)

into a language (ciphertext) that is not recognizable

or cannot be read by unauthorized parties without the

permission of the sender (key). There are different

cryptography methods. In Symmetric cryptography,

the same key is used for encryption and decryption,

where the sender and receiver must share the same

key.

Symmetric cryptography includes two types of ci-

phers: block ciphers and stream ciphers. Block ci-

phers convert plaintext into ciphertext in ﬁxed block

sizes. AES (Rijmen and Daemen, 2001) and DES are

examples of symmetric cryptography that operate on

ﬁxed block sizes of 128 and 64 bits, respectively. The

role of block cipher encryption and decryption is to

provide diffusion and confusion functions. The con-

https://orcid.org/0000-0001-9727-8567

fusion is enforced by establishing a nonlinear func-

tion between the plaintext and the ciphertext; the dif-

fusion consists of spreading the inﬂuence of a small

change to the plaintext throughout the whole cipher-

text. Stream ciphers, on the other hand, convert plain-

text into ciphertext one bit or byte at a time. Asym-

metric cryptography uses a pair of keys for encryp-

tion. A public key for encryption and a private key for

decryption. Difﬁe Hellman, RSA, and RCC are ex-

amples. The Advanced Encryption Standard (AES),

developed by Rijndael and adopted by the National

Institute of Standards and Technology (NIST) since

2001, has been approved as the standard encryption

algorithm (Dubertret, 2023).

Recently, the hardware implementation of encryp-

tion algorithms has gained a wave of attention from

researchers and developers because of their high per-

formance and efﬁciency compared to software-based

solutions. The AES can be implemented efﬁciently

both in hardware and software. Software imple-

mentation takes the smallest resources, but it of-

fers only limited physical security. Because of the

growing requirements for high-speed, high-volume

secure communication combined with physical secu-

rity, the hardware implementation of cryptographic

algorithms becomes essential (Rahimunnisa et al.,

2014). FPGAs are desired because of their low en-

ergy consumption and parallel processing capabili-

ties, which offer an ideal platform for implementing

730

Haroldo, C., David, N., Madani, M. and Bourennane, E.

FPGA Implementation of AES-Based on Optimized Dynamic s-Box.

DOI: 10.5220/0012780300003767

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 21st International Conference on Security and Cryptography (SECRYPT 2024), pages 730-737

ISBN: 978-989-758-709-2; ISSN: 2184-7711

cryptographic algorithms like AES. The Implementa-

tion on FPGA devices can achieve high throughput

rates, making them ideal for confusion and diffusion

in real-time tasks in digital communication. It is use-

ful in areas where greater emphasis is placed on the

speed of communication.

In this study, we improved the design of the AES

block cipher and performed its hardware implemen-

tation. Then, we assessed its material metric and ex-

plored its parallelism properties to accelerate runtime

execution. The main principle consists of replacing

the static S-box with a dynamic one. The proposed

principle consists of the use of the secret key to gen-

erate new dynamic S-boxes by applying bitwise XOR

operations with all 256 bytes of the AES-standardized

S-box. The dynamically generated S-boxes demon-

strate at least the same or greater cryptographic char-

acteristics as the standard AES S-box while increas-

ing the complexity needed to break the algorithm.

Also, no additional information should need to be ex-

changed between the sender and receiver of the en-

crypted data other than the secret key. The choice of

the Dynamic S-box encryption mechanism in this re-

search is due to the security improvement that it can

provide, and we apply the proposed technique to the

AES algorithm because it is a known and widely used

encryption algorithm with weaknesses. The dynamic

s-box introduces variability, which strengthens the se-

curity of the encryption by disrupting the patterns that

can be followed by cryptanalysts to break the encryp-

tion. Also, the dynamic s-box uses some other cryp-

tographic properties, such as bijectivity, nonlinearity,

strict avalanche criteria, and correlation immunity, to

ensure the conﬁdentiality of the encrypted data on the

FPGA and resist attacks.

The proposed architecture is designed using the

Vitis High-Level Synthesis (HLS) with a C++ lan-

guage and implemented on a Field Programmable

Gate Array (FPGA) technology (Smith and Johnson,

2018), (Chen and Wang, 2019) through the Xilinx

XC7Z020 PYNQ-Z2 hardware platform. The robust-

ness of the proposed architecture is tested by evalu-

ating its keystream performance by analyzing three

different dynamic s-boxes.

The remainder of this paper is organized as fol-

lows. Section 2 presents the whole related work,

and Section 3 presents brieﬂy the architecture and

the processing steps of the standard AES block ci-

pher. Section 4 describes the proposed architecture,

including the dynamic S-box designed to enhance

the security of the regular architecture. Section 5

presents the Vitis HLS and FPGA implementation re-

sults and the hardware metrics (logic resources, efﬁ-

ciency, throughput, frequency, etc.). Section 6 inves-

tigates cryptanalytic analysis, allowing us to prove the

robustness of the proposed scheme. Finally, Section 7

summarizes the whole article and gives directions for

our future work.

2 PREVIOUS RELATED WORKS

In the ﬁeld of cryptography, there have been several

studies on the implementation of the Advanced En-

cryption Standard (AES) using hardware-based solu-

tions. The challenging factor has been to increase

throughput with low latency, considering low-cost de-

vices. An adaptive and convenient way to achieve

that is by optimizing the s-box. Hence, various re-

searchers have introduced several methods to achieve

this common goal. A few of these works are discussed

in this section.

An FPGA-based AES accelerator’s comprehen-

sive design and analysis are presented in Wang et

al.’s work (Wang and Ni, 2004). The authors pro-

vide a cutting-edge method for employing a dynamic

S-box to perform the AES algorithm on an FPGA.

Unlike classic ﬁxed-function AES accelerators, this

method enables the accelerator to adjust to various

key sizes and rounds. Memory-mapped I/O (MMIO)

interfaces are used to implement the dynamic S-box,

enabling the CPU to read and write data to the S-box.

To achieve minimal area, various optimization strate-

gies for AES of 32-bit data channels are shown in

(Bui et al., 2017). These techniques involve reducing

the amount of control logic and registers by decreas-

ing activity and implementing a clock gating scheme

for the data storage register. An FPGA with a high-

performance implementation of AES-128 is proposed

by Li et al. (Li et al., 2017). To get high throughput.

The authors combined pipelining and parallelism. In

(Zhang et al., 2016), the authors achieved their objec-

tive of AES implementation on FPGA by combining

techniques such as pipelining, parallelism, and look-

ahead logic to optimize the AES algorithm’s criti-

cal paths. In (Smith and Johnson, 2018), this paper

suggests a dynamic S-Box-based FPGA implementa-

tion of AES that is effective and suitable for Inter-

net of Things (IoT) devices. The implementation’s

major goal is to consume resources as little as pos-

sible while still achieving excellent speed and secu-

rity. In (Chen and Wang, 2019), the authors describe

a pipeline architecture-based, fast FPGA implemen-

tation of AES with Dynamic S-Box. By paralleliz-

ing encryption operations and integrating the dynamic

S-Box technique for increased security, the approach

improves throughput. The secure FPGA implementa-

tion of AES with Dynamic S-Box for embedded de-

FPGA Implementation of AES-Based on Optimized Dynamic s-Box

731

vices is the main emphasis of this work (Zhang and

Li, 2020). The implementation uses FPGA paral-

lelism for effective encryption while addressing secu-

rity concerns in contexts with limited resources. The

AES introduces a composite ﬁeld arithmetic CFA-

based S-box operation to decrease the area (Priya

et al., 2017). To lower the crucial delay and boost

clock frequency and throughput, the sub-pipelining

concept is used in the process. Guzm

an, Nieto, and

Bernal in (Guzman et al., 2016) used a pipelined ar-

chitecture on the Xilinx Virtex 5 FPGA platform to

offer a hardware implementation of the AES-128 al-

gorithm in non-feedback modes of operation, namely

ECB and CTR. In (Mamun et al., 2017), the authors

suggest altering the S-box by adding an extra byte,

which they refer to as the ‘AES-SBOX+.’ The pur-

pose of the improved S-box is to make the AES algo-

rithm more resistant to linear and differential crypt-

analysis. The authors also used power analysis to

assess the security of the AES-SBOX+ against side-

channel attacks and show that it is more resilient to

these types of assaults than the traditional AES S-box.

To produce the S-Box output, the input data is sub-

jected to an afﬁne transformation and bit-permutation

as part of the transformation technique described in

(Nandan and Gowri Shankar Rao, 2022). The au-

thors show that this transformation method is resistant

to various cryptanalytic attacks, such as differential

and linear attacks. Compared to the traditional AES

S-Box design, the suggested S-Box design uses less

power and takes up less space when implemented on

an FPGA platform.

3 STANDARD AES BLOCK

CIPHER ARCHITECTURE

The Advanced Encryption Standard (AES) is a sym-

metric encryption algorithm. This means that both the

sender and receiver use the same key for both encryp-

tion and decryption of the data. It has a ﬁxed block

size of 128 bits and variable key lengths of 128, 192,

or 256 bits. The key is used to initialize a series of

round keys, which are then used in a complex series of

operations to transform the input data (plaintext) into

encrypted data (ciphertext). The matrix used to store

the ciphertext block in all the intermediate and ﬁnal

steps is referred to as a state matrix, 16 × 16 bytes.

In the AES architecture, the encryption and de-

cryption transformations are carried out in a series of

operations. The algorithm consists of 10, 12, or 14

rounds, depending on the size of the key used. These

rounds consist of a series of transformations, which

are substitution, permutation, and mixing of data. The

core operations of AES are SubBytes (byte substitu-

tion), MixColumn (mixing column), ShiftRow (row-

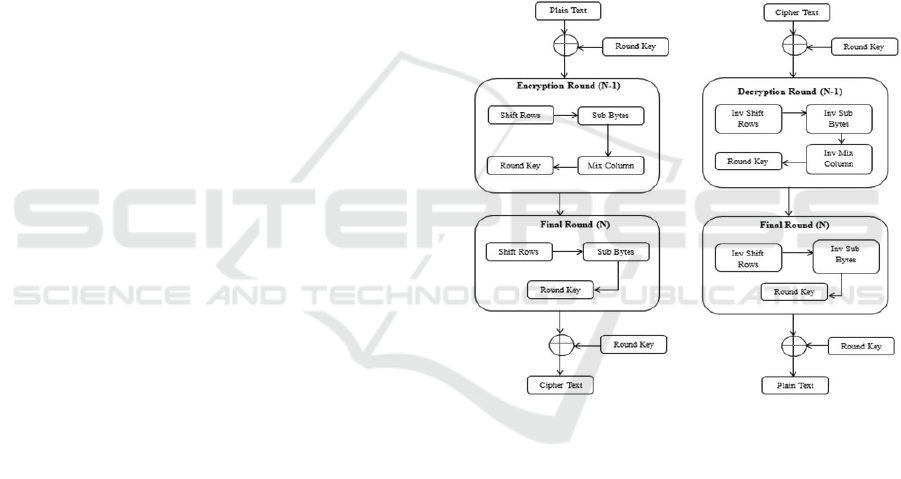
wise permutation), and AddRoundKey (see Figure 1).

Each round provides a different effect on the ﬁnal

ciphertext. The substitution round (SubBytes) is a

nonlinear function, that provides confusion and re-

sistance to linear and differential cryptanalysis, The

Sbox should be carefully designed so that this oper-

ation may be reversible and provide an unequivocal

one-to-one relation between the elements of the Sbox

and its inverse (bijectivity). The permutation steps

ShiftRows and MixColumns are linear functions in-

cluded in the different rounds to spread the inﬂuence

of each plaintext byte over the whole state matrix (dif-

fusion). Finally, the key addition round (AddRound-

Keys) makes the ciphertext dependent on the secret

key.

Figure 1: Encryption and decryption architecture of AES.

The cryptographic properties of S-boxes measure

how randomly the ciphertext bits are changed, some

key ﬁgures of merit are shown below (Webster and

Tavares, 1986), (Waqas et al., 2015):

• Strict Avalanche Criterion SAC: Whenever a sin-

gle bit at the input changes, all the output bits

should have a 50% probability of changing, it is

measured on a scale [0-1], This property is related

to diffusion.

• Bit Independence Criterion-BIC: Output bits j and

k should change independently when any single

input bit i is changed (complemented). Correla-

tion between j and k when i is reversed.

• Nonlinearity-NLM: Complex and non-

proportional relationship between the inputs

and the outputs. This property is related to

confusion [19].

SECRYPT 2024 - 21st International Conference on Security and Cryptography

732

In addition to these requirements, S-boxes should

be reversible to guarantee the bijectivity (complete-

ness) of the encryption-decryption process.

4 PROPOSED ARCHITECTURE

The two main objectives set by this work consist of

improving the AES algorithm by adding dynamic S-

boxes and increasing the runtime performance by im-

plementing the modiﬁed algorithm on an FPGA plat-

form.

It is expected that the dynamically generated S-

boxes demonstrate at least the same or greater cryp-

tographic characteristics as the standard AES S-box

while increasing the complexity needed to break the

algorithm. Also, no additional information needs to

be exchanged between the sender and receiver of the

encrypted data other than the secret key. The FPGA

implementation should exploit parallelism within the

AES algorithm. The approach introduced in (Ar-

rag et al., 2013) will be employed to generate key-

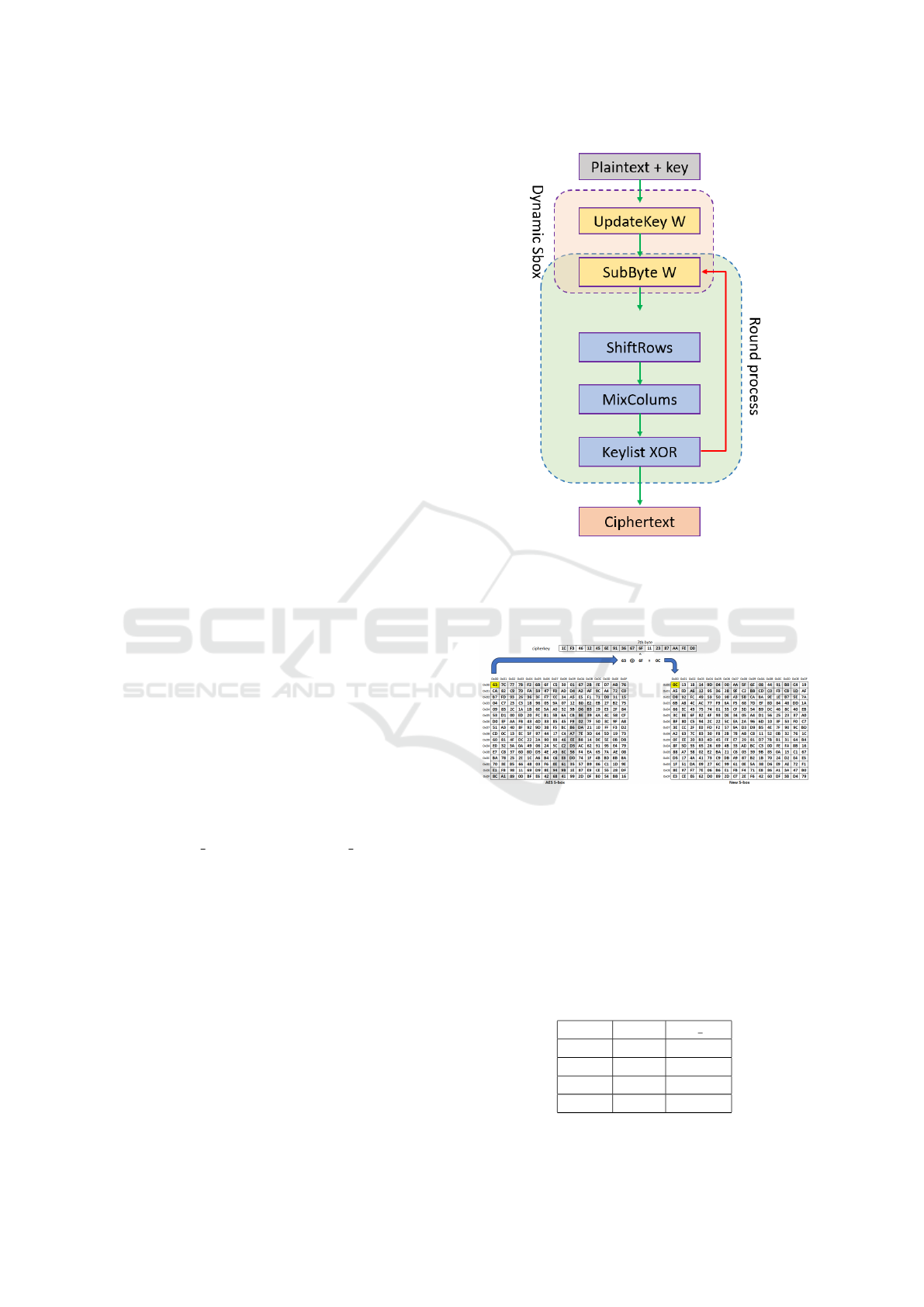
dependent dynamic S-boxes, It consists of the use of

one byte of the cipher key to generate new S-boxes

by applying the XOR operation with all 256 bytes of

the AES S-box. In this work, the 7th byte was used

(but any byte could be used), thus the S-box will be

referred to as S-BOXkey7. In Equation 1 below, the

ith element of the new Dynamic S-box, S-BOXkey7,

corresponds to the ith element of the S-BOXAES,

XORed with the 7th byte of the cipher key.

S − BOXkey7[i] = S − BOXAES[i]⊕ Key7 (1)

To generate the inverse S-box, it is necessary to

use the inverse routine according to Equation 2.

S − BOXkey7 INV [i] = S − BOX AES INV [i ⊕ Key7]

(2)

The algorithm implemented performs standard

AES encryption/decryption, where the updateKey and

SubByte functions have been modiﬁed to dynamically

calculate the new S-box. In Figure 2, a ﬂow diagram

of the implemented AES modiﬁed encryption algo-

rithm with dynamic S-box.

In the updateKey and SubByte routines, in Figure

5, the key’s 7th byte is XORed with the AES S-box

corresponding value to generate the new S-box value.

Any other byte may be selected, as mentioned in the

S-box implementation section. The rest of the encryp-

tion steps are the same. For decryption, the key’s 7th

byte is XORed with the inverse s-box position being

Figure 2: Process of the proposed dynamic s-box.

evaluated and fed to the AES inverse S-box. For bet-

ter understanding, the approach used is illustrated in

Figure 3.

Figure 3: Example of a dynamic S-box.

According to (Arrag et al., 2013), the resulting S-

boxes inherit the cryptographic characteristics of the

AES S-box. To corroborate, a non-linearity and av-

erage SAC tests (Qu et al., 2009) were performed

on 3 S-boxes and compared to the AES S-box value,

concluding that the non-linearity and SAC values are

equivalent (+/-1%) to those of the AES and satisfy the

results of good S-boxes designed for robust block ci-

phers, as prove the results in Table 1.

Table 1: Dynamic Sbox Non-linearity and SAC.

S-box NLM avg sac

AES 112 0.5048

0x23 112 0.499

0x6F 112 0.4954

0xD7 112 0.4982

FPGA Implementation of AES-Based on Optimized Dynamic s-Box

733

Once implemented, the dynamic S-box scheme

would enhance the AES algorithm by adding a 2

256 complexity to its 2

128

complexity (Nissar et al.,

2019), in the case where the cipher key is changed

frequently.

5 VITIS HLS DESIGN

WORKFLOW AND FPGA

IMPLEMENTATION RESULTS

5.1 Vitis HLS Design

The proposed architecture is designed using the Vi-

tis High-Level Synthesis (HLS) with C++ language.

The advantages of this approach are multiple: shorter

development time, easier implementation of recursive

functions, simple hierarchical design, and the possi-

bility that existing primitive libraries may be re-used

to accelerate development time. The design is im-

plemented on the Xilinx XC7Z020 PYNQ-Z2 FPGA

platform. The design process for Vitis HLS is as fol-

lows:

• C Simulation: The C simulation and the co-

simulation allow the designer to compile the code

and test the design behavior without programming

the target device.

• C Synthesis: On the C Synthesis, the target device

resources are allocated based on the design needs

(FF, LUT, and SLICEs).

• Co-simulation: The simulation step consists of

testing the functional behavior of the implemented

module by comparing the generated outputs with

the software or theoretical expected outputs.

• Export RTL (Register Transfer Level): The Ex-

port RTL stage packs the VHDL or Verilog design

into an IP package that may be used in Vivado

(VHDL graphical development tool).

• Implementation: The implementation step takes

care of the layout and routing of the design.

The implemented design is structured as a C/C++

function, which is denominated as the top-level func-

tion. This function may reference other functions

within its deﬁnition. The input and output argu-

ments to the top-level function establish the interac-

tions with the exported design.

5.2 FPGA Implementation Results

After various simulations and synthesis runs, the de-

sign for a CBC mode use of the AES with dynamic

S-box was validated at 833 ns. The resource utiliza-

tion for the design is shown in Table 2.

The maximum frequency was calculated using

Equation 3, where T is the target clock period, T=8

ns in the present design, and WNS is the worst neg-

ative slack calculated after the implementation place

and route in Vivado tools (Mahdi et al., 2023).

Max Freq =

T −W NS

[MHz] (3)

To calculate the throughput, Equation 4 is em-

ployed, where N is the number of bits per block.

T hroughput = N × Max Freq [Mbps] (4)

The Efﬁciency of the design was evaluated using

Equation 5.

E f f iciency =

T hroughput

Slices

[Mbps/Slices] (5)

The comparison of hardware metrics of several

AES implementations is summarized in Table 3. De-

spite the comparative study with other FPGA targets

with different timing and logic resource characteris-

tics is difﬁcult to carry out, we try to give an ob-

jective analysis. Therefore, considering the timing

metrics, we remark that the proposed implementa-

tion presents one of the better throughput achieve-

ments (70 Gb/s) but uses largely low logic resources

compared to (Qu et al., 2009), (Liu et al., 2013). In

addition, both the timing performances and logic re-

sources are better than those obtained by (Guzman

et al., 2016), (Fan and Hwang, 2007). Whereas the

(Elsayed et al., 2008) implementation achieved bet-

ter performances than our architecture. However, the

frequency of the used device in (Elsayed et al., 2008)

(425 Mhz from the datasheet) is greater than the fre-

quency of the used board in this work (125 Mhz). By

considering those remarks, we can consider that the

proposed architecture has good hardware metrics and

timing performance.

6 CRYPTOGRAPHIC ANALYSIS

In this section, an analysis of the cryptographic prop-

erties of the proposed algorithm is performed. A set

of 3 test images was encrypted using the AES-128 dy-

namic S-box algorithm in CBC block mode. The im-

ages employed are 256x256 pixel, 8-bit grayscale pic-

tures. The experiments were performed using a Vitis

HLS testbench written in C++, and the data was ex-

tracted and plotted using MATLAB and Excel on an

Intel (R) Core (TM) i5-8250U CPU operating at 1.60

GHz, running Microsoft Windows 11 (64-bit), with

16 GB of RAM.

SECRYPT 2024 - 21st International Conference on Security and Cryptography

734

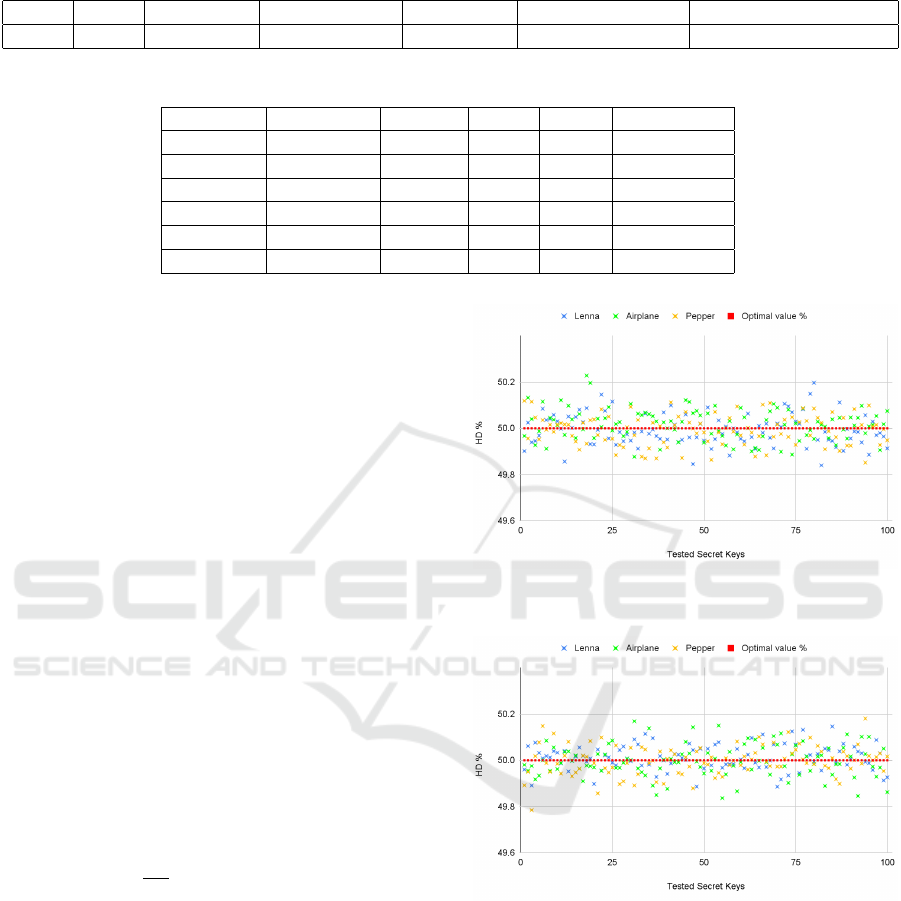
Table 2: Resource utilization for the Zynq xc7z020.

Mode Slices Slice LUTs Slice Registers Fmax MHz Throughput Gbit/s Efﬁciency Mbps/Slices

CBC 3287 10102 7795 540.54 69.19 21.04

Table 3: Comparison of results with other AES architecture designs.

Reference Device F/MHz Mode LUTs Throughput

[26] xc5vlx85 576.07 CTR 22994 73.73Gb/s

[27] xc4vlx200 250 ECB 86806 32.00 Gb/s

[14] xc5vlx110t 272.59 CTR 11677 34.89 Gb/s

[28] xc2vp30 405.277 CBC 6361 108.59 Gb/s

[29] xc7vx690t 516.8 ECB 3436 66.10 Gb/s

This work xc7z020 540.54 CBC 10102 69.19 Gb/s

6.1 Hamming Distance and Key

Sensitivity Analysis

The Hamming Distance (HD) is used in cryptogra-

phy to measure the difference between two-bit strings

(keys) of the same size. Figure 4 shows the hamming

distance between plain and encrypted images. To un-

derstand how sensitive the algorithm is to the secret

key, two tests were performed, by measuring the dis-

tance between the same encrypted plaintext twice by

slightly changing one bit of the secret key. This pro-

cess gives two different encrypted texts, which are

compared to measure the effect of the key change on

the encrypted output (Mahdi et al., 2023). Ideally,

half of the bits, or 50%, should change by just chang-

ing one bit of the secret key. We repeated this process

for 100 different pairs of random keys to understand

how a slight change (one bit) in the secret key can

cause a change in the encrypted texts. Figure 5 shows

the hamming distance between two encrypted images,

where only one bit of the secret key was changed.

Equation 6 was used to calculate the hamming dis-

tance.

HD(C

) =

∑

k=1

[k] ⊕C

[k]) × 100% (6)

The results obtained are robust and close to the

optimal value of 50% within a small variation of

+0.2/ − 0.22%.

6.2 Analysis of the Uniformity of the

Keystream Distribution

Analyzing the uniformity of the keystream distribu-

tion gives us a better understanding of how evenly dis-

tributed the keystream generated by the stream cipher

is across its possible values. The original three plain

images (Lena, Airplane, an Pepper) (see Figures 6 (a),

Figure 4: Hamming distance between plain and encrypted

images.

Figure 5: Hamming distance for key sensitivity analysis.

(i), and (q)) and their corresponding distributions are

shown in Figures 6 (e), (m), and (u), respectively. The

encrypted images from Lena using three different s-

boxes (0x23, 0x6f, and 0xd7) are shown in Figures

6 (c), (d), and (e) and their corresponding distribu-

tions are shown in Figures 6 (g), (h), and (i), respec-

tively. Similarly for images encrypted from Airplane,

and Pepper. Analyzing distribution of each of the en-

crypted images, it is easy to remark that represents a

uniform distribution.

FPGA Implementation of AES-Based on Optimized Dynamic s-Box

735

256x256x8

Sbox-0x23 Sbox-0x6f Sbox-0xd7

(b) Lena (c) (d) (e)

(f) (g) (h) (i)

(j) Airplane (k) (l) (m)

(n) (o) (p) (q)

(r) Pepper (s) (t) (u)

(v) (w) (x) (y)

Figure 6: Distribution of plain and encrypted images.

6.3 CHI-Square Analysis

A Chi-square analysis was tested using Equation 7

over 100 different random keys, to conﬁrm the uni-

formity of encrypted images in our proposed design

and the results obtained in the histograms of Figure

10. The Chi-square test, or analysis, is a statistical ap-

proach used to compare observed frequencies of oc-

currence against expected frequencies of occurrence.

exp

−1

∑

i=1

− E

)

(7)

exp

: chi squared,O

: observed value,E

: ex-

pected value, N

= 256 levels, E

= n

65536 for 256 × 256 images.

Given that the theoretical value for α = 0.05 and

= 256 is χ

(255,0.05) = 293.24, and the experi-

mental Chi-Square results from Table 4 are χ

exp

257.04, 257.29, and 253.25, respectively. We can

conclude that the uniformity of the cipher-text is con-

ﬁrmed because the experimental values are smaller

than the theoretical ones.

Table 4: Comparison of results with other AES architecture

designs.

Image HD χ

exp

Lenna 0.499923 257.04312

Airplane 0.500170 257.2930

Pepper 0.499911 253.2499

6.4 Key Space Analysis

The key space is a method to determine the number of

combinations to perform on an algorithm to determine

its ability to stand against cryptographic attacks such

as brute force. Our proposed dynamic s-box contains

128

different key combinations as in standard 128-

bit AES, but this complexity is compounded by 2

with the presented scheme of dynamic S-boxes, for

a ﬁnal complexity of 2

136

, which makes the relation-

ship between the plain images, secret keys, and the

encrypted images, very complex and robust. Making

it resistant to brute force attacks even when a pair of

plain-encrypted data is known (Mahdi et al., 2023).

7 CONCLUSIONS

In this paper, a method for adding dynamic S-boxes

to AES was evaluated and implemented on an FPGA

target device. The cryptographic characteristics of

the dynamic S-boxes were compared to those of the

AES S-box and found to be equivalent. The FPGA

design implementation for the modiﬁed AES algo-

rithm was evaluated, and the resource utilization and

performance were reported and compared with those

of previous works. An overall cryptographic analysis

was performed on the modiﬁed algorithm, evaluating

key aspects such as uniformity of the keystream, key

sensitivity analysis, and key space analysis, obtaining

results that conﬁrmed the robustness of the proposed

algorithm.

In the future, we will explore ways to optimize the

HLS design and extend the tests performed to the 192-

bit and 256-bit variants. It is possible to modularize

the exported design to use it as a testbed for differ-

ent S-box research based on AES. Another additional

step that would speed testing and evaluation, would

be the design of a PYNQ overlay to perform faster

tests by using the Python programming language. Ad-

ditional functionality, such as padding, may be in-

cluded, but it was not considered in this work. All the

SECRYPT 2024 - 21st International Conference on Security and Cryptography

736

sample data fed to the algorithm has been formatted

to multiples of 16 bytes (128 bits).

ACKNOWLEDGEMENTS

We would like to thank Xilin university donation pro-

gram for the send Pynq-Z2 board, and the IEM De-

partment of Computer Science, Electronics, and Me-

chanics of the UFR Sciences and Techniques, of the

University of Burgundy which opened the doors of

its classes and laboratories to AESE (Advanced Elec-

tronics Systems Engineering) Master 2 students to

successfully complete this project.

REFERENCES

Arrag, S., Hamdoun, A., Tragha, A., and Khamlich, S.

(2013). Implementation of stronger aes by using

dynamic s-box dependent of master key. Journal

of Theoretical and Applied Information Technology,

53:196–204.

Bui, D.-H., Puschini, D., Bacles-Min, S., Beign

e, E.,

and Tran, X.-T. (2017). Aes datapath optimization

strategies for low-power low-energy multisecurity-

level internet-of-things applications. IEEE Transac-

tions on Very Large Scale Integration (VLSI) Systems,

25(12):3281–3290.

Chen, W. and Wang, L. (2019). High-speed fpga imple-

mentation of aes with dynamic s-box using pipeline

architecture. Journal of Cryptographic Engineering,

9(4):289–302.

Dubertret, G. (2023). Initiation

a la cryptographie avec

Python. De Boeck sup

erieur.

Elsayed, G., Elramly, S., Hasan, B., and Shehata, K. (2008).

An efﬁcient implementation of cbc mode rijndeal aes

on an fpga. pages 1–8. IEEE Xplore.

Fan, C.-P. and Hwang, J.-K. (2007). Implementations of

high throughput sequential and fully pipelined aes

processors on fpga. pages 353 – 356. IEEE Xplore.

Guzman, I., Nieto, R., and Norena, A. (2016). Fpga imple-

mentation of the aes-128 algorithm in non-feedback

modes of operation. Dyna (Medellin, Colombia),

83:37–43.

Li, Y., Zhang, Y., and Tian, Y. (2017). A high-performance

fpga implementation of aes-128. In In 2017 IEEE

10th Annual Computing and Communication Work-

shop and Conference (CCWC), pages 0228–0232.

Liu, Q., Xu, Z., and Yuan, Y. (2013). A 66.1 gbps single-

pipeline aes on fpga. pages 378–381. IEEE Xplore.

Mahdi, M., Safwan, E. A., Camel, T., Mark Joseph, V.,

El-Bay, B., and Olivier, D. (2023). Fpga-based im-

plementation of enhanced zuc stream cipher based on

dynamic s-box. In Proc. of the 9th International Con-

ference on Engineering and Emerging Technologies

(ICEET). IEEE Xplore.

Mamun, A., Rahman, S., Shaon, T., and Hossain, M. A.

(2017). Security analysis of aes and enhancing its se-

curity by modifying s-box with an additional byte. In-

ternational journal of Computer Networks & Commu-

nications, 9:69–88.

Nandan, V. and Gowri Shankar Rao, R. (2022). Low-power

and area-efﬁcient design of aes s-box using enhanced

transformation method for security application. Inter-

national Journal of Communication Systems, 35(2).

Nissar, G., Garg, D., and Khan, B. (2019). Implementation

of security enhancement in aes by inducting dynamic-

ity in aes s-box. International Journal of Innovative

Technology and Exploring Engineering, 8.

Priya, S. S., Karthigaikumar, P., Siva Mangai, N. M., and

Kirti Gaurav Das, P. (2017). An efﬁcient hardware

architecture for high throughput aes encryptor using

mux based sub pipelined s-box. In Wireless personal

communications, volume 94, pages 2259–2273.

Qu, S., Shou, G., Hu, Y., Guo, Z., and Qian, Z. (2009). High

throughput, pipelined implementation of aes on fpga.

2009 International Symposium on Information Engi-

neering and Electronic Commerce, pages 542–545.

Rahimunnisa, K., Karthigaikumar, P., Soumiya, R., Jayaku-

mar, J., and Kumar, S. S. (2014). Fpga implementa-

tion of aes algorithm for high throughput using folded

parallel architecture. In Security and communication

networks, volume 7, pages 2225–2236.

Rijmen, V. and Daemen, J. (2001). Advanced encryption

standard. In Proceedings of federal information pro-

cessing standards publications, national institute of

standards and technology.

Smith, J. and Johnson, R. (2018). Efﬁcient fpga implemen-

tation of aes with dynamic s-box for iot devices. IEEE

Transactions on Very Large Scale Integration (VLSI)

Systems, 26(6):1123–1135.

Wang, S.-S. and Ni, W.-S. (2004). An efﬁcient fpga imple-

mentation of advanced encryption standard algorithm.

In 2004 IEEE International Symposium on Circuits

and Systems (ISCAS), volume 2, pages 11–597.

Waqas, U., Afzal, S., Mir, M., and Yousaf, M. (2015). Gen-

eration of aes-like s-boxes by replacing afﬁne matrix.

pages 159–164.

Webster, A. F. and Tavares, S. E. (1986). On the design

of s-boxes. In Williams, H. C., editor, Advances in

Cryptology — CRYPTO ’85 Proceedings, pages 523–

534, Berlin, Heidelberg. Springer Berlin Heidelberg.

Zhang, Q. and Li, H. (2020). Secure fpga implementa-

tion of aes with dynamic s-box for embedded systems.

ACM Transactions on Embedded Computing Systems,

19(3):Article 15.

Zhang, Y., Wang, Z., and Yang, J. (2016). A high-speed

and low-area aes implementation on fpga. In In 2016

10th International Conference on Computer Science

and Network Technology (ICCSNT), pages 1–4.

FPGA Implementation of AES-Based on Optimized Dynamic s-Box

737