Amun: Securing E-Voting Against Over-the-Shoulder Coercion
Riccardo Longo
1 a
and Chiara Spadafora
2 b
1
Fondazione Bruno Kessler, Center for Cybersecurity, Trento, Italy
2
Department of Mathematics, University of Trento, 38123 Povo, Trento, Italy
Keywords:
E-Voting, Over-the-Shoulder Attack, Coercion-Resistance, End-to-End Verifiability, Formal Proof of Security.
Abstract:
In an election where each voter may express P preferences among M possible choices, the Amun protocol
allows to secure vote casting against over-the-shoulder adversaries, retaining privacy, fairness, end-to-end
verifiability, and correctness. We prove the security of the construction under the standard Decisional Diffie
Hellman assumption in the random oracle model.
1 INTRODUCTION
Remote voting, enhanced by advanced cryptographic
techniques, offers more security than traditional
paper-based voting but raises privacy concerns when
voting outside secure booths.
Although many systems protect against various
adversaries who try to bribe electors, we found that
it is more difficult to counter opponents that closely
monitor voters during the voting phase (over-the-
shoulder attacks). The main mitigation technique
against coercion is the usage of fake credentials (Juels
et al., 2010), which are indistinguishable from real
ones but that do not produce valid votes. However, if
the adversary keeps the voter under control until the
end of the voting period, it becomes impossible to re-
vote with the valid credential.
Here we present the Amun
1
protocol, which hides
the real choice expressed by a voter even if an adver-
sary is physically monitoring the elector during vote
casting. This feature protects the elector against over-
the-shoulder attacks without the need to re-vote. The
Amun protocol aims to achieve end-to-end verifiabil-
ity, universal verifiability, privacy, correctness, fair-
ness, and coercion resistance.
The authors in (Spadafora et al., 2021) suggest
a blockchain-based remote e-voting protocol for two
candidates, where voters have two voting tokens (v-
a
https://orcid.org/0000-0002-8739-3091
b
https://orcid.org/0000-0003-3352-9210
1
Amun was a major ancient Egyptian deity. The name
Amun meant something like “the hidden one” or
“invisible”.
tokens): one is valid and the other is a decoy, but only
the voter knows which is which. The Amun protocol
extends this concept to support multiple candidates
and choices.
In a setting where the voter can choose P out of M
candidates, extra care has to be taken in the design of
the v-tokens. In fact, a naïve straightforward adapta-
tion of (Spadafora et al., 2021) might reveal whether
two v-tokens have the same validity, since there are
multiple valid and decoy v-tokens. To deal with this
we had to introduce extra masking steps and another
authority to fully hide the v-tokens validity. So, in
Amun, three authorities share the administration of
the election: they setup the parameters, manage vot-
ers’ registration, and compute the final tally at the
end of the voting phase. Privacy is preserved even if
an attacker colludes with one authority, limiting their
power. As in (Spadafora et al., 2021), votes are cast
by assigning to the candidates some “voting tokens”
generated during registration. Among these tokens,
only a few are valid and express the real preference
of the voter, but they are indistinguishable from the
other, decoy, tokens. This trick disguises the actual
choice made, even if the adversary is watching.
1.1 Related Work
Protocols for electronic election systems have been
abundantly proposed in recent years. Many have
addressed the problem of coercion resistance, giv-
ing a plurality of definitions (Gardner et al., 2009;
Haines and Smyth, 2019; Juels et al., 2010; Krips
and Willemson, 2019; Kusters et al., 2010). Civ-
itas (Clarkson et al., 2008), which derives from
508
Longo, R. and Spadafora, C.
Amun: Securing E-Voting Against Over-the-Shoulder Coercion.
DOI: 10.5220/0012786800003767
Paper published under CC license (CC BY-NC-ND 4.0)
In Proceedings of the 21st International Conference on Security and Cryptography (SECRYPT 2024), pages 508-517
ISBN: 978-989-758-709-2; ISSN: 2184-7711
Proceedings Copyright © 2024 by SCITEPRESS – Science and Technology Publications, Lda.

JCJ (Juels et al., 2010), deals with coercion by allow-
ing voters to vote multiple times via a mechanism of
real and fake credentials. Selene (Ryan et al., 2016)
associates to every vote a unique tracker: the idea is
that, in case of an attack, every voter is able to open
up its commitment to a fake tracker in order to deceive
the attacker. Belenios (Cortier et al., 2019) itself is not
coercion resistant: voters can keep the randomness
used to encrypt the ballot to prove how they voted.
This limitation has been overcome with BeleniosRF
(Chaidos et al., 2016).
Organization. We present some preliminaries in
Section 2. We describe our protocol in Section 3 and
we provide a proof of security in Section 5. Finally,
in Section 6 we draw some conclusions.
2 PRELIMINARIES
Most of the algebraic preliminaries we need to build
the protcol, such as the Decisional Diffie-Hellmann
Assumption (DDH) and commitment schemes, can be
found in (Spadafora et al., 2021). Here we report the
additional tools required for the generalization, for
more details see (Longo and Spadafora, 2021).
We use the following notation for the indexes:
[n] = {i ∈ N : 1 ≤ i ≤ n}, (t
j
)
j∈[m]
= (t
1
,... ,t
m
).
2.1 Equality of Discrete Logarithms
In the protocol it is used a Zero-Knowledge
Proof (ZKP) for the equality of two discrete loga-
rithms (Spadafora et al., 2021; Longo and Spadafora,
2021), which is a variation of the Schnorr interactive
protocol (Schnorr, 1991; Shoup and Alwen, 2007).
2.2 Non-Interactive ZKP
Non-Interactive ZKP (NIZKP) are a special type of
ZKPs that allow the prover to publish a proof that
can be independently verified by all the relevant par-
ties later on. The Fiat-Shamir technique (Iovino and
Visconti, 2019) can be used to transform an interac-
tive sigma protocol into a NIZKP by exploiting a hash
function modeled as a random oracle (RO).
2.3 Designated-Verifier ZKP
Designated-Verifier Non-Interactive ZKP systems
(DVNIZKPs (Jakobsson et al., 2001)) are protocols
which retain most of the security properties of a
NIZKP, but are not publicly verifiable: only the owner
of some secret (the designated verifier) can check the
proof. This property is useful in the context of e-
voting to achieve end-to-end verifiability while still
preventing the voter from transferring some proofs.
In (Longo and Spadafora, 2021) there is a complete
description of the protocol.
2.4 General Requirements for Remote
Voting Systems
A trustworthy e-voting protocol has to satisfy con-
flicting requirements: it should preserve both in-
tegrity of election results and confidentiality of votes.
In (Longo and Spadafora, 2021) are defined the prop-
erties that a trustworthy e-voting protocol should ful-
fill (namely Correctness, Fairness, Privacy, Verifia-
bility). We define here only Vote-Coercion Resistance
since we adopt a non-standard definition, the proof
that our proposed protocol satisfies it is in Section 5.2.
Coercion resistance (Haines and Smyth, 2019) re-
quires that an adversary cannot learn any additional
information about the votes other than what is re-
vealed by the results of tabulation. In other words,
voters cannot prove whether or how they voted, even
if they can interact with the adversary while vot-
ing. The Amun protocol protects against coercers that
wish to sway elections towards specific candidates,
but is not very effective against randomization and
forced abstention. In this simplified model, we use
a slightly weaker adaptation of the definition of Coer-
cion Resistance given in (Juels et al., 2010):
Definition 1 (Vote-Coercion Resistance). Let A
be a coercer, V
c
the set of coerced voters, and
(C
i,1
,. .. ,C
i,P
) the choices that A wants to impose to
the voter corresponding to v
i
∈ V
c
. Let Ψ
1
be the sce-
nario in which A has access only to the final tally. Let
Ψ
2
be the scenario in which A has access to the whole
Bulletin Board, and can see all the actions performed
by the voters in V
c
, with the exception of the ones
carried out in a protected environment (or through
an untappable channel). A voting protocol is Vote-
Coercion Resistant if the probability of A detecting
that a voter in V
c
has not followed its instruction is
the same in Ψ
1
and Ψ
2
.
3 MULTI-CANDIDATE E-VOTING
This section presents our proposal for a remote e-
voting protocol that manages an election with N vot-
ers, where each one expresses P preferences among
M candidates (obviously P < M). The basic idea is
that every voter owns M voting tokens (v-tokens): P
Amun: Securing E-Voting Against Over-the-Shoulder Coercion
509

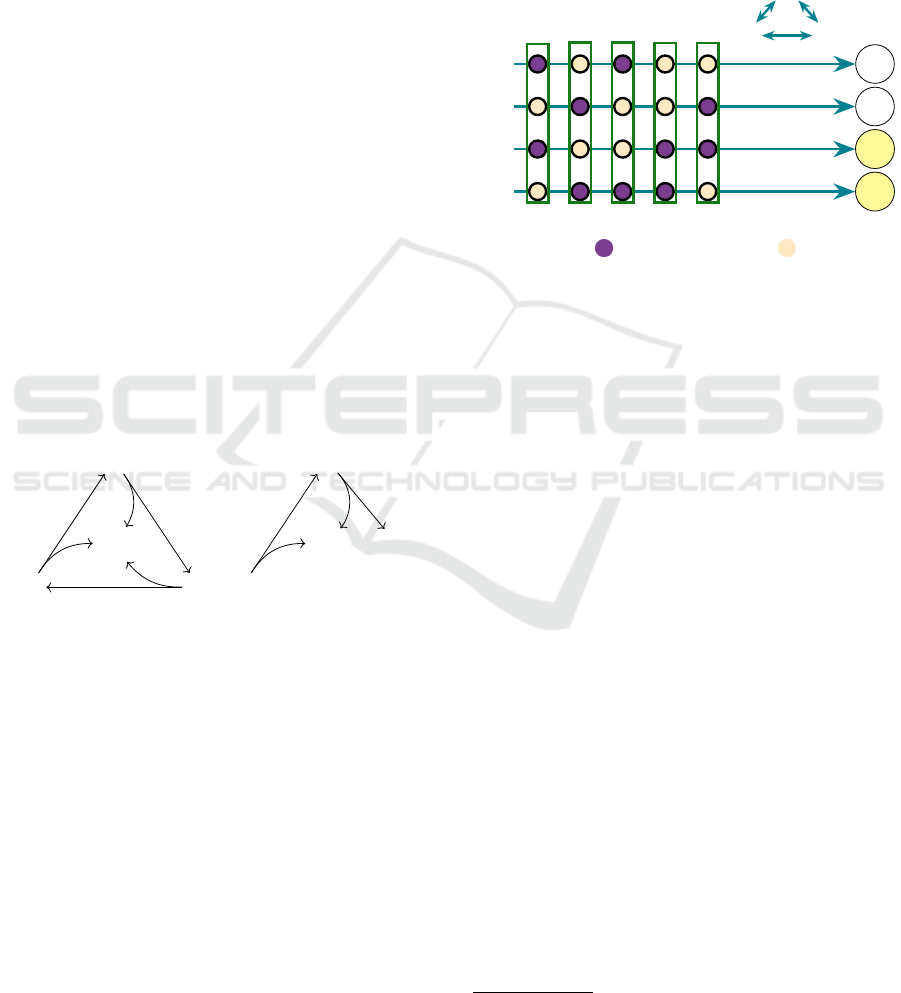
are valid, the others are a decoy, but only the voter
knows which is which. When voting, voters express
their preferences assigning the valid v-tokens to the
chosen candidates and the decoy ones to the others.
The protocol allows for re-voting: before tallying
duplicate ballots (i.e. with the same v-tokens ignoring
their order) are discarded, keeping only the most re-
cent. After the voting phase, when counting the votes,
the decoy v-tokens do not contribute to the tally, so
only valid v-tokens are counted. The whole process is
publicly auditable and fully verifiable, and preserves
privacy as long as at most one authority is corrupt.
The protocol is divided into four phases:
• Setup. Three authorities, knowing a list of eli-
gible voters, generate the values for the creation
of both the v-tokens and the masks associated to
the candidates. These masks guarantee the voters’
privacy, and prevent early tallying.
• Registrar Phase. In this phase, the three author-
ities engage in a 5-step protocol (see Figure 1) to
create M indistinguishable v-tokens (P are valid
and M − P are a decoy) employing masking and
shuffling so that at the end the authorities will
not be able to identify which tokens are valid.
The voter can check the validity of these v-tokens
thanks to DVNIZKPs issued by the authorities.
These proofs are worthless for a coercer because
the voter can forge them.
A
0
A
2
A
1
v
i
A
0
A
1
v
i
BB
I: init & mask
II: mask
III: shuffle
IV: unmask
V: unmask
Figure 1: The main steps of the ballot generation procedure,
which correspond to steps 3-7 of the Registrar Phase as de-
scribed in Section 3.1.2.
• Voting Phase. During this phase the voter express
their preferences by assigning each of their M v-
tokens to the candidates. All v-tokens of a voter
must be assigned together, each to a distinct can-
didate. After the v-tokens have been assigned, the
voter gets a transcript that reports the assignment
of the v-tokens to the candidates. This transcript is
worthless for a coercer since the v-tokens are in-
distinguishable. Here we assume that every can-
didate receives at least one legitimate vote (with a
valid v-token), otherwise it is trivial to discern the
validity of some tokens from the election results.
• Tallying. The v-tokens are processed (see Fig-
ure 2), removing the candidate masks, which al-
lows to count the number of valid and decoy
tokens assigned to each candidate. The results
and the intermediate computations are published,
alongside a set of NIZKPs that allow anyone to
check that the results are correct and there has
not been any tampering. Every voter can also
check, by examining the bulletin board, that their
v-tokens have been cast and counted correctly.
C
4
C
3
C
2
C
1
3
3
2
2
v
1
v
2
v
3
v
4
v
5
A
0
A
2
A
1
Figure 2: Example of voting and tallying. Each voter has
two valid tokens and two decoy tokens . After the tal-
lying it is revealed that candidates C
3
and C
4
are elected
having received more preferences (3) with respect to the
other two candidates (who received only 2).
3.1 Protocol Description
The key components involved in the protocol are:
1. a finite set of voters V = {v
i
}
i∈[N]
(where v
i
is a
pseudonymous id), with N ∈ N the number of eli-
gible voters;
2. a finite set of candidates C = {c
ℓ
}
ℓ∈[M]
with M ∈ N
the number of candidates;
3. three trusted authorities
2
A
0
, A
1
, and A
2
.
4. one ballot b
i
(comprising M v-tokens) for every
i ∈ [N], i.e. one for each eligible voter.
Throughout the protocol we implicitly assume that
every public value (including a description of the key
components presented above) are published in the
BB. The protocol is divided into four phases.
3.1.1 Setup
The authority A
0
selects and publishes:
1. a secure group G of prime order p in which the
DDH assumption holds, with a generator g ∈ G;
2. a commitment scheme Comm to be used to commit
to the values computed before publishing them, in
order to improve security.
2
We use a weak concept of trust here, since the conduct
of these authorities can be checked by voters.
SECRYPT 2024 - 21st International Conference on Security and Cryptography
510

Then A
0
performs the following operations:
1. chooses uniformly at random two values k and λ
in Z
∗
p
. A
0
knows that the v-tokens computed using
k are valid, while the ones computed using λ are
decoys, but this information is kept secret;
2. chooses uniformly at random N ·M distinct values
¯z
i,ℓ
∈ Z
∗
p
, with i ∈ [N], ℓ ∈ [M];
3. finally, A
0
commits to the values g
k
, g
λ
, and, for
every i ∈ [N], it commits to

v
i
,(g
¯z
i,ℓ
)
ℓ∈[M]

.
An honest authority A
0
is supposed to keep private all
the values ¯z
i,ℓ
, k, λ.
The authority A
1
performs the following operations:
1. chooses uniformly at random M distinct values
α
′
ℓ
∈ Z
∗
p
, with ℓ ∈ [M], these will be the first half
of the candidates’ masks;
2. chooses uniformly at random N distinct values
x
′
i
∈ Z
∗
p
, with i ∈ [N];
3. chooses uniformly at random two sets of N ·M dis-
tinct values z
′
i,ℓ
,y
′
i,ℓ
∈ Z
∗
p
, with i ∈ [N],ℓ ∈ [M];
4. finally, A
1
commits to the values g
α
′
ℓ
, ∀ℓ ∈ [M],
and for every i ∈ [N] it commits to the tuple

v
i
,g
x
′
i
,(g
z
′
i,ℓ
)
ℓ∈[M]
,(g
y
′
i,ℓ
)
ℓ∈[M]

.
An honest authority A
1
is supposed to keep private
the values α
′
ℓ
, x
′
i
, z
′
i,ℓ
, y
′
i,ℓ
.
The authority A
2
performs the following operations:
1. chooses uniformly at random M distinct values
α
′′
ℓ
∈ Z
∗
p
, with ℓ ∈ [M], these will be the second
half of the candidates’ masks;
2. chooses uniformly at random N distinct values
x
′′
i
∈ Z
∗
p
, with i ∈ [N];
3. chooses uniformly at random N ·M distinct values
y
′′
i,ℓ
∈ Z
∗
p
, with i ∈ [N], ℓ ∈ [M];
4. Finally A
2
commits to the values g
α
′′
ℓ
, ∀ℓ ∈ [M],
and for every i ∈ [N] it commits to the tuple

v
i
,g
x
′′
i
,(g
y
′′
i,ℓ
)
ℓ∈[M]

.
An honest authority A
2
is supposed to keep private all
the values α
′′
ℓ
, x
′′
i
, y
′′
i,ℓ
.
Once that all the commitments have been published,
the authorities can decommit the values:
• A
0
publishes the decommitments for the
values g
k
, g
λ
, alongside all the tuples

v
i
,(g
¯z
i,ℓ
)
ℓ∈[M]

∀i ∈ [N];
• A
1
publishes the decommitments for
the values g
α
′
ℓ
∀ℓ ∈ [M], and the tuples

v
i
,g
x
′
i
,(g
z
′
i,ℓ
)
ℓ∈[M]
,(g
y
′
i,ℓ
)
ℓ∈[M]

∀i ∈ [N];
• A
2
publishes the decommitments for
the values g
α
′′
ℓ
∀ℓ ∈ [M], and the tuples

v
i
,g
x
′′
i
,(g
y
′′
i,ℓ
)
ℓ∈[M]

∀i ∈ [N].
All these published values are accompanied by
NIZKPs which prove that the authority who pub-
lished them knows the corresponding secret expo-
nents. These NIZKPs can be constructed using the
Schnorr protocol and the Fiat-Shamir transformation
just like in Section 2.2.
To simplify notation we introduce some defini-
tions for aggregate values for all i ∈ [N] and ℓ ∈ [M]:
x
i
= x
′
i
+ x
′′
i
, α
ℓ
= α
′
ℓ
· α
′′
ℓ
,
z
i,ℓ
= ¯z
i,ℓ
· z
′
i,ℓ
, y
i,ℓ
= y
′
i,ℓ
· y
′′
i,ℓ
.
3.1.2 Registrar Phase
For every pseudonymous id v
i
∈ V the following steps
are performed:
1. Let Alice be the person associated to the
pseudonymous id v
i
, note that the authorities do
not need to know this association. She goes in a
safe and controlled environment (see Section 6 for
further discussion on this requirement) where she
is identified and authenticated as the eligible and
not yet registered pseudonymous id v
i
. In this en-
vironment she can interact with all three authori-
ties without fear of eavesdropping or interference.
2. Alice creates a signing key-pair (s
i
,K
i
), a desig-
nated verifier key-pair (e
i
,D
i
), and gives K
i
,D
i
to
the authorities proving the knowledge of s
i
(e.g.
by signing a challenge message), and of e
i
via
a NIZKP (which includes the challenge message
among the public values). The authorities asso-
ciate K
i
,D
i
to v
i
in their respective voters lists.
3. A
0
performs the following steps:
(a) A
0
chooses, for every i ∈ [N], a random subset
V
i
⊂ [M] with cardinality is exactly P, then sets:
σ
i,ℓ
=
(
k ⇐⇒ ℓ ∈ V
i
λ ⇐⇒ ℓ /∈ V
i
i.e. the random choice of the V
i
determines
which tokens will be valid and which a decoy;
(b) A
0
takes the (publicly available) values g
x
′
i
and g
x
′′
i
and creates the step 0 of the ballot
¯
b
0,i
= (
¯
b
0,i,ℓ
)
ℓ∈[M]
where, ∀ℓ ∈ [M]:
¯
b
0,i,ℓ
=

g
σ
i,ℓ
· g
x
′
i
· g
x
′′
i

¯z
i,ℓ
= g
¯z
i,ℓ
(σ
i,ℓ
+x
i
)
;
(c) A
0
sends to A
1
the initial ballot
¯
b
0,i
and sends
to Alice
¯
b
0,i
and V
i
;
Amun: Securing E-Voting Against Over-the-Shoulder Coercion
511

(d) A
0
proves its computations correct with multi-
ple instances of the DVNIZKP of Section 2.3:
i. A
0
proves that the g
¯z
i,ℓ
σ
i,ℓ
are correct (using
σ
i,ℓ
= k or σ
i,ℓ
= λ) with:
ω = k, u = g, z = g
k
,
¯u = g
¯z
i,ℓ
, ¯z = g
¯z
i,ℓ
k
, ∀ℓ ∈ V
i
,
ω = λ, u = g, z = g
λ
,
¯u = g
¯z
i,ℓ
, ¯z = g
¯z
i,ℓ
λ
∀ℓ ∈ [M] \V
i
,
ii. then A
0
proves that the
¯
b
0,i,ℓ
are correct using
for all ℓ ∈ [M]:
ω = ¯z
i,ℓ
, u = g, z = g
¯z
i,ℓ
,
¯u = g
σ
i,ℓ
· g
x
′
i
· g
x
′′
i
, ¯z =
¯
b
0,i,ℓ
.
4. A
1
computes the step 1 of the ballot
¯
b
1,i
= (
¯
b
1,i,ℓ
)
ℓ∈[M]
where:
¯
b
1,i,ℓ
=

¯
b
0,i,ℓ

z
′
i,ℓ
= g
z
i,ℓ
(σ
i,ℓ
+x
i
)
∀ℓ ∈ [M]
and sends it to Alice and to A
2
. Then A
1
proves
that the
¯
b
1,i,ℓ
are correct with the DVNIZKP of
Section 2.3, using:
ω = z
′
i,ℓ
, u = g, z = g
z
′
i,ℓ
,
¯u =
¯
b
0,i,ℓ
, ¯z =
¯
b
1,i,ℓ
∀ℓ ∈ [M].
5. A
2
chooses uniformly at random a permutation
π
i
∈ Sym([M]) and computes the step 2 of the bal-
lot
¯
b
2,i
= (
¯
b
2,i,ℓ
)
ℓ∈[M]
where, ∀ℓ ∈ [M]:
¯
b
2,i,ℓ
=

¯
b
1,i,ℓ

y
′′
i,π
−1
i
(ℓ)
= g
z
i,ℓ
y
′′
i,π
−1
i
(ℓ)
(σ
i,ℓ
+x
i
)
and sends it to Alice and to A
0
, π
i
is sent to Alice
and A
1
. Then A
2
proves that the
¯
b
2,i,ℓ
are correct
with the DVNIZKP of Section 2.3, using:
ω = y
′′
i,π
−1
i
(ℓ)
, u = g, z = g
y
′′
i,π
−1
i
(ℓ)
,
¯u =
¯
b
1,i,ℓ
, ¯z =
¯
b
2,i,ℓ
∀ℓ ∈ [M].
6. A
0
computes the step 3 of the ballot
¯
b
3,i
= (
¯
b
3,i,ℓ
)
ℓ∈[M]
where, ∀ℓ ∈ [M]:
¯
b
3,i,ℓ
=

¯
b
2,i,ℓ

1
¯z
i,ℓ
= g
z
′
i,ℓ
y
′′
i,π
−1
i
(ℓ)
(σ
i,ℓ
+x
i
)
and sends it to Alice and to A
1
. Then A
0
proves
that the
¯
b
3,i,ℓ
are correct with the DVNIZKP of
Section 2.3, using:
ω =
1
¯z
i,ℓ
, u = g
¯z
i,ℓ
, z = g,
¯u =
¯
b
2,i,ℓ
, ¯z =
¯
b
3,i,ℓ
∀ℓ ∈ [M].
7. A
1
computes the final ballot b
i
= (b
i,ℓ
)
ℓ∈[M]
, with:
b
i,ℓ
=

¯
b
3,i,π
i
(ℓ)

y
′
i,ℓ
z
′
i,π
i
(ℓ)
= g
y
i,ℓ
(σ
i,π
i
(ℓ)
+x
i
)
∀ℓ ∈ [M]
and sends it to Alice and publishes on the BB the
pair (K
i
,b
i
). Then A
1
proves that the b
i,ℓ
are cor-
rect with the DVNIZKP of Section 2.3 and using:
ω =
y
′
i,ℓ
z
′
i,π
i
(ℓ)
, u = g
z
′
i,π
i
(ℓ)
, z = g
y
′
i,ℓ
,
¯u =
¯
b
3,i,π
i
(ℓ)
, ¯z = b
i,ℓ
∀ℓ ∈ [M].
Note that Alice, thanks to the proofs and the knowl-
edge of the intermediate values, knows which ones are
a valid token (the ones with σ
i,ℓ
= k), but thanks to the
random choices of V
i
and π
i
the authorities cannot dis-
tinguish the tokens unless they collude. Effectively,
the DVNIZKPs prove to Alice that the ballot has been
created by A
0
with the correct number of valid and
decoy tokens, and that it has been correctly shuffled
by A
2
. Moreover the properties of the DVNIZKP al-
low Alice to forge the transcript changing which to-
kens are valid, making them useless for proving the
validity of a token. In fact, since Alice is in a pro-
tected environment, she can manipulate the received
data without being able to prove or disprove any ma-
nipulation.So, given that she knows e
i
, she can forge a
proof that states the presumed validity of any P of the
M tokens, making any proof worthless to a coercer.
3.1.3 Voting Phase
Voters assign their valid tokens to preferred candi-
dates and decoy tokens to the others. Each voter signs
this assignment with their private key and publishes it
on the BB for verification. After voting, duplicate, in-
complete, and forged ballots are filtered out (relying
on public data only).
3.1.4 Tallying
Once the voting phase is over, the tallying can start.
In order to count the votes, the authorities have to
process the tokens received by each candidate, sub-
stituting the voter’s masks y
i,ℓ
with the appropriate
candidate mask α
ℓ
. Suppose that T ≤ N participants
voted. Without loss of generality, we can assume that
only the participants with index i ∈ [T ] voted, while
the remaining N − T abstained from voting.
For every i ∈ [T ], let φ
i
: [M] −→ [M] be the bi-
jective map that associates to each candidate index
ℓ the index of the token b
i,φ
i
(ℓ)
that the voter asso-
ciated to v
i
sent to the candidate C
ℓ
. Then, for ev-
ery i ∈ [T ], ℓ ∈ [M], the authorities process the token
b
i,φ
i
(ℓ)
by performing the following steps:
SECRYPT 2024 - 21st International Conference on Security and Cryptography
512

1. A
1
computes and publishes the preliminary vote
¯
t
ℓ,i
as:
¯
t
ℓ,i
=

b
i,φ
i
(ℓ)

α
′
ℓ
y
′
i,φ
i
(ℓ)
= g
α
′
ℓ
y
′′
i,φ
i
(ℓ)
(σ
i,π
i
(φ
i
(ℓ))
+x
i
)
,
alongside a NIZKP that proves this computation
correct. A
1
proves that
¯
t
ℓ,i
is correct with the
NIZKP version of Section 2.1 and using:
ω =
α
′
ℓ
y
′
i,φ
i
(ℓ)
, u = g
y
′
i,φ
i
(ℓ)
, z = g
α
′
ℓ
,
¯u = b
i,φ
i
(ℓ)
, ¯z =
¯
t
ℓ,i
.
2. A
2
then computes and publishes the final vote t
ℓ,i
:
t
ℓ,i
= (
¯
t
ℓ,i
)
α
′′
ℓ
y
′′
i,φ
i
(ℓ)
= g
α
ℓ
(σ
i,π
i
(φ
i
(ℓ))
+x
i
)
,
alongside a NIZKP that proves this computation
correct. A
2
proves that t
ℓ,i
is correct with the
NIZKP version of Section 2.1 and using:
ω =
α
′′
ℓ
y
′′
i,φ
i
(ℓ)
, u = g
y
′′
i,φ
i
(ℓ)
, z = g
α
′′
ℓ
,
¯
t = b
ℓ,i
, ¯z = t
ℓ,i
.
Once that all final votes have been computed, the ac-
tual tallying is performed.
Let R
ℓ
be the number of valid tokens given to the
ℓ-th candidate (i.e. the number of preferences re-
ceived by said candidate), and let F
ℓ
be the number
of decoy tokens given to the ℓ-th candidate. Clearly
T = R
ℓ
+ F
ℓ
∀ℓ ∈ [M]. The count R
ℓ
can be com-
puted with the following steps:
1. Both A
1
and A
2
can compute g
α
ℓ
(as (g
α
′′
ℓ
)
α
′
ℓ
and
(g
α
′
ℓ
)
α
′′
ℓ
respectively). A
1
can prove the correct-
ness of this value by publishing a NIZKP. A
2
can
prove the correctness of this value by publishing
a NIZKP. In practice, each authority may publish
half of the values.
2. A
0
computes and publishes g
α
ℓ
k
= (g
α
ℓ
)
k
and
g
α
ℓ
λ
= (g
α
ℓ
)
λ
. Then A
0
proves that g
α
ℓ
k
and that
g
α
ℓ
λ
are correct by publishing two NIZKPs.
3. A
1
computes
∑
T
i=1
x
′
i
, and publishes g
α
ℓ
∑
T
i=1
x
′
i
.
Then A
1
proves that g
α
ℓ
∑
T
i=1
x
′
i
is correct by pub-
lishing a NIZKP, noting that any observer can
compute the value g
∑
T
i=1
x
′
i
=
∏
T
i=1
g
x
′
i
.
4. Similarly, A
2
computes
∑
T
i=1
x
′′
i
and publishes
g
α
ℓ
∑
T
i=1
x
′′
i
. Then A
2
proves that g
α
ℓ
∑
T
i=1
x
′′
i
is cor-
rect by publishing a NIZKP, again, anyone can
compute g
∑
T
i=1
x
′′
i
=
∏
T
i=1
g
x
′′
i
.
5. Given that any observer can compute the value:
g
α
ℓ
(
∑
T
i=1
x
i
+R
ℓ
k+F
ℓ
λ)
=
T
∏
i=1
t
ℓ,i
,
and that:
g
α
ℓ
∑
T
i=1
x
i
= g
α
ℓ
∑
T
i=1
(x
′
i
+x
′′
i
)
= g
α
ℓ
∑
T
i=1
x
′
i
· g
α
ℓ
∑
T
i=1
x
′′
i
,
then anyone can compute:
T =

g
α
ℓ
∑
T
i=1
x
i

−1
· g
α
ℓ
(
∑
T
i=1
x
i
+R
ℓ
k+F
ℓ
λ)
=

g
α
ℓ
k

R
ℓ
·

g
α
ℓ
λ

F
ℓ
.
6. R
ℓ
and F
ℓ
can now be computed by brute force,
giving the number of preferences received by the
ℓ-th candidate.
Given a positive integer T ∈ N, it is possible to rep-
resent it in T + 1 ways as a sum of two non-negative
integers. Given that the number of valid and decoy
votes must sum up to the number of actual voters T ,
it follows that the number of possible values for T is
T +1, so the effort of computing R
ℓ
and F
ℓ
is linear in
the number of actual votes.
4 USABILITY
In order to cast a vote, the voter has to remember
which are the P valid v-tokens among the M in their
ballot. This can be an usability issue when P and
M grow. To help the voter remembering the posi-
tion of the valid tokens, we can exploit error correct-
ing codes. We can see the information on which to-
kens are valid as a binary vector of F
M
2
with constant
weight P. We can exploit constant-weight codes (Fis-
cher and Stern, 1996) to encode these vectors as a
vector of the space F
κ
q
and then use a [n,κ]
q
short-
ened Reed-Solomon code (Roth, 2006) to add error-
correction capabilities. With this approach the voter
has only to remember n elements of F
q
, with the
added bonus that up to
n−κ
2
errors can be automati-
cally corrected.
Finally, we highlight that, with the DVNIZKPs
and the permutation received during the registrar
phase, the voter can check whether they remember
correctly the positions of the valid tokens.
5 SECURITY ANALYSIS
The goal is to prove that an adversary cannot dis-
tinguish between valid and decoy v-tokens and guess
Amun: Securing E-Voting Against Over-the-Shoulder Coercion
513

how voters cast their preferences. Since election re-
sults are obviously public, we have to avoid some triv-
ial cases in which the adversary can deduce the votes
by simply observing the results.
Therefore we assume that the adversary controls
one authority and all but two voters, and that these
two voters express distinct preferences. In particu-
lar, we let the adversary select two distinct sets of
preferences, then we randomly assign to each of the
two uncorrupted voters one set of these sets of pref-
erences. The adversary wins the security game if it
guesses correctly which voter expressed which set of
preferences, i.e. guesses the random assignment.
5.1 Security Model
The security of the protocol will be proven in terms
of vote indistinguishability (VI), as detailed in Defi-
nition 3. We will assume the presence of a malicious
authority, so the simulator in the proof will take on
the roles of the two honest authorities and of the two
voters that the adversary does not control.
To simplify our analysis we assume that the
adversary-controlled authority does not intentionally
fail decommitments or (DV)NIZKPs, so the protocol
does not abort. This is a reasonable assumption con-
sidering the application context, however it is not nec-
essary to attain security. In fact, if the adversary wins
the security game with non-negligible advantage, then
it must run the protocol smoothly with non-negligible
probability (since it outputs its guess only once the
protocol has correctly terminated).
Definition 2 (Security Game). The security game for
the election protocol proceeds as follows:
• Init. The adversary A chooses the authority and
the N − 2 voters that it will control (i.e. the ad-
versary knows which are the valid and decoy v-
tokens of these voters). The remaining two voters
are called free voters. The challenger C takes the
role of the other authorities and the free voters.
• Phase 0. A and C run the Setup and Registrar
phases of the protocol, interacting as needed.
• Phase 1. The adversary votes with some or all of
the voters it controls.
• Challenge. The challenge phase is articulated as
follows:
1. A selects two distinct sets of preferences
˜
P
0
̸=
˜
P
1
, with
˜
P
i
⊂ [M], #
˜
P
i
= P for i = 0,1, and
sends them to C;
2. C flips a random coin µ ∈ {0,1} to determine
which preference set the first free voter will use,
i.e. P
1
=
˜
P
µ
, setting also P
2
=
˜
P
µ⊕1
;
3. C constructs two random ballot assignment
maps
˜
φ
1
,
˜
φ
2
: [M] −→ [M] such that
˜
φ
i
(ℓ) refers
to a valid token if and only if ℓ ∈ P
i
, for i = 1,2;
4. finally, C votes by sending to the candidate C
ℓ
,
∀ℓ ∈ [M], the
˜
φ
1
(ℓ)-th and
˜
φ
2
(ℓ)-th tokens of
the first and second free voter respectively.
.
• Phase 2. The adversary votes with some or all of
the voters it controls.
• Phase 3. A and C run the Tallying phase of the
protocol, and the election result is published.
• Guess. The adversary outputs a guess µ
′
of the
coin flip that randomly assigned the voting pref-
erences of the two free voters.
A wins if µ
′
= µ.
Definition 3 (Vote Indistinguishability). An E-Voting
Protocol with security parameter θ is VI-secure if, for
every probabilistic polynomial-time adversary A that
outputs a guess µ
′
of the coin flip µ (as described in
the security game of Definition 2), there exists a neg-
ligible function η such that P[µ
′
= µ] ≤
1
2
+ η(θ).
In the following theorem we prove our voting pro-
tocol VI-secure under the DDH assumption in the se-
curity game defined above.
Theorem 1. In the Random Oracle Model (ROM), if
the DDH assumption holds, then the protocol of Sec-
tion 3.1 is VI-secure, as per Definition 3.
Proof. Suppose there exists a polynomial time adver-
sary A, that can attack the scheme with advantage ε.
We claim that a simulator S can be built to play the
decisional DH game with advantage
ε
2
. The simula-
tor controls the random oracle that defines the hash
function H, and starts by taking in a DDH challenge:
(g,A = g
a
,B = g
b
,Ξ),
with Ξ = g
ab
or Ξ = R = g
ξ
.
First we consider the case in which the adversary
controls A
0
, the simulation proceeds as follows.
• Init. The adversary chooses the N − 2 voters to
control. Without loss of generality we assume that
the two free voters are associated to v
1
and v
2
.
• Setup. S chooses uniformly at random in Z
∗
p
the
values ˜x
i
,
˜
α
ℓ
, ˜y
i,ℓ
, and ˜z
i,ℓ
for all i ∈ [2], ℓ ∈ [M],
and implicitly sets for all i ∈ [2], ℓ ∈ [M]:
x
′′
i
= ˜x
i
+ (−1)
i
b, α
′
ℓ
= a ·
˜
α
ℓ
,
y
′
i,ℓ
= a · ˜y
i,ℓ
, z
′
i,ℓ
= a · ˜y
i,ℓ
.
S chooses the other values for authorities A
1
and
A
2
following the protocol.
In the improbable case that a = 0, the DDH prob-
lem is trivially solvable (g
a
= g
ab
= 1). If a ̸= 0,
SECRYPT 2024 - 21st International Conference on Security and Cryptography
514

since a and b come from an uniform distribution,
then also these implicit values are uniformly dis-
tributed, so the choices of the simulator are indis-
tinguishable from a real protocol execution.
Note that S can compute all the values g
x
′′
i
, g
α
′
ℓ
,
g
y
′
i,ℓ
, g
z
′
i,ℓ
, either normally (when the parameter has
been explicitly chosen) or as follows:
g
x
′′
i
= g
˜x
i
· B
(−1)
i
, g
α
′
ℓ
= A
˜
α
ℓ
,
g
y
′
i,ℓ
= A
˜y
i,ℓ
, g
z
′
i,ℓ
= A
˜z
i,ℓ
.
for all i ∈ [2], ℓ ∈ [M]. Therefore, S can simulate
the setup phase, exploiting the RO to simulate the
NIZKPs for x
′′
i
, α
′
ℓ
, y
′
i,ℓ
z
′
i,ℓ
for i ∈ [2], ℓ ∈ [M].
• Registrar Phase. For the voters associated to v
i
with 3 ≤ i ≤ N, S can simulate this phase follow-
ing the protocol normally (since all relevant pa-
rameters have been explicitly chosen), while for
i ∈ [2] S does the following:
1. A computes the initial step of the ballot
¯
b
0,i
on
behalf of A
0
and proves its correctness with the
appropriate DVNIZKPs. By rewinding A and
exploiting the control of the random oracle, S is
able to extract from the DVNIZKPs the values
of k,λ, and ¯z
i,ℓ
for all ℓ ∈ [M] (see (Spadafora
et al., 2021)). Moreover, since A
0
communi-
cates the set of indexes of valid tokens V
i
to the
voter associated to v
i
(that is controlled by the
simulator), S can reconstruct the values of the
σ
i,ℓ
for all ℓ ∈ [M].
2. S computes step 1 of the ballot
¯
b
1,i
= (
¯
b
1,i,ℓ
)
ℓ∈[M]
as:
¯
b
1,i,ℓ
= A
¯z
i,ℓ
˜z
i,ℓ
(σ
i,ℓ
+x
′
i
+ ˜x
i
)
· Ξ
¯z
i,ℓ
˜z
i,ℓ
(−1)
i
∗
= g
z
i,ℓ
(σ
i,ℓ
+x
i
)
∀ℓ ∈ [M] (1)
where
∗
= of Equation (1) holds iff Ξ = g
ab
in
the DDH challenge. Since it controls the voter
associated to v
i
, S can forge the DVNIZKPs ex-
ploiting the value e
i
. In order to hide from A
which tokens are valid, these DVNIZKPs are
forged using random values.
3. S can perform step 2 on behalf of A
2
normally,
then A computes step 3 on behalf of A
0
and
proves its correctness.
4. Finally S computes the final ballot
b
i
= (b
i,ℓ
)
ℓ∈[M]
as:
b
i,ℓ
= A
˜y
i,ℓ
y
′′
i,ℓ
(σ
i,π
i
(ℓ)
+x
′
i
+ ˜x
i
)
· Ξ
˜y
i,ℓ
y
′′
i,ℓ
(−1)
i
∗
= g
y
i,ℓ
(σ
i,π
i
(ℓ)
+x
i
)
(2)
where again
∗
= of Equation (2) holds if and only
if Ξ = g
ab
in the DDH challenge.
• Voting: Phases 1, 2, and the Challenge are per-
formed as in Definition 2.
• Tallying. Without loss of generality, suppose that
only the v
i
with i ∈ [T ] have voted. For ℓ ∈ [M], S
carries on with the simulation as follows:
1. S computes the preliminary and final votes on
behalf of A
1
and A
2
following the protocol
without problems. In fact, for i ∈ [2], we have:
α
′
ℓ
y
′
i,
˜
φ
i
(ℓ)
=
a
˜
α
ℓ
a ˜y
i,
˜
φ
i
(ℓ)
=
˜
α
ℓ
˜y
i,
˜
φ
i
(ℓ)
∀ℓ ∈ [M],
and these values are known to S.
2. S computes and publishes the values
g
α
ℓ
= A
˜
α
ℓ
α
′′
ℓ
∀ℓ ∈ [M], and simulates the
proofs of correctness.
3. Finally note that S can compute:
T
∑
i=1
x
′′
i
= ˜x
1
−b+ ˜x
2
+b+
T
∑
i=3
x
′′
i
= ˜x
1
+ ˜x
2
+
T
∑
i=3
x
′′
i
,
so for the rest of the tallying phase S can follow
the protocol.
• Guess Eventually A will output a guess µ
′
of the
coin flip performed by S during the Challenge. S
then outputs 0 to guess that Ξ = g
ab
if µ
′
= µ, oth-
erwise it outputs 1 to indicate that Ξ is a random
group element R ∈ G.
The case in which the adversary controls A
1
and the
case in which the adversary controls A
2
, proceed sim-
ilarly. If A
1
is corrupted, the main difference is that S
implicitly sets:
α
′′
ℓ
= a ·
˜
α
ℓ
, y
′′
i,ℓ
= a · ˜y
i,ℓ
, ¯z
i,ℓ
= a · ˜y
i,ℓ
,
while α
′
ℓ
, y
′
i,ℓ
, z
′
i,ℓ
are chosen normally.
If A
2
is corrupted, the main difference is that S
implicitly sets:
x
′
i
= ˜x
i
+ (−1)
i
b,
while x
′′
i
is chosen normally.
Essentially, in all three cases when Ξ is not ran-
dom the simulator S gives a perfect simulation. This
means that the advantage is preserved, so it holds that:
P[S(g,A,B, Ξ = g
ab
) = 0] =
1
2
+ ε.
On the contrary, when Ξ is a random element R ∈ G,
every token and vote belonging to the free voters be-
comes independent from the values that would have
been computed by following the protocol (since they
are simulated using the random value R), so A can
gain no information about the votes from them, while
the tally is always correct. Since the security game is
structured in such a way that the tally and the tokens
Amun: Securing E-Voting Against Over-the-Shoulder Coercion
515

of the other voters (i.e. the values where Ξ is not used
in the computation by S) do not give any information
about the coin flip µ, we have that:
P[S(g,A,B, Ξ = R) = 0] =
1
2
.
Therefore, S can play the DDH game with non-
negligible advantage
ε
2
.
5.2 General Properties of the Protocol
The general properties of a vote system introduced
in Section 2.4, can all be proved for the proto-
col described in Section 3.1. Here we prove only
Vote-Coercion Resistance, we refer to (Longo and
Spadafora, 2021) for the other proofs.
Proposition 1 (Vote-Coercion Resistance). In the
ROM, if the DDH assumption holds, then the proto-
col is vote-coercion resistant, as per Definition 1.
Proof. In order to comply with the coercer’s request,
a voter associated to v
i
∈ V
c
has to assign the valid
tokens to (C
i,1
,. .. ,C
i,P
). Since the Registrar Phase is
performed in a protected environment, only the voter
associated to v
i
knows which tokens are valid, and
cannot give a meaningful proof of this fact to A as dis-
cussed at the end of the registrar phase (Section 3.1.2).
Thanks to Theorem 1, in the ROM, if the
DDH assumption holds, then the protocol has vote-
indistinguishability and the only way to determine if a
vote expresses a specific choice is to distinguish valid
and decoy tokens. Since A cannot do so, all the infor-
mation that can be gained from the votes is given by
the final tally. This means exactly that the probability
of A detecting that a voter in V
c
has not followed its
instruction is the same in Ψ
1
and Ψ
2
.
6 CONCLUSIONS
In this paper we have generalized the two-candidates-
one-preference e-voting protocol of (Spadafora et al.,
2021) into an M-candidates-P-preferences protocol.
We have tweaked the system of ZKPs that ensure
transparency and full auditability of the process by
using non-interactive proofs to enhance efficiency, ex-
ploiting designated-verifier proofs to preserve plausi-
ble deniability against coercers. Moreover, we have
abandoned the blockchain infrastructure in favor of a
more traditional bulletin board.
Compared with the two-candidates protocol, our
generalization introduces an additional authority, that
is required in order to properly mask the multiple
valid and decoy tokens in each ballot, so that the sys-
tem remains secure even if one authority is corrupt.
Note that the authorities can perform the setup
phase asynchronously, and possible DOS attacks may
be mitigated with a long-lasting Registrar phase. We
can also adopt the strategy of dividing the authorities
in independent triplets that manage restricted pools
of voters (much like how large-scale elections are di-
vided in voting districts). This approach limits the
damage in case that more than one authority is cor-
rupted, speeds up the final step of tallying (whose
computational cost is linear in the number of votes
managed by a triplet of authorities), and enhances the
overall efficiency by distributing the workload.
Security. The protocol fulfills all the security prop-
erties required for an e-voting protocol to be consid-
ered secure, proven in the random oracle model under
the classical Decisional Diffie-Hellman Assumption.
Regarding coercion resistance, the differences be-
tween definitions are subtle. In its strongest form,
coercion resistance includes protection against forced
abstention attacks and randomized voting. Random-
ized vote attacks are less effective in swaying an
election result with respect to other coercion attacks,
while forced abstention may be more effective, but it
would require more effort, since more voters have to
be controlled in order to achieve an impacting result.
In fact, in our protocol the attacker should identify ev-
ery coerced voter by requesting a signature, in order
to link the voter’s identity with a public key and its
ballot, as published in the BB.
Although our definition of coercion resistance
seems weaker, we remark that the most prominent e-
voting protocols with stronger defence against coer-
cion assume that there is a moment during the vot-
ing phase when the voter is not under control of the
attacker. The Amun protocol, instead, protects the
voter even if during the voting period there is con-
stant surveillance from the coercer. Therefore, this
may be preferable when the voting period is limited,
since, in this scenario, it is more likely for the attacker
to maintain continuous control.
To have any kind of anti-coercion resistance is es-
sential that there is a moment where the voter receives
some private information that can then be concealed
from the coercer with plausible deniability. In the de-
scription of the protocol we have assumed that the
communication between the voter and the authorities
during the registrar phase happens in a safe and con-
trolled environment, where the coercer has no power.
This requirement is equivalent to exchanging infor-
mation through untappable channels. This is a com-
mon assumption in coercion-resistant protocols (Juels
et al., 2010; Clarkson et al., 2008).
In the scenario where the voting period is limited,
SECRYPT 2024 - 21st International Conference on Security and Cryptography
516

some voters may struggle to access a secure physical
voting booth, potentially leading to disenfranchise-
ment. However, the longer duration of the registration
phase provides more opportunities for voters to reach
a secure registration booth.
The authors of (Longo et al., 2022; Bitussi et al.,
2023) propose a method to protect voters from coer-
cion by exploiting surveillance gaps. They assume
that an adversary cannot maintain constant surveil-
lance over a voter, allowing the voter to act freely
during these gaps. In particular, when a voter reg-
isters, the voting credential is not issued immediately,
but after a random delay. A DVNIZKP is sent after
another random wait to prove the credential’s correct-
ness. These random waiting periods allow a coerced
voter to exploit surveillance gaps to forge a credential
and its DVNIZKP. This approach can also be applied
to our protocol, where the credential can be seen as
the set of indexes of the valid v-tokens.
Final Remarks. Many election systems allow vot-
ers to cast a blank ballot or to leave some of the P
possible preferences unexpressed. This feature can
be easily added to the protocol presented here by sim-
ply adding P dummy candidates that represent blank
choices.
ACKNOWLEDGMENTS
This work has been partially supported by project
SERICS (PE00000014) under the MUR National Re-
covery and Resilience Plan funded by the European
Union - NextGenerationEU. This work has been par-
tially supported by a joint laboratory between Fon-
dazione Bruno Kessler and the Italian Government
Printing Office and Mint, Italy. The authors are mem-
bers of the INdAM Research Group GNSAGA.
REFERENCES
Bitussi, M., Longo, R., Marino, F. A., Morelli, U., Sharif,
A., Spadafora, C., and Tomasi, A. (2023). Coercion-
resistant i-voting with short pin and oauth 2.0. In E-
Vote-ID 2023, LNI. Herausgeber et al. Bonn. to ap-
pear.
Chaidos, P., Cortier, V., Fuchsbauer, G., and Galindo, D.
(2016). Beleniosrf: A non-interactive receipt-free
electronic voting scheme. In Proceedings of the 2016
ACM SIGSAC Conference on Computer and Commu-
nications Security.
Clarkson, M. R., Chong, S., and Myers, A. C. (2008). Civ-
itas: Toward a secure voting system. In IEEE Sympo-
sium on Security and Privacy.
Cortier, V., Gaudry, P., and Glondu, S. (2019). Belenios: a
simple private and verifiable electronic voting system.
In Foundations of Security, Protocols, and Equational
Reasoning. Springer.
Fischer, J.-B. and Stern, J. (1996). An efficient
pseudo-random generator provably as secure as
syndrome decoding. In Advances in Cryptol-
ogy—EUROCRYPT’96: International Conference on
the Theory and Application of Cryptographic Tech-
niques Saragossa, Spain, May 12–16, 1996 Proceed-
ings 15. Springer.
Gardner, R. W., Garera, S., and Rubin, A. D. (2009). Co-
ercion resistant end-to-end voting. In International
Conference on Financial Cryptography and Data Se-
curity. Springer.
Haines, T. and Smyth, B. (2019). Surveying definitions of
coercion resistance. Cryptology ePrint Archive.
Iovino, V. and Visconti, I. (2019). Non-interactive zero
knowledge proofs in the random oracle model. In
Codes, Cryptology and Information Security: Third
International Conference, C2SI 2019, Rabat, Mo-
rocco, April 22–24, 2019, Proceedings-In Honor of
Said El Hajji. Springer.
Jakobsson, M., Sako, K., and Impagliazzo, R. (2001).
Designated verifier proofs and their applications. In
Advances in Cryptology—EUROCRYPT’96: Interna-
tional Conference on the Theory and Application of
Cryptographic Techniques Saragossa, Spain, May 12–
16, 1996 Proceedings. Springer.
Juels, A., Catalano, D., and Jakobsson, M. (2010).
Coercion-resistant electronic elections. In Towards
Trustworthy Elections. Springer.
Krips, K. and Willemson, J. (2019). On practical as-
pects of coercion-resistant remote voting systems. In
International Joint Conference on Electronic Voting.
Springer.
Kusters, R., Truderung, T., and Vogt, A. (2010). A game-
based definition of coercion-resistance and its appli-
cations. In 2010 23rd IEEE Computer Security Foun-
dations Symposium.
Longo, R., Morelli, U., Spadafora, C., and Tomasi, A.
(2022). Adaptation of an i-voting scheme to ital-
ian elections for citizens abroad. University of Tartu
Press.
Longo, R. and Spadafora, C. (2021). Amun: Securing e-
voting against over-the-shoulder coercion. Cryptology
ePrint Archive.
Roth, R. M. (2006). Introduction to coding theory. IET
Communications, 47(18-19).
Ryan, P. Y., Rønne, P. B., and Iovino, V. (2016). Selene:
Voting with transparent verifiability and coercion-
mitigation. In International Conference on Financial
Cryptography and Data Security. Springer.
Schnorr, C. (1991). Efficient signature generation by smart
cards. Journal of Cryptology, 4:161–174.
Shoup, V. and Alwen, J. (2007). Σ-Protocols Continued and
Introduction to Zero Knowledge.
Spadafora, C., Longo, R., and Sala, M. (2021). A coercion-
resistant blockchain-based E-voting protocol with re-
ceipts (2021). In Advances in Mathematics of Com-
munications. AIMS, doi:10.3934/amc.2021005.
Amun: Securing E-Voting Against Over-the-Shoulder Coercion
517