Strategic Placement of Data Centers for Economic Analysis: An Online

Algorithm Approach

Christine Markarian and Claude Fachkha

College of Engineering and Information Technology Department, University of Dubai, Dubai, U.A.E.

Keywords:

Data Center Location, Economic Growth, Data Analytics, Competitive Analysis, Online Algorithms.

Abstract:

Governments worldwide have increasingly recognized the transformative potential of data analytics in eco-

nomics, leading to the establishment of specialized research centers dedicated to economic analysis. These

centers serve as hubs for experts to dissect economic indicators, inform policymaking, and foster sustainable

growth. With data analytics playing a pivotal role in understanding economic trends and formulating policy

responses, the strategic placement of data centers becomes crucial. In this paper, we address the strategic

placement of data centers in urbanized environments within the framework of online algorithms. Online algo-

rithms are designed to make sequential decisions without complete information about future inputs, making

them suitable for dynamic urban environments. Speciﬁcally, we formulate the problem as the Online Data

Center Placement problem (ODCP) and design a novel online algorithm for it. To gauge our algorithm’s

effectiveness, we use competitive analysis, a standard method for assessing online algorithms. This method

compares our algorithm’s solutions with those of the optimal ofﬂine solution. Our study aims to provide a sys-

tematic approach for informed decision-making, optimizing resource usage, and fostering economic growth.

1 INTRODUCTION

Governments globally have acknowledged the power

of data analytics in economics. This led to the cre-

ation of research centers focused on analyzing eco-

nomic data, forecasting trends, and guiding policy-

making. These efforts highlight data analytics’ vi-

tal role in shaping economic policy, fostering inno-

vation, and promoting sustainable growth (Johnson

et al., 2021).

These specialized research centers are hubs of

economic analysis. They gather experts in statistics,

econometrics, and data science. Together, they dis-

sect economic indicators, understand market dynam-

ics, and identify emerging trends. Institutions like

central banks, ﬁnance ministries, and economic plan-

ning departments have set up dedicated research units.

These units have expertise in data analytics. They

support evidence-based policymaking and economic

analysis.

The beneﬁts of data analytics in economics are

manifold. It helps governments gain valuable in-

sights into the economy’s health, make informed pol-

icy decisions, and respond effectively to economic

challenges. Economic indicators like Gross domes-

tic product (GDP) growth and inﬂation rates are an-

alyzed to understand economic trends, identify ar-

eas of concern, and formulate appropriate policy re-

sponses. Data analytics also facilitates the assessment

of policy interventions, the evaluation of program ef-

fectiveness, and the monitoring of progress towards

economic goals (Awan et al., 2021).

Recent government initiatives have witnessed the

establishment of new centers for data analytics in eco-

nomics globally. Examples range from the Bank of

England’s Data and Statistics Division (Bank of Eng-

land, 2024) to the United States (U.S.) Census Bu-

reau’s specialized units (United States Census Bu-

reau, 2024), alongside institutions like the German

Institute for Economic Research (DIW Berlin) (Ger-

man Institute for Economic Research (DIW Berlin),

2024) and the National Institute of Economic and

Social Research (NIESR) in the United Kingdom

(UK) (National Institute of Economic and Social Re-

search (NIESR), 2024). Moreover, governments in

Singapore, Australia, and other countries have in-

vested in data analytics capabilities to support eco-

nomic research, policy analysis, and forecasting (Liu

et al., 2023).

The focus of this paper centers around the strate-

gic placement of data centers to harness the transfor-

mative potential of data analytics in economics. As

Markarian, C. and Fachkha, C.

Strategic Placement of Data Centers for Economic Analysis: An Online Algorithm Approach.

DOI: 10.5220/0012788500003756

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 13th International Conference on Data Science, Technology and Applications (DATA 2024), pages 425-433

ISBN: 978-989-758-707-8; ISSN: 2184-285X

425

governments worldwide increasingly recognize the

importance of data-driven insights in shaping eco-

nomic policy and fostering sustainable growth, the es-

tablishment of specialized research centers dedicated

to analyzing economic data has become paramount.

The strategic placement of data centers presents

challenges and objectives for governments. They aim

to maximize the effectiveness and accessibility of data

analytics capabilities while ensuring equitable access

to resources across regions. This involves considering

geographic distribution, population centers, partner-

ships, infrastructure, economic factors, and strategic

priorities.

Geographic distribution is crucial for govern-

ments. They aim to ensure equitable access to data

analytics resources across diverse regions, promot-

ing inclusivity and regional development initiatives.

Major urban areas serve as hubs of economic activ-

ity and innovation. They drive the placement of data

centers to leverage existing infrastructure and talent

pools. Collaborative initiatives with academic institu-

tions and private-sector partners shape the placement

of data centers. This ampliﬁes the impact of data an-

alytics initiatives.

Robust infrastructure and connectivity are crucial

for data analytics platforms to work effectively, im-

pacting where data centers are located Governments

focus on places with good economic conditions and

incentives to attract investment, spurring economic

growth and job creation. Data center locations are

chosen to support strategic goals like regional de-

velopment, innovation clusters, and speciﬁc industry

sectors, aiming for sustainable economic progress.

Online algorithms and competitive analysis are

crucial in decision-making processes, notably in sit-

uations like placing research centers in urban areas

(Borodin and El-Yaniv, 2005; Albers, 2003). Online

algorithms decide sequentially without information

about future inputs. They’re vital in dynamic settings

where real-time decisions are needed based on incom-

plete or uncertain data. In location problems, like data

center placement, online algorithms help ﬁnd the best

locations as demands change over time (Borodin and

El-Yaniv, 2005; Albers, 2003).

Competitive analysis uses the competitive ratio to

measure how well online algorithms work compared

to optimal ofﬂine ones. It gives insights into their ef-

fectiveness in real-world scenarios. The competitive

ratio compares the cost of the online algorithm to that

of an optimal ofﬂine solution. A ratio of 1 means the

online algorithm matches the ofﬂine one’s cost in the

worst-case scenario (Borodin and El-Yaniv, 2005; Al-

bers, 2003).

Achieving a competitive ratio of 1 is tough due to

real-world uncertainties. In location problems, chang-

ing demands, resource limits, and geography affect

online algorithm performance (Borodin and El-Yaniv,

2005; Albers, 2003). Analyzing the competitive ra-

tio in data center placement helps understand how on-

line algorithms handle dynamic decisions and uncer-

tainties. It helps governments and organizations im-

prove decision-making and resource allocation for ur-

banization and economic development (Borodin and

El-Yaniv, 2005; Albers, 2003).

Using online algorithms for data placement, es-

pecially in urbanization contexts, is advantageous

because they operate effectively under uncertainty.

These algorithms can make decisions without know-

ing the future, which suits dynamic and unpredictable

urban environments. While regrets may occur, evalu-

ating them with competitive analysis guarantees per-

formance.

2 OUR CONTRIBUTION

Data center placement in urban environments is a

complex problem that requires careful consideration

of many factors in order to achieve the best possi-

ble technological and economic outcomes. Let’s take

an example where a city administration has to choose

where to locate 100 possible data centers within its

urban area. Each data center’s establishment incurs

signiﬁcant costs, covering initial construction, equip-

ment procurement, and infrastructure development,

averaging around C500,000 per center. Moreover,

annual operational expenses, including utility bills,

maintenance, and stafﬁng, amount to approximately

C50,000 per center. Additionally, connecting these

data centers to 50 strategically located hubs intro-

duces further ﬁnancial complexity, with connectiv-

ity costs averaging C100,000 per connection. These

costs ﬂuctuate based on factors such as distance and

technological requirements. Furthermore, each data

center must handle incoming demands for data ana-

lytics services, incurring transportation and process-

ing complexity costs. Transportation costs, associ-

ated with data movement to and from the centers,

are estimated at C10,000 per demand-center pair,

while processing complexity costs amount to approx-

imately C20,000 per pair. The overarching objective

is to minimize establishment, operation, connectivity,

transportation, and processing complexity costs, en-

suring efﬁcient delivery of data analytics services.

In this paper, we tackle the problem of strate-

gically positioning data centers in urbanized envi-

ronments from the perspective of online algorithms.

Speciﬁcally, we formulate the latter as the Online

DATA 2024 - 13th International Conference on Data Science, Technology and Applications

426

Data Center Placement problem (ODCP), outlined

below. We design an online algorithm for ODCP and

assess its performance using the competitive analy-

sis framework, widely recognized as the standard ap-

proach for evaluating online algorithms.

In this rapidly urbanizing world, the dynamic na-

ture of urban environments, characterized by continu-

ous population growth, evolving infrastructure needs,

and shifting socio-economic dynamics, presents a

complex challenge in strategically placing data cen-

ters. Our study aims to offer a systematic approach

to navigate this complexity, enabling informed deci-

sions that optimize resource utilization and stimulate

economic growth.

3 PROBLEM DESCRIPTION:

ONLINE DATA CENTER

PLACEMENT PROBLEM

(ODCP)

Given:

• A set L = {l

,... ,l

} of potential locations

where data centers can be established. This set

represents the available locations where data cen-

ters can be built to serve the demands for data an-

alytics services.

• A set H = {h

,. .. ,h

} of hub locations. These

locations serve as focal points for managing and

coordinating the network of data centers, facili-

tating communication, data aggregation, and cen-

tralized decision-making.

• Each potential data center location l

can be con-

nected to one of the hubs in H, incurring a con-

nectivity cost cc

associated with establishing

and maintaining the network connection between

the potential data center l

and the hub h in H.

• A sequence D = {d

,. .. ,d

} of demands rep-

resenting the arrival of data analytics needs over

time. These demands correspond to various fac-

tors such as geographical regions, population cen-

ters, economic hubs, and social or environmen-

tal contexts where data analytics services are re-

quired.

• Establishment costs ec

associated with estab-

lishing a data center at location l

. These costs

represent the expenses involved in setting up a

data center at each location l

. They include initial

construction costs, equipment procurement, and

infrastructure development.

• Operation costs oc

are expenses related to main-

taining and running a data center at location l

They encompass ongoing expenditures necessary

for efﬁcient operations, including utility bills,

equipment maintenance, stafﬁng, security mea-

sures, and other recurring expenses essential for

sustained functionality of the data center.

• Transportation costs tc

i j

associated with each

demand and data center pair. This cost represents

the expenses associated with transporting data or

resources to and from the data center to fulﬁll de-

mand d

. These costs include factors such as ship-

ping, logistics, and distribution expenses required

to move data or equipment to the designated data

center and deliver services to customers or de-

mands efﬁciently.

• Processing complexity costs pcc

i j

associated

with each demand and data center pair. This cost

reﬂects the computational resources and expertise

required to analyze and process the data associ-

ated with a particular demand at a speciﬁc data

center.

4 OBJECTIVE

In the online setting, demands arrive sequentially and

decisions regarding data center establishment, data

center-hub connections, and demand assignment must

be made without knowledge of future demands. Ad-

ditionally, once decisions are made, they cannot be

reversed. Upon the arrival of each demand, a decision

must be made whether to assign it to an existing data

center or to establish a new one and allocate the de-

mand accordingly. Furthermore, once a data center is

established, it must be promptly connected to one of

the designated hubs to ensure network functionality.

This can be more formally expressed as follows:

1. Each demand d

must be assigned to one data cen-

ter.

∑

i∈L

i j

= 1 for all j ∈ D

2. Each data center l

used for serving demands must

be connected to one hub. U is used to denote the

set of data centers to which demands are assigned.

∑

h∈H

= 1 for all i ∈ U

Minimizing the total sum of establishment, op-

eration, connectivity, transportation, and processing

complexity costs associated with setting up and main-

taining the network of data centers, ensuring efﬁcient

delivery of data analytics services across diverse geo-

graphical regions and demand scenarios, is our objec-

tive. This can be more formally expressed as follows:

Strategic Placement of Data Centers for Economic Analysis: An Online Algorithm Approach

427

Minimize:

∑

i∈L

∑

i∈L

∑

i∈L

∑

h∈H

∑

i∈L

∑

j∈D

i j

∑

i∈L

∑

j∈D

i j

The aim is to construct an online algorithm that

has a competitive ratio as close to 1 as possible. In this

pursuit, we adopt the oblivious adversary model for

our online algorithm, wherein the adversary’s actions

are predetermined and independent of the algorithm’s

decisions. Below is a summary of the Online Data

Center Placement problem (ODCP).

Online Data Center Placement Problem

Input:

• Set L = {l

,. .. ,l

} of potential data

center locations.

• Set H = {h

,. .. ,h

} of hub

locations.

• Sequence D = {d

,. .. ,d

} of

demands.

• Establishment costs ec

• Operation costs oc

• Connectivity costs cc

• Transportation costs tc

i j

• Processing complexity costs pcc

i j

Output:

• Demands arrive sequentially, prompting

decisions made without knowledge of

future demands.

• Upon each demand arrival d

, a decision

must be made to assign it to an existing

data center or establish a new one.

• Once a data center is established, it

must be promptly connected to one of

the designated hubs.

• The goal is to minimize establishment,

operation, connectivity, transportation,

and processing complexity costs, aiming

for a competitive ratio as close to 1 as

possible.

5 RELATED WORK

The problem at hand, the Online Data Center Place-

ment problem (ODCP), represents a broader form

of the Non-metric Online Facility Location problem

(NOCF). NOCF entails a scenario where a set of po-

tential facility locations, a set of client locations (ar-

riving sequentially over time), and a function repre-

senting the facility opening cost are given. The objec-

tive is to assign each client to an open facility while

aiming to minimize the total assignment and facility

opening costs. This broadness becomes evident when

we consider a speciﬁc instance of ODCP. Setting the

operation costs, the connectivity costs, the process-

ing complexity costs, and the number of hubs to zero

transforms the problem into NOCF. In this transfor-

mation, the transportation costs would correspond to

assignment costs and establishment costs to facility

opening costs.

NOCF, along with its variants, has garnered sig-

niﬁcant attention within the online algorithm commu-

nity. Its lower bounds are followed by those for the

Online Set Cover problem (OSC) (Alon et al., 2003;

Korman, 2004). On the positive side, Alon et al. de-

vised a randomized O(log m log n)-competitive online

algorithm for NOCF., with m denoting the number of

facility locations and n the number of client locations.

Another approach involves reducing NOCF instances

to OSC instances and employing a deterministic al-

gorithm for OSC. This yields an O((logn + log m) ·

(logn + loglog m))-competitive ratio. More recently,

Bienkowski et al. (Bienkowski et al., 2021) intro-

duced an online deterministic polynomial-time algo-

rithm surpassing this bound, achieving an O(logm ·

(logn + loglog m))-competitive ratio. Other variants

of NOCF have been explored in the context of service

installation, service quality, and leasing (Markarian,

2021; Markarian, 2022; Markarian and auf der Heide,

2019).

It is important to note that the decisions in ODCP

regarding data center establishment, hub connectivity,

and demand assignment are interrelated. The choice

to establish a new data center impacts connectivity

costs, as it necessitates establishing connections with

one of the designated hubs. Therefore, these decisions

cannot be made independently but must be considered

together to optimize the overall cost and performance

of the network. Hence, while algorithms designed for

NOCF may provide insights, they cannot be directly

applied to ODCP due to the unique constraints and

interdependencies inherent in data center placement

and network optimization.

6 GRAPH-BASED

FORMULATION FOR ODCP

In this section, we formulate ODCP as an edge-

weighted graph problem, outlining the nodes, edges,

and objective of the problem.

DATA 2024 - 13th International Conference on Data Science, Technology and Applications

428

Nodes:

• We designate r as the root node.

• We pair each potential data center location l

from

the set L = {l

,. .. ,l

} with two nodes. One is

identiﬁed as the original data center node l

, while

the other is its replica denoted as l

′

. Here, the set

L denotes the original data center nodes, while L

′

represents their corresponding replicas.

• We pair each hub h

from the set H =

,. .. ,h

} with a node, which we denote as

the hub node h

. Here, the set H represents the

hub nodes.

• Whenever a demand d

from the set D =

,. .. ,d

} arrives, we create a node for it,

denoted as the demand node d

. Here, the set D

represents the demand nodes.

Edges:

• An edge directed from each demand node to each

data center node is added. The edges’ weight is

set to the sum of the associated transportation and

processing complexity costs corresponding to the

demand and data center.

• An edge directed from each demand node d

each data center node l

is added. The edges’

weight corresponds to the sum of transportation

and processing complexity costs, denoted as tc

i j

and pcc

i j

respectively, for demand d

and data

center l

• An edge directed from each data center node l

its replica l

′

is added. The edges’ weight corre-

sponds to the sum of the establishment and op-

eration costs, denoted as ec

and oc

respectively,

associated with the data center l

• An edge directed from each replica data center

node l

′

to each hub node h

is added. The edges’

weight corresponds to the connectivity cost asso-

ciated with the data center and hub, denoted as

i j

• An edge directed from each hub node h

to the root

node r is added and the weights of these edges are

adjusted to zero.

Figure 1 presents an example of a graph generated

from an input consisting of two demands, ﬁve data

center locations, and two hubs.

Objective: The problem asks the following. When-

ever a demand arises, the objective is to ﬁnd, from

the demand node to the root node r, a directed path.

According to the problem formulation, this path com-

prises a data center node and a hub node. Once this

path is determined, we can identify the associated hub

with the hub node and the data center location with the

data center node along the path. The costs associated

with the solution are equivalent to the weights on the

edges. Speciﬁcally, we pay the costs associated with

the data center and the hub chosen along the path de-

termined by the solution. This mapping allows us to

derive a solution for the original non-graph problem,

the Online Data Center Placement problem (ODCP).

This strategic mapping not only enables us to de-

rive a solution for the original non-graph problem, the

Online Data Center Placement problem (ODCP), but

also ensures that the competitive ratio remains consis-

tent. This is achieved by inherently maintaining the

cost alignment within the formulation itself, thereby

preserving parity between the graph-based problem

and the original non-graph problem formulation.

7 ONLINE ALGORITHM DESIGN

We introduce, in this section, an online algorithm for

the Online Data Center Placement problem (ODCP),

utilizing the graph formulation outlined earlier.

An instance of ODCP consists of a set L of po-

tential data center locations and a set H of hub loca-

tions, accompanied by their respective establishment,

operation, and connectivity costs. The sequence D of

demands unfolds incrementally as the algorithm ad-

vances. Each step introduces a new demand, along

with its associated transportation and processing com-

plexity costs.

The algorithm initiates by building the nodes,

edges, and their associated weights for the data center

and hub sets. Subsequently, as each demand is un-

veiled, the algorithm generates a node, incorporating

its relevant edges and weights.

A demand d

∈ D arrives. We represent the graph

created by the aforementioned formulation as G =

(V,E). We refer to the graph problem variant of

ODCP as ODCP

. The algorithm associates each

edge e ∈ E with a fractional value that is set to 0

and increases gradually as the algorithm progresses.

These fractions collectively form a fractional solution

for ODCP

. The algorithm primarily focuses on con-

structing a fractional solution for ODCP

and incre-

mentally converting it into an integral solution upon

the arrival of new demands. We let c

denote the cost

and f

the fraction of edge e. For each demand that ar-

rives, the algorithm outputs a collection of edges that

form a path from the demand node d

to the root node

r. Once such a path is established, we can identify the

corresponding hub and data center nodes along the

path.

Strategic Placement of Data Centers for Economic Analysis: An Online Algorithm Approach

429

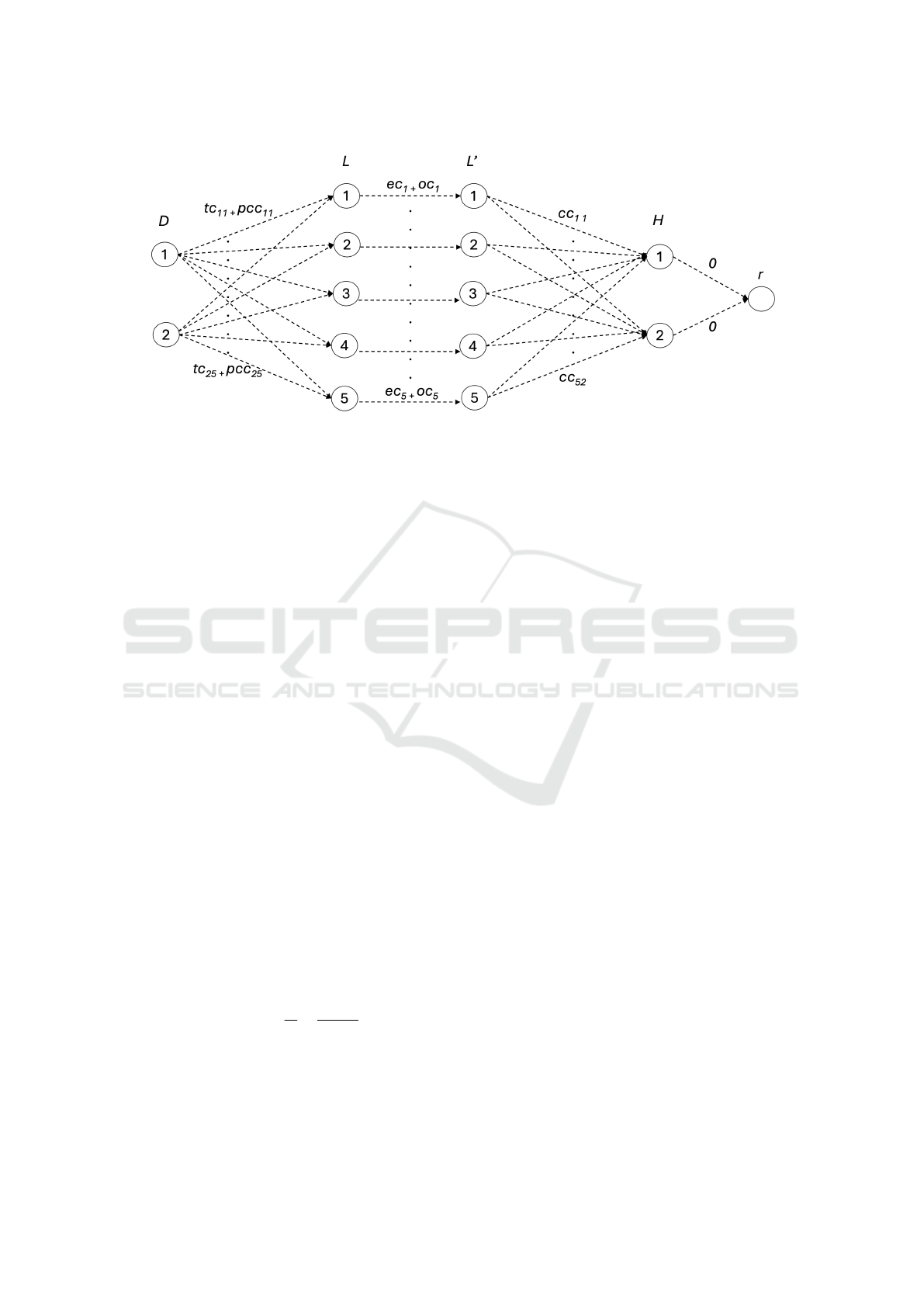
Figure 1: ODCP Instance - Graph Formulation.

The algorithm utilizes a stochastic decision-

making procedure governed by a parameter α. This

parameter is calculated as the smallest value within

2⌈log(n + 1)⌉ independently selected random vari-

ables, with uniform distribution between 0 and 1, with

n denoting the count of demands. Further clariﬁcation

regarding this selection is provided in the competitive

analysis segment.

The algorithm involves concepts related to net-

work ﬂows and connectivity, speciﬁcally focusing on

the principles of maximum ﬂow and minimum cut.

The maximum ﬂow between node u and node v in a

graph represents the minimum cut from u to v—the

smallest total fraction of edges that, if do not exist

anymore, would disconnect u from v.

Input: L = {l

,. .. ,l

}, H = {h

,. .. ,h

∈ D, and the associated establishment, operation,

connectivity, transportation, and processing complex-

ity costs.

Output: Set E

′

⊂ E of edges of G = (V, E) corre-

sponding to the data centers, hubs, and demand-data

center assignments forming the current solution for

ODCP

The algorithm works as follows:

1. As long as the maximum ﬂow from d

to r in G

is below 1, form a minimum cut Q from d

to r

in G. Observe every edge e ∈ Q and augment the

following fraction:

= f

· c

2. Output every edge e if f

exceeds α.

3. If the edges in the current solution do not create a

feasible path for demand d

, ﬁnd a feasible path of

minimum cost and add its edges to the solution.

4. Add the data center(s) and hub(s) associated with

the edges outputted in the previous phase. Assign

the demand to the data center associated with the

solution path.

8 COMPETITIVE ANALYSIS AND

PERFORMANCE EVALUATION

In the third and fourth phases of the algorithm, edges

are acquired. In the third phase, selections are in-

ﬂuenced by a stochastic process, while in the fourth

phase, choices are tailored to ensure a feasible output.

Let Optimal

solution

represent the cost of the opti-

mal ofﬂine solution and f rac signify the cost of the

fractional solution formed by the algorithm.

Selections Based on Stochastic Process: Consider

′

as the collection of edges acquired in the algo-

rithm’s third phase, with C

′

denoting its anticipated

cost. These edges are procured according to the

stochastic process previously outlined. Let’s desig-

nate l as an integer ranging from 1 to 2

⌈

log(n + 1)

⌉

and e as an edge. We deﬁne X

e,l

as the variable indi-

cating whether e is selected by the algorithm through

the stochastic process.

′

∑

e∈S

′

2⌈log(n+1)⌉

∑

l=1

Expectation[X

e,l

] · c

= 2

⌈

log(n + 1)

⌉

∑

e∈S

′

(1)

Consider that the summation of c

over all edges

in S

′

is bounded above by the cost of the fractional so-

lution. This comparison can be drawn against the op-

timal ofﬂine solution. The underlying concept is that

DATA 2024 - 13th International Conference on Data Science, Technology and Applications

430

whenever the algorithm increases a fraction, it does

not surpass 2. Additionally, the total count of fraction

increments can be gauged in relation to the cost of the

optimal ofﬂine solution.

Each edge e in a minimum cut Q contributes to

a fraction increase, quantiﬁed as



·c



. The

algorithm executes a fraction increase solely when the

maximum ﬂow is under 1. Thus,

∑

e∈Q

< 1 before

any such increment. Consequently, the upper limit for

each fraction increase is:

∑

e∈Q



· c



· c

< 2 (2)

Ultimately, in each minimum cut Q, the algorithm

is ensured to include an edge e from the optimal of-

ﬂine solution, as Q necessitates having an edge from

every path by deﬁnition. Referring to the equation

governing the fraction increase, once O(log |Q|) frac-

tion increases occur, the fraction f

for e reaches 1,

and further increments are precluded since e won’t

appear in any subsequent minimum cut. The magni-

tude of any minimum cut is limited by m, denoting the

number of facilities or the maximum available paths

from d

to the root r. Consequently, we are now able

to constrain the fractional solution:

O(logm ·Optimal

solution

) ≥ frac (3)

Equations 1, 2, and 3 allow us to deduce an up-

per bound for the expected cost C

′

of the edges pur-

chased in the third phase of the algorithm:

O(log(kn)logm ·Optimal

solution

) ≥ C

′

(4)

Choices Ensuring Feasibility: Consider S

′′

as the

collection of edges acquired in the fourth phase of the

algorithm, with C

′′

representing its anticipated cost.

These edges are procured by the algorithm solely

when a path hasn’t been acquired via the stochastic

process in the third phase. With each path purchase in

this stage, the algorithm ensures that its cost doesn’t

surpass Optimal

solution

, as it acquires a path of mini-

mum cost.

Consider a speciﬁc demand d

. Let Q

j+1

denote a

minimum cut created after the algorithm has procured

a path from d

to r and has ﬁnished the ﬁrst phase.

The probability of acquiring this path in the l-th trial,

where 1 ≤ l ≤ 2

⌈

log(n + 1)

⌉

, is:

∏

e∈Q

j+1

(1 − f

) ≤ e

−

∑

e∈Q

j+1

−

∑

e∈Q

j+1

≤

It’s notable that the last inequality is true because

the algorithm guarantees that

∑

e∈Q

j+1

≥ 1 by the

end of the ﬁrst phase (as per the Max-ﬂow min-cut

theorem). The expected cost of acquiring the ( j + 1)

path across all 1 ≤ l ≤ 2

⌈

log(n + 1)

⌉

trials is less than

1/n

· Optimal

solution

– (individual demand cost) Let’s initiate by assess-

ing the anticipated cost attributed to a single de-

mand. Select a demand d

. Assume Q

j+1

as the

minimum cut formed after the algorithm procures

a path and concludes the ﬁrst phase. The probabil-

ity of acquiring the path for a single trial, denoted

by 1 ≤ l ≤ 2

⌈

log(n + 1)

⌉

, can be expressed as:

∏

e∈Q

j+1

(1 − f

) ≤ e

−

∑

e∈Q

j+1

≤ 1/e

– (cumulative cost of all demands) The total ex-

pected cost incurred by all n

′

incoming demands

is bounded by:

′

·1/n

·Optimal

solution

≤ n·1/n

·Optimal

solution

= 1/n · Optimal

solution

Consequently, the expected cost C

′′

of the edges

purchased in the fourth phase of the algorithm is

given by:

′′

≤ 1/n · Optimal

solution

(5)

Hence, we can infer the subsequent theorem.

Theorem 1. For the Online Data Center Place-

ment problem (ODCP), a randomized algorithm oper-

ates online with a competitive ratio of O(log n log m).

Here, m refers to the number of data center locations

and n denotes the quantity of demands.

9 NUMERICAL EXAMPLE

Consider an urbanized area with signiﬁcant economic

activity and technological infrastructure. In this sce-

nario, there are 1000 potential locations suitable for

data center deployment and 500 hub locations strate-

gically positioned to ensure efﬁcient network connec-

tivity. With the increasing reliance on digital ser-

vices in urban environments, there are 5000 demands

for various digital applications, reﬂecting the diverse

needs of the population.

Applying competitive analysis for the Online Data

Center Placement problem (ODCP), we ﬁnd that a

randomized algorithm operates online with a compet-

itive ratio of O(log n log m), with m denoting the num-

ber of data center locations (1000) and n the quantity

of demands (5000). Thus, in our numerical example,

the competitive ratio is O(log5000×log 1000), which

ensures the algorithm’s efﬁciency and effectiveness in

Strategic Placement of Data Centers for Economic Analysis: An Online Algorithm Approach

431

handling the substantial demands and data center lo-

cations in the urban environment.

Moreover, the scalability of the algorithm is ev-

ident in its ability to handle even larger numbers of

demands and potential data center locations. No mat-

ter how many more demands arise or how many ad-

ditional potential data center locations are identiﬁed,

the algorithm’s competitive ratio remains consistent,

making it a highly scalable solution for data center

placement in urbanized environments.

10 ALGORITHMIC

TECHNIQUES AND KEY

INSIGHTS

The techniques we use are commonly used to tackle

problems within the realm of online algorithm design.

Our algorithm utilizes network ﬂow analysis princi-

ples to determine the path from each demand node to

the root node in a graph representing the Online Data

Center Placement problem. It employs a stochastic

decision-making process introducing randomness to

enhance decision ﬂexibility. By constructing frac-

tional solutions iteratively, the algorithm incremen-

tally converts them into integral solutions, facilitat-

ing adaptability to evolving demands. Employing a

greedy augmentation strategy, the algorithm gradu-

ally increases the ﬂow along edges forming minimum

cuts, aiming to approach the maximum ﬂow limit ef-

ﬁciently. Additionally, it constructs minimum-cost

paths when the current solution does not form a fea-

sible solution for the current demand, ensuring cost-

effective connectivity. These algorithmic techniques

collectively enable the algorithm to efﬁciently solve

the Online Data Center Placement problem.

Several mathematical methods, such as graph the-

ory, stochastic processes, and probabilistic theory, are

integrated in the evaluation of the algorithm for the

Online Data Center Placement problem. The prob-

lem is modeled as a graph using the concepts of graph

theory, where nodes stand in for data centers, hubs,

and demand locations, and edges for the connections

and expenses that exist between them. In the third

stage of the algorithm, edge selection is guided by

stochastic processes, which introduce randomness to

adjust to changing conditions and optimize cost. This

stochastic process is supported by probability the-

ory, which allows the algorithm to make probabilis-

tic decisions based on random variables and distribu-

tions. These mathematical methods are combined by

the algorithm to produce a competitive ratio analysis,

which sheds light on how well it functions in online

scenarios.

We provide a comprehensive framework for data

center placement in urban environments using our al-

gorithmic approach, which has demonstrable bene-

ﬁts for cost-effectiveness, scalability, ﬂexibility, and

real-time decision-making as well as urban devel-

opment planning. By leveraging online algorithms,

our approach facilitates prompt responses to chang-

ing demands and emerging trends in dynamic ur-

ban environments, enhancing agility and adaptability

in decision-making processes. Through competitive

analysis, our algorithm provides cost-effective solu-

tions relative to optimal ofﬂine algorithms, empower-

ing governments and organizations to make informed

decisions within budgetary constraints and resource

allocations. With its scalable and ﬂexible nature, our

algorithm accommodates diverse demand levels, ge-

ographical distributions, and infrastructure require-

ments, ensuring adaptability to evolving urban land-

scapes and economic dynamics. Moreover, our al-

gorithm contributes to evidence-based urban develop-

ment planning by analyzing data-driven insights and

economic indicators to strategically place data cen-

ters, fostering economic growth, innovation, and re-

gional development in alignment with broader urban

planning objectives and sustainability goals.

11 CONCLUSION AND FUTURE

DIRECTIONS

In conclusion, our study sheds light on the criti-

cal role of data analytics in shaping economic pol-

icy and fostering sustainable growth, underscored by

the strategic placement of data centers. Through the

lens of online algorithms, we address the challenge

of dynamically situating data centers in urbanized en-

vironments, considering factors such as geographic

distribution, infrastructure, and economic priorities.

Our novel approach, encapsulated in the Online Data

Center Placement problem formulation and algorithm

design, offers a systematic framework for decision-

making amidst uncertainty and evolving demands.

One possible future direction is to investigate the

application of our algorithm in data centers and ur-

banized environments, either in real or simulated en-

vironments. Practical testing allows for evaluation

under real-world conditions, taking into account fac-

tors like data variability and constraints related to

urban infrastructure, while competitive analysis of-

fers insightful information about theoretical worst-

case scenarios. We can learn more about the algo-

rithm’s performance in dynamic urban landscapes and

its strengths and limitations in handling real-time data

DATA 2024 - 13th International Conference on Data Science, Technology and Applications

432

and decision-making in the context of data center

placement strategies by conducting practical evalua-

tions in urbanized environments.

Further research could expand our model to in-

corporate data security and infrastructure resilience.

Infrastructure resilience is the process of strategically

placing data centers to fortify urban infrastructure net-

works against external shocks such as cyberattacks

and natural disasters. To reduce failures and increase

redundancy, this involves determining key sites. In-

tegrating data security goals also guarantees privacy

requirements are followed and sensitive data is pro-

tected. By taking these aspects into account, data cen-

ter location techniques are improved and help create

safe and dependable urban data ecosystems, which

are essential for reliable data-driven urban develop-

ment projects.

Combining data center location methods with

more general smart city initiatives to improve urban

efﬁciency, sustainability, and quality of life is an in-

triguing new direction for future research. With this

integration, there is a chance to use data analytics to

improve public services, transit networks, urban in-

frastructure, and even data center locations. Cities

may optimize the beneﬁts of data-driven approaches

to societal issues and create synergies by matching

data center site decisions with smart city objectives.

REFERENCES

Albers, S. (2003). Online algorithms: a survey. Mathemat-

ical Programming, 97:3–26.

Alon, N., Awerbuch, B., and Azar, Y. (2003). The on-

line set cover problem. In Proceedings of the Thirty-

Fifth Annual ACM Symposium on Theory of Comput-

ing, STOC ’03, page 100–105, New York, NY, USA.

Association for Computing Machinery.

Awan, U., Shamim, S., Khan, Z., Zia, N. U., Shariq, S. M.,

and Khan, M. N. (2021). Big data analytics capabil-

ity and decision-making: The role of data-driven in-

sight on circular economy performance. Technologi-

cal Forecasting and Social Change, 168:120766.

Bank of England (Accessed: 2024). Bank of England

Statistics Research Datasets.

Bienkowski, M., Feldkord, B., and Schmidt, P. (2021). A

nearly optimal deterministic online algorithm for non-

metric facility location. In Bl

aser, M. and Monmege,

B., editors, 38th International Symposium on Theoret-

ical Aspects of Computer Science (STACS 2021), vol-

ume 187 of Leibniz International Proceedings in In-

formatics (LIPIcs), pages 14:1–14:17, Dagstuhl, Ger-

many. Schloss Dagstuhl – Leibniz-Zentrum f

ur Infor-

matik.

Borodin, A. and El-Yaniv, R. (2005). Online computation

and competitive analysis. cambridge university press.

German Institute for Economic Research (DIW Berlin) (Ac-

cessed: 2024). German Institute for Economic Re-

search (DIW Berlin).

Johnson, M., Jain, R., Brennan-Tonetta, P., Swartz, E., Sil-

ver, D., Paolini, J., Mamonov, S., and Hill, C. (2021).

Impact of big data and artiﬁcial intelligence on indus-

try: developing a workforce roadmap for a data driven

economy. Global Journal of Flexible Systems Man-

agement, 22(3):197–217.

Korman, S. (2004). On the use of randomization in the on-

line set cover problem. Weizmann Institute of Science,

Liu, R., Sun, W., and Hu, W. (2023). Placement of high

availability geo-distributed data centers in emerging

economies. IEEE Transactions on Cloud Computing.

Markarian, C. (2021). Online non-metric facility location

with service installation costs. In ICEIS (1), pages

737–743.

Markarian, C. (2022). Online non-metric facility location

with service-quality costs. In ICEIS (1), pages 616–

622.

Markarian, C. and auf der Heide, F. M. (2019). Online algo-

rithms for leasing vertex cover and leasing non-metric

facility location. In ICORES, pages 315–321.

National Institute of Economic and Social Research

(NIESR) (Accessed: 2024). National Institute of Eco-

nomic and Social Research (NIESR).

United States Census Bureau (Accessed: 2024). United

States Census Bureau Special Census Program.

Strategic Placement of Data Centers for Economic Analysis: An Online Algorithm Approach

433