Research on Pricing of Automatic Redemption Structured Deposit
Products Based on Monte Carlo Simulation
Wenlu Chen
School of Economics and Finance, Tianjin University of Finance and Economics, 300222, Tianjin, China
Keywords: Automatic Redemption Structured Deposit Products, Research on Pricing, Monte Carlo.
Abstract: Structured deposit is one of the priorities today. It provides better options for investors and fills a gap in the
market. However, due to his short development in the market, it lacks a unified understanding. Therefore,
the topic of this paper is the pricing of structured deposit products. The research methods of this paper are as
follows: First of all, the paper simulates the income of the product and introduces the basic information and
income of a product to better explain the structured deposit product. Then, nine different market
environments and various parameters are assumed, and the Monte Carlo method is used to simulate the
price path of assets. According to the circumstances of nine different market environments, the annual
expected return rate and annual volatility and estimated, and their sensitivity analysis is carried out. Finally,
it is concluded which market environment has the highest product return, and the annual expected return is
positively correlated with exercise price 1, and negatively correlated with exercise price 2, and the annual
volatility has nothing to do with the exercise price.
1 INTRODUCTION
In 2002, China Everbright Bank launched a foreign
currency structured deposit product. In 2005, it
issued China’s first structural deposit structure of
RMB after becoming the first bank in China to be
eligible to trade cross-currency derivatives of RMB
(Zhang 2022 & Qin 2023). In April 2018, the
People’s Bank of China issued on its official website
the “Guiding Opinions on Regulation the Asset
Management Business of Financial Institutions”
(referred to as the “New Regulations”), article 6 of
which stipulated that financial institutions should
pass on the of “seller is responsible, buyer is
responsible” to investors, break the rigid payment,
and guide financial products to realize the
transformation to net worth products (Li 2023). This
means that investors who are more inclined to
capital-prot protection financial products will
gradually withdraw from the market. Based on the
characteristics of structural deposits, breaking
through the interest rate ceiling to give investors
higher benefits than general deposits are also in line
with the reform requirements of relevant policies,
which can fill the vacancy of capital protection
products of commercial banks, and has a good
market demand and market prospects.
Structured deposit refers to the deposit of RMB
or foreign currency funds legally held by investors in
banks, and the bank can embed financial derivatives
(including but not limited to forwards, swaps,
options or futures, etc.) based on ordinary deposits
(Zhao 2022). Financial products with certain risks
link investors’ returns to interest rates, exchange
rates, stock prices, commodity prices credit indices,
and other financial or non-financial subjects (Zhao
2022). Structured deposits are not ordinary deposits
and are different from bank wealth management.
Structured deposits are embedded in financial
derivatives based on deposits, and are linked to the
fluctuations of interest rates, exchange rates, indices,
etc., so that depositors can obtain higher returns
based on bearing certain risks.
The pricing method is one of the important
problems in the study of structured products, and
also one of the difficulties in the study of structured
products. Domestic scholars have adopted different
research methods to analyze the pricing situation and
influencing factors of products. In 2007, Li Chang
selected two foreign currency range products issued
by different banks, applied the GARCH model and
Monte Carlo simulation, and studied the pricing
methods, income characteristics, and the sources of
price differences of the two products based on
Chen, W.
Research on Pricing of Automatic Redemption Structured Deposit Products Based on Monte Carlo Simulation.
DOI: 10.5220/0012815500004547
Paper published under CC license (CC BY-NC-ND 4.0)
In Proceedings of the 1st International Conference on Data Science and Engineering (ICDSE 2024), pages 17-21
ISBN: 978-989-758-690-3
Proceedings Copyright © 2024 by SCITEPRESS – Science and Technology Publications, Lda.
17

modern option pricing theory (Zhang 2022). In 2011,
Liu Fengqin decomposed the value of structured
foreign exchange deposits based on the combination
decomposition principle of financial engineering and
believed that the value of the ordinary
interest-bearing part could be calculated by the
Monte Carlo simulation method, while the part that
could be redeemed in advance should be priced by
the improved least squares Monte Carlo simulation
method (Zhang 2023). In 2012, Ma Ying took a
structured product of Everbright Bank as an
example, conducted a pricing analysis with the
Monte Carlo simulation method, found that it was
issued at a premium, and concluded that the reason
for this was caused by the procedure fees charged by
the bank and the compensation charged to cover its
risks (Wang 2023). In 2018, Chen Tingting et al.
studied the pricing of exchange-linked structured
deposits, used the principle of no arbitrage to
construct a partial differential equation suitable for
product value, and gave the pricing formula in the
paper (Sang 2022). In 2020, Feng Ling et al.
calculated the theoretical value of equity-linked
products based on quantum field theory, and the
results showed that the forward interest rate
calculated by the quantum field theory model was
closer to the Chinese financial market with better
goodness-of-fit (Zhang 2022).
Due to the release of new regulations on capital
management, capital protection financial products
have gradually withdrawn from the market, while
structured deposits can fill the gap in the market and
meet the needs of investors. However, the
development time of structural deposits in China is
relatively short, and investors do not have a good
understanding of structural deposits, and the income
of structural deposits, which leads to blind
investment.
This paper will study the pricing of a class of
self-redemption structured deposits in a variety of
market environments to give investors a more
comprehensive perspective. The purpose of this
paper is to provide some help for investors’ deposit
selection.
2 GUANGFA BANK
ZZGYCAO1613 STRUCTURAL
DEPOSIT DETAILS
2.1 Product Introduction
The product has two exercise prices,
1
K
and 𝐾

;
There are three expected annualized returns, namely
1
r , 𝑟

and
3
r (𝑟

> 𝑟

> 𝑟

); There are i
observation days and the fixing price of the
underlying object on observation day (i) is denoted
as
1 n
ii− ; The product principal is C . Structured
deposit income is
R
. The actual term of structured
deposits is
t . There are two revenue scenarios for
the product:
1. The structured deposit will automatically
terminate and stop observation, and the structured
deposit will in principle return the principal and the
corresponding structured deposit income to the
investor on the first early termination maturity date.
The calculation is as follows:
1
R=C r t/365×× (1)
2. The structured deposit matures naturally, and
in principle returns the principal and the
corresponding structured deposit income to the
investor on the maturity date of the structured
deposit. The calculation is as follows:
12 2
,R=C r t/365
n
iK
+
≥×× (2)
12 3
,R=C r t/365
n
iK
+
<×× (3)
2.2 Case Product Introduction
The selected case product is the bullish automatic
redemption 276 days structured deposit
ZZGYCAAO1613 product of Guangfa Bank. As
shown in Table 1, the basic information of bullish
automatic redemption 276 days structured deposit
ZZGYCAAO1613 product of Guangfa Bank.
Table 1: Basic Product Information.
product name
“Guangyin Wealth creation” section D The 362 RMB structural deposit in 2023
hook mar
k
China Securities 500 Index
subscription
￥10,000.00, the amount above the subscription starting point should be an
integral multiple of ￥1,000.00
earnings
It is linked to the price level of the CIS 500
expected annualized rate of return
0.5% or 2.7% or 3.9%
issuance size
The lower limit is ￥10，000，000.00
The upper limit is ￥100，000，000.00
ICDSE 2024 - International Conference on Data Science and Engineering
18

subscri
p
tion Perio
d
2023.11.20-2023.11.26
launch da
y
2023.11.28
due day 2024.08.30
de
p
osit term 276 da
y
s
structured de
p
osit tradin
g
da
y
186 da
y
s
exercise
p
rices 1 O
p
enin
g
p
rice*100.01%
exercise prices 2 Opening price*97.0%
early termination triggers the condition
The fixing price of the underlying object on the observation date (i) (
8i ≤ )
is higher than or equal to the exercise prices 1
earnings are calculated on a basis A/365
Data source: Guangfa Bank official website collation
As shown in Table 2, Guangfa Bank’s call automatic
redemption 276 days structured deposit
ZZGYCAAO1613 product observation date and
structured deposit trading day.
Table 2: Product Observation Date and Structured Deposit
Trading Day.
i observation date trading day
1 2024.01.03 26
2 2024.01.30 45
3 2024.02.20 55
4 2024.03.19 75
5 2024.04.23 99
6 2024.05.21 116
7 2024.06.25 138
8 2024.07.29 162
As shown in Figure 1, the income information of
the 276-day structured deposit ZZGYCAAO1613 of
Guangfa Bank.
Figure 1: Product Revenue Information (Original).
The yield of this product is linked to the price of
China Securities 500.
On the i (i = 1,2,3,4,5,6,7,8) observation day, if
an early termination trigger event occurs, the
structured deposit will automatically terminate and
stop observation, in principle, the structured deposit
will return the principal and corresponding
structured deposit income to the investor on the i (l)
early termination maturity date. Investors’ return on
structured deposits is calculated as follows:
Expected annualized returns = 3.9000%.
Revenue = principal × 3.9000% × the actual term
of structured deposits / 365.
If no early termination trigger event occurs for
the structured deposit, the structured deposit matures
naturally, and in principle, the principal and the
corresponding structured deposit income will be
returned to the investor on the maturity date of the
structured deposit. The calculation is as follows:
If on the product observation date (i = 9), the
underlying closing price is greater than or equal to
the exercise prices 2, expected annualized returns =
2.7000%.
If on the product observation date (i = 9), the
underlying closing price is less than or equal to the
exercise prices 2, expected annualized returns =
0.5000%.
Revenue = principal × 3.9000% × the actual term
of structured deposits / 365.
3 MONTE CARLO SIMULATION
This paper will simulate nine different market
environments in Monte Carlo. The parameters are:
μ is the expected annual return on the underlying
asset,
123
2%, 0%, 2% μμμ =− = = ;
σ
is the annual volatility of the underlying asset,
12 3
1%, 5%, 10% σσ σ === .
01 2 123
100, 110 /100, 90 /100, 4%, 3%, 0.5%SK K rrr== = ===
.
A total of 250 days were simulated, with
observation days 26, 46, 66, 86, 106, 126, 146, 166
and 186.
The main idea of Monte Carlo simulation is to
classify the price movement of the underlying asset
into different computation values (
12
, ...
T
SS S ). At
time within the term, the underlying asset price at
each time node is predicted by the following price
formula (Li 2022):
Research on Pricing of Automatic Redemption Structured Deposit Products Based on Monte Carlo Simulation
19

2
exp[( )
2
tt t t
SS t t
σ
μσε
+Δ
=−Δ+Δ
(4)
Using the Monte Carlo simulation method to
simulate the underlying asset price steps are as
follows:
1. Generate random numbers through Python
software, and calculate the closing price of the
second trading day according to the formula (4), and
obtain the closing price of the second day. Based on
this, the closing price of each trading day within the
term of the product is obtained.
2. Repeat Step 1 for 10,000 times. According to
the return determination method in the above part,
the probability, annual expected return rate, and the
annual volatility of the three scenarios are
determined.
4 RESULT
4.1 Monte Carlo Simulation Result
Based on the methodology described above, the
results obtained are shown in Table 3.
When
μ remains the same and
σ
continues
to rise, the expected annual rate of return will decline,
but when
3
μμ =
, the expected annual rate of return
will first rise and the decline. The annual volatility
decreases gradually, but when 𝜇𝜇

, the annual
volatility increases gradually.
When
σ
remains the same and μ continues
to rise, the expected annual rate of return will first
rise and then decline. the annual volatility also goes
up and then down.
In these nine market environments, the annual
expected annual rate of return is highest when 𝜇
𝜇

 0%, 𝜎𝜎

 1%.
4.2 Sensitivity Analysis
By changing the values of
1
K
and
2
K
, the annual
expected rate of return and annual volatility are
observed, and the sensitivity analysis is carried out.
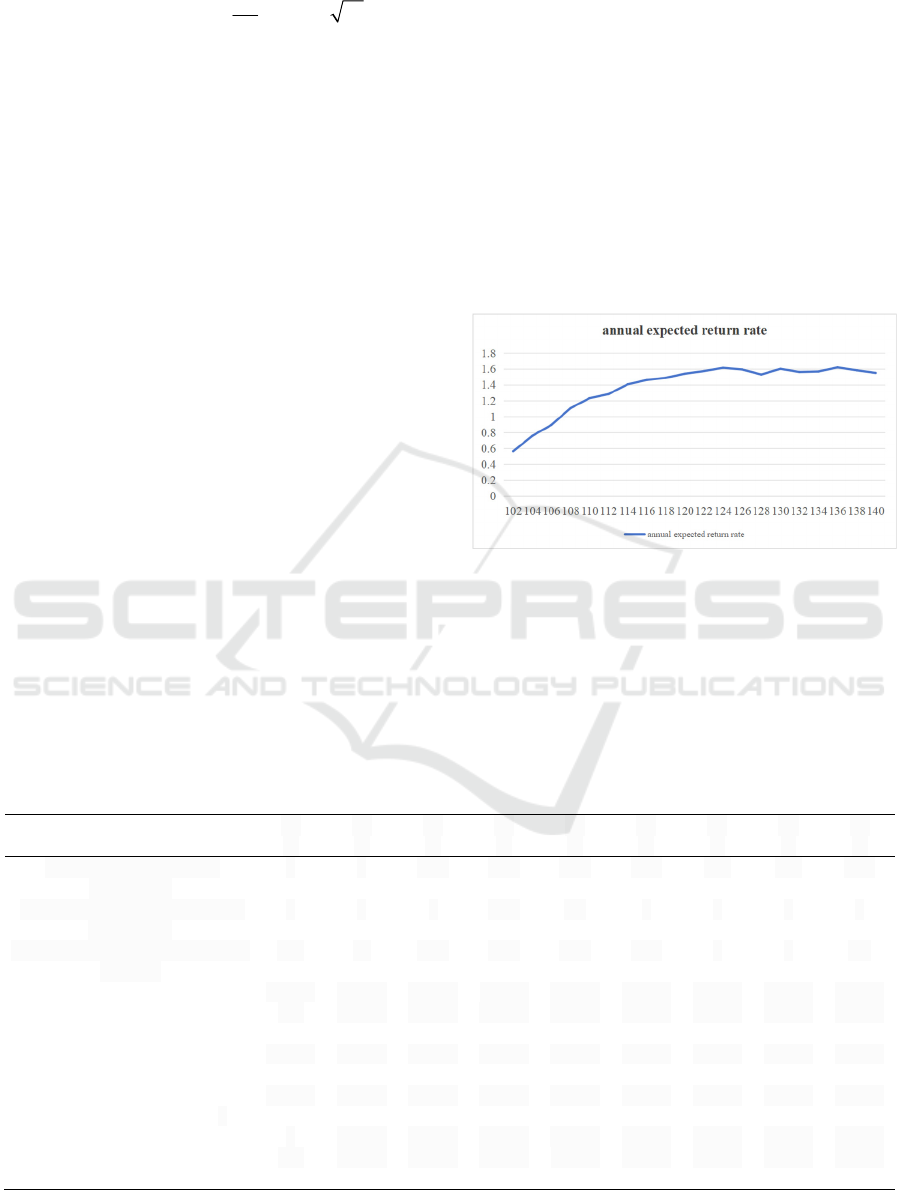
As shown in Figure 2, the annual expected return
rate of
1
K
.
Figure 2: The annual expected return rate of 𝐾

(Original).
As shown in figure 3, the annual volatility of 𝐾

.
Table 3: Simulation Result.
μ
1
,
σ
1
μ
1
,
σ
2
μ
1
,
σ
3
μ
2
,
σ
1
μ
2
,
σ
2
μ
2
,
σ
3
μ
3
,
σ
1
μ
3
,
σ
2
μ
3
,
σ
3
The probability of early
termination
0 7 28.4 49.6 77.5 75.1 100 100 99.9
The probability of a high yield
on maturit
y
0 0 0 22.9 0.7 0 0 0 0
The probability of a low yield on
maturit
y
100 93 71.6 27.5 21.8 24.9 0 0 0.1
Expected annual rate of return
0.3425 0.3262 0.2828 1.2311 0.4389 0.3175 0.0792 0.1098 0.1852
Expected annual rate of return
u
p
on earl
y
termination
nan 0.1096 0.1324 1.3436 0.4514 0.3092 0.0792 0.1098 0.1852
Expected annual rate of return
for hi
g
h
y
ield at maturit
y
2.0548 2.0548 2.0548 2.0548 2.0548 2.0548 2.0548 2.0548 2.0548
Expected annual rate of return
for low
y
ield at maturit
y
0.3425 0.3425 0.3425 0.3425 0.3425 0.3425 0.3425 0.3425 0.3425
Annual volatilit
y
0 0.0639 0.1276 0.8568 0.5397 0.4405 0.0272 0.0831 0.2327
Annual volatility upon early
termination
nan 0.0888 0.1604 0.8464 0.5911 0.5081 0.0272 0.0831 0.2327
ICDSE 2024 - International Conference on Data Science and Engineering
20

Figure 3: The annual expected return rate of 𝐾

(Original).
As shown in figure 4, the annual expected return rate
of
2
K
.
Figure 4: The annual expected return rate of 𝐾

(Original).
As shown in figure 5, the annual volatility of 𝐾

.
Figure 5: The annual volatility of 𝐾

(Original).
The results show that the annual expected rate of
return is positively correlated with 𝐾

and
negatively correlated with 𝐾

. and it have no
significant impact on the annual volatility, indicating
that 𝐾

and 𝐾

have no linear relationship with the
annual volatility.
The sensitivity analysis of this paper is mainly to
study how the annual expected rate of return and the
annual volatility of structured deposit products are
affected by single factor fluctuations. After a single
factor sensitivity analysis, investors should pay
special attention to certain factors when buying
structured deposit products. In the above analysis of
the return of structured deposit products, it can be
seen that the exercise price 1 and exercise price 2 of
the product are relatively analysis of this paper takes
these two factors as research objects.
5 CONCLUSION
This paper selects nine different market
environments, uses Monte Carlo method to simulate
the structured deposit products in different market
environments, and obtains its the annual rate of
return and the annual volatility. The sensitivity
analysis of exercise price 1 and exercise price 2
shows that exercise prices 1 is positively correlated
to the annual expected rate of return, and exercise
price 2 is negatively correlated to the annual
expected rate of return, and the two are unrelated to
the annual volatility. Therefore, both investors and
banks need to pay more attention to the impact of the
exercise price on the annual expected return. This
paper first makes a brief introduction to the income
methods of structured deposit products, so the
investors can better understand structured deposit
products. Secondly, results are obtained under
different market conditions, and sensitivity analysis
is carried out so that banks can refer to them when
designing products. Finally, this study is only a
single linked object, which can analyzed in different
investment portfolios in the future, to obtain greater
benefits.
REFERENCES
Y. D. Zhang, Suzhou University of Science and
Technology, pp. 1 (2022).
H. Qin, Shihezi University, pp. 1 (2023).
Q. Y. Li, South China University of Technology, pp. 1
(2023).
Y. S. Zhao, Beijing Jiaotong University, pp. 12 (2022).
B. B. Zhang, Anhui University, pp. 5 (2022).
J. W. Zhang, Southwest University, pp. 9 (2023).
Z. L. Wang, Anhui University of Finance and Economics,
pp. 4 (2023).
Y. Sang, South-Central Minzu University, pp.6 (2022).
Q. Zhang, Zhongnan University of Economics and Law,
pp. 4 (2022).
Z. J. Li, Shihezi University, pp. 32 (2022).
Research on Pricing of Automatic Redemption Structured Deposit Products Based on Monte Carlo Simulation
21