Integration of CAPM and ANN in the Application of Stock

Forecasting

Wenzhen Fan

and Jiayan Wang

2,a

CUHK Business School, The Chinese University of Hong Kong, Sha Tin, New Territories, Hong Kong, China

School of Computer Science and Engineering, Faculty of Innovation Technology,

Macau University of Science and Technology, Avenida Wai Long, Taipa, Macau SAR, China

Keywords: CAPM (Capital Asset Pricing Model), ANN (Artificial Neural Networks), Stock Market Forecasting,

Integration Challenges, Market Dynamics.

Abstract. The goal of this review is to integrate the two models of capital asset pricing model (CAPM) and artificial

neural network (ANN) to predict stocks. First, the article introduces the basic theories of CAPM and ANN,

their traditional roles in stock market analysis, and their respective advantages. This article emphasizes that

although both CAPM and ANN have their advantages in stock prediction, their integration can bring

comprehensive insights. The paper used CAPM's in-depth analysis capabilities in risk assessment and ANN's

ability to process large-scale complex data and found that the accuracy and efficiency of stock market

predictions can be significantly improved. However, this integrated approach also comes with new challenges

and difficulties. It includes not only how to find the complexity of the model, but also how to meet the

requirements for data quality, and how to find a way to integrate the two models to predict stocks effectively.

This article further discusses future research directions, which can optimize the structure of the integrated

model and improve its adaptability to market dynamics, including how to use this integrated model to promote

more effective investment decisions in the rapidly developing financial technology field.

1 INTRODUCTION

Stock market prediction is very important. Because

the stock market, as the core of capital flows, not only

provides a key area for financial activity but also an

important indicator of economic health. For retail

investors, financial institutions, and policymakers, it

is important to accurately predict stock price trends,

impact, and contribute to investment decisions.

However, the complexity of the stock market is

influenced by a variety of factors. Macroeconomic

conditions, company performance, political events,

and market sentiment all cause price fluctuations,

making stock prices often difficult to predict. Stock

market prediction will become a major challenge in

the field of financial research.

Traditional stock market prediction methods such

as moving averages and linear regression, although

they have certain effectiveness in historical data and

statistical analysis, have limited effectiveness in

dealing with complex and non-linear market

behavior. They always not fully consider the market

sentiment, emergency, or even the macroeconomic

fluctuations and so on. These key factors play a

crucial role in predicting the stocks. In addition, these

methods depend too much on historical data and the

past trends in many stocks around the world, so they

cannot capture the future changes in the markets,

especially during situations of market conditions and

economic environments change rapidly.

As technology is growing by leaps and bounds,

especially in the fields of big data and machine

learning, the tools and methods to predict stocks also

develop fast. First of all, the Capital Asset Pricing

Model (CAPM) is a classic financial theoretical

model, which plays an important role in quantifying

investment risks and evaluating expected returns

(Sharpe 1964, Lintner 1965, Mossin 1966). Despite

some limitations in these fields, their simplicity and

universality are indispensable for market risks and

asset pricing (Muhammad Ahmed Saleem 2016).

However, when considering the complexity of the

markets and their dynamic changes, it is unlikely to

only use CAPM to predict the price of stocks (Yang

et al. 2021). In this situation, artificial neural

networks and other cutting-edge technologies are

Fan, W. and Wang, J.

Integration of CAPM and ANN in the Application of Stock Forecasting.

DOI: 10.5220/0012818000004547

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 1st International Conference on Data Science and Engineering (ICDSE 2024), pages 32-39

ISBN: 978-989-758-690-3

more used to predict and show their strong power in

processing complex data and pattern recognition.

Thus using artificial neural networks in the field of

financial analysis and forecasting shows big potential

(Wang 2017).

However, although ANN shows advantages in

these fields, some obvious limitation also exists. For

example, they need a high dependence on large

amounts of high-quality data, the opacity of the

decision-making process, the risk of overfitting, or

even the sensitivity of parameter adjustment (Yang et

al. 2021, Nabipour et al. 2020, Luyang et al. 2019,

Ndikum 2020, Agrawal et al. 2016). At the same time,

CAPM still has a key role in the stock price analysis

and also provides the framework for assessing market

risks and expecting returns. Thus integrating the

CAPM and ANN, not only shows the theoretical

depth of CAPM and data analysis capabilities in ANN

but also offers new possibilities for stock market

analysis and forecasting to achieve a qualitative leap

in accuracy and efficiency (Yang et al. 2021, Ayub et

al. 2020, Chen et al. 2022, Jan et al. 2022, Wang &

Chen 2023).

By integrating CAPM and ANN, researchers not

only overcome the limitations of traditional methods

but also benefit from ANN in handling complex and

nonlinear data when preserving the theoretical depth

and risk assessment of the CAPM market (Loo 2020,

Gunasekaran et al. 2013). This interdisciplinary

approach offers a new perspective on stock market

forecasting and promises significant improvements in

precision and efficiency.

2 RELATED WORK

2.1 Classic Models

2.1.1 CAPM Model

Emerged in the 1960s, the CAPM (Capital Asset

Pricing Model) was independently proposed by

William Sharpe, John Lintner, and Jan Mossin

(Sharpe 1964, Lintner 1965, Mossin 1966). As an

imperative extension of modern portfolio theory,

especially the portfolio selection theory according to

Harry Markowitz, the core idea of CAPM is that the

expected return of an asset can be evaluated by

calculating its correlation with the overall market

(Markowitz 1952).

𝐸(𝑅𝑡) = 𝑅𝑓, 𝑡 + (𝐸(𝑅𝑚, 𝑡) − 𝑅𝑓, 𝑡) × 𝛽𝑖 (1)

This is the traditional CAPM model formula. E

(Rt) here is the expected return on assets at time t, Rf,

t is the risk-free interest rate time t, E (Rm, t) is the

market expected return time t, beta is the beta value

of assets, we used to measure the relative to the

sensitivity of market movement.

Using the risk-free interest rate, the CAPM model

calculates the expected return of an asset, which is

generally represented by the output on short-term

government bonds. The correlation coefficient

between the asset and the market portfolio, like the

beta coefficient and the expected return of the market

portfolio. This beta reflects the risk of individual

assets relative to the market. In CAPM, the risk

coefficient (beta, β) of the asset can be obtained by

calculating the covariance between the asset return

rate and the market return rate, and then dividing by

the variance of the market return rate: 𝛽



(



,



)







The cov(Ri, Rm) is the covariance of the return

rate (Ri) of the asset ( i ) and the return rate ( Rm ) of

the market, which represents the difference between

these two variables Common Volatility. The 𝜎





the variance of market returns, it indicates the

volatility of market returns.

The CAPM assumes that investors are not willing

to take the risks, but the investors also understand that

higher risks can lead to higher returns. Therefore, the

model plays a crucial role in evaluating investment

options for investors, especially in deciding whether

stocks are worth investing in.

Time flies, the CAPM has been expanded several

times to adapt to the complexity of financial markets.

Robert C. Merton made an important extension of the

CAPM by introducing continuous-time models

(Merton 1973). Its continuous-time CAPM model

focuses on the stochastic development of asset prices

and is suitable for analyzing financial assets whose

prices fluctuate frequently.

The Fama-French three-factor model is another

important extension of the traditional CAPM. This

model was proposed in the 1990s by Eugene Fama

and Kenneth French to enhance its capability to

explain differences in asset returns by introducing

two additional risk factors (Fama & French 1993).

These two factors are the size of the company (size)

and the book-to-market ratio (book-to-market ratio).

CAPM as a theoretical framework, not only plays

an important role in academic research but also holds

a key position in the actual functioning of financial

markets to help investors better understand market

dynamics and value assets.

2.1.2 ANN Model

The origin of ANN dates back to the 1940s, initially

inspired by research on the human brain and nervous

Integration of CAPM and ANN in the Application of Stock Forecasting

system (McCulloch & Pitts 1990). As a

computational model that imitates the information

processing function of the human brain, ANN has

showcased extraordinary capabilities in pattern

recognition and nonlinear data processing. ANN

incorporates an input layer, several hidden layers, and

an output layer, and each layer encompasses multiple

neurons, which interact with each other through

weighted connections.

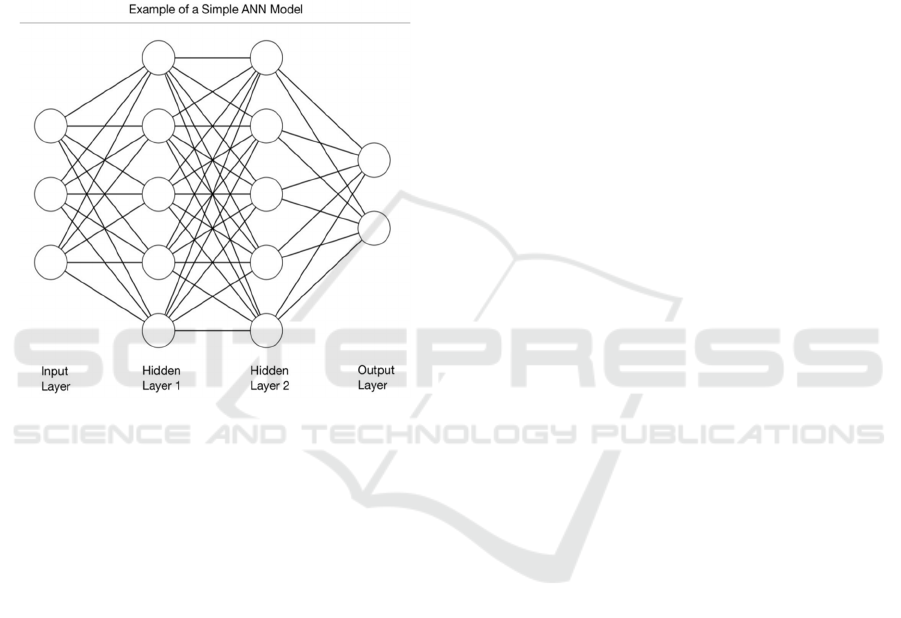
The simple structure of the ANN model is as

Figure 1.

Figure 1: The simple structure of the ANN model (Picture

credit: Original).

2.2 Input Layer

The input layer consists of three neurons, labeled I1,

I2, and I3. This layer is responsible for receiving

external input signals. In a variety of application

scenarios, these signals can be in the form of image

pixels, sensor data, or other digital inputs. Each

neuron represents an independent input feature, for

this model, can be regarded as a 3 d vector data

processing.

Hidden Layer 1 consists of five neurons, labeled

H1 to H5. It serves as the primary processing layer

between the input layer and the output layer, and the

neurons in this layer perform weighted and nonlinear

transformations of the input data. Hidden layers in the

multi-layer network play a key role and can be

extracted and processed in the complicated features

of the input data.

Hidden Layer 2 also consists of five neurons,

labeled H1 to H5. This layer further processes

information from the first hidden layer, increasing the

depth of the network in terms of data processing and

helping to capture more complex features and

patterns.

Output Layer consists of two neurons, labeled O1

and O2. As the final layer of the network, the output

layer converts the information processed by the

hidden layer into the final output, which can be

classified as results, predicted values, or other forms

according to the different application scenarios.

In this simple ANN model, the data processing

process demonstrates the basic mechanism of ANN.

First, the data starts in the input layer, which consists

of three neurons, each neuron corresponding to a

characteristic dimension of the input data. For

example, when people process financial market data,

these neurons can represent various market indicators

such as stock prices, trading volumes, or technical

indicators.

Then the data flows to hidden layers that are

responsible for discovering sophisticated patterns and

relationships in the input data. In the model, there are

two hidden layers and 5 neurons each. These neurons

weigh the input from the previous layer, where the

weight represents the importance of the input features

relative to the output. The output of each neuron is a

weighted sum of its inputs, which is then transformed

by an activation function. The alteration of activation

functions is critical to the network's capabilities

because they introduce nonlinearity and allow the

network to learn complex data relationships.

Common activation functions include the Rectified

Linear Unit (ReLU) or the sigmoid function.

After that, the data is transferred to the output

layer. In the model, the output layer consists of two

neurons, which represent the final output of the

network. In different application scenarios, these

results may represent different things. For example,

in a classification task, they can represent different

class probabilities; In a regression task, they can

represent the prediction of a continuous value.

This data flow from the input layer to the hidden

layer to the output layer allows the network to adapt

and recognize complex patterns in the data by

learning the optimal weights between different layers.

For this reason, ANN has demonstrated strong

capabilities in various machine learning tasks such as

image and speech recognition, natural language

processing, financial market analysis, etc. In addition,

its flexibility makes this architecture suitable for

many different data types and tasks, from simple

binary classification to complex time series

prediction.

Over time, many classic articles have gradually

advanced the development of the field of modern

artificial neural networks and introduced key

ICDSE 2024 - International Conference on Data Science and Engineering

concepts and technological advances. Rosenblatt's

work on the perceptron laid the foundation for further

theoretical and practical development (Rosenblatt,

1958). The error backpropagation algorithm by David

E. Rumelhar is a multi-layer feed-forward neural

network—effective impact training (Rumelhart et al.

1986). Sepp Hochreiter and Jürgen Schmidhuber's

LSTM paper proposed a special type of recurrent

neural network that had a profound impact on natural

language processing and sequence analysis

(Hochreiter 1997). Research by Yann LeCun et al.

applied convolutional neural networks (CNNs) to

document recognition and image processing, making

CNNs widely used in the fields of computer vision

and image recognition (Lecun et al. 1998). And Alex

Net’s success in the ImageNet competition. Excellent

performance marks a breakthrough in deep learning

in the field of computer vision (Krizhevsky et al.

2012).

These groundbreaking articles illustrate the

evolution of the original simple perceptron to

complex deep learning architectures. Each article has

played a crucial role in the understanding and

development of modern neural network models.

3 INTEGRATION METHOD OF

CAPM AND ANN

3.1 CAPM Review Methodology

3.1.1 Estimation Method and Empirical

Research

In the field of modern financial analysis, when

combining estimation methods and empirical

research play an important role in stock forecasting.

As shown in the research of Man Fang, the expected

return rate and systemic risk of stocks are estimated

by combining multiple models such as E-V, E-S, and

GLS, especially in specific markets such as the

Shanghai A-share market and the Tehran Stock

Exchange. Its value has been shown in empirical

research (Wang 2017). The main advantage of this

approach is its ability to provide an in-depth

understanding of the effectiveness of CAPM in a

specific market or scenario and to take into account

market-specific factors and conditions. However, this

method also has certain limitations, mainly

manifested in its over-reliance on historical data and

market-specific scenarios, which may result in

limited generalization capabilities in different

markets or different periods. Furthermore, combining

multiple models may increase model complexity and

computational difficulty.

3.1.2 Standard Formula and Market

Complexity Analysis

Researchers such as Yajuan Yang, and R

Jagannathan, when they used the standard formula of

CAPM to calculate expected returns, emphasized the

importance of considering market complexity in

practical applications (Yang et al. 2021, Jagannathan,

& Wang 1996). The advantage of this approach is that

it provides a concise and generally accepted way to

estimate a stock's expected return. However, it may

not fully take into account the complexity and

dynamics of the market, especially during periods of

high volatility or atypical market events. For

example, the conditional CAPM model proposed by

R Jagannathan, although it considers the time changes

in β coefficient and market risk premium and

additional factors (such as human capital return rate),

there may be challenges in accurately capturing rapid

changes in market conditions.

3.1.3 Market Portfolio and Beta Analysis

Market portfolio and beta analysis are other important

method for stock prediction. Researchers such as P

Ndikun, Smita Agrawal, L Chen, and others use

market portfolios (such as the US S&P 500 Index)

and risk-free rates of return to estimate the beta value

of assets and calculate the CAPM of stocks Beta and

volatility to predict stock prices (Luyang et al. 2019,

Ndikum 2020, Agrawal et al. 2016). The advantage

of this approach is its ease of implementation,

especially in standardized large markets such as the

S&P 500. The beta analysis provides an intuitive

understanding of the correlation between individual

stocks and the market as a whole. However, this

approach may not adequately represent the dynamics

of the market in small or unconventional markets. In

addition, the calculation of Beta value relies on

historical data and may not accurately reflect future

market conditions when market conditions change

rapidly.

3.2 ANN Review Methodology

3.2.1 Stock Price Prediction Based on

Traditional and Efficient ANN

Architecture

Recent studies, especially those conducted by

Ndikun, have shown that the use of backpropagation

neural network (BPNN) based on opening price, high

Integration of CAPM and ANN in the Application of Stock Forecasting

price, low price, volume, and closing price and

efficient ANN architecture to process Publicly traded

U.S. stock data can effectively predict stock prices

(Ndikum 2020). These methods achieve predictions

by analyzing patterns and trends in historical data.

Advantages include being able to effectively learn

patterns in historical price data, adapting to different

types of stock and market data, and being relatively

easy to implement and apply to actual trading

systems. However, these methods also have some

limitations, such as the risk of overfitting, dependence

on high-quality historical data, and possible

insufficient response to market emergencies and new

information.

3.2.2 Application of Deep Learning

Technology in Stock Price Prediction

The application of deep learning techniques,

especially in research conducted by L Chen and

Prakash K. Aithal, demonstrated feedforward

networks, recurrent neural networks (RNN), long

short-term memory networks (LSTM), and

generative adversarial Networks (GAN) and other

technologies have the potential to handle non-linear

relationships and time series dynamics of stock price

data (Luyang et al. 2019, Gunasekaran & Ramaswami

2014). These deep learning models are capable of

processing more complex patterns and larger data

sets, are particularly suitable for processing time

series data of stock prices, and effectively capture the

non-linear relationships of stock price data. However,

these models also face several challenges, including

requiring significant computing resources and time to

train, model building and optimization requiring deep

expertise, and the model's decision-making process

potentially lacking transparency and explainability.

3.2.3 Application of Artificial Neural

Networks in Processing Raw Data and

Simulating Nonlinear Relationships

In terms of the application of ANN, especially

research conducted by Smita Agrawal and Yajuan

Yang has shown that ANN can directly process raw

data, thereby reducing the need for complex feature

extraction (Yang et al. 2021, Agrawal et al. 2016). At

the same time, a multi-layer feedforward neural

network is used to adapt to the nonlinearity and

complexity of the stock market. The merits of this

way include the ability to directly process raw stock

market data, identify and simulate complex nonlinear

relationships, and have a flexible network structure

that can adapt to different data characteristics.

However, this method also has some disadvantages,

such as the large amount of data required to train the

model, the complexity of network structure and

parameter selection, and the challenge of updating the

model in real-time in a rapidly changing market

environment.

3.3 CAPM and ANN Integration

Review Methodology

3.3.1 Beta Classification Prediction Method

Combining CAPM Theory and ANN

Usman Ayub and colleagues relying on the CAPM

theory, divided stocks into different Beta portfolios

based on systematic risk (Ayub et al. 2020). This

classification is based on the core assumption of

CAPM, which is that the expected return of a stock is

directly proportional to its market risk (Beta value).

Through this classification, researchers can focus on

analyzing stock portfolios with similar risk

characteristics, thereby providing more accurate risk

assessments and predictions.

Next, use ANN to process the stock data for these

different beta combinations. ANN plays a key role

here, especially in identifying and processing non-

linear features in stock market data. By training ANN

models, especially using the backpropagation

algorithm, researchers can fine-tune model

parameters to more accurately capture the complex

relationship between market risk and stock returns.

J Wang applied a similar approach, emphasizing

the ability of ANN in capturing the nonlinear

dynamics of stock market data (Wang & Chen 2023).

This method allows researchers to learn from

historical stock market data and predict future market

trends, especially for stocks that are affected by

market fluctuations and external economic factors.

The advantage of this method is that it combines

the systematic risk assessment of CAPM theory with

the efficient ability of ANN in data processing. It can

provide deep insights into the non-linear dynamics of

stock markets, thereby improving the accuracy and

reliability of forecasts. Especially in analyzing market

risks and predicting stock prices, this method is more

efficient and accurate than traditional financial

models.

3.3.2 Integrated Analysis Method of

Advanced Neural Network and CAPM

YC Chen applied the combination of BPNN and

CAPM to improve the accuracy of stock price

prediction (Chen et al. 2022). This method first uses

BPNN to analyze and predict the price and growth

ICDSE 2024 - International Conference on Data Science and Engineering

trends of stocks. In this process, BPNN exerts its

advantages in identifying complex patterns in market

data and processing large amounts of data. These

prediction results are then used as input to the CAPM

model to integrate the prediction capabilities of

BPNN and the theoretical basis of CAPM in stock

pricing and market risk assessment. This integrated

approach is particularly suitable for those situations

that require in-depth market data analysis and highly

accurate stock price predictions.

WK Loo adopted a similar approach, combining

ANN technology and CAPM to predict the yield of

Hong Kong Real Estate Investment Trusts (HK-

REITs) ((Loo 2020). The ANN technology here is not

limited to BPNN but covers a wider range of neural

network applications to identify and process complex

patterns in market data. This approach leverages the

capabilities of ANN in data processing and pattern

recognition while incorporating the theoretical

framework of CAPM in assessing market risk and

stock pricing. Through this integration, the study can

provide a deeper understanding of HK-REIT market

dynamics and improve forecast accuracy.

The main advantage of this method is that it

combines the data processing capabilities of neural

networks and the theoretical framework of CAPM to

provide a more comprehensive and accurate stock

price prediction method. It is particularly suitable for

complex and dynamic market environments, capable

of processing and analyzing large amounts of data,

and providing predictions based on in-depth analysis.

3.3.3 Dynamic Market Forecasting Method

of Three-Layer ANN and CAPM

Jan's methods use the structure of a three-layer neural

network, including the input layer, hidden layer, and

output layer, to analyze and predict dynamic changes

in the stock market (Jan et al. 2022, Gunasekaran &

Ramaswami 2014). This structure takes advantage of

the advanced data processing capabilities of ANN and

is particularly suitable for capturing complex patterns

and non-linear relationships in market data.

The input layer is responsible for receiving market

data, such as stock prices, trading volumes,

macroeconomic indicators, etc. Hidden Layers

analyzes this data in-depth and learns the relationship

between market dynamics and potential influencing

factors. The output layer ultimately generates

predictions that provide insights into the future

direction of the stock.

Combined with the CAPM model, this method

can not only analyze historical data but also predict

the future performance of stocks, especially in

assessing market risks and expected returns. In

addition, through the rolling window method, the

model can adapt to new market information to ensure

the timeliness and accuracy of predictions. To

evaluate the performance of the model, statistical

tools such as mean square error and the Diebold-

Mariano test were used. These tools help quantify

forecast errors and ensure that models reliably reflect

the true dynamics of the market.

The advantage of this method is that it can

comprehensively process large amounts of market

data and predict stock prices by learning hidden

patterns in the data. It can adapt to rapid changes in

the market, provide timely and accurate stock price

predictions, and is especially suitable for dynamic

and changing market environments.

3.3.4 CAPM Integrated Strategy Method of

Fuzzy Logic and ANN Optimization

M Gunasekaran and R Barua integrated the

technologies of Adaptive Neuro-Fuzzy Inference

System (ANFIS) and Elman Recurrent Neural

Network (ERNN) respectively and combined them

with the CAPM (Gunasekaran et al. 2013, Markowitz

1952). This integrated strategy optimizes the

application of the CAPM model so that it can more

accurately reflect stock values in complex and

dynamic market environments. The ANFIS method

combines the learning ability of neural networks and

the processing ability of fuzzy logic to optimize the

parameters in the fuzzy logic system. This process

covers the various steps starting from fuzzifying the

input data, establishing fuzzy rules, and then using the

rules for reasoning. Next, these rule parameters are

trained and adjusted through the neural network and

finally defuzed to obtain the final prediction output.

The application of ERNN emphasizes the efficient

processing of time series data, especially when

dealing with dynamic changes in the stock market.

ERNN can capture the time correlation in stock price

movements, providing the model with deeper market

insights.

Combining these two methods, this strategic

approach not only enhances the predictive power of

the CAPM model under static market conditions but

also enables it to adapt and reflect more complex and

changing market environments. This approach

provides greater accuracy and reliability in predicting

stock market risk and returns and is particularly good

at predicting stocks that are affected by multiple

market factors.

The main advantage is that it combines the

advantages of fuzzy logic and neural networks to

Integration of CAPM and ANN in the Application of Stock Forecasting

improve the adaptability and accuracy of the

prediction model under complex market conditions.

By combining time series analysis capabilities,

dynamic changes in the stock market can be better

understood and predicted.

4 CHALLENGES AND

LIMITATIONS

This approach holds significant advantages when

integrating the CAPM and the ANN for stock market

forecasting. First of all, by combining CAPM's

market risk analysis with ANN's advanced data

processing capabilities, this integrated approach is

capable of providing detailed insights into market

dynamics, including the capture and analysis of

market characteristics—non-linear market data. Also,

the flexibility and learning ability of ANN makes this

method excellent for dealing with complex market

situations and large amounts of data, especially when

market conditions change quickly.

Nevertheless, this integrated method does face

certain challenges. Highly dependent on the quality

of the input data, any inaccuracies or even

incompleteness of the data can affect the accuracy of

the forecast outcome. The ANN may be at risk of

overfitting historical data, which may result in a

reduced ability of the model to generalize to new data.

On top of that, the process of integrating CAPM and

ANN can be excessively complex and time-

consuming, especially when data is large.

Due to the “black box” nature of the ANN, this

integrated model lacks transparency and

interpretability, which causes uncertainty in the

investment decision-making process. ANN

performance depends heavily on the selection and

adjustment of network parameters, thus they require

a lot of experimentation and expertise. Furthermore,

the effective implementation and application of this

integrated approach requires extensive technical

knowledge and expertise. Although the integrated

approach improves forecasting capabilities,

uncertainties remain in forecasting under extreme

market conditions or emergencies.

Although the integrated approach of CAPM and

ANN to stock market forecasting presents some

challenges, it is an overall valuable tool due to its

significant advantages in terms of providing detailed

market analysis and processing complex data. When

using these methods in practice, these issues must be

fully considered and handled carefully to ensure the

accuracy and reliability of the forecasts.

5 CONCLUSION

Challenges exist such as data quality dependencies,

model overfitting, and computational resource

requirements. However, its significant advantages in

providing in-depth market analysis and processing

complex data make it a valuable tool for predicting

stocks. In the future, people more willing to see

further integration and innovation of CAPM and

ANN, especially in improving model adaptability,

incorporating more data types and sources, applying

deep learning and other advanced machine learning

techniques, enhancing model interpretability and

transparency, and more Adapt well to developments

in irrational market behavior.

Challenges exist such as data quality

dependencies, model overfitting, and computational

resource requirements. However, its significant

advantages in providing in-depth market analysis and

processing complex data make it a valuable tool for

predicting stocks. In the future, people more willing

to see further integration and innovation of CAPM

and ANN, especially in improving model

adaptability, incorporating more data types and

sources, applying deep learning and other advanced

machine learning techniques, enhancing model

interpretability and transparency, and more Adapt

well to developments in irrational market behavior.

Deeper integration of ANN with other traditional

financial models such as the Fama-French model and

arbitrage pricing theory (APT) is also expected. For

example, utilize LSTM-RNN to analyze and predict

stock returns based on the Fama-French 5-factor

model, or combine APT and ANN to improve the

efficiency and accuracy of portfolio management.

These integrated approaches not only improve

understanding of market behavior but also show

potential in predicting market trends and stock

returns.

Future research will focus on how to better

integrate traditional financial theory with advanced

data analysis techniques to respond to the changing

and emerging challenges of global financial markets.

With the development of financial technology, this

approach will play a more important role in the field

of financial market analysis and prediction, especially

in providing people with more powerful and flexible

tools.

By way of conclusion, the integration of CAPM

and ANN represents an important development

ICDSE 2024 - International Conference on Data Science and Engineering

direction in the field of financial market analysis and

prediction. Future research and applications will

likely focus on how to better integrate traditional

financial theory with advanced data analysis

techniques, not only CAPM and ANN to respond to

the changing and emerging challenges of the global

financial market. This process will require close

collaboration between financial professionals, data

scientists, and technology experts to jointly drive

innovation and progress in the field of financial

analytics.

AUTHORS CONTRIBUTION

All the authors contributed equally and their names

were listed in alphabetical order.

REFERENCES

A. Krizhevsky, I. Sutskever, G. E. Hinton, ImageNet

classification with deep convolutional neural networks,

2012, available at https://proceedings.neurips.cc/

paper_files/paper/2012/file/c399862d3b9d6b76c8436e

924a68c45b-Paper.pdf

B. Muhammad Ahmed Saleem, The CAPM is Not Dead,

2016, available at https://digitalcommons.usu.edu/

gradreports/775

C. Luyang, P. Markus. Z. Jason, Available at SSRN,

(2019).

D. Rumelhart, G. Hinton, R. Williams, Nature 323, 533-

536, (1986).

E. F. Fama, K. R. French, Journal of Financial Economics,

33(1), 3-56, (1993).

F. Rosenblatt, Psychological Review, 65(6), 386-408,

1958.

H. Markowitz, The Journal of Finance, 7(1), 77-91, (1952).

J. Lintner, The Review of Economics and Statistics, 47(1),

13–37, (1965).

J. Mossin, Econometrica, 34(4), 768-783, (1966).

J. Wang, Z. Chen, Mathematics (Basel), 11(14), 3220,

(2023).

M. Gunasekaran, K. S. Ramaswami, Journal of Intelligent

& Fuzzy Systems, 26(1), 277-286, (2014).

M. Gunasekaran, K. S. Ramaswami, S. Karthik, CSI

Transactions on ICT, 1(4), 291-300, (2013).

M. N. Jan, M. Tahir, M. Shariq, M. Asif, Research Square

Platform LLC, (2022).

M. Nabipour, P. Nayyeri, H. Jabani, A. Mosavi, E.

Salwana, Entropy (Basel, Switzerland), 22(8), 840,

(2020).

P. Ndikum, ArXiv.Org, (2020).

R. C. Merton, Econometrica, 41(5), 867-887, (1973).

R. Jagannathan, Z. Wang, The Journal of Finance (New

York), 51(1), 3-53, (1996).

S. Agrawal, D. Goyal, P. Murarka, Ciência e Técnica

Vitivinícola, 31, 20, (2016).

S. Hochreiter, J. Schmidhuber, 9(8), 1735-1780, (1997).

U. Ayub, M. Naveed Jan, A. Afridi, I. A. Jadoon, Pakistan

Journal of Social Sciences, 40, 673-688, (2020).

W. F. Sharpe, The Journal of Finance, 19(3), 425-442,

(1964).

W. K. Loo, Journal of Property Investment & Finance,

38(4), 291-307, (2020).

W. S. McCulloch, W. Pitts, Bulletin of Mathematical

Biology, 52(1/2), 99-115, (1990).

Y. C. Chen, S. M. Kuo, Y. Liu, Z. Wu, F. Zhang,

International Journal of Financial Studies, 10(4), 99,

2022.

Y. j. Yang, B. Chen, L. L. Zhang, 2021 17th International

Conference on Computational Intelligence and Security

(CIS), Chengdu, China, 168-172, (2021).

Y. Lecun, L. Bottou, Y. Bengio, P. Haffner, Proceedings of

the IEEE, 86(11), 2278-2324, (1998).

Y. Wang, ArXiv. Org, (2017).

Y. Yang, B. Chen, L. L. Zhang, 2021 17th International

Conference on Computational Intelligence and Security

(CIS), 168-172, (2021).

Integration of CAPM and ANN in the Application of Stock Forecasting