Analysis and Control of Airport Runway Intrusion

Yutianyang Jia

Air Traffic Control, Civil Aviation University of China, Tianjin, China

Keywords: Runway Incursion, ARIMA Model, Least Squares Method, Safety, Prediction.

Abstract: In order to improve the accuracy of runway incursion predictions and identify the key factors influencing

such incidents, this study employed a comprehensive approach. Firstly, an ARIMA model was established

by analyzing runway incursion data from fiscal year 2019 to fiscal year 2023 in the United States. This time

range allowed for a robust analysis of trends and patterns in runway incursions. Secondly, the least squares

method was applied to conduct multiple regression analysis on the results and influencing factors of runway

incursions specifically at the top 15 airports in China's civil transport network during the year 2011.The

integration of these two methodologies resulted in the development of a reliable ARIMA prediction model,

which effectively captured the complexities of runway incursions. Notably, the research findings

highlighted those typical errors emerged as the primary contributing factor to these incidents. Such insights

provide valuable directions and suggestions for targeted strengthening and training programs aimed at

enhancing the competency of relevant practitioners within China's civil aviation safety departments. By

adopting preventive measures based on this study's recommendations, it is expected that runway incursion

accidents can be significantly reduced, ultimately bolstering the overall safety of China's civil aviation

sector.

1 INTRODUCTION

Runway incursion is a problem that cannot be

ignored in the field of aviation safety. In recent

years, with the growth of global air traffic, the

number of runway incursion incidents has been on

the rise, posing a serious threat to flight safety.

In China, the aviation industry is rapidly

developing, and runway incursion incidents occur

from time to time. Runway incursion is not a newly

emerged phenomenon, but it has become an

important issue that has drawn abundant attention in

recent decades. With the increase in air traffic

volume and the workload of controllers, coupled

with some human errors and equipment failures, the

possibility of runway incursion has increased.

Several severe runway incursion incidents that

have occurred internationally have not only caused

significant economic losses, but also posed a serious

threat to people's lives. According to Simple Flying,

the US FAA confirmed 19 severe runway incursion

incidents from January to October 2023, the highest

number since 2016.

On January 2, 2023, an Airbus A350 passenger

plane operated by Japan Airlines collided with a

plane of the Japan Coast Guard at Tokyo Haneda

Airport and caught fire, becoming the first ever total

loss accident of an Airbus A350 passenger plane.379

passengers on the passenger plane narrowly escaped,

14 people were injured, and 5 people on the plane of

the Japan Coast Guard died. According to the latest

released call records by the Ministry of Land,

Infrastructure, Transport and Tourism in Japan, the

plane of the Japan Coast Guard entered the runway

without permission, leading to a collision with the

just landed JL516 passenger plane. It can be

basically confirmed that this was an accident caused

by runway incursion.

According to the ICAO in 2007, runway

incursions occur when an aircraft, vehicle, or person

is present on the runway incorrectly, posing a

significant challenge to the safe operation of the

airport surface, including the runway and taxiway

system (Sabine et al. 2019). The Federal Aviation

Administration (FAA) declares in the 2015 National

Runway Safety Plan that the objective of runway

safety is to improve safety by decreasing both the

number and the severity of runway intrusions

(Mathew et al. 2017, Seraphin 2019).

Jia, Y.

Analysis and Control of Airport Runway Intrusion.

DOI: 10.5220/0012819700004547

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 1st International Conference on Data Science and Engineering (ICDSE 2024), pages 459-463

ISBN: 978-989-758-690-3

459

The importance of preventing runway incursions

is self-evident. For the aviation industry, every

runway incursion could potentially become a

disaster. Therefore, in-depth research on the causes,

development process, and effective prevention of

runway incursions has become an important topic in

the field of aviation safety.

2 ANALYSE DATA

2.1 Analyzing the Influencing Factors

of Runway Intrusion

Due to the relatively short time for runway incursion

safety construction in China and the data being

specific to airports, making it difficult to find from

official websites, the analysis was conducted using

runway incursion data published by the Federal

Aviation Administration (FAA) website for fiscal

years 2019-2023 (Cheng et al. 2019). The universal

nature of the data makes the analysis results valuable

in terms of runway incursion construction in China.

The data in Table 1 is obtained from the statistics of

runway incursions published on the official website

of the Federal Aviation Administration (FAA).

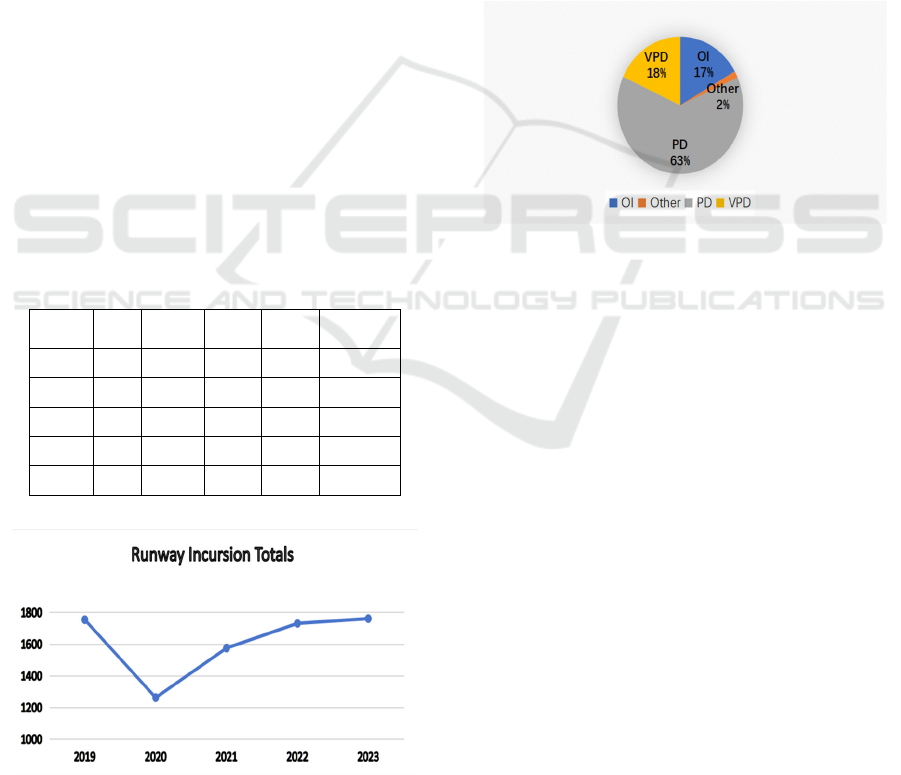
Table 1: Runway intrusion data for fiscal years 2019-2023

published on the official website of the Federal Aviation

Administration (FAA) of the United States

Years Ol Other PD VPD TOTAL

2019 324 16 1118 295 1753

2020 164 15 841 241 1261

2021 226 30 1033 285 1574

2022 309 26 1084 311 1730

2023 338 44 1070 380 1760

Figure 1: Line graph showing the number of runway

incursions in the United States from fiscal year 2019 to

fiscal year 2023 (Picture credit: Original).

From Figure 1, it can be observed that the

number of runway incursions decreased significantly

from 2019 to 2020 and gradually increased to the

level of 2019 from 2020 to fiscal year 2023. The

decline in runway incursions in fiscal year 2020 can

be attributed to the impact of the COVID-19

pandemic, which led to a 60.1% decline in air

passenger traffic and a significant decrease in flight

operations (Daniel et al. 2021). The aviation industry

in the United States was heavily affected by the

pandemic from fiscal year 2020 to fiscal year 2022,

resulting in significant lay-offs of controllers. With

the recovery of the aviation industry in 2023, there

was an increase in civil aviation passenger traffic,

leading to a significant increase in the workload of

controllers and an increase in runway incursion

accidents.

Figure 2: Pie chart depicting the types of runway incursion

incidents in the United States from fiscal year 2019 to

fiscal year 2023 (Picture credit: Original).

Based on Figure 1 and Figure 2, it can be

concluded that pilot deviation (PD) is the primary

cause of runway incursions in the United States from

fiscal year 2019 to fiscal year 2023, accounting for

63% of the total. The human factor is a crucial

element in ensuring the safety of air operations. The

European Union Safety Agency report (Harris and

Li, 2011) reveals that approximately a quarter of

large commercial air transport accidents and serious

incidents attribute to human factors (HF) or human

performance (HP) issues (Paulina & Skorupski

2022). Therefore, it is crucial to enhance prevention

and management measures related to pilot deviation.

Runway incursions often occur due to human errors,

particularly those made by pilots. By identifying

pilot risk factors in runway incursion accidents, it is

possible to significantly reduce the number of

fatalities and financial losses caused by airlines, as

well as the frequency of general airline runway

incursion accidents and incidents (Yu-Hern & Wong

2019).

ICDSE 2024 - International Conference on Data Science and Engineering

460

2.2 Establishment of ARIMA Model

The author selected data on the number of runway

incursions for the first to third quarters of the fiscal

years 2019 to 2023, as published by the FAA, to

conduct time series analysis and establish an

ARIMA model for runway incursions, as shown in

table 2. The ARIMA model, an acronym for

AutoRegressive Integrated Moving Average Model,

was introduced in the early 1970s by Box and

Jenkins (Ivan et al. 2023). It is a widely recognized

time series prediction technique, also known as the

Box-Jenkins model or the Box-Jenkins method (Gao

& Yang 2008). Using the autocorrelation and partial

autocorrelation analysis methods, the characteristics

of the runway incursion time series model were

analysed.

Table 2: Quarterly runway intrusion data for fiscal years

2019-2023 published on the official website of the Federal

Aviation Administration (FAA) in the United States.

2019.1 2019.2 2019.3 2019.4

440 382 445 486

2020.1 2020.2 2020.3 2020.4

419 295 217 330

2021.1 2021.2 2021.3 2021.4

318 296 485 475

2022.1 2022.2 2022.3 2022.4

401 399 445 485

2023.1 2023.2 2023.3 2023.4

367 408 481 504

In this model, At the zeroth order of differencing,

the significance p-value was 0.561, indicating non-

significance. The null hypothesis cannot be rejected,

suggesting that the sequence is not stationary. At the

first order of differencing, the significance p-value

was 0.000, indicating significance. The null

hypothesis can be rejected, suggesting that the

sequence is stationary. At the second order of

differencing, the significance p-value was 0.067,

indicating non-significance. The null hypothesis

cannot be rejected, suggesting that the sequence is

not stationary.

Based on the above analysis and using the AIC

information criterion to find the optimal parameters,

the author concluded that the ARIMA (1,0,0) model

is appropriate, as shown in table 3.

Table 3: ADF Inspection Form.

ADF Ins

ection Form

variable Differe

ntial

order

t P AIC critical value

1% 5% 10

TOTAL 0 -

1.445

0.561 123.

171

3.88

3.05

2.6

1 -

4.703

0.000

***

122.

725

4.06

3.12

2.7

2 -2.74 0.067

120.

683

4.13

3.15

2.7

2.3 Model Evaluation and Testing

According to the AIC information criterion, the Q-

statistic results suggest that Q6 is not significant at

the 0.05 level. Therefore, author cannot reject the

hypothesis that the model's residuals constitute a

white noise sequence. Furthermore, the goodness of

fit R² value is 0.243, indicating that the model

satisfies the basic requirements, as shown in table 4.

Table 4: ARIMA model (1,0,0) validation table.

Term Symbol Value

Df Residuals 18

Number of

samples

N 20

Q statistic

Q6(P value) 0.509(0.475)

Q12(P value) 7.606(0.268)

Q18(P value) 13.536(0.331)

Information

Criterion

AIC 231.234

BIC 234.221

Goodness of fit R² 0.243

The model equation is as follows: y(t) = 206.872

+ 0.495 * y(t-1)

Through graphical analysis, it can be observed

that the trend of the actual values is similar to that of

the model's fitted values, as shown figure 3. Thus,

the model can be used for prediction and is

considered accurate.

Analysis and Control of Airport Runway Intrusion

461

Figure 3: Runway incursion ARIMA model Least Squares

Method Safety Original data values of time series model

(blue) and fitted values of the model (green) (Picture

credit: Original).

This model can be employed to forecast future

runway incursion frequencies, providing valuable

insights for prevention, monitoring, and

management.

2.4 Establishment of Multiple Linear

Regression Model

Fifteen airports with the highest number of aircraft

takeoffs and landings in China in 2011 were selected

as the research objects. Relevant data on runway

incursions in these fifteen airports over the past five

years were collected, as shown table 5.

The author aims to determine whether typical

threats or typical errors are more important factors

contributing to runway incursions. Therefore, a

multiple linear regression model was developed to

investigate the relationship between the independent

variables (typical threat occurrences and typical

error occurrences) and the dependent variable

(runway incursion occurrences).

Table 5: 15 Runway intrusion data from Chinese airports.

typical threats

typical errors

runway

incursions

AIRP

ORT

CODE

Quantity/

Starting

Quantity/

Starting

number

of times

1 418 109 22

2 511 132 28

3 475 121 25

4 561 117 30

5 359 102 19

6 431 93 20

7 354 95 18

8 399 103 24

9 418 110 23

10 409 95 21

11 565 97 27

12 251 69 11

13 315 83 22

14 387 91 19

15 477 87 25

min𝑄𝑦



𝑏





𝑏





𝑥



𝑏





𝑥











Make





























0，to obtain

Simplifying the system of equations mentioned

above:

⎩

⎪

⎨

⎪

⎧

∂𝑄

∂𝑏



∗

2 



𝑦



𝑏



𝑏



𝑥



𝑏



𝑥









∂𝑄

∂𝑏



2 



𝑦



𝑏



𝑏



𝑥



𝑏



𝑥









𝑥



∂𝑄

∂𝑏



2 



𝑦



𝑏



𝑏



𝑥



𝑏



𝑥









𝑥



⎩

⎪

⎨

⎪

⎧

𝑛𝑏





𝑥







𝑏





𝑥







𝑏





𝑦







𝑥







𝑏





𝑥









𝑏





𝑥







𝑥



𝑏





𝑥







𝑦



𝑥







𝑏





𝑥







𝑥



𝑏





𝑥









𝛽





𝑥



𝑦







Solving the first equation yields:

𝑏





𝑦‾𝑏





𝑥‾



𝑏





𝑥‾



In the above equation system：

𝑦‾

𝑛

𝑦







; 𝑥‾





𝑛

𝑥







; 𝑥‾





𝑛

𝑥







Substituting b

into the second and third equations

gives:

𝑙



𝑏





𝑙



𝑏





𝑙



𝑙



𝑏





𝑙



𝑏





𝑙



Wherein：

𝑙





∑

𝑥



𝑥‾









𝑥



𝑥‾



 𝑘, 𝑗1, 2

𝑙





∑

𝑥



𝑥‾











𝑦



𝑦‾



𝑘1, 2

Thus, b0, b1, and b2can be solved as follows:

(1) By solving the above equation, it can be

concluded that the parameters of the binary linear

regression model in the case are:b1=0.040121 ，

b2=0.068627 ， b0=-1.5452Therefore, the two-

variable linear regression model for the case is

ICDSE 2024 - International Conference on Data Science and Engineering

462

represented as:y = 0.040121x1 + 0.068627x2 -

1.5452.

(2) From Table 6, the calculated F-statistic value

is 29.71081. Considering a significance level of α =

0.05, using the FINV function in Excel, author find

that F0.95（2，13） = 3.885294. Since F > F0.95

（2，13）, the model's confidence level is 95%.

(3) As shown in Table 6, the coefficient of

determination (R²) for the two-variable linear

regression equation is 0.8319836. This indicates that

the model performs well and satisfies the

requirements for handling collinearity among

variables.

(4) Additionally, all the VIF values for the two

independent variables are below 10, indicating that

there is no issue of multicollinearity in the model.

Thus, the model is well-constructed.

Table 6: Linear regression equation parameters.

Regression Statistics

Multiple R 0.912131

R Square 0.831984

Adjusted R Square 0.803981

error 2.073037

Observations 15

By establishing a multiple linear regression model,

author can determine the relationship between

typical errors and typical threats with runway

incursions. From the model in this case, it is evident

that the regression coefficient for typical errors is

greater than that for typical threats. This implies

those typical errors have a stronger influence on

runway incursions. Therefore, effective monitoring

and reduction of runway incursions should focus on

controlling and mitigating typical errors.

3 CONCLUSION

Based on the relationship between the number of

runway incursions in the United States and time

series, an ARIMA prediction model has been

established. Using least squares method, multiple

regression analysis was performed on the results and

influencing factors based on the runway incursion

data of the top 15 airports in China's civil transport

airports in 2011.The research conclusions are as

follows:

(1) Using the obtained ARIMA time prediction

model to predict runway incursion events can obtain

relatively reliable results.

(2) Using least squares method to perform

multiple regression analysis on the results and

influencing factors can show that typical errors are

the main influencing factors of runway incursions.

(3) Through the above two methods, some

references can be provided for runway safety issues

in China's civil aviation industry.

REFERENCES

W. Sabine, et al. Accident Analysis and Prevention 79,

88–99 (2019).

K. Mathew, et al.Journal of Air Transport Management

65, 54–62 (2017).

C. Seraphin, Accident Analysis and Prevention 45,305–

316 (2019).

W. Cheng, et al. Collegiate Aviation Review International

36, 2 (2019).

L. Daniel, et al. Research in Transportation Economics

(2021).

C. Paulina, J. Skorupski. Journal of Air Transport

Management 105, (2022).

C. Yi. Frontiers in Psychology 13, 4 (2022).

C. Yu-Hern, K.M. Wong. Journal of Air Transport

Management 24, 25–30 (2019.)

S. Ivan, E. John, Boylan. International Journal of

Production Research 58, 818–827 (2023).

Y. Gao, Y. Yang, The Chinese Journal of Safety Sciences

11, 25-30 (2008)

Analysis and Control of Airport Runway Intrusion

463