
Research on the Influencing Factors of GDP in Anhui Province Based
on Statistical Analysis
Kaifeng Zhou
Faculty of Science, Wuhan University of Technology, Wuhan, 430070, China
Keywords: Influencing Factors, Correlation Analysis, Factor Analysis, Multiple Linear Regression Analysis, GDP.
Abstract: This article is based on the statistical data of Anhui Province from 2003 to 2022, aiming to explore the
influencing factors of Anhui Province’s GDP. The data comes from the Anhui Provincial Bureau of Statistics,
and five impact indicators are selected: total import and export volume, number of colleges and universities,
per capita consumption expenditure of urban residents, general budget revenue, and highway mileage. First,
Pearson correlation analysis was performed on the data set and it was found that there is a strong correlation
between different indicators. Then the factor analysis method was used to reduce the dimensionality of the
above indicators, and two factors, social finance and social construction, were obtained. Finally, a binary
linear regression model with standardized GDP as the dependent variable and the above two factors as
independent variables was established through multiple linear regression analysis. These analyzes provide an
important basis for an in-depth understanding of the influencing factors of Anhui Province's GDP, identify
the main factors and put forward guiding suggestions, which will help relevant departments formulate targeted
policies to promote economic growth in Anhui Province.
1 INTRODUCTION
Regional GDP refers to the final results of the
production activities of all resident units in the region
within a certain period of time. The GDP of a region
is equal to the sum of the added value of various
industries and is usually used to reflect the level of
economic development of a region (Dynan and
Sheiner 2018). The Anhui Provincial National
Economic and Social Development Statistical
Bulletin in 2022 stated that the province's gross
product (GDP) for the whole year was 4.5045 billion
yuan, an increase of 3.5% over the previous year
(Wang et al 2023). Anhui's economy has achieved a
historic transformation from "being in the middle in
terms of total volume but lagging behind in per
capita" to "being in the forefront in terms of total
volume and being in the middle on per capita", and its
economic strength has achieved a major leap (Wang
and Shi 2021). However, compared with other
economically developed provinces and cities in the
"Yangtze River Delta" region, there is still a large gap
(Ren and Zhou 2022). Additionally, Anhui Province's
digital economy has developed rapidly in recent
years, but there is still the problem of unbalanced
development between the north and the south (Luo
2019). In order to implement comprehensive high-
quality development and build a modern and beautiful
Anhui, Anhui's economy must maintain a stable and
positive development trend. Therefore, it is of great
significance to explore the influencing factors of GDP
in Anhui Province, and to adopt and implement
relevant effective economic measures to promote the
economic development of Anhui Province.
There is no shortage of statistical research on the
factors influencing Anhui Province’s economic
vitality in China. For example, by establishing a
stepwise regression model, Ren and Zhou proposed
that per capita consumption expenditure and
technology contract turnover have a greater impact on
Anhui Province's GDP (Wang et al 2021). In addition,
Jingyu Luo established a factor analysis model on the
comprehensive urban strength of 16 cities in Anhui
Province and concluded that social welfare
investment and sustainable development capabilities
affect economic development to a certain extent
(Wang and Cai 2022). Wang et al. established
evaluation indicators through emergy models and
obtained that the slow improvement of ecological
civilization caused by the large proportion of the
secondary industry is a major obstacle to Anhui's
economic development. Thus, there is an urgent need
Zhou, K.
Research on the Influencing Factors of GDP in Anhui Province Based on Statistical Analysis.
DOI: 10.5220/0012820200004547
Paper published under CC license (CC BY-NC-ND 4.0)
In Proceedings of the 1st International Conference on Data Science and Engineering (ICDSE 2024), pages 267-274
ISBN: 978-989-758-690-3
Proceedings Copyright © 2024 by SCITEPRESS – Science and Technology Publications, Lda.
267

Table 1: Variable names.
variable name impact indicators (unit)
𝑦
GDP of Anhui Province (100 million yuan)
𝑥
total import and export volume (100 million U.S. dollars)
𝑥
number of colleges and universities
𝑥
per capita consumption expenditure of urban residents (yuan)
𝑥
general budget revenue (100 million yuan)
𝑥
highway mileage (thousand kilometers)
to optimize the industrial structure and develop a
circular economy (Trani and Holsworth 2010).
Moreover, Wang and Cai also acquired good results
by establishing the entropy weight TOPSIS model.
They concluded that the main factors affecting
regional economic vitality are the four categories of
economic efficiency, science and technology and
education, opening up to the outside world, and the
living standard of residents. Among them, the two
aspects of science and technology, education
investment and opening up have greater weight
(Zhang et al 2020). Based on the existing research
results, this article selects five indicators: total import
and export volume, number of colleges and
universities, per capita consumption expenditure of
urban residents, general budget revenue, and highway
mileage to explore the statistical data of relevant
indicators from 2003 to 2022. This article
innovatively selects the number of colleges and
universities and highway mileage as some of the
impact indicators. As the development of higher
education and highway construction can greatly
affect the local economy (Cheng 2023). It is planned
to conduct a series of statistical analyzes based on the
inherent relationship between the data.
2 METHODOLOGY
2.1 Data Source
The data used in this article all come from the Anhui
Statistical Yearbook published by the Anhui
Provincial Bureau of Statistics over the years. The
data on the five impact indicators released by it from
2003 to 2022 were integrated to obtain the data set
used in the study.
2.2 Data Preprocessing
This article takes Anhui Province’s GDP as the
explained variable and the five selected impact
indicators as explanatory variables. Since the selected
unit of the original highway mileage data is 10,000
kilometers, all data are decimals. Now it is expanded
ten times and the unit of 1,000 kilometers is selected
to ensure the readability and beauty of the data. The
variables are named as shown in Table 1 below.
2.3 Descriptive Statistical Analysis
First, SPSS was used to conduct descriptive statistical
analysis on the data, and the following Table 2 was
obtained. It can be seen from Table 2: (1) The
skewness of general budget revenue is close to 0, and
it is basically symmetrically distributed; the skewness
of GDP and total import and export volume are both
large positive values, and they are right-skewed data.
Except for the total import and export volume, the
kurtosis of the rest of the data is negative, indicating
that the data is more distributed in parts farther from
the mean. (2) For the number of colleges and
universities and highway mileage, the standard
deviation and coefficient of variation of these two
data are small, indicating that the growth of these two
data is relatively gentle; the coefficient of variation
and standard deviation of other data are large,
indicating that the data distribution is highly discrete.
The above data can illustrate that Anhui
Province's economy has been developing steadily and
for the better in the past 20 years, and residents'
quality of life has improved.
In view of the obvious differences between the
various indicators used in this article and the
measurement units of GDP, direct statistical analysis
will be inconsistent with the actual situation, making
the conclusion erroneous. Therefore, before
subsequent analysis, the data were first standardized
by Z-score. Record the standardized GDP as 𝑦
∗
, and
the five standardized impact indicators are
𝑥
∗
,𝑥
∗
,𝑥
∗
,𝑥
∗
,𝑥
∗
.
In the following, correlation analysis, factor
analysis and multiple linear regression analysis will
be carried out in sequence according to the internal
relationship of the data.
ICDSE 2024 - International Conference on Data Science and Engineering
268

Table 2: Descriptive statistics.
variable
name
maximum
value
minimum
value
mean
standard
deviation
median kurtosis skewness
coefficient of
variation (CV)
𝑦
45045.02 4307.8 20863.02 13255.162 19462.85 -1.097 0.417 0.635
𝑥
1131.27 59.43 426.152 314.033 418.295 0.259 0.897 0.737
𝑥
121 73 107.7 16.442 117.5 -0.408 -1.104 0.153
𝑥
26832 5064.34 15185.98 7037.696 15559.365 -1.225 0.149 0.463
𝑥
3589.1 220.75 1828.154 1192.308 1933.895 -1.575 0.009 0.652
𝑥
5.5 1.1 3.405 1.39 3.35 -1.249 -0.193 0.408
3 RESULTS AND DISCUSSION
3.1 Correlation Analysis
Since the data taken are all continuous numerical
data, the Pearson correlation coefficient can be used
for correlation analysis. Pearson correlation analysis
is a statistical method used to measure the strength
and direction of a linear relationship between two
variables. This method is based on the concept of
covariance, which measures whether the changing
trends of two variables are consistent. To facilitate the
use of notation, let 𝑦
∗
=𝑥
∗
.
And let 𝑥
∗
,𝑥
∗
(
𝑖,𝑗=0,1,2,⋯,5,𝑖≠𝑗
)
be a
two-dimensional population. Obtain observation data
from it: 𝑥
,
∗
,𝑥
,
∗
,𝑥
,
∗
,𝑥
,
∗
,⋯,𝑥
,
∗
,𝑥
,
∗
(
𝑛=
20
)
. Denote,
𝑥̅
()
=
∑
𝑥
,
∗
,𝑥̅
()
=
∑
𝑥
,
∗
(1)
Correlation Coefficient is usually represented by
𝑟, and its calculation formula is:
𝑟
∗
∗
=
∗
∗
∗
∗
∗
∗
(2)
In formula (2),
𝑆
∗
∗
=
∑
𝑥
,
∗
−𝑥̅
()
𝑥
,
∗
−𝑥̅
()
(3)
𝑆
∗
∗
=
∑
𝑥
,
∗
−𝑥̅
()
,
𝑆
∗
∗
=
∑
𝑥
,
∗
−𝑥̅
()
(4)
They represent the covariance of 𝑥
∗
,𝑥
∗
and the
variance of 𝑥
∗
,𝑥
∗
respectively.
It is generally believed that when the absolute
value of the Pearson correlation coefficient is greater
than 0.5, it is considered that there is a strong linear
relationship between the two variables; when the
absolute value of the Pearson correlation coefficient
is between 0.3 and 0.5, it is considered that there is a
moderate degree of linear relationship between the
two variables. linear relationship; when the absolute
value of the Pearson correlation coefficient is less
than 0.3, it is considered that the linear relationship
between the two variables is weak and there is no
linear relationship.
Perform hypothesis testing on correlation,
assuming the null hypothesis is 𝐻
:𝜌
∗
∗
=0, and
the alternative hypothesis is 𝐻
: 𝜌
∗
∗
≠0. When
𝑋
,𝑋
is a two-dimensional normal population, and
𝐻
is true, the statistic 𝑡=
∗
∗
√
∗
∗
~𝑡
(
𝑛−2
)
.
Assuming that the 𝑡 value obtained from actual
observation data is 𝑡
, then 𝑝=𝑃
(|
𝑡
|
≥𝑡
)
. At the
significance level 𝛼=0.05, 𝐻
is rejected when 𝑝<
𝛼. And it is considered that 𝑥
∗
,𝑥
∗
are related and the
calculated correlation coefficient reflects the strength
of the linear correlation between the two variables.
The correlation coefficients between pairs of
𝑦
∗
,𝑥
∗
,𝑥
∗
,𝑥
∗
,𝑥
∗
,𝑥
∗
are obtained by solving. The
obtained correlation coefficient matrix is shown in
Table 3 below.
It can be seen from the correlation coefficient
matrix in Table 3 that the 𝑝 values of the correlation
coefficient test between each variable are all less than
the significance level 𝛼=0.05. Therefore, the null
hypothesis is rejected. Therefore, it can be supposed
that there is a correlation between variables, and the
calculated correlation coefficient reflects the strength
of the linear correlation between the two variables.
Research on the Influencing Factors of GDP in Anhui Province Based on Statistical Analysis
269

Table 3: Correlation coefficient matrix.
𝒚
∗
𝒙
𝟏
∗
𝒙
𝟐
∗
𝒙
𝟑
∗
𝒙
𝟒
∗
𝒙
𝟓
∗
𝑦
∗
1 0.974** 0.808** 0.992** 0.985** 0.967**
𝑥
∗
1 0.754** 0.959** 0.939** 0.914**
𝑥
∗
1 0.86** 0.868** 0.905**
𝑥
∗
1 0.993** 0.984**
𝑥
∗
1 0.985**
𝑥
∗
1
Note: ** indicates significant correlation at the 0.05 level
Noting that the values of the correlation
coefficients are all greater than 0.5, it can be
considered that there is a strong positive linear
relationship between the variables. This shows that
there is strong collinearity among the five different
impact indicators selected in this article. In order to
further select factors that influence GDP with greater
weight, the five influencing indicators need to be
dimensionally reduced to eliminate strong
collinearity and make the final conclusion accurate
and effective. The purpose is achieved through factor
analysis below.
3.2 Factor Analysis
Since the number of selected impact indicators is
small, it is determined that the number of public
factors to be selected in the factor analysis of this
article is 2, recorded as 𝐹
,𝐹
. That is, the five impact
indicators 𝑥
∗
𝑥
∗
are dimensionally reduced into
two public factors 𝐹
,𝐹
through factor analysis to
facilitate subsequent multiple linear regression
analysis.
The orthogonal factor analysis model based on
this study is,
𝑥
∗
=𝑎
𝐹
+𝑎
𝐹
+𝜀
𝑥
∗
=𝑎
𝐹
+𝑎
𝐹
+𝜀
⋮
𝑥
∗
=𝑎
𝐹
+𝑎
𝐹
+𝜀
(5)
Expressed in matrix as:
𝑥
∗
𝑥
∗
⋮
𝑥
∗
=
𝑎
𝑎
𝑎
𝑎
⋮
𝑎
⋮
𝑎
𝐹
𝐹
+
𝜀
𝜀
⋮
𝜀
, abbreviated as 𝑥
×
∗
=𝐴
×
𝐹
×
+𝜀
×
. In
addition, equation (2) should also satisfy: ①
𝐶𝑜𝑣
(
𝐹,𝜀
)
=𝑂, that is, 𝐹 and 𝜀 are uncorrelated; ②
𝐹
,𝐹
are uncorrelated and both have variances of 1;
③ 𝜀
,𝜀
,…,𝜀
are uncorrelated and have different
variances. The corresponding steps and results of
factor analysis are as follows:
Applicability test: The test results are shown in
Table 4 below.
From Table 4, it can be seen that the KMO value
is 0.83 greater than 0.6, and the Bartlett sphericity test
shows that the 𝑝 value is equal to 0.000 and less than
0.05, which is significant. Therefore, this problem can
be considered suitable for factor analysis.
Table 4: Applicability test results.
KMO and Bartlett's test
KMO 0.83
Bartlett's test of
sphericity
Approximate chi-square 211.514
𝑑𝑓
10
𝑝
0.000***
Note: *** represents the 1% significance level
Table 5: variance explained.
component
% of Variance (Unrotated) % of Variance (Rotated)
Eigen
Value
% of
Variance
Cumulative % of
Variance
Eigen
Value
% of
Variance
Cumulative % of
Variance
1 4.671 93.417 93.417 286.373 57.275 57.275
2 0.264 5.278 98.695 207.102 41.42 98.695
3 0.05 1.01 99.705
4 0.011 0.213 99.918
5 0.004 0.082 100
ICDSE 2024 - International Conference on Data Science and Engineering
270

Factor extraction: The variance explanation table
obtained from data processing is shown in Table 5
above.
It can be observed from Table 5 that the
cumulative contribution rate of the first two
components reaches 98.695%, which is higher than
95%, and the contribution rate of the last three
components can be approximately ignored.
Therefore, it is feasible to select two public factors.
Factor rotation and naming: Further process the
data to obtain the rotated factor loading coefficient
table, as shown in Table 6 below.
Table 6: Rotated component matrix.
Factor loading (Rotated)
𝐹
𝐹
𝑥
∗
0.909 0.387
𝑥
∗
0.432 0.897
𝑥
∗
0.821 0.567
𝑥
∗
0.796 0.593
𝑥
∗
0.737 0.665
Note that in Table 6, the public factor 𝐹
in the
rotated component matrix has large loadings on the
three indicators 𝑥
(total import and export volume),
𝑥
(per capita consumption expenditure of urban
residents), and 𝑥
(general budget revenue). It
reflects relevant information at the macroeconomic
and trade levels, so 𝐹
can be named the social
financial factor. The other public factor 𝐹
has large
loadings on the two indicators 𝑥
(number of colleges
and universities) and 𝑥
(highway mileage), which
reflects relevant information at the level of social
infrastructure construction, so 𝐹
can be named the
social construction factor.
Factor score calculation: The calculated component
score coefficient matrix is shown in Table 7 below:
Table 7: Component score coefficient matrix.
𝑭
𝟏
𝑭
𝟐
𝑥
∗
0.847 -0.7
𝑥
∗
-0.852 1.325
𝑥
∗
0.382 -0.126
𝑥
∗
0.294 -0.021
𝑥
∗
0.068 0.25
From Table 7, the linear combination expression
of the two public factors regarding each indicator is
obtained, namely:
𝐹
=0.847𝑥
∗
− 0.852𝑥
∗
+ 0.382𝑥
∗
+ 0.294𝑥
∗
+ 0.068𝑥
∗
𝐹
=−0.7𝑥
∗
+ 1.325𝑥
∗
− 0.126𝑥
∗
− 0.021𝑥
∗
+0.25𝑥
∗
(6)
3.3 Multiple Linear Regression
Analysis
In order to avoid severe collinearity affecting the
analysis results, the social financial factor 𝐹
and
social construction factor 𝐹
after factor analysis
dimensionality reduction are selected as independent
variables, and the standardized GDP data 𝑦
∗
is used
as the dependent variable to conduct multiple linear
regression analysis.
Through the above analysis, it can be roughly
concluded that 𝐹
,𝐹
and 𝑦
∗
have a strong linear
relationship. Under this premise, a multiple linear
regression model can be established:
𝑦
∗
=𝛽
+𝛽
𝐹
+𝛽
𝐹
+𝜀
,
𝜀~𝑁
(
0,𝜎
)
(7)
In equation (3), 𝛽
(
𝑖=1,2
)
represents the
regression coefficient, and 𝛽
represents the
intercept. Then use the least squares method to
estimate 𝛽
(
𝑖=1,2
)
,𝛽
. Find the optimal function by
minimizing the sum of squared errors. Solve the
approximate solution 𝛽
of the coefficient matrix 𝛽=
(
𝛽
,𝛽
,𝛽
)
through matrix operations 𝛽
=
(
𝐹
𝐹
)
𝐹
𝑌
∗
. where 𝑌
∗
=
𝑦
∗
𝑦
∗
⋮
𝑦
∗
, 𝐹=
1𝑓
𝑓
1𝑓
𝑓
⋮
1
⋮
𝑓
,
⋮
𝑓
,
. The results of the multiple linear
regression analysis are shown in Table 8 below:
Table 8: Regression coefficient.
Beta
t Significance
(constant)
0.000 1.000
𝐹
0.871 45.455 0.000
𝐹
0.485 25.324 0.000
It can be concluded from Table 8 that the
approximate solution 𝛽
=(0,0.871,0.485)
of the
coefficient matrix. Subsequent model testing will be
performed on this model to ensure that the model is
successfully established. 𝐻
: 𝛽
=𝛽
=𝛽
=0, 𝐻
:
Research on the Influencing Factors of GDP in Anhui Province Based on Statistical Analysis
271
There is at least one 𝛽
≠0. Under the condition of
𝐻
, construct the test statistic 𝐹=
=
/()
/()
~𝐹
(
3 − 1,20 −3
)
. In the above formula.
Where 𝑆
=
∑(
𝑦
∗
−𝑦
∗
)
is the regression sum of
squares, 𝑆
=
∑(
𝑦
∗
−𝑦
∗
)
is the residual sum of
squares.
It can be obtained from the ANOVA table in SPSS
that the 𝑝 value of this test is approximately 0.000<
𝛼=0.05. It means that the regression coefficient
corresponding to at least one independent variable is
not equal to 0, that is, there is a linear relationship
between at least one independent variable and the
dependent variable, and the model is successfully
established.
Meanwhile, it is not difficult to find from Table 8
that the calculated 𝑝 values corresponding to 𝛽
,𝛽
are all 0.000 and less than 𝛼=0.05, indicating that
the model is well established and has a reasonable
binary linear relationship. The linear regression effect
of independent variables 𝐹
,𝐹
on 𝑦
∗
is significant.
The resulting binary linear regression equation is as
follows,
𝑦
∗
=0.871𝐹
+ 0.485𝐹
(8)
𝑦
∗
is the approximate estimate of the dependent
variable. For multiple linear regression, the modified
multiple determination coefficient is used to
determine the degree of linear regression, as shown in
the following formula, where 𝑆
=𝑆
+𝑆
, and
𝑅
=1−
⁄
⁄
.
Since the basic assumption of the linear regression
model also requires that each random error 𝜀
(
𝑖=
1,2,…,20
)
is independent of each other, the Durbin-
Watson test is used to test the independence of the
errors. Construct the DW statistic as shown in the
following formula:
𝐷𝑊=
∑(
)
∑
(9)
The results of the goodness-of-fit judgment and
Durbin-Watson test are obtained as shown in Table 9
below:
Table 9: Model summary.
Model R R S
q
uare Ad
j
usted R S
q
uare DW
1 0.997 0.994 0.993 0.964
From Table 9, the calculated 𝑅
=0.994 is very
close to 1, which demonstrates that the linear fitting
effect is very good. The model is reasonably
established and can make more effective predictions.
The obtained Durbin-Watson test result is 0.964,
which conforms to the value range of 0<DW<4.
However, there is a weak positive correlation
between the residuals of two adjacent points, which
can be approximately regarded as the absence of
serial autocorrelation, that is, each random error can
be considered independent of each other.
Finally, residual analysis is performed. In order to
test whether the studentized residuals, that is, the
regression standardized residuals, obey the standard
normal distribution, a normal P-P plot is made for the
regression standardized residuals, as depicted in
Figure 1. In order to test that the variances of the
normal distributions obeyed by the random errors
𝜀
(
𝑖=1,2,…,20
)
are the same, in other words, they
have variance consistency. Make a residual scatter
plot with the fitted value of the dependent variable 𝑌
as the abscissa, as depicted in Figure 2.
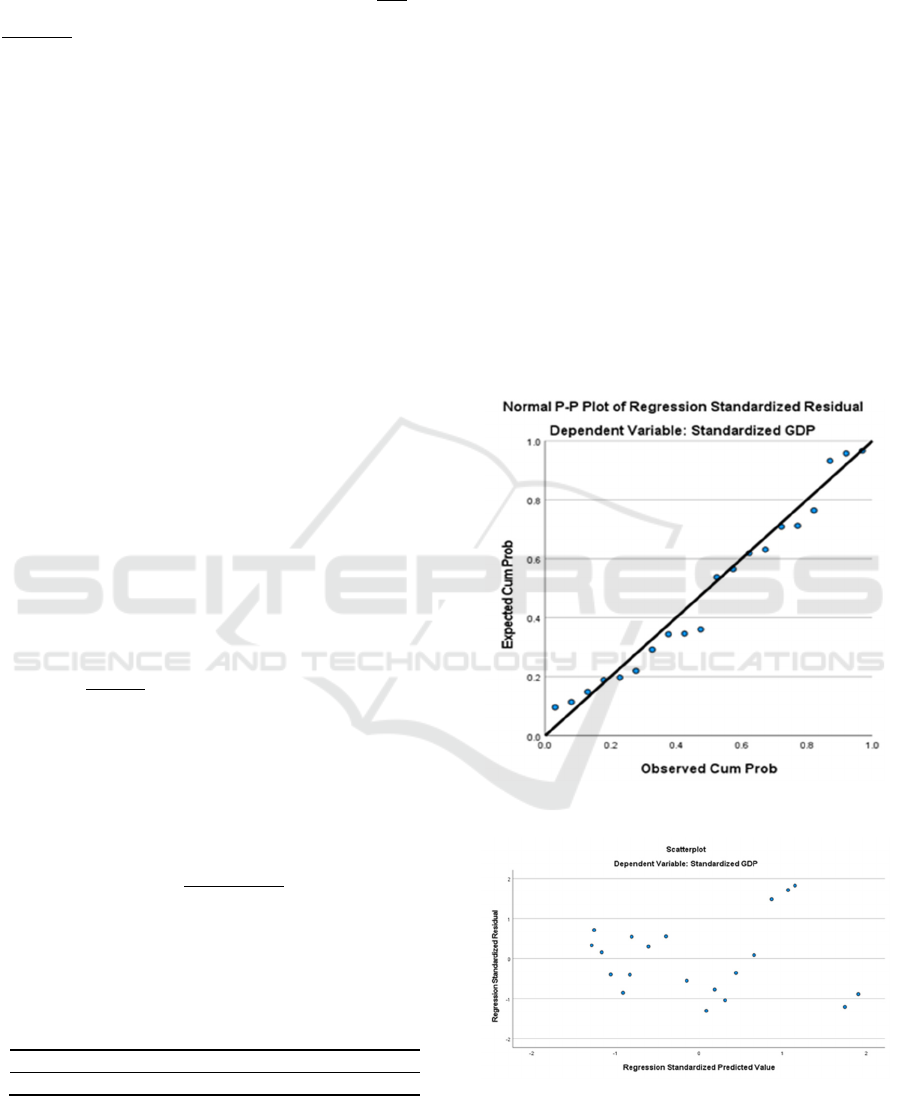
Figure 1: Normal P-P diagram (Picture credit: Original).
Figure 2: Residual scatter plot (Picture credit: Original).
As can be seen from Figure 1, the residual points
are basically distributed along the diagonal straight
line, indicating that the expected cumulative
ICDSE 2024 - International Conference on Data Science and Engineering
272

probability closely matches the observed cumulative
probability. Therefore, it follows the normal
distribution. It can be found in Figure 2 that the
standardized residual scatter points are distributed
around the 0 value, roughly within a band-shaped
area, and there is no obvious trend. This means that
the variances of the random errors are homogeneous,
there is no heteroscedasticity problem, and the fit is
good.
4 CONCLUSION
This article obtains a series of research results
through statistical data analysis of Anhui Province’s
GDP and five impact indicators. After conducting
descriptive statistics on the data, it was found through
correlation analysis that there is strong correlation
and collinearity between the indicators. In order to
eliminate the impact of collinearity on the results, the
five indicators were dimensionally reduced through
factor analysis and finally two common factors were
obtained. These two public factors are named social
financial factors and social construction factors
respectively. Finally, by establishing a multiple linear
regression model, the binary linear regression
equation of standardized GDP with respect to the
above two factors was obtained. After testing, it can
be proved that the equation has a good fitting degree.
It can be seen from the obtained regression
equation that Anhui Province's GDP has a certain
positive linear correlation with social
macroeconomics, such as consumption, trade, and
social infrastructure, such as school and highway
construction. Therefore, in order to implement
economic construction as the center and promote
high-quality economic development in Anhui
Province, the following guiding opinions are put
forward for reference.
Deepen opening to the outside world and expand
foreign trade cooperation: Promote the in-depth
integration of Anhui Province with the international
market and strengthen economic and trade
cooperation with countries along the Belt and Road.
It is recommended to formulate more flexible trade
policies, attract foreign investment and technology
introduction, and improve the level of opening up to
the outside world. At the same time, we will
strengthen the development of cross-border e-
commerce and digital economy and improve the
efficiency of import and export.
Stimulate residents’ consumption vitality:
Stimulate residents' consumption by increasing
residents' income levels and improving employment
rates. Encourage the development of cultural tourism,
health care and other consumer fields, and cultivate
new consumption growth points. In addition, promote
consumer confidence, strengthen brand building, and
improve product and service quality.
Increase public budget investment: Increase
government financial investment, especially in the
fields of education, medical care, science and
technology and other social undertakings. Increase
support for innovative enterprises and scientific
research institutions to promote technological
innovation and industrial upgrading. At the same
time, the fiscal expenditure structure should be
optimized to ensure the effectiveness and
sustainability of capital investment.
Accelerate the construction of transportation
infrastructure and improve the connectivity of the
province: Improve infrastructure levels and shorten
transportation time between urban and rural areas and
between provinces. Accelerate the planning and
construction of transportation infrastructure such as
highways and railways, promote smooth logistics,
and promote coordinated development of industries.
This will help reduce logistics costs, improve
production efficiency, and enhance Anhui Province’s
competitiveness in the global value chain.
Optimize the education system and promote talent
cultivation: Increase investment in higher education
and improve the overall level of educational
resources. At the same time, enterprises are
encouraged to cooperate with universities to
strengthen the integration of industry, education,
research and application, and improve the practicality
and employment rate of higher education. Cultivate
more high-quality talents, provide intellectual support
for upgrading the economic structure, and build an
innovation highland.
REFERENCES
K. Dynan and L. Sheiner, Hutchins Center Working Paper,
(2018).
C. Wang, F. Liu and Y. Wang, Environmental Engineering
Research 28(1), (2023).
Z. Wang and P. Shi, Complexity, 1-8 (2021).
J. Ren and Z. Zhou, International Journal of Education and
Humanities 2(1), 7-11 (2022).
J. Luo, Tourism Management and Technology Economy
2(1), 13-21 (2019).
C. Wang, Y. Zhang, C. Liu, et al., Sustainability 13(5), 2988
(2021).
W. Wang and X. Cai, Journal of Natural Sciences of Harbin
Normal University 38(3), 9-19 (2022).
Research on the Influencing Factors of GDP in Anhui Province Based on Statistical Analysis
273

E. P. Trani and R. D. Holsworth, R&L Education, 9-11
(2010).
X. Zhang, Y. Hu and Y. Lin, Journal of Transport
Geography 82, 102600 (2020).
H. L. Cheng, Cooperative Economy and Technology 23,
30-32 (2023).
ICDSE 2024 - International Conference on Data Science and Engineering
274
