Advertising Optimization and Feature Analysis Based on Machine

Learning

Yao Li

Jinan University – University of Birmingham Joint Institute at Jinan University, Jinan University, Guangzhou, 511443,

China

Keywords: Machine Learning, Random Forest, Advertising Optimization.

Abstract: Under the impact of the pandemic for three years, the market economy has shown an overall downward trend,

and the consumption level of the public has decreased. Maintaining product sales and stimulating consumer

desire have become the main problem for the industry. By using machine learning algorithms to optimize

advertisements, industry costs can be reduced and better sales can be achieved. This study first associates the

objectives with features to facilitate relevant practitioners to carry out corresponding optimizations. Secondly,

prioritizing the importance of data features is beneficial for relevant practitioners to have a bias towards their

work and facilitate subsequent model building. Finally, based on the importance of the corresponding features,

select the features with higher importance to establish a click-through rate prediction model for advertising

rating. The random forest model can achieve an accuracy of 95% in predicting advertising click-through rates.

Then the experimental results show that using machine learning methods to construct a model can predict the

subsequent click-through rate of advertisements to optimize them. By predicting and rating existing

advertisements and observing the expected results, it is convenient for relevant advertising design and

placement personnel to make improvements, to achieve optimal efficiency in advertising.

1 INTRODUCTION

Against the backdrop of a three-year pandemic

impact, the market economy is experiencing an

overall downturn, leading to a reduction in consumer

spending levels among the masses. To maintain

product sales, stimulating consumer desire has

emerged as a primary challenge for industries.

Advertising, as one of the primary means to boost

consumer desire and enhance product sales, poses

potential pressure on industries when additional

personnel are hired to optimize and upgrade product

advertisements, incurring extra costs. Utilizing

Machine Learning (ML) algorithms for

advertisement optimization. In addition, it presents a

viable solution to mitigate industry costs and achieve

improved sales outcomes (Gao et al. 2023).

Pannu indicated that Artificial Intelligence (AI)

possesses enduring capabilities, maintains

consistency, and is cost-effective (Pannu 2015).

Additionally, it can be easily replicated and

distributed. There are instances where AI outperforms

human activities in terms of speed and efficiency,

thereby establishing its superiority over natural

intelligence. ML, a subset of AI (Jha 2019, Pathan et

al. 2020, Pandya et al. 2020), involves machines

comprehending decision-making processes by

meticulously observing outputs and engaging in

extensive simulations (Sukhadia et al. 2020, Patel et

al. 2020, Kundalia et al. 2020). Kietzmann et al.

(2018) discussed how businesses leverage ML to

translate data streams into valuable consumer

insights. However, such practices may carry adverse

consequences, as seen in cases like the privacy

infringement allegations against Cambridge

Analytica.

This paper primarily focuses on employing ML in

Display Advertising. This study first associates the

objectives with features to facilitate relevant

practitioners to carry out corresponding

optimizations. Secondly, sorting the importance of

data features through random forests is beneficial for

relevant practitioners to have a bias in their work and

facilitate subsequent model building. This paper

conducts a particular analysis and contrast of the

predictive performance of different models and

selects five models. Firstly, because logistic

regression is widely used in binomial classification

Li, Y.

Advertising Optimization and Feature Analysis Based on Machine Learning.

DOI: 10.5220/0012822000004547

Paper published under CC license (CC BY-NC-ND 4.0)

In Proceedings of the 1st International Conference on Data Science and Engineering (ICDSE 2024), pages 70-76

ISBN: 978-989-758-690-3

problems, logistic regression is first adopted.

Secondly, decision tree classifiers and random forest

classifiers from classification models are used.

Finally, it is used Gradient Boosting classifier and

XGB classifier. The features are selected with higher

importance to establish a click-through rate

prediction model for advertising rating. Meanwhile,

this paper compares various models and selects the

optimal model. In conclusion, ML has significant

advantages in advertising optimization. These

findings not only provide innovative solutions for the

advertising industry but also provide strong support

for advertising optimization in practical applications,

improving advertising performance The benefits of

advertising have brought significant economic and

user experience improvements to the industry.

2 METHODOLOGY

2.1 Dataset Description and

Preprocessing

The dataset use includes virtual advertising data

(Dataset 2023). Firstly, 'Daily Time Spent on Site' and

'Daily Internet Usage' are adopted to consider. Then

'Age’, ‘Area Income', 'Ad Topic Line', 'City’, ‘Male'

and 'Country'; 'Timestamp' is introduced later.

Preliminary processing is carried out on the data,

including time splitting for subsequent processing

and detection of duplicate or missing data. It has been

detected that there are no duplicate or missing

datasets in this dataset. There is no need for

subsequent data cleaning.

2.2

Proposed Approach

In the field of advertising, establishing a more

accurate click-through rate prediction model is

crucial for evaluating and optimizing advertisements.

To solve the problem of comparing the importance of

various features, the Random Forest algorithm is

adopted to extract the importance of features. By

arranging the features in descending order of

importance, the relative importance of each feature is

obtained, guiding subsequent advertising

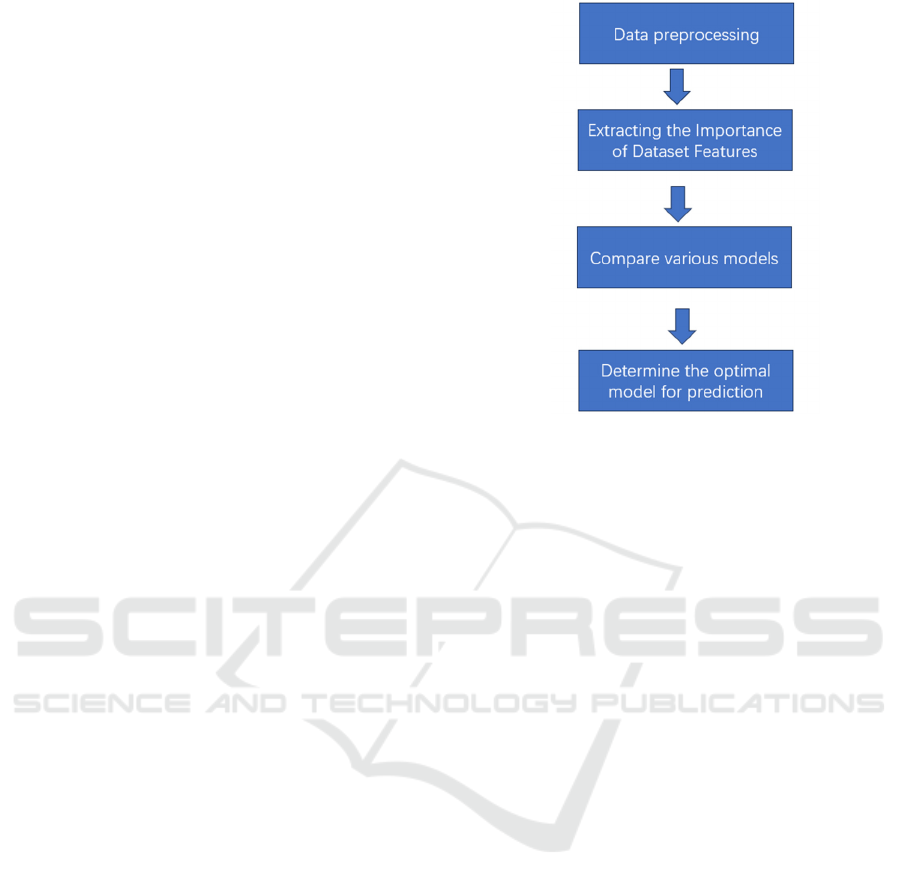
optimization. This study is divided into several parts,

including model construction, model optimization,

and function comparison. Figure 1 shows the process

of the study.

Figure 1: The process of the study (Picture credit: Original).

First, preliminary processing is carried out on the

data, including time splitting for subsequent

processing and detection of duplicate or missing data.

It has been detected that there are no duplicate or

missing datasets in this dataset. There is no need for

subsequent data cleaning.

Extracting the Importance of Dataset Features: To

address the issue of comparing the importance of

various features, a random forest algorithm is used to

extract feature importance. By arranging the features

in descending order, the relative importance of each

feature is obtained, guiding subsequent advertising

optimization. Second, in the model construction

stage, five models are selected. Firstly, because

logistic regression is widely used in binomial

classification problems, logistic regression is first

adopted. Secondly, decision tree classifiers and

random forest classifiers from classification models

are used. Finally, it is used Gradient Boosting

classifier and XGB classifier. Predict click-through

rates through these models and compare their

performance. Because of the comprehensive grade

and accuracy of each model, the optimal classifier -

the Random Forest classifier is selected. The model is

going to calculate the possible click-through rate of

advertisements, achieving optimization of

advertisements. Third, random forest is a formidable

ensemble learning algorithm that can handle complex

feature relationships and noise, making it the optimal

model. Its feature importance ranking provides a clear

direction for subsequent advertising optimization.

This detailed and comprehensive modeling process

ensures the robustness and accuracy of the final

model, providing strong support for advertising

Advertising Optimization and Feature Analysis Based on Machine Learning

placement. Through this systematic approach,

enterprises can gain a more precise understanding of

advertising effectiveness, optimize advertising

strategies, increase ad click-through rates, and

achieve more effective advertising placement.

2.2.1 Logistic Regression

In handling binary classification tasks, it is Logistic

regression that is widely used. Although its name

contains the word "regression," it is actually a

classification algorithm specifically designed to

predict the probabilities of outcomes, which are

typically between 0 and 1. The algorithm uses logical

functions to map linear combinations of features into

probability Spaces. Then performs binary

classification by setting thresholds. Logistic

regression is simple and efficient, so it is often used

as a baseline model for classification problems, or for

ranking the importance of features.

2.2.2 Decision Tree

Decision Trees are tree-based classification

algorithms that recursively split the data into different

nodes based on feature selection. The hierarchical

structure is formed by nodes in the tree, where each

node represents a decision stemming from a specific

feature value. Decision Trees are simple to

understand and explain, but they can suffer from

overfitting.

Firstly, information entropy serves as a widely

used metric for assessing the purity of a sample set,

where smaller values indicate higher purity in the

dataset. The ratio of the k-th class of samples in the

set D, denoted as pk, further contributes to this

measure.

Secondly, information gain comes into play by

considering the varied sample sizes in different

branch nodes and assigning weights accordingly. The

significance of a discrete attribute 'a' with V possible

values is emphasized, and a higher information gain

is favored, highlighting the importance of attributes

in the decision tree, as:

𝑒𝑛𝑡(𝐷) = −

∑

𝑝



𝑙𝑜𝑔



𝑝







(1)

Moving on, the gain rate criterion introduces a

preference for attributes with fewer values, in contrast

to the information gain criterion. The C4.5 algorithm

uses a strategic approach that does not directly select

the candidate partition attribute with the highest gain

rate. Instead, the algorithm first propagates those

properties that have a higher-than-average

information gain for candidate partition properties,

and then selects the properties with the highest gain

rate from them, as:

𝐺𝑎𝑖𝑛

(

𝐷,𝑎

)

=𝑒𝑛𝑡

(

𝐷

)

−

∑







𝑒𝑛𝑡

(

𝐷



)





(2)

In conclusion, the Gini Index offers an evaluation

of the data's purity by precisely determining the

likelihood that two randomly chosen samples from

dataset D would have contradictory class labels. A

lower Gini (D) score suggests that the dataset is purer.

The attribute that minimizes the Gini coefficient is

chosen after partitioning, resulting in the

identification of the ideal partitioning attribute. This

is why the Gini coefficient of the attribute "a" is

significant in the context of attribute partitioning,

𝐺𝑎𝑖𝑛



(

,

)

(,)

()

(3)

𝐼𝑉

(

𝑎

)

=−

∑















𝑙𝑜𝑔









(4)

According to attribute a's Gini index, the optimum

partitioning attribute will be identified by minimizing

the Gini index following partitioning, as:

𝐺𝑖𝑛𝑖

(

𝐷

)

=1−

∑

𝑝









(5)

𝐺𝑖𝑛𝑖



(

,

)

∑















𝐺𝑖𝑛𝑖(𝐷



) (6)

2.2.3 Random Forest

An ensemble learning technique called random forest

uses many decision trees. By randomly selecting

features and data samples, the random forest

constructs several decision trees., and then combines

the results through averaging or voting to enhance

accuracy and robustness. Random Forest is suitable

for large datasets and performs well with high-

dimensional data and numerous features.

Here are the specific steps for a random forest.

Firstly, problems with regression and classification

can be resolved with random forests. In classification,

the input consists of a training dataset with labels,

while in regression, it includes a training dataset with

target variables. Secondly, bootstrapped sampling

involves randomly selecting samples from the

training data with replacement, creating a new dataset

of the same size as the original. This process allows

some samples to appear multiple times in the new

dataset, while others may not appear. Thirdly, random

feature selection occurs at each decision tree node,

where a subset of features is randomly chosen for

splitting. This ensures that each decision tree does not

overly rely on specific features, adding diversity to

the model. Next, as the base learner, decision trees are

ICDSE 2024 - International Conference on Data Science and Engineering

used. At each node, a decision tree is built by splitting

on a random subset of features. This process

continues until the tree reaches a specified maximum

depth or the number of samples in a node falls below

a threshold. Fifthly, for classification problems, a

voting mechanism is employed, where the majority

vote determines the final classification result. In

regression problems, averaging is used, taking the

average of outputs from multiple decision trees as the

final prediction. Sixthly, the process involves

repeating steps 2-5 to build multiple decision trees

through repeated random sampling and random

feature selection. These decision trees constitute the

Random Forest. Finally, for classification problems,

the final result is determined based on the majority

vote of multiple decision trees. For regression

problems, the output is the average result of multiple

decision trees.

Here are the advantages of random forests. Firstly,

the high accuracy of Random Forest is attributed to

the aggregation of multiple decision trees, leading to

robust predictive performance. Secondly, Random

Forest demonstrates resistance to overfitting by

employing strategies such as randomly selecting data

and features, effectively reducing the risk of

overfitting. Thirdly, Random Forest is particularly

effective in handling large datasets with numerous

features and samples, showcasing its capability to

manage extensive data scenarios.

2.2.4 Gradient Boosting Classifier

Gradient Boosting is an ensemble learning technique

that sequentially trains weak classifiers (usually

decision trees) to correct errors made by previous

models. Each new classifier aims to correct the

residual errors of the previous one, ultimately

forming a powerful ensemble model. Gradient

Boosting often yields high predictive accuracy.

2.2.5 XGB Classifier

XGB Classifier is an enhanced variant of the Gradient

Boosting algorithm known for its higher speed and

power. XGB Classifier incorporates regularization

and pruning on top of gradient boosting, speeding up

training by optimizing an approximation of the

objective function while effectively preventing

overfitting.

2.3 Implementation Details

This study uses the Jupiter editor in the Python

environment to build the model. This study uses

Seaborn's chart-building function to demonstrate the

relationship between features and click-through rates

in feature representation. Lastly, The Random Forest

model relies on several hyperparameters that

significantly impact its performance. The number of

subtrees, or n estimators, the maximum growth depth

of the tree, the minimum number of leaf samples, the

minimum number of branch node samples, the

minimum number of split samples, and the maximum

number of selected features are the main parameters

of a random forest. This study fine-tuned

hyperparameters using grid search to find the optimal

configuration that maximizes prediction accuracy.

3 RESULT AND DISCUSSION

3.1 The Analysis of the Data

The correlation between age and click-through rate,

regional income and click-through rate, daily internet

usage time, and click-through rate is demonstrated

through chart analysis.

As shown in Figure 2, the probability of clicking

reaches a peak of 60 around the age of 40. Instead of

reaching a peak click-through rate of 100 around the

age of thirty, as shown in Figure 3, the highest click-

through value reaches 60 when the regional income

reaches 50000. When the regional income reaches

65000, the maximum nonclick value reaches 80.

From all figures 2-4, it is easy to draw the

following conclusion: click-through rates generally

increase with age; The click-through rate decreases as

regional revenue increases; The click-through rate

decreases as the time spent on the website increases.

Although this can distinguish the relationship

between each feature and the target, it cannot

determine the importance of each feature. The

inability to provide biased guidance for optimization

work also poses difficulties in establishing a more

accurate model. So, it needs to extract the importance

of features.

Advertising Optimization and Feature Analysis Based on Machine Learning

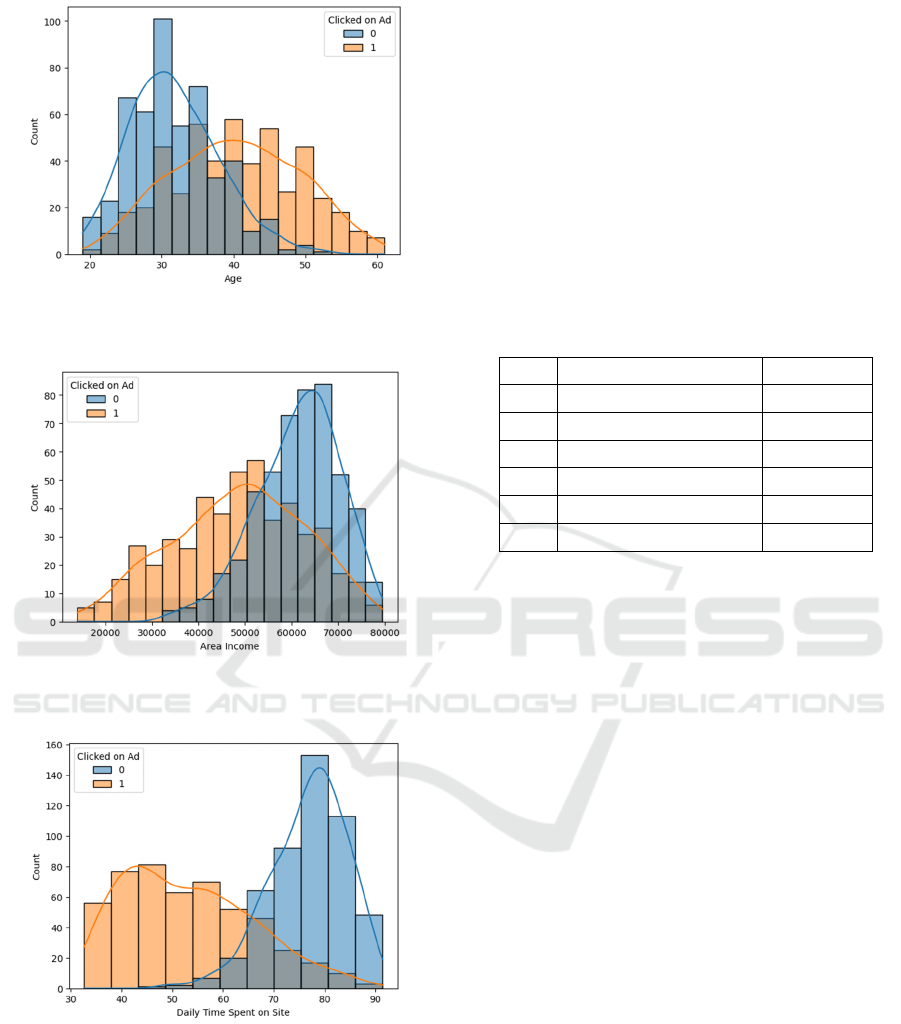
Figure 2: The relationship between age and ctr (Picture

credit: Original).

Figure 3: The relationship between area income and ctr

(Picture credit: Original).

Figure 4: The relationship between daily time spent on site

and ctr (Picture credit: Original).

3.2 The Arrangement of Feature

Importance

As shown in Table 1, the importance of this dataset is

ranked in descending order as daily Internet usage;

Daily time spend on site; Area income; Age; Month;

and Male.

The greatest important feature which is Daily

internet usage is 0.432184. Daily internet usage has a

significant impact on whether clicks are being made

or not. The most irrelevant feature is male reaching

0.004885.

To address the issue of comparing the importance

of various features, a random forest algorithm is used

to extract feature importance. By arranging the

features in descending order, the relative importance

of each feature is obtained, providing guidance for

subsequent advertising optimization.

Table 1: The arrangement of feature importance.

rank feature importance

5 Daily internet usage 0.432184

4 Daily Time Spent on Site 0.337208

1 Area Income 0.120775

0 Age 0.093234

3 Month 0.011714

2 Male 0.004885

The above Table 2- 6 shows the scores of each

model under the same feature construction model.

‘No_clicked’ represents that the advertisement

cannot be clicked, and ‘Clicked’ represents that the

advertisement can be clicked. ‘Accuracy Rate’ refers

to the number of correctly classified samples as a

proportion of the total number of samples. "Pre"

evaluates the ratio of samples predicted by the model

to the actual positive category. The "recall" is the

proportion of the actual positive sample that is

correctly predicted by the model to be positive. The

F1 value is the harmonic average of accuracy and

recall, which comprehensively reflects the

performance of the model in predicting the positive

category, taking into account both factors. ‘Ma_avg’

is stranded for Macro averaging which calculates the

indicators for each category, and then takes the

average of all categories. For each category, it

independently calculates indicators and then averages

them. This is equally weighted for all categories.

Macro averaging does not consider category

imbalance. Weighted averaging calculates the

indicators for each category, but takes into account

the sample size of each category, assigning greater

weights to categories with more samples. This is to

address the situation of imbalanced categories. The

calculation method of weighted average is to multiply

the indicators of each category by the support (sample

ICDSE 2024 - International Conference on Data Science and Engineering

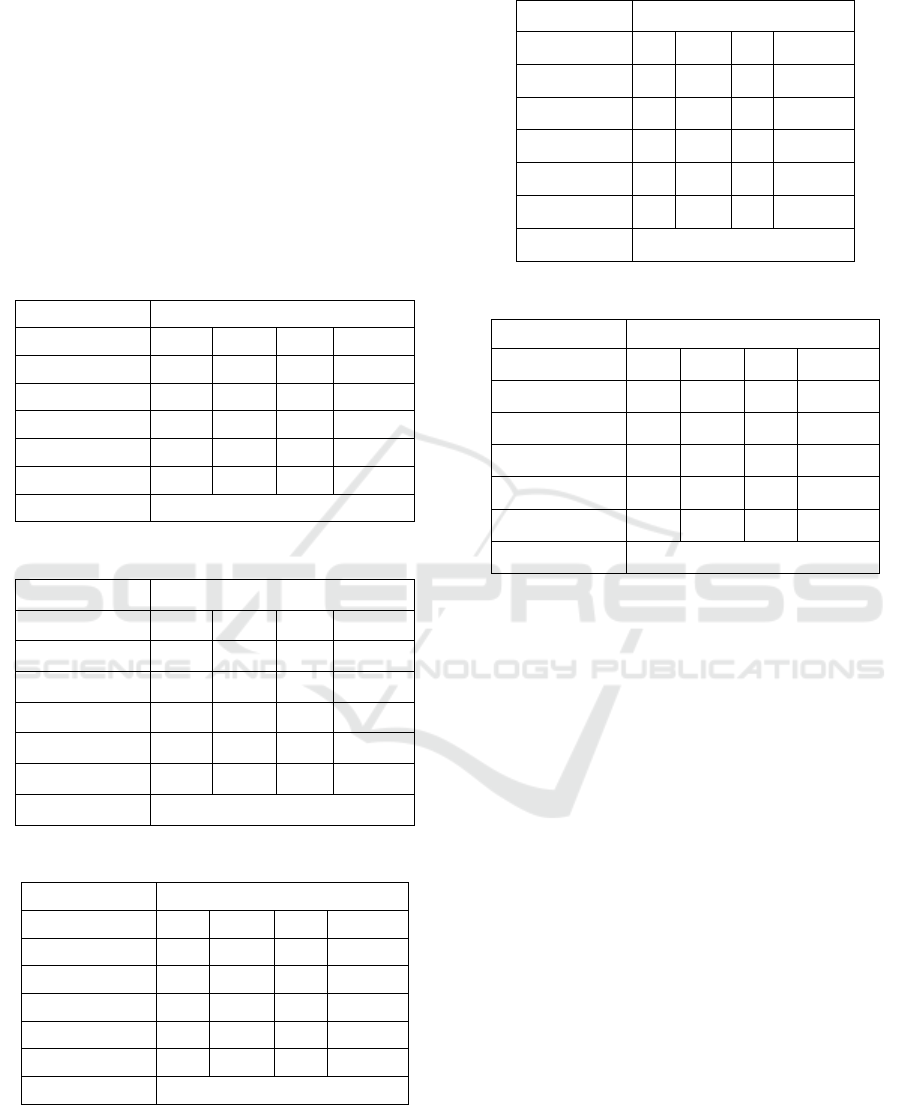
size) of that category, and then take the weighted

average of all categories.

The rates of Logistic Regression, Decision Tree

Classifier, Random Forest Classifier, Gradient

Boosting Classifier, and XGB Classifier are 0.9071,

0.9425, 0.9548, 0.9426, and 0.9426. For predicting

advertising click-through rates, this study focuses

more on accuracy ratings. From the table above, this

study indicates that the random forest model achieves

the highest accuracy, reaching 0.95. The

comprehensive rating of the model is also 0.9548,

which is the highest value among the five models.

Table 2: The rate of Logistic Regression.

Logistic Regression

pre recall f1 support

No_clicked 0.86 0.96 0.91 162

Clicked 0.96 0.85 0.9 168

Accuracy Rate

0.91 330

Ma_avg 0.91 0.91 0.91 330

We_avg 0.91 0.91 0.91 330

AUC 0.9071

Table 3: The rate of Decision Tree Classifier.

Decision Tree Classifier

pre recall

f1 support

No_clicked 0.94 0.94

0.94 162

Clicked 0.95 0.94

0.94 168

Accuracy Rate

0.94 330

Ma_avg 0.94 0.94

0.94 330

We_avg 0.94 0.94

0.94 330

AUC 0.9425

Table 4: The rate of Random Forest Classifier.

RandomForestClassifier

pre

recall f1 su

ort

No_clicked 0.94

0.97 0.95 162

Clicked 0.97

0.94 0.95 168

Accuracy Rate

0.95 330

Ma_avg 0.95

0.95 0.95 330

We_avg 0.95

0.95 0.95 330

AUC 0.9548

Table 5: The rate of Gradient Boosting Classifier.

Gradient Boosting Classifier

re recall f1 Su

ort

No_clicked 0.93 0.95 0.94 162

Clicked 0.95 0.93 0.94 168

Accuracy Rate

0.94 330

0.94 0.94 0.94 330

We_avg 0.94 0.94 0.94 330

AUC 0.9426

Table 6: The rate of XGB Classifier.

XGB Classifier

re recall f1 su

ort

clicked 0.93 0.95 0.94 162

Clicked 0.95 0.93 0.94 168

Accurac

Rate

0.94 330

0.94 0.94 0.94 330

We_avg 0.94 0.94 0.94 330

AUC 0.9426

4 CONCLUSION

To optimize advertising and increase industry

revenue, this study first associates the objectives with

features to facilitate relevant practitioners to carry out

corresponding optimizations. Secondly, prioritizing

the importance of data features is beneficial for

relevant practitioners to have a bias towards their

work and facilitate subsequent model building.

Finally, based on the importance of the corresponding

features, select the features with higher importance to

establish a click-through rate prediction model for

advertising rating. The random forest model can

achieve an accuracy of 95% in predicting advertising

click-through rates. Then the experimental results

show that using machine learning methods to

construct a model can predict the subsequent click-

through rate of advertisements to optimize them. For

the future, provide suggestions for model deployment

and monitoring to ensure robust operation in actual

production environments. Otherwise, discuss how to

adapt the model to real-time changing user behavior

and market conditions.

Advertising Optimization and Feature Analysis Based on Machine Learning

REFERENCES

B. Gao, et al. SAGE Open (2023) p. 21582440231210759.

A. Pannu, International Journal of Engineer Innovation

Technology (2015) pp. 79–84

K. Jha, A. Doshi, P. Patel, Artificial Intelligence in

Agriculture (2019) pp. 1–12

M. Pathan, N. Patel, H. Yagnik, M. Shah Artificial

Intelligence in Agriculture (2020) pp. 81–95.

R. Pandya, S. Nadiadwala, R. Shah, M. Shah, Augmented

Human Research (2020) p. 3.

A. Sukhadia, K. Upadhyay, M. Gundeti et. al, Augmented

Human Research (2020) p.13.

D. Patel, Y. Shah, N. Thakkar, et. al, Augmented Human

Research (2020) p. 6.

K. Kundalia, Y. Patel, M. Shah Augmented Human

Research (2020) p. 11.

J. Kietzmann, J. Paschen, E. Treen, Journal of

Advertisement Research (2018) pp. 263–267.

Dataset,

https://www.kaggle.com/datasets/gabrielsantello/adver

tisement-click-on-ad/data (2023).

ICDSE 2024 - International Conference on Data Science and Engineering